Experimental Study of the Effect of Slope on the Spread and Burning Characteristics of a Continuous Oil Spill Fire
Abstract
:1. Introduction
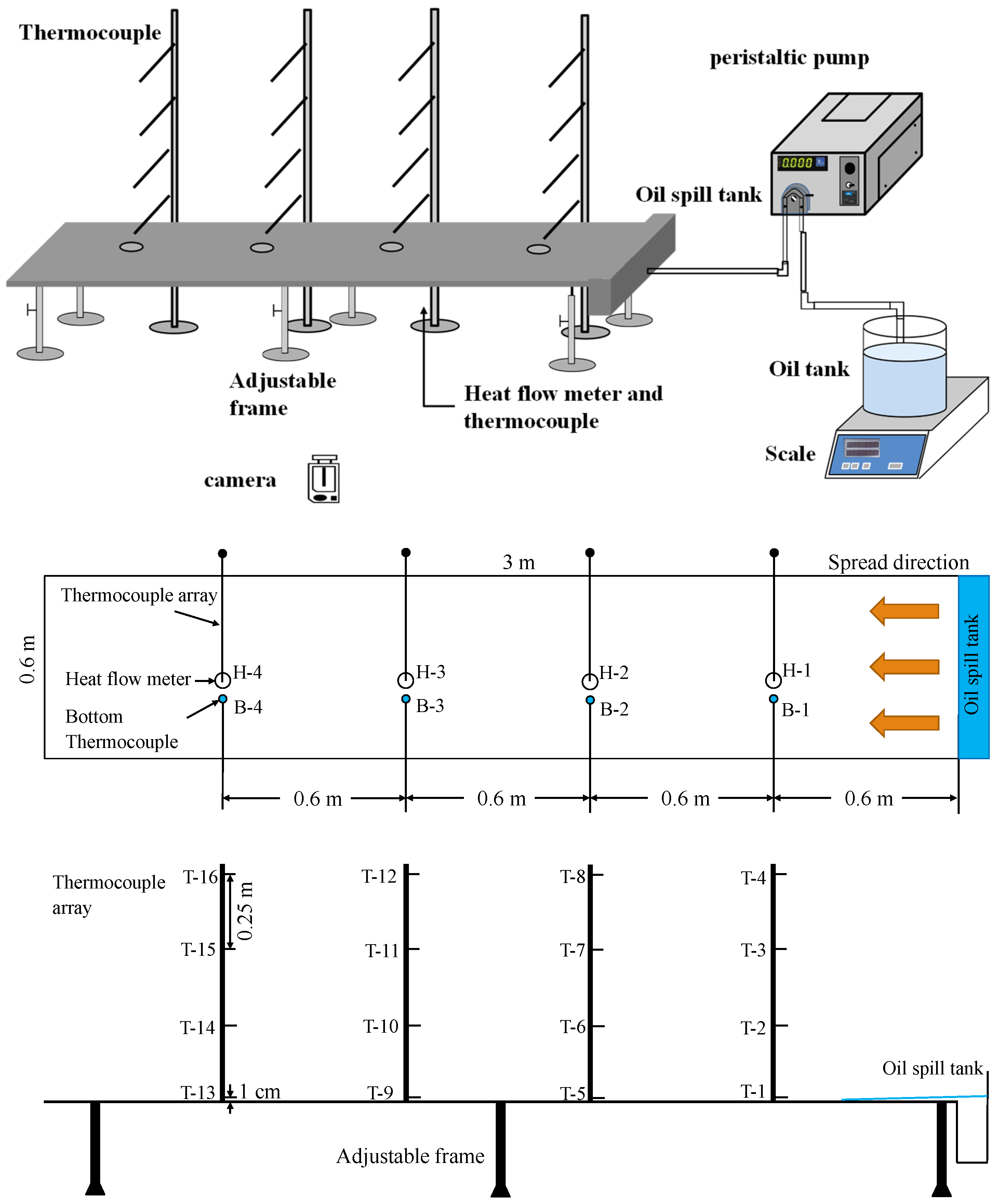
2. Experimental Setup
3. Results and Discussion
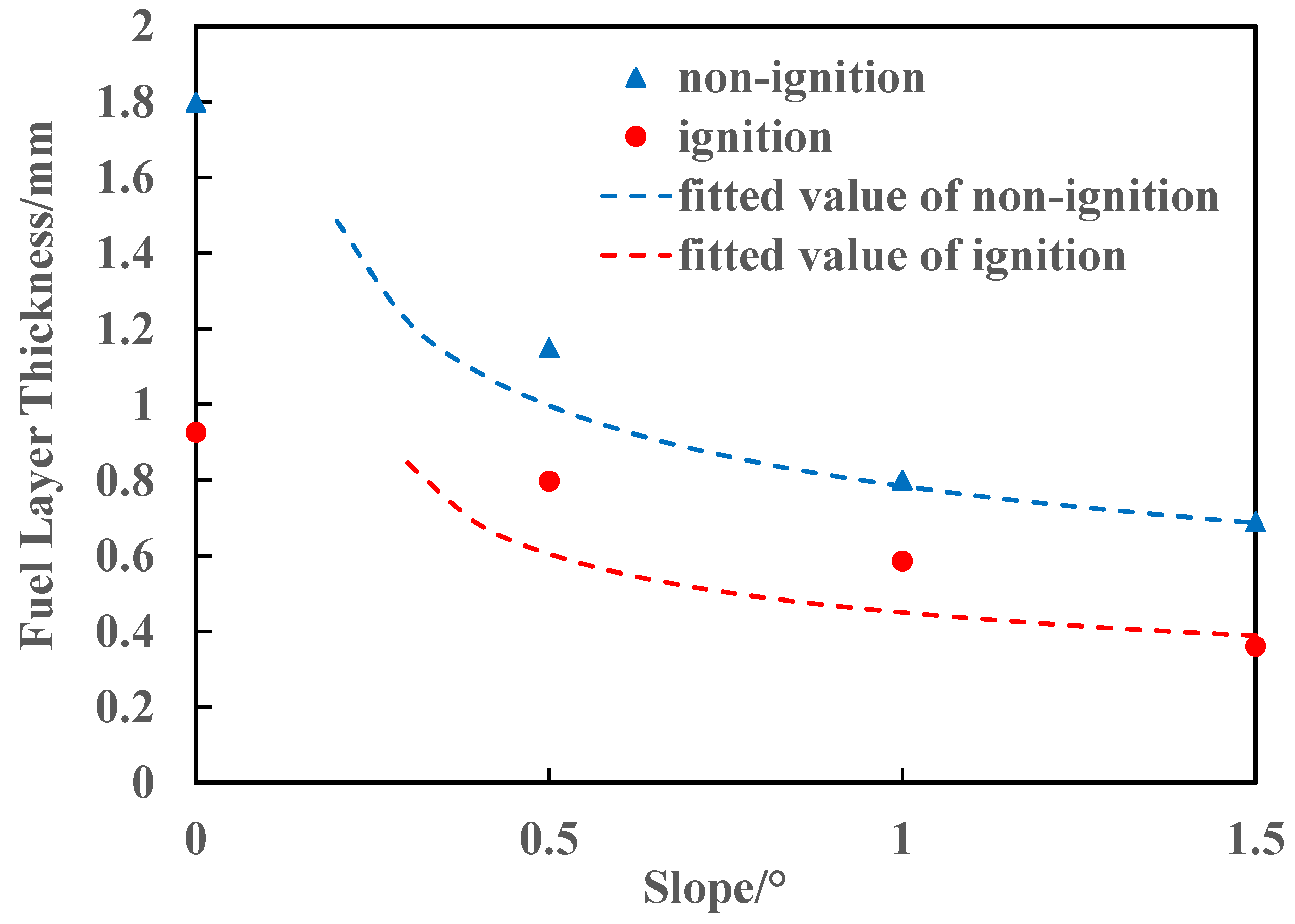
3.1. Experimental Phenomena
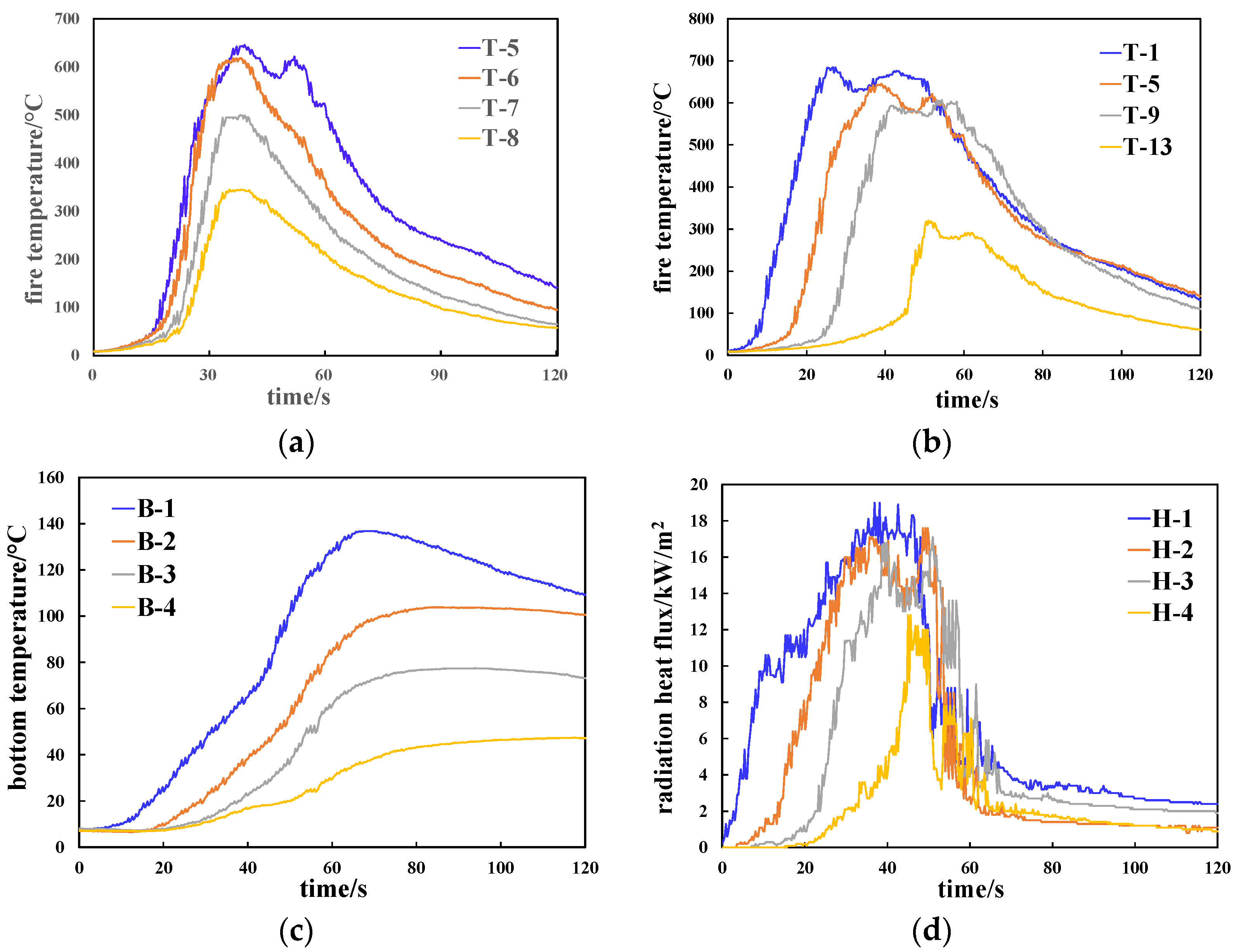
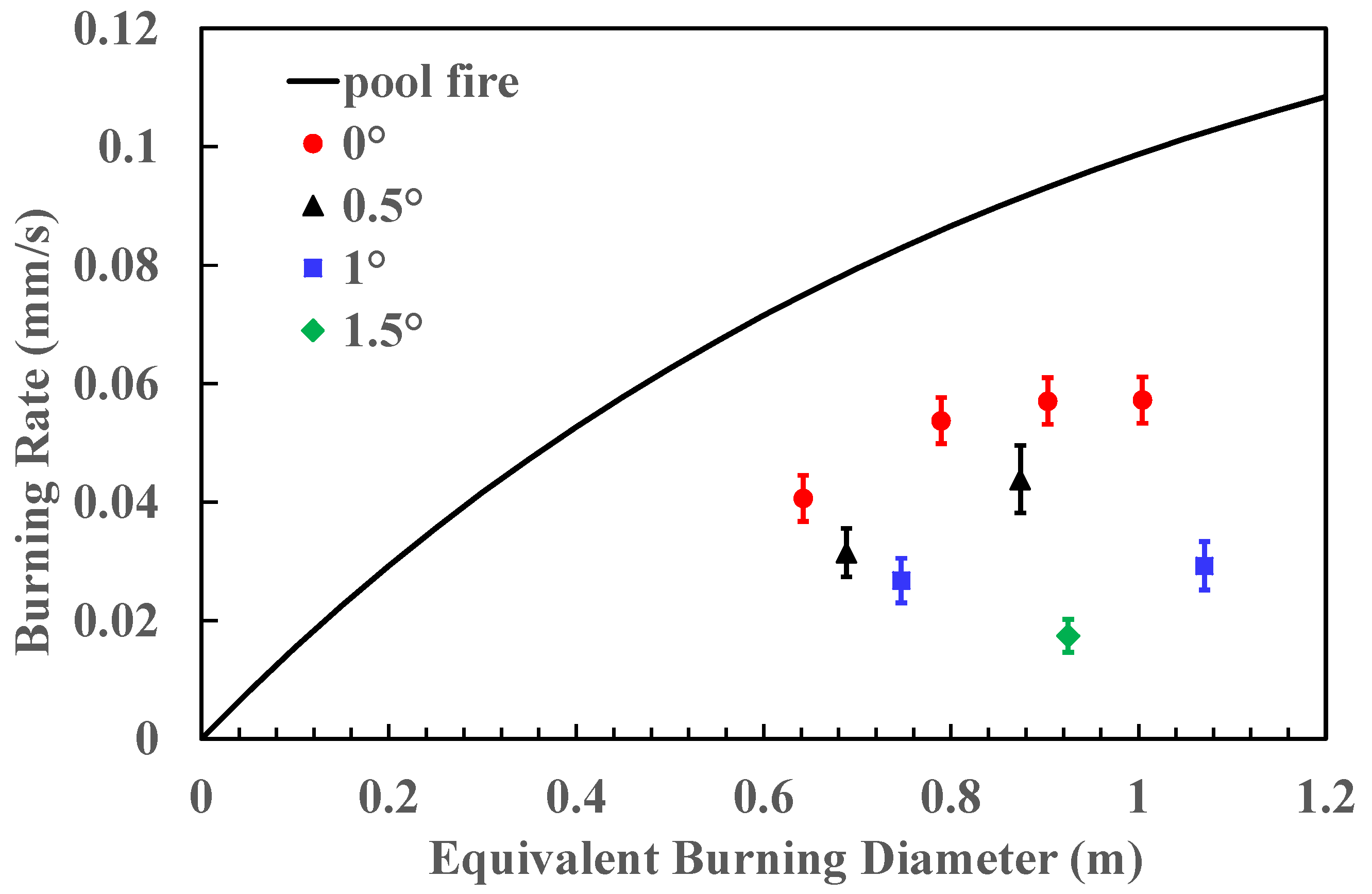
3.2. Burning Process
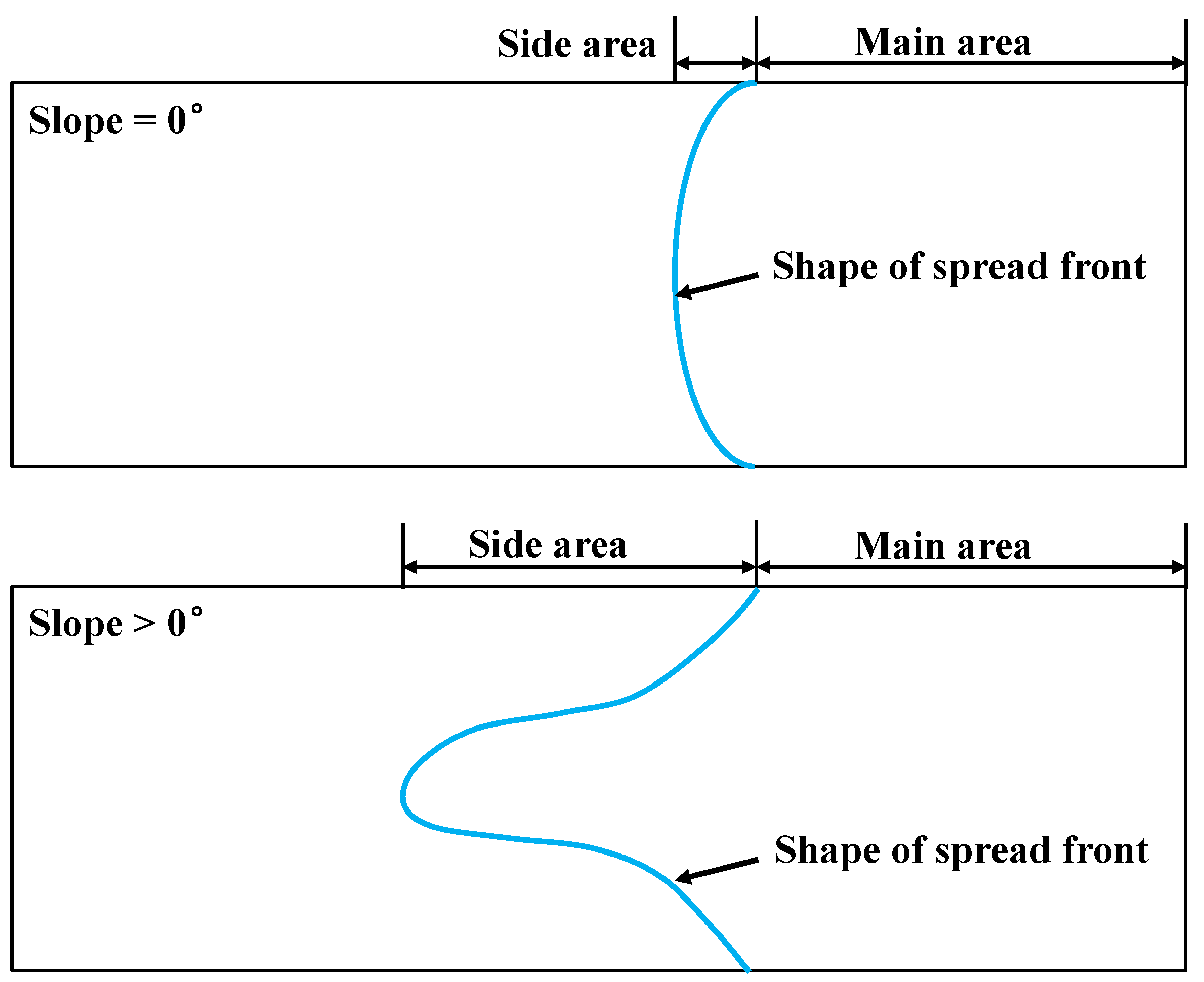
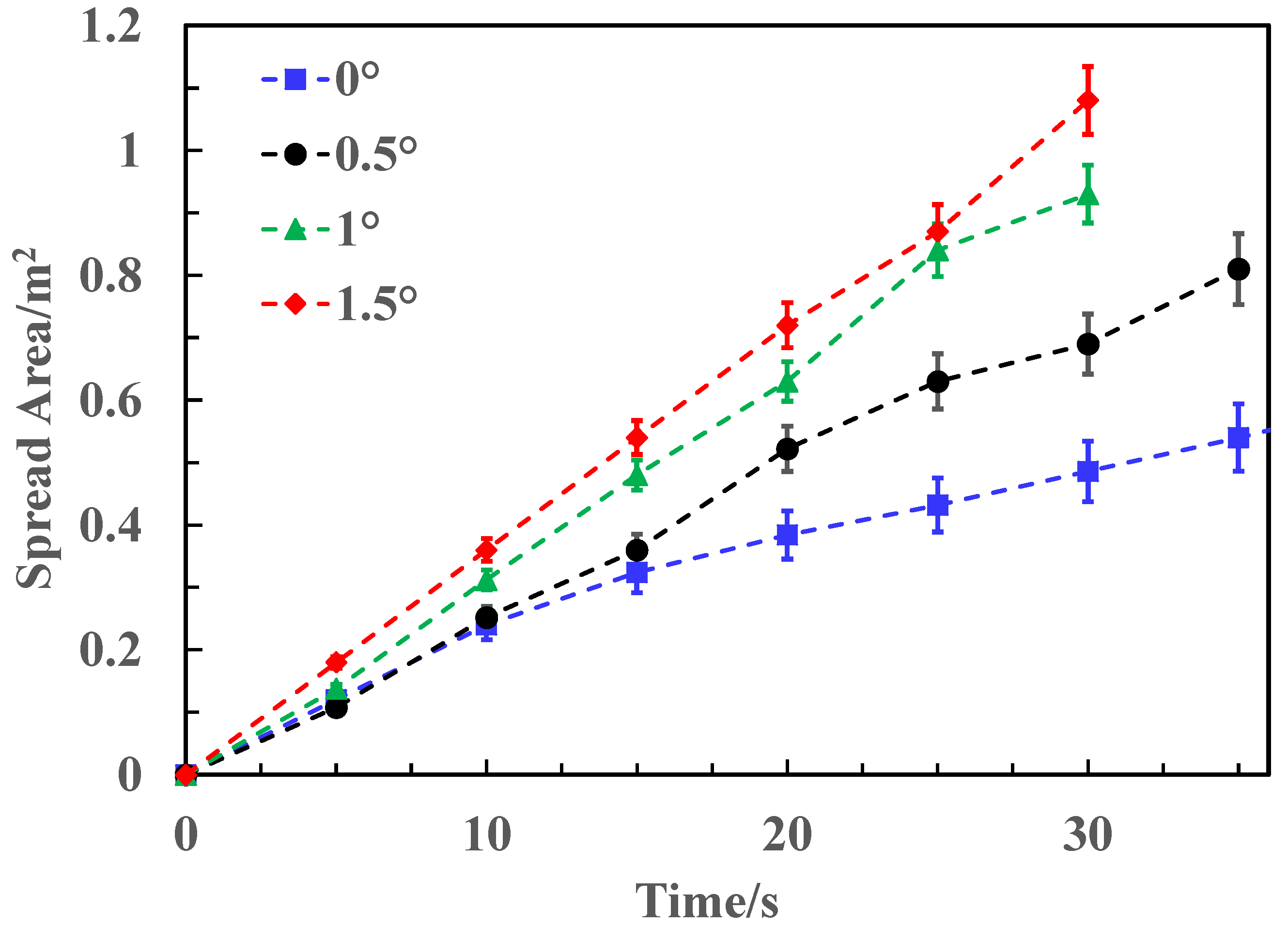
3.3. Spread Process
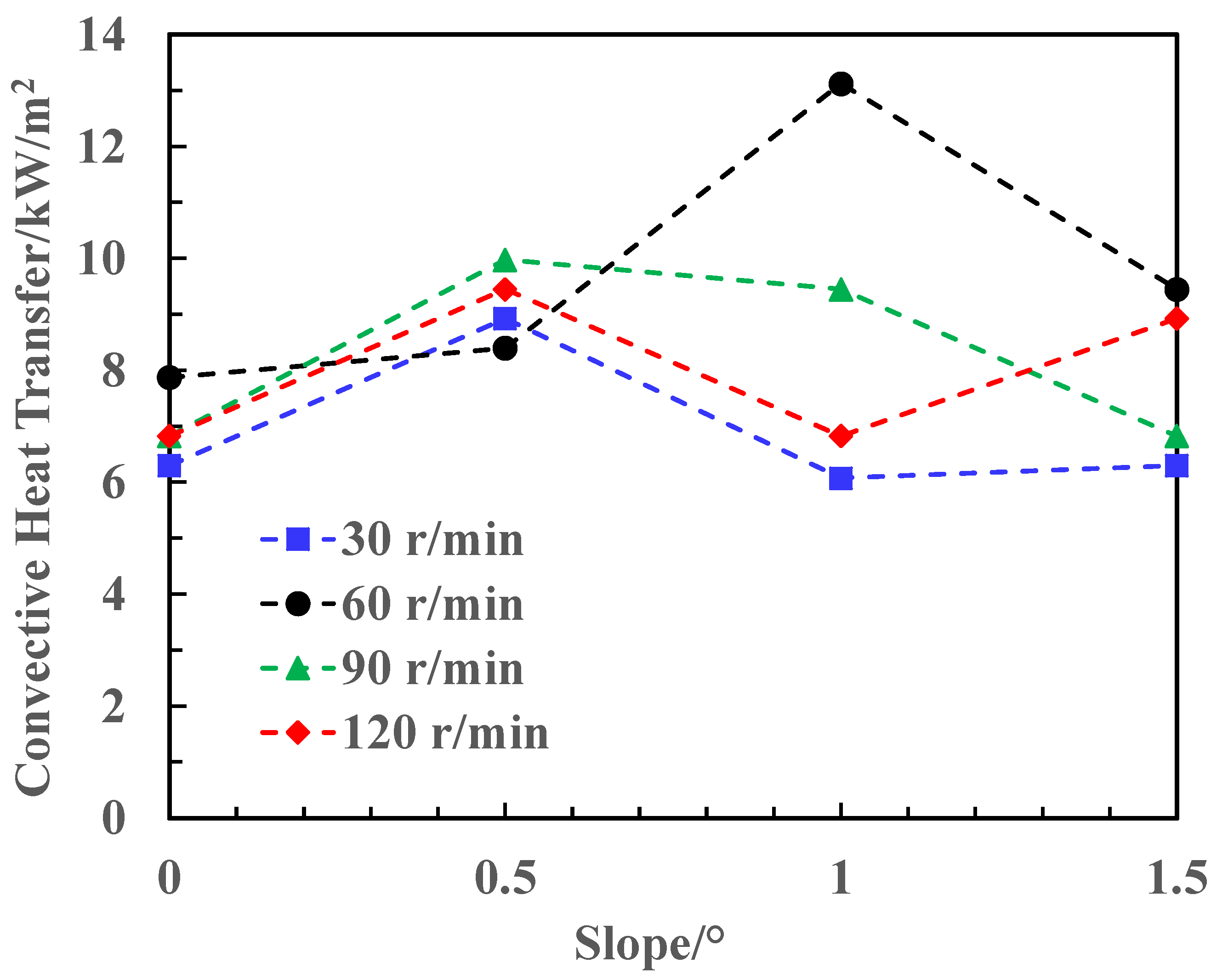
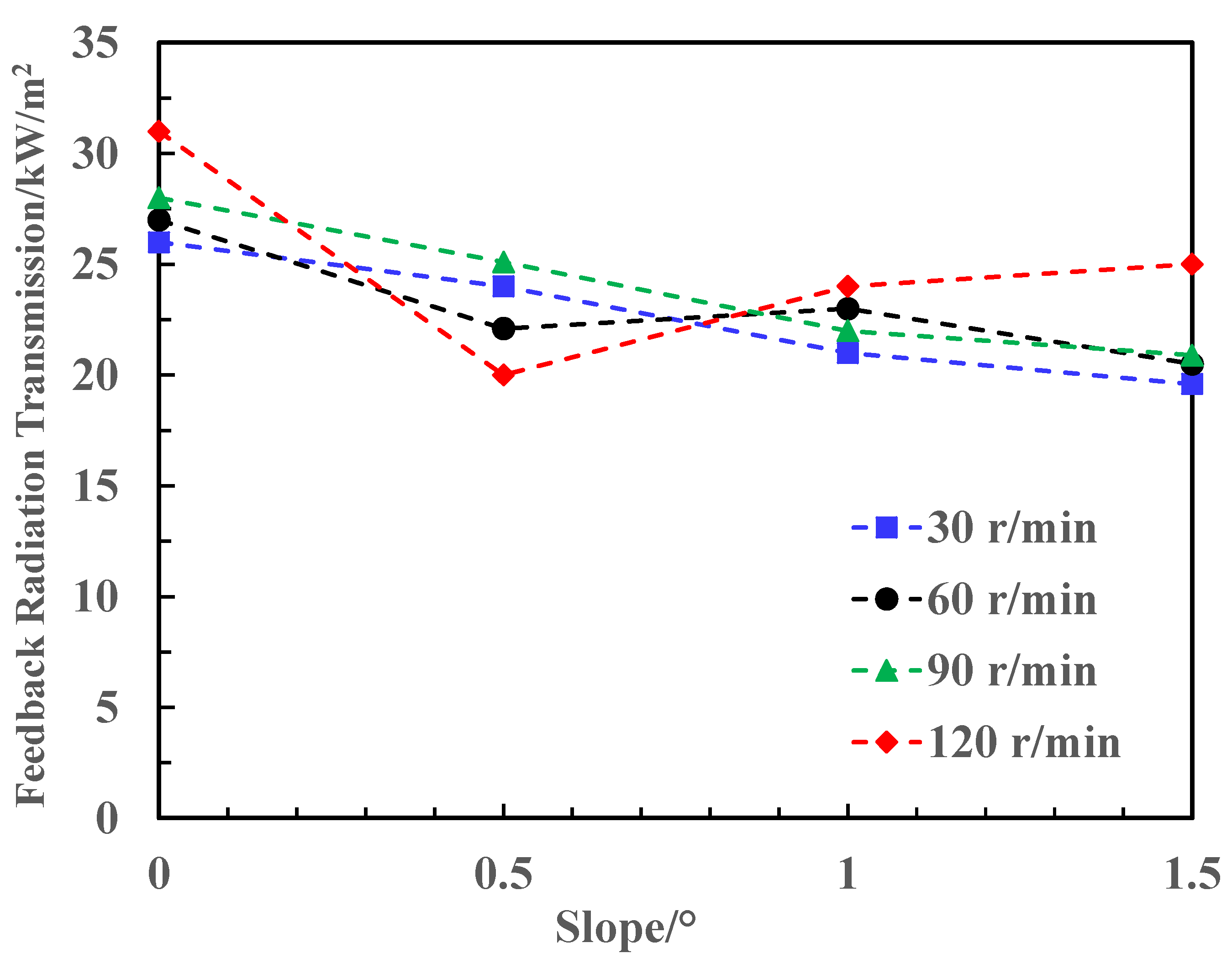
3.4. Effect of Slope
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, J.; Zhao, Y.; Bi, Y.; Li, C.; Kong, D.; Lu, S. Effect of initial pressure on the burning behavior of ethanol pool fire in the closed pressure vessel. Process Saf. Environ. Prot. 2021, 153, 159–166. [Google Scholar] [CrossRef]
- Liu, C.X. Effects of Ullage Height on Burning Behaviors of Pool Fires. Ph.D. Thesis, University of Science and Technology of China, Hefei, China, 2021. [Google Scholar]
- Lin, Y.J. Investigation of Flame Geometry and Downstream Heat Flux Evolution of Pool Fires under Cross FLOW and inclined Surface. Ph.D. Thesis, University of Science and Technology of China, Hefei, China, 2021. [Google Scholar]
- Kuang, C. Investigation into Burning Rate, Heat Feedback Mechanisms and Radiation Properties of Pool Fire in Cross Flow. Ph.D. Thesis, University of Science and Technology of China, Hefei, China, 2021. [Google Scholar]
- Li, Y.T.; Huang, H. Experimental and Model Study on the Spread and Burning Behavior of Liquid Fuel Spill Fires. Ph.D. Thesis, Tsinghua University, Beijing, China, 2015. [Google Scholar]
- Li, Y.T.; Xu, D.; Huang, H.; Zhao, J.; Shuai, J. An experimental study on the burning rate of a continuously released n-heptane spill fire on an open water surface. J. Loss Prev. Process Ind. 2020, 63, 104033. [Google Scholar] [CrossRef]
- Li, Y.T.; Huang, H.; Shuai, J.; Zhao, J.; Su, B. Experimental study of continuously released liquid fuel spill fires on land and water in a channel. J. Loss Prev. Process Ind. 2018, 52, 21–28. [Google Scholar] [CrossRef]
- Zhao, J.L.; Huang, H. Experimental and Model Study on the Spread and Burning Behavior of Continuous Liquid Spill Fires. Ph.D. Thesis, Tsinghua University, Beijing, China, 2018. [Google Scholar]
- Zhao, J.L.; Huang, H.; Jomaas, G.; Zhong, M.; Ji, Y. Spread and burning behavior of continuous spill fires. Fire Saf. J. 2017, 91, 347–354. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.L.; Zhu, H.; Huang, H.; Zhong, M.; Yang, R. Experimental study on the liquid layer spread and burning behaviors of continuous heptane spill fires. Process Saf. Environ. Prot. 2019, 122, 320–327. [Google Scholar] [CrossRef]
- Zhao, J.L.; Zhu, X.; Zhang, J.; Huang, H.; Yang, R. Experimental study on the spread and burning behaviors of continuously discharge spill fires under different slopes. J. Hazard. Mater. 2020, 392, 122352. [Google Scholar] [CrossRef] [PubMed]
- Li, H.H.; Liu, X.; Liu, J.; Ge, J.; Tang, F. Spread and burning characteristics of continuous spill fires in a tunnel. Tunn. Undergr. Space Technol. 2021, 109, 103754. [Google Scholar] [CrossRef]
- Li, H.H.; Liu, J.; Ge, J. Phenomenological characteristics of continuous spill fires in a tunnel with longitudinal ventilation. Process Saf. Environ. Prot. 2020, 138, 108–116. [Google Scholar] [CrossRef]
- Liu, Q.Y. Review on liquid fuel spill fire. Sci. Technol. Eng. 2017, 17, 138–144. [Google Scholar]
- Liu, Q.Y.; Lu, Z.H.; Zhi, M.U. Study on thermal radiation model of large-scale continuously released jet fuel spill fire. J. China Univ. Pet. Ed. Nat. Sci. 2020, 44, 149–155. [Google Scholar]
- Liu, Q.Y.; Zhao, J.L.; Lv, Z.; Zhu, H.; Yang, R. Experimental study on the effect of substrate slope on continuously released heptane spill fires. J. Therm. Anal. Calorim. 2020, 140, 2497–2503. [Google Scholar] [CrossRef]
- Li, M.H.; Luo, Q.Y.; Wang, C.J.; Pan, Y. Study on unsteady combustion behavior of stationary spilling fire of n-butanol under condition of variable slope. J. Saf. Sci. Technol. 2020, 16, 5–10. [Google Scholar]
- Fay, J.A. Unusual Fire Hazard of LNG Tanker Spills. Combust. Sci. Technol. 1973, 7, 47–49. [Google Scholar] [CrossRef]
- Fay, J.A. Physical Processes in the Spread of Oil on a Water Surface. In Proceedings of the Joint Conference on Prevention and Control of Oil Spills, International Oil Pill Conference, Washington, DC, USA, 15–17 June 1971; American Petroleum Institute: Washington, DC, USA, 1971; pp. 463–467. [Google Scholar]
- Briscoe, F.; Shaw, P. Spread and evaporation of liquid. Prog. Energy Combust. Sci. 1980, 6, 127–140. [Google Scholar] [CrossRef]
- Webber, D.M. A Model for Pool Spreading and Vaporization and its Implementation in the Computer Code G*A*S*P; AEA Technology, SRD/HSE/R507; Safety and Reliability Directorate: Washington, DC, USA, 1990. [Google Scholar]
- Witlox, H.W.M. Model for Pool Spreading, Evaporation and Solution on Land and Water (PVAP)—Theory Manual, Consequence Modeling Documentation; PHAST Technical Reference; PHAST: Homberg, Germany, 2000. [Google Scholar]
- Webber, D.M. On models of spreading pools. J. Loss Prev. Process Ind. 2012, 25, 923–926. [Google Scholar] [CrossRef]
- Burgess, D.S.; Strasser, A.; Grumer, J. Diffusive burning of liquids in open trays. Fire Res. Abstr. Rev. 1961, 3, 177–192. [Google Scholar]
- Babrauskas, V. Estimating large pool fire burning rates. Fire Technol. 1983, 19, 251–261. [Google Scholar] [CrossRef]
- Benfer, M. Spill and Burning Behavior of Flammable Liquids. Master’s Thesis, University of Maryland, College Park, MD, USA, 2010. [Google Scholar]
- Mealy, C.; Benfer, M.; Gottuk, D. Fire Dynamics and Forensic Analysis of Liquid Fuel Fires; Bureau of Justice Statistics: Washington, DC, USA, 2011.
- Mealy, C.; Benfer, M.; Gottuk, D. Liquid Fuel Spill Fire Dynamics. Fire Technol. 2014, 50, 419–436. [Google Scholar] [CrossRef]
- Gottuk, D.T.; Scheffey, J.L.; Williams, F.W.; Gott, J.E.; Tabet, R.J. Optical Fire Detection (OFD) for Military Aircraft Hangars: Final Report on OFD Performance to Fuel Spill Fires and Optical Stresses; NRL/MR/6180-00-8457; Naval Research Laboratory: Washington, DC, USA, 2000. [Google Scholar]
- Hissong, D.W. Keys to modeling LNG spills on water. J. Hazard. Mater. 2007, 140, 465–477. [Google Scholar] [CrossRef] [PubMed]






| N-Heptane | Alcohol | |
|---|---|---|
| Density (g/cm3) | 0.678 | 0.789 |
| Boiling point (°C) | 98.4 | 78.3 |
| Heat of combustion (kJ/mol) | 4806.6 | 1365.5 |
| Rotation Speed r/min | Quality g/s | Volume L/min |
|---|---|---|
| 30 | 9 | 0.79 |
| 60 | 18 | 1.58 |
| 90 | 25 | 2.19 |
| 120 | 30 | 2.63 |
| No. | Type of Fuel | Revolutions (r/min) | Slope (°) |
|---|---|---|---|
| 1 | n-heptane | 30 | 0 |
| 2 | n-heptane | 60 | 0 |
| 3 | n-heptane | 90 | 0 |
| 4 | n-heptane | 120 | 0 |
| 5 | n-heptane | 30 | 0.5 |
| 6 | n-heptane | 60 | 0.5 |
| 7 | n-heptane | 90 | 0.5 |
| 8 | n-heptane | 120 | 0.5 |
| 9 | n-heptane | 30 | 1 |
| 10 | n-heptane | 60 | 1 |
| 11 | n-heptane | 90 | 1 |
| 12 | n-heptane | 120 | 1 |
| 13 | n-heptane | 30 | 1.5 |
| 14 | n-heptane | 60 | 1.5 |
| 15 | n-heptane | 90 | 1.5 |
| 16 | n-heptane | 120 | 1.5 |
| 17 | n-heptane | 30 | 2 |
| 18 | n-heptane | 60 | 2 |
| 19 | n-heptane | 90 | 2 |
| 20 | n-heptane | 120 | 2 |
| 21 | alcohol | 30 | 0 |
| 22 | alcohol | 60 | 0 |
| 23 | alcohol | 90 | 0 |
| 24 | alcohol | 120 | 0 |
| 25 | alcohol | 30 | 0.5 |
| 26 | alcohol | 60 | 0.5 |
| 27 | alcohol | 90 | 0.5 |
| 28 | alcohol | 120 | 0.5 |
| 29 | alcohol | 30 | 1 |
| 30 | alcohol | 60 | 1 |
| 31 | alcohol | 90 | 1 |
| 32 | alcohol | 120 | 1 |
| 33 | alcohol | 30 | 1.5 |
| 34 | alcohol | 60 | 1.5 |
| 35 | alcohol | 90 | 1.5 |
| 36 | alcohol | 120 | 1.5 |
| 37 | alcohol | 30 | 2 |
| 38 | alcohol | 60 | 2 |
| 39 | alcohol | 90 | 2 |
| 40 | alcohol | 120 | 2 |
| Slope (°) | N-Heptane | Alcohol |
|---|---|---|
| 0 | Shrinking and steady burning phases were observed | Shrinking and steady burning phases were observed |
| 0.5 | Steady burning phase was observed when fuel discharge rate was low | Steady burning phase was observed when fuel discharge rate was low |
| 1 | Steady burning phase was observed when fuel discharge rate was low | Steady burning phase was not observed |
| 1.5 | Steady burning phase was observed when fuel discharge rate was low | Steady burning phase was not observed |
| 2 | Steady burning phase was not observed | Steady burning phase was not observed |
| Non-Burning Situation | Burning Situation | |
|---|---|---|
| n | ||
| /(°) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Huang, H.; Zhao, J.; Song, G. Experimental Study of the Effect of Slope on the Spread and Burning Characteristics of a Continuous Oil Spill Fire. Fire 2022, 5, 112. https://doi.org/10.3390/fire5040112
Sun X, Huang H, Zhao J, Song G. Experimental Study of the Effect of Slope on the Spread and Burning Characteristics of a Continuous Oil Spill Fire. Fire. 2022; 5(4):112. https://doi.org/10.3390/fire5040112
Chicago/Turabian StyleSun, Xiaoxiao, Hong Huang, Jinlong Zhao, and Guangheng Song. 2022. "Experimental Study of the Effect of Slope on the Spread and Burning Characteristics of a Continuous Oil Spill Fire" Fire 5, no. 4: 112. https://doi.org/10.3390/fire5040112
APA StyleSun, X., Huang, H., Zhao, J., & Song, G. (2022). Experimental Study of the Effect of Slope on the Spread and Burning Characteristics of a Continuous Oil Spill Fire. Fire, 5(4), 112. https://doi.org/10.3390/fire5040112






