Beads and Globules from Fires: Can They Be Differentiated through Metallurgical Analysis Based on Machine Learning Algorithms?
Abstract
:1. Introduction
2. The Metallurgical Data Collection
2.1. Experiment Conditions and Metallurgical Image Dataset
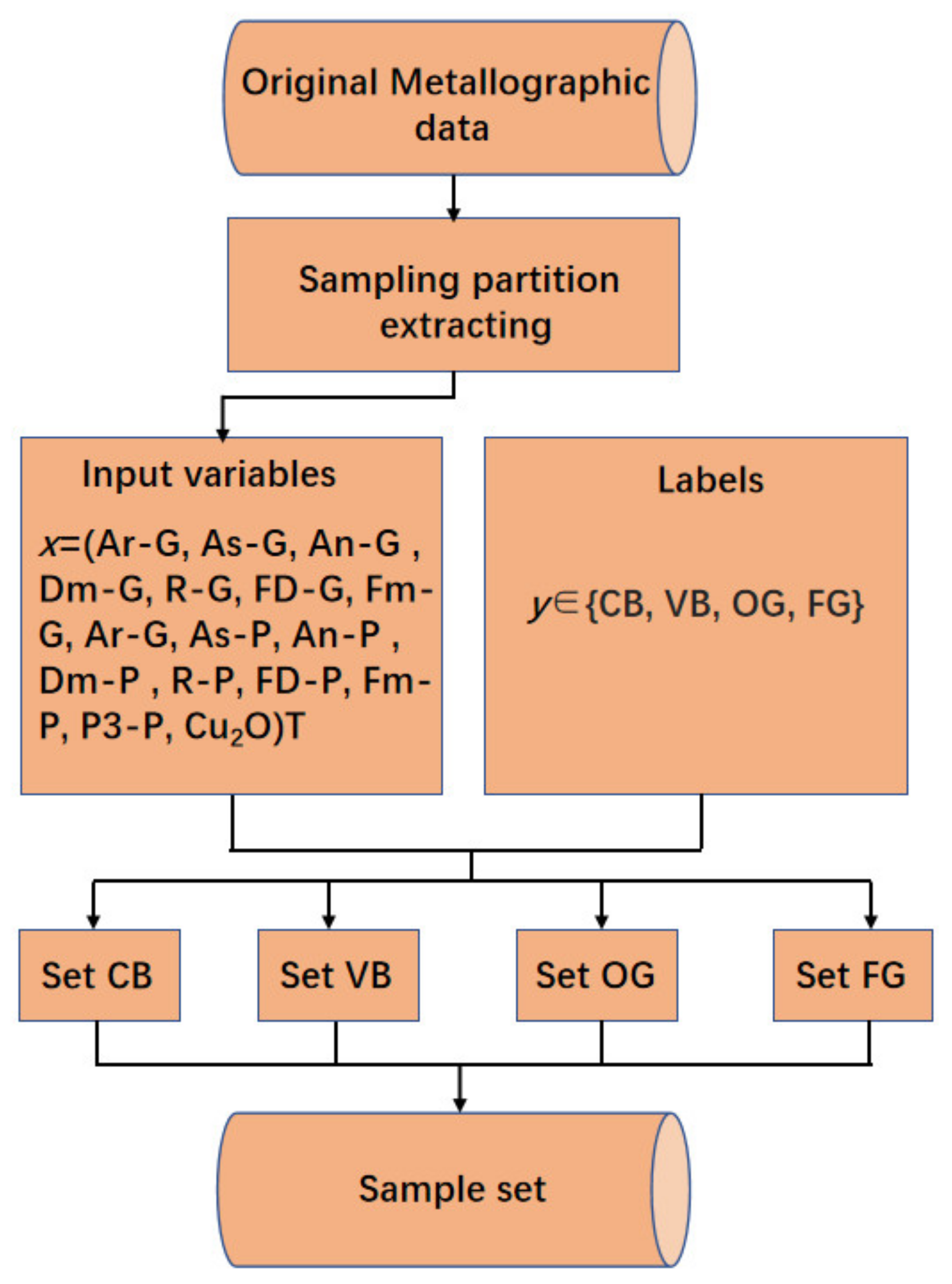
2.2. Selection of Input Variables
3. Development of Classification Model
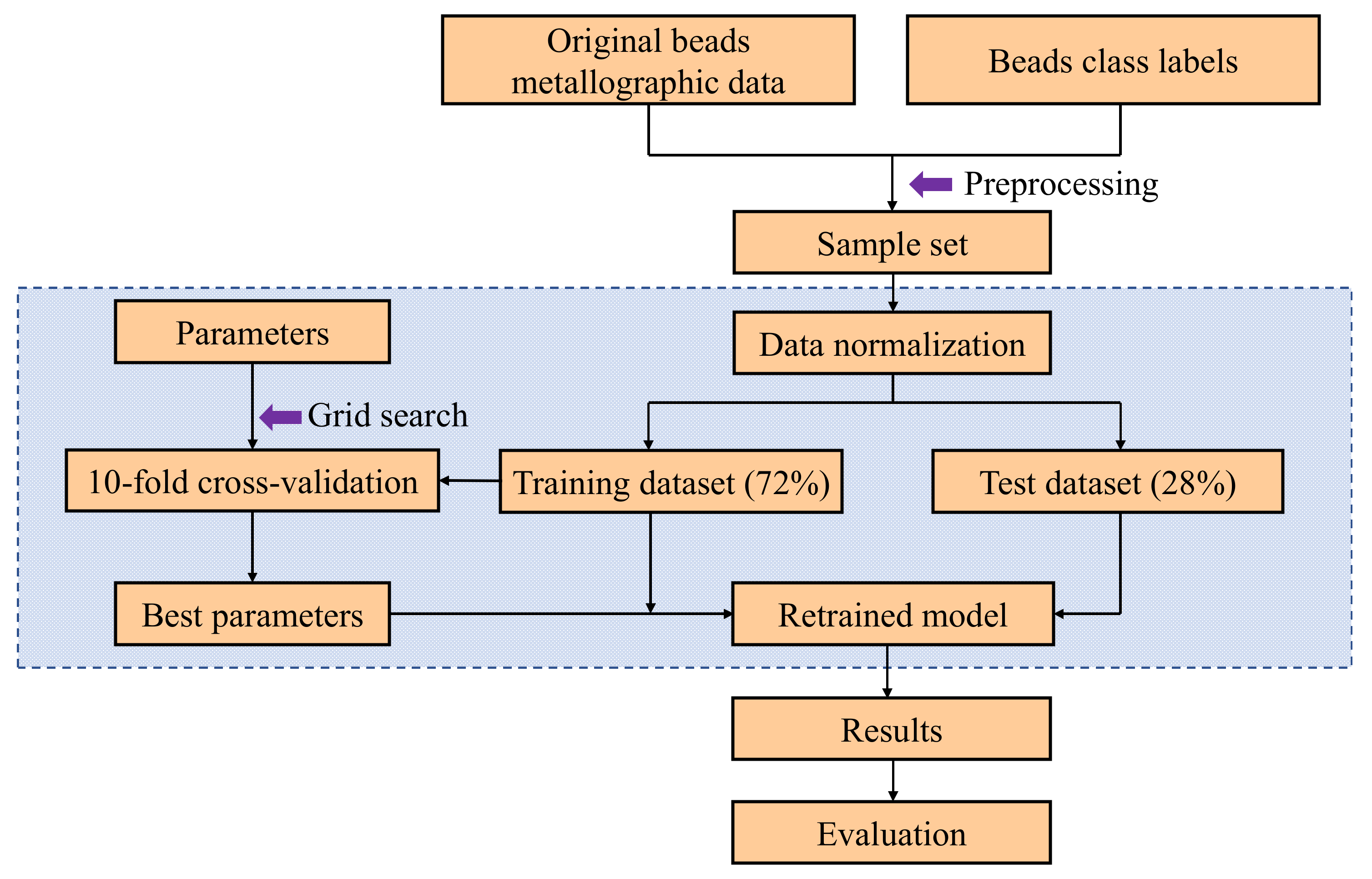
Model Training and Evaluation
4. Results and Discussion
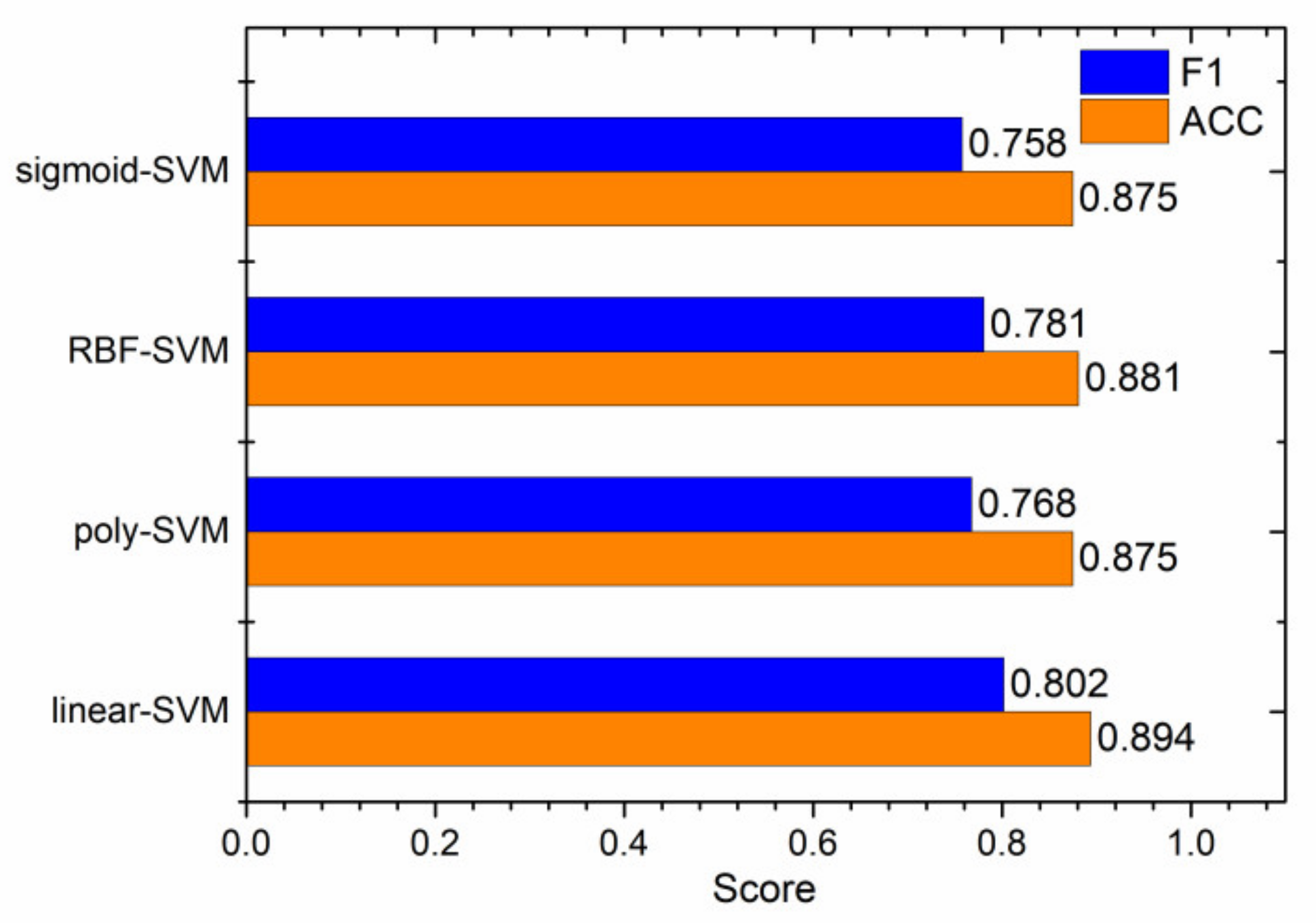
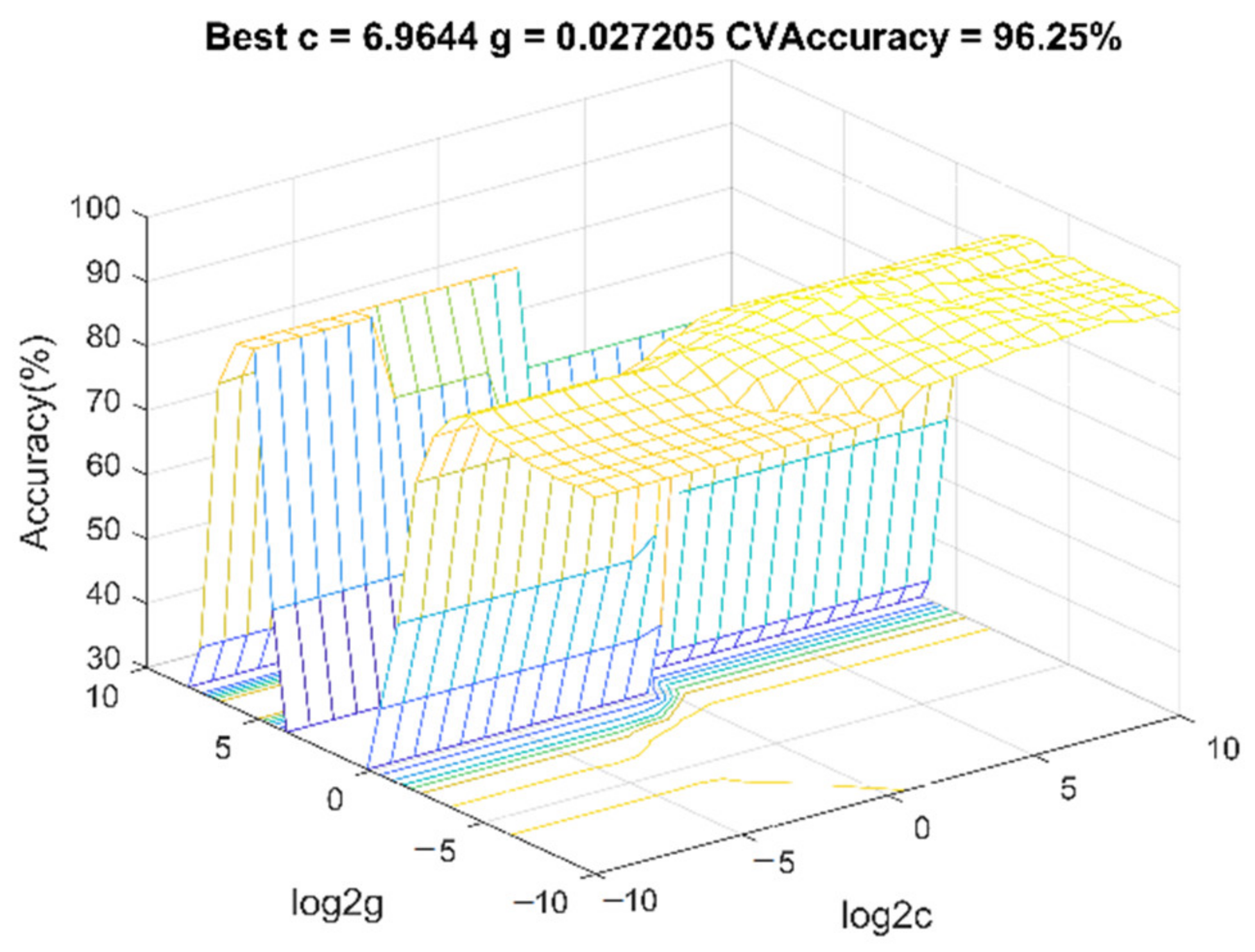
4.1. Prediction Results of SVMs
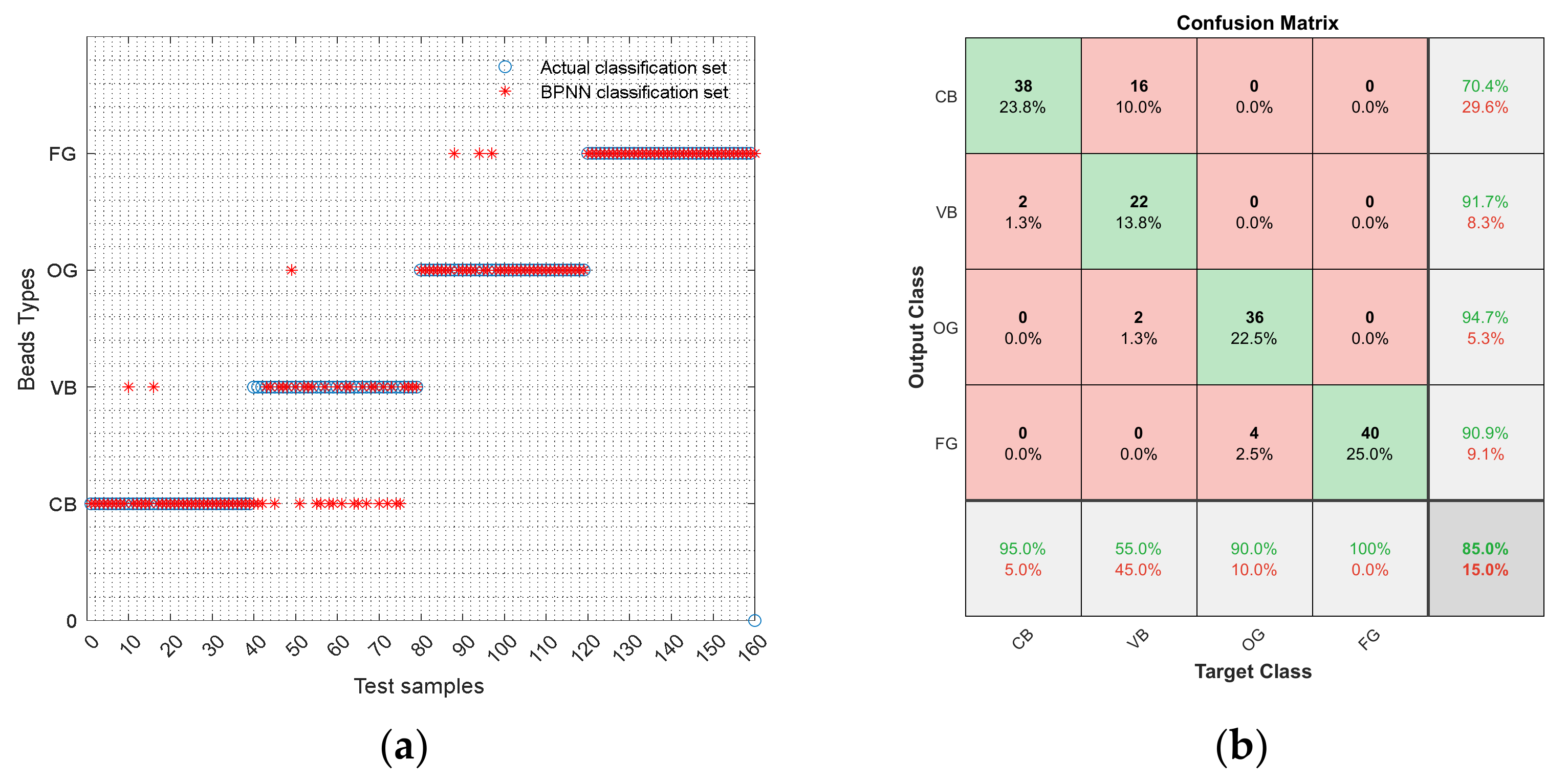
4.2. Prediction Results of BPNN
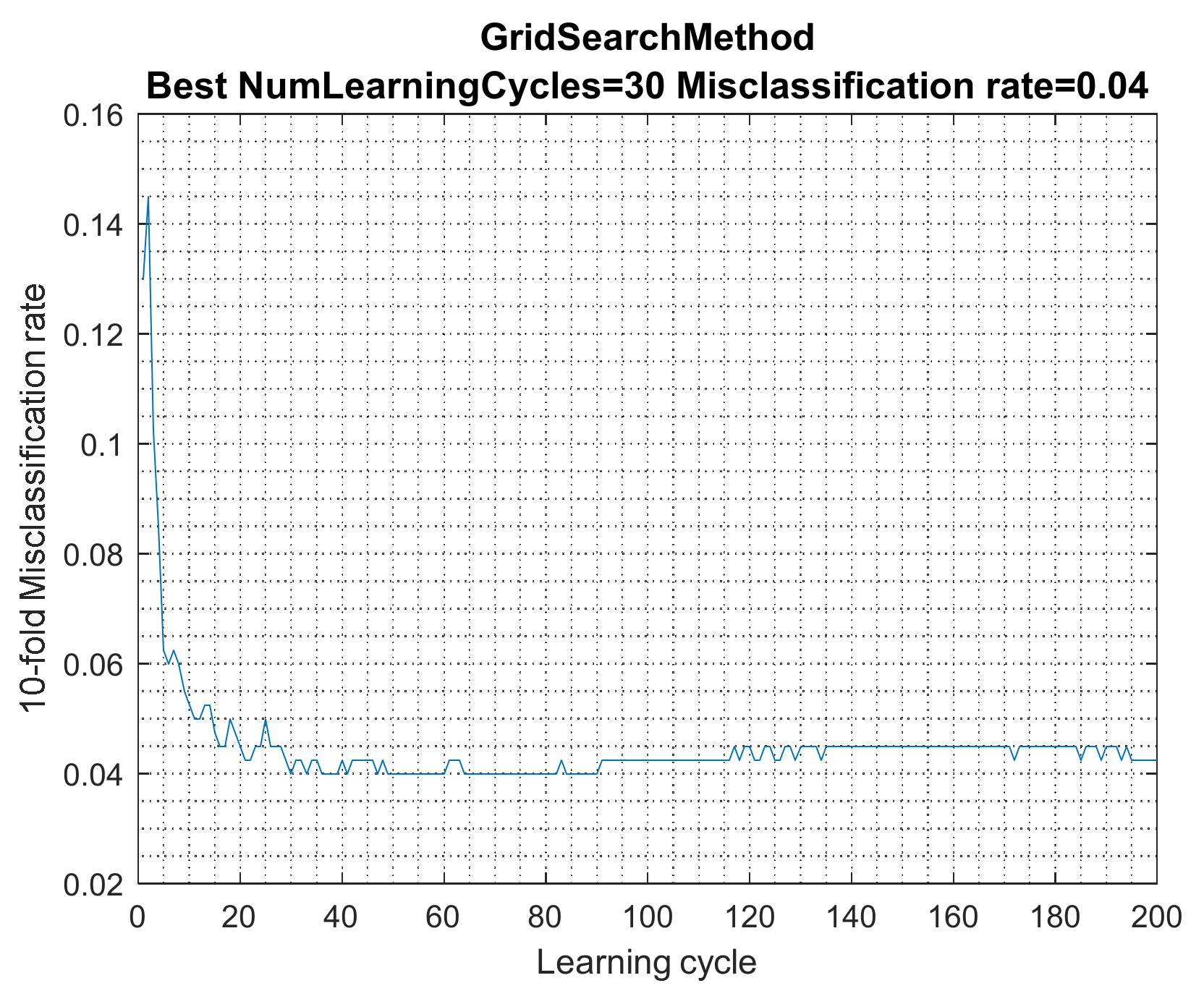
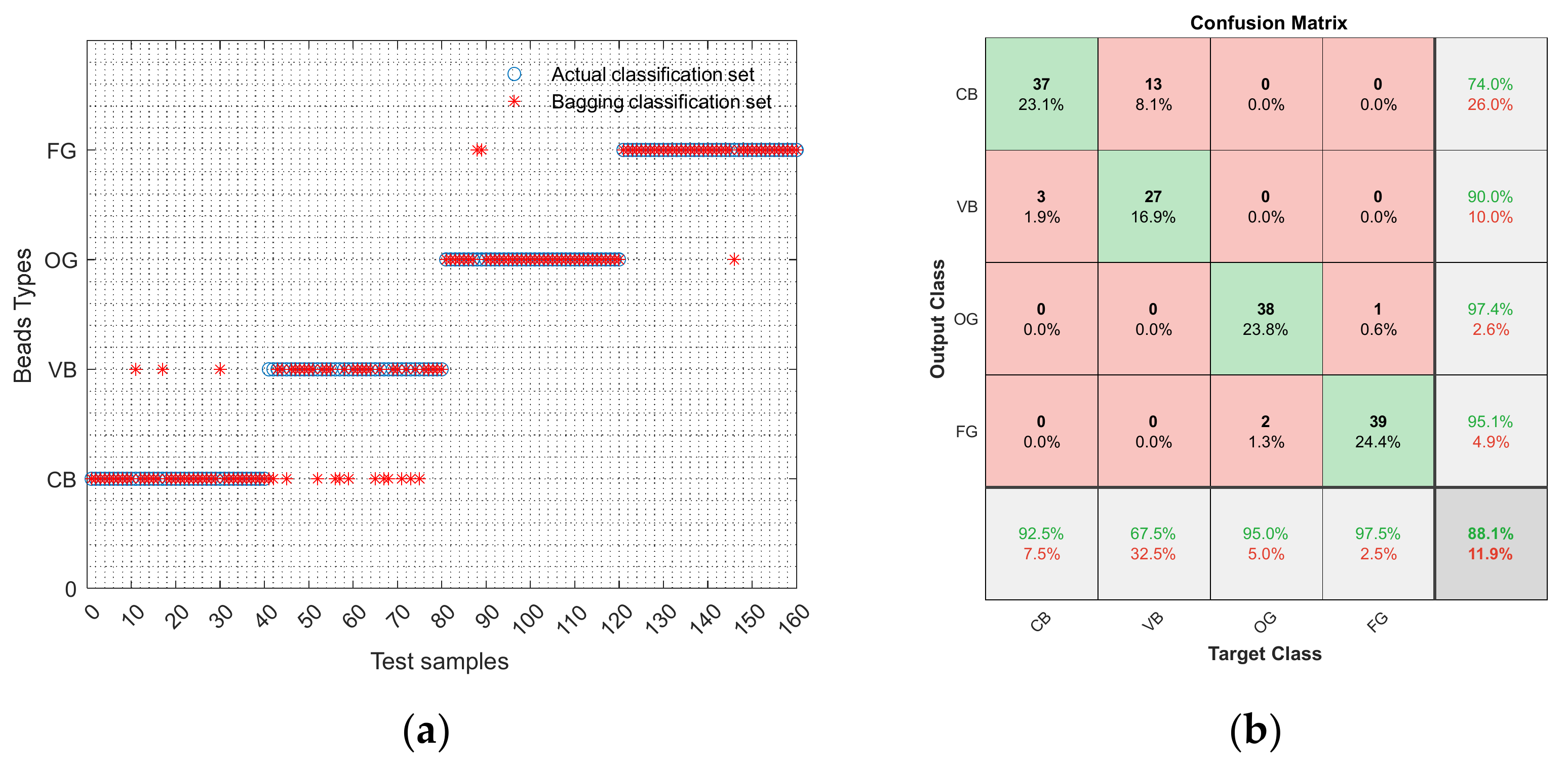
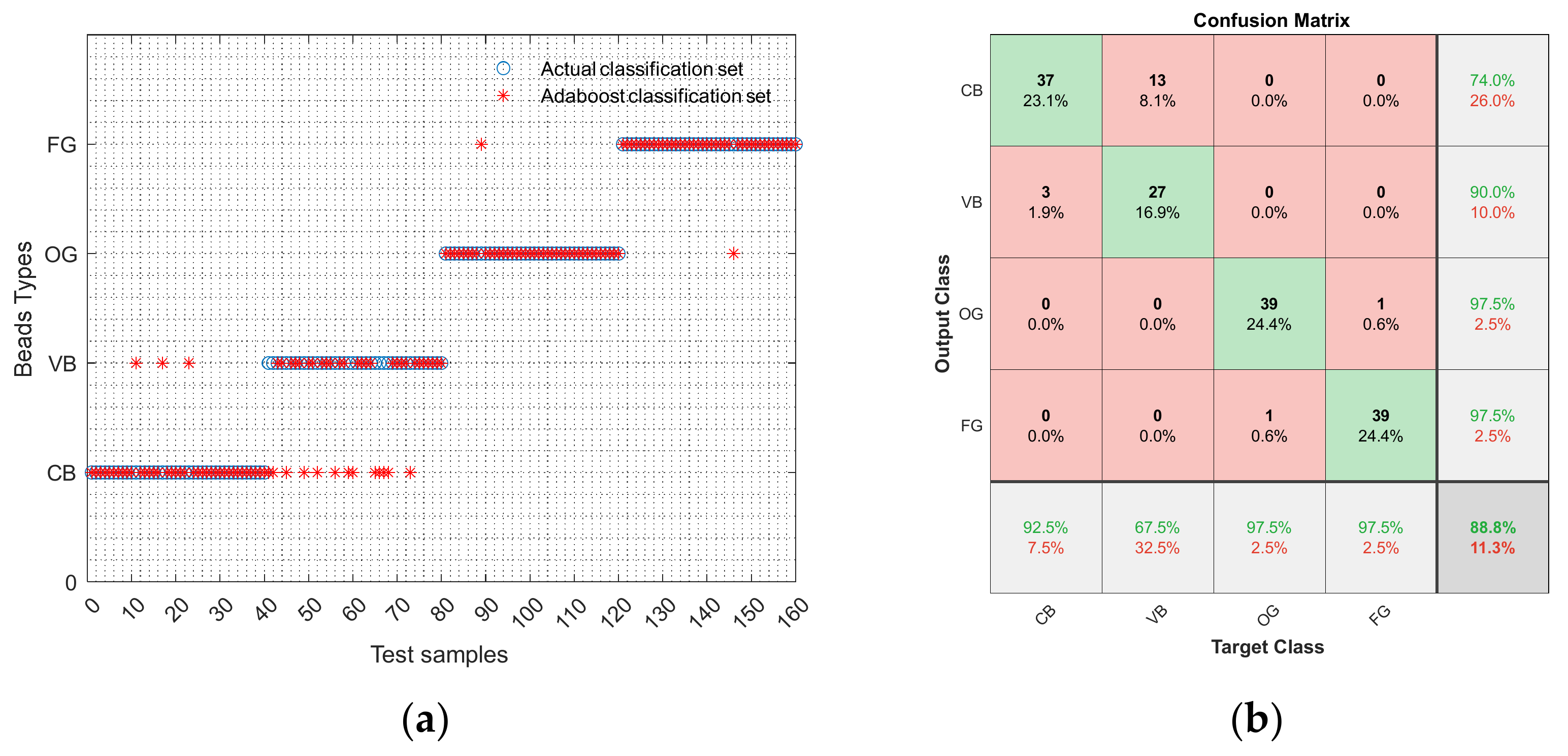
4.3. Prediction Results of Bagging and AdaBoost
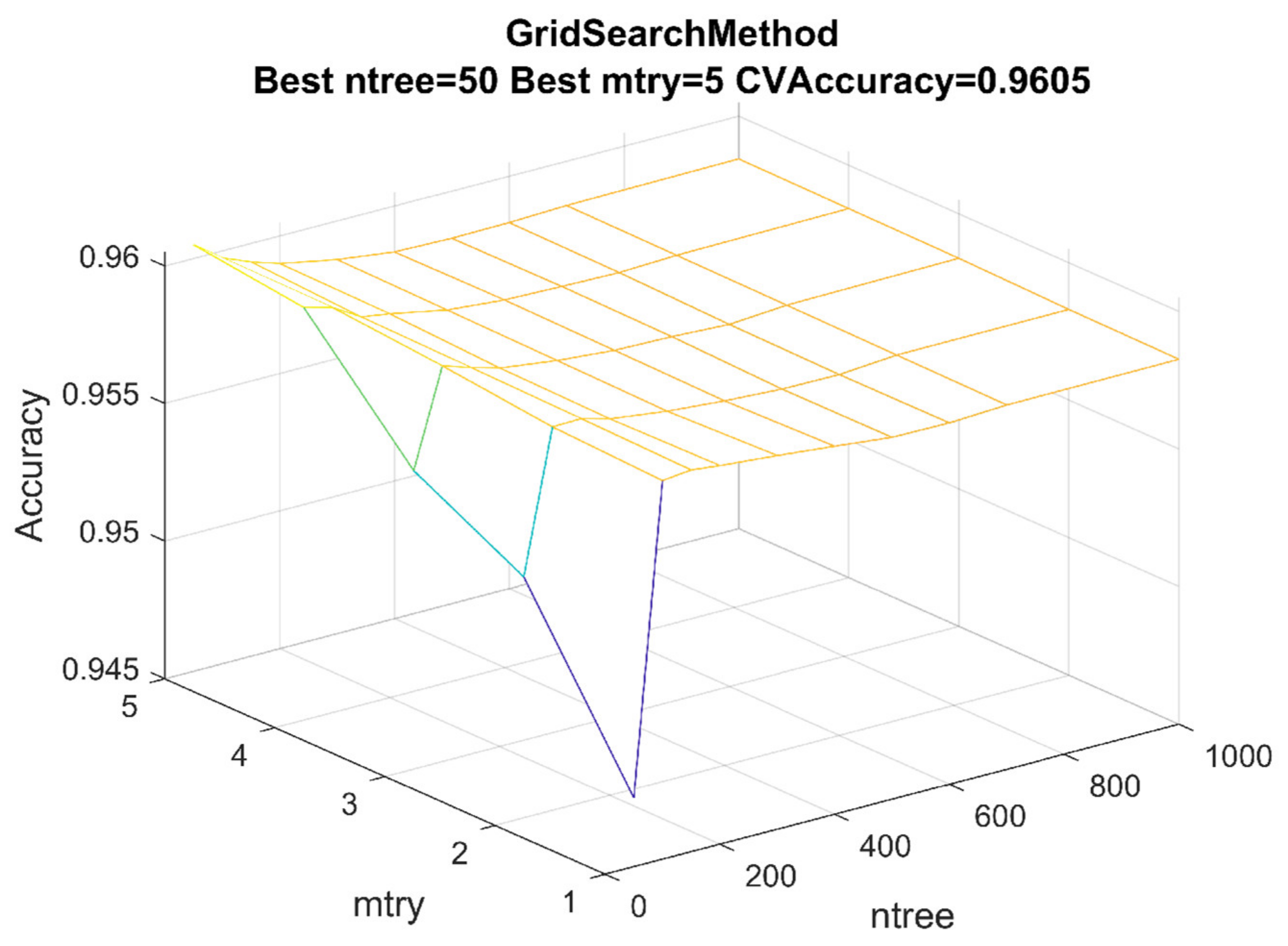
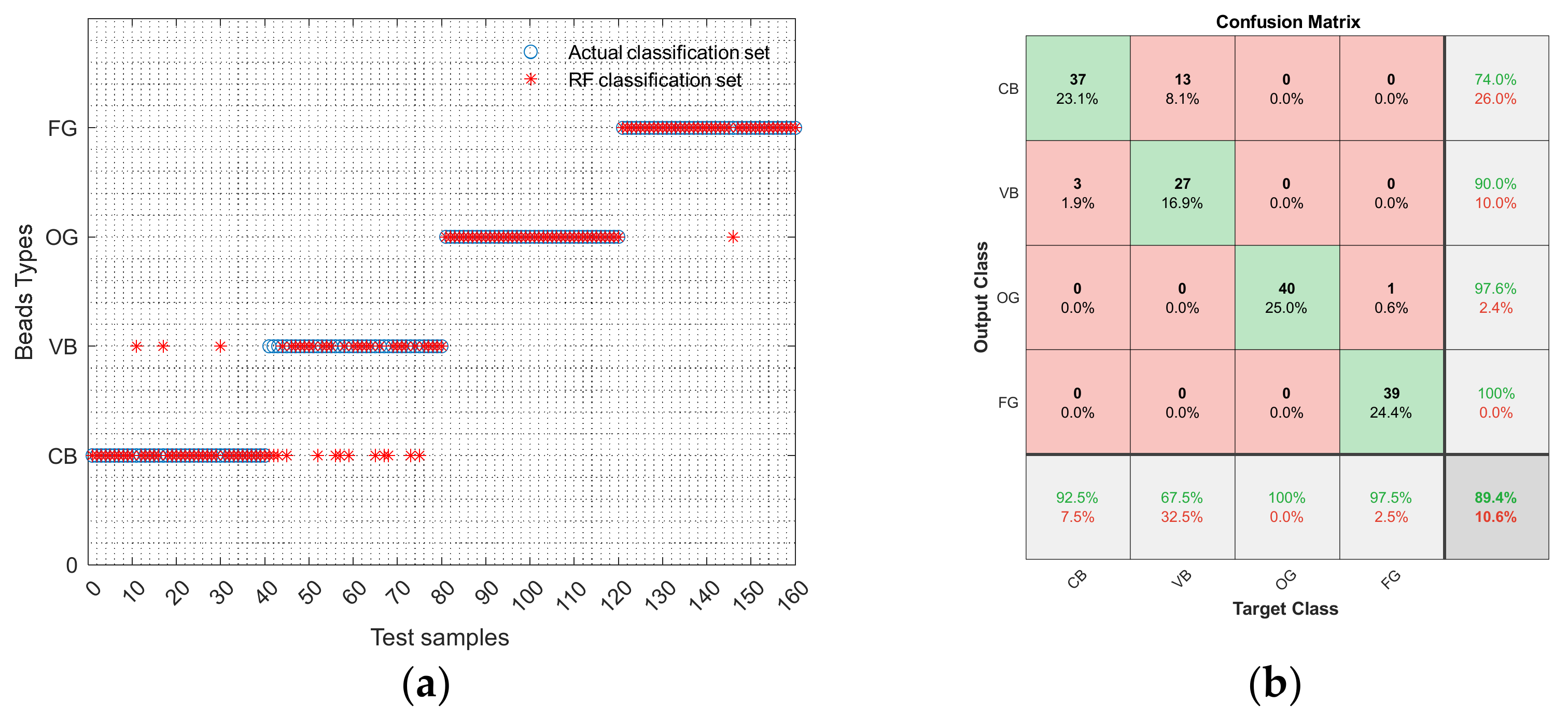
4.4. Prediction Results of RF
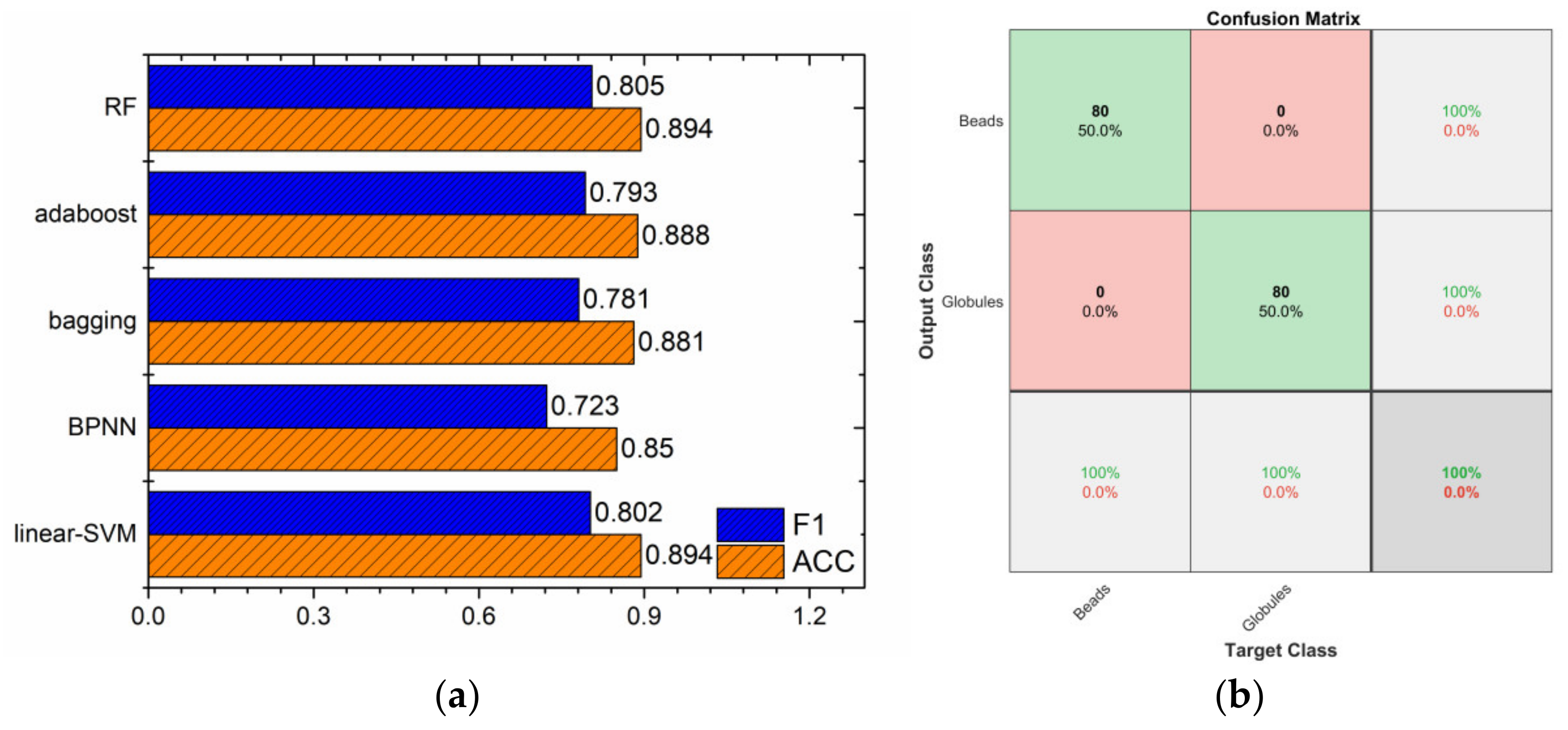
4.5. Performance Comparison among Classifiers
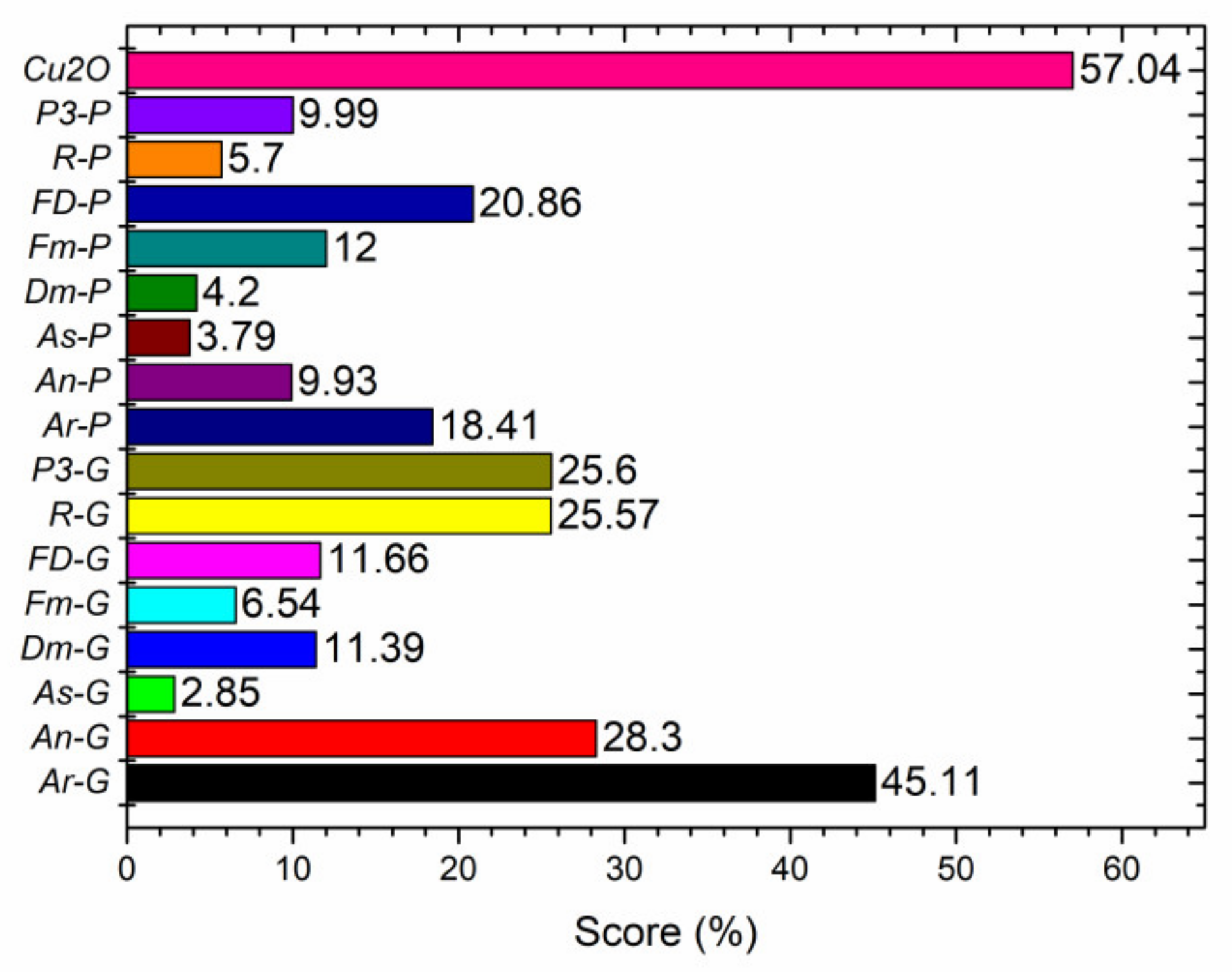
4.6. Variable Importance Analysis
5. Conclusions
- Among the machine learning classifiers used in this work, RF has the great potential to differentiate among melted beads. ACC/F1 of RF model were 0.894/0.805, respectively, which are better than SVM, BPNN, AdaBoost, and bagging. For RF classifier, the recall rates of CB, VB, OG, and FG were 92.5%, 67.5%, 100%, and 97.5%, respectively, indicating that RF has best potential to predict OG and FG. It is also worth noting that the RF used in this work could completely distinguish between beads and globules.
- Through variables importance measure analysis, it is concluded that Cu2O has a relatively high impact on bead classification, while some parameters like As-G, As-P, Dm-P, R-P, Fm-G, and P3-P have relatively low impacts on the prediction results of the model.
- More importantly, we cannot find much promise with this method that uses multiple metallurgical and morphological parameters proposed in this paper for distinguishing between CB and VB. It is confirmed that none of machine learning classifiers used in this paper combined with metallurgical analysis could do this work well.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hossain, M.D.; Hassan, M.K.; Akl, M.; Pathirana, S.; Rahnamayiezekavat, P.; Douglas, G.; Bhat, T.; Saha, S. Fire Behaviour of Insulation Panels Commonly Used in High-Rise Buildings. Fire 2022, 5, 81. [Google Scholar] [CrossRef]
- Silva-Junior, C.H.; Buna, A.T.M.; Bezerra, D.S.; Costa, O.S., Jr.; Santos, A.L.; Basson, L.O.D.; Santos, A.L.S.; Alvarado, S.T.; Almeida, C.T.; Freire, A.T.G.; et al. Forest Fragmentation and Fires in the Eastern Brazilian Amazon–Maranhão State, Brazil. Fire 2022, 5, 77. [Google Scholar] [CrossRef]
- Xie, D.; Wang, W.; Lv, S.; Deng, S. Visual and oxide analysis for identification of electrical fire scene. Forensic Sci. Int. 2018, 285, e21–e24. [Google Scholar] [CrossRef] [PubMed]
- Wright, S.A.; Loud, J.D.; Blanchard, R.A. Globules and Beads: What Do They Indicate About Small-Diameter Copper Conductors that Have Been Through a Fire? Fire Technol. 2015, 51, 1051–1070. [Google Scholar] [CrossRef]
- Henderson, R.; Manning, C.; Barnhill, S. Questions Concerning the use of Carbon Content to Identify “Cause” vs. “Result” Beads in Fire Investigations. Fire Arson Investig. 1998, 48, 26–27. [Google Scholar]
- Babrauskas, V. Fires due to electric arcing: Can ‘cause’ beads be distinguished from ‘victim’ beads by physical and chemical testing. In Proceedings of the Fire and Materials: Eighth International Conference, San Francisco, CA, USA, 27–28 January 2003. [Google Scholar]
- DeCost, B.L.; Holm, E.A. A computer vision approach for automated analysis and classification of microstructural image data. Comput. Mater. Sci. 2015, 110, 126–133. [Google Scholar] [CrossRef]
- Chowdhury, A.; Kautz, E.; Yener, B.; Lewis, D. Image driven machine learning methods for microstructure recognition. Comput. Mater. Sci. 2016, 123, 176–187. [Google Scholar] [CrossRef]
- Bangaru, S.S.; Wang, C.; Hassan, M.; Jeon, H.W.; Ayiluri, T. Estimation of the degree of hydration of concrete through automated machine learning based microstructure analysis—A study on effect of image magnification. Adv. Eng. Inform. 2019, 42, 100975. [Google Scholar] [CrossRef]
- Gupta, S.; Sarkar, J.; Kundu, M.; Bandyopadhyay, N.; Ganguly, S. Automatic recognition of SEM microstructure and phases of steel using LBP and random decision forest operator. Measurement 2020, 151, 107224. [Google Scholar] [CrossRef]
- Jain, P.; Coogan, S.C.P.; Subramanian, S.G.; Crowley, M.; Taylor, S.W.; Flannigan, M.D. A review of machine learning applications in wildfire science and management. Environ. Rev. 2020, 28, 478–505. [Google Scholar] [CrossRef]
- Jiao, Z.; Hu, P.; Xu, H.; Wang, Q. Machine learning and deep learning in chemical health and safety: A systematic review of techniques and applications. ACS Chem. Health Saf. 2020, 27, 316–334. [Google Scholar] [CrossRef]
- Al-Kahlout, M.M.; Ghaly, A.M.A.; Mudawah, D.Z.; Abu-Naser, S.S. Neural network approach to predict forest fires using meteorological data. Int. J. Acad. Eng. Res. IJAER 2020, 4, 68–72. [Google Scholar]
- Chen, Y.; Xu, W.; Zuo, J.; Yang, K. The fire recognition algorithm using dynamic feature fusion and IV-SVM classifier. Clust. Comput. 2019, 22, 7665–7675. [Google Scholar] [CrossRef]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef]
- Bradley, P.S.; Mangasarian, O.L. Massive data discrimination via linear support vector machines. Optim. Methods Softw. 2000, 13, 1–10. [Google Scholar] [CrossRef]
- Wang, S.; Liu, S.; Che, X.; Wang, Z.; Zhang, J.; Kong, D. Recognition of polycyclic aromatic hydrocarbons using fluorescence spectrometry combined with bird swarm algorithm optimization support vector machine. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 224, 117404. [Google Scholar] [CrossRef]
- Yu, Z.; Qin, L.; Chen, Y.; Parmar, M. Stock price forecasting based on LLE-BP neural network model. Phys. A Stat. Mech. Its Appl. 2020, 553, 124197. [Google Scholar] [CrossRef]
- Wang, S.; Wu, T.; Shao, T.; Peng, Z. Integrated model of BP neural network and CNN algorithm for automatic wear debris classification. Wear 2019, 426–427, 1761–1770. [Google Scholar] [CrossRef]
- Liu, H.; Liu, J.; Wang, Y.; Xia, Y.; Guo, Z. Identification of grouting compactness in bridge bellows based on the BP neural network. Structures 2021, 32, 817–826. [Google Scholar] [CrossRef]
- Rokach, L.; Schclar, A.; Itach, E. Ensemble methods for multi-label classification. Expert Syst. Appl. 2014, 41, 7507–7523. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Pham, B.T.; Nguyen, M.D.; Nguyen-Thoi, T.; Ho, L.S.; Koopialipoor, M.; Quoc, N.K.; Armaghani, D.J.; Van Le, H. A novel approach for classification of soils based on laboratory tests using Adaboost, Tree and ANN modeling. Transp. Geotech. 2021, 27, 100508. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, X.; Huang, X.; Yin, X. Prediction model of rock mass class using classification and regression tree integrated AdaBoost algorithm based on TBM driving data. Tunn. Undergr. Space Technol. 2020, 106, 103595. [Google Scholar] [CrossRef]
- Prabhakar, S.K.; Rajaguru, H. Alcoholic EEG signal classification with Correlation Dimension based distance metrics approach and Modified Adaboost classification. Heliyon 2020, 6, e05689. [Google Scholar] [CrossRef]
- Yousaf, M.S.; Ahmad, I.; Khurshid, A.; Ikram, M. Machine assisted classification of chicken, beef and mutton tissues using optical polarimetry and Bagging model. Photodiagn. Photodyn. Ther. 2020, 31, 101779. [Google Scholar] [CrossRef]
- Ashour, A.S.; Eissa, M.M.; Wahba, M.A.; Elsawy, R.A.; Elgnainy, H.F.; Tolba, M.S.; Mohamed, W.S. Ensemble-based bag of features for automated classification of normal and COVID-19 CXR images. Biomed. Signal Process. Control 2021, 68, 102656. [Google Scholar] [CrossRef]
- Louzada, F.; Anacleto-Junior, O.; Candolo, C.; Mazucheli, J. Poly-bagging predictors for classification modelling for credit scoring. Expert Syst. Appl. 2011, 38, 12717–12720. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Roshan, E.; Kattan, M. Random forest swarm optimization-based for heart diseases diagnosis. J. Biomed. Inform. 2021, 115, 103690. [Google Scholar]
- Guo, Z.; Yu, B.; Hao, M.; Wang, W.; Jiang, Y.; Zong, F. A novel hybrid method for flight departure delay prediction using Random Forest Regression and Maximal Information Coefficient. Aerosp. Sci. Technol. 2021, 116, 106822. [Google Scholar] [CrossRef]
- Jadhav, D.A. An enhanced and secured predictive model of Ada-Boost and Random-Forest techniques in HCV detections. Mater. Today Proc. 2021, 51, 186–195. [Google Scholar] [CrossRef]
- Deng, J.; Li, Y.; Lü, H.-F.; Wang, W.-F.; Bai, L.; Shu, C.-M. Metallurgical analysis of the ‘cause’arc beads pattern characteristics under different short-circuit currents. J. Loss Prev. Process. Ind. 2020, 68, 104339. [Google Scholar] [CrossRef]
- Yu, Z.; Chen, S.; Deng, J.; Xu, X.; Wang, W. Microstructural characteristics of arc beads with overcurrent fault in the fire scene. Materials 2020, 13, 4521. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Y.; Gao, Y.; Sun, J.; Lyu, H.-F.; Yu, T.; Yang, S.; Wang, Y. Analysis of overload induced arc formation and beads characteristics in a residential electrical cable. Fire Saf. J. 2022, 131, 103626. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, T.; Su, G.; Li, C.; Zhao, F.; Mi, W. Microstructure and component analysis of glowing contacts in electrical fire investigation. Eng. Fail. Anal. 2022, 140, 106539. [Google Scholar] [CrossRef]
- Liang, W.; Wang, G.; Ning, X.; Zhang, J.; Li, Y.; Jiang, C.; Zhang, N. Application of BP neural network to the prediction of coal ash melting characteristic temperature. Fuel 2020, 260, 116324. [Google Scholar] [CrossRef]
- Zhang, Y.-G.; Tang, J.; Liao, R.-P.; Zhang, M.-F.; Zhang, Y.; Wang, X.-M.; Su, Z.-Y. Application of an enhanced BP neural network model with water cycle algorithm on landslide prediction. Stoch. Environ. Res. Risk Assess. 2021, 35, 1273–1291. [Google Scholar] [CrossRef]
- Chen, Y. Prediction algorithm of PM2.5 mass concentration based on adaptive BP neural network. Computing 2018, 100, 825–838. [Google Scholar] [CrossRef]
- Babrauskas, V. Arc beads from fires: Can ‘cause’ beads be distinguished from ‘victim’ beads by physical or chemical testing? J. Fire Prot. Eng. 2004, 14, 125–147. [Google Scholar] [CrossRef]

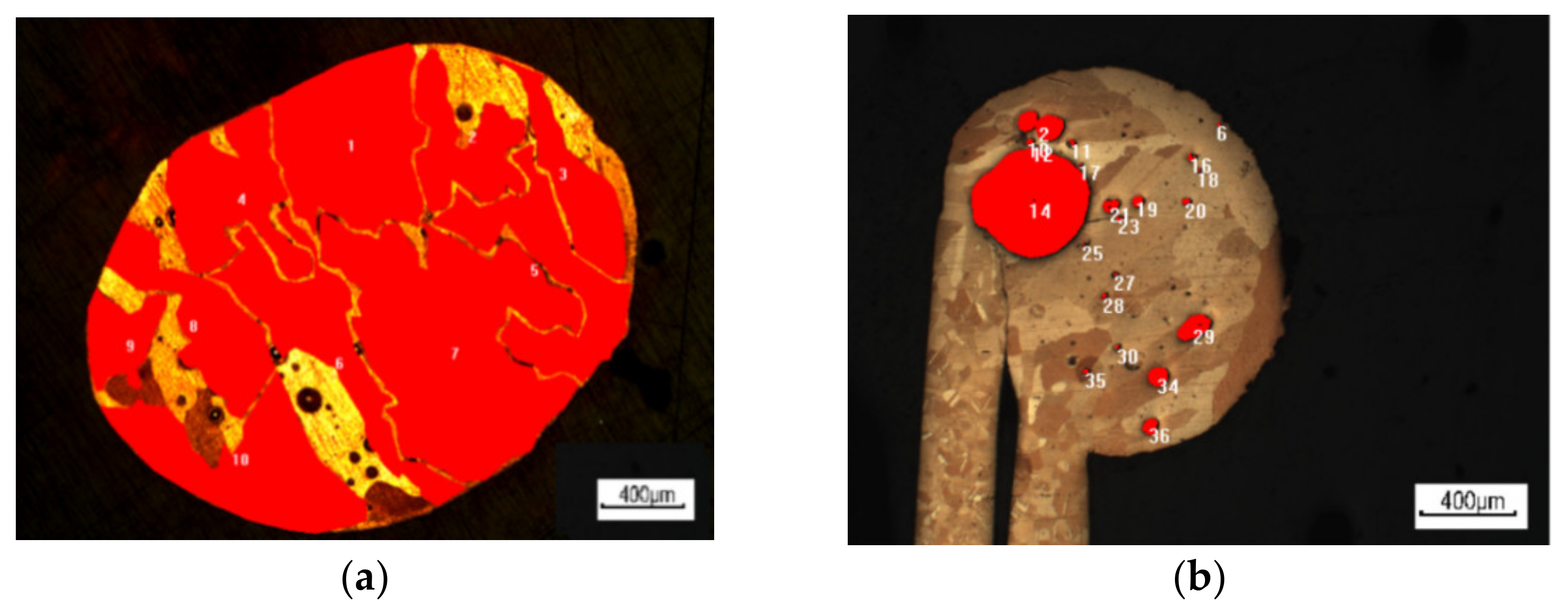







| No. | Type | Item | Code | Implication |
|---|---|---|---|---|
| 1 | Parameters of grains | Area | Ar-G | Reports the area of each object (minus any holes) |
| 2 | Angle | An-G | Reports the angle between the vertical axis and the major axis of the ellipse equivalent to the object (i.e., an ellipse with the same area, first and second degree moments), where 0° ≤ Angle° ≤ 180° | |
| 3 | Aspect | As-G | Reports the ratio between the major axis and the minor axis of the ellipse equivalent to the object (i.e., an ellipse with the same area, first and second degree moments), as determined by Major Axis/Minor Axis. Aspect is always ≥1 | |
| 4 | Diameter (mean) | Dm-G | Reports the average length of the diameters measured at two degree intervals joining two outline points and passing through the centroid | |
| 5 | Feret (mean) | Fm-G | Reports the shortest caliper (feret) length | |
| 6 | Fractal Dimension | FD-G | Reports the fractal dimension of the object’s outline | |
| 7 | Roundness | R-G | Reports the roundness of each object, as determined by the following formula: (perimeter2)/(4 × pi × area). Circular objects will have a roundness = 1; other shapes will have a roundness > 1 | |
| 8 | Perimeter3 | P3-G | Reports a corrected chain code length of the object perimeter, not including holes | |
| 9 | Parameters of poles | Area | Ar-P | The same as before |
| 10 | Angle | An-P | The same as before | |
| 11 | Aspect | As-P | The same as before | |
| 12 | Diameter (mean) | Dm-P | The same as before | |
| 13 | Feret (mean) | Fm-P | The same as before | |
| 14 | Fractal Dimension | FD-P | The same as before | |
| 15 | Roundness | R-P | The same as before | |
| 16 | Perimeter3 | P3-P | The same as before | |
| 17 | Cu2O Content | Cu2O Ratio | Cu2O | The proportion of Cu2O after content binary extraction and measurement in polarized-field under the magnification of 50× |
| Model | Parameter | Optional Values | N |
|---|---|---|---|
| BP neutral network | Number of hidden layers | 1, 2, 3 | 72 |
| Hidden layer size | [10 20 30] | ||
| Train function | traingd, traingda, traingdm, traingdx | ||
| Transfer function | logsig, tansig | ||
| SVM | Kernel function | poly, linear, RBF, Sigmoid | 884 |
| c | 2−2, 2−1.5, 2−1, 2−0.5, 1, 20.5, 21, 21.5, 22, 22.5, 23, 23.5, 24 | ||
| g | 2−4, 2−3.5, 2−3, 2−2.5,2−2, 2−1.5, 2−1, 2−0.5, 1, 20.5, 21, 21.5, 22, 22.5,23, 23.5, 24 | ||
| Bagging | NumLearningCycles | 1–200 | 200 |
| AdaBoost | NumLearningCycles | 1–200 | 200 |
| Random forest | ntree | 50, 100, 150, 200, 300, 400, 500, 600, 700, 1000 | 50 |
| mtry | 1, 2, 3, 4, 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Chen, T.; Wang, Z.; Gao, Z.; Mi, W. Beads and Globules from Fires: Can They Be Differentiated through Metallurgical Analysis Based on Machine Learning Algorithms? Fire 2022, 5, 123. https://doi.org/10.3390/fire5040123
Wang G, Chen T, Wang Z, Gao Z, Mi W. Beads and Globules from Fires: Can They Be Differentiated through Metallurgical Analysis Based on Machine Learning Algorithms? Fire. 2022; 5(4):123. https://doi.org/10.3390/fire5040123
Chicago/Turabian StyleWang, Guanning, Tao Chen, Zhidong Wang, Zishan Gao, and Wenzhong Mi. 2022. "Beads and Globules from Fires: Can They Be Differentiated through Metallurgical Analysis Based on Machine Learning Algorithms?" Fire 5, no. 4: 123. https://doi.org/10.3390/fire5040123
APA StyleWang, G., Chen, T., Wang, Z., Gao, Z., & Mi, W. (2022). Beads and Globules from Fires: Can They Be Differentiated through Metallurgical Analysis Based on Machine Learning Algorithms? Fire, 5(4), 123. https://doi.org/10.3390/fire5040123





