Investigation of the Temperature Beneath Curved Tunnel Ceilings Induced by Fires with Natural Ventilation
Abstract
:1. Introduction
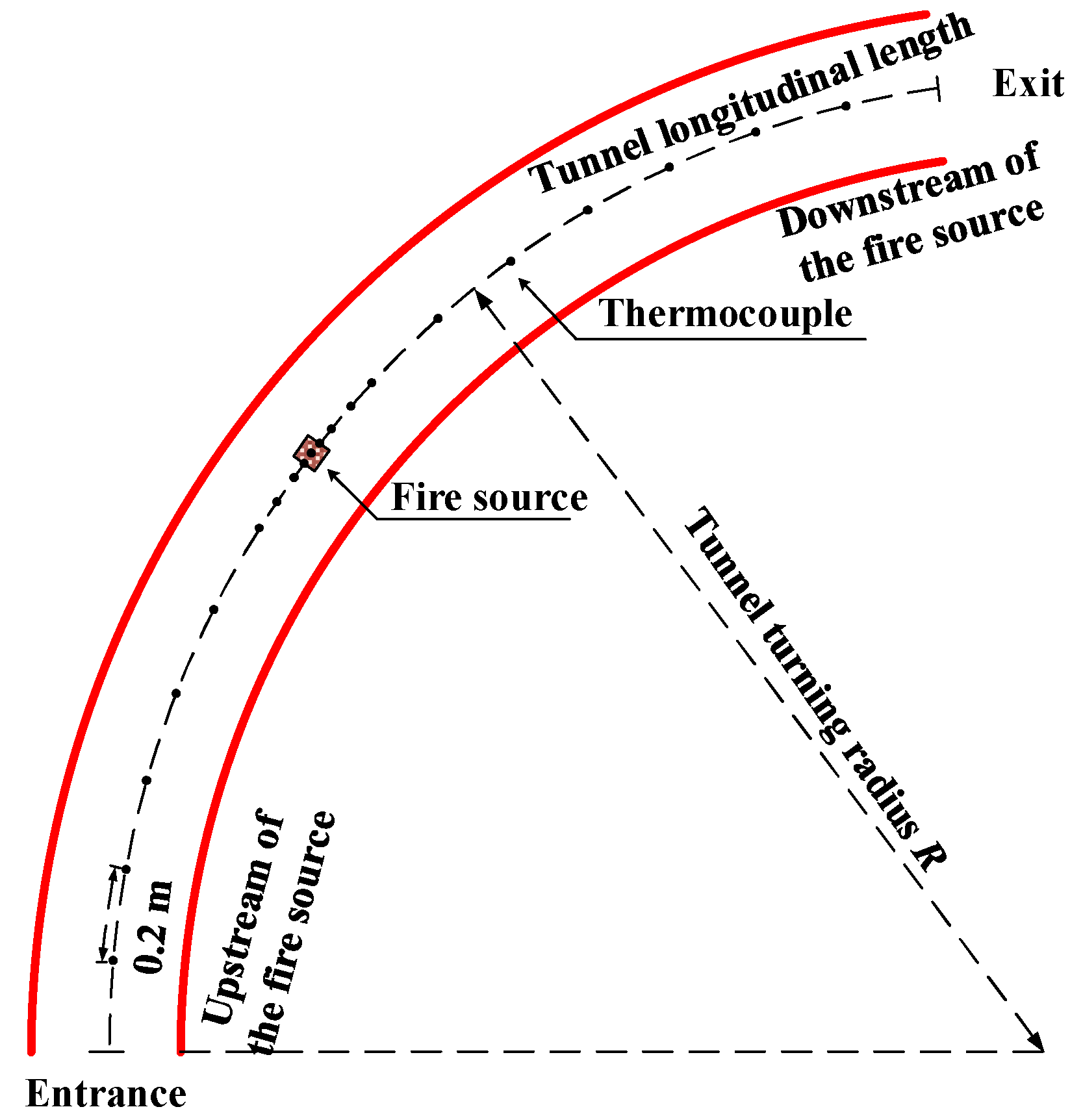
2. Experimental Setup
2.1. Small-Scale Curved Tunnel
2.2. Experimental Scenarios
3. Results and Discussion
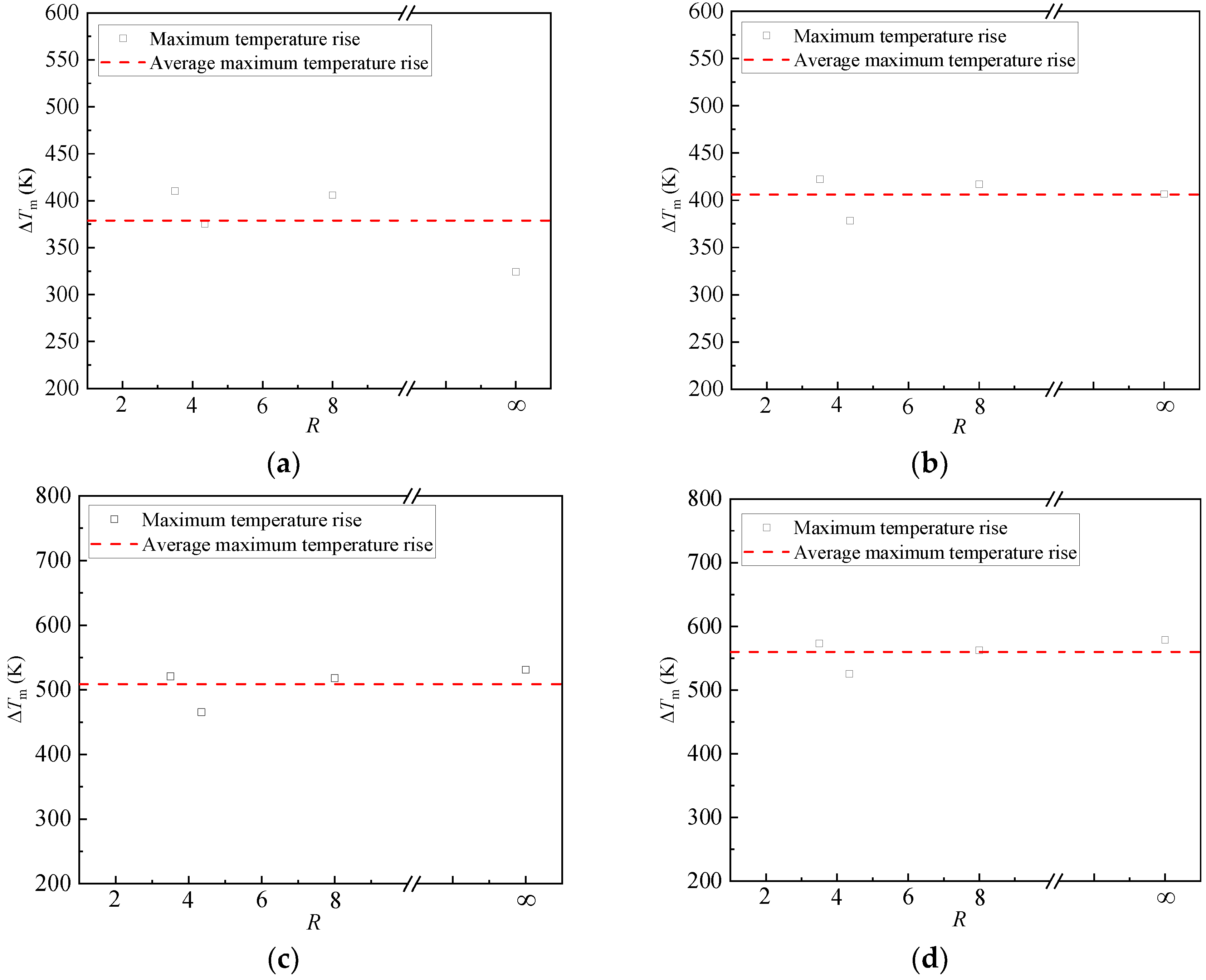
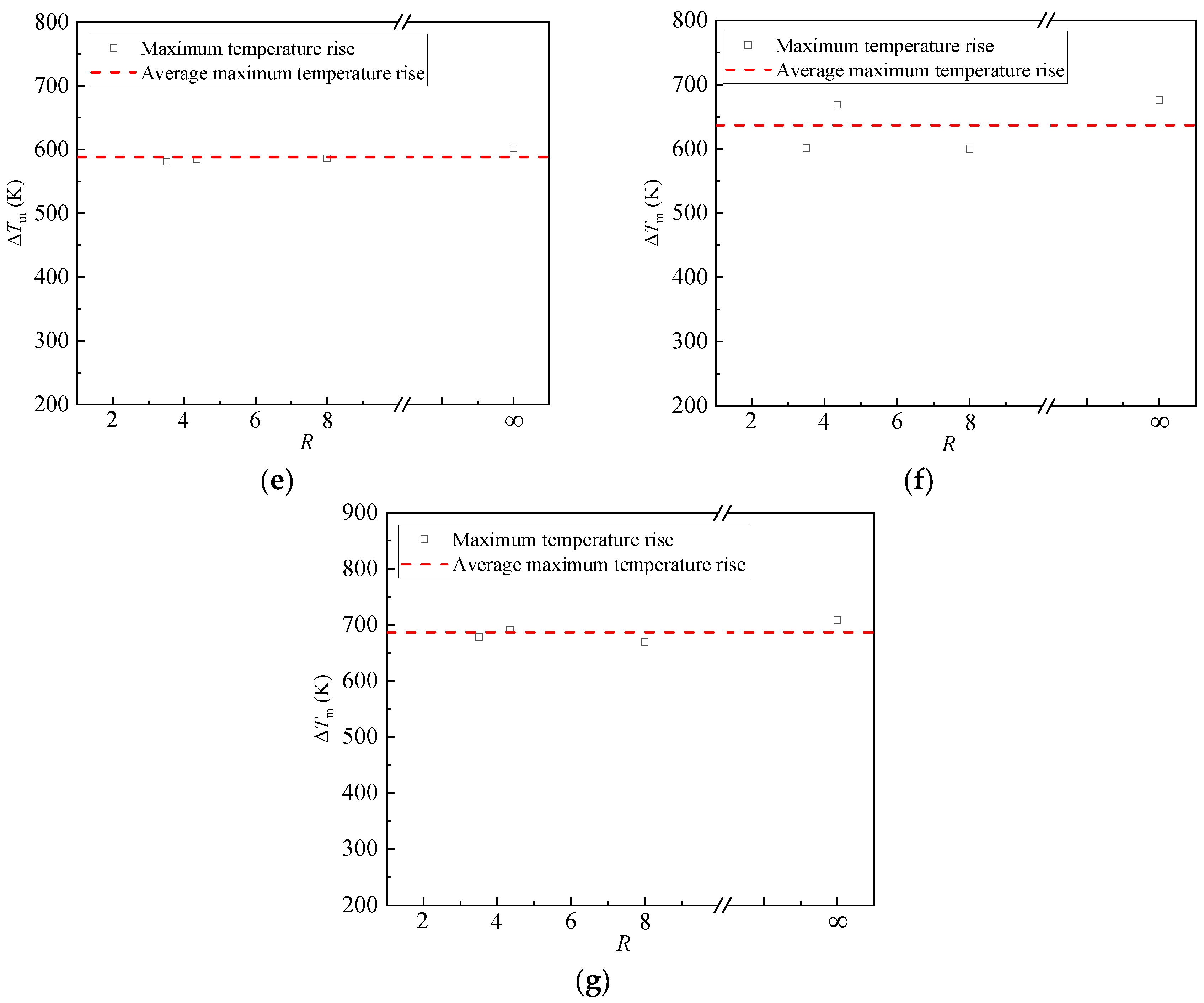
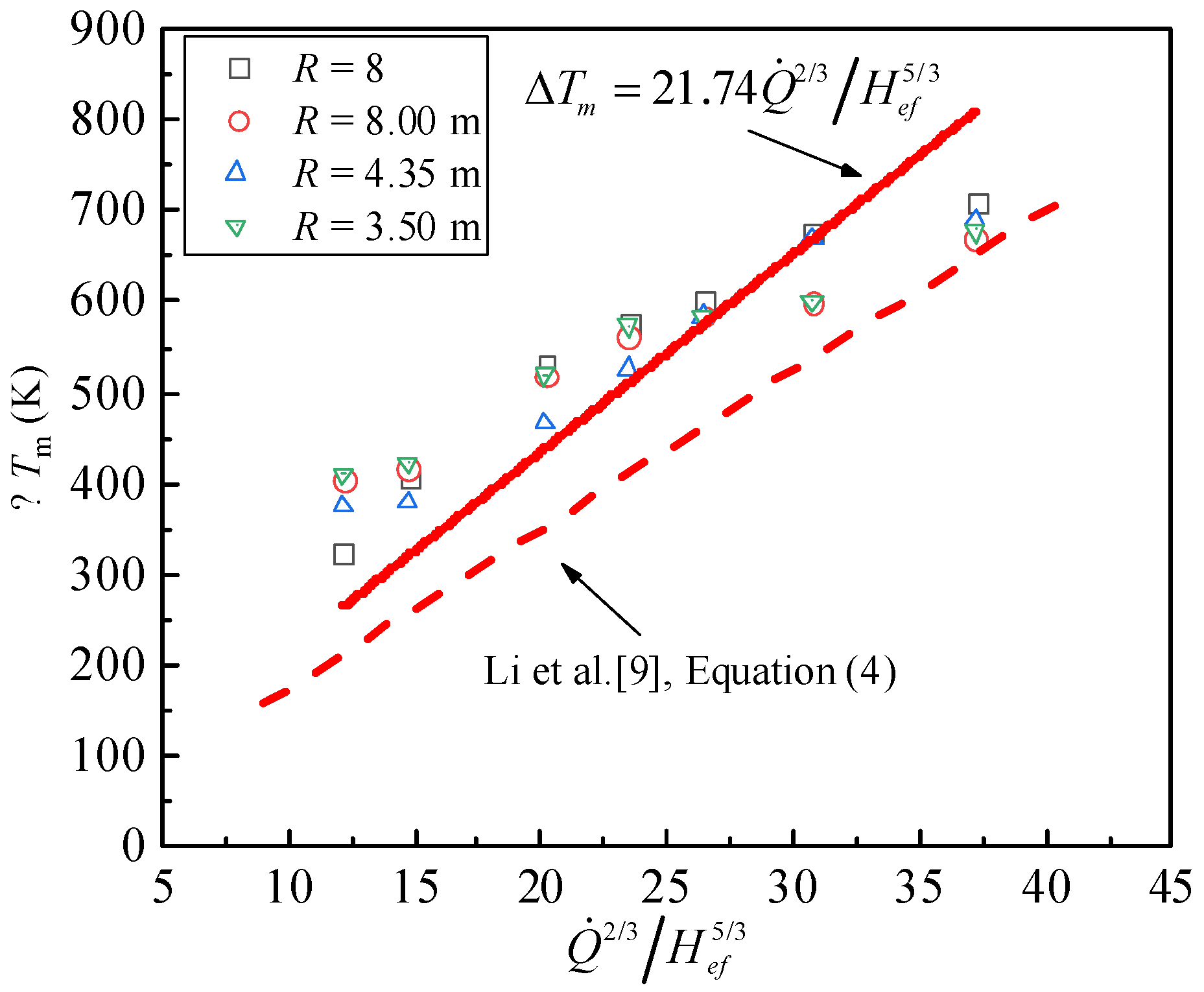
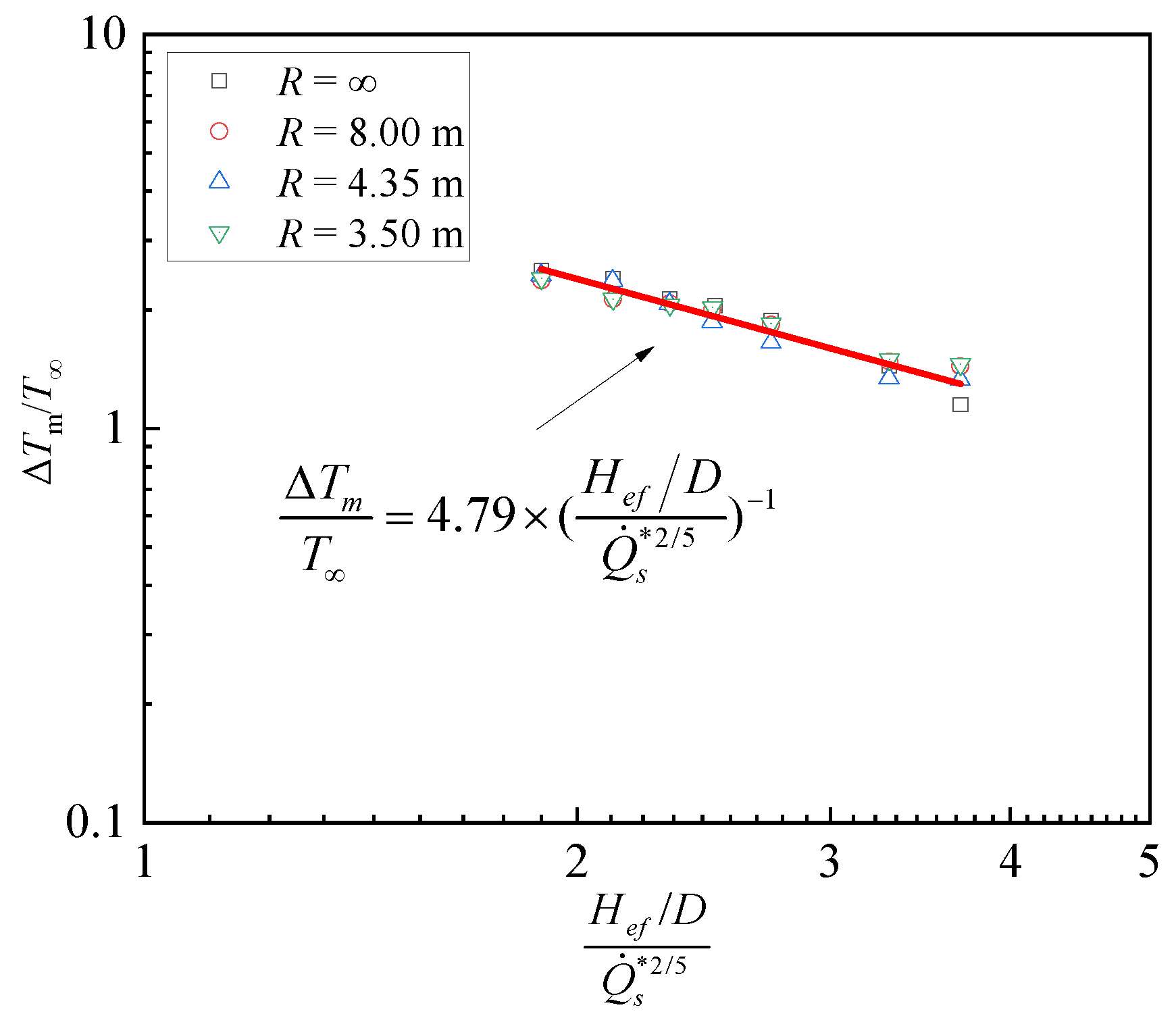
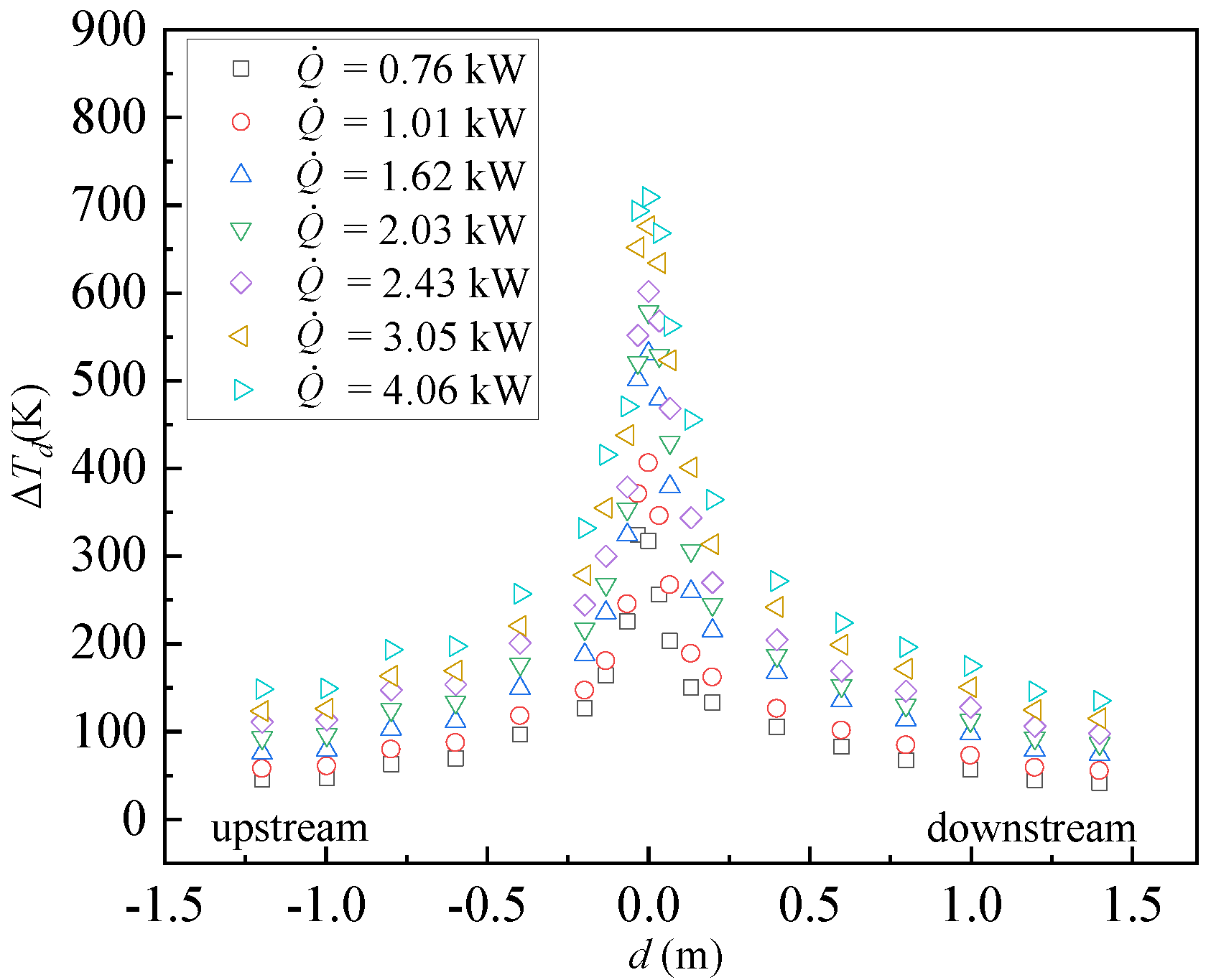
3.1. Variations in Maximum Temperature
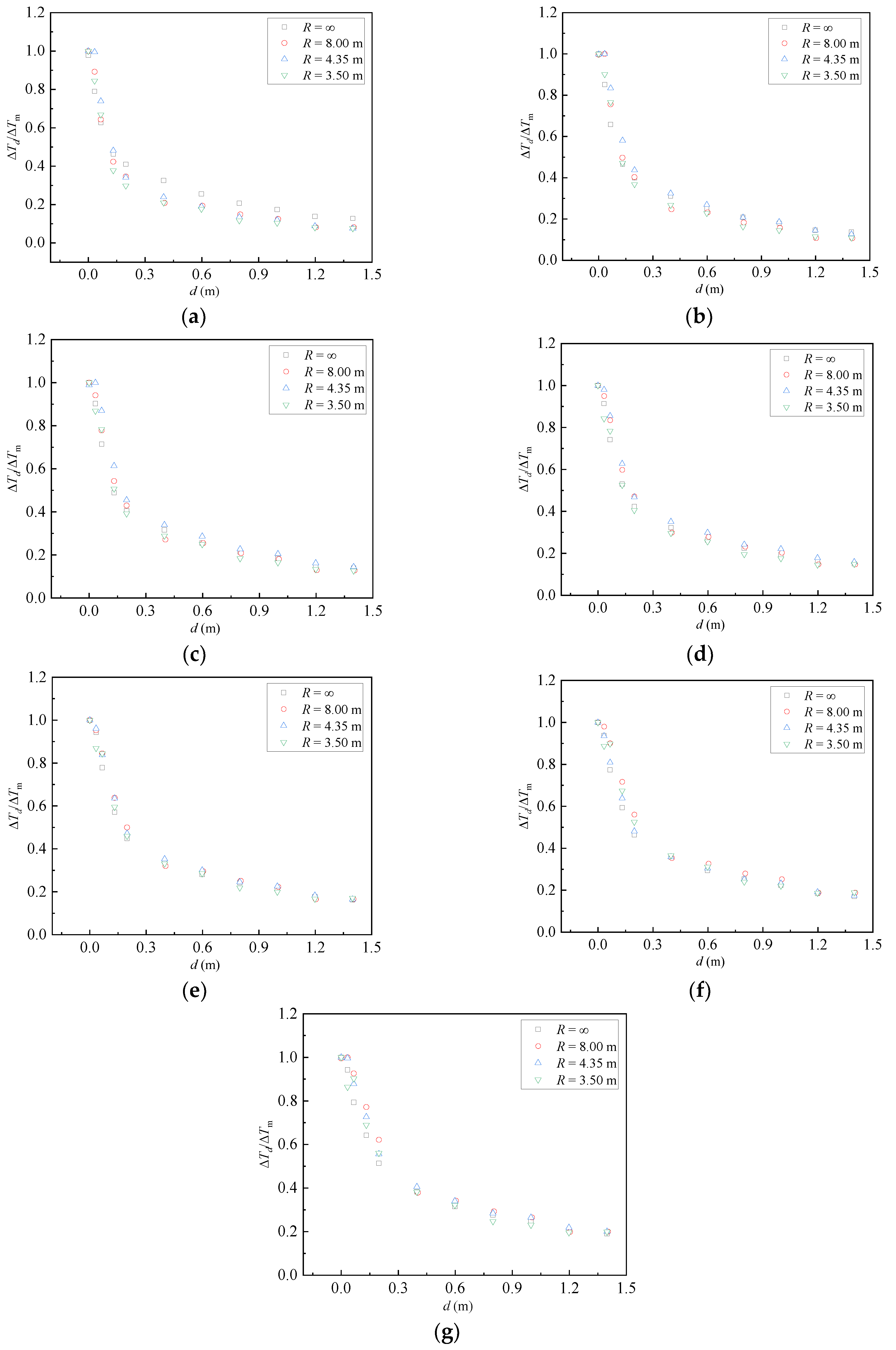
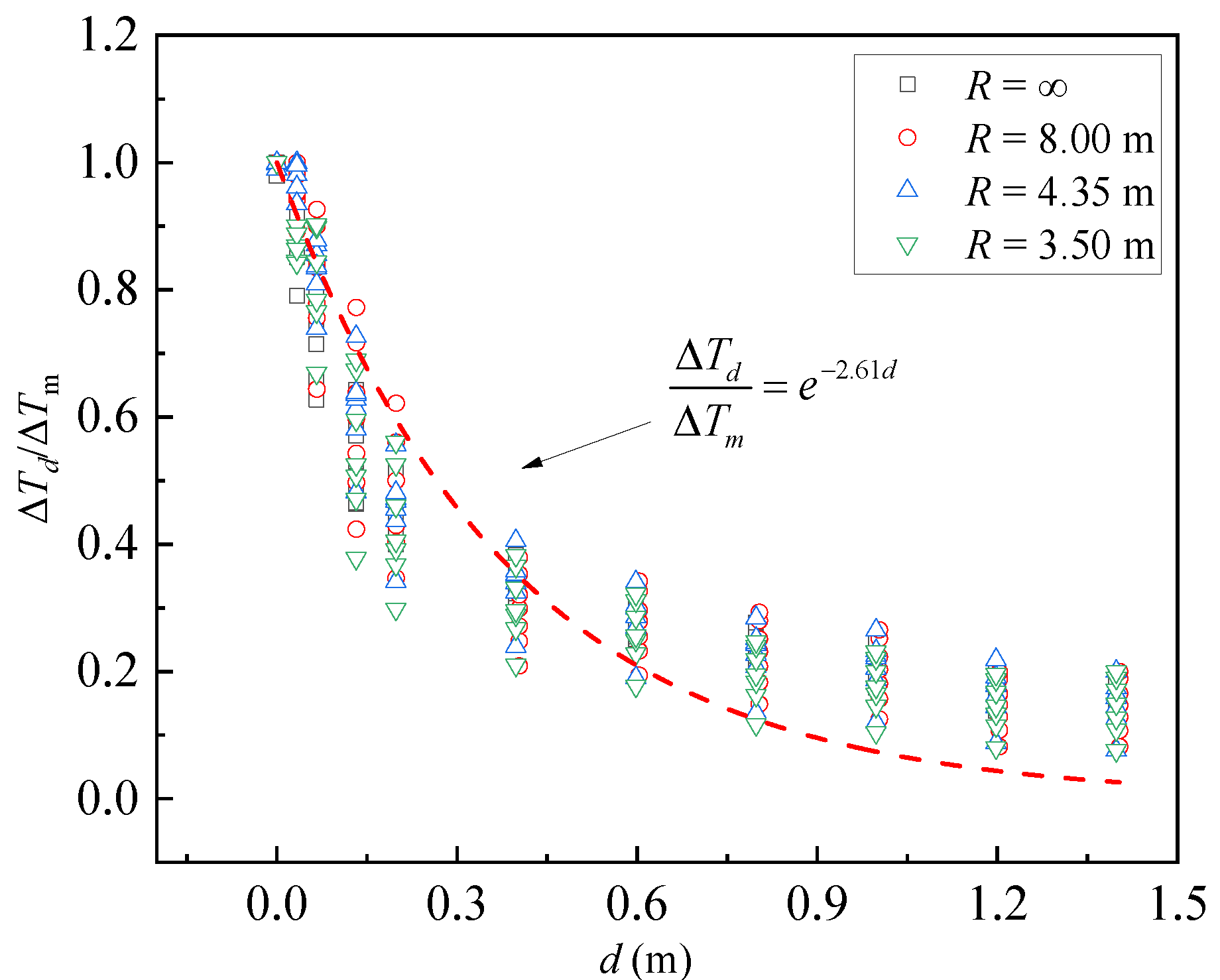
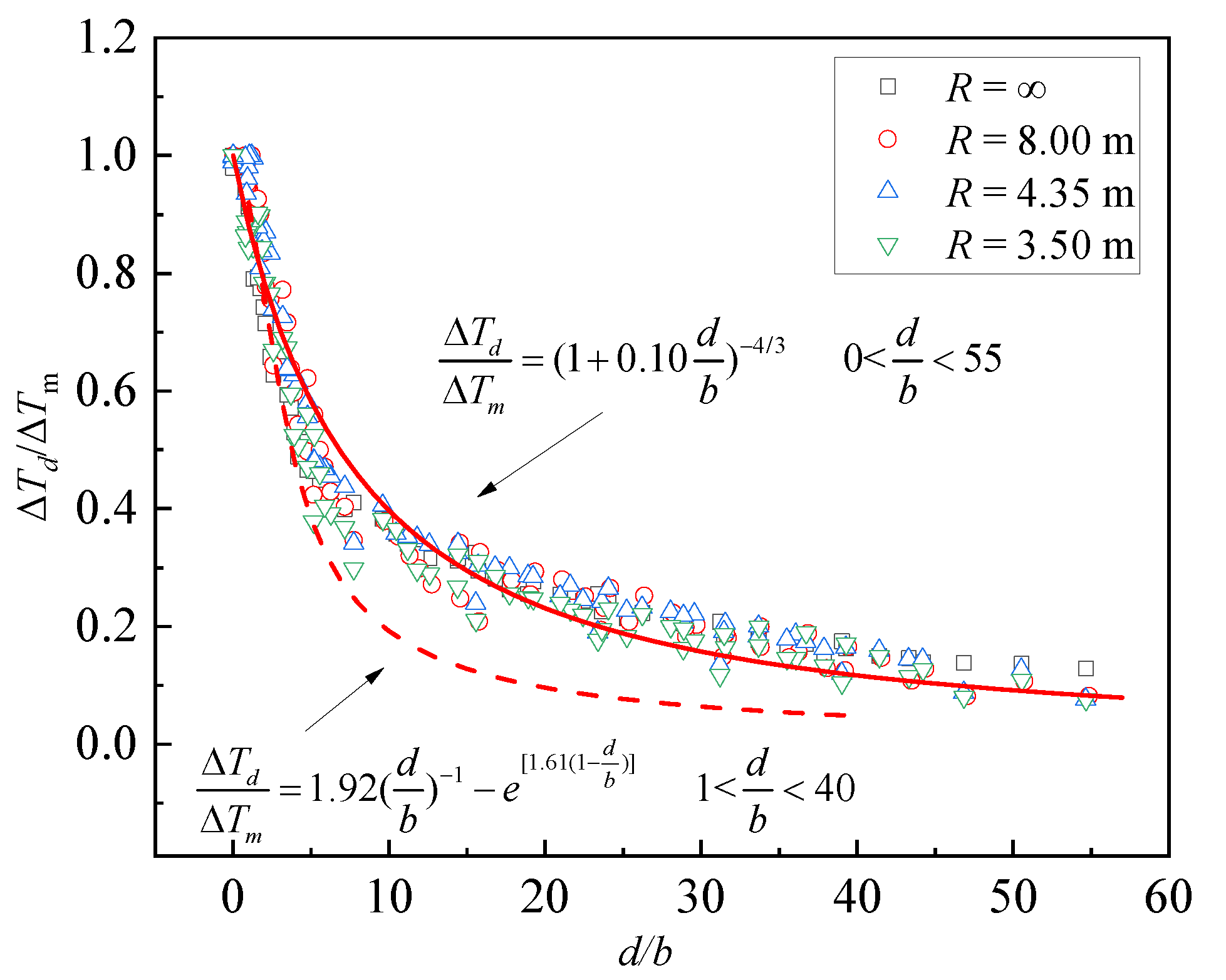
3.2. The Longitudinal Attenuation of Temperature
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Du, T.; Yang, D.; Peng, S.N.; Xiao, Y.M. A method for design of smoke control of urban traffic link tunnel (UTLT) using longitudinal ventilation. Tunn. Undergr. Space Technol. 2015, 48, 35–42. [Google Scholar] [CrossRef]
- Ren, F.; Shi, C.L.; Li, J.; Che, H.L.; Xu, X. Numerical study on the flow characteristics and smoke temperature evolution under double fires condition with a metro train in tunnel. Tunn. Undergr. Space Technol. 2021, 114, 104553. [Google Scholar] [CrossRef]
- Zhang, X.C.; Hu, L.H.; Zhu, W.; Zhang, X.L.; Yang, L.Z. Flame extension length and temperature profile in thermal impinging flow of buoyant round jet upon a horizontal plate. Appl. Therm. Eng. 2014, 73, 15–22. [Google Scholar] [CrossRef]
- Du, T.; Yang, D.; Peng, S.N.; Liu, Y.L.; Xiao, Y.M. Performance evaluation of longitudinal and transverse ventilation for thermal and smoke control in a looped urban traffic link tunnel. Appl. Therm. Eng. 2016, 96, 490–500. [Google Scholar] [CrossRef]
- Tang, F.; He, Q.; Chen, L.F.; Li, P.C. Experimental study on maximum smoke temperature beneath the ceiling induced by carriage fire in a tunnel with ceiling smoke extraction. Sustain. Cities Soc. 2019, 44, 40–45. [Google Scholar] [CrossRef]
- Alpert, R.L. Calculation of response time of ceiling-mounted fire detectors. Fire Technol. 1972, 8, 181–195. [Google Scholar] [CrossRef]
- Heskestad, G.; Delichatsios, M.A. The initial convective flow in fire. Symp. Int. Combust. 1979, 17, 1113–1123. [Google Scholar] [CrossRef]
- Delichatsios, M.A. The flow of fire gases under a beamed ceiling. Combust. Flame 1981, 43, 1–10. [Google Scholar] [CrossRef]
- Li, Y.Z.; Lei, B.; Ingason, H. The maximum temperature of buoyancy-driven smoke flow beneath the ceiling in tunnel fires. Fire Saf. J. 2011, 46, 204–210. [Google Scholar] [CrossRef]
- Hu, L.H.; Huo, R.; Li, Y.Z.; Wang, H.B.; Chow, W.K. Full-scale burning tests on studying smoke temperature and velocity along a corridor. Tunn. Undergr. Space Technol. 2005, 20, 223–229. [Google Scholar] [CrossRef]
- Li, L.M.; Cheng, X.D.; Wang, X.G.; Zhang, H.P. Temperature distribution of fire-induced flow along tunnels under natural ventilation. J. Fire Sci. 2012, 30, 121–136. [Google Scholar] [CrossRef]
- Huang, Y.B.; Li, Y.F.; Dong, B.Y.; Li, J.M.; Liang, Q. Numerical investigation on the maximum ceiling temperature and longitudinal decay in a sealing tunnel fire. Tunn. Undergr. Space Technol. 2018, 72, 120–130. [Google Scholar] [CrossRef]
- Zhang, X.L.; Lin, Y.J.; Shi, C.L.; Zhang, J.P. Numerical simulation on the maximum temperature and smoke back-layering length in a tilted tunnel under natural ventilation. Tunn. Undergr. Space Technol. 2021, 107, 103661. [Google Scholar] [CrossRef]
- Zhang, T.H.; Wang, G.Y.; Hu, H.H.; Huang, Y.D.; Zhu, K.; Wu, K. Study on temperature decay characteristics of fire smoke backflow layer in tunnels with wide-shallow cross-section. Tunn. Undergr. Space Technol. 2021, 112, 103874. [Google Scholar] [CrossRef]
- Tang, F.; Li, L.J.; Chen, W.K.; Tao, C.F.; Zhan, Z. Studies on ceiling maximum thermal smoke temperature and longitudinal decay in a tunnel fire with different transverse gas burner locations. Appl. Therm. Eng. 2017, 110, 1674–1681. [Google Scholar] [CrossRef]
- Tang, F.; Chen, L.; Chen, Y.H.; Pang, H.P. Experimental study on the effect of ceiling mechanical smoke extraction system on transverse temperature decay induced by ceiling jet in the tunnel. Int. J. Therm. Sci. 2020, 152, 106294. [Google Scholar] [CrossRef]
- Ingason, H.; Li, Y.Z. Model scale tunnel fire tests with longitudinal ventilation. Fire Saf. J. 2010, 45, 371–384. [Google Scholar] [CrossRef]
- Chen, L.; Tang, F. Experimental study on the longitudinal temperature decay beneath ceiling in ventilated tunnel fire. J. Therm. Anal. Calorim. 2020, 139, 3179–3184. [Google Scholar] [CrossRef]
- Tao, L.L.; Zeng, Y.H.; Li, J.; Yang, C.C.; Fang, Y.; Li, B.J. Study on the maximum temperature and temperature decay in single-side centralized smoke exhaust tunnel fires. Int. J. Therm. Sci. 2022, 172, 107277. [Google Scholar] [CrossRef]
- Tang, F.; Cao, Z.L.; Chen, Q.; Meng, N.; Wang, Q.; Fan, C.G. Effect of blockage-heat source distance on maximum temperature of buoyancy-induced smoke flow beneath ceiling in a longitudinal ventilated tunnel. Int. J. Heat Mass Transf. 2017, 109, 683–688. [Google Scholar] [CrossRef]
- Zhang, S.G.; Yang, H.; Yao, Y.Z.; Zhu, K.; Zhou, Y.; Cheng, X.D. Numerical Investigation of Back-Layering Length and Critical Velocity in Curved Subway Tunnels with Different Turning Radius. Fire Technol. 2017, 53, 1465–1793. [Google Scholar] [CrossRef]
- Wang, F.; Wang, M.N.; Carvel, R.; Wang, Y. Numerical study on fire smoke movement and control in curved road tunnels. Tunn. Undergr. Space Technol. 2017, 67, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.S.; Zhou, D.M.; Tao, H.W.; Zhang, X.C.; Hu, W.B. Investigation of critical velocity in curved tunnel under the effects of different fire locations and turning radiuses. Tunn. Undergr. Space Technol. 2022, 126, 104553. [Google Scholar] [CrossRef]
- Tang, F.; He, Q.; Sun, X.P.; Jiang, L.; Hu, P.; Hu, L.H. Experimental study of carriage fire in a tunnel: Evolution of flame geometry characteristics under relative strong crosswinds. Proc. Combust. Inst. 2021, 38, 4963–4970. [Google Scholar] [CrossRef]
- Li, Y.S.; Zhang, X.L.; Sun, X.P.; Zhu, N. Maximum temperature of ceiling jet flow in longitudinal ventilated tunnel fires with various distances between fire source and cross-passage. Tunn. Undergr. Space Technol. 2021, 113, 103953. [Google Scholar] [CrossRef]
- Hu, L.H.; Wang, Q.; Tang, F.; Delichatsios, M.A.; Zhang, X.C. Axial temperature profile in vertical buoyant turbulent jet fire in a reduced pressure atmosphere. Fuel 2013, 106, 779–786. [Google Scholar] [CrossRef]
- Heskestad, G.; Hamada, T. Ceiling Jets of Strong Fire Plumes. Fire Saf. J. 1993, 21, 69–82. [Google Scholar] [CrossRef]
- He, L.; Xu, Z.S.; Markert, F.; Zhao, J.M.; Xie, E.; Liu, Q.L.; Fan, C.G. Ceiling jet velocity during the whole process of fire development in a tunnel. J. Wind Eng. Ind. Aerodyn. 2021, 212, 104588. [Google Scholar] [CrossRef]


| Scenarios No. | Fire Heat Release Rates (kW) | Tunnel Turning Radius R (m) |
|---|---|---|
| 1–4 | 0.76 | 3.5, 4.35, 8, ∞ |
| 5–8 | 1.01 | |
| 9–12 | 1.62 | |
| 13–16 | 2.03 | |
| 17–20 | 2.43 | |
| 21–24 | 3.05 | |
| 25–28 | 4.06 |
| Zone | κ | C | η |
|---|---|---|---|
| Continuous flame | 6.9 | 0.9 | 1/2 |
| Intermittent flame | 1.9 | 0.9 | 0 |
| Buoyant plume | 1.1 | 0.9 | −1/3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, H.; Xu, Z.; Zhou, D. Investigation of the Temperature Beneath Curved Tunnel Ceilings Induced by Fires with Natural Ventilation. Fire 2022, 5, 90. https://doi.org/10.3390/fire5040090
Tao H, Xu Z, Zhou D. Investigation of the Temperature Beneath Curved Tunnel Ceilings Induced by Fires with Natural Ventilation. Fire. 2022; 5(4):90. https://doi.org/10.3390/fire5040090
Chicago/Turabian StyleTao, Haowen, Zhisheng Xu, and Dongmei Zhou. 2022. "Investigation of the Temperature Beneath Curved Tunnel Ceilings Induced by Fires with Natural Ventilation" Fire 5, no. 4: 90. https://doi.org/10.3390/fire5040090
APA StyleTao, H., Xu, Z., & Zhou, D. (2022). Investigation of the Temperature Beneath Curved Tunnel Ceilings Induced by Fires with Natural Ventilation. Fire, 5(4), 90. https://doi.org/10.3390/fire5040090






