1. Introduction
Fire remains an actual and important threat to humans and their infrastructure. It is estimated that 5000 fires ignite each day in the European Union, generating a yearly loss of €126 billion [
1]. They are a growing threat to building infrastructures as more and more of them are built to sustain the world population and economic growth. Many protection devices against indoor fires exist, most of them relying on a nozzle delivering a fluid onto the fire, be it water, gas or foam. Halon-based extinguishing agents such as Halon 1301 have been used extensively in the past due to their efficiency to suppress fires, but their role in the destruction of the ozone layer has led to their ban by the Montreal Protocol in 1989 [
2]. Since then, research on fire safety has focused on finding efficient and environment friendly alternatives.
Water is a prime candidate as a clean extinguishing agent as it is an abundant, inexpensive, and non-dangerous product, and sprinklers are already a mature and common way to protect indoor infrastructures. Today 96% of fires in sprinkler-protected buildings are controlled or extinguished by the system on the premises [
3]. However, this technology is ineffective against oil and electrical fires and is not suitable to protect water sensitive infrastructure because the droplets’ diameter is too large and would cause further damage to the equipment. Water mists can provide a solution in this regard. They are defined by the NFPA 750 standard as a spray whose 99% of the flow-weighted cumulative volumetric distribution of water droplets have a diameter less than 1000
[
4]. Many experiments go well below this limit and produce ultra-fine water mists whose droplets diameter is less than 10
. As the median droplet diameter decreases, the suppression mechanisms change. Traditional sprinklers suppress the fire by cooling the burning material because their droplets are large enough to go through the flame without evaporating. Water mists also have a cooling effect but the heat extraction source comes from the evaporation of the small droplets. This extracted heat turns the water droplets to steam, which expands and smothers the fire through oxygen displacement. Finally, the numerous and fine droplets form an opaque mist and block the radiative effect of the fire. Cui and Liu detailed the research progress on suppression rules of water mists on different types of fires [
5]. Detailed reviews of fire suppression by sprinklers and water mists also exist [
6,
7].
Numerical studies have been conducted by fire safety engineers and researchers as both a cost-effective alternative to experiments and a way to explore new configurations on the fly. In their review, Shen et al. [
8] detail many applications of CFD (Computational Fluid Dynamics) codes ranging from enclosure, jet and pool fires, gas dispersion and different types of explosions. While numerous codes related to fire and smoke development exist, the same cannot be said about fire suppression codes. CFD codes related to fire suppression can be divided into two categories: CFD and zone codes. Zone codes divide the combustion compartment into two layers, a “hot” upper one made up of the smoke and a “cold” lower one. They are often used to determine the transport of the smoke layer and related phenomena such as ceiling-jet or the possibility of a backdraft. Such codes are CFAST (National Institute of Standards and Technology), MAGIC (Électricité de France) and OEIL (Direction Générale de l’Armement). Apart from CFAST, which is free and open source, the others are either commercial or closed. CFD codes describe localized behaviors and Lagrangian particles more accurately than zone codes. They are more complete and versatile tools, but the associated computation time is usually higher than a zone code. Example codes are FDS (National Institute of Standards and Technology), OpenFOAM (OpenCFD Ltd.), SMARTFIRE (Fire Safety Engineering Group) and KFX (DNV). FDS and OpenFOAM are free and open source whereas KFX and SMARTFIRE are commercial. CFD codes can then be used to highlight water mist suppression mechanisms through the study of the influence of droplet size because they can be modeled using the Lagrangian paradigm [
9,
10,
11]. Between the four presented CFD codes, the code FDS (Fire Dynamics Simulator) in its version 6.7.6 is used for the present work [
12]. It is a well-tested and recognized large eddy simulation (LES) code in the fire safety domain when it comes to fire suppression.
Regarding the type of indoor environments typically studied in the available literature, they come in plenty of sizes and conditions. In the last decade, a lot of research has been done to explore different configurations. The effects of a confined space on water mists performance [
13,
14] as well as room geometry [
15], ventilation conditions [
16], the presence of objects shielding the fire [
17], the type of burning material [
18], the presence of added chemicals to the water [
19] or the fire offset relative to the nozzle [
20] were studied. They conducted parametric studies capable of describing water mist mechanisms, but more could be learned from CFD using sensitivity analysis.
Sensitivity analysis provides information as to which parameter has the most influence on the variation of one output quantity related to a model. It can be local, where the sensitivity of the parameters are relative to a fixed set of parameters, or global, where the entire space formed from the ranges taken by the parameters is explored. It is already used extensively in other fields of research. In fire science, it was used to determine a wildfire propagation model sensitivity using the factorial design [
21] and a compartment fire scenario using global sensitivity analysis [
22]. Nonetheless, fire suppression by water aspersion has never been investigated using such techniques.
CFD is used to save time in the design process of experiments and monitor a virtually unlimited amount of quantities in space over time. In turn, experiments improve the understanding of the fire suppression science and the results are used to improve numerical models. In this regard, the authors think that the use of sensitivity analysis in conjunction with CFD can hasten the understanding of the process of fire suppression. It speeds up the process of designing experiments by providing quantitative information between parameters and quantities of interest. This quantitative information allows the fine tuning of future experiments because they provide a precise range of values to explore and numerical models through the use of constants. For CFD itself, sensitivity analysis can be used to validate numerical models and compare the results to experimental data. Irregularities between numerical models and experimental conditions, especially the limiting cases of the model, can be explored using sensitivity analysis and are a source of ideas for future experiments.
In this article, CFD capabilities to model a simple water mist geometry are studied by reproducing as well as possible the experimental conditions of a small compartment fire and water suppression obtained by Yinshui et al. [
23]. A series of sensitivity analyses will be conducted to demonstrate the feasibility and potential of this technique in the field of water mists fire safety and identify the most important parameters on water mists performances. Different sensitivity analysis techniques will be used and compared to determine which one provides the best results.
2. FDS Numerical Modeling
2.1. Governing Equations
The CFD code FDS solves a form of the Navier–Stokes equations of conservation of species, mass, momentum and energy appropriate for low-speed, thermally-driven flow with an emphasis on smoke and heat transport from fires. Turbulence is treated by means of LES. FDS uses the concept of “lumped species”, where a mixture of gas species for the air transport react together [
24], pages 7–10. For example, air is a lumped species that consists of nitrogen, oxygen, and trace amounts of water vapor and carbon dioxide. The lumped species mass fractions Z are linearly related to the primitive species mass fractions Y using a matrix multiplication. From there all conservation equations can be derived. From there, all conservation equations can be derived. Here is the transport equation for a lumped species:
The summation of Equation (
1) over all species gives the mass conservation equation:
Because of the low Mach number approximation, the internal energy and enthalpy may be related. The energy conservation equation can then be written in terms of the sensible enthalpy:
Finally, the momentum conservation equation can be written as:
Liquid droplets associated with water mist systems are modeled within the Lagrangian formalism [
24] pages 100–101. Drag and drag reduction phenomenon are accounted as well. The liquid droplets diameter is represented by a combination of log-normal and Rosin–Rammler distributions using the cumulative volume diameter:
The longitude angle of the initial droplet position between 0 and
is randomly chosen from a uniform distribution. The latitude between 0 and
is randomly selected from the following distribution:
with
controlling the peak of the distribution while
is the spread parameter. If
, the distribution is uniform. Each particle is assigned an initial velocity and direction normal to the position on the sphere. In its linearized form, the velocity of a particle is then dependent on the gas phase velocity, the gravitational acceleration and the drag force:
2.2. Computational Domain and Conditions
Before the different sensitivity analysis methods can be carry out, a FDS simulation must first be built. FDS 6.7.6 was used. Initial and boundary conditions were left at the default.
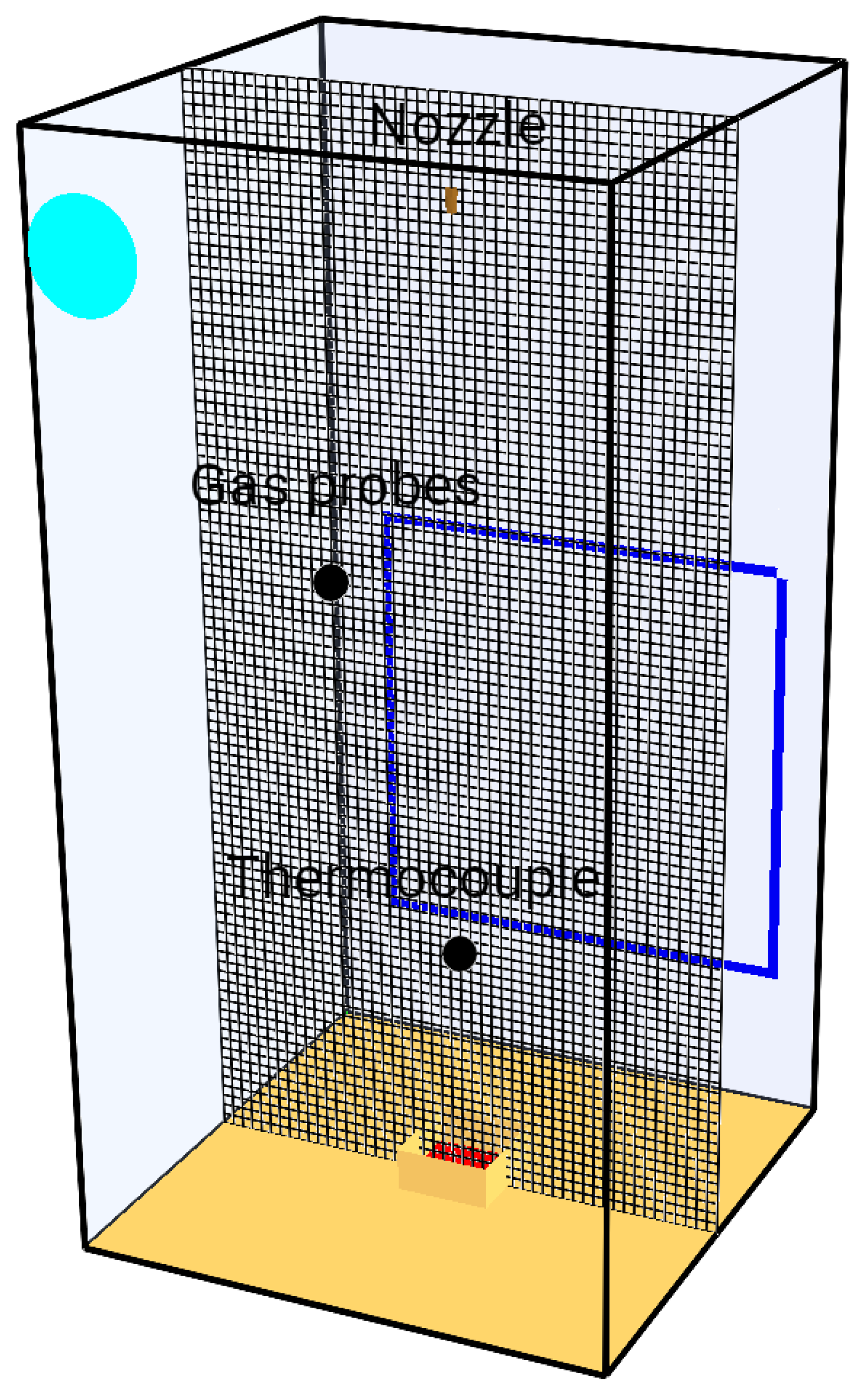
Figure 1 shows the domain considered in the present work, based on Yinshui et al.’s [
23] work. It consists of a 1 m × 1 m × 2 m compartment with acrylic walls. Ambient temperature is 20 °C. An exhaust vent (cyan) 20 cm in diameter is located at 1.80 m with an flow rate of 59
/
. Because the aforementioned authors did not notice a pressure drop, air leaks coming from the 0.8 m × 0.8 m door (blue) were added.
On the floor lies a 314
diesel pool fire with a heat release rate of 516
. For the diesel pool fire, no indication of heat release rate (HRR) or mass loss was given by Yinshui et al. [
23]. The standard t-squared model for the fire growth was therefore used. Dodecane was used as a surrogate as it has a close molecular formulation and is already well implemented in FDS. Fire growth rate for the dodecane is 0.047
[
25]. The rise to a full-grown fire is achieved after 19 s.
In this preliminary work, the heat release rate approach was chosen and a ramp was prescribed for the growth and decrease of this quantity. First, an increasing ramp with a t-squared growth was applied until the maximum HRR was achieved. The points of this increasing ramp were specified each second. The ramp was then held constant until the water mist activation to model the full-grown phase of the fire. Next, a decreasing ramp with a linear profile was applied to model the fire suppression until the HRR reached zero. The time between maximum and zero HRR was aligned on what was specified in the experimental work as fire extinguishing time, a time after which the water discharge was halted. Because the fire was extinguished, the HRR was assumed to be close to zero. Furthermore, because the extinguishing time of 3 s is fast, a simple linear profile was chosen for the decreasing HRR ramp.
Although the authors are aware of the shortcomings of this approach in terms of fire suppression accuracy, we believe it is still sufficiently accurate as a first approach to provide general information on the dynamics of fires and their extinction by water, the objective of this work being to test sensitivity analysis methods on water mist systems. The HRR model could be improved using empirical data or numerical techniques such as described by Jenft et al. [
9]. In their work, they relate the pyrolysis rate and the temperature of each fuel cell on the free burning phase. When water impinges a fuel cell, the computed temperature is used to force the corresponding pyrolysis rate. Another solution to further improve the numerical predictions would be to use a model based on the diesel characteristics and volume available rather than on the heat release rate, but it requires dedicated ignition.
A high-pressure water mist nozzle with an orifice of 1.0 mm, a solid spray angle of 60° and a flow rate of 2 is positioned 1.80 m above the fire. A thermocouple is located 0.45 m above the fire. Gas probes monitoring the O, CO and CO concentrations are situated at 1.30 m near the wall. An exhaust vent is located at 1.80 m from the ground. Free burning is allowed for 60 s before the water mist nozzle is activated for 3 s.
2.3. Mesh Sensitivity Analysis
In any CFD case, it is important to choose the correct mesh resolution. It is usually the best compromise between precision, computation time and computation power available. The FDS User Guide recommends an optimal mesh size by the non-dimensional number
with
the mesh size and
the characteristic fire diameter related to the fire heat release rate.
In the NUREG-1824 [
26], the United States Nuclear Regulatory Commission documents that
is a reasonable condition and gives the range of mesh sizes (1.15 cm; 4.61 cm) to explore for the present study. In the present work, the best test case from Yinshui et al. in terms of suppression time was selected as the reference case. Five meshes were chosen for the mesh sensitivity analysis. Starting from the mesh size 4.0 cm producing a total of 31,250 total cells into the domain, we multiplied by 1.5, 2, 6 and 8 for the respective mesh sizes 3.3 cm, 3.1 cm, 2.2 cm and 2.0 cm. Finer meshes were not considered as the computational time of multiple days becomes prohibitive in the scope of the current study with dozens of simulation runs to perform for the sensitivity analysis. The resulting comparisons of temperature profile between the experimental result and the different meshes are presented in
Figure 2. The results of the sensitivity mesh analysis are presented in
Table 1.
The absolute error computed between the experimental and the numerical average temperature decreases as the mesh size decreases, ranging from 40.3% to 2.0%. The calculation time ranges from 2.1 h to 26.3 h. There is a substantial gap between mesh sizes 2.2 cm and 2.0 cm in terms of absolute error, which is divided by 13, from 26.9% to 2.0%, whereas the computation time is only multiplied by 1.5, from 17.6 h to 26.3 h. Therefore, the mesh size of 2cm was selected as reference for the validation case. The time step based on the CFL criterion was automatically adjusted by FDS through the mesh sensitivity analysis.
2.4. Validation Case
FDS capabilities to reproduce the water mist fire suppression mechanisms are discussed here. Efforts are focused on reproducing the results of the first test of Yinshui et al. [
23] that has one of the best extinguishing times and for which both temperature and O
, CO
, and CO gas concentrations are given.
Figure 3 presents the evolution of the temperature inside the compartment for times 10 s (fire development), 45 s (fully developed fire), 62 s (on-going suppression) and 70 s (extinguished fire) using a vertical median plane. It can be seen that the exhaust ventilation has an effect on the water mist droplets spatial distribution inside the volume. Instead of being centered on the fire, the spray cone highlighted in red is tilted from its nominal axis, probably under the influence of the exhaust air flow.
Figure 4a presents the evolution of the O
volume fraction inside the compartment for the same time steps as
Figure 3. The oxygen displacement is visible if the comparison between 45 s and 62 s is made for region of the flame, because the located green and cyan colors are replaced with a diffuse and turbulent yellow tint. The phenomenon affects the whole lower half of the compartment as even regions with an orange tint around the flame turned to yellow. The same conclusion can be made about the concentrations of carbon dioxide (
Figure 4b) and monoxide (
Figure 4c). Overall, the high-pressure nozzle homogenizes an otherwise localized accumulation or lack of gaseous species.
Temperature and species quantities have also been monitored over time from the sensor positions described above and are compiled in
Figure 5. The temperature profile is presented on
Figure 5a and is accurately reproduced from 0 to 60 s. The peak of the temperature is higher in the simulation (563 °C) than in the experiment (530 °C). The decrease in temperature following the water mist activation is sharper in the simulation than the observed experimental results, which is due to the imposed decrease of HRR. This is the largest variation of all four studied quantities in the fire suppression time period and is an indication of the limits of our FDS model. The gas concentrations presented in
Figure 5b–d are well reproduced by the FDS simulations.
The oxygen concentration decreases linearly as the fire burns. It reaches a constant value of 18.5% after the fire suppression. This behavior highlights the oxygen displacement because no more oxygen is consumed by the fire after suppression. The carbon dioxide concentration rise becomes noticeable after 40 s of free burn and continues to rise after the fire suppression up until 100 s. After this time, it also reaches a constant value of 1.0%. The rise of carbon monoxide concentration is also slow with a slightly sharper rise in the simulation. As for the carbon dioxide, the concentration rises after the fire suppression that happens after 60 s. The final value of concentration is around 215 ppm.
5. Conclusions
Sensitivity analysis methods were applied with success to fire suppression by water mist systems using numerical tools. New quantitative insights into the relations between several key parameters of the fire suppression system were obtained. The results show that spray angle is a quantity of interest for the design of experiments and temperature decrease and that the importance of quantities such as the droplet size can sometimes be overestimated for some configuration. A concrete application of the current result is that the spray cone angle should be more influential in the fire protection design of a small room and might have more impact than the flow rate or the droplet size. This novel approach was made in two times.
The suppression of a diesel compartment fire by a water mist system based on experimental results produced by Yinshui et al. [
23] was first numerically investigated using the CFD code FDS and a heat release rate approach. After conducting a mesh sensitivity analysis, a validation case was performed. The gas concentrations of O
, CO
and CO were correctly reproduced from start to finish. The predicted temperature decrease was overestimated.
Sensitivity analyses were then conducted using the factorial design and a statistical global method using the variance decomposition of a chosen model. Linear model, non-linear model and chaos expansion were investigated. The water flow rate Q, spray cone angle , discharge duration and the droplet size served as input parameters.
The obtained results for the temperature indicate that the discharge duration is the most influential parameter with the linear model and that the spray cone angle is dominant when quadratic terms are added in the model. This is supported by the quadratic relationship that exists between the spray cone angle and the surface area covered on the ground by the water mist. The expected results can be obtained using sensitivity analysis, and thus confirm that such techniques are suitable for fire suppression studies.
Since the feasibility has been assessed, future works will focus on improving and refining the techniques presented in this article. The combustion models of numerical simulations will be improved and compared to our own experimental results, in order to rely on more accurate data. Concurrently, efforts will be made to refine the aforementioned sensitivity analysis techniques and develop new ones, for examples based on fractional design or chaos polynomials with extended numbers of parameters and different distributions.