Experimental Investigation on the Heat Dissipation and Postfire Structural Performance of a Reinforced Concrete Column with Biomimicked Geometry
Abstract
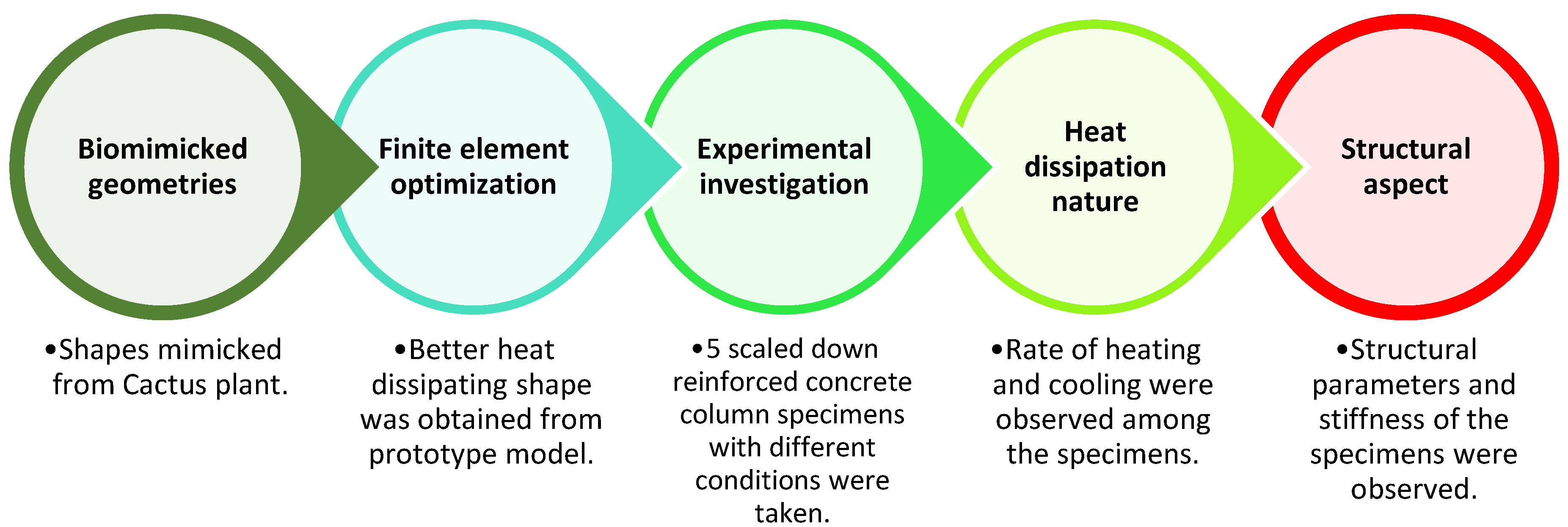
:1. Introduction
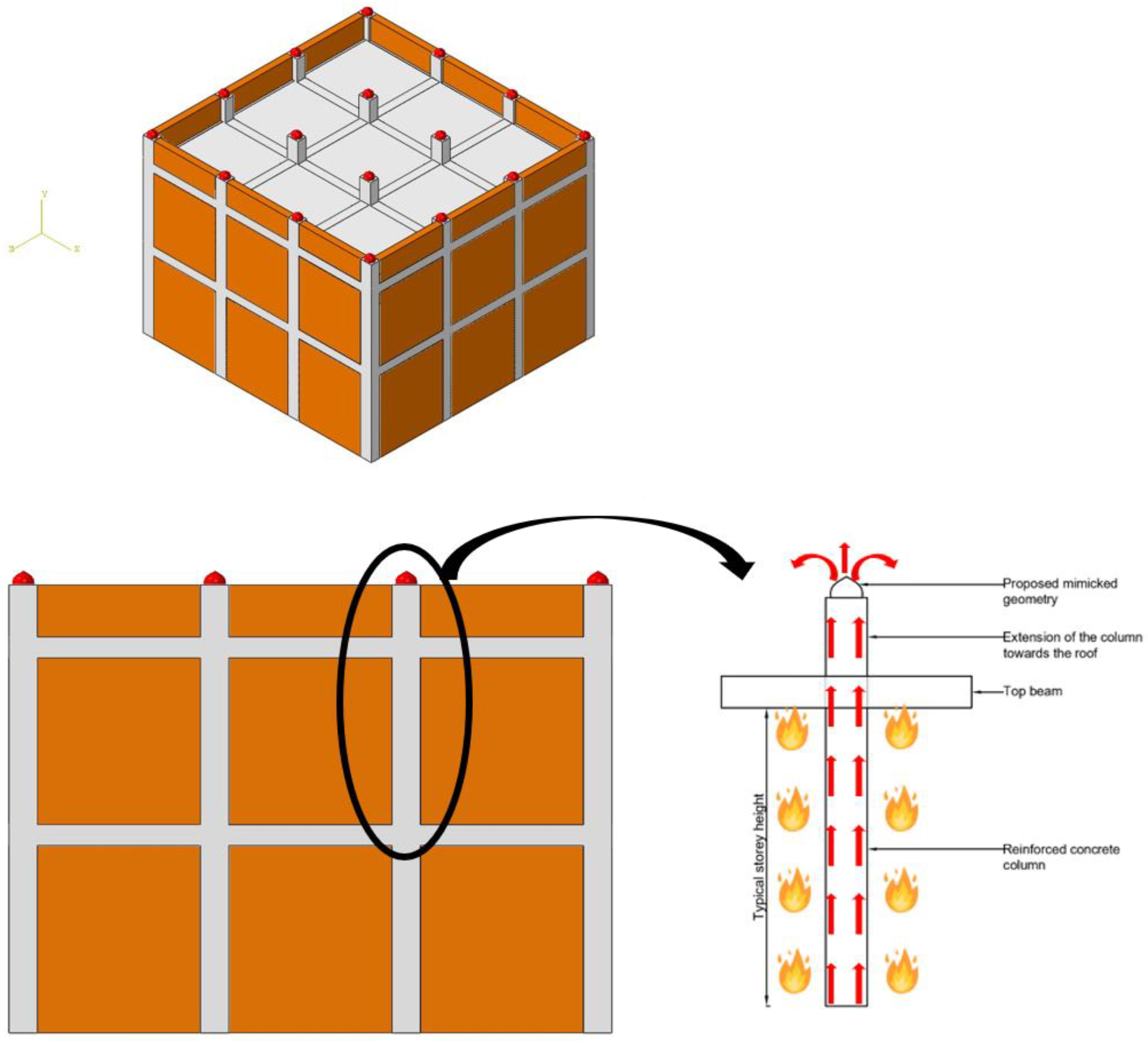
Application of the Proposed Concept in Prototype Buildings
2. Materials, Methods, and Experiments
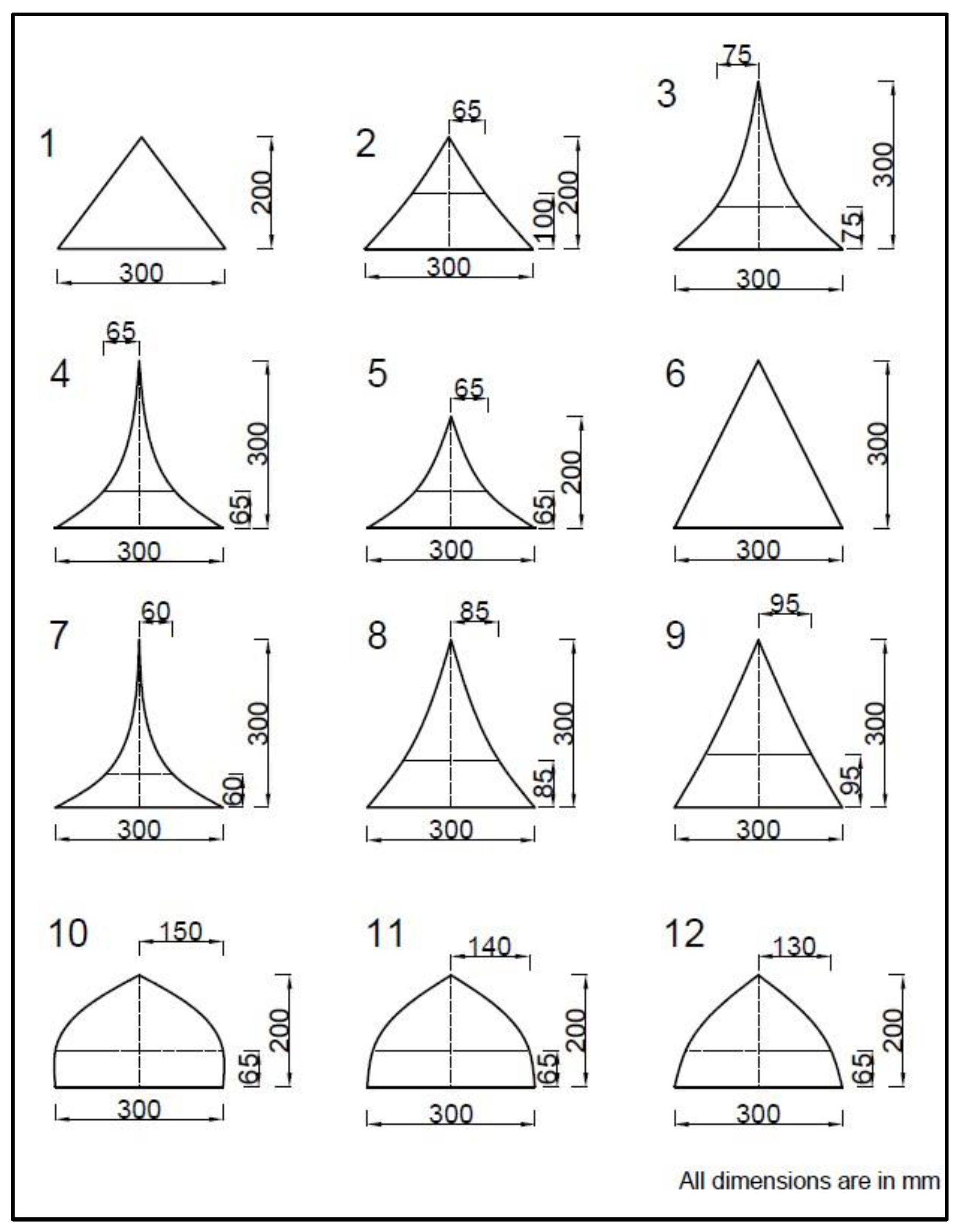
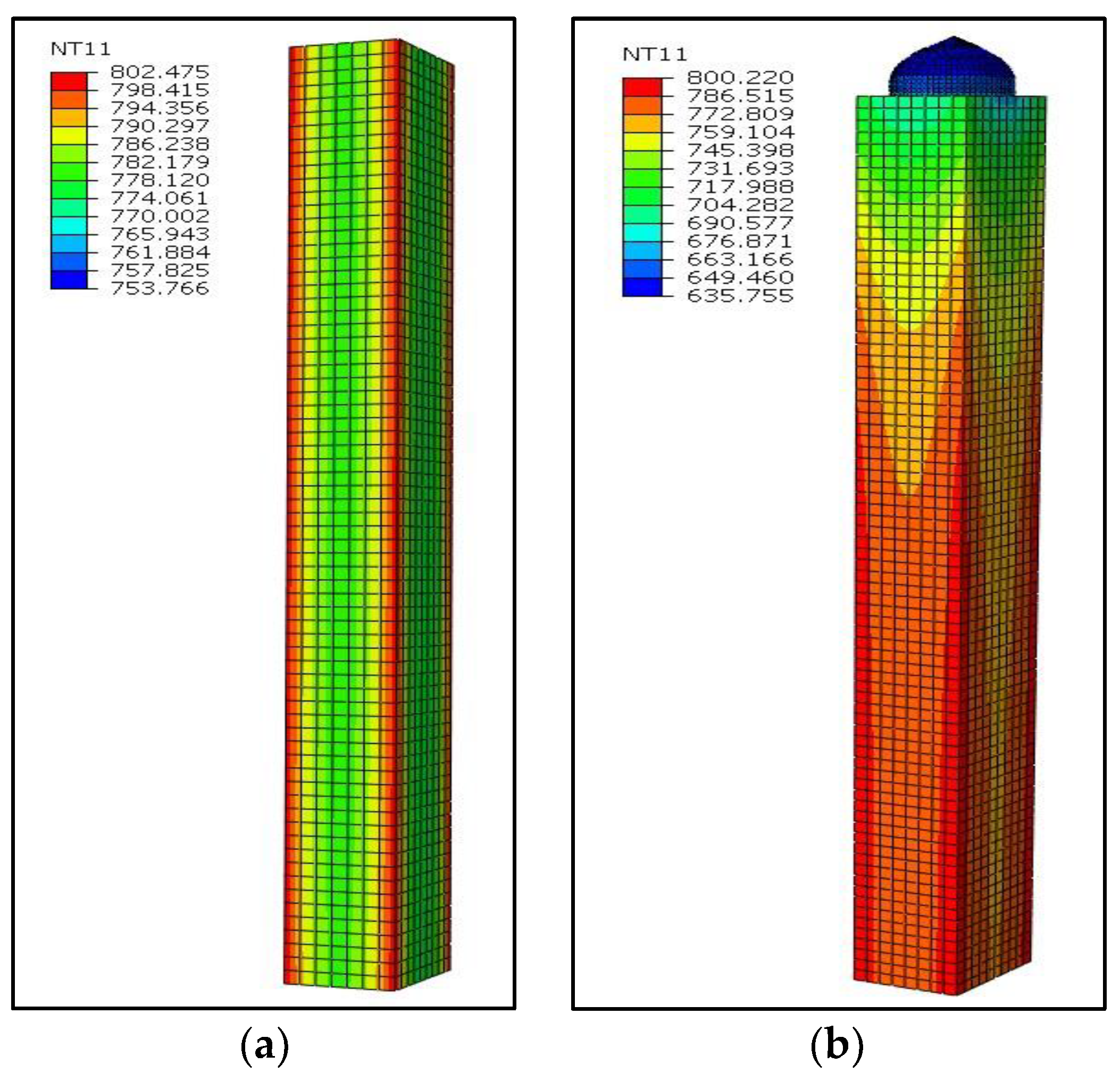
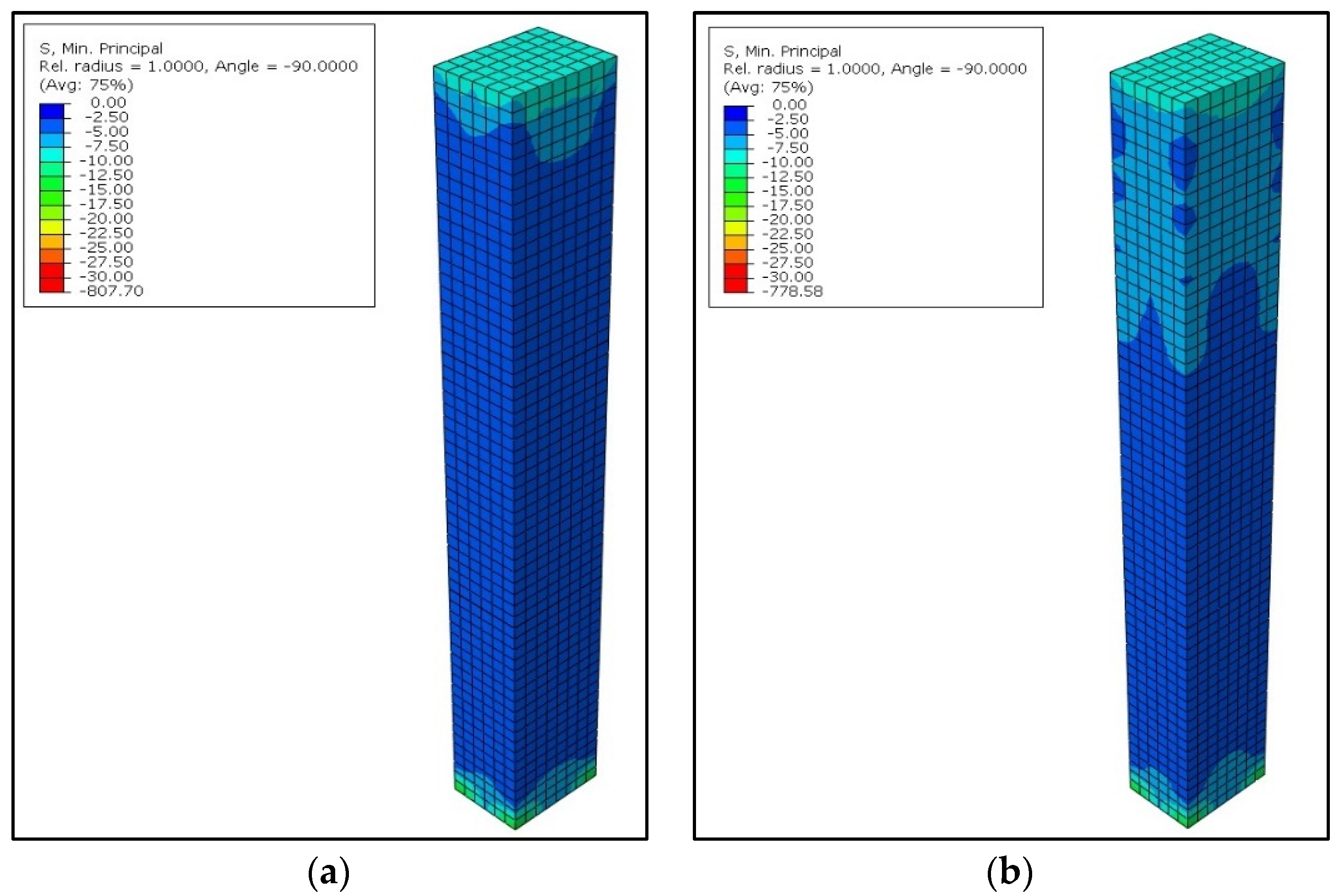
3. Optimization through Finite Element Analysis
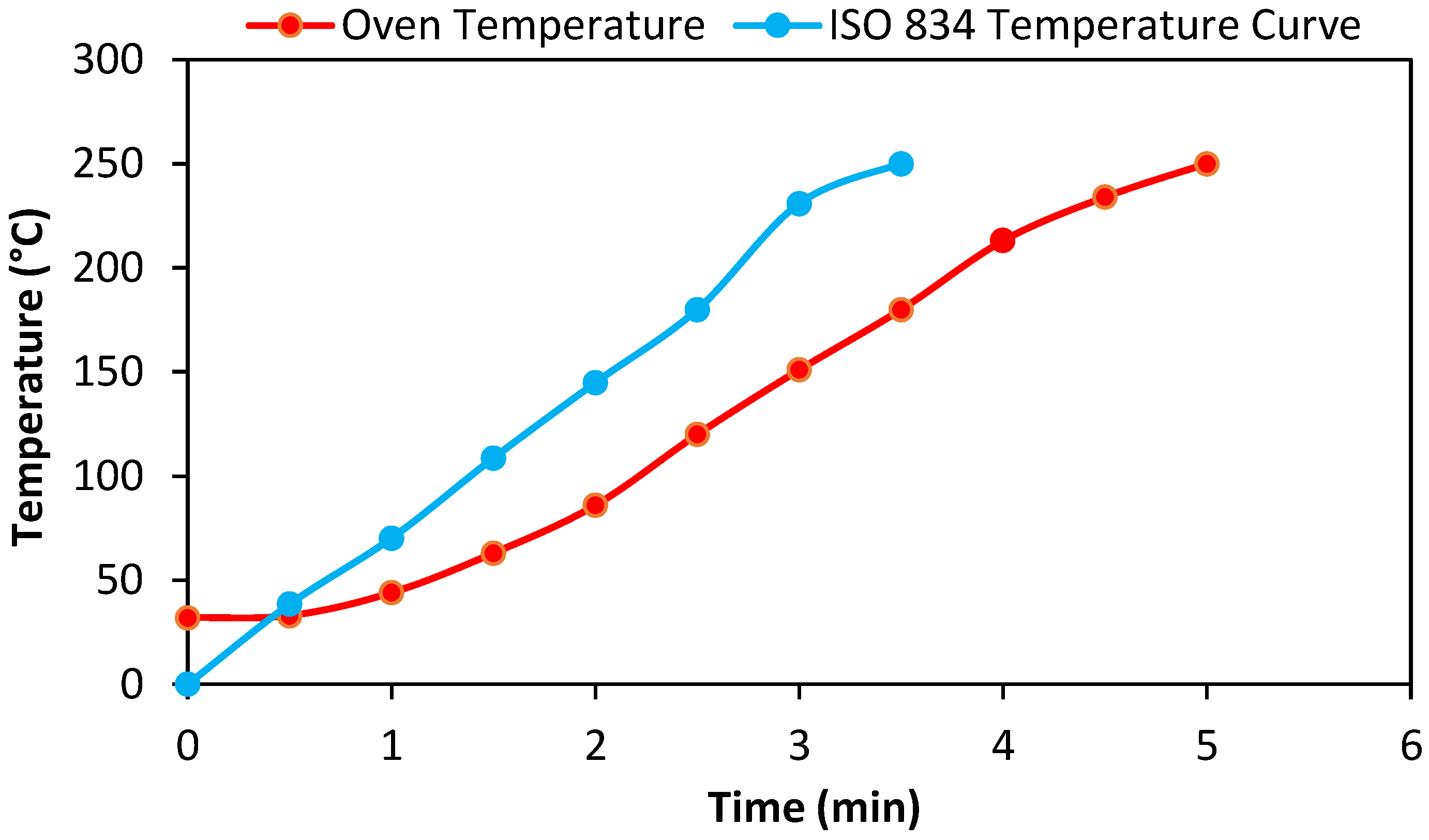
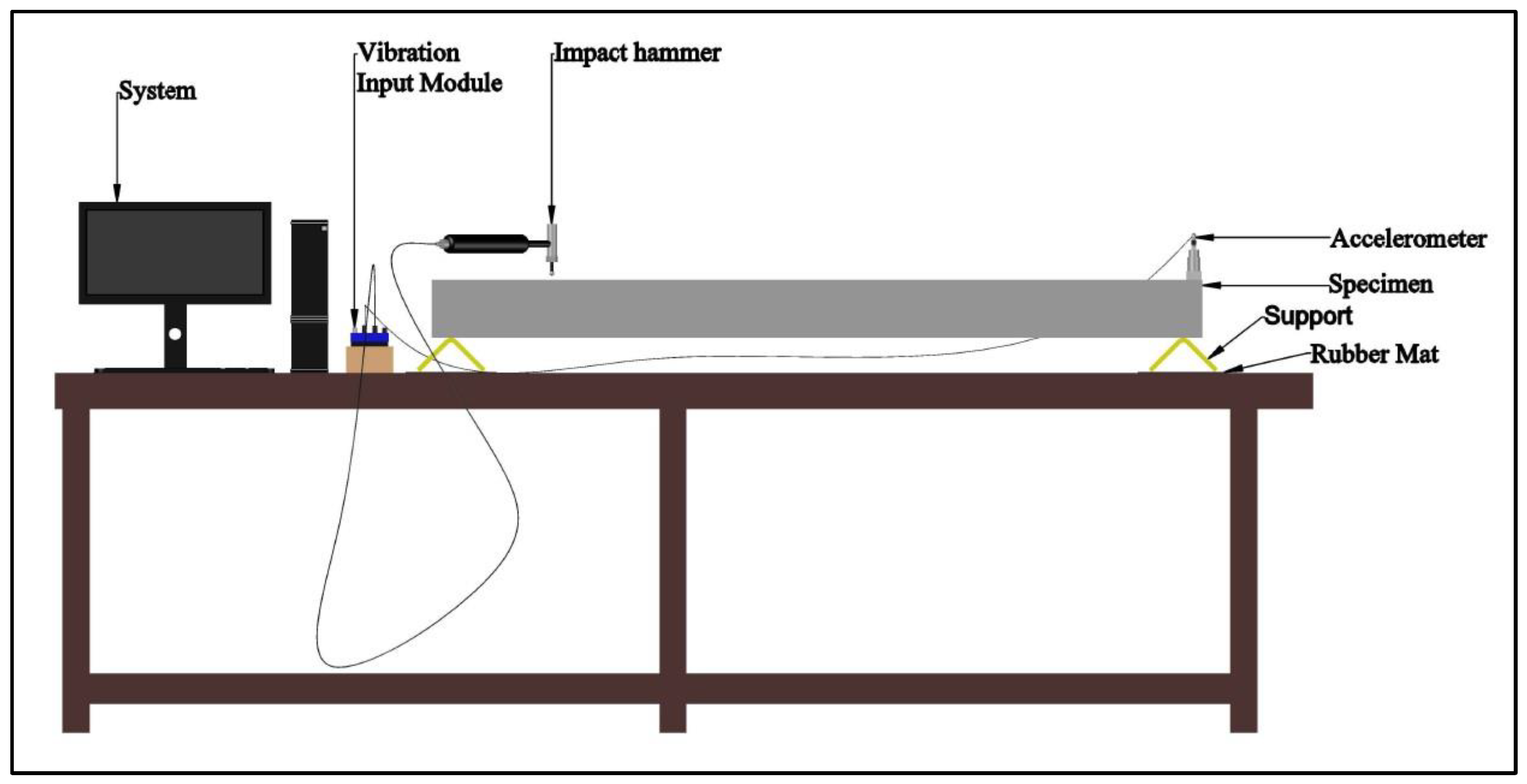
4. Experimental Setup
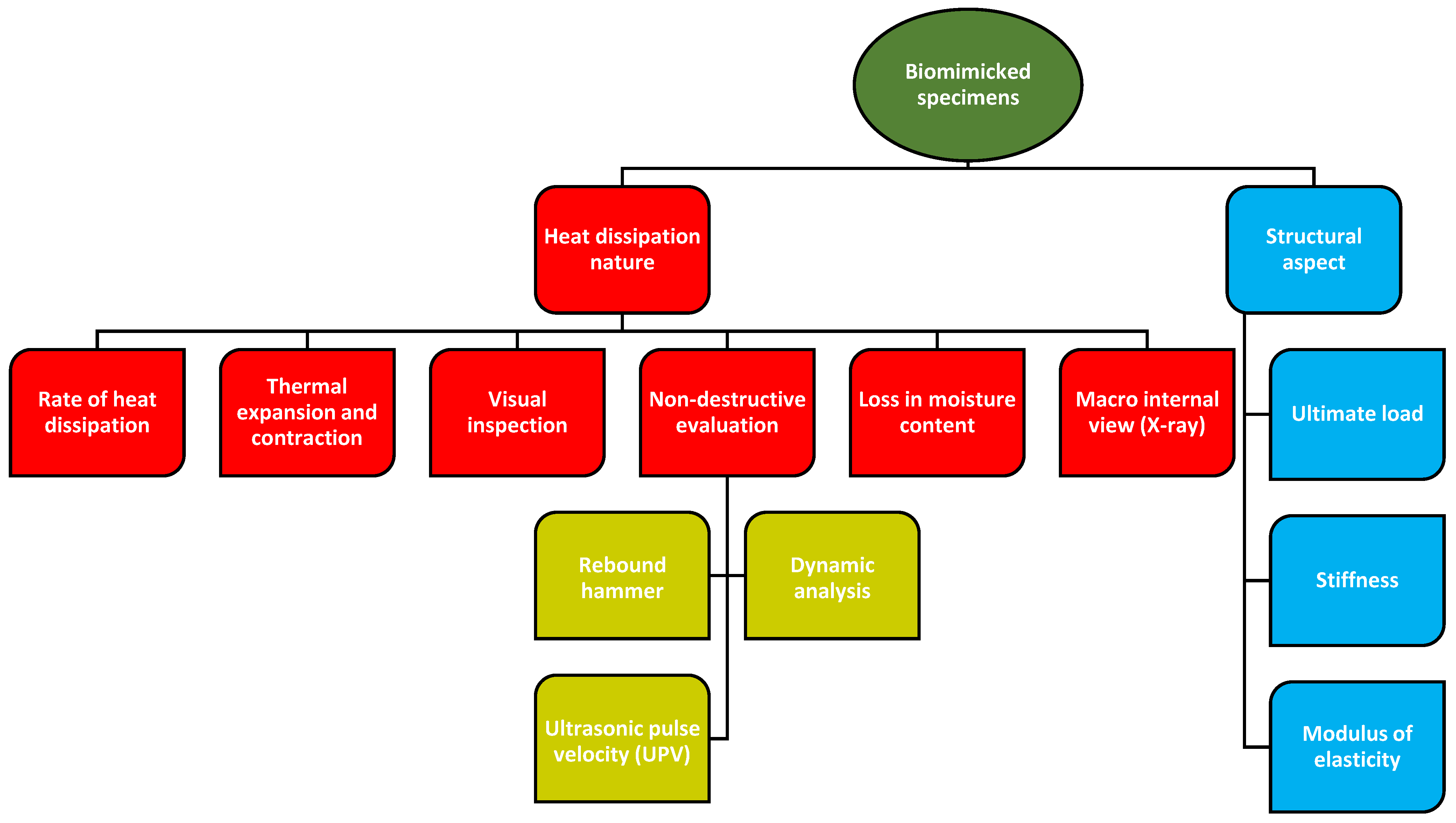
5. Results and Discussion
5.1. Initial Observation
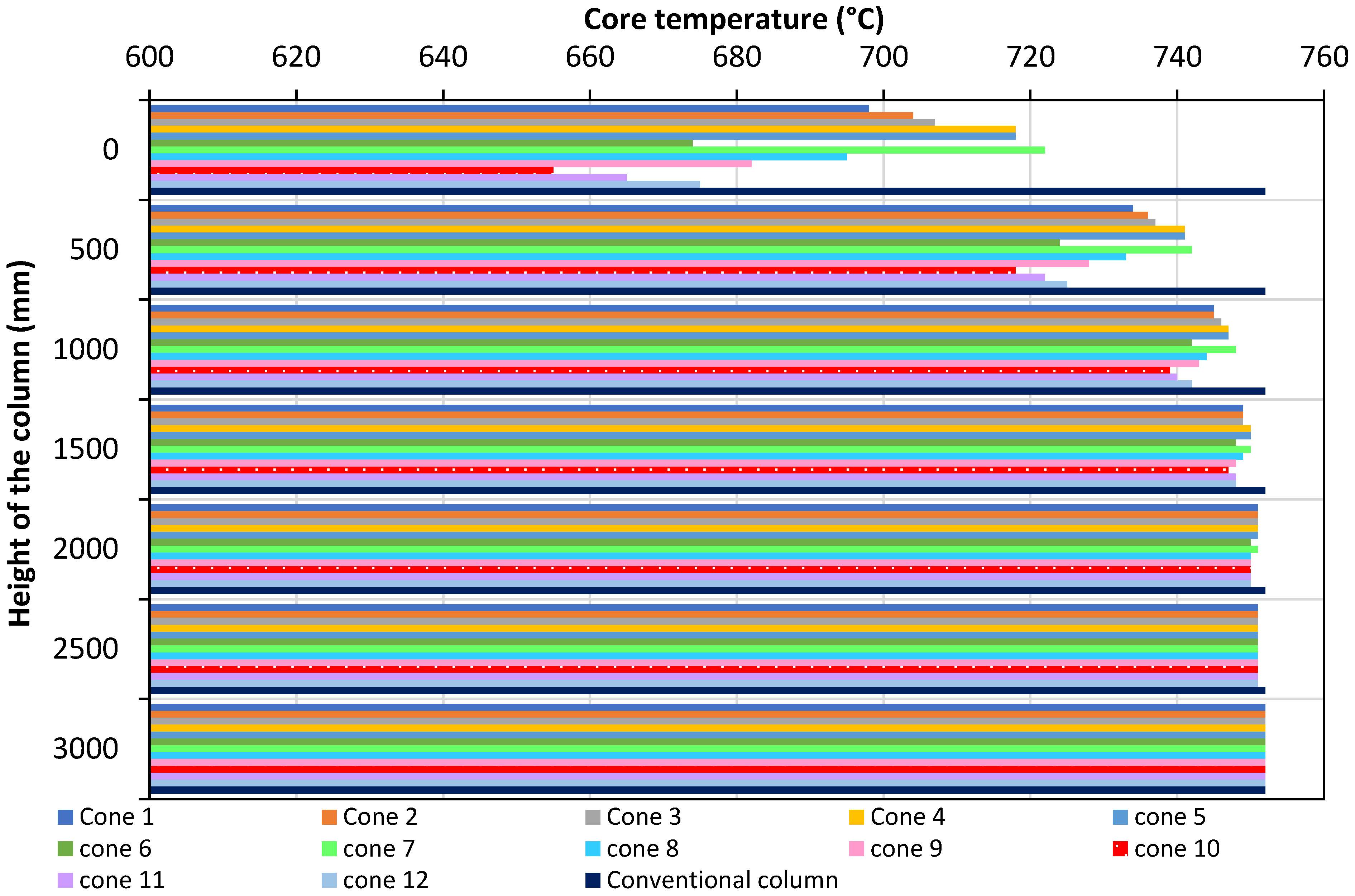
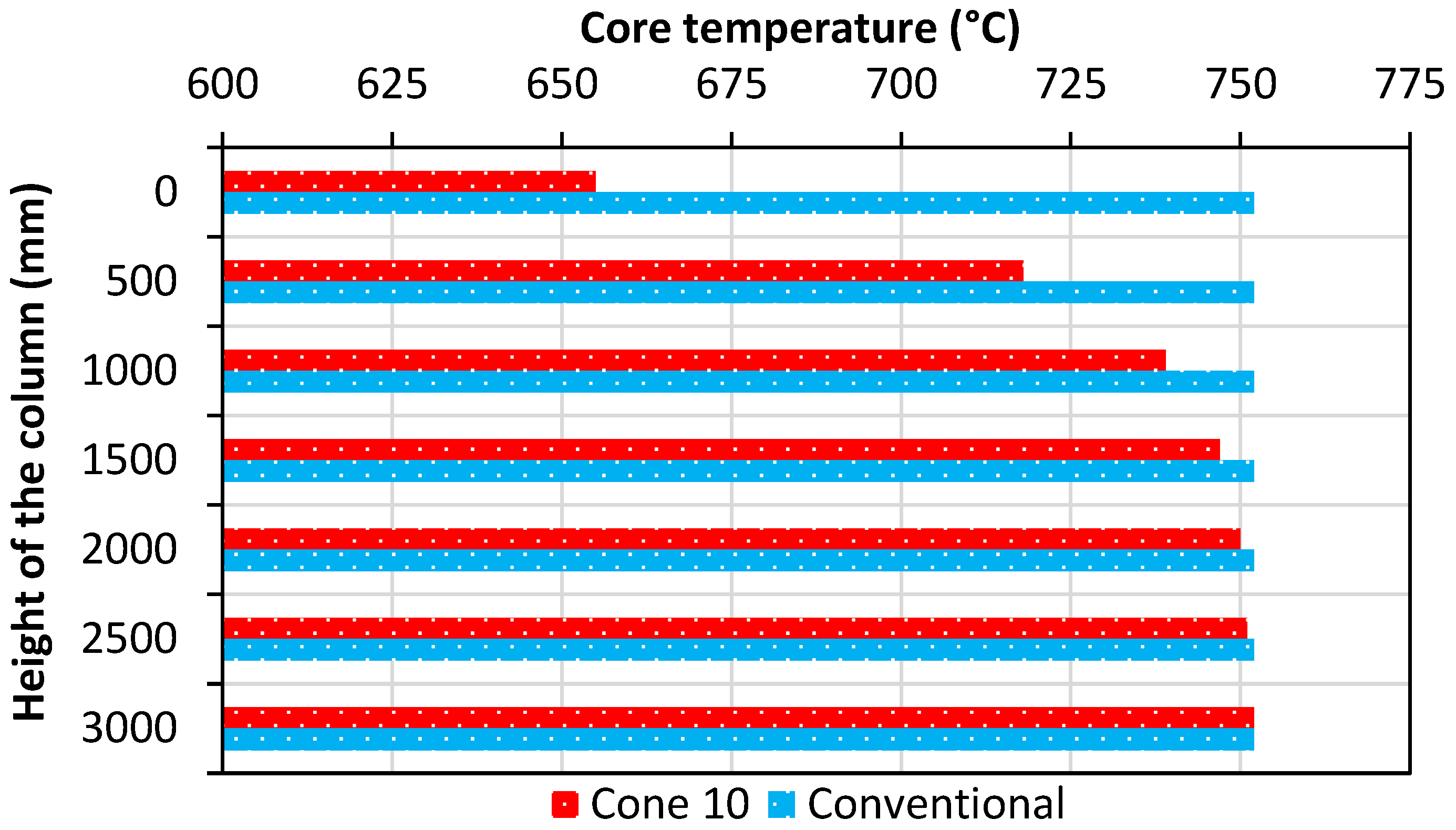
5.2. Time Versus Temperature Characteristics of the Specimens
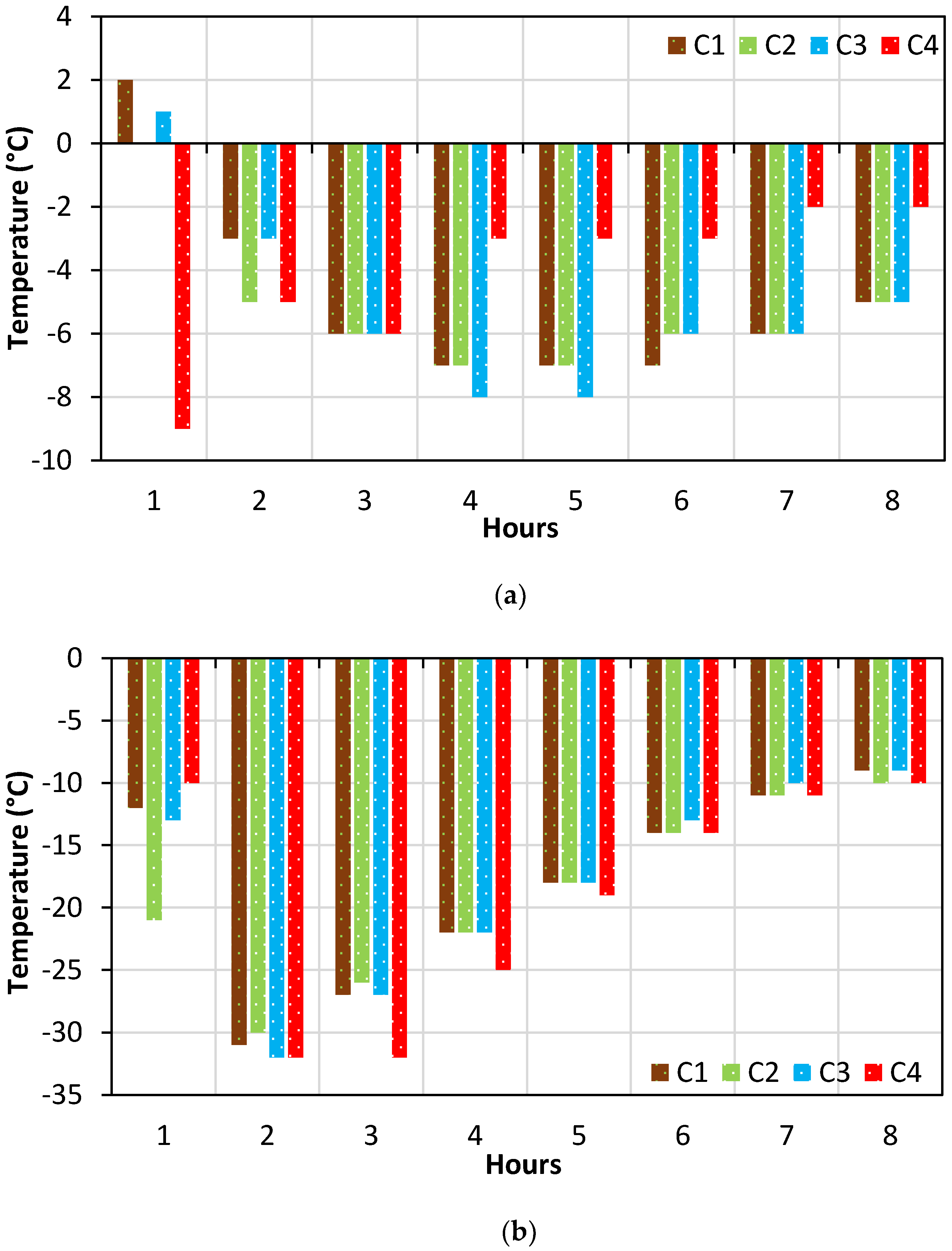
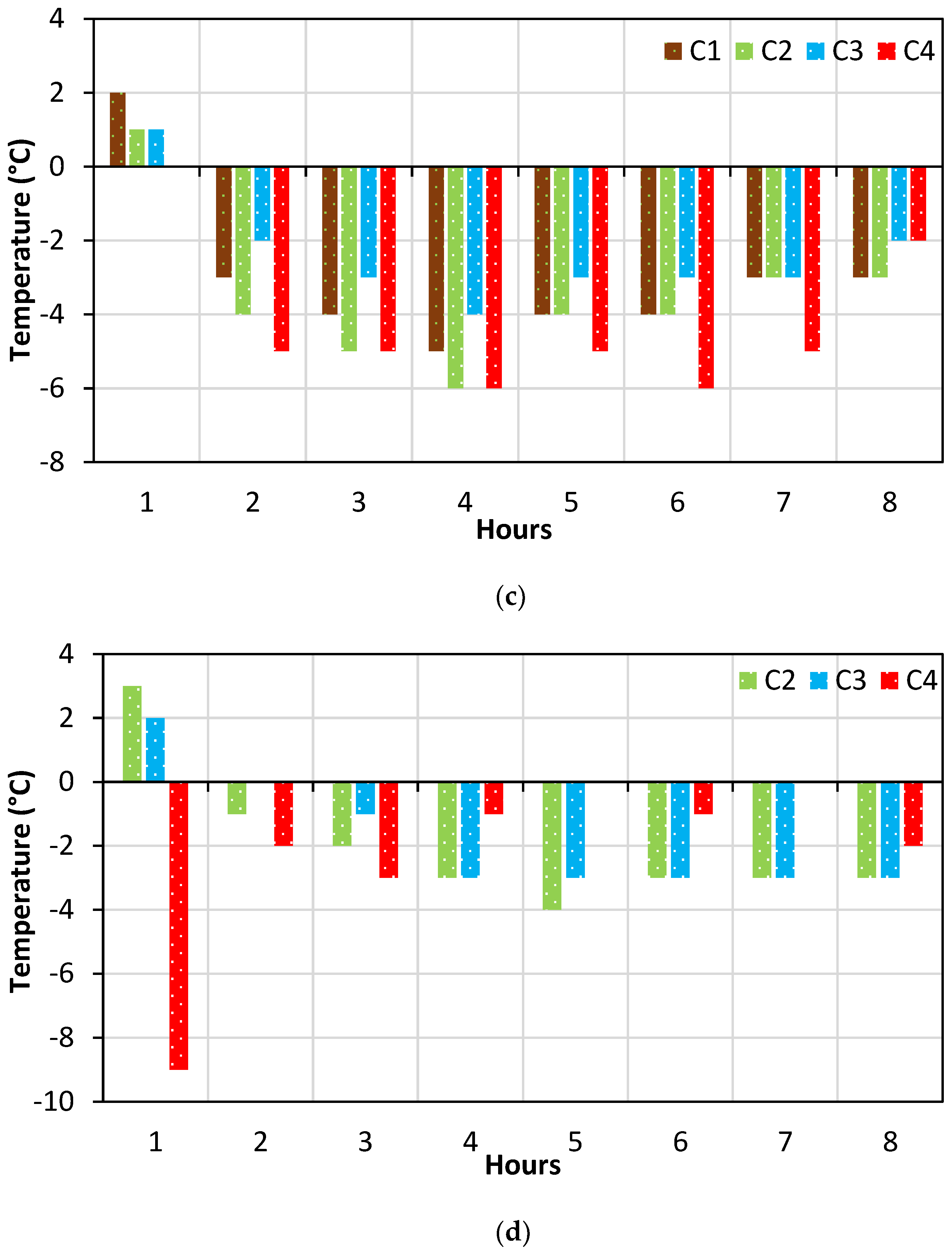
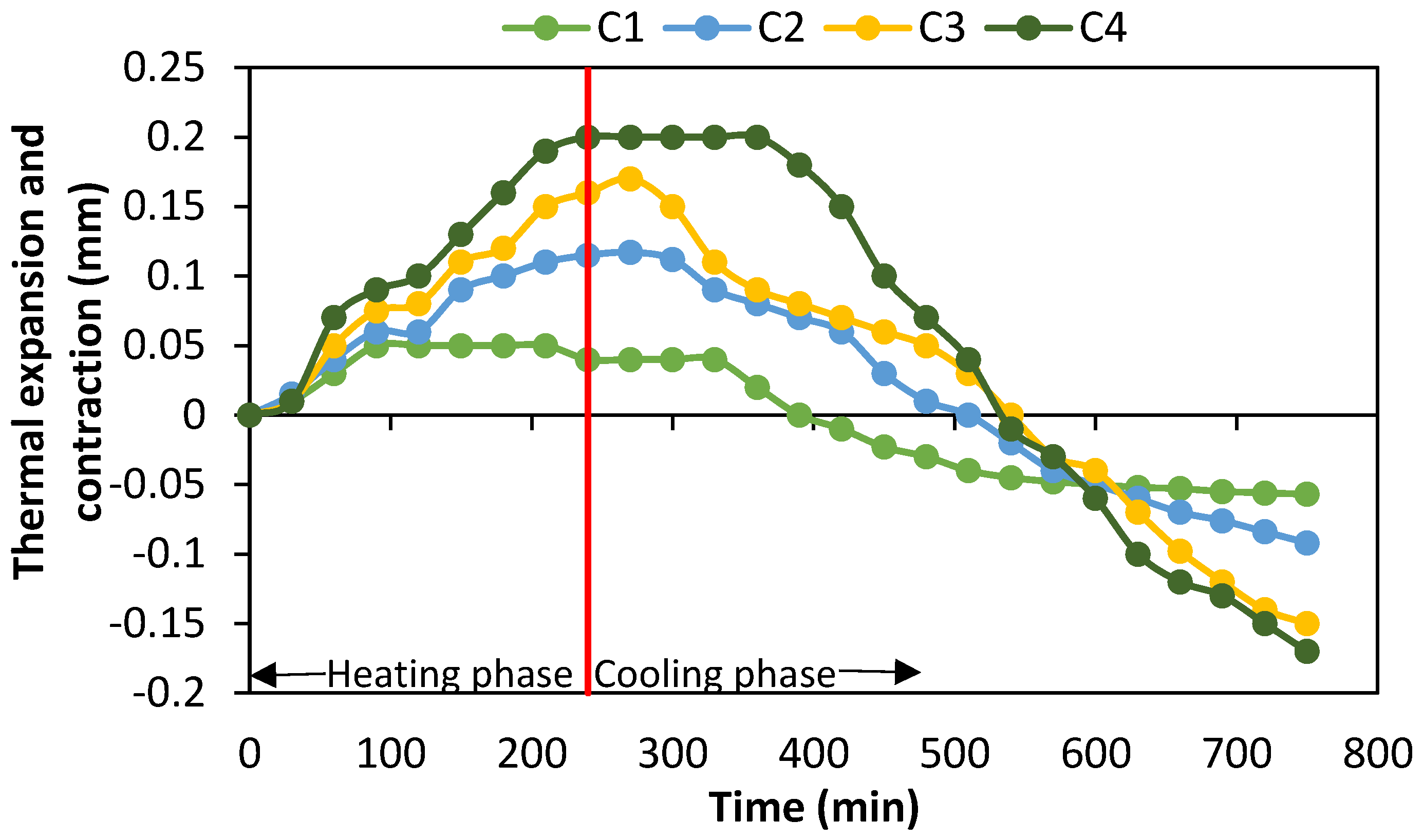
5.3. Thermal Expansion and Contraction
5.4. Visual Inspection
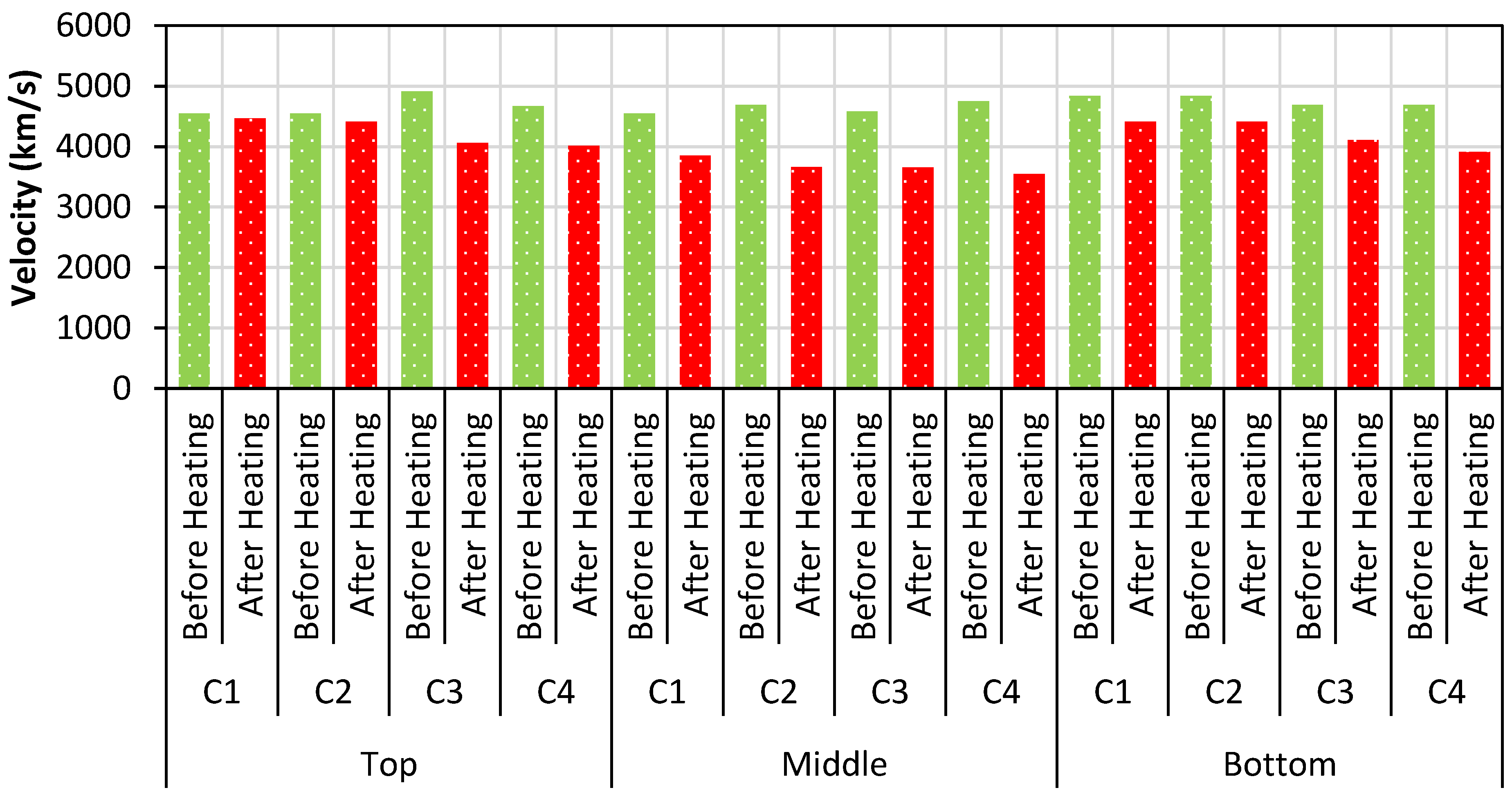
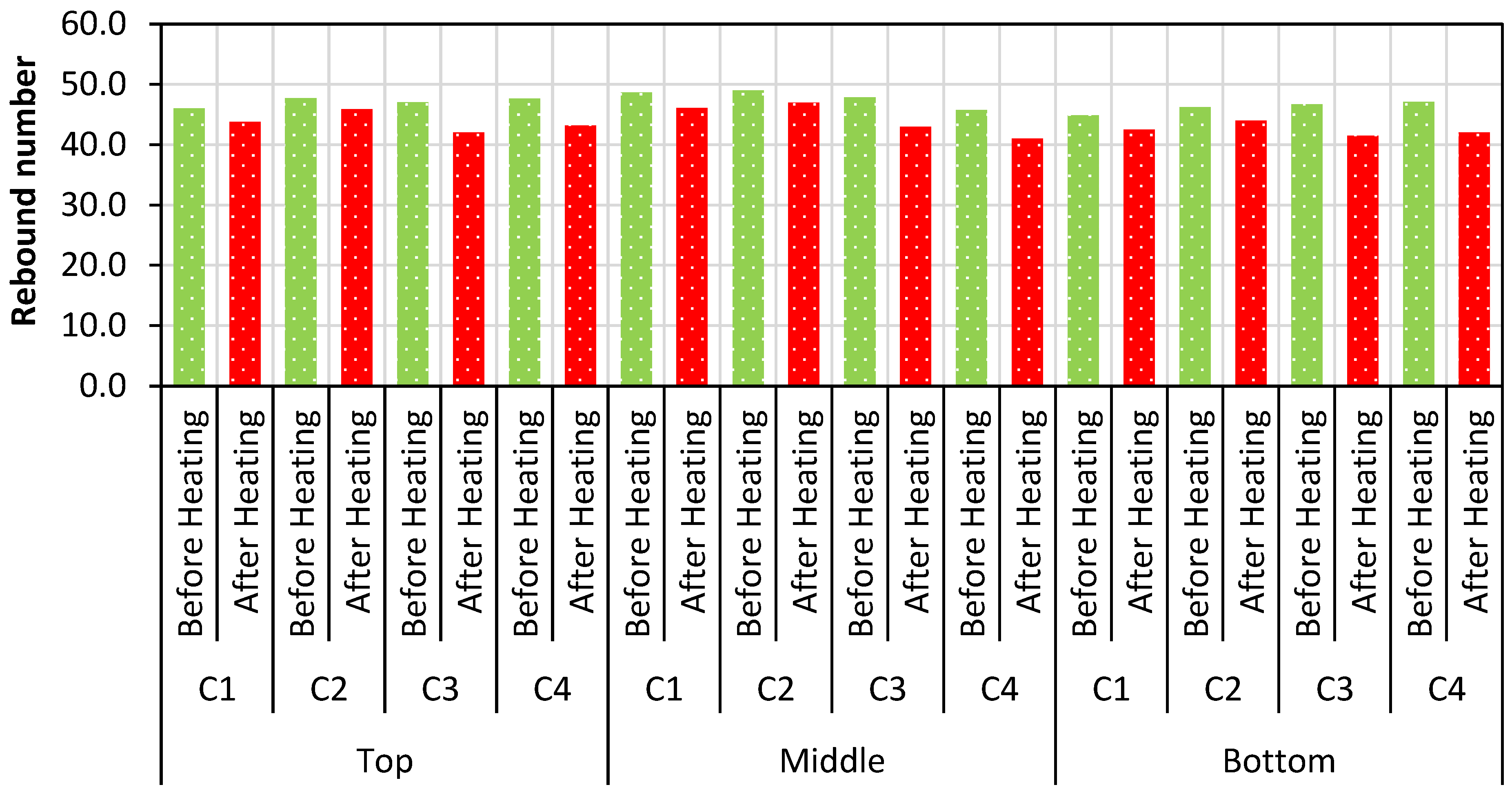
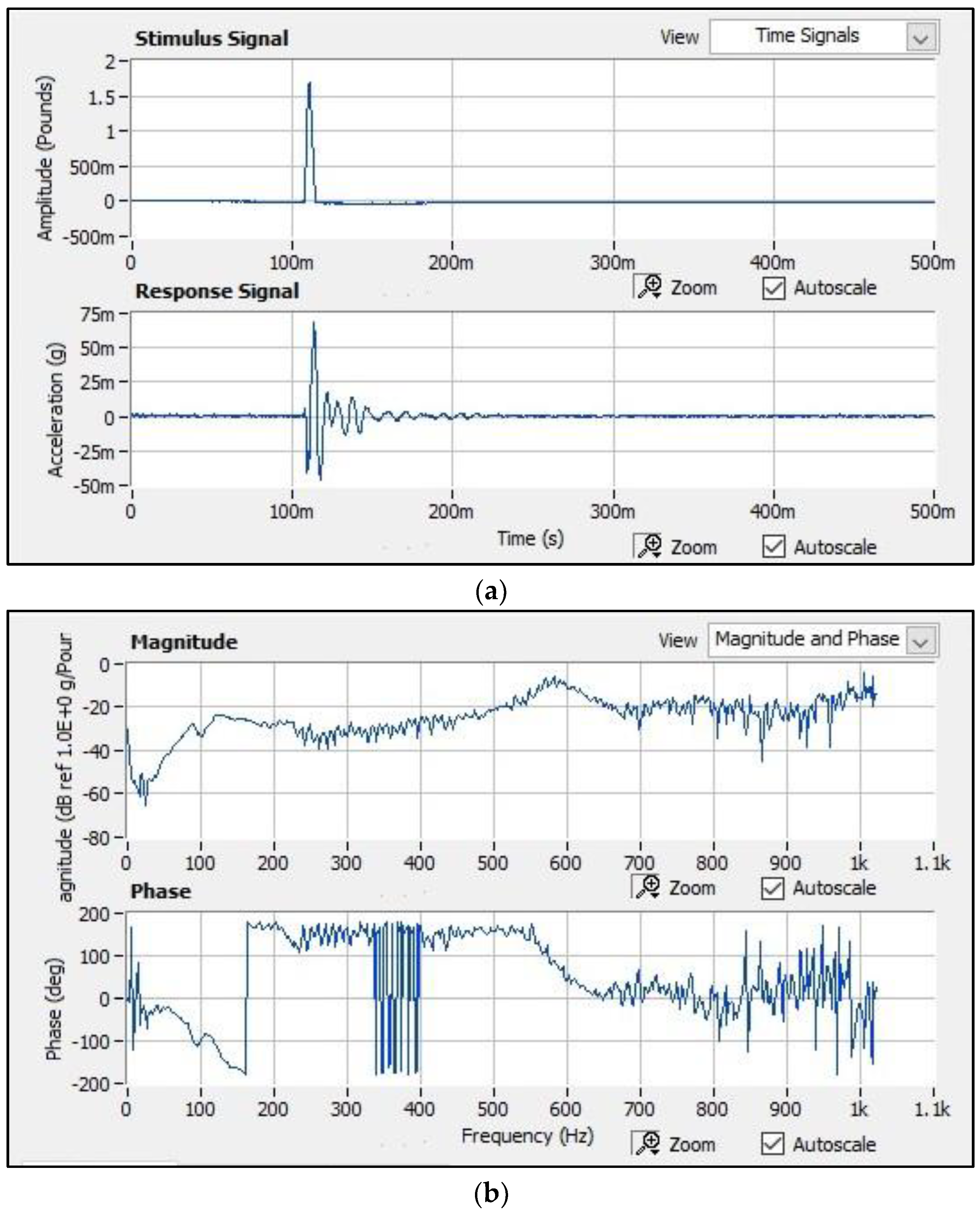
5.5. Nondestructive Evaluation
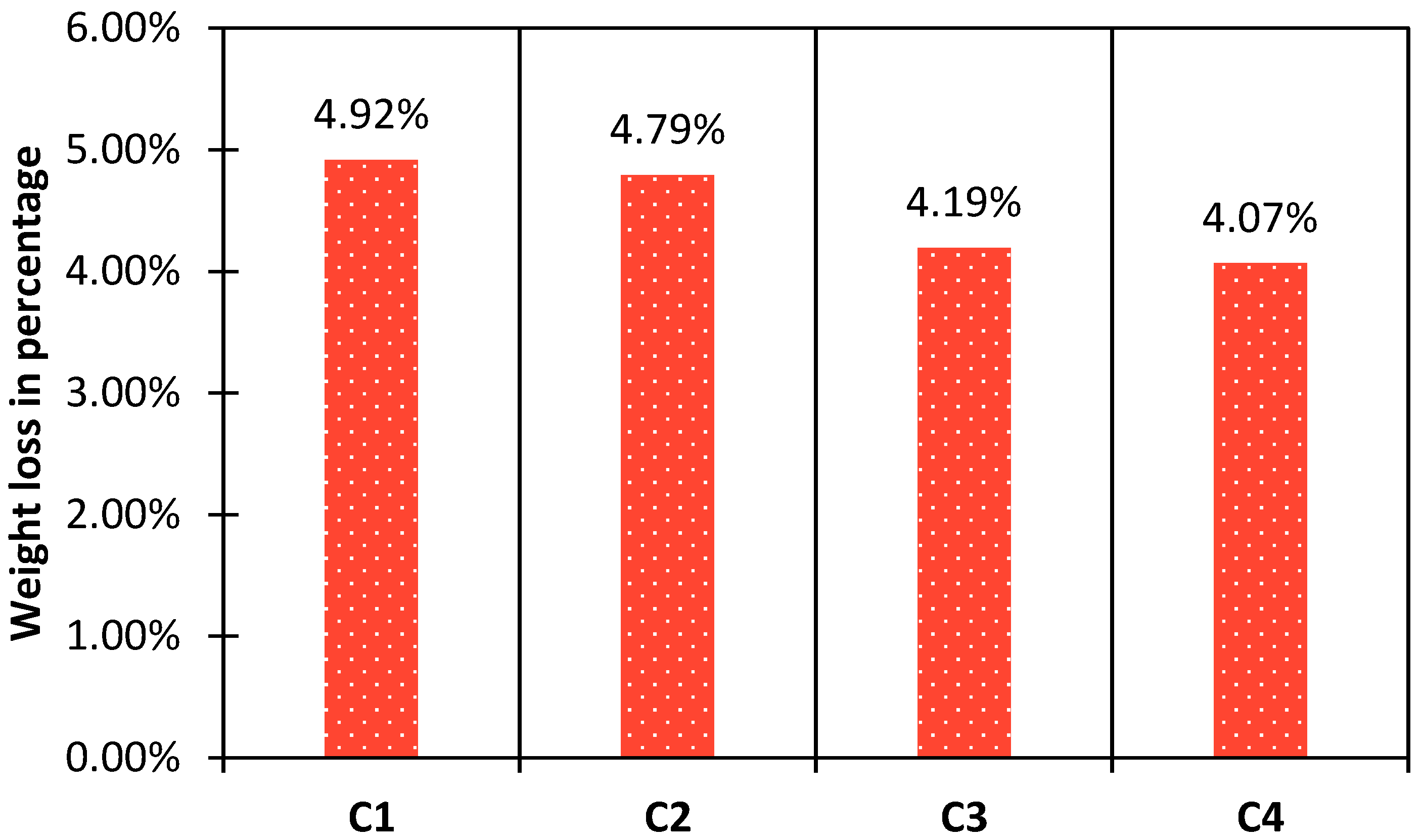
5.6. Weight Loss in the Specimens after Heating
5.7. X-ray of the Specimens
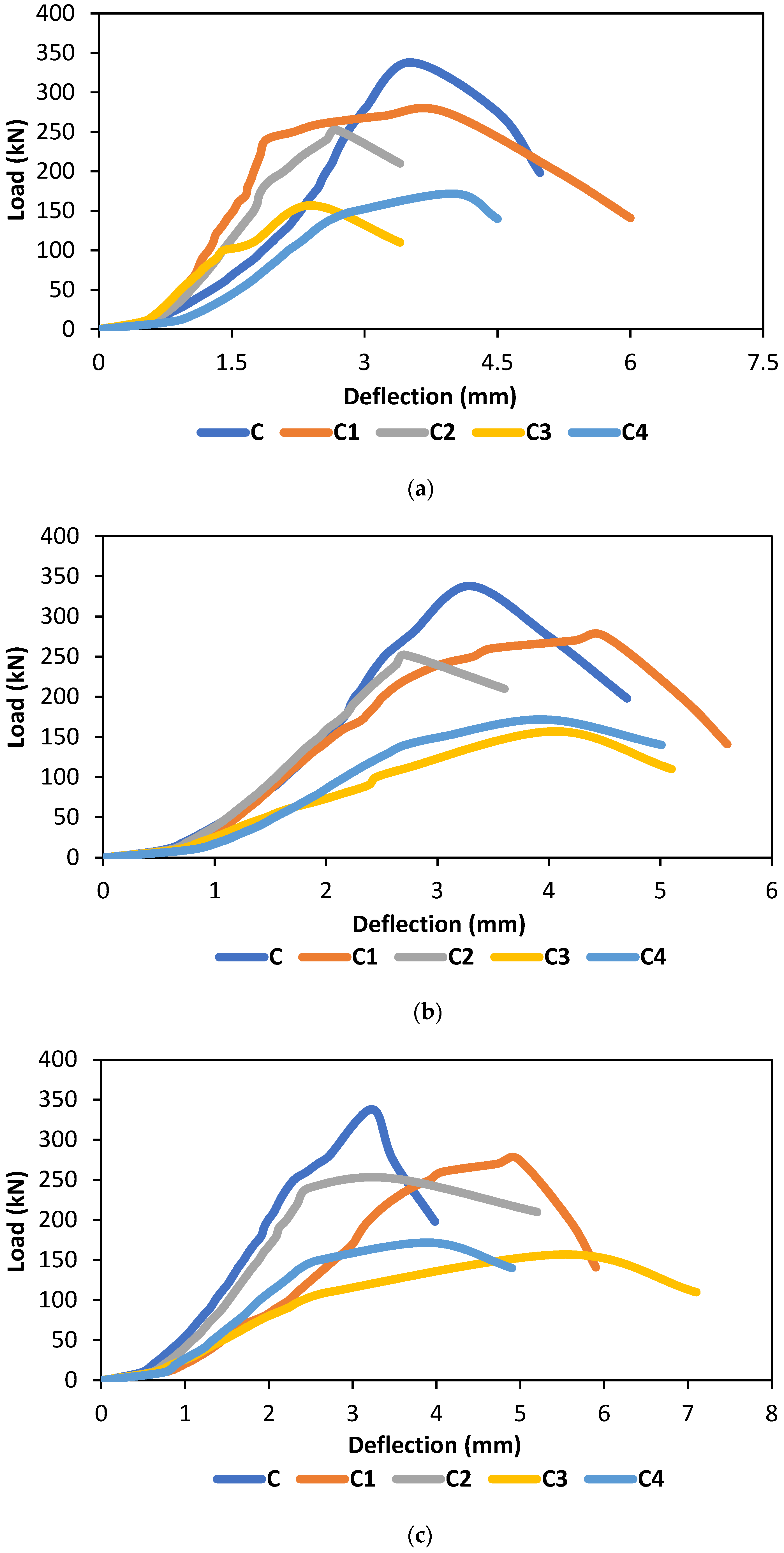
5.8. Ultimate Load Capacity of the Columns
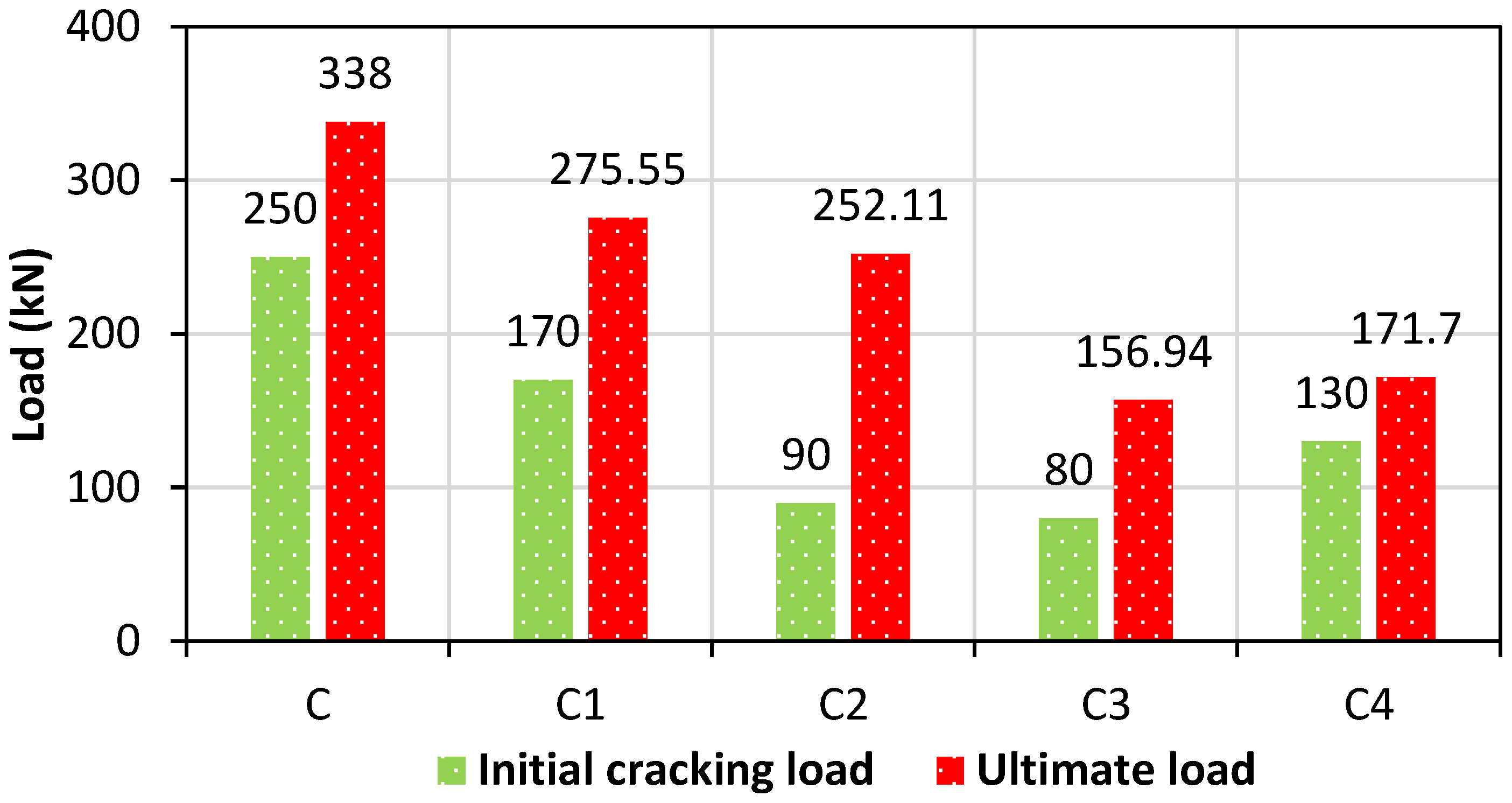
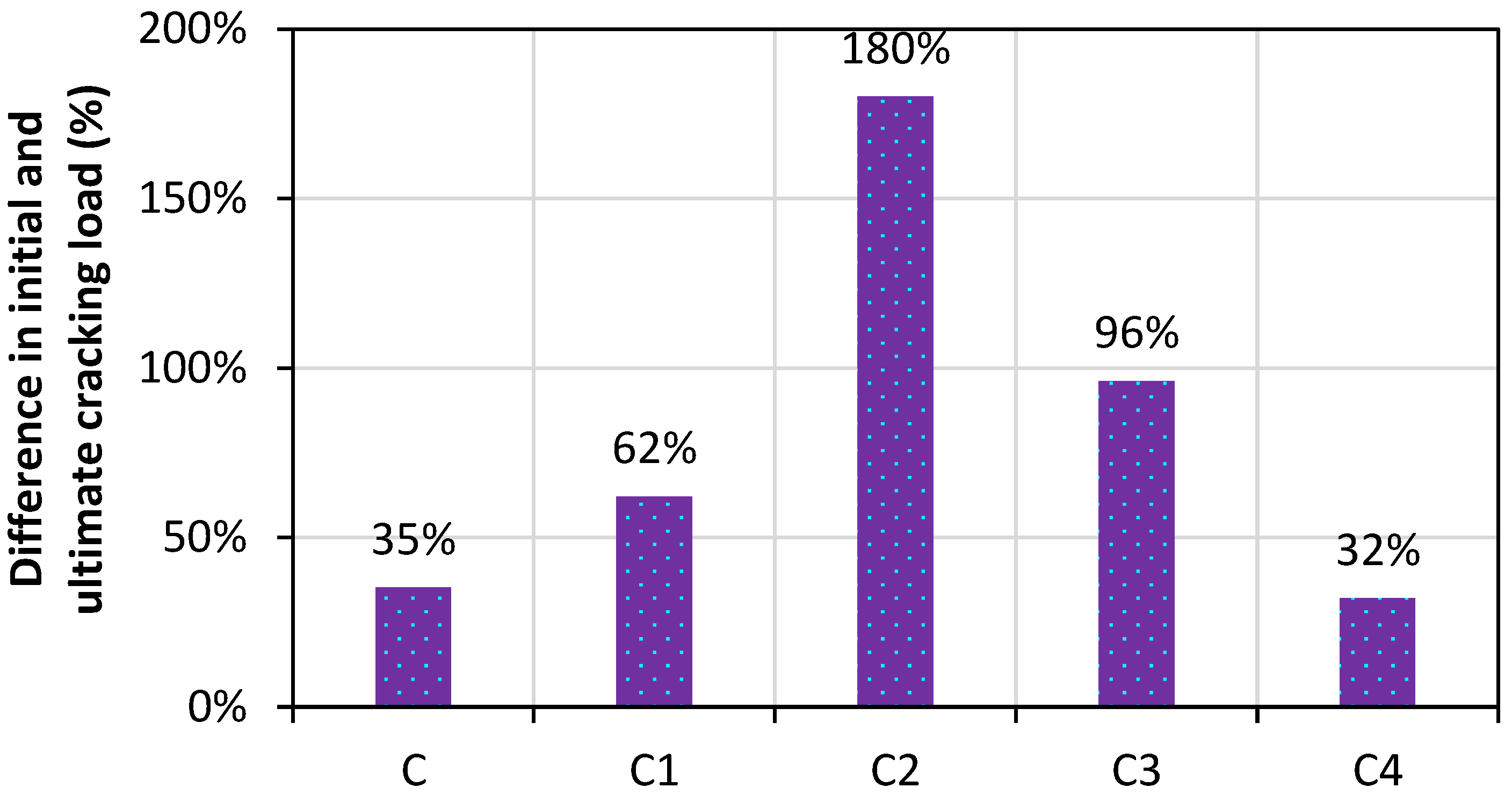
5.9. Initial and Final Cracking Loads
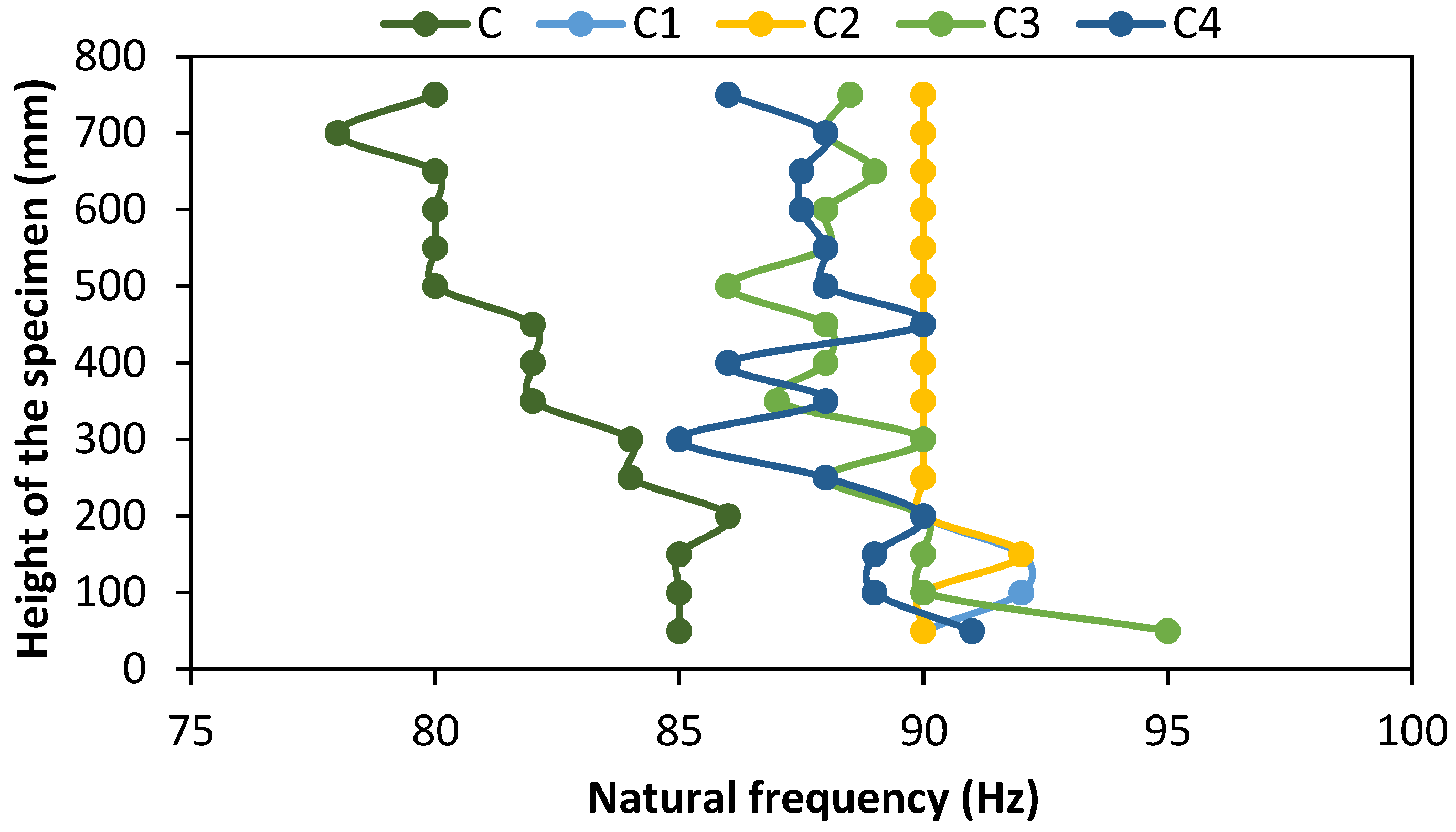
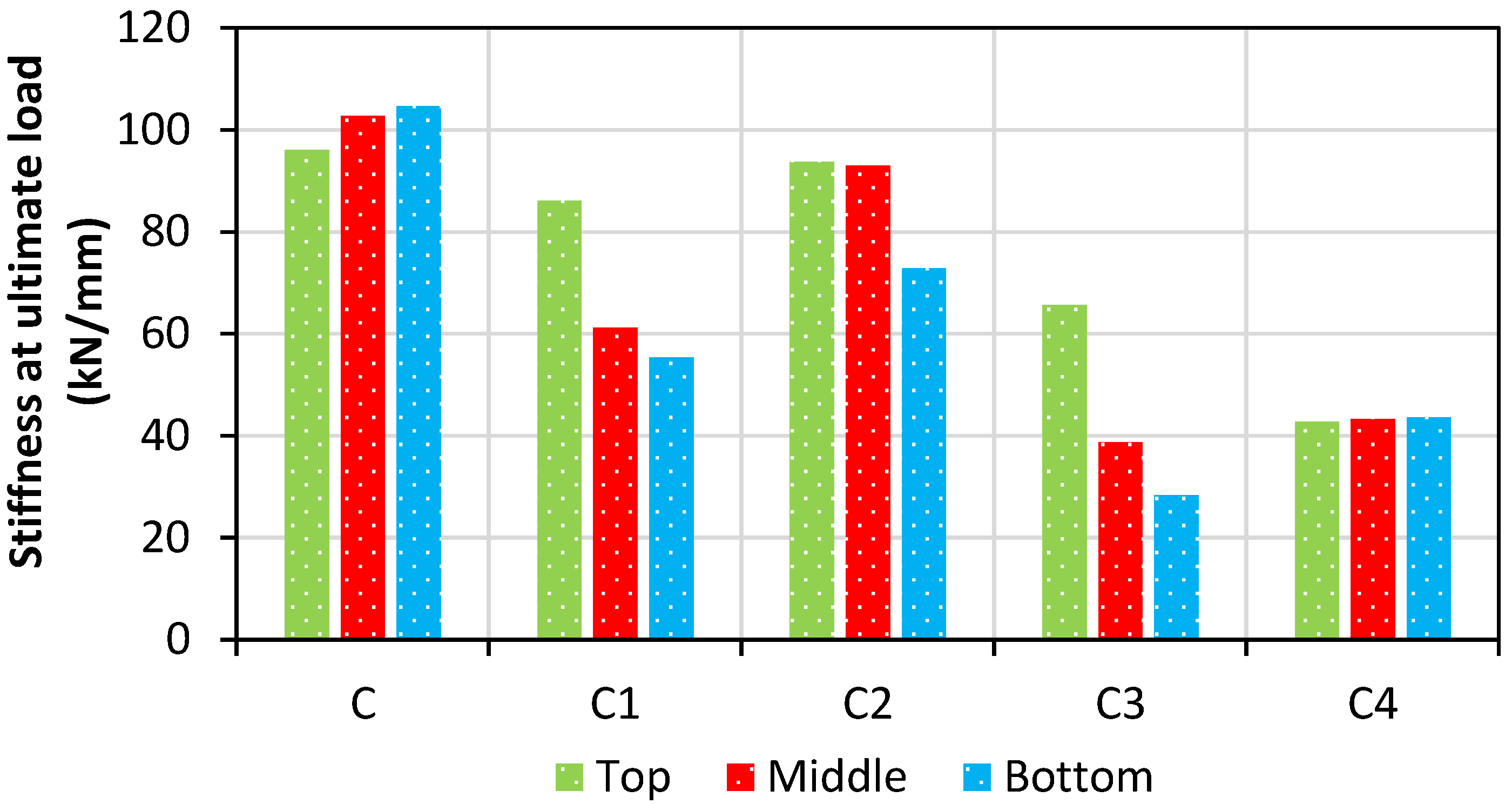
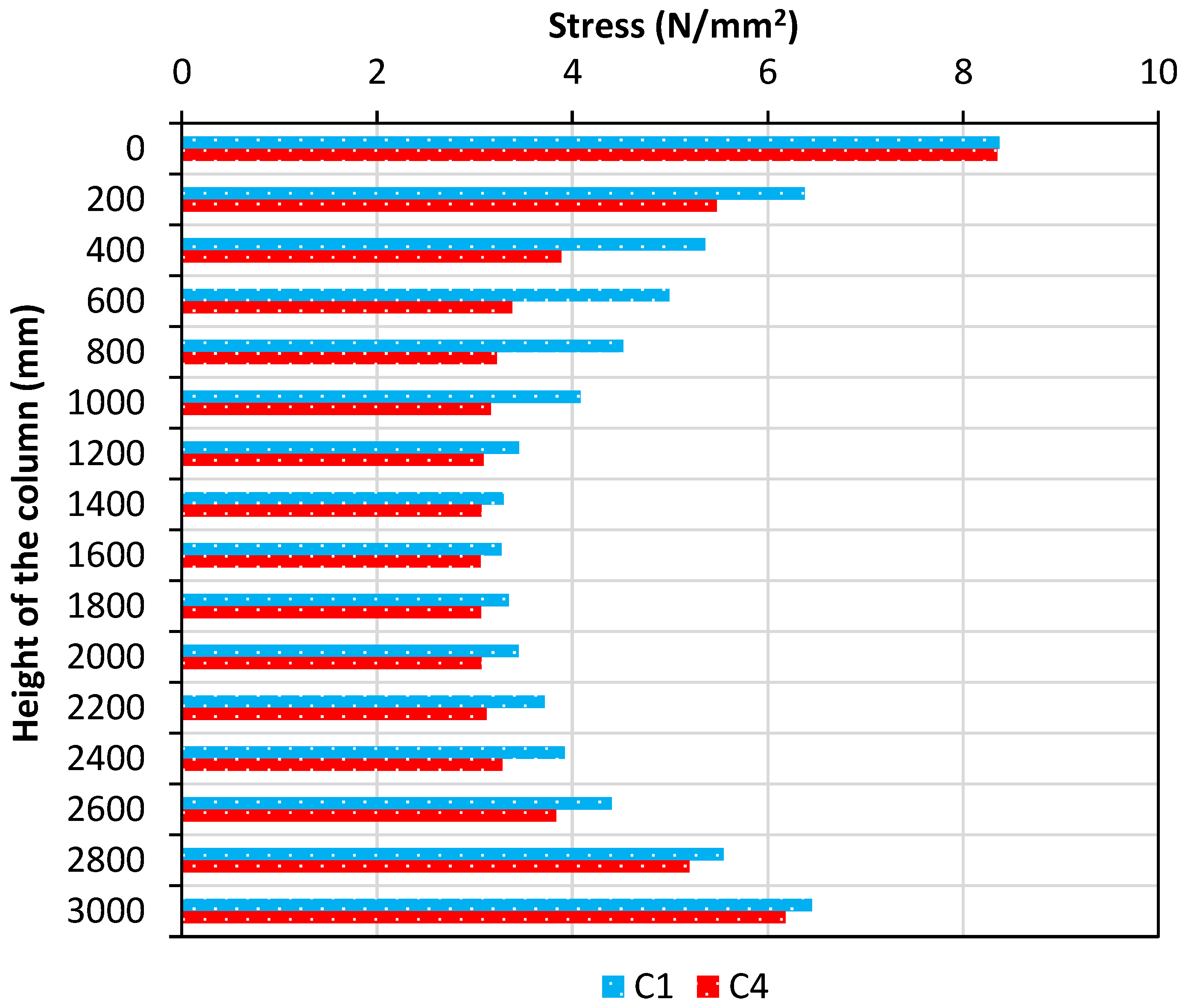
5.10. Stiffness of the Specimens
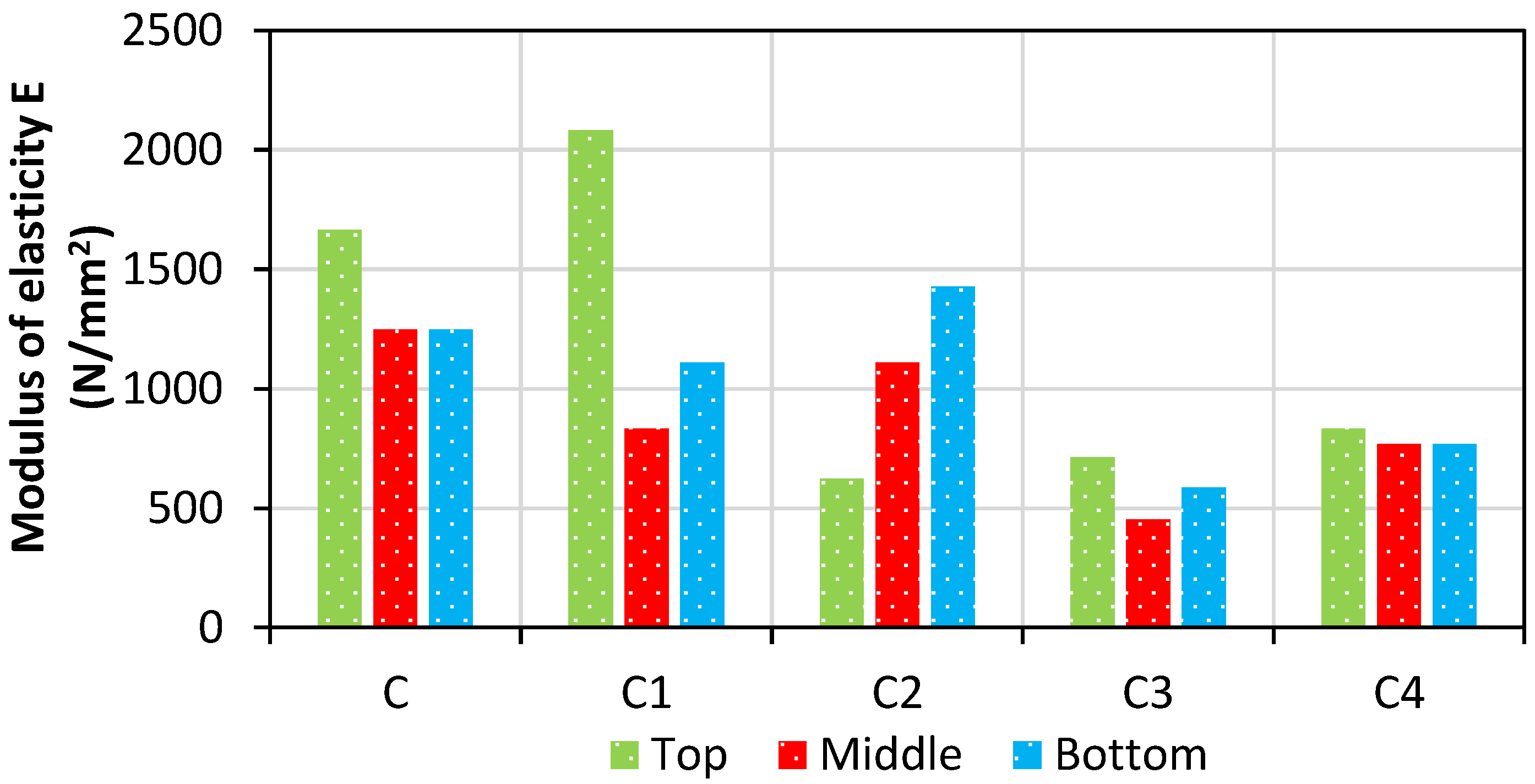
5.11. Modulus of Elasticity of the Specimens
6. Conclusions
- The mimicked specimens show a better heat dissipation nature than the conventional specimen. The rate of cooling was faster in the quenched specimen.
- The quenched specimen undergoes more thermal elongation and contraction as a result of faster heat dissipation; as a result, it generates more cracks on the better heat dissipated specimens.
- The dynamic analysis proved to be one the best structural health monitoring technique and nondestructive testing evaluation method, as the results were found to be satisfactory in the case of fire damage evaluation.
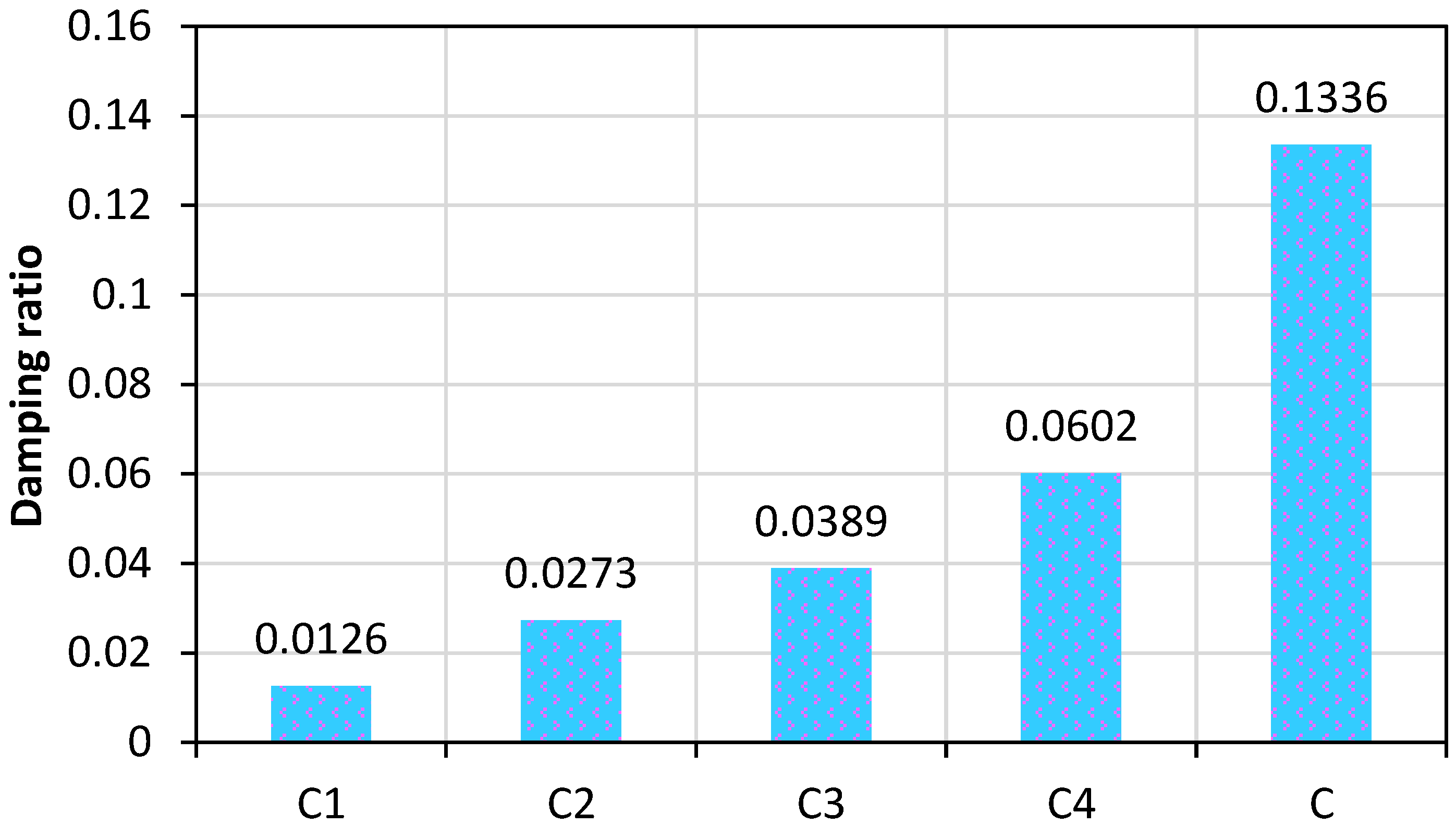
- From the dynamic analysis, the damping ratio of the quenched specimen was reclaimed to be higher than that of the other heated specimens. The damping ratio of the quenched specimen was higher than that of the conventional heated specimen. This eventually shows the intensity of fire damage and the presence of moisture content inside. The X-ray images also prove the presence of moisture content, and they were in good covenant with the results of dynamic analysis.
- The ultimate load of the quenched specimen was found to be less than that of the conventional heated and nonheated specimen, as the quenching effect reduces the overall load-carrying capacity of the column.
- The stiffness of the columns at different regions shows major variation except for the quenched and nonheated column. The quenching effect helps the member maintain its stiffness at almost the same level over the height. Although the stiffness was quantitatively less than that of the nonheated specimen, they followed the same trend. This could eventually prevent the uneven collapse of the member under localized fire conditions.
- The modulus of elasticity calculated at the regions also shows that the quenched specimen maintains uniform strength throughout the height, similar to that of the nonheated specimen.
7. Patents
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, Z.; Shen, J.; Wang, C.; Wu, H. Characterization of sustainable mortar containing high-quality recycled manufactured sand crushed from recycled coarse aggregate. Cem. Concr. Compos. 2022, 132, 104629. [Google Scholar] [CrossRef]
- Ahamed, M.K.; Wang, H.; Hazell, P.J. From biology to biomimicry: Using nature to build better structures—A review. Constr. Build. Mater. 2022, 320, 126195. [Google Scholar] [CrossRef]
- Oguntona, O.A.; Aigbavboa, C.O. Biomimetic reinvention of the construction industry: Energy management and sustainability. Energy Procedia 2017, 142, 2721–2727. [Google Scholar] [CrossRef]
- Charkas, M.N. Towards Environmentally Responsive Architecture: A Framework for Biomimic Design of Building’S Skin. JES J. Eng. Sci. 2019, 47, 371–388. [Google Scholar] [CrossRef]
- Gorb, S.N.; Gorb, E.V. Insect-inspired architecture to build sustainable cities. Curr. Opin. Insect Sci. 2020, 40, 62–70. [Google Scholar] [CrossRef]
- Grigorian, M. Biomimicry and theory of structures-design methodology transfer from trees to moment frames. J. Bionic Eng. 2014, 11, 638–648. [Google Scholar] [CrossRef]
- Yiatros, S.; Wadee, M.A.; Hunt, G.R. The load-bearing duct: Biomimicry in structural design. Proc. Inst. Civ. Eng. Eng. Sustain. 2007, 160, 179–188. [Google Scholar] [CrossRef]
- Hu, Z.; Thiyagarajan, K.; Bhusal, A.; Letcher, T.; Fan, Q.H.; Liu, Q.; Salem, D. Design of ultra-lightweight and high-strength cellular structural composites inspired by biomimetics. Compos. Part B Eng. 2017, 121, 108–121. [Google Scholar] [CrossRef]
- Soltan, D.G.; Ranade, R.; Li, V.C. A Bio-inspired Cementitious Composite for High Energy Absorption in Infrastructural Applications. Blucher Mater. Sci. Proc. 2014, 1, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Nachiar, S.S.; Satyanarayanan, K.S.; Lakshmipathy, M.; Pavithra, S.S. Study on behaviour of compression members based on concept of biomimics. Mater. Today Proc. 2018, 34, 518–524. [Google Scholar] [CrossRef]
- Nachiar, S.S.; Satyanarayanan, K.S.; Lakshmipathy, M. Study on the behaviour of tension member based on the concept of biomimics. Mater. Today Proc. 2018, 34, 371–378. [Google Scholar] [CrossRef]
- Nachiar, S.S.; Satyanarayanan, K.S.; Lakshmipathy, M. Experimental investigation on the behavior of biomimicked columns subjected to compression. Int. J. Civ. Eng. Technol. 2018, 9, 771–778. [Google Scholar]
- Nachiar, S.S.; Shilpa, P.; Satyanarayanan, K.S.; Anandh, S. Modeling and analysis of a pin jointed plane frame using Biomimicked structural elements. Mater. Today Proc. 2021, 50, 259–268. [Google Scholar] [CrossRef]
- Abed, M.S.; Resan, S.F.; Zemam, S.K. Developing knotted slender reinforced concrete column based on bamboo culm biomimicry. Asian J. Civ. Eng. 2022, 23, 99–111. [Google Scholar] [CrossRef]
- Kaluvan, S.; Park, C.Y.; Choi, S.B. Bio-inspired device: A novel smart MR spring featuring tendril structure. Smart Mater. Struct. 2015, 25, 01LT01. [Google Scholar] [CrossRef]
- Fan, J.; He, J.H. Biomimic design of multi-scale fabric with efficient heat transfer property. Therm. Sci. 2012, 16, 1349–1352. [Google Scholar] [CrossRef]
- Reichert, S.; Menges, A.; Correa, D. Meteorosensitive architecture: Biomimetic building skins based on materially embedded and hygroscopically enabled responsiveness. CAD Comput. Aided Des. 2015, 60, 50–69. [Google Scholar] [CrossRef]
- Mathews, M.E.; Kiran, T.; Anand, N.; Lubloy, E.; Naser, M.Z.; Arulraj, G.P. Effect of protective coating on axial resistance and residual capacity of self-compacting concrete columns exposed to standard fire. Eng. Struct. 2022, 264, 114444. [Google Scholar] [CrossRef]
- Li, Y.; Du, P.; Tan, K.H. Fire resistance of ultra-high performance concrete columns subjected to axial and eccentric loading. Eng. Struct. 2021, 248, 113158. [Google Scholar] [CrossRef]
- Xu, L.; Bao, Y.H. Experimental study on the fire resistance of concrete filled steel tube reinforced concrete (CFSTRC) column-RC beam frames. Adv. Struct. Eng. 2021, 24, 2413–2426. [Google Scholar] [CrossRef]
- Yang, D.; Liu, F.; Huang, S.-S.; Yang, H. Structural fire safety design of square and rectangular tubed-reinforced-concrete columns. Structures 2020, 29, 1286–1321. [Google Scholar] [CrossRef]
- Wen, B.; Zhang, L.; Wu, B.; Niu, D.; Wang, L.; Zhang, Y. Fire resistance of earthquake damaged reinforced concrete columns. Struct. Infrastruct. Eng. 2021, 18, 1–23. [Google Scholar] [CrossRef]
- Du, P.; Yang, Y.; Tan, K.H. Fire behaviour and design of hybrid fibre reinforced high-performance concrete columns subjected to uniaxial bending. Eng. Struct. 2022, 251, 113425. [Google Scholar] [CrossRef]
- Chen, Z.; Liao, H.; Zhou, J.; Ye, P. Eccentric compression behavior of reinforced recycled aggregate concrete columns after exposure to elevated temperatures: Experimental and numerical study. Structures 2022, 43, 959–976. [Google Scholar] [CrossRef]
- Gernay, T. Fire resistance and burnout resistance of reinforced concrete columns. Fire Saf. J. 2019, 104, 67–78. [Google Scholar] [CrossRef]
- Tan, K.H.; Yao, Y. Fire Resistance of Four-Face Heated Reinforced Concrete Concrete Columns. Beton-Und Stahlbetonbau 2003, 103, 472–481. [Google Scholar] [CrossRef]
- Buch, S.H.; Sharma, U.K. Statistical Review of the Fire Resistance of Concrete Columns. Arab. J. Sci. Eng. 2022. [Google Scholar] [CrossRef]
- Naser, M.Z.; Kodur, V.K. Explainable machine learning using real, synthetic and augmented fire tests to predict fire resistance and spalling of RC columns. Eng. Struct. 2022, 253, 113824. [Google Scholar] [CrossRef]
- Buch, S.H.; Sharma, U.K. Empirical model for determining fire resistance of Reinforced Concrete columns. Constr. Build. Mater. 2019, 225, 838–852. [Google Scholar] [CrossRef]
- Bajc, U.; Kolšek, J.; Planinc, I.; Bratina, S. Fire resistance of RC columns with regard to spalling of concrete. Fire Saf. J. 2022, 130, 103568. [Google Scholar] [CrossRef]
- Yu, M.; Hu, X.; Xu, L.; Cheng, S. A general unified method for calculating fire resistance of CFST columns considering various types of steel and concrete. J. Build. Eng. 2022, 59, 105125. [Google Scholar] [CrossRef]
- Rahnavard, R.; Craveiro, H.D.; Simões, R.A.; Laím, L.; Santiago, A. Fire resistance of concrete-filled cold-formed steel (CF-CFS) built-up short columns. J. Build. Eng. 2021, 48, 103854. [Google Scholar] [CrossRef]
- Fellouh, A.; Bougara, A.; Piloto, P.; Benlakehal, N. Fire resistance of partially encased composite columns subjected to eccentric loading. J. Struct. Fire Eng. 2022, 13, 451–469. [Google Scholar] [CrossRef]
- Shao, Z.; Zha, X.; Wan, C. Design method of fire-resistance capacity of reinforced-concrete-filled steel tube column under axial compression. Fire Saf. J. 2022, 129, 103572. [Google Scholar] [CrossRef]
- Kong, W.; Fu, C.; Liu, W. Study on the Deformation Behaviour of Reinforced Concrete Beam-Supporting Column Transfer Structures during Fire Exposure. KSCE J. Civ. Eng. 2022, 26, 2765–2779. [Google Scholar] [CrossRef]
- Possidente, L.; Weiss, A.; de Silva, D.; Pustorino, S.; Nigro, E.; Tondini, N. Fire safety engineering principles applied to a multi-storey steel building. Proc. Inst. Civ. Eng. Struct. Build. 2021, 174, 725–738. [Google Scholar] [CrossRef]
- Santarpia, L.; Bologna, S.; Ciancio, V.; Golasi, I.; Salata, F. Fire temperature based on the time and resistance of buildings—predicting the adoption of fire safety measures. Fire 2019, 2, 19. [Google Scholar] [CrossRef] [Green Version]
- Mullins-jaime, C.; Smith, T.D. Nanotechnology in Residential Building Materials for Better Fire Protection and Life Safety Outcomes. Fire 2022, 5, 174. [Google Scholar] [CrossRef]
- van Coile, R.; Hopkin, D.; Elhami-Khorasani, N.; Gernay, T. Demonstrating adequate safety for a concrete column exposed to fire, using probabilistic methods. Fire Mater. 2021, 45, 918–928. [Google Scholar] [CrossRef]
- Parthasarathi, N.; Satyanarayanan, K.S.; Prakash, M.; Farsangi, E.N.; Thirumurugan, V.; Srinivasasenthil, S. Progressive collapse evaluation of RC frames under high-temperature conditions: Experimental and finite element investigations. Structures 2022, 41, 375–388. [Google Scholar] [CrossRef]
- Wickström, U. Temperature Calculation in Fire Safety Engineering; Springer Nature: Berlin, Germany, 2016. [Google Scholar] [CrossRef]
- Chetti, M.B.; Nobel, P.S. Recovery of photosynthetic reactions after high-temperature treatments of a heat-tolerant cactus. Photosynth. Res. 1988, 18, 277–286. [Google Scholar] [CrossRef]
- Lewis, D.A.; Nobel, P.S. Thermal Energy Exchange Model and Water Loss of a Barrel Cactus, Ferocactus acanthodes. Plant Physiol. 1977, 60, 609–616. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Walker, L.R. The Saguaro Cactus: A Natural History. By David Yetman, Alberto Búrquez, Kevin Hultine, and Michael Sanderson. West. Hist. Q. 2020, 51, 487–488. [Google Scholar] [CrossRef]
- IS 456. Concrete, Plain and Reinforced. Bur. Indian Stand. Dehli 2000, 1–114.
- Vishal, M.; Satyanarayanan, K.; Thirumurugan, V. Analytical investigation on behavior of three-dimensional reinforced concrete frames under thermal effect. Mater. Today: Proc. 2021, 50, 248–252. [Google Scholar] [CrossRef]
- Murugan, V.; Srinivasan, S.K. Influence of cover thickness in structural frames exposed to fire and service loads. Environ. Sci. Pollut. Res. 2021, 29, 85955–85968. [Google Scholar] [CrossRef]
- Vishal, M.; Satyanarayanan, K.S. Analytical Investigation on Progressive Collapse of 3-D Reinforced Concrete Frames under High Temperature. In Resilient Infrastructure; Springer: Singapore, 2022; pp. 269–279. [Google Scholar]
- Cuong-Le, T.; le Minh, H.; Sang-To, T. A nonlinear concrete damaged plasticity model for simulation reinforced concrete structures using ABAQUS. Frat. ed Integrita Strutt. 2021, 16, 232–242. [Google Scholar] [CrossRef]
- EN 1991-1-7. Eurocode 1—Action on structures—Part 1–7: General actions—Accidental actions. Eur. Comm. Stand. 2006, 54, 18–20. [CrossRef] [Green Version]
- ISO 834-11; Fire Resistance Tests—Elements of Building Construction. Part 11 Specif. Requir. Assess. Fire Prot. to Strucutral Steel Elem. ISO: Geneva, Switzerland, 2014.
- Usmani, A.S.; Rotter, J.M.; Lamont, S.; Sanad, A.M.; Gillie, M. Fundamental principles of structural behaviour under thermal effects. Fire Saf. J. 2001, 36, 721–744. [Google Scholar] [CrossRef]
- Singh, T.; Sehgal, S.; Prakash, C.; Dixit, S. Real-Time Structural Health Monitoring and Damage Identification Using Frequency Response Functions along with Finite Element Model Updating Technique. Sensors 2022, 22, 4546. [Google Scholar] [CrossRef]
- Pranno, A.; Greco, F.; Lonetti, P.; Luciano, R.; de Maio, U. An improved fracture approach to investigate the degradation of vibration characteristics for reinforced concrete beams under progressive damage. Int. J. Fatigue 2022, 163, 107032. [Google Scholar] [CrossRef]
- Altunişik, A.C.; Akbulut, Y.E.; Başağa, H.B.; Mostofi, S.; Mosallam, A.; Wafa, L.F. Experimental Investigation on Dynamic Characteristics Changes of Fire Exposed Reinforced Concrete and Steel Members. Fire Technol. 2021, 58, 1169–1208. [Google Scholar] [CrossRef]
- Pul, S.; Atasoy, A.; Senturk, M.; Hajirasouliha, I. Structural performance of reinforced concrete columns subjected to high-temperature and axial loading under different heating-cooling scenarios. J. Build. Eng. 2021, 42, 102477. [Google Scholar] [CrossRef]
- Li, Y.; Yang, E.H.; Tan, K.H. Effects of heating followed by water quenching on strength and microstructure of ultra-high performance concrete. Constr. Build. Mater. 2019, 207, 403–411. [Google Scholar] [CrossRef]








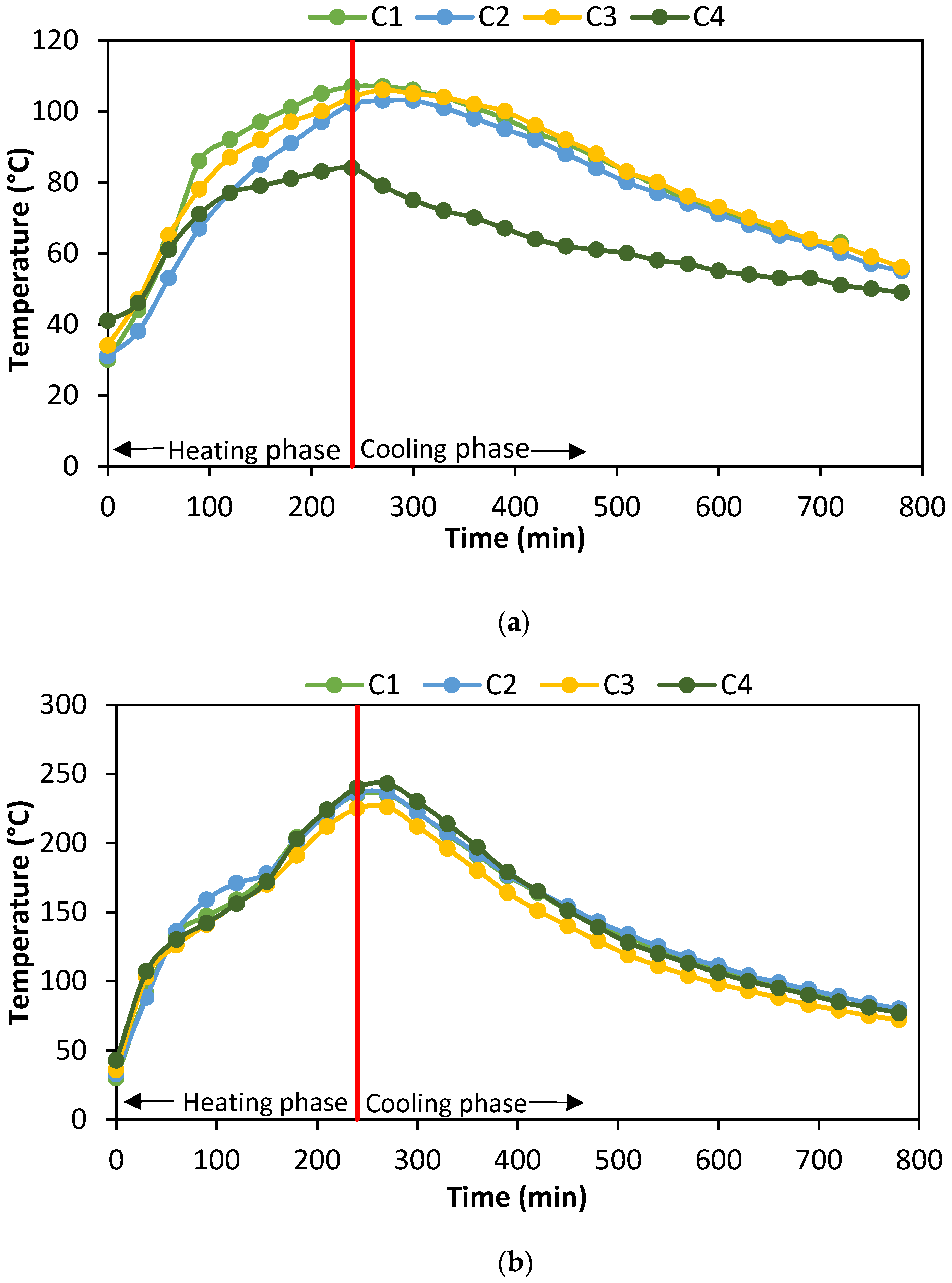
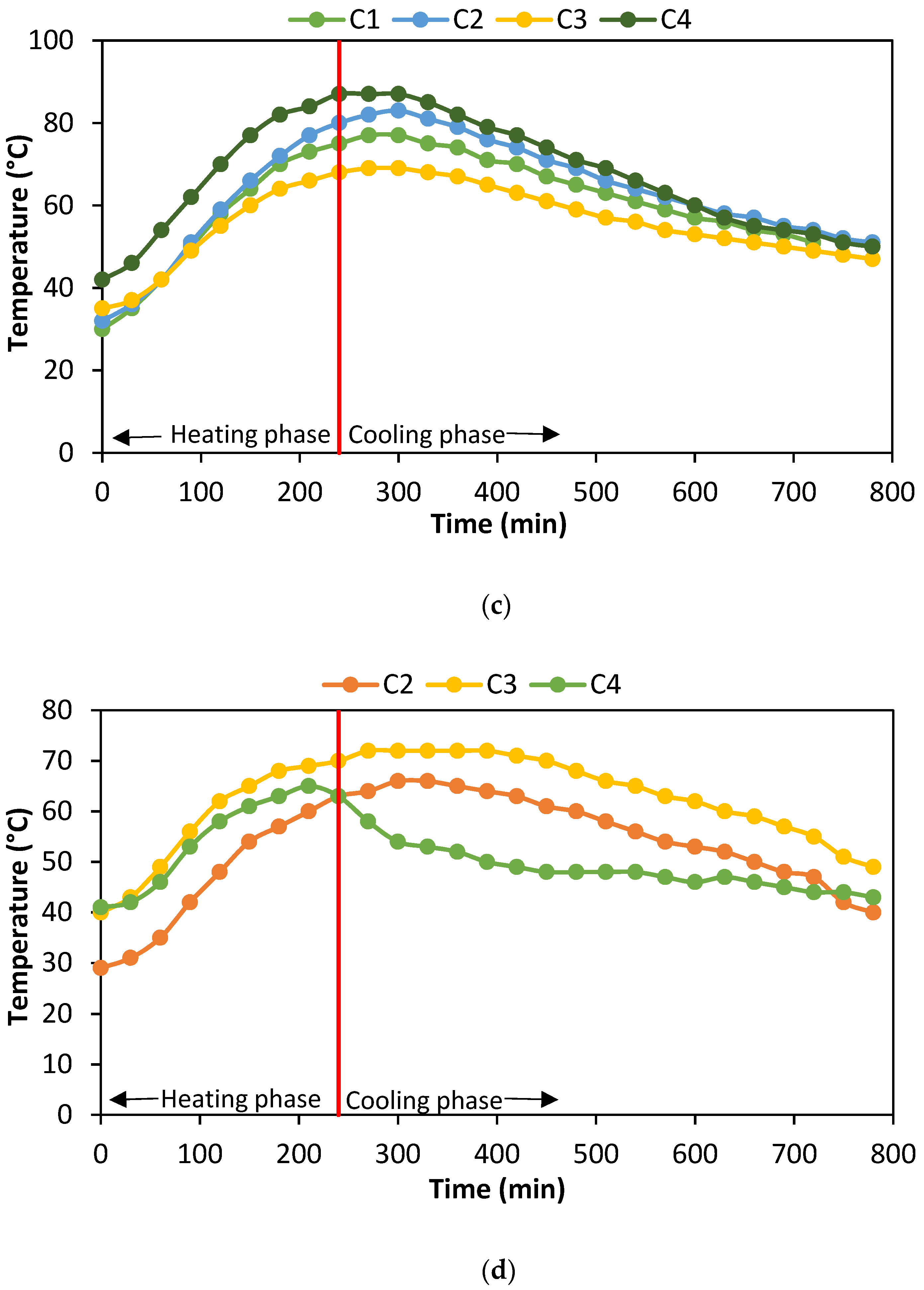
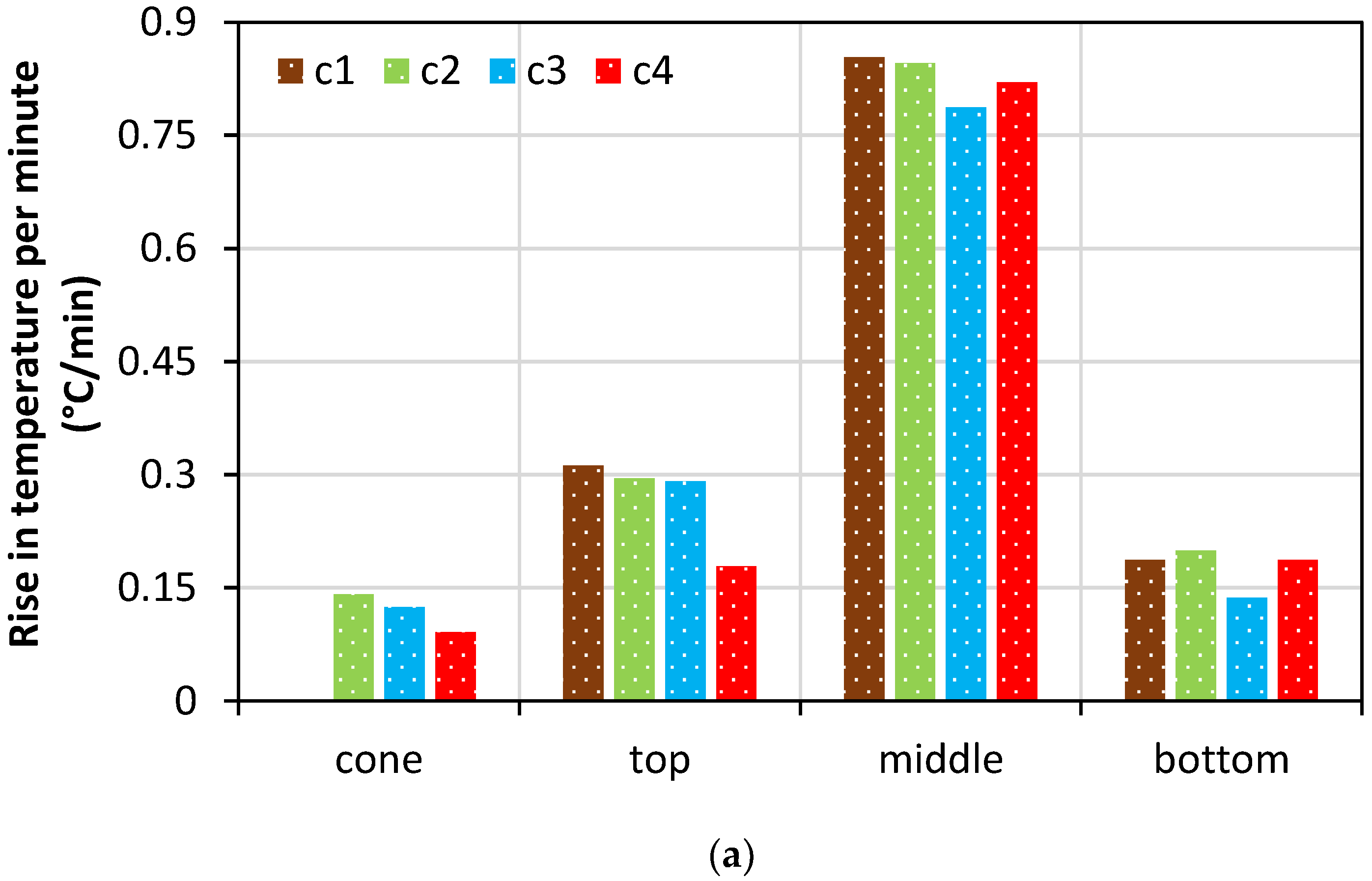
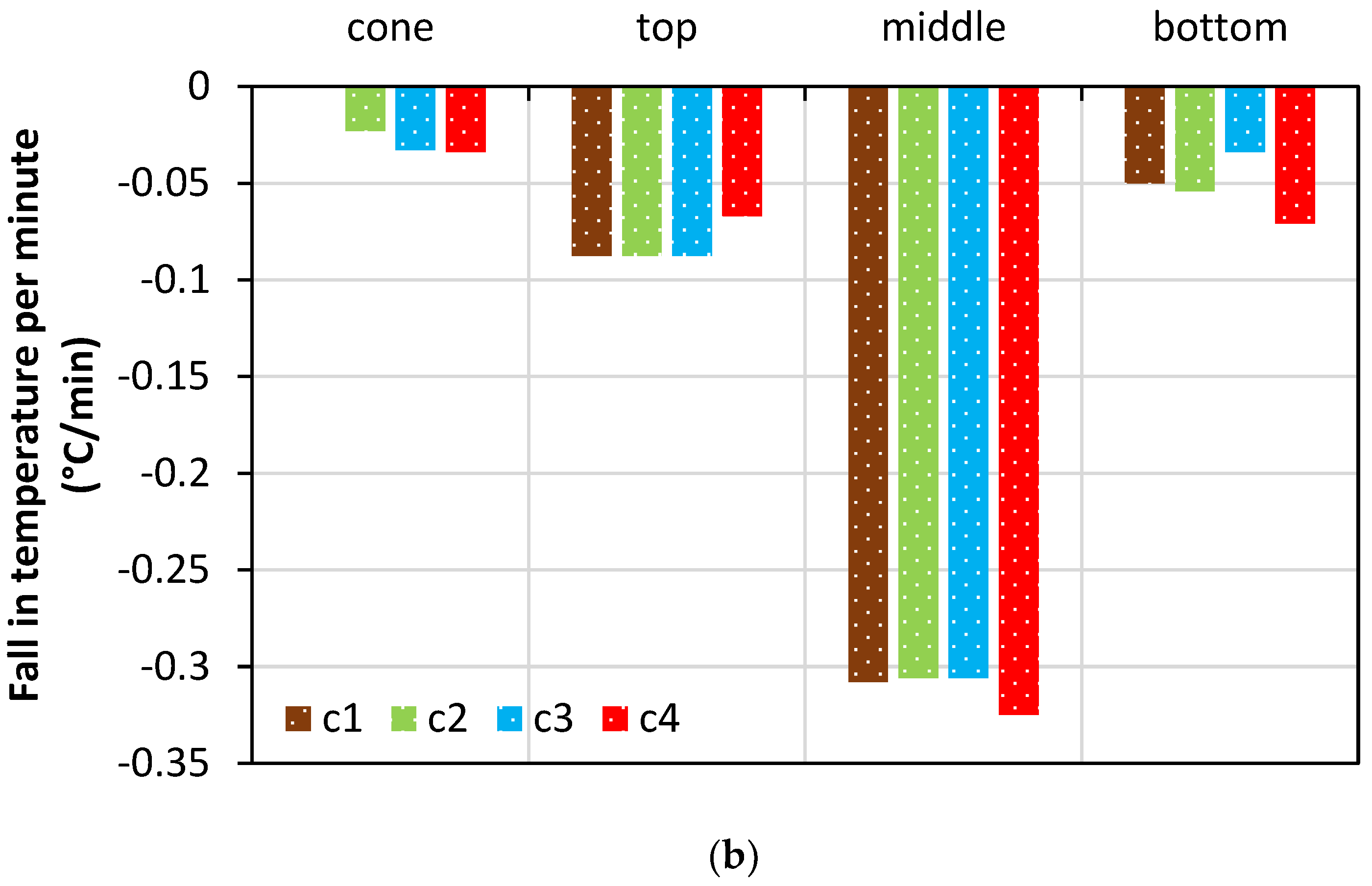
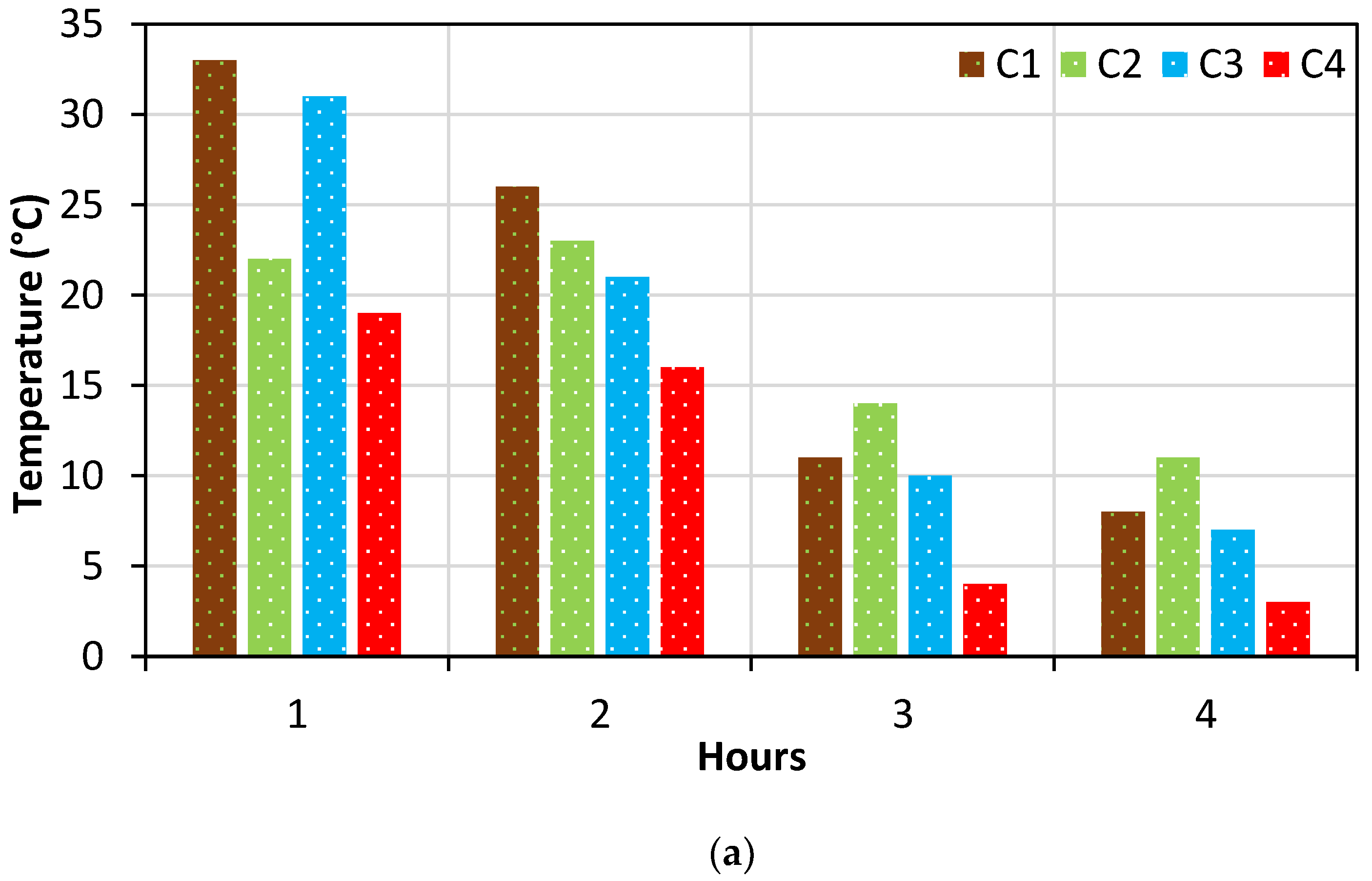
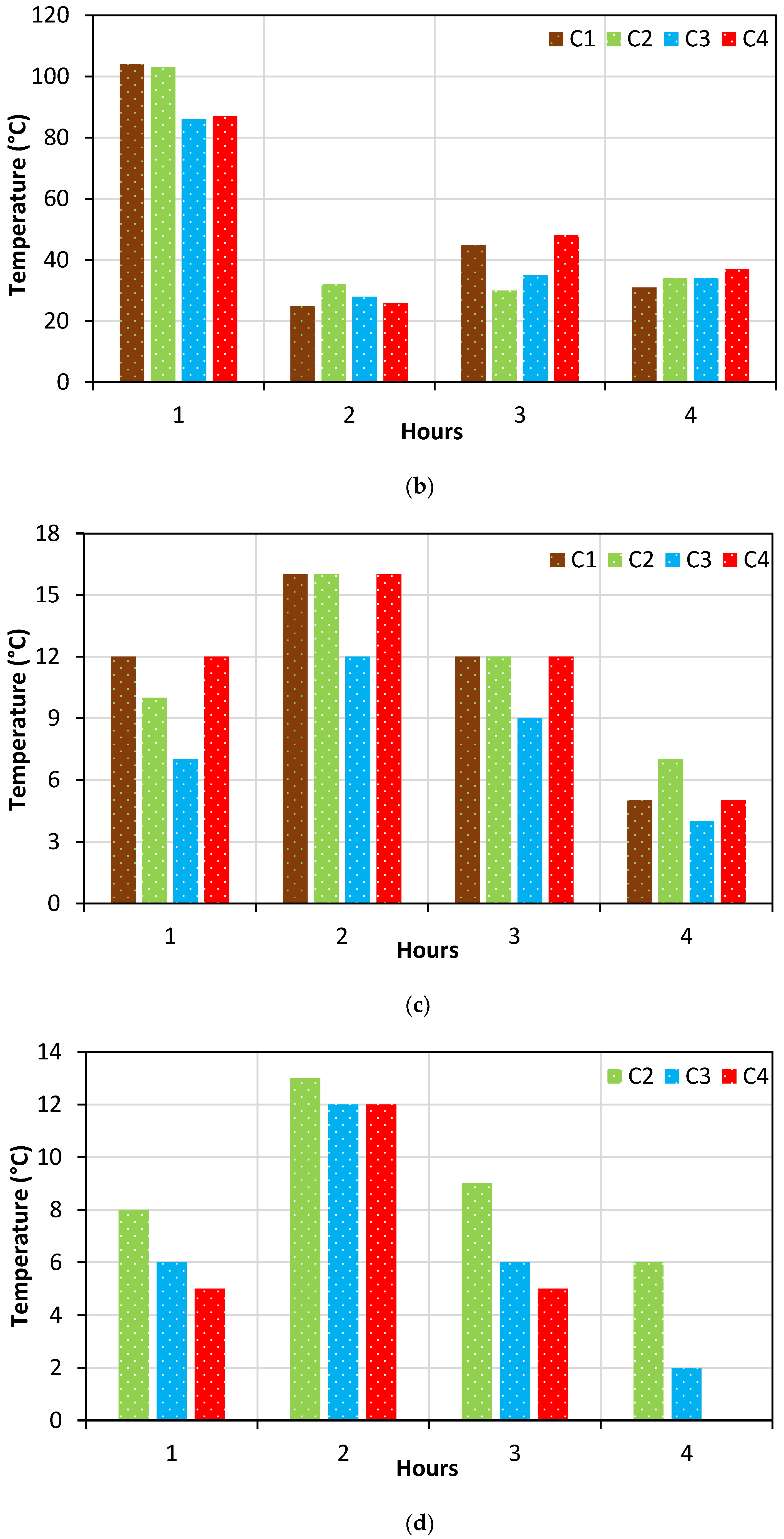





| Room Temperature ( °C) | Humidity (%) | Temperature in Cone ( °C) | Temperature in Top ( °C) | Temperature in Middle ( °C) | Temperature in Bottom ( °C) | |
|---|---|---|---|---|---|---|
| C1 | 31 | 69 | - | 30 | 30 | 30 |
| C2 | 29 | 71 | 29 | 31 | 33 | 32 |
| C3 | 39 | 66 | 40 | 34 | 36 | 35 |
| C4 | 39 | 90 | 41 | 41 | 43 | 42 |
| Specimen | Maximum Temperature Reached with Respect to Time | |||
|---|---|---|---|---|
| Cone | Top | Middle | Bottom | |
| C1 | - | 108 °C at 280 min | 238 °C at 250 min | 78 °C at 280 min |
| C2 | 66 °C at 290 min | 103 °C at 256 min | 239 °C at 250 min | 83 °C at 292 min |
| C3 | 73 °C at 312 min | 106 °C at 264 min | 230 °C at 254 min | 69 °C at 248 min |
| C4 | 64 °C at 190 min | 84 °C at 212 min | 245 °C at 256 min | 87 °C at 228 min |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vishal, M.; Satyanarayanan, K.S. Experimental Investigation on the Heat Dissipation and Postfire Structural Performance of a Reinforced Concrete Column with Biomimicked Geometry. Fire 2022, 5, 205. https://doi.org/10.3390/fire5060205
Vishal M, Satyanarayanan KS. Experimental Investigation on the Heat Dissipation and Postfire Structural Performance of a Reinforced Concrete Column with Biomimicked Geometry. Fire. 2022; 5(6):205. https://doi.org/10.3390/fire5060205
Chicago/Turabian StyleVishal, M., and K.S. Satyanarayanan. 2022. "Experimental Investigation on the Heat Dissipation and Postfire Structural Performance of a Reinforced Concrete Column with Biomimicked Geometry" Fire 5, no. 6: 205. https://doi.org/10.3390/fire5060205
APA StyleVishal, M., & Satyanarayanan, K. S. (2022). Experimental Investigation on the Heat Dissipation and Postfire Structural Performance of a Reinforced Concrete Column with Biomimicked Geometry. Fire, 5(6), 205. https://doi.org/10.3390/fire5060205






