Wildfire Risk Zone Mapping in Contrasting Climatic Conditions: An Approach Employing AHP and F-AHP Models
Abstract
:1. Introduction
2. Materials and Methods
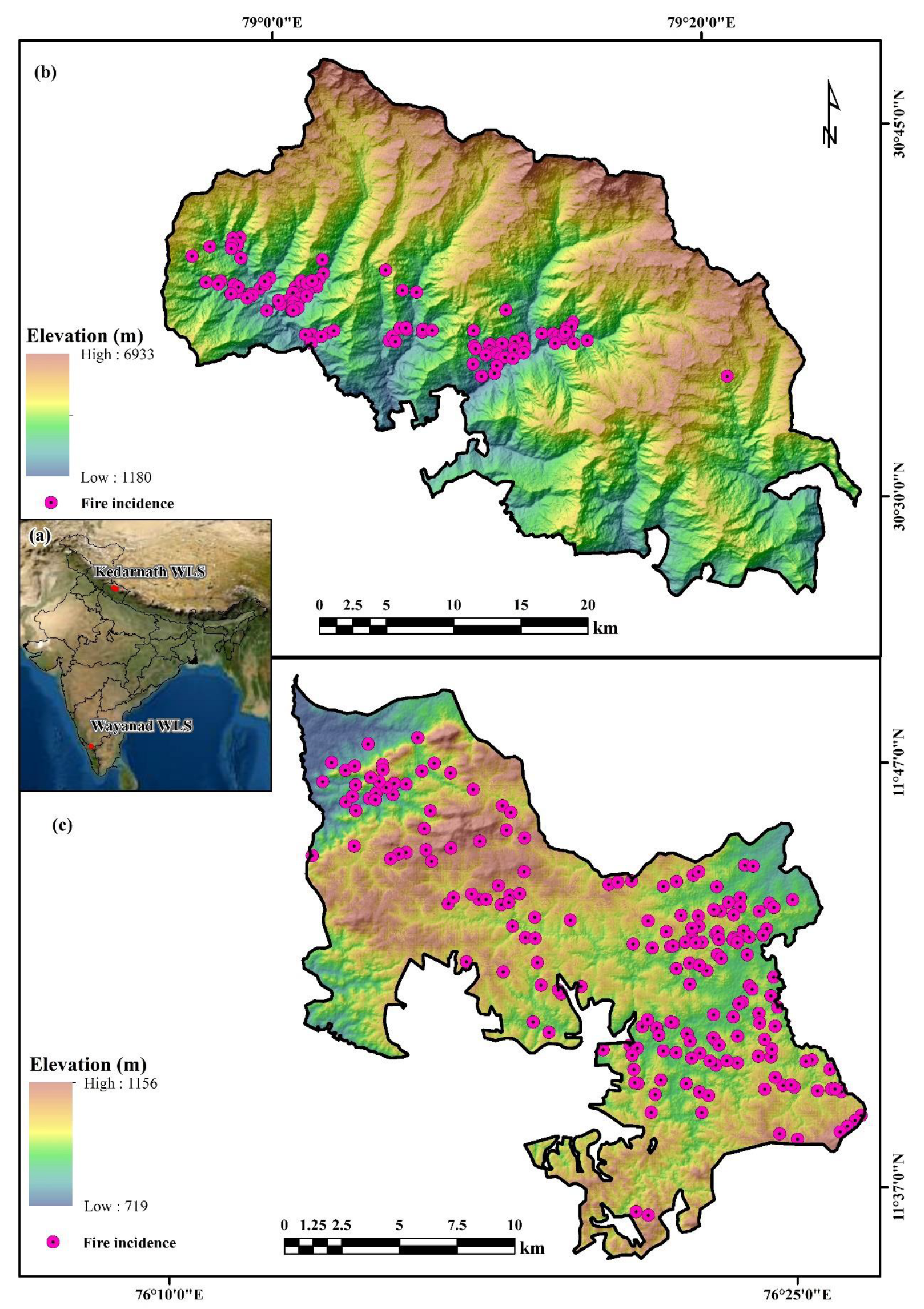
2.1. Study Area
2.1.1. Kedarnath Wildlife Sanctuary (KWLS)
2.1.2. Wayanad Wildlife Sanctuary (WWLS)
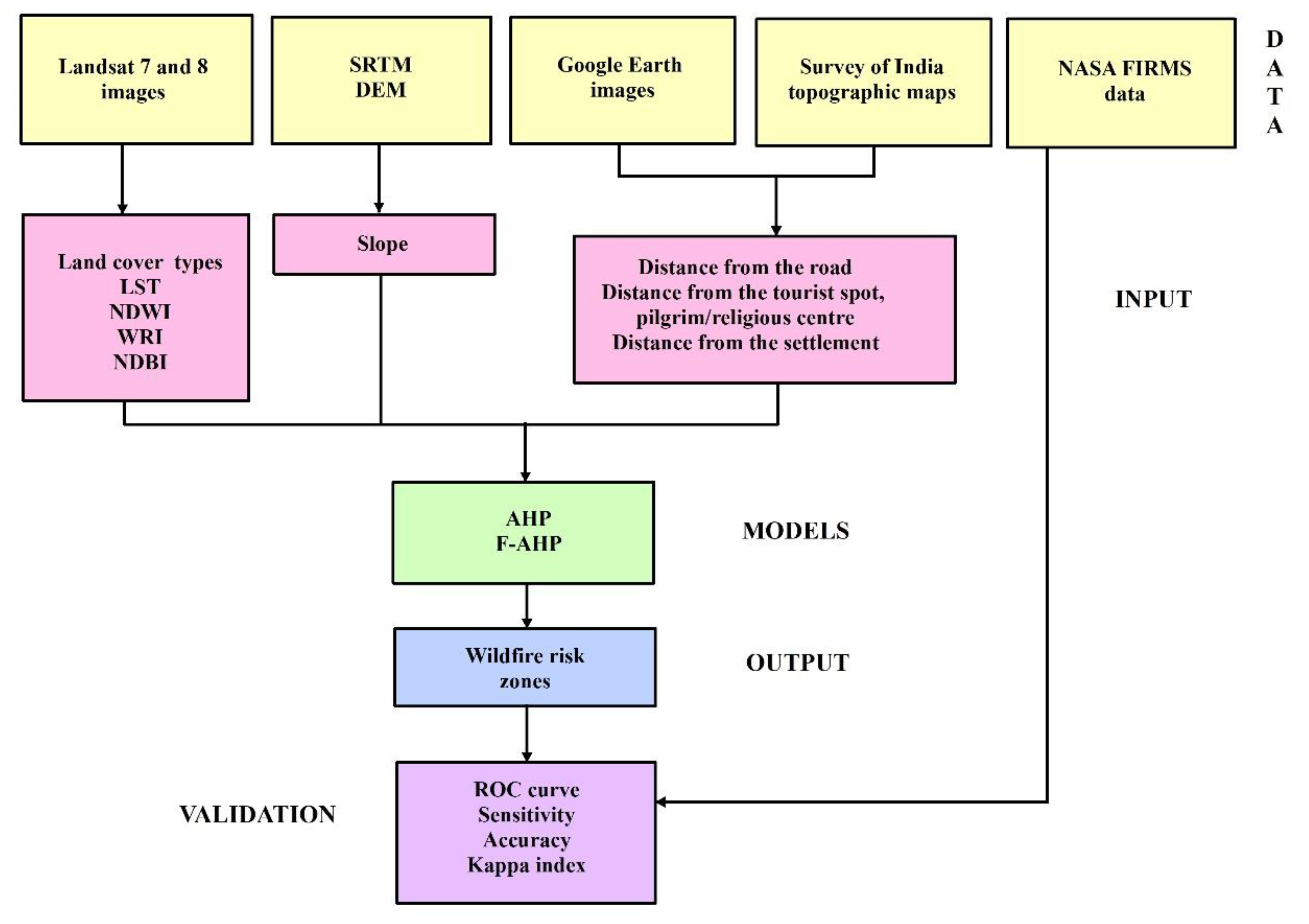
2.2. Data Source and Major Steps
- 1.
- Data were gathered from a variety of sources; both primary and secondary (Table 1). ArcGIS 10.8 (Esri, Inc., Redlands, CA, USA) and ERDAS Imagine 9.2 (Hexagon AB, Stockholm, Sweden) were used to create the thematic layers for these different factors.
- 2.
- The layers of continuous factors such as the slope, Land Surface Temperature (LST), Normalized Difference Water Index (NDWI), distance from the road, distance from the major tourist spot and pilgrim/religious center, distance from the settlement, Water Ratio Index (WRI), and Normalized Difference Built-up Index (NDBI) were classified using the Natural breaks method [57,68].
- 3.
- The multicollinearity of factors was tested employing the Variance Inflation Factor (VIF) and tolerance.
- 4.
- The risk zone maps were created employing the AHP and F-AHP models. MS Excel and FisPro 3.8 (https://www.fispro.org/en/ (accessed on 11 August 2022)) [69,70] were employed to derive the weights of the AHP and F-AHP models, respectively (Figure 2).
- 5.
- 6.
- The risk zone maps were validated utilizing the ROC curve method and other statistical validation matrices such as sensitivity, accuracy, and Kappa index, and the R 4.2.1 (The R Foundation for Statistical Computing, Vienna, Austria) software was employed for the validation of the maps.
2.3. Creation of Wildfire Inventory
2.4. Derivation of Conditioning Factors
- i.
- Transformation of the Digital Number (DN) to Spectral Radiance (Lλ)
- ii.
- Transformation of Spectral Radiance to At-Satellite Brightness Temperatures
- iii.
- LST Estimation
- iv.
- Conversion of Kelvin to Degree Celsius
2.5. Multi-Collinearity Test
2.6. AHP Modeling
2.7. F-AHP Modelling
2.8. Validation of the Maps
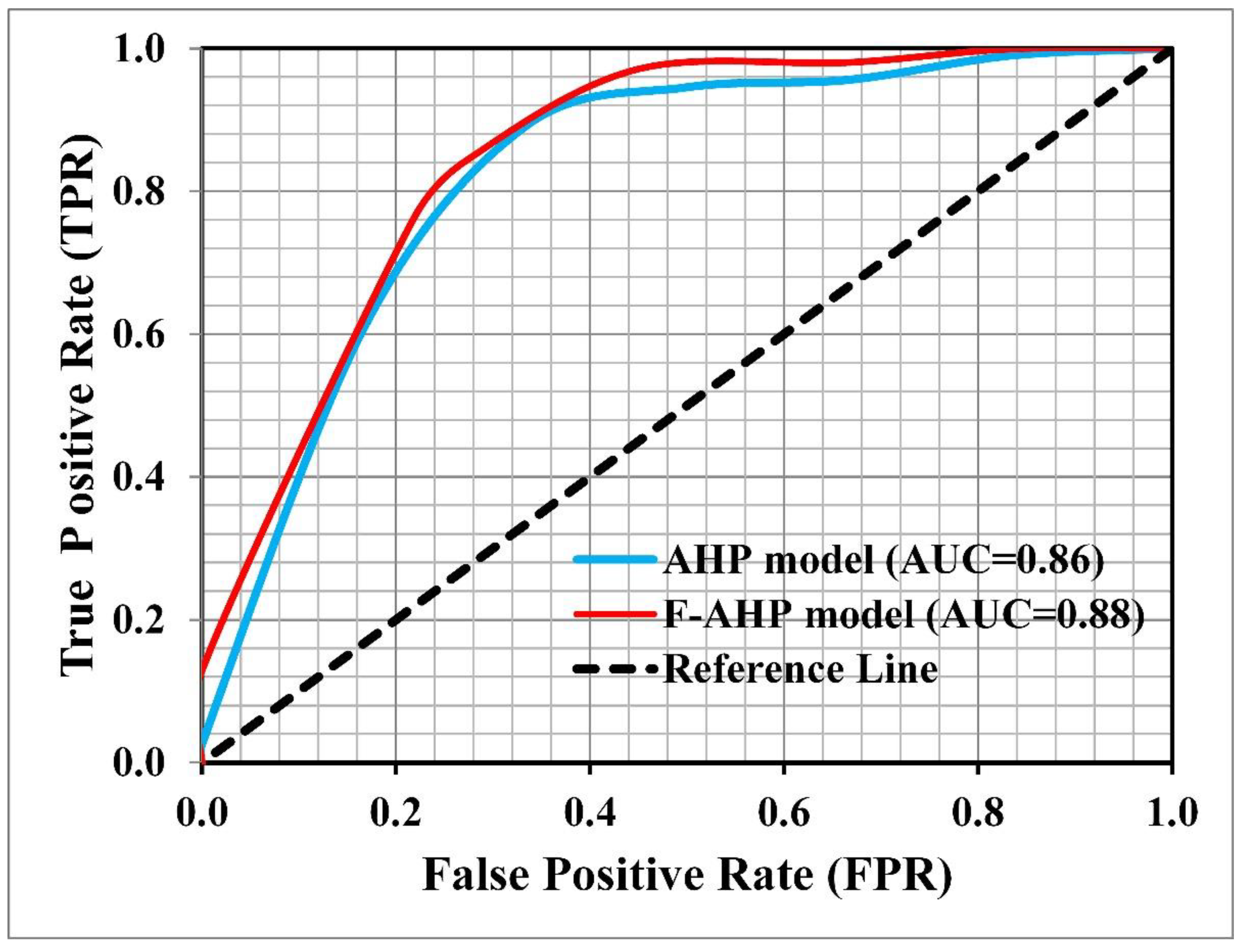
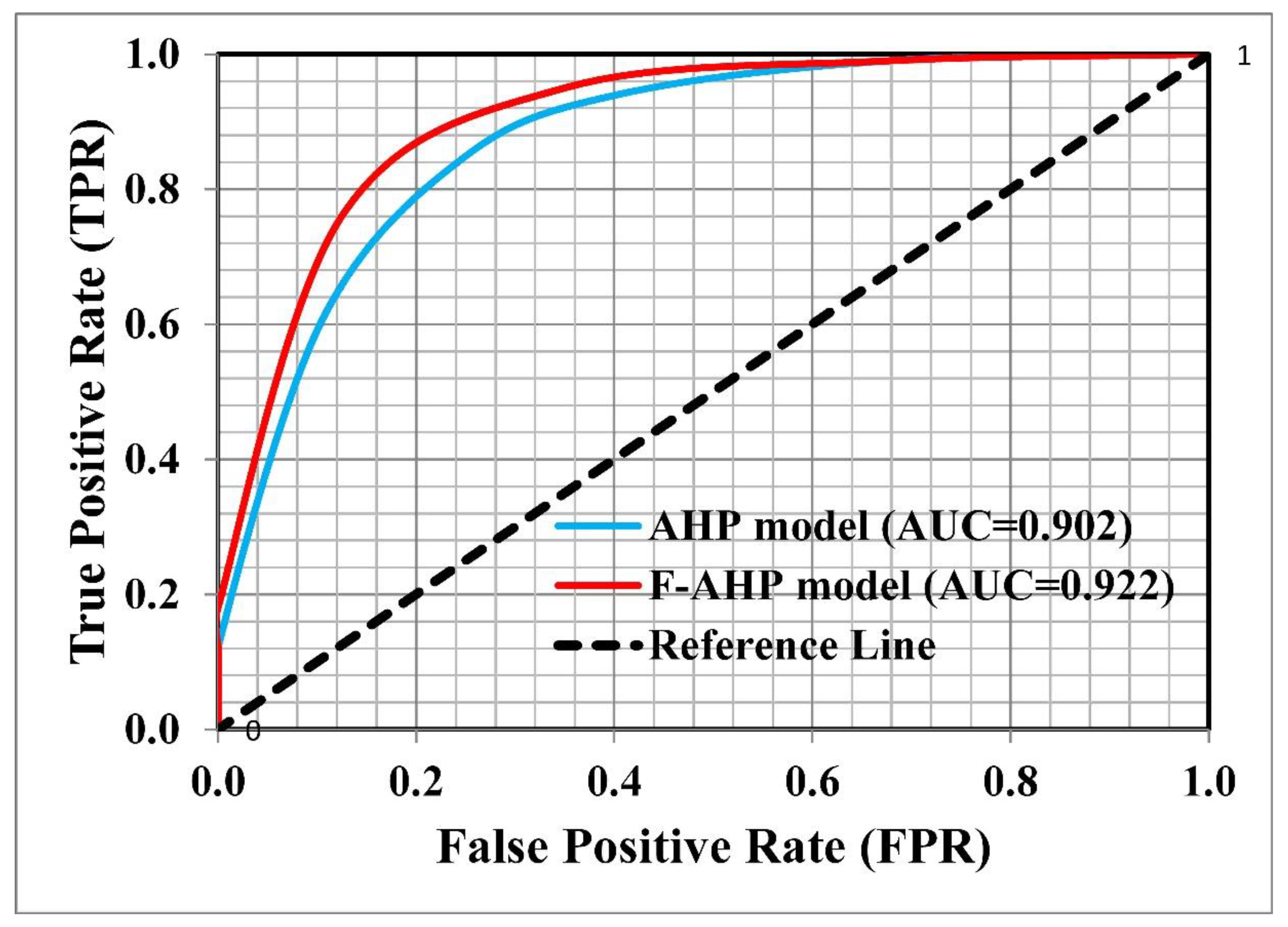
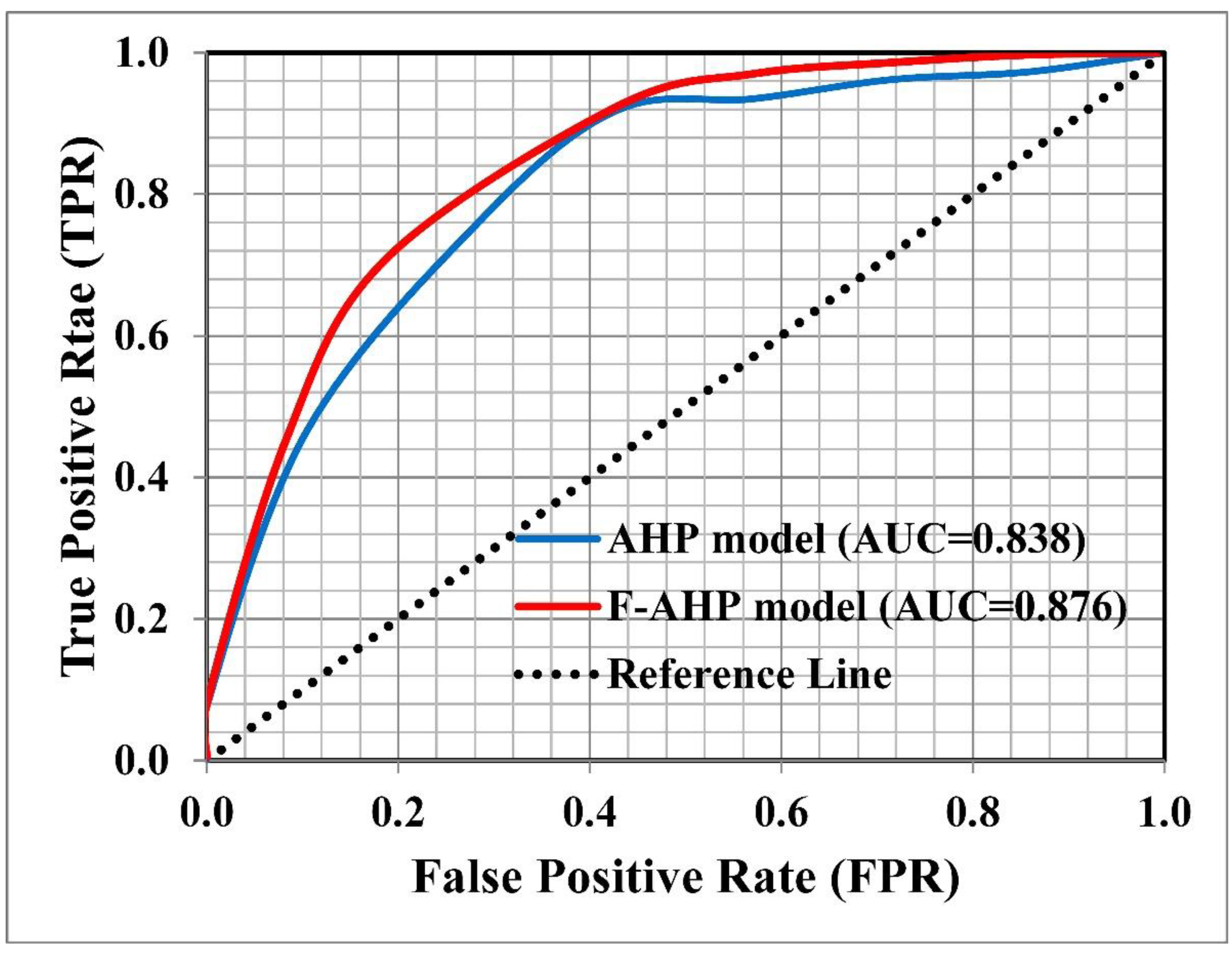
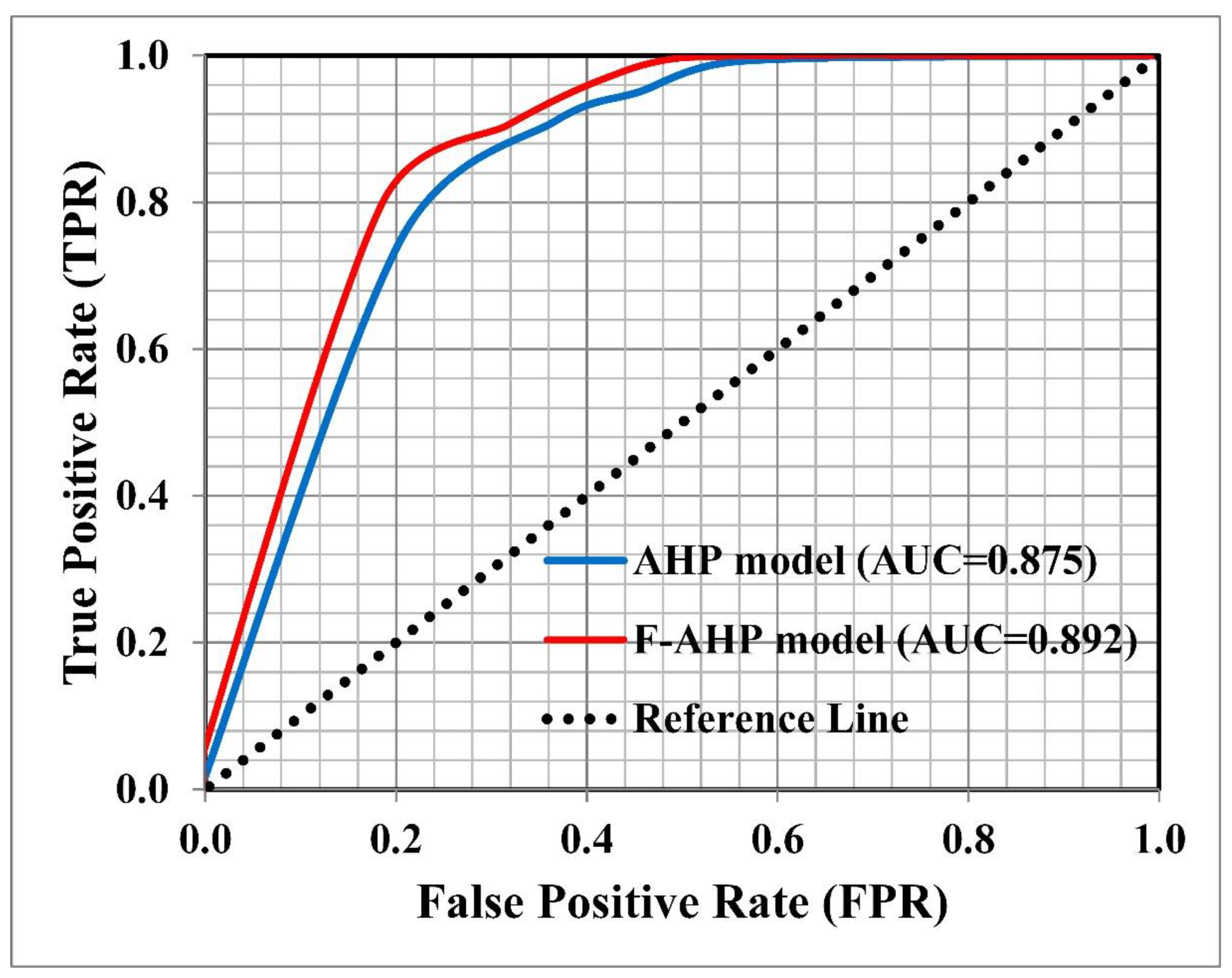
2.8.1. ROC Curve
2.8.2. Sensitivity and Accuracy
2.8.3. Kappa Index
3. Results
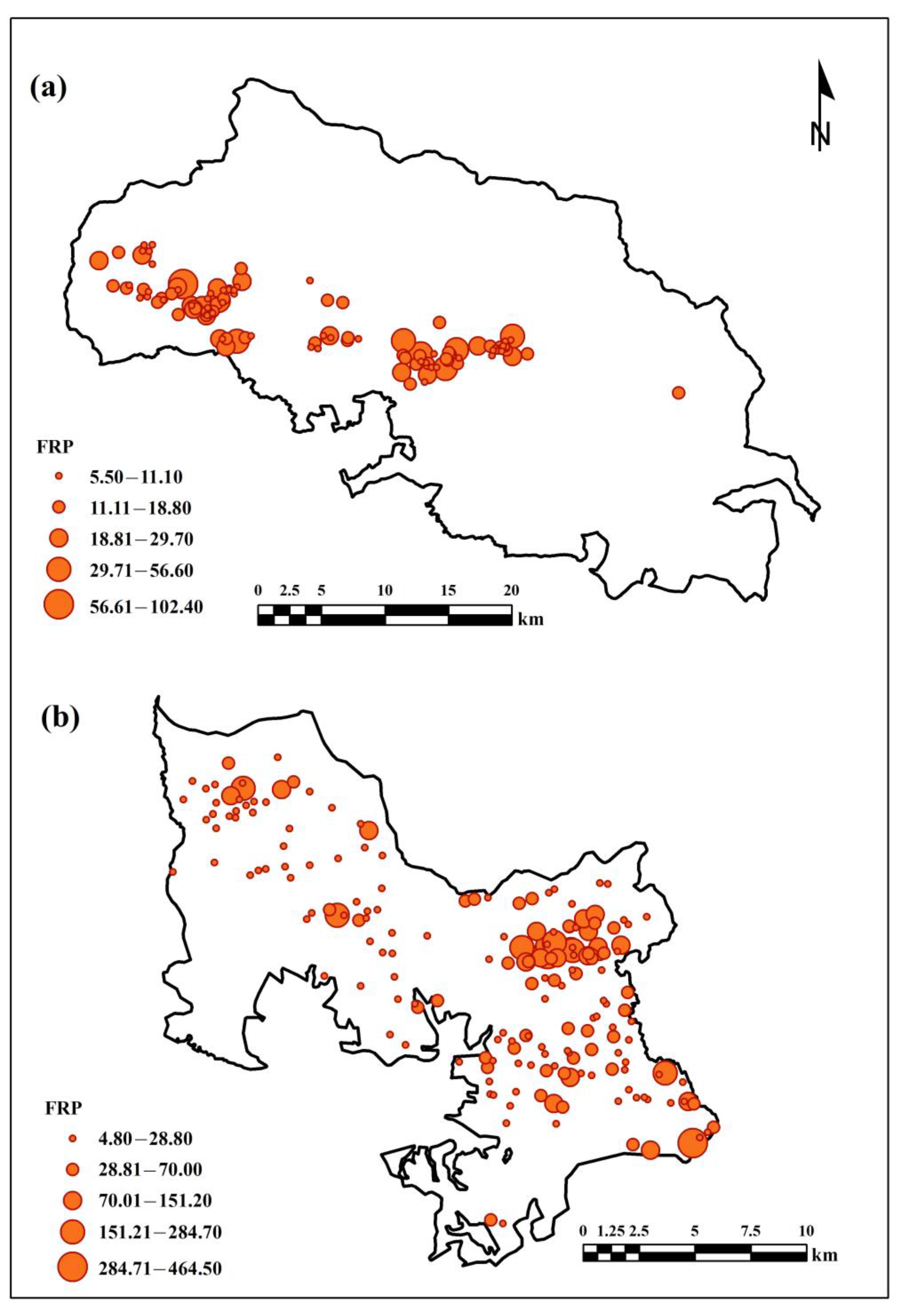
3.1. Fire Radiative Power (FRP) Distribution
3.2. Multi-Collinearity Analysis
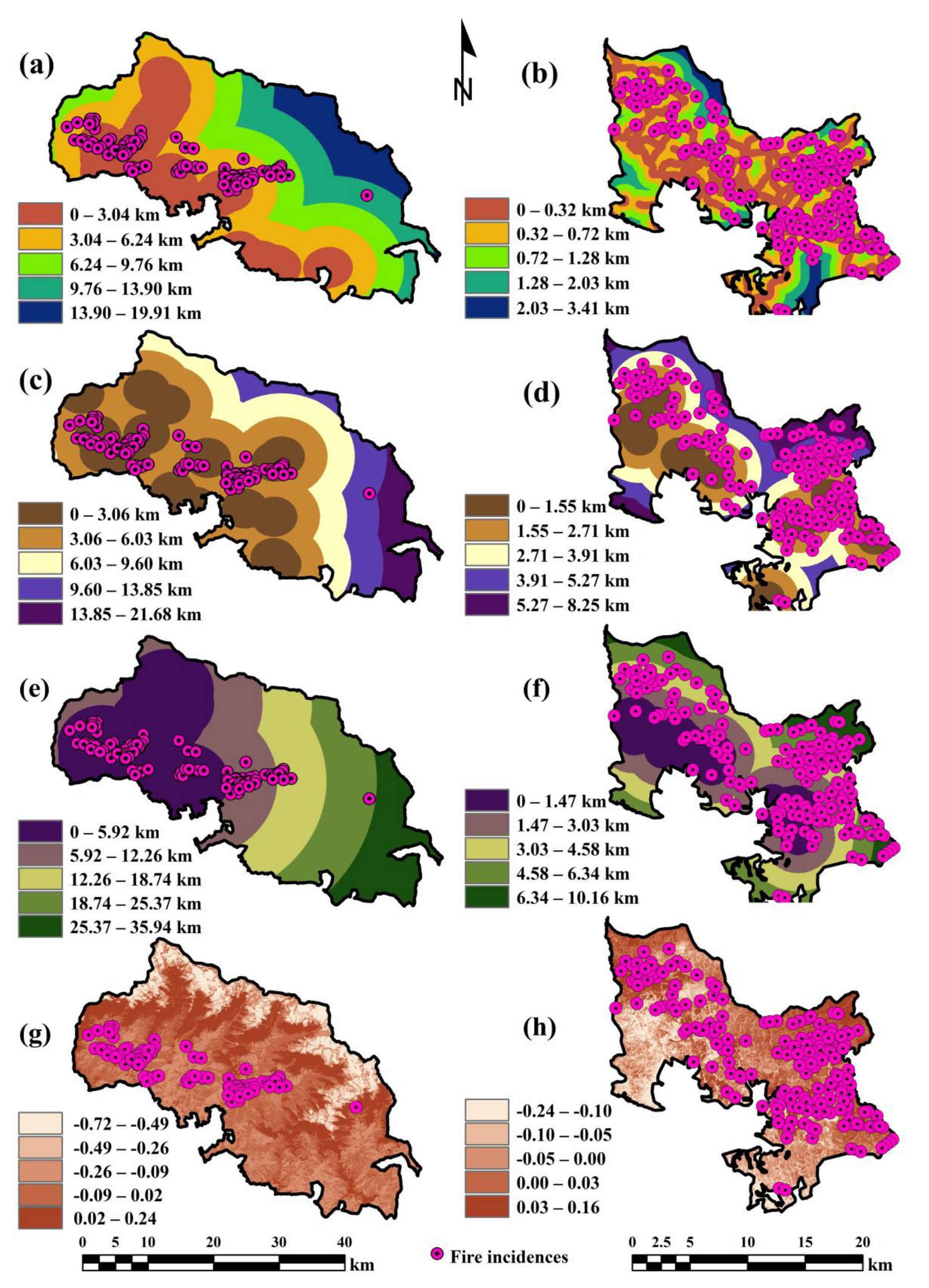
3.3. Conditioning Factors
3.3.1. LST
3.3.2. Land Cover Types
3.3.3. Slope
3.3.4. WRI
3.3.5. NDWI
3.3.6. Distance from the Road
3.3.7. Distance from the Tourist Spot, and Pilgrim/Religious Center
3.3.8. Distance from the Settlement
3.3.9. NDBI
3.4. Wildfire Risk Zones
3.5. Validation of the Risk Zone Maps
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reddy, C.S.; Bird, N.G.; Sreelakshmi, S.; Manikandan, T.M.; Asra, M.; Krishna, P.H.; Jha, C.S.; Rao, P.V.N.; Diwakar, P.G. Identification and characterization of spatio-temporal hotspots of forest fires in South Asia. Environ. Monit. Assess. 2019, 191, 791. [Google Scholar] [CrossRef] [PubMed]
- Yadav, I.C.; Devi, N.L. Biomass burning, regional air quality, and climate change. In Encyclopedia of Environmental Health, 2nd ed.; Nriagu, J., Ed.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 386–391. [Google Scholar] [CrossRef]
- Cai, Y.F.; Zhang, H.; Feng, Z.; Shen, S.Z. Intensive Wildfire Associated With Volcanism Promoted the Vegetation Changeover in Southwest China During the Permian−Triassic Transition. Front. Earth Sci. 2021, 9, 615841. [Google Scholar] [CrossRef]
- Zhao, H.; Li, X.; Hall, V.A. Holocene vegetation change in relation to fire and volcanic events in Jilin, Northeastern China. Sci. China Earth Sci. 2015, 58, 1404–1419. [Google Scholar] [CrossRef]
- Satendra; Kaushik, A.D. Forest Fire Disaster Management; National Institute of Disaster Management, Ministry of Home Affairs: New Delhi, India, 2014.
- Morgan, J.; Artemieva, N.; Goldin, T. Revisiting wildfires at the K-Pg boundary. J. Geophys. Res. Biogeosci. 2013, 118, 1508–1520. [Google Scholar] [CrossRef]
- Tedim, F.; Xanthopoulos, G.; Leone, V. Forest fires in Europe: Facts and challenges. In Wildfire Hazards, Risks and Disasters; Shroder, J.F., Paton, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 77–99. [Google Scholar] [CrossRef]
- Xu, R.; Yu, P.; Abramson, M.J.; Johnston, F.H.; Samet, J.M.; Bell, M.L.; Haines, A.; Ebi, K.L.; Li, S.; Guo, Y. Wildfires, global climate change, and human health. N. Engl. J. Med. 2020, 383, 2173–2181. [Google Scholar] [CrossRef]
- Wang, B.; Luo, X.; Yang, Y.M.; Liu, J. Historical change of El Niño properties sheds light on future changes of extreme El Niño. Proc. Natl. Acad. Sci. USA 2019, 116, 22512–22517. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Z.; Ziegler, A.D.; Searchinger, T.; Yang, L.; Chen, A.; Ju, K.; Piao, S.; Li, L.Z.X.; Ciais, P.; Chen, D.; et al. A reversal in global terrestrial stilling and its implications for wind energy production. Nat. Clim. Chang. 2019, 9, 979–985. [Google Scholar] [CrossRef]
- Karnauskas, K.B.; Lundquist, J.K.; Zhang, L. Southward shift of the global wind energy resource under high carbon dioxide emissions. Nat. Geosci. 2018, 11, 38–43. [Google Scholar] [CrossRef]
- Bowman, D.M.J.S.; Kolden, C.A.; Abatzoglou, J.T.; Johnston, F.H.; van der Werf, G.R.; Flannigan, M. Vegetation fires in the Anthropocene. Nat. Rev. Earth Environ. 2020, 1, 500–515. [Google Scholar] [CrossRef]
- Hurteau, M.D.; Liang, S.; Westerling, A.L.; Wiedinmyer, C. Vegetation-fire feedback reduces projected area burned under climate change. Sci. Rep. 2019, 9, 2838. [Google Scholar] [CrossRef] [Green Version]
- Sun, Q.; Miao, C.; Hanel, M.; Borthwick, A.G.L.; Duan, Q.; Ji, D.; Li, H. Global heat stress on health, wildfires, and agricultural crops under different levels of climate warming. Environ. Int. 2019, 128, 125–136. [Google Scholar] [CrossRef] [PubMed]
- Turco, M.; Rosa-Cánovas, J.J.; Bedia, J.; Jerez, S.; Montávez, J.P.; Llasat, M.C.; Provenzale, A. Exacerbated fires in Mediterranean Europe due to anthropogenic warming projected with non-stationary climate-fire models. Nat. Commun. 2018, 9, 3821. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cieslik, S.; Tuovinen, J.P.; Baumgarten, M.; Matyssek, R.; Brito, P.; Wieser, G. Gaseous exchange between forests and the atmosphere. In Developments in Environmental Science; Matyssek, R., Clarke, N., Cudlin, P., Mikkelsen, T.N., Tuovinen, J.P., Wieser, G., Paoletti, E., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; Volume 13, pp. 19–36. [Google Scholar] [CrossRef]
- Harper, A.R.; Doerr, S.H.; Santin, C.; Froyd, C.A.; Sinnadurai, P. Prescribed fire and its impacts on ecosystem services in the UK. Sci. Total Environ. 2018, 624, 691–703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Junaidi, S.N.; Khalid, N.; Othman, A.N.; Hamid, J.R.A.; Saad, N.M. Analysis of the relationship between forest fire and land surface temperature using Landsat 8 OLI/TIRS imagery. IOP Conf. Ser. Earth Environ. Sci. 2005, 767, 012005. [Google Scholar] [CrossRef]
- Liu, Z.; Ballantyne, A.P.; Cooper, L.A. Biophysical feedback of global forest fires on surface temperature. Nat. Commun. 2019, 10, 214. [Google Scholar] [CrossRef] [Green Version]
- Vlassova, L.; Pérez-Cabello, F.; Mimbrero, M.R.; Llovería, R.M.; García-Martín, A. Analysis of the relationship between land surface temperature and wildfire severity in a series of Landsat images. Remote Sens. 2014, 6, 6136–6162. [Google Scholar] [CrossRef] [Green Version]
- Chuvieco, E.; Aguado, I.; Jurdao, S.; Pettinari, M.L.; Yebra, M.; Salas, J.; Hantson, S.; de la Riva, J.; Ibarra, P.; Rodrigues, M.; et al. Integrating geospatial information into fire risk assessment. Int. J. Wildland Fire 2014, 23, 606–619. [Google Scholar] [CrossRef]
- Nikhil, S.; Danumah, J.H.; Saha, S.; Prasad, M.K.; Rajaneesh, A.; Mammen, P.C.; Ajin, R.S.; Kuriakose, S.L. Application of GIS and AHP method in forest fire risk zone mapping: A study of the Parambikulam Tiger Reserve, Kerala, India. J. Geovis. Spat. Anal. 2021, 5, 14. [Google Scholar] [CrossRef]
- Eskandari, S. A new approach for forest fire risk modeling using fuzzy AHP and GIS in Hyrcanian forests of Iran. Arab. J. Geosci. 2017, 10, 190. [Google Scholar] [CrossRef]
- Pradeep, G.S.; Danumah, J.H.; Nikhil, S.; Prasad, M.K.; Patel, N.; Mammen, P.C.; Rajaneesh, A.; Oniga, V.E.; Ajin, R.S.; Kuriakose, S.L. Forest fire risk zone mapping of Eravikulam National Park in India: A comparison between frequency ratio and analytic hierarchy process methods. Croat. J. For. Eng. 2022, 43, 199–217. [Google Scholar] [CrossRef]
- Gheshlaghi, H.A.; Feizizadeh, B.; Blaschke, T. GIS-based forest fire risk mapping using the analytical network process and fuzzy logic. J. Environ. Plan. Manage. 2020, 63, 481–499. [Google Scholar] [CrossRef]
- Jafari Goldarag, Y.; Mohammadzadeh, A.; Ardakani, A.S. Fire risk assessment using neural network and logistic regression. J. Indian Soc. Remote Sens. 2016, 44, 885–894. [Google Scholar] [CrossRef]
- Shao, Y.; Feng, Z.; Sun, L.; Yang, X.; Li, Y.; Xu, B.; Chen, Y. Mapping China’s forest fire risks with machine learning. Forests 2022, 13, 856. [Google Scholar] [CrossRef]
- Chen, W.; Zhou, Y.; Zhou, E.; Xiang, Z.; Zhou, W.; Lu, J. Wildfire risk assessment of transmission-line corridors based on naïve bayes network and remote sensing data. Sensors 2021, 21, 634. [Google Scholar] [CrossRef] [PubMed]
- Janiec, P.; Gadal, S. A comparison of two machine learning classification methods for remote sensing predictive modeling of the forest fire in the North-Eastern Siberia. Remote Sens. 2020, 12, 4157. [Google Scholar] [CrossRef]
- Song, B.; Kang, S. A method of assigning weights using a ranking and nonhierarchy comparison. Adv. Decis. Sci. 2016, 2016, 8963214. [Google Scholar] [CrossRef] [Green Version]
- Gavade, R.K. Multi-criteria decision making: An overview of different selection problems and methods. Int. J. Comput. Sci. Inf. Technol. 2014, 5, 5643–5646. [Google Scholar]
- Olson, D.L. Opportunities and limitations of AHP in multiobjective programming. Math. Comput. Model. 1988, 11, 206–209. [Google Scholar] [CrossRef]
- Carnero, M.C. Benchmarking of the maintenance service in health care organizations. In Handbook of Research on Data Science for Effective Healthcare Practice and Administration; Noughabi, E., Raahemi, B., Albadvi, A., Far, B., Eds.; IGI Global: Hershey, PA, USA, 2017; pp. 1–25. [Google Scholar] [CrossRef]
- Abrams, W.; Ghoneim, E.; Shew, R.; LaMaskin, T.; Al-Bloushi, K.; Hussein, S.; AbuBakr, M.; Al-Mulla, E.; Al-Awar, M.; El-Baz, F. Delineation of groundwater potential (GWP) in the northern United Arab Emirates and Oman using geospatial technologies in conjunction with simple additive weight (SAW), analytical hierarchy process (AHP), and probabilistic frequency ratio (PFR) techniques. J. Arid Environ. 2018, 157, 77–96. [Google Scholar] [CrossRef]
- Kumar, R.; Dwivedi, S.B.; Gaur, S. A comparative study of machine learning and Fuzzy-AHP technique to groundwater potential mapping in the data-scarce region. Comput. Geosci. 2021, 155, 104855. [Google Scholar] [CrossRef]
- Amrutha, K.; Danumah, J.H.; Nikhil, S.; Saha, S.; Rajaneesh, A.; Mammen, P.C.; Ajin, R.S.; Kuriakose, S.L. Demarcation of forest fire risk zones in Silent Valley National Park and the effectiveness of forest management regime. J. Geovis. Spat. Anal. 2022, 6, 8. [Google Scholar] [CrossRef]
- Çoban, H.O.; Erdin, C. Forest fire risk assessment using GIS and AHP integration in Bucak forest enterprise, Turkey. Appl. Ecol. Environ. Res. 2020, 18, 1567–1583. [Google Scholar] [CrossRef]
- Kayet, N.; Chakrabarty, A.; Pathak, K.; Sahoo, S.; Dutta, T.; Hatai, B.K. Comparative analysis of multi-criteria probabilistic FR and AHP models for forest fire risk (FFR) mapping in Melghat Tiger Reserve (MTR) forest. J. For. Res. 2020, 31, 565–579. [Google Scholar] [CrossRef]
- Kumari, B.; Pandey, A.C. Geo-informatics based multi-criteria decision analysis (MCDA) through analytic hierarchy process (AHP) for forest fire risk mapping in Palamau Tiger Reserve, Jharkhand state, India. J. Earth Syst. Sci. 2020, 129, 204. [Google Scholar] [CrossRef]
- Lamat, R.; Kumar, M.; Kundu, A.; Lal, D. Forest fire risk mapping using analytical hierarchy process (AHP) and earth observation datasets: A case study in the mountainous terrain of Northeast India. SN Appl. Sci. 2021, 3, 425. [Google Scholar] [CrossRef]
- Mohammadi, F.; Shabanian, N.; Pourhashemi, M.; Fatehi, P. Risk zone mapping of forest fire using GIS and AHP in a part of Paveh forests. Iran. J. For. Poplar Res. 2011, 18, 569–586. [Google Scholar] [CrossRef]
- Novo, A.; Fariñas-Álvarez, N.; Martínez-Sánchez, J.; González-Jorge, H.; Fernández-Alonso, J.M.; Lorenzo, H. Mapping forest fire risk—A case study in Galicia (Spain). Remote Sens. 2020, 12, 3705. [Google Scholar] [CrossRef]
- Nuthammachot, N.; Stratoulias, D. A GIS- and AHP-based approach to map fire risk: A case study of Kuan Kreng peat swamp forest, Thailand. Geocarto Int. 2021, 36, 212–225. [Google Scholar] [CrossRef]
- Nuthammachot, N.; Stratoulias, D. Multi-criteria decision analysis for forest fire risk assessment by coupling AHP and GIS: Method and case study. Environ. Dev. Sustain. 2021, 23, 17443–17458. [Google Scholar] [CrossRef]
- Sivrikaya, F.; Küçük, Ö. Modeling forest fire risk based on GIS-based analytical hierarchy process and statistical analysis in Mediterranean region. Ecol. Inform. 2022, 68, 101537. [Google Scholar] [CrossRef]
- Van Hoang, T.; Chou, T.Y.; Fang, Y.M.; Nguyen, N.T.; Nguyen, Q.H.; Xuan Canh, P.; Ngo Bao Toan, D.; Nguyen, X.L.; Meadows, M.E. Mapping forest fire risk and development of early warning system for NW Vietnam using AHP and MCA/GIS methods. Appl. Sci. 2020, 10, 4348. [Google Scholar] [CrossRef]
- Eskandari, S.; Miesel, J.R. Comparison of the fuzzy AHP method, the spatial correlation method, and the Dong model to predict the fire high-risk areas in Hyrcanian forests of Iran. Geomat. Nat. Hazards Risk 2017, 8, 933–949. [Google Scholar] [CrossRef] [Green Version]
- Güngöroğlu, C. Determination of forest fire risk with fuzzy analytic hierarchy process and its mapping with the application of GIS: The case of Turkey/Çakırlar. Hum. Ecol. Risk Assess. 2017, 23, 388–406. [Google Scholar] [CrossRef]
- Kumi-Boateng, B.; Peprah, M.S.; Larbi, E.K. Prioritization of forest fire hazard risk simulation using hybrid grey relativity analysis (HGRA) and fuzzy analytical hierarchy process (FAHP) coupled with multicriteria decision analysis (MCDA) techniques—A comparative study analysis. Geod. Cartogr. 2021, 47, 147–161. [Google Scholar] [CrossRef]
- Mehta, D.; Baweja, P.K.; Aggarwal, R.K. Forest fire risk assessment using fuzzy analytic hierarchy process. Curr. World Environ. 2018, 13, 307–316. [Google Scholar] [CrossRef] [Green Version]
- Sharma, L.K.; Kanga, S.; Nathawat, M.S.; Sinha, S.; Pandey, P.C. Fuzzy AHP for forest fire risk modeling. Disaster Prev. Manage. 2012, 21, 160–171. [Google Scholar] [CrossRef]
- Tiwari, A.; Shoab, M.; Dixit, A. GIS-based forest fire susceptibility modeling in Pauri Garhwal, India: A comparative assessment of frequency ratio, analytic hierarchy process and fuzzy modeling techniques. Nat. Hazards 2021, 105, 1189–1230. [Google Scholar] [CrossRef]
- Akshaya, M.; Danumah, J.H.; Saha, S.; Ajin, R.S.; Kuriakose, S.L. Landslide susceptibility zonation of the Western Ghats region in Thiruvananthapuram district (Kerala) using geospatial tools: A comparison of the AHP and Fuzzy-AHP methods. Saf. Extrem. Environ. 2021, 3, 181–202. [Google Scholar] [CrossRef]
- Abdı, A.; Bouamrane, A.; Karech, T.; Dahri, N.; Kaouachi, A. Landslide susceptibility mapping using GIS-based fuzzy logic and the analytical hierarchical processes approach: A case study in Constantine (North-East Algeria). Geotech. Geol. Eng. 2021, 39, 5675–5691. [Google Scholar] [CrossRef]
- Bouamrane, A.; Derdous, O.; Dahri, N.; Tachi, S.E.; Boutebba, K.; Bouziane, M.T. A comparison of the analytical hierarchy process and the fuzzy logic approach for flood susceptibility mapping in a semi-arid ungauged basin (Biskra basin: Algeria). Int. J. River Basin Manage. 2022, 20, 203–213. [Google Scholar] [CrossRef]
- Vilasan, R.T.; Kapse, V.S. Evaluation of the prediction capability of AHP and F-AHP methods in flood susceptibility mapping of Ernakulam district (India). Nat. Hazards 2022, 112, 1767–1793. [Google Scholar] [CrossRef]
- Senan, C.P.C.; Ajin, R.S.; Danumah, J.H.; Costache, R.; Arabameri, A.; Rajaneesh, A.; Sajinkumar, K.S.; Kuriakose, S.L. Flood vulnerability of a few areas in the foothills of the Western Ghats: A comparison of AHP and F-AHP models. Stoch. Environ. Res. Risk Assess. 2022. [Google Scholar] [CrossRef] [PubMed]
- Malik, Z.A.; Bhat, J.A.; Bhatt, A.B. Forest resource use pattern in Kedarnath wildlife sanctuary and its fringe areas (a case study from Western Himalaya, India). Energy Policy 2014, 67, 138–145. [Google Scholar] [CrossRef]
- Bhat, J.A.; Kumar, M.; Bussmann, R.W. Ecological status and traditional knowledge of medicinal plants in Kedarnath Wildlife Sanctuary of Garhwal Himalaya, India. J. Ethnobiol. Ethnomed. 2013, 9, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kittur, S.; Sathyakumar, S.; Rawat, G.S. Assessment of spatial and habitat use overlap between Himalayan tahr and livestock in Kedarnath Wildlife Sanctuary, India. Eur. J. Wildl. Res. 2010, 56, 195–204. [Google Scholar] [CrossRef]
- Misra, S.; Maikhuri, R.K.; Dhyani, D.; Rao, K.S. Assessment of traditional rights, local interference and natural resource management in Kedarnath Wildlife Sanctuary. Int. J. Sustain. Dev. World Ecol. 2009, 16, 404–416. [Google Scholar] [CrossRef]
- Bahuguna, Y.M.; Gairola, S.; Uniyal, P.L.; Bhatt, A.B. Moss Flora of Kedarnath Wildlife Sanctuary (KWLS), Garhwal Himalaya, India. Proc. Natl. Acad. Sci. India Sect. B Biol. Sci. 2016, 86, 931–943. [Google Scholar] [CrossRef]
- Singh, G.; Rawat, G.S. Ethnomedicinal survey of Kedarnath Wildlife Sanctuary in Western Himalaya, India. Indian J. Fundam. Appl. Life Sci. 2011, 1, 35–46. [Google Scholar]
- Najar, M.U.I.; Rahim, A. Effect of canopy cover on understory invasive alien species in the Wayanad Wildlife Sanctuary, Kerala, India. J. Biodivers. Manage. For. 2018, 7, 1. [Google Scholar] [CrossRef]
- Arjun, M.S.; Ravindran, R.; Zachariah, A.; Ashokkumar, M.; Varghese, A.; Deepa, C.K.; Chandy, G. Gastrointgestinal parasites of Tigers (Panthera tigristigris) in Wayanad Wildlife Sanctuary, Kerala, India. Int. J. Current Microbiol. Appl. Sci. 2017, 6, 2502–2509. [Google Scholar] [CrossRef] [Green Version]
- Narayanan, M.K.R.; Mithunlal, S.; Sujanapal, P.; Kumar, N.A.; Sivadasan, M.; Alfarhan, A.H.; Alatar, A.A. Ethnobotanically important trees and their uses by Kattunaikka tribe in Wayanad Wildlife Sanctuary, Kerala, India. J. Med. Plant. Res. 2011, 5, 604–612. [Google Scholar]
- Vinod, P.G.; Ajin, R.S.; Jacob, M.K. RS and GIS Based Spatial Mapping of Forest Fires in Wayanad Wildlife Sanctuary, Wayanad, North Kerala, India. Int. J. Earth Sci. Eng. 2016, 9, 498–502. [Google Scholar]
- Babitha, B.G.; Danumah, J.H.; Pradeep, G.S.; Costache, R.; Patel, N.; Prasad, M.K.; Rajaneesh, A.; Mammen, P.C.; Ajin, R.S.; Kuriakose, S.L. A framework employing the AHP and FR methods to assess the landslide susceptibility of the Western Ghats region in Kollam district. Saf. Extreme Environ. 2022, 4, 171–191. [Google Scholar] [CrossRef]
- Guillaume, S.; Charnomordic, B. Learning interpretable fuzzy inference systems with FisPro. Inf. Sci. 2011, 181, 4409–4427. [Google Scholar] [CrossRef] [Green Version]
- Guillaume, S.; Charnomordic, B. Fuzzy inference systems: An integrated modeling environment for collaboration between expert knowledge and data using FisPro. Expert Syst. Appl. 2012, 39, 8744–8755. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.S.; Hult, J.; Picotte, J.; Peterson, B. Potential underestimation of satellite fire radiative power retrievals over gas flares and wildland fires. Remote Sens. 2020, 12, 238. [Google Scholar] [CrossRef] [Green Version]
- Li, F.; Zhang, X.; Roy, D.P.; Kondragunta, S. Estimation of biomass-burning emissions by fusing the fire radiative power retrievals from polar-orbiting and geostationary satellites across the conterminous United States. Atmos. Environ. 2019, 211, 274–287. [Google Scholar] [CrossRef]
- Abebe, G.; Getachew, D.; Ewunetu, A. Analysing land use/land cover changes and its dynamics using remote sensing and GIS in Gubalafito district, Northeastern Ethiopia. SN Appl. Sci. 2022, 4, 30. [Google Scholar] [CrossRef]
- Alam, A.; Bhat, M.S.; Maheen, M. Using Landsat satellite data for assessing the land use and land cover change in Kashmir valley. GeoJournal 2020, 85, 1529–1543. [Google Scholar] [CrossRef] [Green Version]
- Arulbalaji, P. Analysis of land use/land cover changes using geospatial techniques in Salem district, Tamil Nadu, South India. SN Appl. Sci. 2019, 1, 462. [Google Scholar] [CrossRef] [Green Version]
- Landsat 8 Data Users Handbook, Version 5.0; Department of the Interior, U.S. Geological Survey: Liston, VA, USA, 2019. Available online: https://www.usgs.gov/media/files/landsat-8-data-users-handbook (accessed on 1 October 2022).
- Ghosh, S.; Das, A.; Hembram, T.K.; Saha, S.; Pradhan, B.; Alamri, A.M. Impact of COVID-19 induced lockdown on environmental quality in four Indian megacities using Landsat 8 OLI and TIRS-derived data and Mamdani fuzzy logic modelling approach. Sustainability 2020, 12, 5464. [Google Scholar] [CrossRef]
- Nichol, J.E. A GIS-based approach to microclimate monitoring in Singapore’s high-rise housing estates. Photogramm. Eng. Remote Sens. 1994, 60, 1225–1232. [Google Scholar]
- Artis, D.A.; Carnahan, W.H. Survey of emissivity variability in thermography of urban areas. Remote Sens. Environ. 1982, 12, 313–329. [Google Scholar] [CrossRef]
- Snyder, W.C.; Wan, Z.; Zhang, Y.; Feng, Y.Z. Classification-based emissivity for land surface temperature measurement from space. Int. J. Remote Sens. 1998, 19, 2753–2774. [Google Scholar] [CrossRef]
- Gao, B. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Shen, L.; Li, C. Water body extraction from Landsat ETM+ imagery using adaboost algorithm. In Proceedings of the 2010 18th International Conference on Geoinformatics, Beijing, China, 18–20 June 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Zha, Y.; Gao, J.; Ni, S. Use of normalized difference built-up index in automatically mapping urban areas from TM imagery. Int. J. Remote Sens. 2003, 24, 583–594. [Google Scholar] [CrossRef]
- Allen, M.P. The problem of multicollinearity. In Understanding Regression Analysis; Springer: Boston, MA, USA, 1997; pp. 176–180. [Google Scholar] [CrossRef]
- Anonymous. Multicollinearity and partial least squares. In Hebbian Learning and Negative Feedback Networks; Advanced Information and Knowledge Processing; Springer: London, UK, 2005. [Google Scholar] [CrossRef]
- O’brien, R.M. A caution regarding rules of thumb for Variance Inflation Factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Forthofer, R.N.; Lee, E.S.; Hernandez, M. Linear regression. In Biostatistics, 2nd ed.; Forthofer, R.N., Lee, E.S., Hernandez, M., Eds.; Academic Press: Cambridge, MA, USA, 2007; pp. 349–386. [Google Scholar] [CrossRef]
- Ferré, J. 3.02—Regression diagnostics. In Comprehensive Chemometrics; Brown, S.D., Tauler, R., Walczak, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 33–89. [Google Scholar] [CrossRef]
- Kim, J.H. Multicollinearity and misleading statistical results. Korean J. Anesthesiol. 2019, 72, 558–569. [Google Scholar] [CrossRef] [Green Version]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation (Decision Making Series); McGraw Hill: New York, NY, USA, 1980. [Google Scholar]
- Tavana, M.; Soltanifar, M.; Santos-Arteaga, F.J. Analytical hierarchy process: Revolution and evolution. Ann. Oper. Res. 2021. [Google Scholar] [CrossRef]
- Thakkar, J.J. Analytic hierarchy process (AHP). In Multi-Criteria Decision Making. Studies in Systems, Decision and Control; Springer: Singapore, 2021; Volume 336. [Google Scholar] [CrossRef]
- Gao, Z.; Jiang, Y.; He, J.; Wu, J.; Xu, J.; Christakos, G. An AHP-based regional COVID-19 vulnerability model and its application in China. Model. Earth Syst. Environ. 2022, 8, 2525–2538. [Google Scholar] [CrossRef]
- Thomas, A.V.; Saha, S.; Danumah, J.H.; Raveendran, S.; Prasad, M.K.; Ajin, R.S.; Kuriakose, S.L. Landslide susceptibility zonation of Idukki district using GIS in the aftermath of 2018 Kerala floods and landslides: A comparison of AHP and frequency ratio methods. J. Geovis. Spat. Anal. 2021, 5, 21. [Google Scholar] [CrossRef]
- Danumah, J.H.; Odai, S.N.; Saley, B.M.; Szarzynski, J.; Thiel, M.; Kwaku, A.; Kouame, F.K.; Akpa, L.Y. Flood risk assessment and mapping in Abidjan district using multi-criteria analysis (AHP) model and geoinformation techniques, (Côte d’Ivoire). Geoenviron. Disasters 2016, 3, 10. [Google Scholar] [CrossRef] [Green Version]
- Van Laarhoven, P.J.M.; Pedrcyz, W. A fuzzy extension of Saaty’s priority theory. Fuzzy Sets Syst. 1983, 11, 229–241. [Google Scholar] [CrossRef]
- Putra, M.S.D.; Andryana, S.; Fauziah; Gunaryati, A. Fuzzy analytical hierarchy process method to determine the quality of gemstones. Adv. Fuzzy Syst. 2018, 2018, 9094380. [Google Scholar] [CrossRef]
- Maharani, I.S.; Astanti, R.D.; Ai, T.J. Fuzzy analytical hierarchy process with unsymmetrical triangular fuzzy number for supplier selection process. In MEC-APCOMS 2019. Lecture Notes in Mechanical Engineering; Osman Zahid, M., Abd Aziz, R., Yusoff, A., Mat Yahya, N., Abdul Aziz, F., Yazid Abu, M., Eds.; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Lima-Junior, F.R.; Carpinetti, L.C.R. Dealing with the problem of null weights and scores in Fuzzy Analytic Hierarchy Process. Soft Comput. 2020, 24, 9557–9573. [Google Scholar] [CrossRef]
- Jesiya, N.P.; Gopinath, G. A fuzzy based MCDM–GIS framework to evaluate groundwater potential index for sustainable groundwater management—A case study in an urban-periurban ensemble, southern India. Groundw. Sustain. Dev. 2020, 11, 100466. [Google Scholar] [CrossRef]
- Afolayan, A.H.; Ojokoh, B.A.; Adetunmbi., A.O. Performance analysis of fuzzy analytic hierarchy process multi-criteria decision support models for contractor selection. Sci. Afr. 2020, 9, e00471. [Google Scholar] [CrossRef]
- Buckley, J.J. Fuzzy hierarchical analysis. Fuzzy Sets Syst. 1985, 17, 233–247. [Google Scholar] [CrossRef]
- Ayhan, M.B. A fuzzy AHP approach for supplier selection problem: A case study in a gear motor company. Int. J. Manage. Value Supply Chains 2013, 4, 11–23. [Google Scholar] [CrossRef]
- Chou, S.W.; Chang, Y.C. The implementation factors that influence the ERP (Enterprise Resource Planning) benefits. Decis. Support Syst. 2008, 46, 149–157. [Google Scholar] [CrossRef]
- Melo, F. Receiver operating characteristic (ROC) curve. In Encyclopedia of Systems Biology; Dubitzky, W., Wolkenhauer, O., Cho, K.H., Yokota, H., Eds.; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, F.; He, H. Assessing the accuracy of diagnostic tests. Shanghai Arch. Psychiatry 2018, 30, 207–212. [Google Scholar] [CrossRef] [PubMed]
- Boyce, D. Evaluation of medical laboratory tests. In Orthopaedic Physical Therapy Secrets, 3rd ed.; Placzek, J.D., Boyce, D.A., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 125–134. [Google Scholar] [CrossRef]
- Anonymous. Accuracy. In Encyclopedia of Machine Learning; Sammut, C., Webb, G.I., Eds.; Springer: Boston, MA, USA, 2011. [Google Scholar] [CrossRef]
- Bolboacă, S.D.; Jäntschi, L. Sensitivity, specificity, and accuracy of predictive models on phenols toxicity. J. Comput. Sci. 2014, 5, 345–350. [Google Scholar] [CrossRef]
- Baratloo, A.; Hosseini, M.; Negida, A.; El Ashal, G. Part 1: Simple definition and calculation of accuracy, sensitivity and specificity. Emergency 2015, 3, 48–49. [Google Scholar]
- Parikh, R.; Mathai, A.; Parikh, S.; Chandra Sekhar, G.; Thomas, R. Understanding and using sensitivity, specificity and predictive values. Indian J. Ophthalmol. 2008, 56, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Xia, Y. Chapter Eleven—Correlation and association analyses in microbiome study integrating multiomics in health and disease. In Progress in Molecular Biology and Translational Science; Sun, J., Ed.; Academic Press: Cambridge, MA, USA, 2020; Volume 171, pp. 309–491. [Google Scholar] [CrossRef]
- McHugh, M.L. Interrater reliability: The kappa statistic. Biochem. Med. 2012, 22, 276–282. [Google Scholar] [CrossRef]
- Yu, C.H. Test–retest reliability. In Encyclopedia of Social Measurement; Kempf-Leonard, K., Ed.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 777–784. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Peng, J.; Shahabi, H.; Hong, H.; Bui, D.T.; Duan, Z.; Li, S.; Zhu, A.X. GIS-based landslide susceptibility evaluation using a novel hybrid integration approach of bivariate statistical based random forest method. CATENA 2018, 164, 135–149. [Google Scholar] [CrossRef]
- da Costa, B.S.C.; da Fonseca, E.L. The use of fire radiative power to estimate the biomass consumption coefficient for temperate grasslands in the Atlantic forest biome. Rev. Bras. Meteorol. 2017, 32, 255–260. [Google Scholar] [CrossRef] [Green Version]
- Salma; Nikhil, S.; Danumah, J.H.; Prasad, M.K.; Nazar, N.; Saha, S.; Mammen, P.C.; Ajin, R.S. Prediction capability of the MCDA-AHP model in wildfire risk zonation of a protected area in the Southern Western Ghats. Environ. Sustain. 2023, 6, 44. [Google Scholar] [CrossRef]
- Manzo-Delgado, L.; Aguirre-Gómez, R.; Álvarez, R. Multitemporal analysis of land surface temperature using NOAA-AVHRR: Preliminary relationships between climatic anomalies and forest fires. Int. J. Remote Sens. 2004, 25, 4417–4424. [Google Scholar] [CrossRef]
- Veena, H.S.; Ajin, R.S.; Loghin, A.M.; Sipai, R.; Adarsh, P.; Viswam, A.; Vinod, P.G.; Jacob, M.K.; Jayaprakash, M. Wildfire risk zonation in a tropical forest division in Kerala, India: A study using geospatial techniques. Int. J. Conserv. Sci. 2017, 8, 475–484. [Google Scholar]
- Gómez-González, S.; Ojeda, F.; Fernandes, P.M. Portugal and Chile: Longing for sustainable forestry while rising from the ashes. Environ. Sci. Policy 2018, 81, 104–107. [Google Scholar] [CrossRef]
- Egorova, V.N.; Trucchia, A.; Pagnini, G. Fire-spotting generated fires. Part II: The role of flame geometry and slope. Appl. Math. Model. 2022, 104, 1–20. [Google Scholar] [CrossRef]
- Estes, B.L.; Knapp, E.E.; Skinner, C.N.; Miller, J.D.; Preisler, H.K. Factors influencing fire severity under moderate burning conditions in the Klamath Mountains, northern California, USA. Ecosphere 2017, 8, e01794. [Google Scholar] [CrossRef] [Green Version]
- Jaiswal, R.K.; Mukherjee, S.; Raju, K.D.; Saxena, R. Forest fire risk zone mapping from satellite imagery and GIS. Int. J. Appl. Earth Obs. Geoinf. 2002, 4, 1–10. [Google Scholar] [CrossRef]
- Ajin, R.S.; Loghin, A.M.; Jacob, M.K.; Vinod, P.G.; Krishnamurthy, R.R. The risk assessment study of potential forest fire in Idukki Wildlife Sanctuary using RS and GIS techniques. Int. J. Adv. Earth Sci. Eng. 2016, 5, 308–318. [Google Scholar]
- Silander, J.A. Temperate Forests. In Encyclopedia of Biodiversity; Levin, S.A., Ed.; Elsevier: Amsterdam, The Netherlands, 2001; pp. 607–626. [Google Scholar] [CrossRef]
- Currie, W.S.; Bergen, K.M. Temperate Forest. In Encyclopedia of Ecology; Jørgensen, S.E., Fath, B.D., Eds.; Academic Press: Cambridge, MA, USA, 2008; pp. 3494–3503. [Google Scholar] [CrossRef]
- Gu, Y.; Hunt, E.; Wardlow, B.; Basara, J.B.; Brown, J.F.; Verdin, J.P. Evaluation of MODIS NDVI and NDWI for vegetation drought monitoring using Oklahoma Mesonet soil moisture data. Geophys. Res. Lett. 2008, 35, L22401. [Google Scholar] [CrossRef] [Green Version]
- Masinda, M.M.; Sun, L.; Wang, G.; Hu, T. Moisture content thresholds for ignition and rate of fire spread for various dead fuels in northeast forest ecosystems of China. J. For. Res. 2021, 32, 1147–1155. [Google Scholar] [CrossRef]
- Parajuli, A.; Gautam, A.P.; Sharma, S.P.; Bhujel, K.B.; Sharma, G.; Thapa, P.B.; Bist, B.S.; Poudel, S. Forest fire risk mapping using GIS and remote sensing in two major landscapes of Nepal. Geomat. Nat. Hazards Risk 2020, 11, 2569–2586. [Google Scholar] [CrossRef]
- Ajin, R.S.; Loghin, A.M.; Vinod, P.G.; Jacob, M.K. RS and GIS based forest fire risk zone mapping in the Periyar Tiger Reserve, Kerala, India. J. Wetl. Biodivers. 2016, 6, 139–148. [Google Scholar]
- Ajin, R.S.; Loghin, A.M.; Vinod, P.G.; Jacob, M.K. Mapping of forest fire risk zones in Peechi-Vazhani wildlife sanctuary, Thrissur, Kerala, India: A study using geospatial techniques. J. Wetl. Biodivers. 2017, 7, 7–16. [Google Scholar]
- Harsha, G.; Anish, T.S.; Rajaneesh, A.; Prasad, M.K.; Mathew, R.; Mammen, P.C.; Ajin, R.S.; Kuriakose, S.L. Dengue risk zone mapping of Thiruvananthapuram district, India: A comparison of the AHP and F-AHP methods. GeoJournal 2022. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Dai, X.; Wang, Z.; Li, J.; Qu, G.; Li, W.; She, J.; Wang, Y. Landslide susceptibility assessment model construction using typical machine learning for the Three Gorges reservoir area in China. Remote Sens. 2022, 14, 2257. [Google Scholar] [CrossRef]
- Selamat, S.N.; Majid, N.A.; Taha, M.R.; Osman, A. Landslide susceptibility model using artificial neural network (ANN) approach in Langat river basin, Selangor, Malaysia. Land 2022, 11, 833. [Google Scholar] [CrossRef]
- Achu, A.L.; Thomas, J.; Aju, C.D.; Gopinath, G.; Kumar, S.; Reghunath, R. Machine-learning modelling of fire susceptibility in a forest-agriculture mosaic landscape of southern India. Ecol. Inform. 2021, 64, 101348. [Google Scholar] [CrossRef]


| Data | Source | Layers Derived (Factor) | Scale | Spatial Resolution |
|---|---|---|---|---|
| Landsat 8 OLI image | https://earthexplorer.usgs.gov/ (accessed on 21 September 2022) | Land cover types NDWI WRI NDBI | 30 m | |
| Landsat 7 ETM+ | https://earthexplorer.usgs.gov/ (accessed on 21 September 2022) | LST | 60 m | |
| Landsat 8 TIRS image | https://earthexplorer.usgs.gov/ (accessed on 21 September 2022) | LST | 100 m | |
| SRTM DEM | https://earthexplorer.usgs.gov/ (accessed on 5 January 2020) | Slope | 30 m | |
| Topographic map | Survey of India | Distance from the road Distance from the tourist spot, pilgrim/religious center Distance from the settlement | 1: 50,000 | |
| Google Earth Pro | https://earth.google.com/web/ (accessed on 5 October 2022) | Distance from the road (updated) Distance from the tourist spot, pilgrim/religious center (updated) Distance from the settlement (updated) | 15 cm to 15 m | |
| NASA FIRMS data | https://firms.modaps.eosdis.nasa.gov/download/ (accessed on 27 July 2022) | Fire incidence points | 375 m (VIIRS) and1 km (MODIS) |
| LCT | Slp | LST | NDWI | DR | DTSPRC | DS | WRI | NDBI | Vp | Cp | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| LCT | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 4.147 | 0.308 |
| Slp | 1/2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 3.008 | 0.223 |
| LST | 1/3 | 1/2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 2.113 | 0.157 |
| NDWI | 1/4 | 1/3 | 1/2 | 1 | 2 | 3 | 4 | 5 | 6 | 1.459 | 0.108 |
| DR | 1/5 | 1/4 | 1/3 | 1/2 | 1 | 2 | 3 | 4 | 5 | 1.000 | 0.074 |
| DTSPRC | 1/6 | 1/5 | 1/4 | 1/3 | 1/2 | 1 | 2 | 3 | 4 | 0.685 | 0.051 |
| DS | 1/7 | 1/6 | 1/5 | 1/4 | 1/3 | 1/2 | 1 | 2 | 3 | 0.473 | 0.035 |
| WRI | 1/8 | 1/7 | 1/6 | 1/5 | 1/4 | 1/3 | 1/2 | 1 | 2 | 0.332 | 0.025 |
| NDBI | 1/9 | 1/8 | 1/7 | 1/6 | 1/5 | 1/4 | 1/3 | 1/2 | 1 | 0.241 | 0.018 |
| ∑ | 2.83 | 4.72 | 7.59 | 11.45 | 16.28 | 22.08 | 28.83 | 36.50 | 45.00 | 13.46 | 1.00 |
| LCT | Slp | LST | NDWI | DR | DTSPRC | DS | WRI | NDBI | ∑rank | [C] | [D] = [A]*[C] | [E] = [D]/[C] | λmax | CI | CR | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LCT | 0.35 | 0.42 | 0.40 | 0.35 | 0.31 | 0.27 | 0.24 | 0.22 | 0.20 | 2.76 | 0.307 | 2.981 | 9.711 | 9.408 | 0.051 | 0.035 (3.52%) |
| Slp | 0.18 | 0.21 | 0.26 | 0.26 | 0.25 | 0.23 | 0.21 | 0.19 | 0.18 | 1.96 | 0.218 | 2.134 | 9.782 | |||
| LST | 0.12 | 0.11 | 0.13 | 0.17 | 0.18 | 0.18 | 0.17 | 0.16 | 0.16 | 1.39 | 0.154 | 1.499 | 9.715 | |||
| NDWI | 0.09 | 0.07 | 0.07 | 0.09 | 0.12 | 0.14 | 0.14 | 0.14 | 0.13 | 0.98 | 0.109 | 1.040 | 9.548 | |||
| DR | 0.07 | 0.05 | 0.04 | 0.04 | 0.06 | 0.09 | 0.10 | 0.11 | 0.11 | 0.69 | 0.076 | 0.714 | 9.345 | |||
| DTSPRC | 0.06 | 0.04 | 0.03 | 0.03 | 0.03 | 0.05 | 0.07 | 0.08 | 0.09 | 0.48 | 0.053 | 0.489 | 9.168 | |||
| DS | 0.05 | 0.04 | 0.03 | 0.02 | 0.02 | 0.02 | 0.03 | 0.05 | 0.07 | 0.33 | 0.037 | 0.336 | 9.077 | |||
| WRI | 0.04 | 0.03 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.03 | 0.04 | 0.23 | 0.026 | 0.236 | 9.104 | |||
| NDBI | 0.04 | 0.03 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.02 | 0.17 | 0.019 | 0.174 | 9.222 | |||
| ∑ | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 9.00 | 1.000 | 84.672 |
| LCT | Slp | LST | NDWI | DR | DTSPRC | DS | WRI | NDBI | |
|---|---|---|---|---|---|---|---|---|---|
| LCT | (1, 1, 1) | (1, 2, 3) | (2, 3, 4) | (3, 4, 5) | (4, 5, 6) | (5, 6, 7) | (6, 7, 8) | (7, 8, 9) | (9, 9, 9) |
| Slp | (1/3, 1/2, 1) | (1, 1, 1) | (1, 2, 3) | (2, 3, 4) | (3, 4, 5) | (4, 5, 6) | (5, 6, 7) | (6, 7, 8) | (7, 8, 9) |
| LST | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1, 1, 1) | (1, 2, 3) | (2, 3, 4) | (3, 4, 5) | (4, 5, 6) | (5, 6, 7) | (6, 7, 8) |
| NDWI | (1/5, 1/4, 1/3) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1, 1, 1) | (1, 2, 3) | (2, 3, 4) | (3, 4, 5) | (4, 5, 6) | (5, 6, 7) |
| DR | (1/6, 1/5, 1/4) | (1/5, 1/4, 1/3) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1, 1, 1) | (1, 2, 3) | (2, 3, 4) | (3, 4, 5) | (4, 5, 6) |
| DTSPRC | (1/7, 1/6, 1/5) | (1/6, 1/5, 1/4) | (1/5, 1/4, 1/3) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1, 1, 1) | (1, 2, 3) | (2, 3, 4) | (3, 4, 5) |
| DS | (1/8, 1/7, 1/6) | (1/7, 1/6, 1/5) | (1/6, 1/5, 1/4) | (1/5, 1/4, 1/3) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1, 1, 1) | (1, 2, 3) | (2, 3, 4) |
| WRI | (1/9, 1/8, 1/7) | (1/8, 1/7, 1/6) | (1/7, 1/6, 1/5) | (1/6, 1/5, 1/4) | (1/5, 1/4, 1/3) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1, 1, 1) | (1, 2, 3) |
| NDBI | (1/9, 1/9, 1/9) | (1/9, 1/8, 1/7) | (1/8, 1/7, 1/6) | (1/7, 1/6, 1/5) | (1/6, 1/5, 1/4) | (1/5, 1/4, 1/3) | (1/4, 1/3, 1/2) | (1/3, 1/2, 1) | (1, 1, 1) |
| LCT | 3.292 | 4.147 | 4.902 |
| Slp | 2.282 | 3.008 | 3.840 |
| LST | 1.576 | 2.113 | 2.785 |
| NDWI | 1.080 | 1.459 | 1.956 |
| DR | 0.740 | 1.000 | 1.351 |
| DTSPRC | 0.511 | 0.685 | 0.926 |
| DS | 0.359 | 0.473 | 0.634 |
| WRI | 0.260 | 0.332 | 0.438 |
| NDBI | 0.204 | 0.241 | 0.304 |
| 10.305 | 13.460 | 17.136 | |
| 0.058 | 0.074 | 0.097 | |
| LCT | 0.192 | 0.308 | 0.476 |
| Slp | 0.133 | 0.223 | 0.373 |
| LST | 0.092 | 0.157 | 0.270 |
| NDWI | 0.063 | 0.108 | 0.190 |
| DR | 0.043 | 0.074 | 0.131 |
| DTSPRC | 0.030 | 0.051 | 0.090 |
| DS | 0.021 | 0.035 | 0.062 |
| WRI | 0.015 | 0.025 | 0.043 |
| NDBI | 0.012 | 0.018 | 0.029 |
| LCT | 0.325 | 0.299 |
| Slp | 0.243 | 0.223 |
| LST | 0.173 | 0.159 |
| NDWI | 0.120 | 0.111 |
| DR | 0.083 | 0.076 |
| DTSPRC | 0.057 | 0.052 |
| DS | 0.039 | 0.036 |
| WRI | 0.027 | 0.025 |
| NDBI | 0.020 | 0.018 |
| ∑ | 1.09 | 1.00 |
| Factors | Collinearity Statistics of KWLS | Collinearity Statistics of WWLS | ||
|---|---|---|---|---|
| Tolerance | VIF | Tolerance | VIF | |
| LST | 0.209 | 4.782 | 0.503 | 1.988 |
| LCT | 0.707 | 1.415 | 0.668 | 1.497 |
| Slope | 0.890 | 1.124 | 0.849 | 1.177 |
| WRI | 0.230 | 4.354 | 0.600 | 1.666 |
| NDWI | 0.288 | 4.472 | 0.593 | 1.687 |
| Distance from the road | 0.235 | 4.255 | 0.726 | 1.378 |
| Distance from the tourist spot or pilgrim/religious center | 0.576 | 1.735 | 0.881 | 1.135 |
| Distance from the settlement | 0.247 | 4.049 | 0.691 | 1.447 |
| NDBI | 0.278 | 3.597 | 0.772 | 1.295 |
| Risk Zones | Percentage of Risk Zones in KWLS | Percentage of Risk Zones in WWLS | ||
|---|---|---|---|---|
| AHP Model | F-AHP Model | AHP Model | F-AHP Model | |
| Very low | 16.59 | 16.59 | 8.43 | 8.45 |
| Low | 16.70 | 16.54 | 17.92 | 17.70 |
| Moderate | 16.92 | 17.50 | 27.62 | 27.75 |
| High | 26.61 | 26.88 | 29.08 | 28.98 |
| Very high | 23.18 | 22.49 | 16.95 | 17.12 |
| Total | 100 | 100 | 100 | 100 |
| Matrices | Training Dataset | Validation Dataset | ||
|---|---|---|---|---|
| AHP | F-AHP | AHP | F-AHP | |
| Sensitivity | 0.714 | 0.771 | 0.714 | 0.810 |
| Accuracy | 0.742 | 0.806 | 0.737 | 0.842 |
| Kappa index | 0.840 | 0.850 | 0.870 | 0.884 |
| Matrices | Training Dataset | Validation Dataset | ||
|---|---|---|---|---|
| AHP | F-AHP | AHP | F-AHP | |
| Sensitivity | 0.800 | 0.840 | 0.846 | 0.905 |
| Accuracy | 0.813 | 0.845 | 0.875 | 0.926 |
| Kappa index | 0.762 | 0.829 | 0.850 | 0.875 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sinha, A.; Nikhil, S.; Ajin, R.S.; Danumah, J.H.; Saha, S.; Costache, R.; Rajaneesh, A.; Sajinkumar, K.S.; Amrutha, K.; Johny, A.; et al. Wildfire Risk Zone Mapping in Contrasting Climatic Conditions: An Approach Employing AHP and F-AHP Models. Fire 2023, 6, 44. https://doi.org/10.3390/fire6020044
Sinha A, Nikhil S, Ajin RS, Danumah JH, Saha S, Costache R, Rajaneesh A, Sajinkumar KS, Amrutha K, Johny A, et al. Wildfire Risk Zone Mapping in Contrasting Climatic Conditions: An Approach Employing AHP and F-AHP Models. Fire. 2023; 6(2):44. https://doi.org/10.3390/fire6020044
Chicago/Turabian StyleSinha, Aishwarya, Suresh Nikhil, Rajendran Shobha Ajin, Jean Homian Danumah, Sunil Saha, Romulus Costache, Ambujendran Rajaneesh, Kochappi Sathyan Sajinkumar, Kolangad Amrutha, Alfred Johny, and et al. 2023. "Wildfire Risk Zone Mapping in Contrasting Climatic Conditions: An Approach Employing AHP and F-AHP Models" Fire 6, no. 2: 44. https://doi.org/10.3390/fire6020044
APA StyleSinha, A., Nikhil, S., Ajin, R. S., Danumah, J. H., Saha, S., Costache, R., Rajaneesh, A., Sajinkumar, K. S., Amrutha, K., Johny, A., Marzook, F., Mammen, P. C., Abdelrahman, K., Fnais, M. S., & Abioui, M. (2023). Wildfire Risk Zone Mapping in Contrasting Climatic Conditions: An Approach Employing AHP and F-AHP Models. Fire, 6(2), 44. https://doi.org/10.3390/fire6020044










