Experimental Study of Scale Effect in Tunnel Fires at Different Sealing Ratios
Abstract
1. Introduction
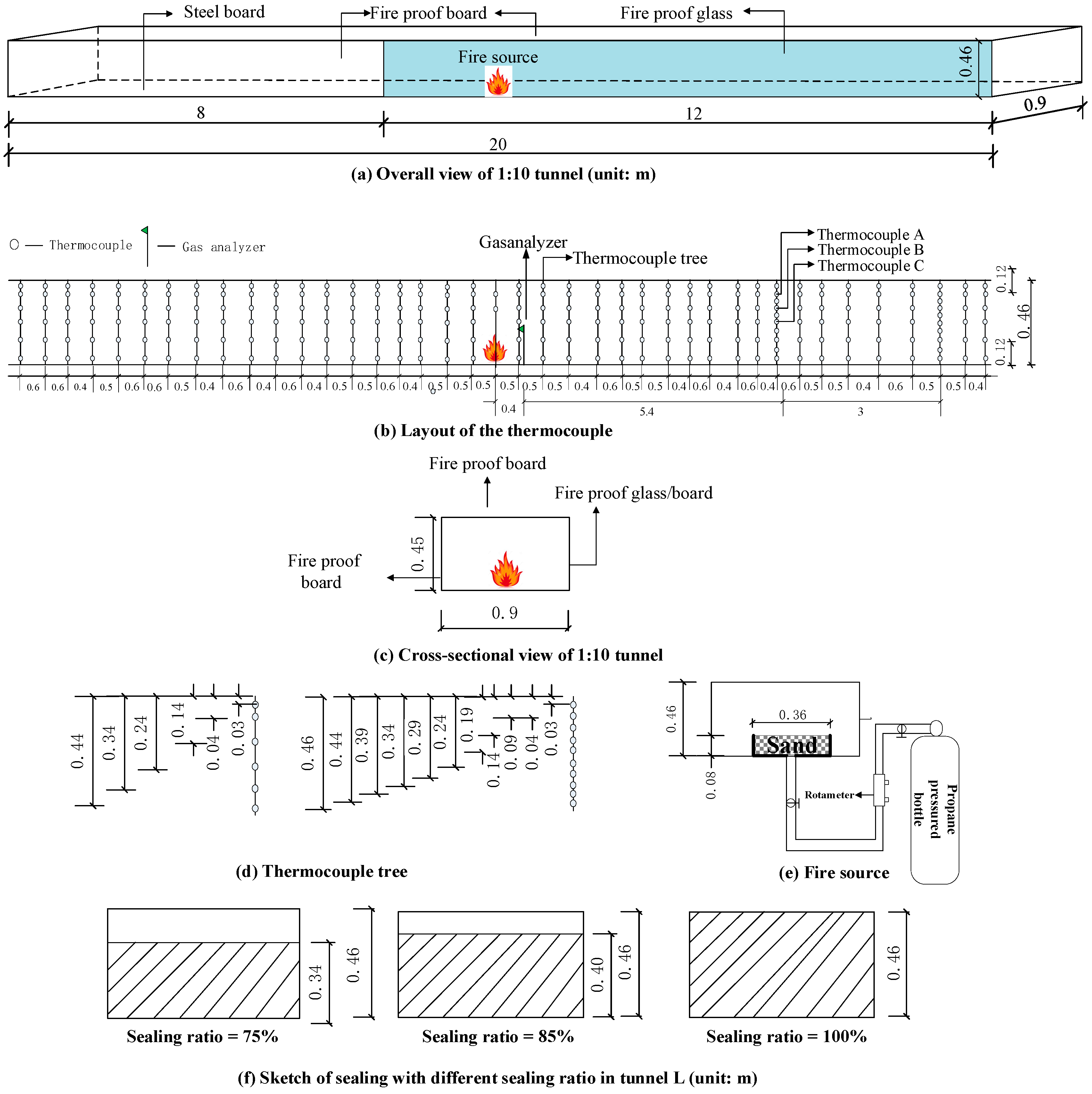
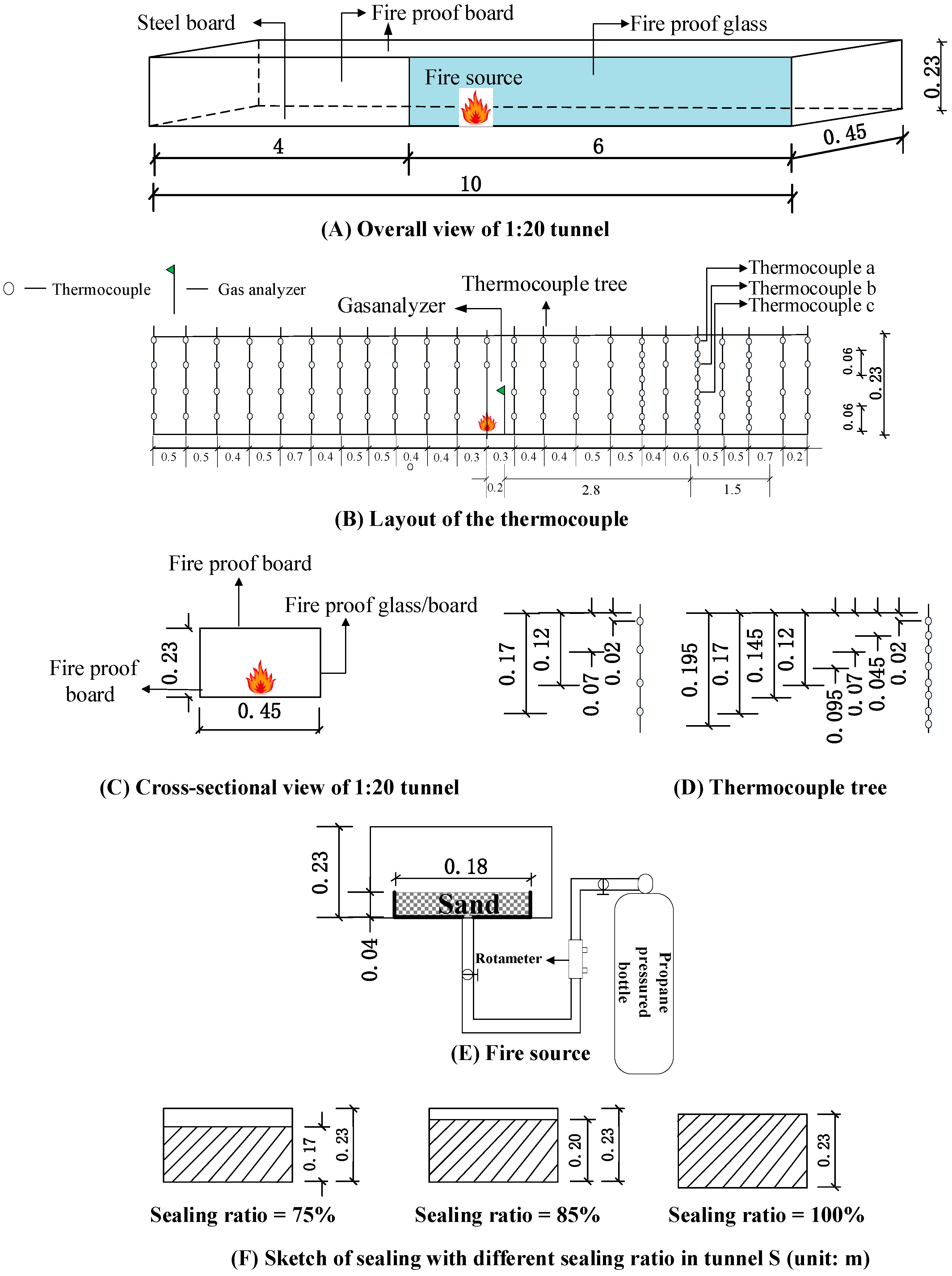
2. Experimental Setup
3. Experimental Results
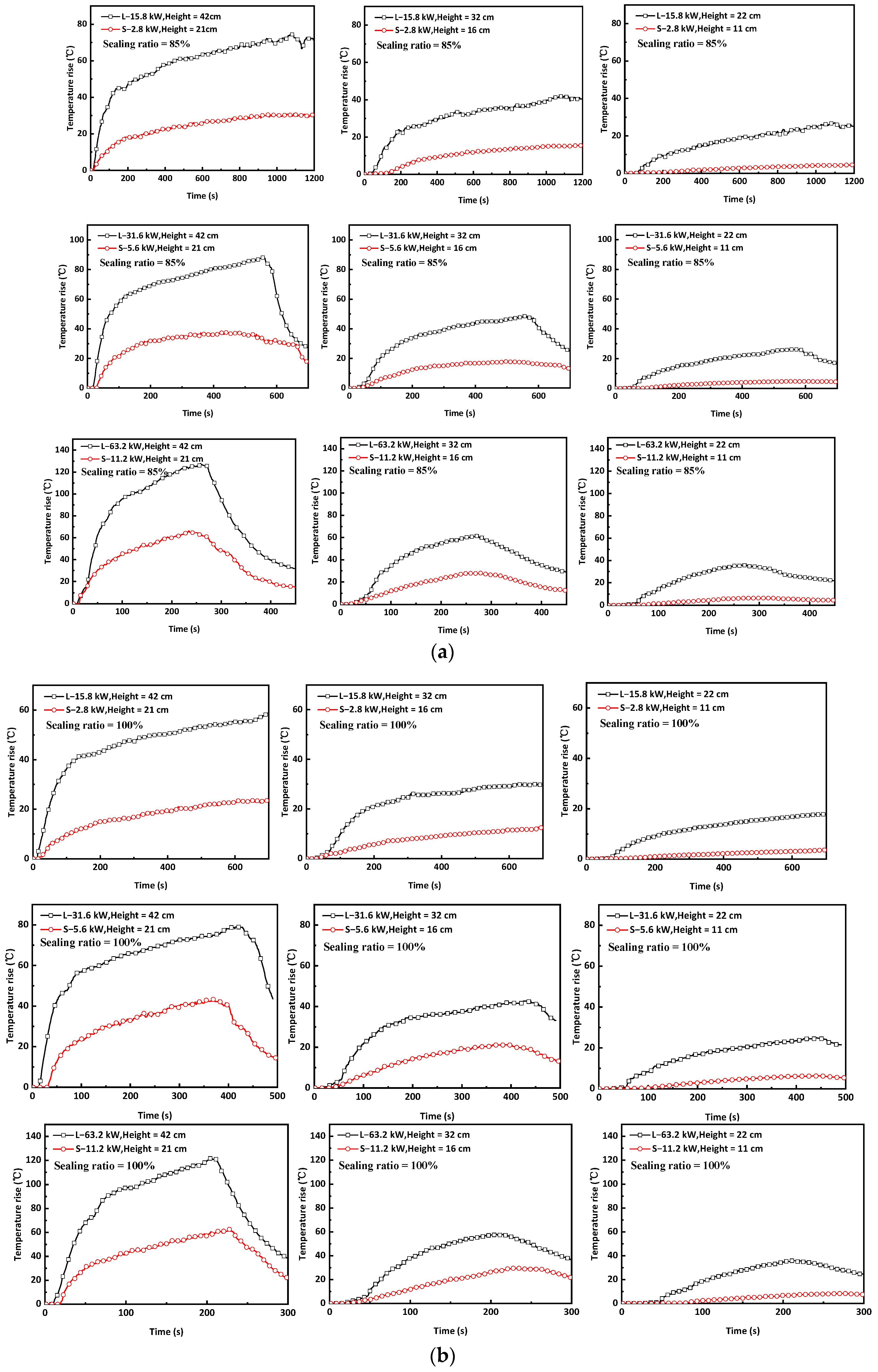
3.1. Peak Temperature Rises above the Fire Source in Tunnel-S
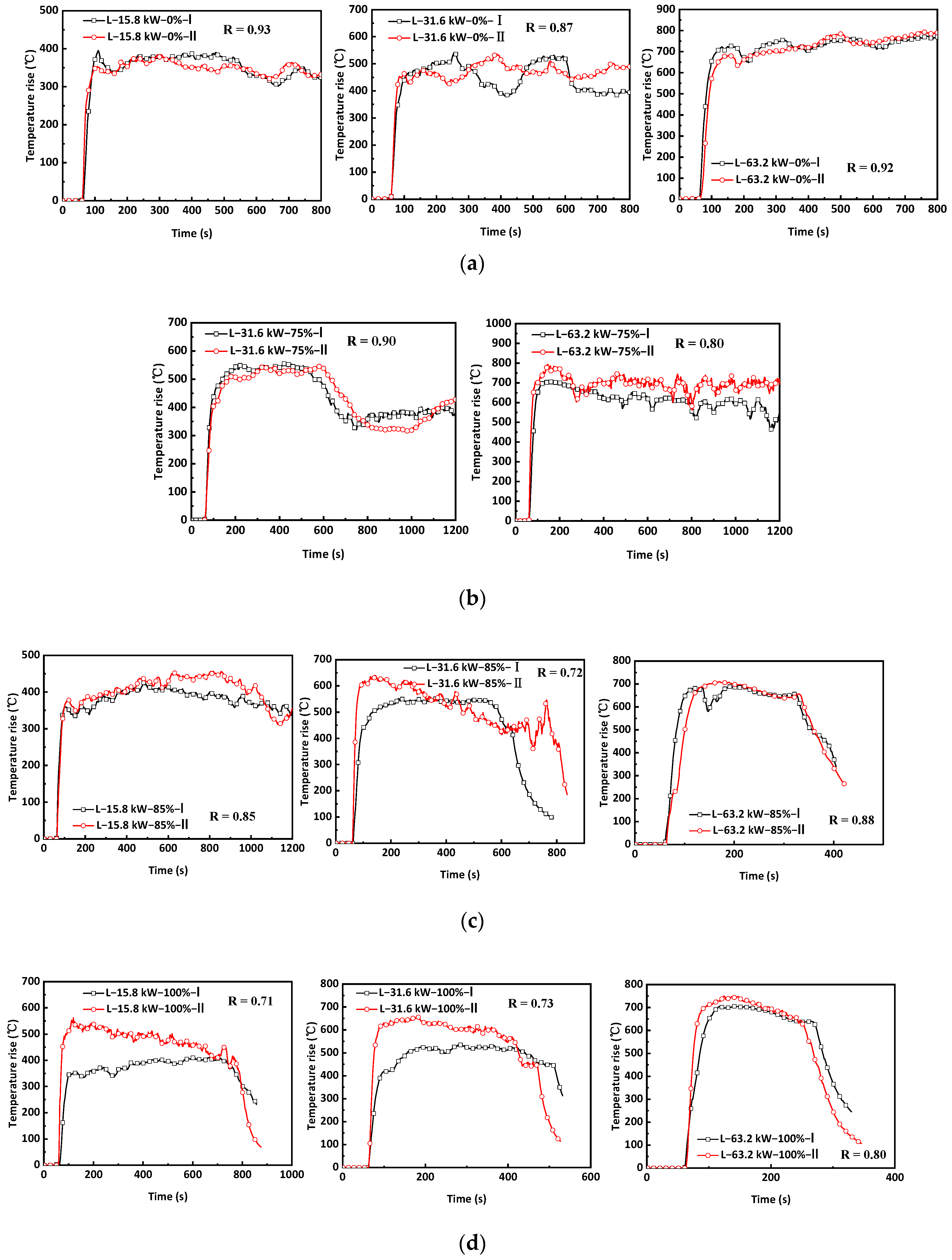
3.2. Peak Temperature Rises above the Fire Source in Tunnel-L
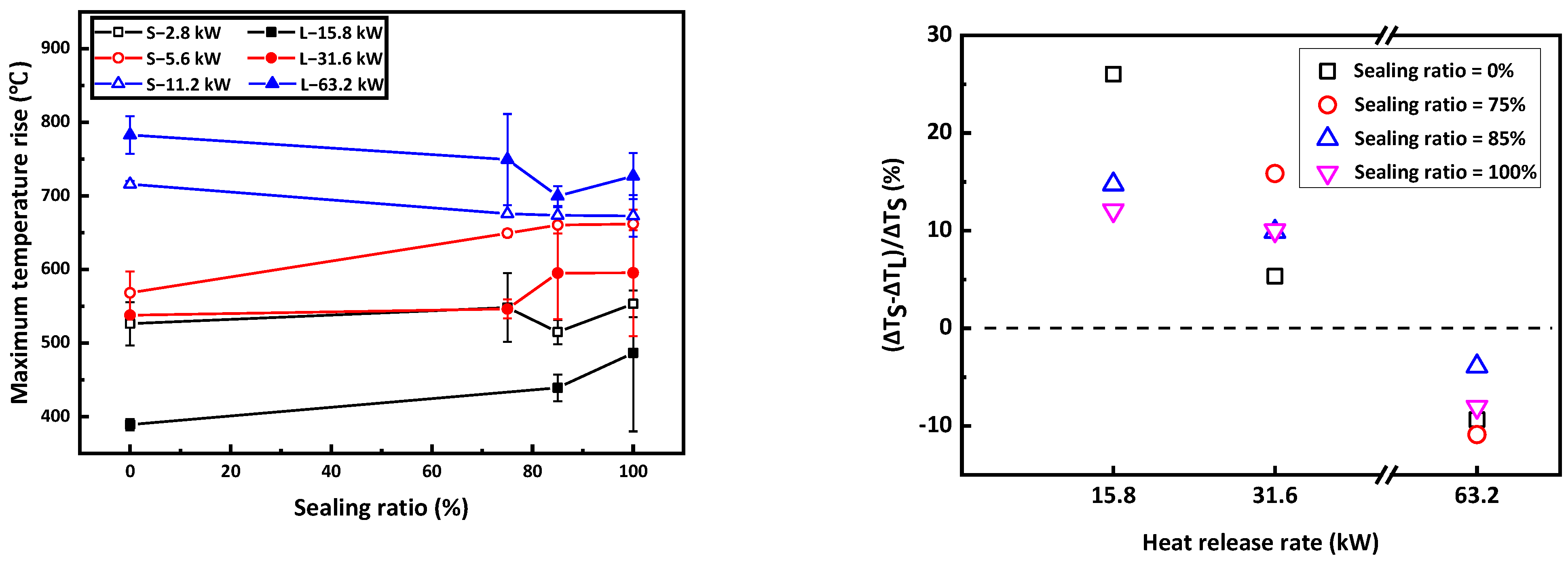
3.3. A Comparision of Peak Temperature Rises above the Fire Source in Two Tunnels
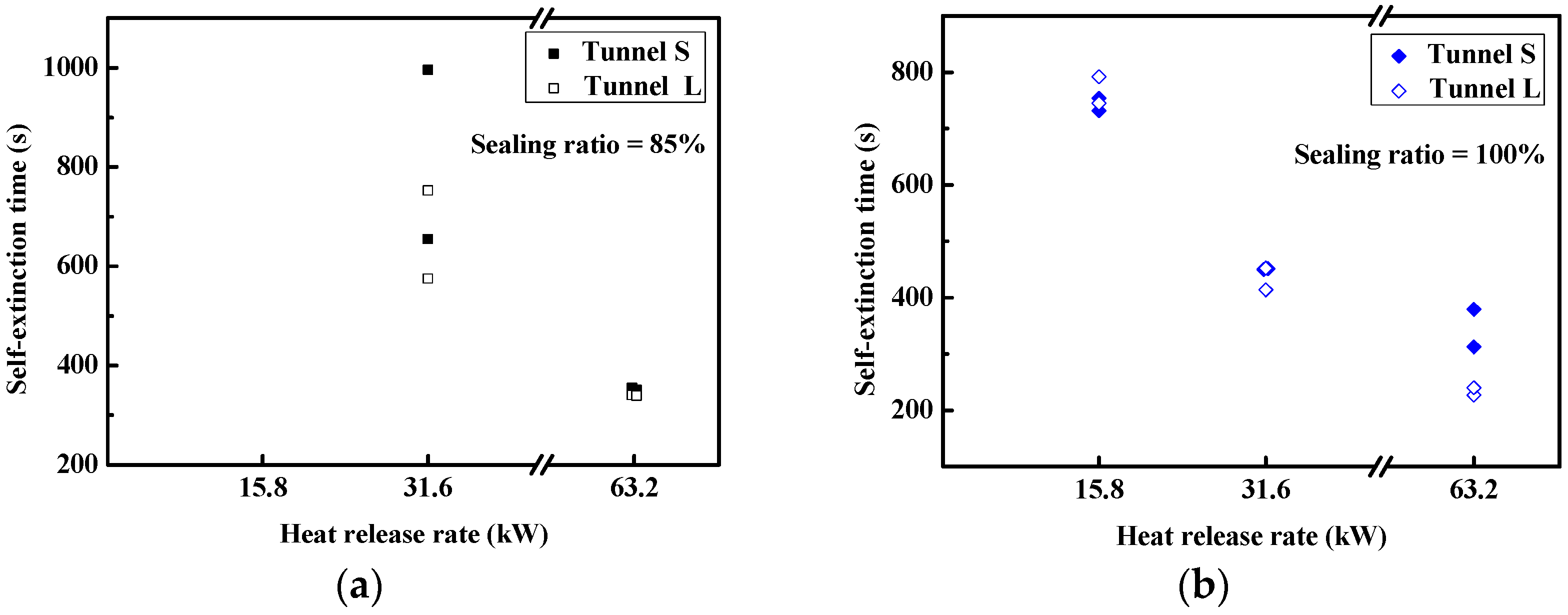
3.4. Extinction Times at Different Sealing Ratios
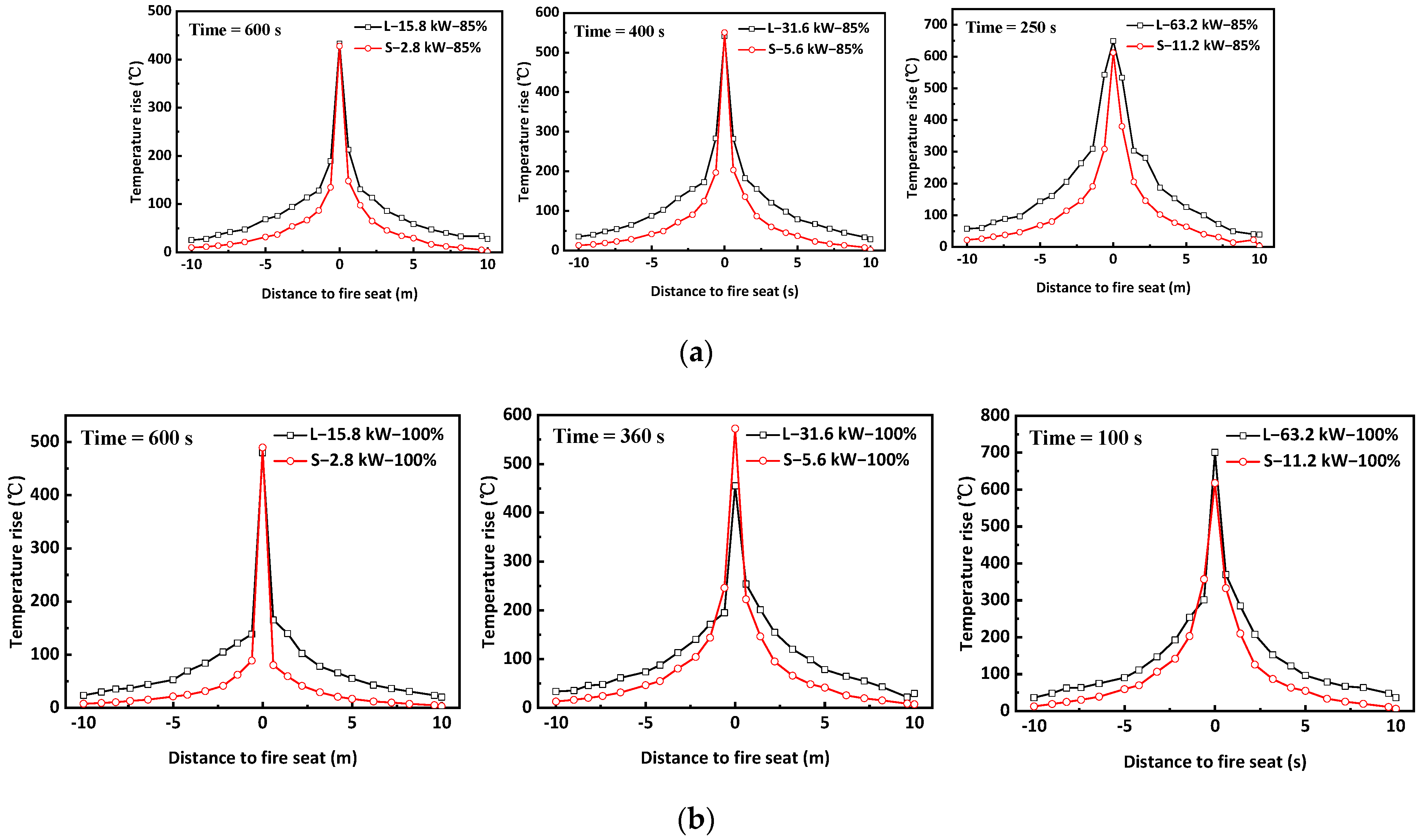
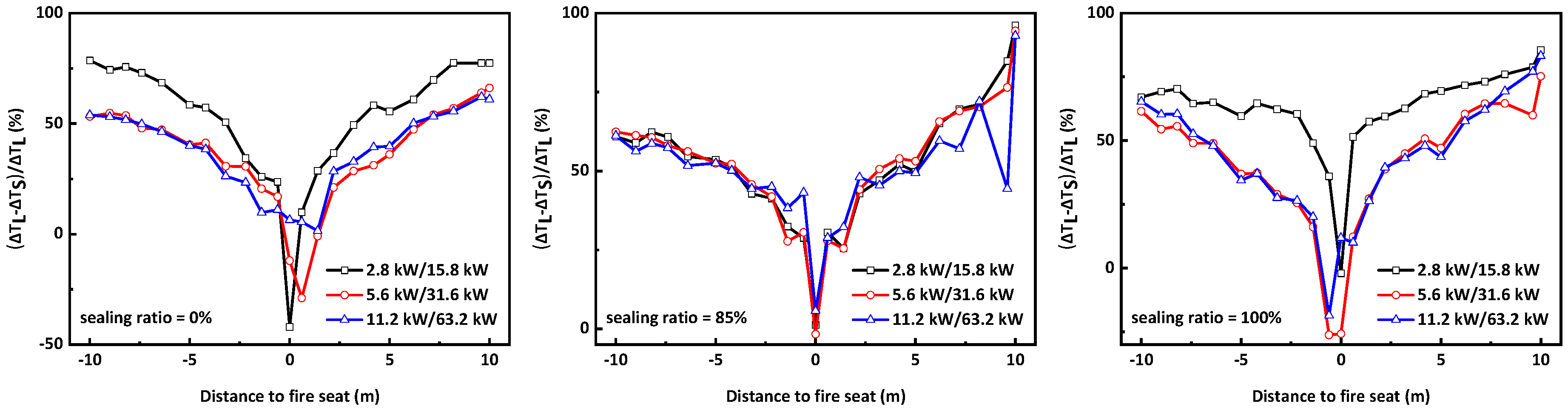
3.5. Attenuation of Temperature Rises along the Tunnels
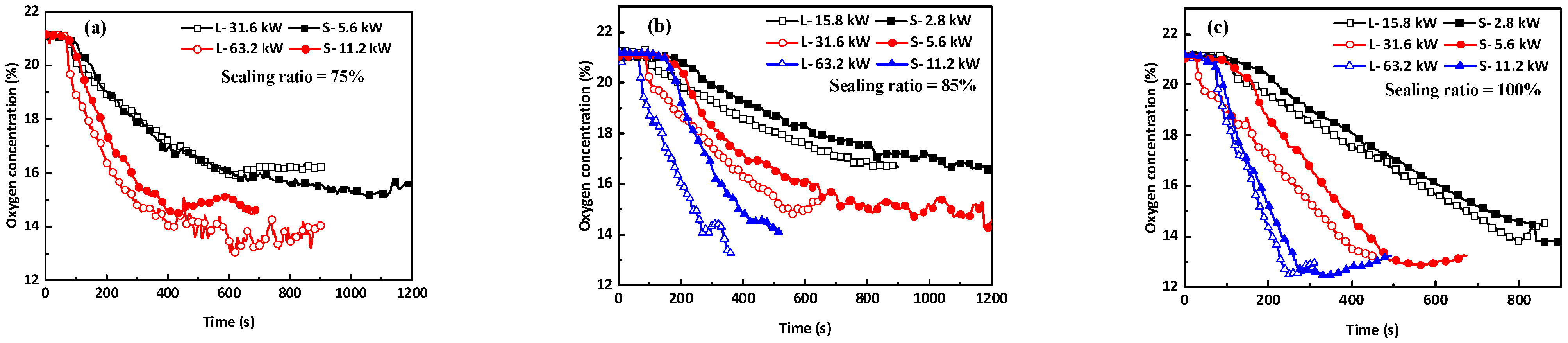
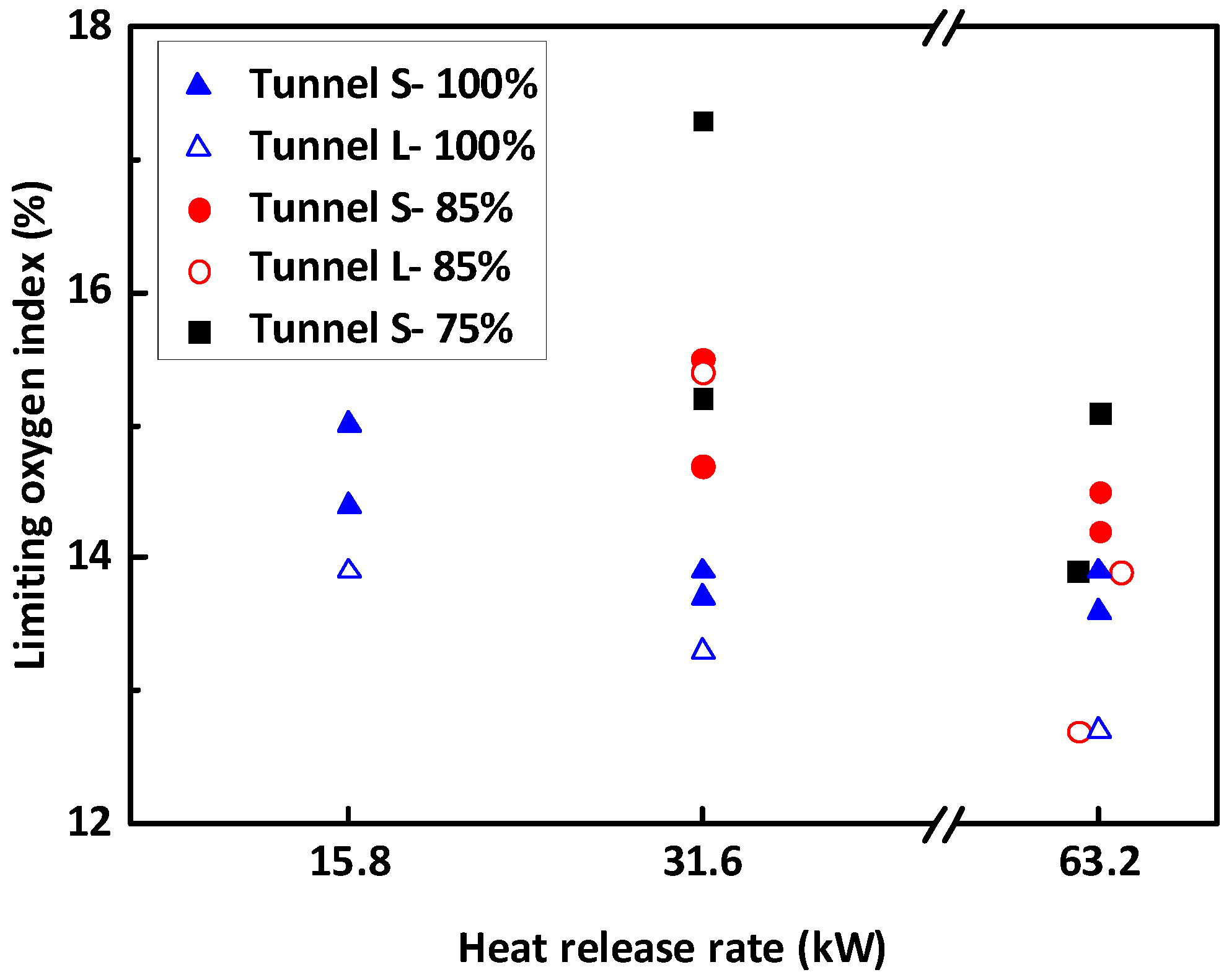
3.6. Similarity in Oxygen Concentration
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Roh, J.S.; Yang, S.S.; Ryou, H.S.; O Yoon, M.; Jeong, Y.T. An experimental study on the effect of ventilation velocity on burning rate in tunnel fires—Heptane pool fire case. Build. Environ. 2008, 43, 1225–1231. [Google Scholar] [CrossRef]
- Lee, S.R.; Ryou, H.S. An Experimental Study of the Effect of the Aspect Ratio on the Critical Velocity in Longitudinal Ventilation Tunnel Fires. J. Fire Sci. 2005, 23, 119–138. [Google Scholar] [CrossRef]
- Yao, Y.; He, K.; Peng, M.; Shi, L.; Cheng, X.; Zhang, H. Maximum gas temperature rise beneath the ceiling in a portals-sealed tunnel fire. Tunn. Undergr. Space Technol. 2018, 80, 10–15. [Google Scholar] [CrossRef]
- Wu, Y.; Bakar, M. Control of smoke flow in tunnel fires using longitudinal ventilation systems—A study of the critical velocity. Fire Saf. J. 2000, 35, 363–390. [Google Scholar] [CrossRef]
- Li, Y.Z.; Ingason, H. Model scale tunnel fire tests with automatic sprinkler. Fire Saf. J. 2013, 61, 298–313. [Google Scholar] [CrossRef]
- Ingason, H. Model scale railcar fire tests. Fire Saf. J. 2007, 42, 271–282. [Google Scholar] [CrossRef]
- Hansen, R.; Ingason, H. Heat release rates of multiple objects at varying distances. Fire Saf. J. 2012, 52, 1–10. [Google Scholar] [CrossRef]
- Choi, B.; Oh, C.; Kim, M.; Han, Y.; Choi, J. A new design criterion of fire ventilation for transversely ventilated tunnels. Tunn. Undergr. Space Technol. 2006, 21, 277–278. [Google Scholar] [CrossRef]
- Chen, C.-K.; Zhu, C.-X.; Liu, X.-Y.; Yu, N.-H. Experimental investigation on the effect of asymmetrical sealing on tunnel fire behavior. Int. J. Heat Mass Transf. 2016, 92, 55–65. [Google Scholar] [CrossRef]
- Chen, C.-K.; Xiao, H.; Wang, N.-N.; Shi, C.-L.; Zhu, C.-X.; Liu, X.-Y. Experimental investigation of pool fire behavior to different tunnel-end ventilation opening areas by sealing. Tunn. Undergr. Space Technol. 2017, 63, 106–117. [Google Scholar] [CrossRef]
- Huang, Y.; Li, Y.; Dong, B.; Li, J.; Liang, Q. Numerical investigation on the maximum ceiling temperature and longitudinal decay in a sealing tunnel fire. Tunn. Undergr. Space Technol. 2018, 72, 120–130. [Google Scholar] [CrossRef]
- Yao, Y.; Cheng, X.; Zhang, S.; Zhu, K.; Zhang, H.; Shi, L. Maximum smoke temperature beneath the ceiling in an enclosed channel with different fire locations. Appl. Therm. Eng. 2017, 111, 30–38. [Google Scholar] [CrossRef]
- Yao, Y.; Cheng, X.; Shi, L.; Zhang, S.; He, K.; Peng, M.; Zhang, H. Experimental study on the effects of initial sealing time on fire behaviors in channel fires. Int. J. Therm. Sci. 2018, 125, 273–282. [Google Scholar] [CrossRef]
- Wang, K.-H.; Chen, J.-M.; Wang, Z.-K.; Gao, D.-L.; Wang, G.-Y.; Lin, P. An experimental study on self-extinction of tunnel fire under natural ventilation condition. Tunn. Undergr. Space Technol. 2018, 84, 177–188. [Google Scholar] [CrossRef]
- Xu, Z.; Zhao, J.; Liu, Q.; Chen, H.; Liu, Y.; Geng, Z.; He, L. Experimental investigation on smoke spread characteristics and smoke layer height in tunnels. Fire Mater. 2019, 43, 303–309. [Google Scholar] [CrossRef]
- Lin, P.; Wang, Z.-K.; Wang, K.-H.; Gao, D.-L.; Shi, J.-K.; You, S.-H.; Chen, Z.-N.; Wang, G.-Y.; Mei, X.-J. An experimental study on self-extinction of methanol fire in tilted tunnel. Tunn. Undergr. Space Technol. 2019, 91, 102996. [Google Scholar] [CrossRef]
- You, S.-H.; Wang, K.-H.; Shi, J.-K.; Chen, Z.-N.; Gao, D.; Chen, J.-M.; Lin, P. Self-extinction of methanol fire in tunnel with different configuration of blocks. Tunn. Undergr. Space Technol. 2020, 98, 103343. [Google Scholar] [CrossRef]
- Shi, J.-K.; Zuo, C.; Xiong, Y.-Y.; Zhou, M.; Lin, P. Experimental study of different sealing ratios on the self-extinction of tunnel fires. Tunn. Undergr. Space Technol. 2021, 112, 103894. [Google Scholar] [CrossRef]
- Li, Y.Z.; Hertzberg, T. Scaling of internal wall temperatures in enclosure fires. J. Fire Sci. 2015, 33, 113–141. [Google Scholar] [CrossRef]
- Ingason, H.; Li, Y.Z.; Lönnermark, A. Tunnel Fire Dynamics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Vauquelin, O.; Michaux, G.; Lucchesi, C. Scaling laws for a buoyant release used to simulate fire-induced smoke in laboratory experiments. Fire Saf. J. 2008, 44, 665–667. [Google Scholar] [CrossRef]
- Tilley, N.; Rauwoens, P.; Fauconnier, D.; Merci, B. On the extrapolation of CFD results for smoke and heat control in reduced-scale set-ups to full scale: Atrium configuration. Fire Saf. J. 2013, 59, 160–165. [Google Scholar] [CrossRef]
- Lin, P.; Xiong, Y.-Y.; Zuo, C.; Shi, J.-K. Verification of Similarity of Scaling Laws in Tunnel Fires with Natural Ventilation. Fire Technol. 2021, 57, 1611–1635. [Google Scholar] [CrossRef]
- Kile, G.W.; Gonzalez, J.A. The memorial tunnel fire ventilation test program: The longitudinal and natural tests. J. Ashrae Trans. 1997, 103, 701–713. [Google Scholar]
- Hurley, M.J. SFPE Handbook of Fire Protection Engineering; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Li, Y.Z.; Lei, B.; Ingason, H. The maximum temperature of buoyancy-driven smoke flow beneath the ceiling in tunnel fires. Fire Saf. J. 2011, 46, 204–210. [Google Scholar] [CrossRef]
- Hu, L.H.; Wu, L.; Liu, S. Flame length elongation behavior of medium hydrocarbon pool fires in cross air flow. Fuel. 2013, 111, 613–620. [Google Scholar] [CrossRef]
- Emori, R.I.; Saito, K. A Study of Scaling Laws in Pool and Crib Fires. Combust. Sci. Technol. 1983, 31, 217–231. [Google Scholar] [CrossRef]


| Type | Scaling Law | Unit |
|---|---|---|
| Heat-release rate | kW | |
| Velocity | m/s | |
| Time | s | |
| Temperature | K | |
| Gas concentration | - |
| No. | HRR/kW | Self-Extinction or Not | Self-Extinction Time/s | Limiting Oxygen Concentration/% |
|---|---|---|---|---|
| L-15.8–0%-Ⅰ | N | - | - | |
| L-15.8–75%-Ⅰ | N | - | - | |
| L-15.8–85%-Ⅰ | N | - | - | |
| L-15.8–85%-Ⅱ | 15.8 | N | - | - |
| L-15.8–100%-Ⅰ | Y | 745 | - | |
| L-15.8–100%-Ⅱ | Y | 792 | 13.9 | |
| L-31.6–0%-Ⅰ | N | - | - | |
| L-31.6–75%-Ⅰ | N | - | - | |
| L-31.6–75%-Ⅱ | N | - | - | |
| L-31.6–85%-Ⅰ | Y | 753 | - | |
| L-31.6–85%-Ⅱ | 31.6 | Y | 575 | 15.4 |
| L-31.6–100%-Ⅰ | Y | 414 | NA | |
| L-31.6–100%-Ⅱ | Y | 452 | 13.3 | |
| L-63.2–0%-Ⅰ | N | - | - | |
| L-63.2–75%-Ⅰ | N | - | - | |
| L-63.2–75%-Ⅱ | N | - | - | |
| L-63.2–85%-Ⅰ | 63.2 | Y | 340 | 13.9 |
| L-63.2–85%-Ⅱ | Y | 339 | 12.7 | |
| L-63.2–100%-Ⅰ | Y | 227 | NA | |
| L-63.2–100%-Ⅱ | Y | 240 | 12.7 |
| No. | HRR/kW | Self-Extinction or Not | Self-Extinction Time/s | Limiting Oxygen Concentration/% |
|---|---|---|---|---|
| S-2.8–0%-Ⅰ | 2.8 | N | - | - |
| S-2.8–75%-Ⅰ | N | - | - | |
| S-2.8–75%-Ⅱ | N | - | - | |
| S-2.8–85%-Ⅰ | N | - | - | |
| S-2.8–85%-Ⅱ | N | - | - | |
| S-2.8–100%-Ⅰ | Y | 517 | 15 | |
| S-2.8–100%-Ⅱ | Y | 533 | 14.4 | |
| S-5.6–0%-Ⅰ | 5.6 | N | - | - |
| S-5.6–75%-Ⅰ | Y | 746 | 15.2 | |
| S-5.6–75%-Ⅱ | Y | 788 | 17.3 | |
| S-5.6–85%-Ⅰ | Y | 463 | 15.5 | |
| S-5.6–85%-Ⅱ | Y | 704 | 14.7 | |
| S-5.6–100%-Ⅰ | Y | 319 | 13.9 | |
| S-5.6–100%-Ⅱ | Y | 318 | 13.7 | |
| S-11.2–0%-Ⅰ | 11.2 | N | - | - |
| S-11.2–75%-Ⅰ | Y | 406 | 15.1 | |
| S-11.2–75%-Ⅱ | Y | 726 | 13.9 | |
| S-11.2–85%-Ⅰ | Y | 251 | 14.5 | |
| S-11.2–85%-Ⅱ | Y | 248 | 14.2 | |
| S-11.2–100%-Ⅰ | Y | 221 | 13.6 | |
| S-11.2–100%-Ⅱ | Y | 168 | 13.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Wang, X.; Li, B.; Lin, P. Experimental Study of Scale Effect in Tunnel Fires at Different Sealing Ratios. Fire 2023, 6, 92. https://doi.org/10.3390/fire6030092
Chen L, Wang X, Li B, Lin P. Experimental Study of Scale Effect in Tunnel Fires at Different Sealing Ratios. Fire. 2023; 6(3):92. https://doi.org/10.3390/fire6030092
Chicago/Turabian StyleChen, Ling, Xuan Wang, Baiyi Li, and Peng Lin. 2023. "Experimental Study of Scale Effect in Tunnel Fires at Different Sealing Ratios" Fire 6, no. 3: 92. https://doi.org/10.3390/fire6030092
APA StyleChen, L., Wang, X., Li, B., & Lin, P. (2023). Experimental Study of Scale Effect in Tunnel Fires at Different Sealing Ratios. Fire, 6(3), 92. https://doi.org/10.3390/fire6030092









