A Comparison of Four Spatial Interpolation Methods for Modeling Fine-Scale Surface Fuel Load in a Mixed Conifer Forest with Complex Terrain
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data Collection
2.2. Spatial Interpolation Methods
2.2.1. Classification
2.2.2. Multiple Linear Regression
2.2.3. Ordinary Kriging
2.2.4. Regression Kriging
2.3. Comparison of Interpolation Methods
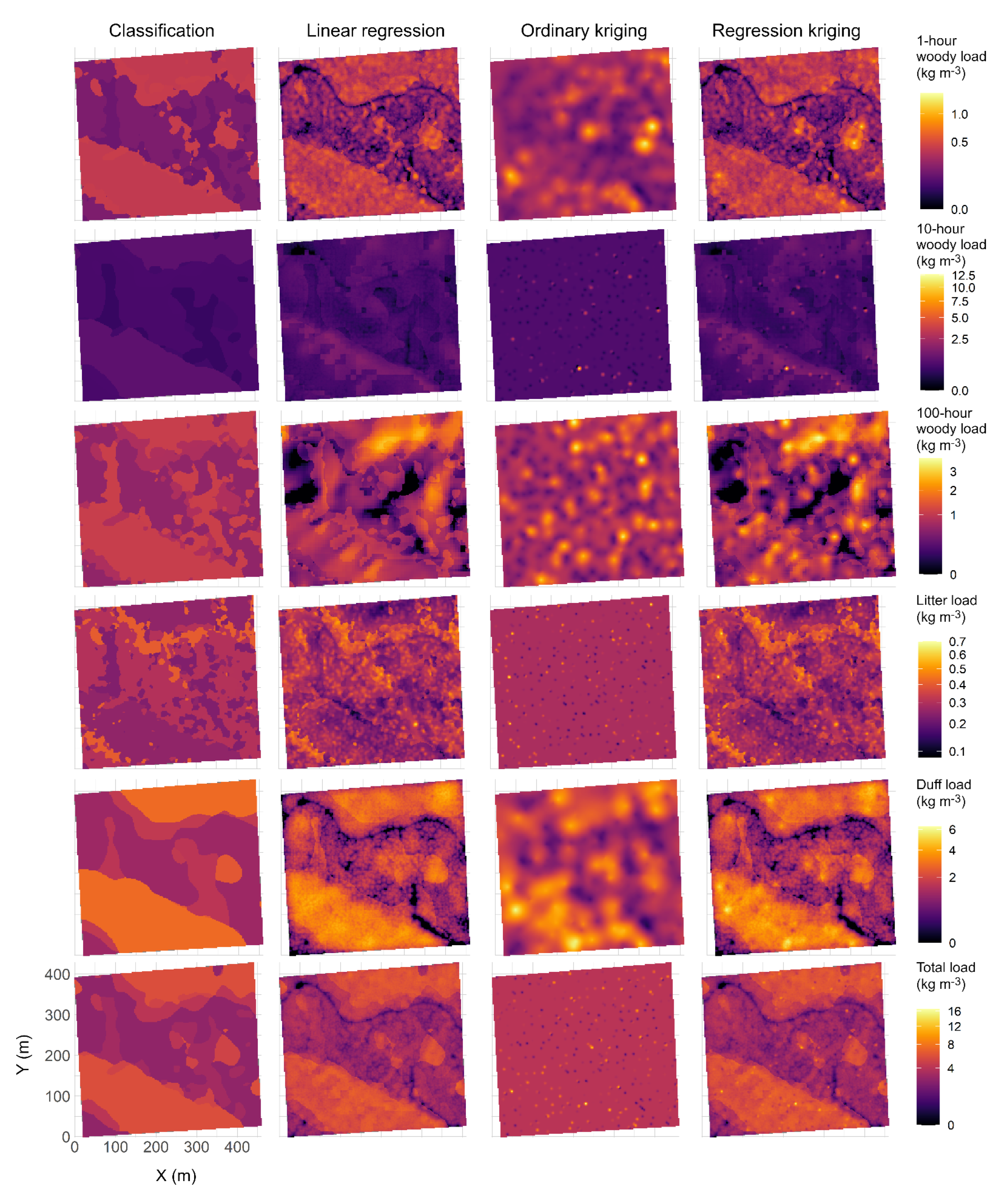
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Burgan, R.E. Concepts and Interpreted Examples in Advanced Fuel Modeling; Gen. Tech. Rep. INT-GTR-238; USDA Forest Service, Intermountain Research Station: Ogden, UT, USA, 1987. [Google Scholar]
- Ucitel, D.; Christian, D.P.; Graham, J.M. Vole Use of Coarse Woody Debris and Implications for Habitat and Fuel Management. J. Wildl. Manag. 2003, 67, 65–72. [Google Scholar] [CrossRef]
- de Groot, W.J.; Landry, R.; Kurz, W.A.; Anderson, K.R.; Englefield, P.; Fraser, R.H.; Hall, R.J.; Banfield, E.; Raymond, D.A.; Decker, V.; et al. Estimating direct carbon emissions from Canadian wildland fires. Int. J. Wildland Fire 2007, 16, 593–606. [Google Scholar] [CrossRef]
- Keane, R.E.; Herynk, J.M.; Toney, C.; Urbanski, S.P.; Lutes, D.C.; Ottmar, R.D. Evaluating the performance and mapping of three fuel classification systems using Forest Inventory and Analysis surface fuel measurements. For. Ecol. Manag. 2013, 305, 248–263. [Google Scholar] [CrossRef]
- Hobbs, R.J.; Atkins, L. Spatial variability of experimental fires in south-west Western Australia. Aust. J. Ecol. 1988, 13, 295–299. [Google Scholar] [CrossRef]
- Rebertus, A.J.; Williamson, G.B.; Moser, E.B. Fire-Induced Changes in Quercus Laevis Spatial Pattern in Florida Sandhills. J. Ecol. 1989, 77, 638–650. [Google Scholar] [CrossRef]
- Fernandes, P.A.M.; Loureiro, C.A.; Botelho, H.S. Fire behaviour and severity in a maritime pine stand under differing fuel conditions. Ann. For. Sci. 2004, 61, 537–544. [Google Scholar] [CrossRef] [Green Version]
- Arroyo, L.A.; Pascual, C.; Manzanera, J.A. Fire models and methods to map fuel types: The role of remote sensing. For. Ecol. Manag. 2008, 256, 1239–1252. [Google Scholar] [CrossRef] [Green Version]
- Hiers, J.K.; O’Brien, J.J.; Mitchell, R.J.; Grego, J.M.; Loudermilk, E.L. The wildland fuel cell concept: An approach to characterize fine-scale variation in fuels and fire in frequently burned longleaf pine forests. Int. J. Wildland Fire 2009, 18, 315–325. [Google Scholar] [CrossRef]
- Keane, R.E.; Gray, K.; Bacciu, V.; Leirfallom, S. Spatial scaling of wildland fuels for six forest and rangeland ecosystems of the northern Rocky Mountains, USA. Landsc. Ecol. 2012, 27, 1213–1234. [Google Scholar] [CrossRef]
- Lydersen, J.M.; Collins, B.M.; Knapp, E.E.; Roller, G.B.; Stephens, S. Relating fuel loads to overstorey structure and composition in a fire-excluded Sierra Nevada mixed conifer forest. Int. J. Wildland Fire 2015, 24, 484–494. [Google Scholar] [CrossRef]
- O’Brien, J.J.; Loudermilk, E.L.; Hiers, J.K.; Pokswinski, S.; Hornsby, B.; Hudak, A.; Dexter, S.; Rowell, E.; Bright, B.C. Canopy-Derived Fuels Drive Patterns of In-Fire Energy Release and Understory Plant Mortality in a Longleaf Pine (Pinus palustris) Sandhill in Northwest Florida, USA. Can. J. Remote Sens. 2016, 42, 489–500. [Google Scholar] [CrossRef]
- Keane, R.E.; Burgan, R.; van Wagtendonk, J. Mapping wildland fuels for fire management across multiple scales: Integrating remote sensing, GIS, and biophysical modeling. Int. J. Wildland Fire 2001, 10, 301–319. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. A Review of Spatial Interpolation Methods for Environmental Scientists; Geoscience Australia: Canberra, Australia, 2008; p. 137. [Google Scholar]
- Legendre, P. Spatial autocorrelation: Trouble or new paradigm? Ecology 1993, 74, 1659–1673. [Google Scholar] [CrossRef]
- Reich, R.M.; Lundquist, J.E.; Bravo, V.A. Spatial models for estimating fuel loads in the Black Hills, South Dakota, USA. Int. J. Wildland Fire 2004, 13, 119–129. [Google Scholar] [CrossRef]
- Hudak, A.T.; Lefsky, M.A.; Cohen, W.B.; Berterretche, M. Integration of lidar and Landsat ETM+ data for estimating and mapping forest canopy height. Rem. Sens. Environment 2002, 82, 397–416. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Q.; Lin, H.S. Comparing Ordinary Kriging and Regression Kriging for Soil Properties in Contrasting Landscapes. Pedosphere 2010, 20, 594–606. [Google Scholar] [CrossRef]
- Gong, G.; Mattevada, S.; O’Bryant, S.E. Comparison of the accuracy of kriging and IDW interpolations in estimating ground-water arsenic concentrations in Texas. Environ. Res. 2014, 130, 59–69. [Google Scholar] [CrossRef]
- Eldeiry, A.A.; Garcia, L.A. Comparison of ordinary kriging, regression kriging, and cokriging techniques to estimate soil salinity using LANDSAT images. J. Irrig. Drain. Eng. 2010, 136, 355–364. [Google Scholar] [CrossRef]
- Hofstra, N.; Haylock, M.; New, M.; Jones, P.; Frei, C. Comparison of six methods for the interpolation of daily, European climate data. J. Geophys. Res. Atmos. 2008, 113, D21110. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Heap, A.D. A review of comparative studies of spatial interpolation methods in environmental sciences: Performance and impact factors. Ecol. Inform. 2011, 6, 228–241. [Google Scholar] [CrossRef]
- Banwell, E.M.; Varner, M.J.; Knapp, E.E.; Van Kirk, R.W. Spatial, seasonal, and diel forest floor moisture dynamics in Jeffrey pine-white fir forests of the Lake Tahoe Basin, USA. For. Ecol. Manag. 2013, 305, 11–20. [Google Scholar] [CrossRef]
- Banwell, E.M.; Varner, J.M. Structure and composition of forest floor fuels in long-unburned Jeffrey pine-white fir forests of the Lake Tahoe Basin, USA. Int. J. Wildland Fire 2014, 23, 363–372. [Google Scholar] [CrossRef]
- Keane, R.E. Spatiotemporal variability of wildland fuels in US Northern Rocky Mountain forests. Forests 2016, 7, 129. [Google Scholar] [CrossRef] [Green Version]
- Riccardi, C.L.; Ottmar, R.D.; Sandberg, D.V.; Andreu, A.; Elman, E.; Kopper, K.; Long, J. The fuelbed: A key element of the Fuel Characteristic Classification System. Can. J. For. Res. 2007, 37, 2394–2412. [Google Scholar] [CrossRef]
- Prichard, S.J.; Kennedy, M.C.; Andreu, A.G.; Eagle, P.C.; French, N.H.; Billmire, M. Next-Generation Biomass Mapping for Regional Emissions and Carbon Inventories: Incorporating Uncertainty in Wildland Fuel Characterization. J. Geophys. Res.–Biogeosciences 2019, 124, 3699–3716. [Google Scholar] [CrossRef]
- Brown, J.K.; Bevins, C.D. Surface Fuel Loadings and Predicted Fire Behavior for Vegetation Types in the Northern Rocky Mountains; Research Note INT-RN-358; USDA Forest Service, Intermountain Research Station: Ogden, UT, USA, 1986. [Google Scholar]
- Fry, D.L.; Stephens, S.L. Stand-level spatial dependence in an old-growth Jeffrey pine–mixed conifer forest, Sierra San Pedro Mártir, Mexico. Can. J. For. Res. 2010, 40, 1803–1814. [Google Scholar] [CrossRef] [Green Version]
- Hall, R.J.; Skakun, R.S.; Arsenault, E.J.; Case, B.S. Modeling forest stand structure attributes using Landsat ETM+ data: Application to mapping of aboveground biomass and stand volume. For. Ecol. Manag. 2006, 225, 378–390. [Google Scholar] [CrossRef]
- Kennard, D.K.; Outcalt, K. Modeling spatial patterns of fuels and fire behavior in a longleaf pine forest in the Southeastern USA. Fire Ecol. 2006, 2, 31–52. [Google Scholar] [CrossRef]
- Vakili, E.; Hoffman, C.M.; Keane, R.E.; Tinkham, W.T.; Dickinson, Y. Spatial variability of surface fuels in treated and untreated ponderosa pine forests of the southern Rocky Mountains. Int. J. Wildland Fire 2016, 25, 1156–1168. [Google Scholar] [CrossRef]
- Pierce, K.B.; Ohmann, J.L.; Wimberly, M.C.; Gregory, M.J.; Fried, J.S. Mapping wildland fuels and forest structure for land management: A comparison of nearest neighbor imputation and other methods. Can. J. For. Res. 2009, 39, 1901–1916. [Google Scholar] [CrossRef]
- Keane, R.E.; Dickinson, L.J. The Photoload Sampling Technique: From Downward-Looking Photographs of Synthetic Fuelbeds; Gen. Tech. Rep. RMRS-GTR-190; USDA Forest Service Rocky Mountain Research Station: Fort Collins, CO, USA, 2007. [Google Scholar]
- Tinkham, W.T.; Hoffman, C.M.; Canfield, J.M.; Vakili, E.; Reich, R.M. Using the photoload technique with double sampling to improve surface fuel loading estimates. Int. J. Wildland Fire 2016, 25, 224–228. [Google Scholar] [CrossRef]
- Matthews, S. Effect of drying temperature on fuel moisture content measurements. Int. J. Wildland Fire 2010, 19, 800–802. [Google Scholar] [CrossRef]
- Hood, S.; Wu, R. Estimating Fuel Bed Loadings in Masticated Areas. In Proceedings of the Fuels Management-How to Measure Success, Portland, OR, USA, 28–30 March 2009; USDA Forest Service Rocky Mountain Research Station: Fort Collins, CO, USA; pp. 333–340. [Google Scholar]
- Diggle, P.J. Statistical Analysis of Spatial Point Patterns, 2nd ed.; Arnold: London, UK, 2003. [Google Scholar]
- Hijmans, R.J. Package ‘Raster’—Geographic Data Analysis and Modeling. 2019. Available online: https://CRAN.R-project.org/package=raster (accessed on 10 August 2022).
- Brenning, A.; Bangs, D.; Becker, M. RSAGA: SAGA Geoprocessing and Terrain Analysis. R Package Version 1.3.0. 2018. Available online: https://CRAN.R-project.org/package=RSAGA (accessed on 10 August 2022).
- Evans, J.S.; Murphy, M.A. _spatialEco_. R Package Version 1.3-6. 2021. Available online: https://github.com/jeffreyevans/spatialEco (accessed on 10 August 2022).
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists, 2nd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2007. [Google Scholar]
- Eberly, L.E. Multiple linear regression. Methods Mol. Biol. 2007, 404, 165–187. [Google Scholar] [CrossRef] [PubMed]
- Pardo-Iguzquiza, E.; Chica-Olmo, M. Geostatistics with the Matern semivariogram model: A library of computer programs for inference, kriging and simulation. Comput. Geosci. 2008, 34, 1073–1079. [Google Scholar] [CrossRef]
- Hengl, T. A Practical Guide to Geostatistical Mapping, 2nd ed.; Scientific and Technical Research Series Report; Office for the Official Publication of the European Communities: Luxembourg, 2009; ISBN 978-92-79-06904-8. [Google Scholar]
- Gotway, C.A.; Stroup, W.W. A Generalized Linear Model Approach to Spatial Data Analysis and Prediction. J. Agric. Biol. En-viron. Stat. 1997, 2, 157–178. [Google Scholar] [CrossRef]
- Berrar, D. Cross-validation. In Encyclopedia of Bioinformatics and Computational Biology; Elsevier: Amsterdam, The Netherlands, 2019; Volume 1, pp. 542–545. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, 2019, Vienna, Austria. Available online: https://www.R-project.org/ (accessed on 10 August 2022).
- Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; McGowan, L.D.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J.; et al. Welcome to the Tidyverse. J. Open Source Softw. 2019, 4, 1686. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Rubio, V. ggplot2—Elegant Graphics for Data Analysis (2nd Edition). J. Stat. Softw. 2017, 77. [Google Scholar] [CrossRef] [Green Version]
- Baddeley, A.; Rubak, E.; Turner, R. Spatial Point Patterns: Methodology and Applications with R; Chapman and Hall/CRC: Boca Raton, FL, USA, 2015. [Google Scholar] [CrossRef] [Green Version]
- Bivand, R.S.; Pebesma, E.; Gómez-Rubio, V. Applied Spatial Data Analysis with R, 2nd ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Zambrano, M.B. hydroGOF: Goodness-of-Fit Functions for Comparison of Simulated and Observed Hydrological Time Series, R package version 0.4-0; R Foundation for Statistical Computing: Vienna, Austria, 2017. [CrossRef]
- Gräler, B.; Pebesma, E.; Heuvelink, G. Spatio-temporal interpolation using gstat. R. J. 2016, 8, 204–218. [Google Scholar] [CrossRef]
- Hiemstra, P.H.; Pebesma, E.J.; Twenhöfel, C.J.W.; Heuvelink, G.B.M. Real-time automatic interpolation of ambient gamma dose rates from the Dutch radioactivity monitoring network. Comput. Geosci. 2009, 35, 1711–1721. [Google Scholar] [CrossRef]
- Thompson, M.P.; Haas, J.R.; Gilbertson-Day, J.W.; Scott, J.H.; Langowski, P.; Bowne, E.; Calkin, D.E. Development and application of a geospatial wildfire exposure and risk calculation tool. Environ. Model. Softw. 2015, 63, 61–72. [Google Scholar] [CrossRef]
- Thompson, M.P.; Riley, K.L.; Loeffler, D.; Haas, J.R. Modeling fuel treatment leverage: Encounter rates, risk reduction, and suppression cost impacts. Forests 2017, 8, 469. [Google Scholar] [CrossRef] [Green Version]
- Linn, R.R.; Winterkamp, J.L.; Furman, J.H.; Williams, B.; Hiers, J.K.; Jonko, A.; O’Brien, J.J.; Yedinak, K.M.; Goodrick, S. Modeling low intensity fires: Lessons learned from 2012 RxCADRE. Atmosphere 2021, 12, 139. [Google Scholar] [CrossRef]
- O’Brien, J.J.; Hiers, J.K.; Varner, J.M.; Hoffman, C.M.; Dickinson, M.B.; Michaletz, S.T.; Loudermilk, E.L.; Bufler, B.W. Advances in mechanistic approaches to quantifying biophysical fire effects. Curr. For. Rep. 2018, 4, 161–177. [Google Scholar] [CrossRef]
- Lin, C.; Ma, S.E.; Huang, L.P.; Chen, C.I.; Lin, P.T.; Yang, Z.K.; Lin, K.T. Generating a baseline map of surface fuel loading using stratified random sampling inventory data through cokriging and multiple linear regression methods. Rem. Sens. 2021, 13, 1561. [Google Scholar] [CrossRef]
- Bright, B.C.; Hudak, A.T.; Meddens, A.J.H.; Hawbaker, T.J.; Briggs, J.S.; Kennedy, R.E. Prediction of forest canopy and surface fuels from Lidar and satellite time series data in a bark beetle-affected forest. Forests 2017, 8, 322. [Google Scholar] [CrossRef] [Green Version]
- Hudak, A.T.; Dickinson, M.B.; Bright, B.C.; Kremens, R.L.; Loudermilk, E.L.; O’Brien, J.J.; Hornsby, B.S.; Ottmar, R.D. Measurements relating fire radiative energy density and surface fuel consumption-RxCADRE 2011 and 2012. Int. J. Wildland Fire 2016, 25, 25–37. [Google Scholar] [CrossRef] [Green Version]
- Arellano-Pérez, S.; Castedo-Dorado, F.; López-Sánchez, C.A.; González-Ferreiro, E.; Yang, Z.; Díaz-Varela, R.A.; Álvarez-González, J.G.; Vega, J.A.; Ruiz-González, A.D. Potential of Sentinel-2A data to model surface and canopy fuel characteristics in relation to crown fire hazard. Rem. Sens. 2018, 10, 1645. [Google Scholar] [CrossRef] [Green Version]
- Keane, R.E. Biophysical controls on surface fuel litterfall and decomposition in northern Rocky Mountains, USA. Can. J. For. Res. 2008, 38, 1431–1445. [Google Scholar] [CrossRef]
- Cornwell, W.K.; Cornelissen, J.H.C.; Amatangelo, K.; Dorrepaal, E.; Eviner, V.T.; Godoy, O.; Hobbie, S.E.; Hoorens, B.; Kurokowa, H.; Herez-Harguindegy, N.; et al. Plant species traits are the predominant control on litter decomposition rates within biomes worldwide. Ecol. Lett. 2008, 11, 1065–1071. [Google Scholar] [CrossRef]
- Weedon, J.T.; Cornwell, W.K.; Cornelissen, J.H.C.; Zanne, A.E.; Wirth, C.; Coomes, D.A. Global meta-analysis of wood decomposition rates: A role for trait variation among tree species? Ecol. Lett. 2009, 12, 45–56. [Google Scholar] [CrossRef]
- Fry, D.L.; Stevens, J.T.; Potter, A.T.; Collins, B.M.; Stephens, S.L. Surface fuel accumulation and decomposition in old-growth pine-mixed conifer forests, northwestern Mexico. Fire Ecol. 2018, 14, 6. [Google Scholar] [CrossRef]
- Rowell, E.; Loudermilk, E.L.; Hawley, C.; Pokswinski, S.; Seielstad, C.; Queen, L.; O’Brien, J.J.; Hudak, A.T.; Goodrick, S.; Hiers, J.K. Coupling terrestrial laser scanning with 3D fuel biomass sampling for advancing wildland fuels characterization. For. Ecol. Manag. 2020, 462, 117945. [Google Scholar] [CrossRef]
- Hiers, Q.A.; Loudermilk, E.L.; Hawley, C.M.; Hiers, J.K.; Pokswinski, S.; Hoffman, C.M.; O’Brien, J.J. Non-destructive fuel volume measurements can estimate fine-scale biomass surface fuel types in a frequently burned ecosystem. Fire 2021, 4, 36. [Google Scholar] [CrossRef]
- Wallace, L.; Hillman, S.; Hally, B.; Taneha, R.; White, A.; McGlade, J. Terrestrial laser scanning: An operational tool for fuel hazard mapping? Fire 2022, 5, 85. [Google Scholar] [CrossRef]
- Swayze, N.P.; Tinkham, W.T.; Creasy, M.B.; Vogeler, J.C.; Hudak, A.T.; Hoffman, C.M. Influence of UAS flight altitude and speed on aboveground biomass prediction. Rem. Sens. 2022, 14, 1989. [Google Scholar] [CrossRef]
- Swayze, N.P.; Tinkham, W.T.; Vogeler, J.C.; Hudak, A.T. Influence of flight parameters on UAS-based monitoring of tree height, diameter, and density. Rem. Sens. Environ. 2021, 263, 112540. [Google Scholar] [CrossRef]
- Tinkham, W.T.; Swayze, N.P. Influence of Agisoft Metashape parameters on individual tree detection using structure from motion canopy height models. Forests 2021, 12, 250. [Google Scholar] [CrossRef]
- Zazali, H.H.; Towers, I.N.; Sharples, J.J. A critical review of fuel accumulation models used in Australian fire management. Int. J. Wildland Fire 2021, 30, 42–56. [Google Scholar] [CrossRef]
- Hoffman, C.M.; Sief, C.H.; Linn, R.R.; Mell, W.; Parsons, R.A.; Ziegler, J.P.; Hiers, J.K. Advancing the science of wildland fire dynamics using process-based models. Fire 2018, 1, 32. [Google Scholar] [CrossRef] [Green Version]

| Fuel Component | Min | First Quartile | Median | Mean | Third Quartile | Max |
|---|---|---|---|---|---|---|
| 1 h woody | 0.02 | 0.10 | 0.18 | 0.29 | 0.34 | 2.42 |
| 10 h woody | 0.12 | 0.24 | 0.44 | 0.67 | 0.73 | 15.00 |
| 100 h woody | 0.03 | 0.03 | 0.14 | 0.87 | 1.20 | 9.16 |
| Litter | 0.00 | 0.15 | 0.25 | 0.29 | 0.38 | 1.08 |
| Duff | 0.00 | 0.55 | 1.65 | 1.91 | 2.80 | 9.88 |
| Total | 0.25 | 1.88 | 3.47 | 4.02 | 5.48 | 19.90 |
| Cover Type * | Fuel Load (kg m−2) | |||||
|---|---|---|---|---|---|---|
| Total | 1 h | 10 h | 100 h | Litter | Duff | |
| PIEN | 5.69 | 0.39 | 0.94 | 1.09 | 0.27 | 3.00 |
| PIPO | 2.30 | 0.17 | 0.49 | 0.46 | 0.29 | 0.88 |
| PIPU | 5.32 | 0.56 | 0.53 | 1.42 | 0.32 | 2.49 |
| POTR | 3.12 | 0.15 | 0.53 | 0.88 | 0.23 | 1.33 |
| PSME | 4.20 | 0.38 | 0.62 | 0.84 | 0.40 | 1.96 |
| Component | Scale (m) | Predictors (p) | r2 | MSE | MAE | CV |
|---|---|---|---|---|---|---|
| Classification | ||||||
| 1 h woody | 6 | Cover type | 0.15 | 0.09 | 0.19 | 104 |
| 10 h woody | 3 | Cover type | 0.04 | 0.98 | 0.46 | 148 |
| 100 h woody | 7 | Cover type | 0.04 | 1.67 | 0.94 | 149 |
| Litter | 4 | Cover type | 0.08 | 0.03 | 0.14 | 61 |
| Duff | 5 | Cover type | 0.29 | 2.16 | 1.11 | 77 |
| Total | 10 | Cover type | 0.24 | 6.48 | 1.86 | 63 |
| Linear regression | ||||||
| 1 h woody | 6 | Cover type; basal area; distance to tree; distance to large tree; slope | 0.24 | 0.08 | 0.18 | 99 |
| 10 h woody | 13 | TPH; distance to tree; aspect; flow direction; topographic wetness | 0.13 | 0.90 | 0.44 | 142 |
| 100 h woody | 3 | Cover type; curvature; flow direction; topographic wetness | 0.08 | 1.61 | 0.90 | 146 |
| Litter | 4 | Cover type; basal area; TPH of large trees; aspect; slope, surface relief ratio; topographic wetness | 0.20 | 0.03 | 0.13 | 58 |
| Duff | 19 | Cover type; basal area; TPH; TPH of large trees; distance to large tree; aspect; slope; curvature; surface relief ratio | 0.51 | 1.62 | 0.90 | 66 |
| Total | 10 | Cover type; basal area; distance to tree; aspect; flow direction | 0.30 | 6.05 | 1.74 | 62 |
| Component | Nugget | Sill | Range |
|---|---|---|---|
| Ordinary kriging | |||
| 1 h woody | 0.04 | 0.06 | 39.70 |
| 10 h woody | 0.00 | 1.18 | 7.96 |
| 100 h woody | 0.85 | 0.91 | 27.80 |
| Litter | 0.01 | 0.02 | 6.08 |
| Duff | 1.20 | 1.64 | 49.50 |
| Total | 0.00 | 7.71 | 6.30 |
| Regression kriging | |||
| 1 h woody | 0.05 | 0.03 | 24.10 |
| 10 h woody | 0.00 | 1.14 | 7.66 |
| 100 h woody | 0.85 | 0.80 | 25.60 |
| Litter | 0.01 | 0.02 | 6.08 |
| Duff | 1.11 | 0.83 | 17.90 |
| Total | 1.33 | 4.94 | 6.29 |
| Component | Method | ME | MAE | MAPE | robs,pred |
|---|---|---|---|---|---|
| 1 h woody | CL | <0.01 | 0.19 | 67% | 0.35 |
| LR | <0.01 | 0.19 | 66% | 0.43 | |
| OK | <0.01 | 0.18 | 65% | 0.36 | |
| RK | <0.01 | 0.18 | 64% | 0.45 | |
| 10 h woody | CL | <0.01 | 0.47 | 70% | 0.14 |
| LR | <−0.01 | 0.46 | 68% | 0.27 | |
| OK | <0.01 | 0.45 | 67% | 0.22 | |
| RK | <0.01 | 0.47 | 70% | 0.27 | |
| 100 h woody | CL | <−0.01 | 0.96 | 110% | 0.11 |
| LR | <0.01 | 0.92 | 106% | 0.22 | |
| OK | <0.01 | 0.89 | 103% | 0.25 | |
| RK | <0.01 | 0.87 | 101% | 0.28 | |
| Litter | CL | <0.01 | 0.14 | 50% | 0.24 |
| LR | <0.01 | 0.14 | 48% | 0.30 | |
| OK | <0.01 | 0.13 | 46% | 0.40 | |
| RK | <−0.01 | 0.13 | 45% | 0.44 | |
| Duff | CL | <0.01 | 1.18 | 62% | 0.42 |
| LR | <0.01 | 1.06 | 55% | 0.59 | |
| OK | <0.01 | 0.98 | 51% | 0.61 | |
| RK | <0.01 | 0.96 | 50% | 0.64 | |
| Total | CL | <0.01 | 1.89 | 47% | 0.47 |
| LR | <0.01 | 1.80 | 45% | 0.51 | |
| OK | 0.04 | 1.91 | 48% | 0.39 | |
| RK | 0.02 | 1.70 | 42% | 0.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoffman, C.M.; Ziegler, J.P.; Tinkham, W.T.; Hiers, J.K.; Hudak, A.T. A Comparison of Four Spatial Interpolation Methods for Modeling Fine-Scale Surface Fuel Load in a Mixed Conifer Forest with Complex Terrain. Fire 2023, 6, 216. https://doi.org/10.3390/fire6060216
Hoffman CM, Ziegler JP, Tinkham WT, Hiers JK, Hudak AT. A Comparison of Four Spatial Interpolation Methods for Modeling Fine-Scale Surface Fuel Load in a Mixed Conifer Forest with Complex Terrain. Fire. 2023; 6(6):216. https://doi.org/10.3390/fire6060216
Chicago/Turabian StyleHoffman, Chad M., Justin P. Ziegler, Wade T. Tinkham, John Kevin Hiers, and Andrew T. Hudak. 2023. "A Comparison of Four Spatial Interpolation Methods for Modeling Fine-Scale Surface Fuel Load in a Mixed Conifer Forest with Complex Terrain" Fire 6, no. 6: 216. https://doi.org/10.3390/fire6060216
APA StyleHoffman, C. M., Ziegler, J. P., Tinkham, W. T., Hiers, J. K., & Hudak, A. T. (2023). A Comparison of Four Spatial Interpolation Methods for Modeling Fine-Scale Surface Fuel Load in a Mixed Conifer Forest with Complex Terrain. Fire, 6(6), 216. https://doi.org/10.3390/fire6060216









