Application of Factorial Analysis to the Study of Vented Dust Explosions in Large Biomass Storage Silos
Abstract
:1. Introduction
2. Materials and Methods
2.1. CFD Code
2.2. Scenario
2.3. Factorial Design
2.3.1. Vent Area
2.3.2. Ignition Location
- Top: ignition in the upper third of the cloud height (at 19.75 m above the silo bottom);
- Bottom: ignition in the lower third of the cloud height (at 1.25 m above the silo bottom).
2.3.3. Initial Turbulence
- Low: the three parameters had lower values, resulting in weak initial turbulence.
- High: this corresponded to a more severe turbulent flow.
2.3.4. Dust Concentration
2.4. Factorial Analysis
- q: the sum of the products of Pred,sim and the corresponding contrast coefficient, considering the 16 cases;
- Q: calculated as q divided by the number of cases (16);
- Q2: the square of Q (the total Q2 is the sum of all Q2 values);
- Y: the percentage of each Q2 in relation to the total Q2.
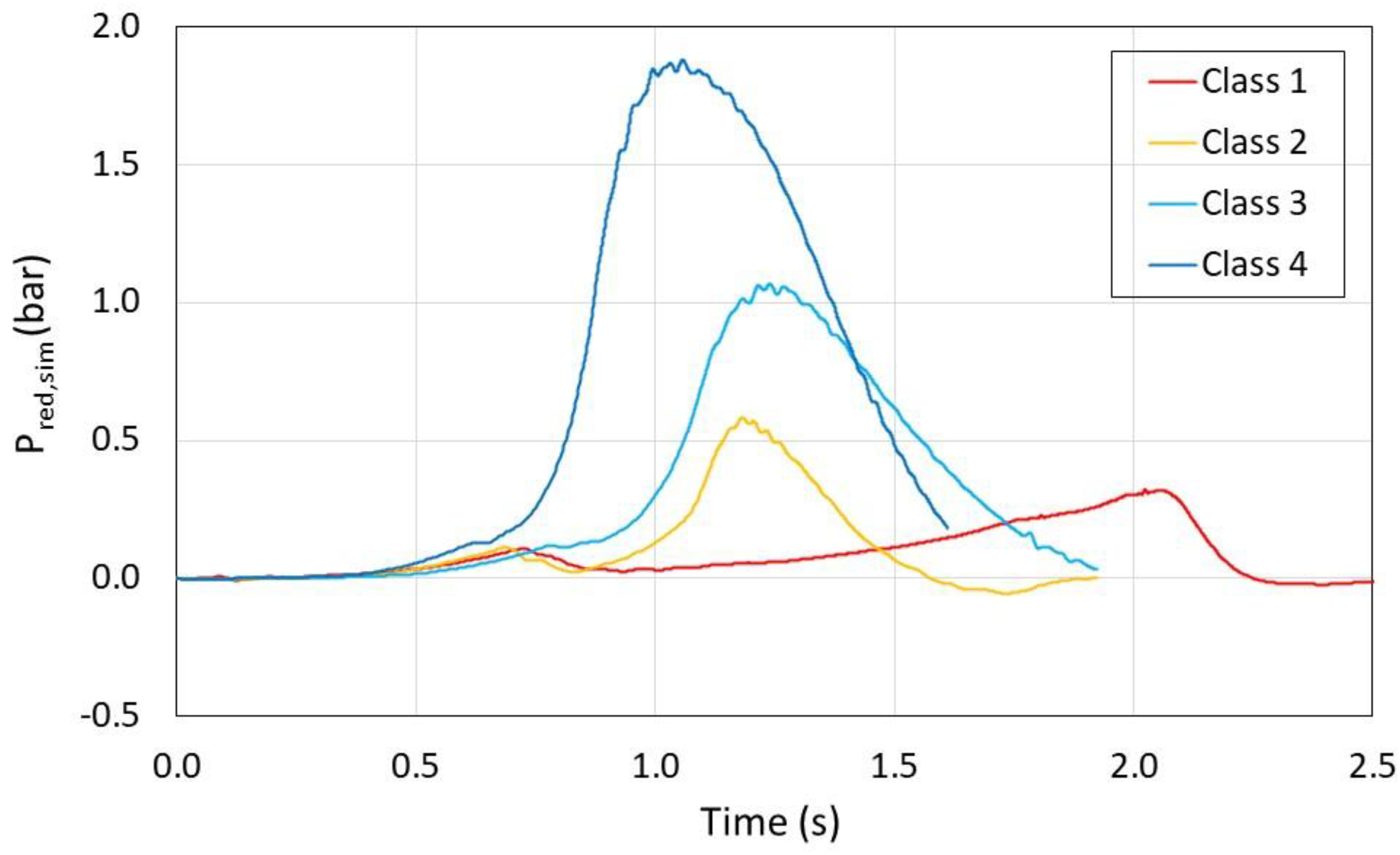
3. Results
- Class 1: Pred,sim ≤ 0.5 bar;
- Class 2: 0.5 bar < Pred,sim ≤ 1.0 bar;
- Class 3: 1.0 bar < Pred,sim ≤ 1.5 bar;
- Class 4: 1.5 bar < Pred,sim.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Eckhoff, R.K. Understanding dust explosions. The role of powder science and technology. J. Loss Prev. Process Ind. 2009, 22, 105–116. [Google Scholar] [CrossRef]
- Klippel, A.; Schmidt, M.; Krause, U. Dustiness in workplace safety and explosion protection—Review and outlook. J. Loss Prev. Process Ind. 2015, 34, 22–29. [Google Scholar] [CrossRef]
- Ilea, C.G.; Kosinski, P.; Hoffmann, A.C. The effect of polydispersity on dust lifting behind shock waves. Powder Technol. 2009, 196, 194–201. [Google Scholar] [CrossRef]
- Amyotte, P.R.; Eckhoff, R.K. Dust explosion causation, prevention and mitigation: An overview. J. Chem. Health Saf. 2010, 17, 15–28. [Google Scholar] [CrossRef]
- Eckhoff, R.K. Dust Explosions in the Process Industries, 3rd ed.; Gulf Professional Publishing/Elsevier: Amsterdam, The Netherlands, 2003; pp. 20–25. [Google Scholar]
- Abbasi, T.; Abbasi, S.A. Dust explosions—Cases, causes, consequences, and control. J. Hazard. Mater. 2007, 40, 7–44. [Google Scholar] [CrossRef]
- García Torrent, J.; Ramírez-Gómez, A.; Fernandez-Anez, N.; Medic Pejic, L.; Tascón, A. Influence of the composition of solid biomass in the flammability and susceptibility to spontaneous combustion. Fuel 2016, 184, 503–511. [Google Scholar] [CrossRef]
- Ferreira, T.; Marques, E.; Monney, J.M.; Pinho, C. A Study on the spontaneous ignition of some ligneous pellets. Fire 2023, 6, 153. [Google Scholar] [CrossRef]
- Casson Moreno, V.; Cozzani, V. Major accident hazard in bioenergy production. J. Loss Prev. Process Ind. 2015, 35, 135–144. [Google Scholar] [CrossRef]
- Krigstin, S.; Wetzel, S.; Jayabala, N.; Helmeste, C.; Madrali, S.; Agnew, J.; Volpe, S. Recent health and safety incident trends related to the storage of woody biomass: A need for improved monitoring strategies. Forests 2018, 9, 538. [Google Scholar] [CrossRef] [Green Version]
- Coffey, C.J.; Price, D.W. Probabilistic risk assessment in combination with CFD modelling of biomass dust explosions within large bulk storage volumes. In Proceedings of the Hazards XXIII Symposium, Southport, UK, 12–15 November 2012. [Google Scholar]
- Siwek, R. Explosion venting technology. J. Loss Prev. Process Ind. 1996, 9, 81–90. [Google Scholar] [CrossRef]
- Yuan, Z.; Khakzad, N.; Khan, F.; Amyotte, P. Domino effect analysis of dust explosions using Bayesian networks. Process Saf. Environ. Prot. 2016, 100, 108–116. [Google Scholar] [CrossRef]
- EN 14491; Dust Explosion Venting Protective Systems. European Committee for Standardization: Brussels, Belgium, 2012.
- NFPA 68; Standard on Explosion Protection by Deflagration Venting. National Fire Protection Association: Quincy, MA, USA, 2023.
- Zalosh, R. Explosion Venting Data and Modeling—Literature Review; The Fire Protection Research Foundation: Quincy, MA, USA, 2008. [Google Scholar]
- Siwek, R. New revised VDI guideline 3673 “Pressure release of dust explosions”. Process Saf. Prog. 1994, 13, 190–201. [Google Scholar] [CrossRef]
- EN 14034-1; Determination of Explosion Characteristics of Dust Clouds—Part 1: Determination of the Maximum Explosion Pressure pmax of Dust Clouds. European Committee for Standardization: Brussels, Belgium, 2011.
- EN 14034-2; Determination of Explosion Characteristics of Dust Clouds—Part 2: Determination of the Maximum Rate of Explosion Pressure Rise (dp/dt)max of Dust Clouds. European Committee for Standardization: Brussels, Belgium, 2011.
- Tascón, A. Design of silos for dust explosions: Determination of vent area sizes and explosion pressures. Eng. Struct. 2017, 134, 1–10. [Google Scholar] [CrossRef]
- Tascón, A.; Aguado, P.J.; Ramírez, A. Dust explosion venting in silos: A comparison of standards NFPA 68 and EN 14491. J. Loss Prev. Process Ind. 2009, 22, 204–209. [Google Scholar] [CrossRef]
- Middha, P.; Samaraweera, R.; Coffey, C.; Price, D.W. The Influence of Explosion Relief Vent Layouts on Explosion Overpressures in Large Biomass Storage Vessels. Chem. Eng. Trans. 2016, 48, 205–210. [Google Scholar] [CrossRef]
- Tascón, A.; Aguado, P.J. Simulations of vented dust explosions in a 5 m3 vessel. Powder Technol. 2017, 321, 409–418. [Google Scholar] [CrossRef]
- Proust, C.; Leprette, E.; Snoeys, J. The role of turbulence in explosion vent system design. In Proceedings of the Hazards XXII Symposium, Liverpool, UK, 11–14 April 2011. [Google Scholar]
- Tamanini, F. Aspect Ratio Effects in Unvented and Vented Dust Explosions. Ind. Eng. Chem. Res. 2012, 51, 7636–7642. [Google Scholar] [CrossRef]
- Tascón, A.; Ramírez-Gómez, A.; Aguado, P.J. Dust explosions in an experimental test silo: Influence of length/diameter ratio on vent area sizes. Biosyst. Eng. 2016, 148, 18–33. [Google Scholar] [CrossRef]
- Castellanos, D.; Skjold, T.; van Winggerden, K.; Echkoff, R.K.; Mannan, M.S. Validation of the DESC code in simulating the effect of vent ducts on dust explosions. Ind. Eng. Chem. Res. 2013, 52, 6057–6067. [Google Scholar] [CrossRef]
- Klippel, A.; Schmidt, M.; Muecke, O.; Krause, U. Dust concentration measurements during filling of a silo and CFD modeling of filling processes regarding exceeding the lower explosion limit. J. Loss Prev. Process Ind. 2014, 29, 122–137. [Google Scholar] [CrossRef]
- Rani, S.I.; Aziz, B.A.; Gimbun, J. Analysis of dust distribution in silo during axial filling using computational fluid dynamics: Assessment on dust explosion likelihood. Process Saf. Environ. Prot. 2015, 96, 14–21. [Google Scholar] [CrossRef] [Green Version]
- Reding, N.S.; Shiflett, M.B. Consequence prediction for dust explosions involving interconnected vessels using computational fluid dynamics modeling. J. Loss Prev. Process Ind. 2020, 65, 104149. [Google Scholar] [CrossRef]
- Olugbemide, D.I. A CFD study of the effects of pipe bending angle on pressure piling in coal dust explosions in interconnected vessels. Fire Saf. J. 2022, 128, 103540. [Google Scholar] [CrossRef]
- Abuswer, M.; Amyotte, P.; Khan, F.; Imtiaz, S. Retrospective risk analysis and controls for Semabla grain storage hybrid mixture explosion. Process Saf. Environ. Prot. 2016, 100, 49–64. [Google Scholar] [CrossRef]
- Ghaffari, M.; van Wingerden, K.; Gjøvåg Hagen, J.T.; Skjold, T.; Storvik, I. Sensitivity Analysis of Dust Explosion Consequences in a Roller Mill using FLACS-DustEx. Chem. Eng. Trans. 2016, 53, 157–162. [Google Scholar] [CrossRef]
- Tascón, A.; Ruiz, A.; Aguado, P.J. Dust explosions in vented silos: Simulations and comparisons with current standards. Powder Technol. 2011, 208, 717–724. [Google Scholar] [CrossRef]
- Huang, C.; Bloching, M.; Lipatnikov, A.N. A vented corn starch dust explosion in an 11.5 m3 vessel: Experimental and numerical study. J. Loss Prev. Process Ind. 2022, 75, 104707. [Google Scholar] [CrossRef]
- Ogunfuye, S.; Sezer, H.; Kodakoglu, F.; Farahani, H.F.; Rangwala, A.S.; Akkerman, V. Dynamics of explosions in cylindrical vented enclosures: Validation of a computational model by experiments. Fire 2021, 4, 9. [Google Scholar] [CrossRef]
- Feroukas, K.; Chiapolino, A.; Saurel, R. Simplified interfacial area modeling in polydisperse two-phase flows under explosion situations. Fire 2023, 6, 21. [Google Scholar] [CrossRef]
- FLACS-CFD v22.1r2 User’s Manual; Gexcon: Bergen, Norway, 2022.
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Hjertager, B.H.; Solberg, T.; Nymoen, K.O. Computer modelling of gas explosion propagation in offshore modules. J. Loss Prev. Process Ind. 1992, 5, 165–174. [Google Scholar] [CrossRef]
- Tascón, A.; Aguado, P.J. CFD simulations to study parameters affecting dust explosion venting in silos. Powder Technol. 2015, 272, 132–141. [Google Scholar] [CrossRef]
- Skjold, T.; Arntzen, B.J.; Hansen, O.R.; Taraldset, O.J.; Storvik, I.E.; Eckhoff, R.K. Simulating dust explosions with the first version of DESC. Process Saf. Environ. Prot. 2005, 83, 151–160. [Google Scholar] [CrossRef] [Green Version]
- Skjold, T. Review of the DESC project. J. Loss Prev. Process Ind. 2007, 20, 291–302. [Google Scholar] [CrossRef]
- Hauert, F.; Vogl, A.; Radant, S. Dust cloud characterization and its influence on the pressure-time-history in silos. Process Saf. Prog. 1996, 15, 178–184. [Google Scholar] [CrossRef]
- Dean, A.; Voss, D.; Draguljić, D. Design and Analysis of Experiments, 2nd ed.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; Wiley: Hoboken, NJ, USA, 2013; pp. 255–259. [Google Scholar]
- Bartknecht, W. Effectiveness of explosion venting as a protective measure for silos. Plant/Oper. Prog. 1985, 4, 4–13. [Google Scholar] [CrossRef]
- Eckhoff, R.K. Use of (dP/dt)max from closed-bomb tests for predicting violence of accidental dust explosions in industrial plants. Fire Saf. J. 1985, 8, 159–168. [Google Scholar] [CrossRef]
- Skjold, T. Dust explosions modeling: Status and prospects. Part. Sci. Technol. 2018, 36, 489–500. [Google Scholar] [CrossRef]
- Dorofeev, S.B. Flame acceleration and explosion safety applications. Proc. Combust. Inst. 2011, 33, 2161–2175. [Google Scholar] [CrossRef]
- Dafnomilis, I.; Lodewijks, G.; Junginger, M.; Schott, D.L. Evaluation of wood pellet handling in import terminals. Biomass Bioenergy 2018, 117, 10–23. [Google Scholar] [CrossRef]
- Brown, K.R.; Whelan, C.; Murray, G.; Laturnus, B.; Yazdanpanah, F.; Cloney, C.; Amyotte, P. Application of process hazard analysis and inherently safer design in wood pellet production. ACS Omega 2022, 7, 47720–47733. [Google Scholar] [CrossRef] [PubMed]
- Jägers, J.; Wirtz, S.; Scherer, V.; Behr, M. Experimental analysis of wood pellet degradation during pneumatic conveying processes. Powder Technol. 2020, 359, 282–291. [Google Scholar] [CrossRef]
- van Wingerden, K. Mechanical sparks as an ignition source of gas and dust explosions. Chem. Eng. Trans. 2019, 77, 133–138. [Google Scholar] [CrossRef]
- Castellanos, D.; Carreto, V.; Skjold, T.; Yuan, S.; Chaudhari, P.; Mannan, M.S.; Mashuga, C. Construction of a 36 L dust explosion apparatus and turbulence flow field comparison with a standard 20 L dust explosion vessel. J. Loss Prev. Process Ind. 2018, 55, 113–123. [Google Scholar] [CrossRef]



| Level | Characteristic Velocity (m/s) | Relative Turbulence Intensity | Turbulence Length Scale (m) |
|---|---|---|---|
| Low | 0.15 | 0.80 | 0.03 |
| High | 0.50 | 1.00 | 0.10 |
| A (Vent Area) | B (Ignition Location) | C (Initial Turbulence) | D (Dust Concentration) | |
|---|---|---|---|---|
| −1 | 56 m2 | Top | Low | 300 g/m3 |
| +1 | 28 m2 | Bottom | High | 500 g/m3 |
| Case | A | B | C | D |
|---|---|---|---|---|
| 01 | −1 | −1 | −1 | −1 |
| 02 | −1 | −1 | −1 | +1 |
| 03 | −1 | −1 | +1 | −1 |
| 04 | −1 | −1 | +1 | +1 |
| 05 | −1 | +1 | −1 | −1 |
| 06 | −1 | +1 | −1 | +1 |
| 07 | −1 | +1 | +1 | −1 |
| 08 | −1 | +1 | +1 | +1 |
| 09 | +1 | −1 | −1 | −1 |
| 10 | +1 | −1 | −1 | +1 |
| 11 | +1 | −1 | +1 | −1 |
| 12 | +1 | −1 | +1 | +1 |
| 13 | +1 | +1 | −1 | −1 |
| 14 | +1 | +1 | −1 | +1 |
| 15 | +1 | +1 | +1 | −1 |
| 16 | +1 | +1 | +1 | +1 |
| Case | Vent Area (m2) | Ignition Location | Initial Turbulence | Dust Concentration (g/m3) | Pred,sim (Bar) | Class |
|---|---|---|---|---|---|---|
| 03 | 56 | Top | High | 300 | 0.108 | 1 |
| 01 | 56 | Top | Low | 300 | 0.155 | 1 |
| 05 | 56 | Bottom | Low | 300 | 0.270 | 1 |
| 02 | 56 | Top | Low | 500 | 0.293 | 1 |
| 04 | 56 | Top | High | 500 | 0.321 | 1 |
| 09 | 28 | Top | Low | 300 | 0.344 | 1 |
| 11 | 28 | Top | High | 300 | 0.439 | 1 |
| 13 | 28 | Bottom | Low | 300 | 0.534 | 2 |
| 07 | 56 | Bottom | High | 300 | 0.578 | 2 |
| 06 | 56 | Bottom | Low | 500 | 0.584 | 2 |
| 10 | 28 | Top | Low | 500 | 0.744 | 2 |
| 15 | 28 | Bottom | High | 300 | 1.067 | 3 |
| 14 | 28 | Bottom | Low | 500 | 1.096 | 3 |
| 12 | 28 | Top | High | 500 | 1.146 | 3 |
| 08 | 56 | Bottom | High | 500 | 1.159 | 3 |
| 16 | 28 | Bottom | High | 500 | 1.878 | 4 |
| A | B | C | D | BC | |
|---|---|---|---|---|---|
| q | 3.780 | 3.616 | 2.676 | 3.726 | 1.720 |
| Q | 0.236 | 0.226 | 0.167 | 0.233 | 0.108 |
| Q2 (a) | 0.056 | 0.051 | 0.028 | 0.054 | 0.012 |
| Y | 26% | 24% | 13% | 25% | 5% |
| Ignition | Turbulence | Additional Effect on Pred,sim |
|---|---|---|
| −1 | −1 | Increment |
| −1 | +1 | Decrement |
| +1 | −1 | Decrement |
| +1 | +1 | Increment |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varela, A.; Arbizu-Milagro, J.; Tascón, A. Application of Factorial Analysis to the Study of Vented Dust Explosions in Large Biomass Storage Silos. Fire 2023, 6, 226. https://doi.org/10.3390/fire6060226
Varela A, Arbizu-Milagro J, Tascón A. Application of Factorial Analysis to the Study of Vented Dust Explosions in Large Biomass Storage Silos. Fire. 2023; 6(6):226. https://doi.org/10.3390/fire6060226
Chicago/Turabian StyleVarela, Alejandro, Julia Arbizu-Milagro, and Alberto Tascón. 2023. "Application of Factorial Analysis to the Study of Vented Dust Explosions in Large Biomass Storage Silos" Fire 6, no. 6: 226. https://doi.org/10.3390/fire6060226
APA StyleVarela, A., Arbizu-Milagro, J., & Tascón, A. (2023). Application of Factorial Analysis to the Study of Vented Dust Explosions in Large Biomass Storage Silos. Fire, 6(6), 226. https://doi.org/10.3390/fire6060226






