Abstract
The key to ensure the reliability of the cloud detonation in high-drop-velocity double-event fuel-air explosives (DEFAEs) is to cause the twice-detonating device (TDD) to detonate in the dispersed fuel. Here, an ejection mechanism for a TDD is designed and the ejection process is analyzed through an outfield ejection test. Accordingly, a simulation model for the description of the ejection process is established and verified to be reliable by comparing it with the experimental results. Based on the model, two extended ensamples for design optimization of the ejection mechanism are developed. The factors influencing the ejection characteristics of the TDD are further analyzed, including the ejection charge mass and screw (for baffle fixing) parameter. The research carried out here provides theoretical and experimental support for the optimal design of the ejection mechanism in high-drop-velocity DEFAEs.
1. Introduction
In the modern military context, warheads equipped with double-event fuel-air explosives (DEFAEs) have great lethality, with the advantages of a large explosive area and high explosive strength [1,2,3,4,5,6]. A DEFAE typically follows two detonation processes to produce an explosive cloud [7,8,9,10,11,12]. The first detonation is used for dispersal of the fuel; the second one is for the timely initiation of the twice-detonating device (TDD) and detonation of the fuel-air mixture, bringing about an explosive cloud and causing shock-wave damage to the target. DEFAEs with low drop velocity have the disadvantage of low penetration ability. Hence, DEFAE equipment on high-drop-velocity weapon platforms such as rockets and ballistic missiles is a developing trend in modern weapon technology. For DEFAEs with high drop velocities, potential problems that may arise include the low reliability of the explosive cloud caused by the inaccurate landing position of the TDD. Therefore, it is of great significance to study the motion trajectory and control method of TDDs.
Research on TDDs is usually classified into static and dynamic explosive characteristics. For static explosives, the detonating device is usually placed in a canister near the ground [13,14,15,16]. The effects of the initiation method, the charging method, and the structure of the device on the cloud’s morphology and state parameters in the static state have been studied [17,18,19,20]. However, with the demand for the application of dynamic explosives in fields such as national defense, research on dynamic explosive characteristics has become a hot topic. Bai et al. [21] studied the formation of the dynamic cloud and detonation effect at a low drop velocity by using the air-drop method (the TDD is located at the center of the deceleration parachute canopy). The motion trajectory of the TDD and the factors influencing the detonation point were analyzed, through which the distribution range of the detonation point was estimated. Liu et al. [22] established a numerical simulation method for full-scale and large-volume fuel dispersal and cloud detonation under a high drop velocity. The dynamic explosive characteristics were studied, including the influence of the initial drop velocity on the fuel dispersal radius and cloud detonation range. Ye and Zhang [23,24] theoretically proposed a dynamic detonation method where a TDD controlled by a decelerating chute was set on the top of the DEFAE, and they established a nonlinear calculation model for the description of the motion state of the TDD. Using the developed MATLAB graphical user interface, the influences of several parameters on the TDD motion process were studied. However, due to the difficulty of parachute control in practice, the application of this method under a high drop velocity needs to be further verified. Zhou et al. [25] proposed a twice-detonating-based fuel–air explosive warhead suitable for a 300 m/s high drop velocity, where the TDD maintains relative motion with the warhead through a cable connection, then is dropped at an appropriate time to detonate the dispersed fuel. This method can effectively detonate the fuel, but there are issues including cable entanglement and the fact that longer cables occupy a larger volume and weight.
To prevent the explosive failure of DEFAEs with a high drop velocity, the TDD is required to fall within the reaction range of the fuel at the appropriate time. Hence, it is essential to study the ejection characteristics of TDDs. Due to the high cost and difficulty of conducting full-scale experiments, studies on TDDs usually require a combination of experimentation and numerical simulation, on the basis of which a suitable model is usually proposed to predict the optimal design parameters.
In this study, the modeling and optimization of ejection characteristics for TDDs in high-drop-velocity DEFAEs is carried out. An ejection mechanism is designed, and the simulation model is accordingly established by LS-DYNA software. Through comparative studies by simulation and experimentation, the model for the optimization of the ejection characteristics is verified to be reliable and two ensamples for the application of the ejection mechanism’s design are further illustrated.
2. Design of the Ejection Mechanism
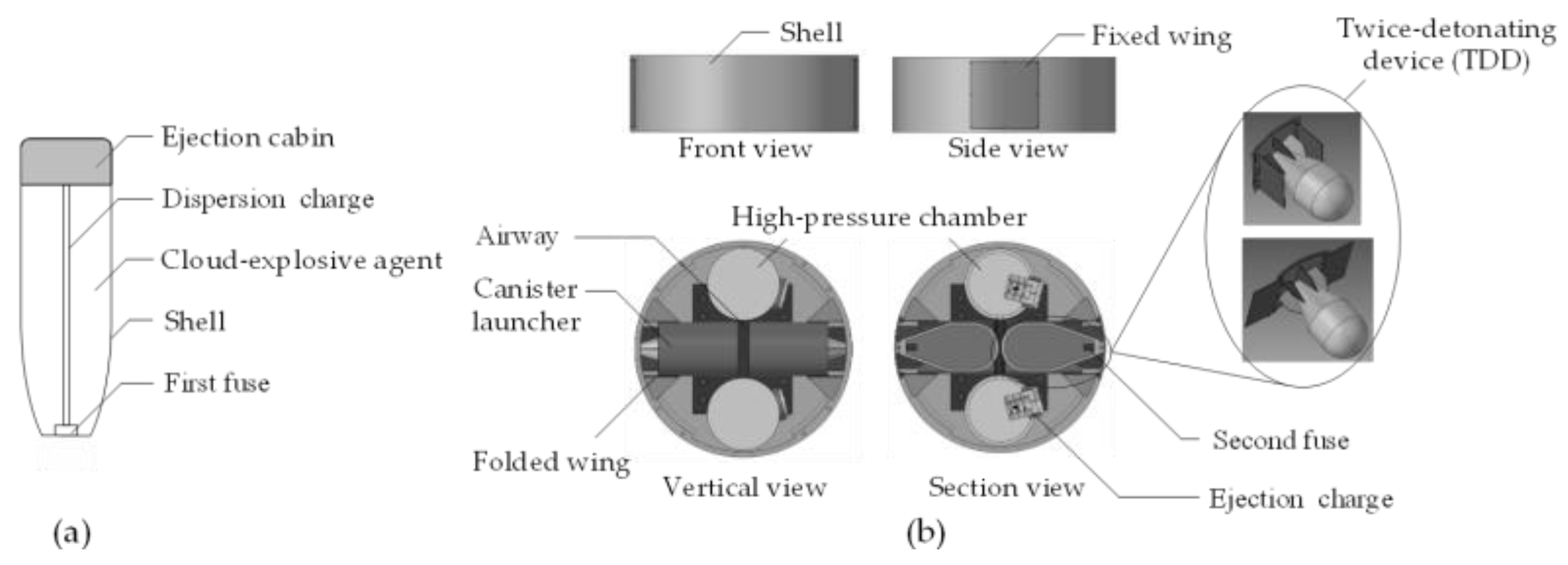
As shown in Figure 1a, a typical DEFAE warhead includes a cluster of cloud-explosive agent, a central tubular fuel for the dispersal of the agent, a primary fuse for the initiation of the charge, a cabin for the ejection of the TDD, and a shell for the integration of the parts. In this study, a TDD is designed to be placed in the ejection cabin which is at the tail end of the warhead (translucent gray area in Figure 1a), separated from the other parts by a partition board. An independent power drive is used to control the ejection of the TDD, causing it to drop within a suitable range and accurately detonate the dispersed agent.
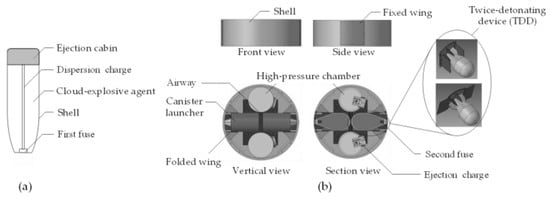
Figure 1.
Diagram of the DEFAE warhead and ejection mechanism. (a) The warhead layout. (b) A pair of integrated ejection mechanisms for the TDD. The partially enlarged view displays the TDD with wings folded and opened.
To ensure a reliable detonation, two sets of identical ejection mechanisms are designed as shown in Figure 1b, each of which includes an ejection cabin, a cluster of the ejection charge, a high-pressure gas chamber, an airway, a canister launcher, and a TDD. Thereinto, the TDD is composed of a fixed wing, a pair of folded wings, and a shell containing a second fuse and detonation charge [26]. The fixed wing is connected to the ejection cabin by screws. The folded wings are connected to the fixed wing by the pin shaft and torsional spring. The size of the folded wings is designed based on the requirements for deceleration after the ejection of the TDD.
The ejection process is described as follows: first, the ejection charge is ignited by an electric igniter, generating a cloud of high-temperature and high-pressure gas and filling the whole sealed chamber. Then, the high-pressure gas pushes the TDD through the airway, leading to the breakage of the screws which form the connection between the fixed wing and the shell. It eventually gives rise to the ejection of the TDD at a certain velocity and executes a subsequent reaction with the dispersed fuel. Specifically, the motion attitude of the TDD can be adjusted by changing the area of the wings to better serve the detonation.
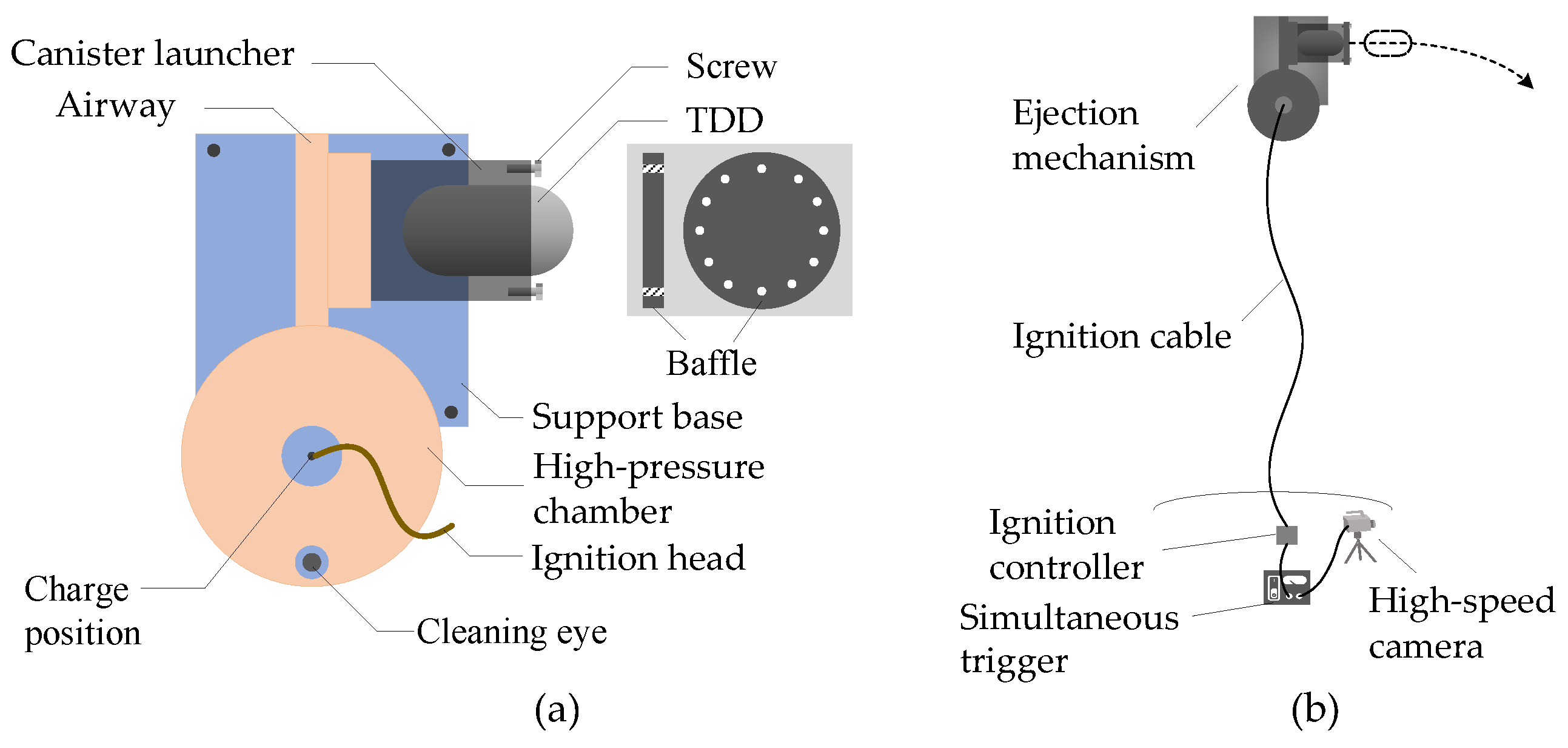
Here, to experimentally investigate the ejection characteristics of the TDD, the ejection mechanism is fabricated, and the experimental layout is shown in Figure 2. In the experiment, the designed ejection mechanism is reasonably simplified to facilitate the series of tests. It mainly involves the removal of the folded wings, because the motion attitude of the TDD in the air is not studied here; only the ejection characteristics are to be explored. The ejection mechanism is depicted in Figure 2a.
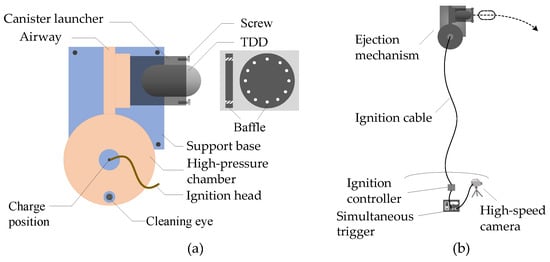
Figure 2.
Diagram of the (a) ejection mechanism and (b) the ejection experimental setup.
Both the ejection mechanism and the TDD are constructed of steel. A threaded hole is cut in the top center of the high-pressure chamber for convenient placement of the charge and a nut with a hole is implemented for easy passage of the ignition head pin. A baffle is added to the front of the ejection cabin using screws. There are 12 through-holes with diameters of 3 mm on the launcher, which are aligned with the corresponding holes on the baffle, and then the two parts are fixed by a threaded connection.
The experimental setup is shown in Figure 2b. A TDD with an explosive charge (black powder) loaded and an ignition head inserted is placed in the center of the high-pressure gas chamber. When the ignition controller is activated, the ignition head detonates the charge, producing a cloud of gas that fills the chamber and the airway. The gas pushes the TDD to move axially along the launcher. As the gas pressure increases, the TDD is ejected from the launcher at a certain initial velocity. The motion process of the TDD is recorded by a high-speed camera once the ignition head is activated, which is realized through a synchronous trigger. The entire experiment was conducted in an open outdoor environment.
3. Results and Discussion
In this section, a simulation model of the ejection mechanism is developed. To verify the reliability of the model, relevant experiments are carried out and compared with the simulation results. Based on the simulation model, two ensamples for design optimization of the ejection mechanism are developed. The factors influencing the ejection characteristics are further analyzed.
3.1. Modeling of the Ejection Mechanism
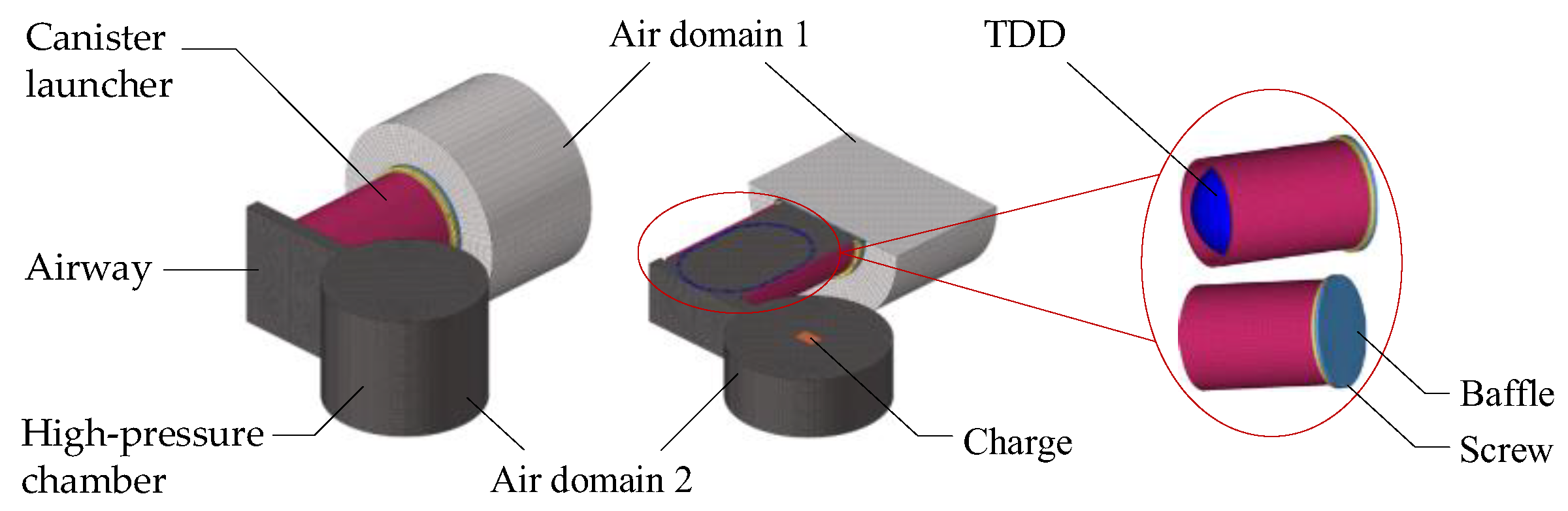
The simulation model is established according to the structure and size of the experimental device, as shown in Figure 3, where the air domains 1 and 2 represent the air setup in the chamber and in the open environment, respectively.
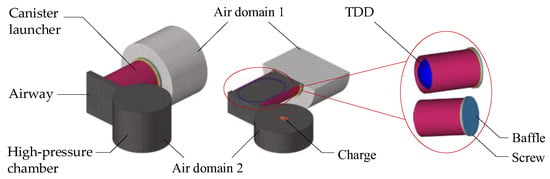
Figure 3.
Simulation model of the ejection mechanism. The partially enlarged view displays the layout of the TDD in the canister launcher.
The fluid–solid coupling algorithm and the ALE (arbitrary Lagrange–Euler) multisubstance element with single point integration are adopted for calculation. The TDD, canister launcher, and baffle are meshed in the Lagrange grid; the charge and air domain are meshed in the Euler grid.
The materials involved in the calculation include the black powder, air, metal structural components, etc. Thereinto, the black powder is replaced by an equivalent TNT charge [27,28] and described by the MAT_HIGH_EXPLOSIVE_BURN model and JWL (Jones–Wilkins–Lee) equation of state [29], whose form is:
where P denotes the pressure of the detonation product, V denotes the initial relative volume, E is the detonation energy per unit volume, and A, B, R1, R2, ω are the parameters of the JWL equation of state. The calculation parameters are shown in Table 1 [20], where ρ0 is the density and D is the detonation velocity.

Table 1.
Detonation properties of the TNT charge and the parameters of the JWL equation of state.
The air is described by the MAT_NULL model and LINEAR_POLYNOMIAL equation of state, which is expressed as:
where C0, C1, C2, C3, C4, C5, C6 are constants, μ = 1/V0 − 1, V0 denotes the initial relative volume, and E0 denotes the initial internal energy per unit reference volume. Detailed calculation parameters are shown in Table 2.

Table 2.
Air parameters used for the simulation.
The baffle is defined by the MAT_PIECEWISE_LINEAR_PLASTICITY model, the TDD and canister launcher are defined by the MAT_RIGID model, and the screws are defined by the MAT_PLASTIC_KINEMATIC model. The screw connection adopts a hyper beam unit structure. The boundary conditions are set as follows: air domains 1 and 2 possess a fixed boundary and a nonreflective boundary, respectively. The canister launcher, baffle, and TDD adopt a surface contact constraint.
3.2. Reliability Verification of the Simulation Model
To verify the simulation, the experimental and simulated ejection characteristics influenced by the number of screws (for baffle fixing) are obtained.
An illustrated example of the motion of the TDD is shown in Figure 4, where 10 video frames (0~72 m/sms) are recorded by a high-speed camera. The TDD is driven by a 15.00 g charge with the baffle fixed by eight screws. Once the TDD is ejected from the launcher, the visible particles disperse and become more diffuse over time. As time goes by, the TDD undergoes a flat throwing motion under the influence of the initial velocity and gravity.

Figure 4.
Motion process of the TDD with 8 screws for baffle fixing.
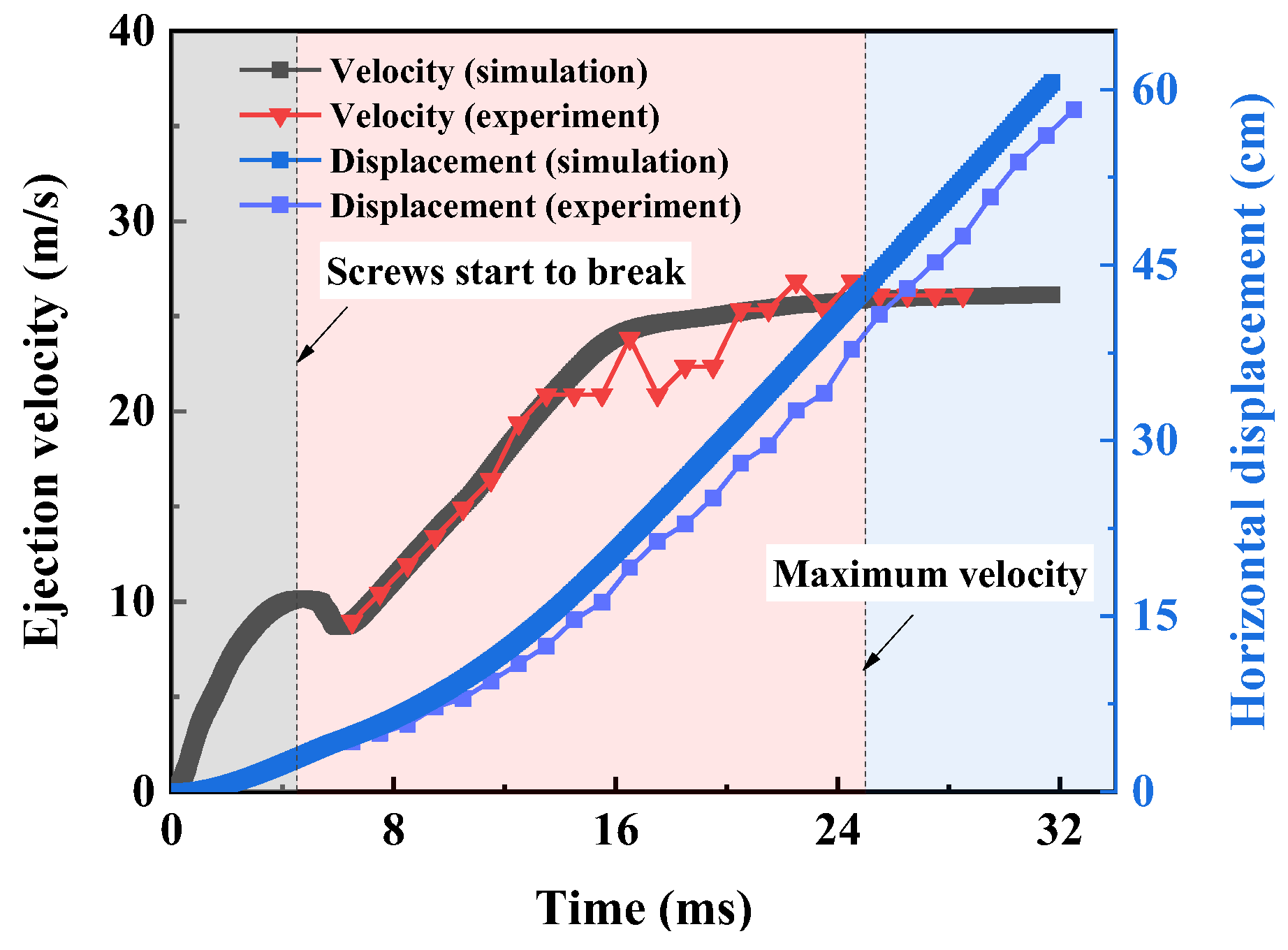
The horizontal displacement and the ejection velocity (converted by the displacement) variation with time is recorded in Figure 5. As is evident from the simulated result, the ejection velocity increases with time until a turning point occurs at around 4.5 m/s when the TDD collides with the baffle. It leads to kinetic energy loss followed by a rapid decrease in the velocity by 1.4 m/s. After a total time of 6 m/s, all the screws are broken, and the curve resumes its upward trend. The released high-pressure gas promotes the continuous increase in velocity. At 25 m/s, the velocity reaches its maximum when the driving force of the gas approaches the air resistance. As for the experiments, only the velocity curve after the TDD collides with the baffle can be obtained because the TDD motion in the launcher cannot be technically tested by the existing device. From the experimental result, the velocity increases rapidly during the effective period of gas driving. After 16 m/s, it increases slowly and reaches its maximum at 22.5 m/s. The variation trend in the experimental and simulated curves is basically consistent.
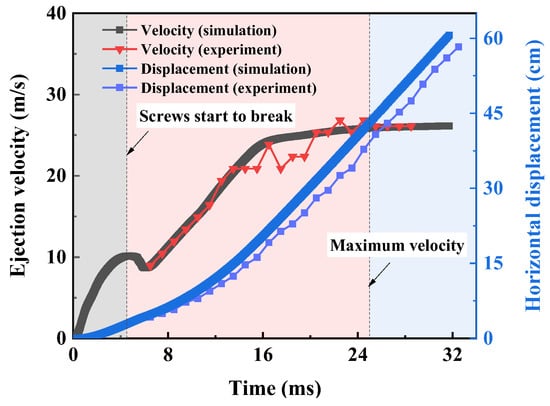
Figure 5.
Horizontal displacement and the converted ejection velocity of the TDD (with 8 screws for baffle fixing) versus time during the ejection process. The translucent areas represent the motion process of the TDD staged by the time of screw breakage and the maximum ejection velocity.
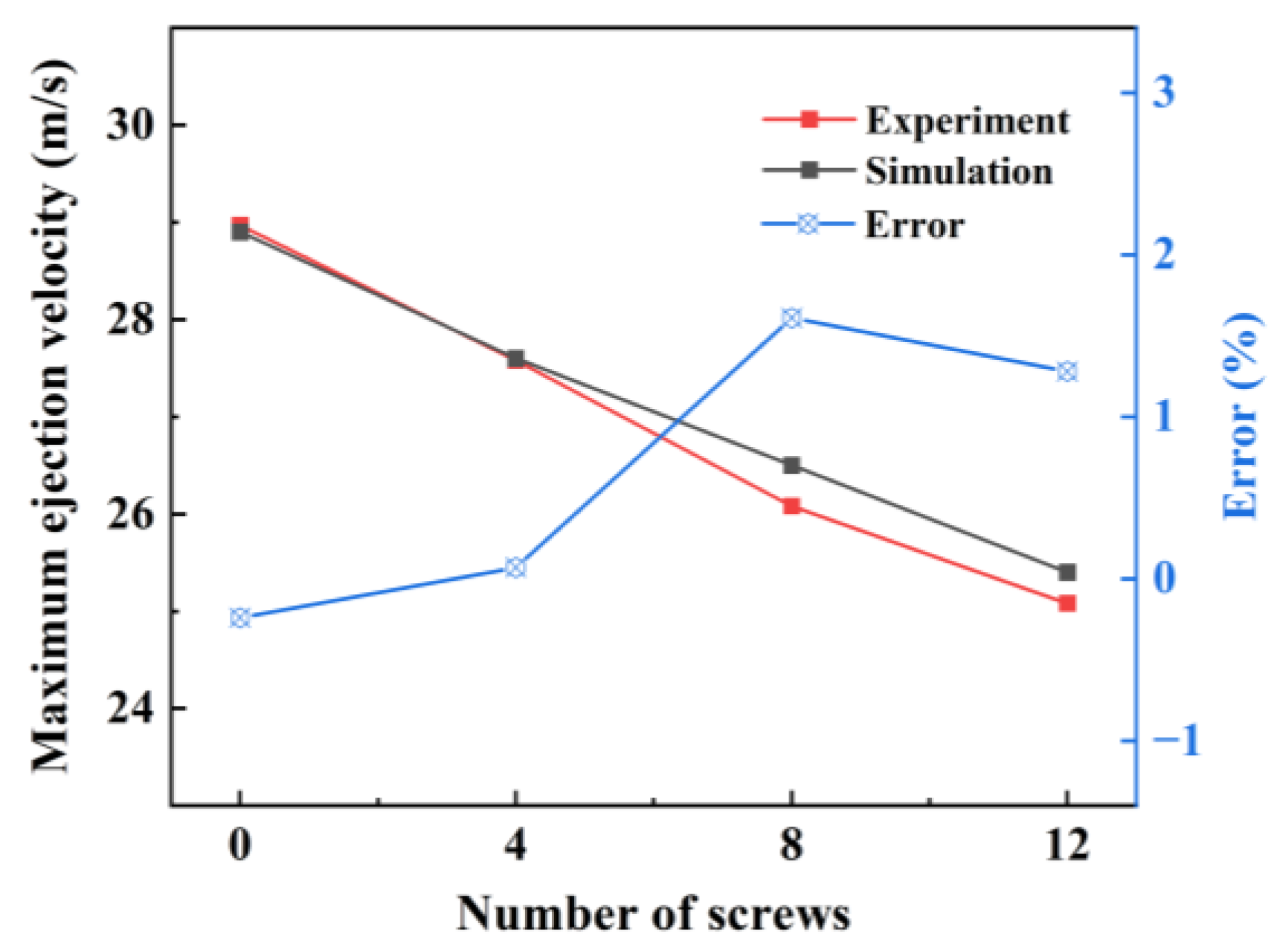
The influence of the number of screws on the maximum ejection velocity of the TDD was further simulated, as shown in Figure 6. It can be seen that the maximum velocity decreases with the increasing number of screws and it has a decrease rate of approximately 1 m/s for every four screws added. As the number of screws increases, the kinetic energy lost by the TDD increases and the maximum ejection velocity decreases. A maximum error of 1.61% occurs between the simulation and the experiment when the baffle is fixed by eight screws. These errors originate from random errors where the screw tightness is different for each test. Consequently, a consistency between the experimental and the simulated maximum ejection velocity is reached, further verifying the reliability of the simulation results.
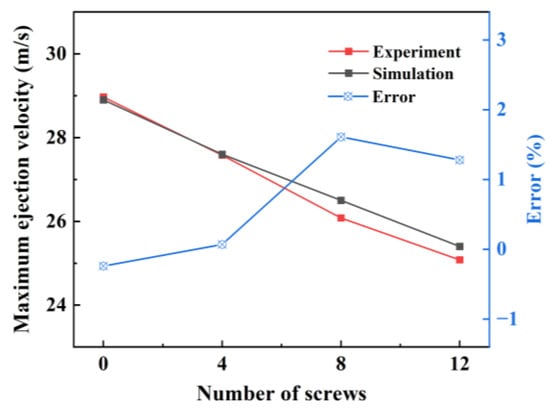
Figure 6.
Maximum ejection velocity versus number of screws by experimentation and simulation.
3.3. Ensamples for Optimization of the Ejection Characteristics
As for the simulation model of the ejection mechanism described in Section 3.1, the TDD is separated from the baffle. When the two collide and the screws break, they will be ejected together at different velocities. However, in practical applications, the TDD is usually equipped with a fixed wing to control the motion attitude after ejection, so the model needs to be modified to more accurately reflect the ejection characteristics.
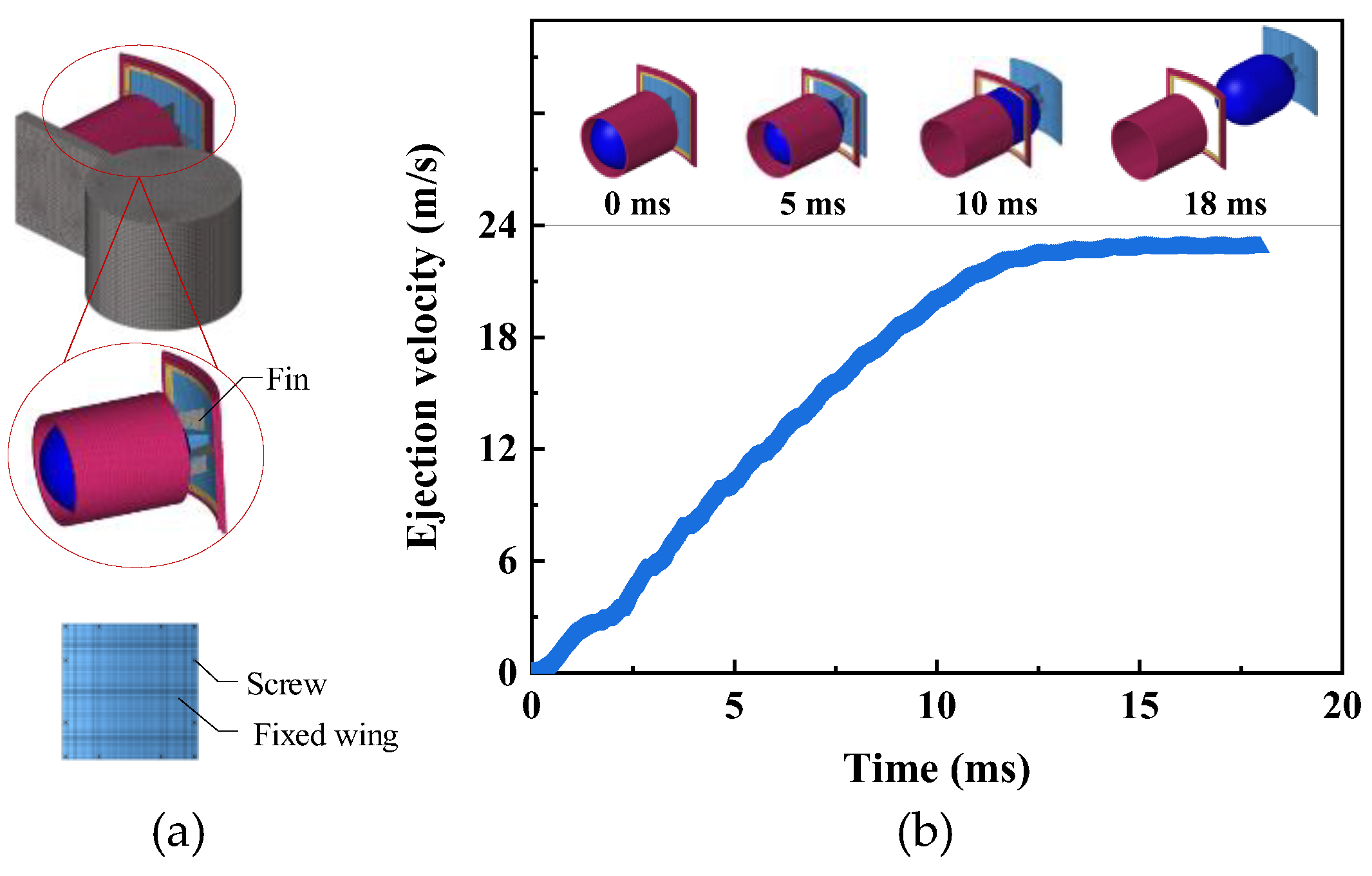
On the basis of the reliability of the previously proposed simulation model, here, a reconstructed model is developed, where the baffle is connected to the TDD and acts as a fixed wing. The reconstructed model is shown in Figure 7a, where a set of fins is added to connect the baffle with the TDD. Additionally, according to the original design concept in Section 2, the baffle is rebuilt to be square.
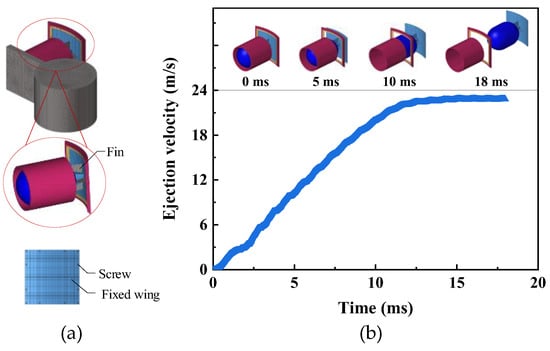
Figure 7.
Ejection velocity versus time during the ejection process of the reconstructed simulation model. (a) The reconstructed simulation model. The partially enlarged view displays the TDD with fins for connection of the shell and the fixed wing. (b) The ejection velocity versus time.
Here, a 15 g charge and eight screws are selected for simulation. The ejection velocity versus time is obtained, as shown in Figure 7b. Different from the results in Figure 5 (black solid square), here, the TDD is not accelerated in the canister launcher since it is integrated with the baffle. Hence, the ejection velocity would not present an obvious trend of decreasing and then increasing. After the screws break at 2 m/s, the ejection velocity tends to increase continuously and reaches its maximum at 13 m/s once the driving gas is lost. Top Figure 7b gives the motion process of the TDD at different times.
3.3.1. Cooperative Parameter Optimization for Charge Mass and Number of Screws
A series of numerical simulations was conducted by changing the number of screws and the charge mass. The maximum ejection velocities of the TDD and the break time of the screws under different working conditions are summarized in Table 3.

Table 3.
Simulated ejection characteristics under different charge mass and number of screws (screw diameter of 3 mm).
As can be seen from the simulated results, with the increase in the charge mass (when the number of screws is constant), the screws start to break earlier. The total break time of the screws is shortened and the maximum ejection velocity increases. When the number of screws is eight and the charge mass increases from 10.00 g to 15.00 g, the total break time is shortened by approximately 487 μs. The maximum ejection velocity increases by 3 m/s. When the number of screws is 12 and the charge mass increases from 10.00 g to 15.00 g, the break time is shortened by approximately 1500 μs. The maximum ejection velocity increases by 5.5 m/s. In order to ensure that there is sufficient energy to cause the screws to break and enable the TDD to be effectively ejected, there is a lower limit for the charge mass under different numbers of screws. When the number of screws is 8, the charge mass should be no less than 6.25 g; when it is 10, the charge mass should be no less than 8.75 g; when it is 12, the charge mass should be no less than 10.00 g.
When the charge mass is constant, the screws start to break later with the increase in the number of screws. The total break time is prolonged, and the maximum ejection velocity is decreased with the increasing number of screws. When the charge mass is 10.00 g and the number of screws increases from 8 to 12, the break time is prolonged by approximately 1600 μs and the maximum ejection velocity decreases by approximately 3.8 m/s.
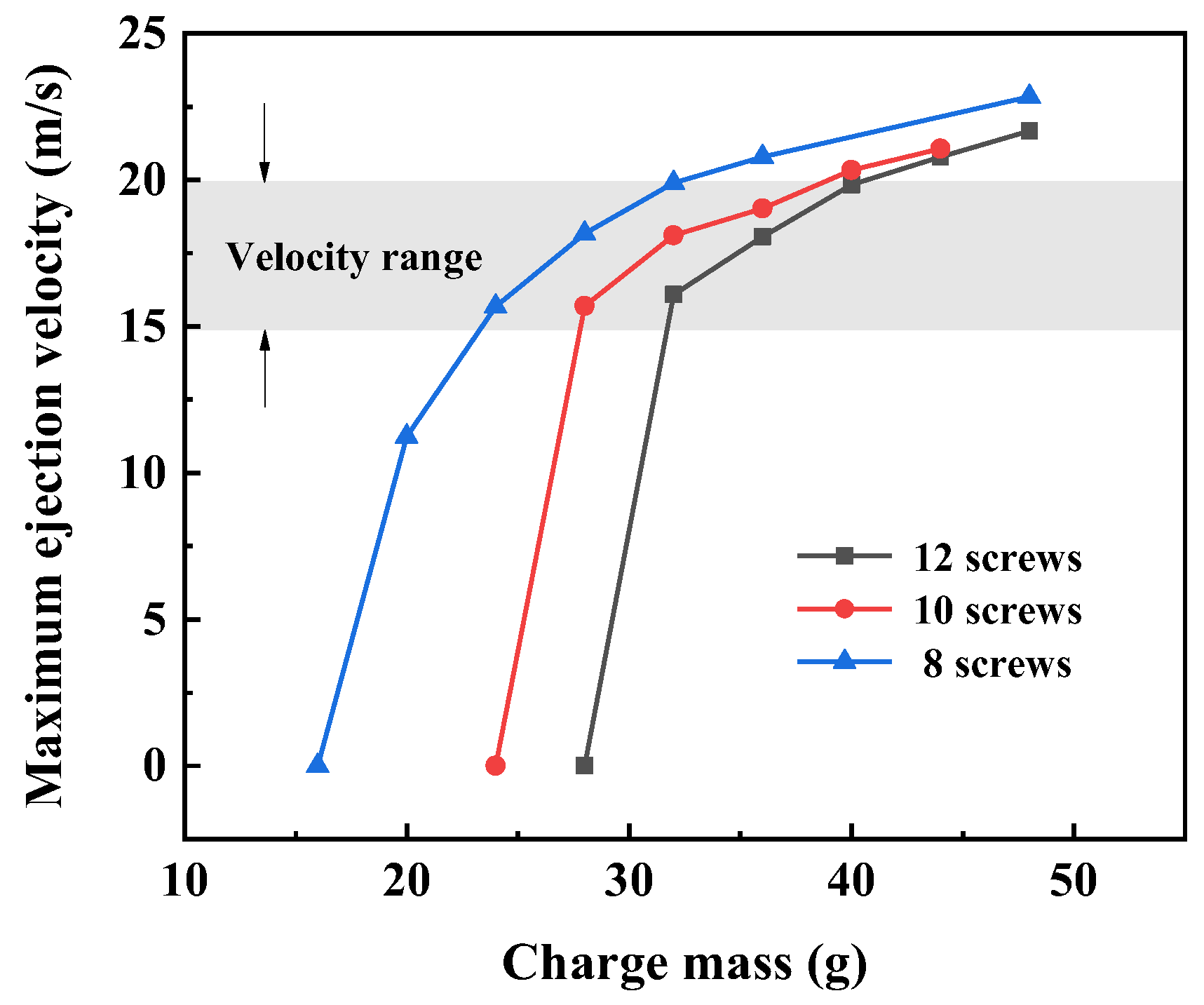
The maximum ejection velocity versus charge mass under different numbers of screws is plotted as a more intuitive scatter diagram in Figure 8. Assume that there is a certain type of DEFAE missile with a twice-detonating time of 300 m/s, and the optimal detonation range is within 4.5~6.0 m away from the center. Consequently, to ensure that the TDD falls within the effective range, the maximum ejection velocity should be within 15~20 m/s (transparent grey area in Figure 8). When the number of screws is 8, the charge mass should be within 6.25~10.00 g; when it is 10, the charge mass should be within 8.75~11.25 g; when it is 12, the charge mass should be within 10.00~12.50 g.
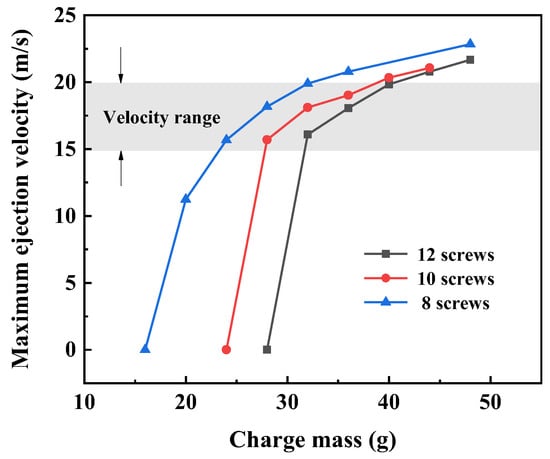
Figure 8.
Simulated maximum ejection velocity versus charge mass under different numbers of screws.
3.3.2. Cooperative Parameter Optimization for Charge Mass and Screw Diameter
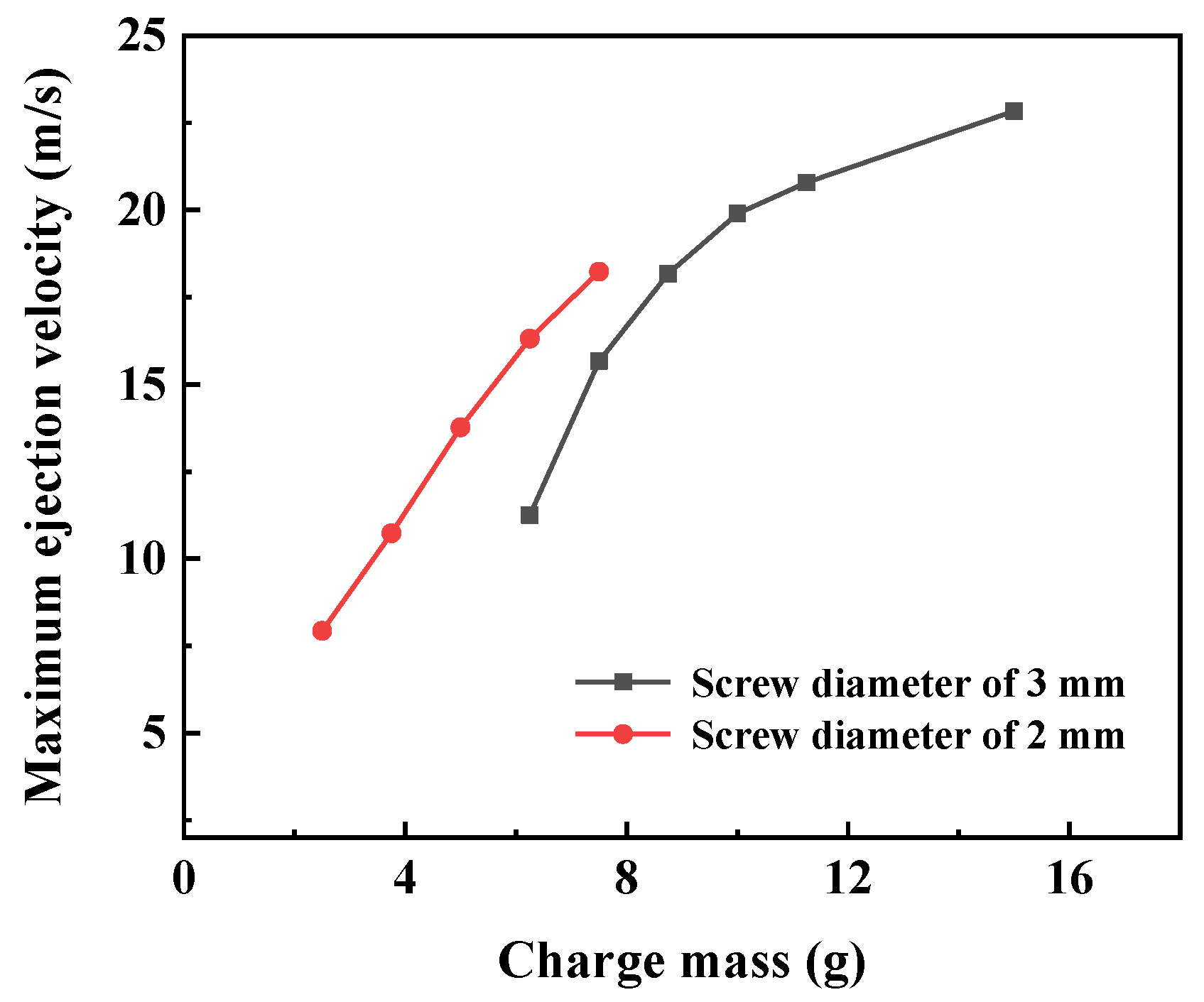
The numerical simulation was conducted by changing the screw diameter and the charge mass. The maximum ejection velocities of the TDD and the break time of the screws under different working conditions are summarized in Table 4. Extracting the maximum ejection velocity from the table, the velocity versus charge mass under different screw diameters is plotted in Figure 9.

Table 4.
Simulated ejection characteristics under different charge mass and screw diameter (8 screws).
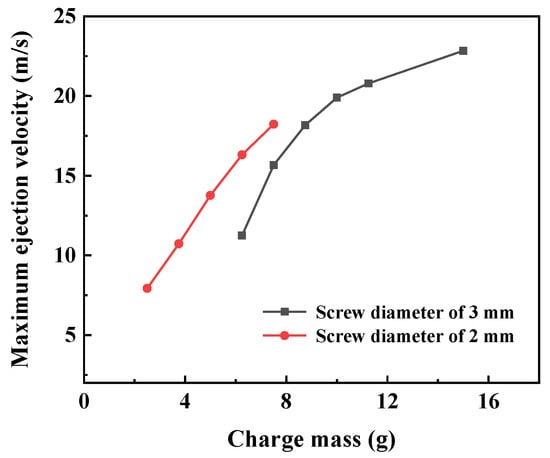
Figure 9.
Simulated maximum ejection velocity versus charge mass under different screw diameters.
As can be seen, when the screw diameter is constant, the screws start to break earlier with the increasing charge mass. The total break time of the screws is shortened, and the maximum ejection velocity is increased. When the charge mass is constant and the diameter of the screws increases, the screws start to break later. When the screw diameter is 3 mm and the charge mass increases from 10.00 g to 15.00 g, the total break time is shortened by approximately 360 μs and the maximum ejection velocity is increased by approximately 3 m/s. When the screw diameter is 2 mm and the charge mass increases from 2.50 g to 7.50 g, the total break time is shortened by approximately 2000 μs and the maximum ejection velocity is increased by approximately 10.3 m/s.
According to the design requirements of a certain type of DEFAE missile mentioned in the end of Section 3.3.1 (the maximum ejection velocity range of 15~20 m/s), when the screw diameter is 3 mm, the charge mass should be within 7.50~10.00 g; when it is 2 mm, the charge mass should be within 6.25~7.50 g.
4. Conclusions
In summary, an ejection mechanism for TDDs in high-drop-velocity DEFAEs is designed. The modeling and optimization method for the ejection characteristics is explored by a combination of experimentation and numerical simulation. Under the given conditions, the maximum error between the numerical simulation and the experimental results is 1.61%. The structure of the ejection mechanism is verified to be feasible, which can meet the requirements for the ejection of a TDD.
By giving two simulated ensamples for application in the optimal design of the ejection mechanism, relative influence factors are analyzed and the appropriate value ranges of these factors for a reliable cloud detonation are obtained. Consequently, the maximum ejection velocity of the TDD is positively correlated with the charge mass, and negatively correlated with the number and diameter of screws. The proposed ejection mechanism and the characteristics optimization method can be useful for reference in improving the success rate and the reliability of high-drop-velocity DEFAEs for weapon equipment technology.
Author Contributions
Conceptualization, B.S. and J.L.; methodology, C.B.; software, C.Z. and B.S.; validation, B.S., J.L. and C.Z.; investigation, C.Z. and X.J.; data curation, C.B.; writing—original draft preparation, B.S.; writing—review and editing, B.S., J.L. and C.Z.; supervision, C.B.; project administration, J.L. and C.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, F. Metalized Heterogeneous Detonation and Dense Reactive Particle Flow. AIP Conf. Proc. 2012, 1426, 27–34. [Google Scholar]
- Milne, A.M.; Parrish, C.; Worland, I. Dynamic Fragmentation of Blast Mitigants. Shock Waves 2010, 20, 41–51. [Google Scholar] [CrossRef]
- Frost, D.L.; Ornthanalai, C.; Zarei, Z.; Tanguay, V.; Zhang, F. Particle Momentum Effects from the Detonation of Heterogeneous Explosives. J. Appl. Phys. 2007, 101, 113529. [Google Scholar] [CrossRef]
- Zhang, F.; Frost, D.L.; Thibault, P.A.; Murray, S.B. Explosive Dispersal of Solid Particles. Shock Waves 2001, 10, 431–443. [Google Scholar] [CrossRef]
- Ritzel, D.V.; Ripley, R.C.; Murray, S.B.; Anderson, J. Near-field Blast Phenomenology of Thermobaric Explosions. In Proceedings of the 26th International Symposium on Shock Waves, Göttingen, Germany, 15–20 July 2009; Hannemann: Berlin, Germany, 2009. [Google Scholar]
- Tsybulenko, E. Fuel Air Explosive Weapons. In International Conflict and Security Law: A Research Handbook; Sayapin, S., Atadjanov, R., Kadam, U., Kemp, G., Zambrana-Tévar, N., Quénivet, N., Eds.; T.M.C. Asser Press: The Hague, The Netherlands, 2022; pp. 379–388. [Google Scholar]
- Zhang, Q.; Wei, K.; Luo, A.; Wang, D.; Qin, B. Numerical Simulation on Dispersal Character of Fuel by Central He. Def. Sci. J. 2007, 57, 425. [Google Scholar]
- Song, X.; Zhang, J.; Zhang, D.; Xie, L.; Li, B. Dispersion and Explosion Characteristics of Unconfined Detonable Aerosol and Its Consequence Analysis to Humans and Buildings. Process Saf. Environ. Prot. 2021, 152, 66–82. [Google Scholar] [CrossRef]
- Bai, C.; Wang, Y.; Li, J.; Chen, M. Influences of the Cloud Shape of Fuel-Air Mixtures on the Overpressure Field. Shock Vib. 2016, 2016, 9748536. [Google Scholar] [CrossRef]
- Apparao, A.; Rao, C.R. Performance of Unconfined Detonable Fuel Aerosols of Different Height to Diameter Ratios. Propellants Explos. Pyrotech. 2013, 38, 818–824. [Google Scholar] [CrossRef]
- Apparao, A.; Saji, J.; Balaji, M.; Devangan, A.; Rao, C. Determination of Minimum Mass and Spatial Location of Initiator for Detonation of Propylene Oxide Aerosols. Shock Waves 2017, 27, 247–255. [Google Scholar] [CrossRef]
- Apparao, A.; Rao, C. TNT Equivalency of Unconfined Aerosols of Propylene Oxide. Def. Sci. J. 2014, 64, 431. [Google Scholar] [CrossRef]
- Samirant, M.; Smeets, G.; Baras, C.; Royer, H.; Oudin, L. Dynamic Measurements in Combustible and Detonable Aerosols. Propellants Explos. Pyrotech. 1989, 14, 47–56. [Google Scholar] [CrossRef]
- Apparao, A.; Rao, C.; Tewari, S.P. Studies on Formation of Unconfined Detonable Vapor Cloud Using Explosive Means. J. Hazard. Mater. 2013, 254, 214–220. [Google Scholar] [CrossRef]
- Zhang, F.; Ripley, R.; Yoshinaka, A.; Findlay, C.; Anderson, J.; Von Rosen, B. Large-Scale Spray Detonation and Related Particle Jetting Instability Phenomenon. Shock Waves 2015, 25, 239–254. [Google Scholar] [CrossRef]
- Liu, G.; Hou, F.; Cao, B.; Xie, L.; Shen, Z.; Zhou, T. Experimental Study of Fuel-Air Explosive. Combust. Explos. Shock Waves 2008, 44, 213–217. [Google Scholar] [CrossRef]
- Huang, Z.; Yu, X. Numerical Simulation Study of Expanding Fracture of 45 Steel Cylindrical Shell under Different Detonation Pressure. Materials 2022, 15, 3980. [Google Scholar] [CrossRef] [PubMed]
- Grady, D.E. Length Scales and Size Distributions in Dynamic Fragmentation. Int. J. Fract. 2010, 163, 85–99. [Google Scholar] [CrossRef]
- Wang, F.; Bai, C.; Yan, H. The Study for the Effect of the Thickness of Cylindrical Shell on the Fuel Dispersing in the FAE Warhead Design by Simulation. J. Proj. Rocket. Missiles Guid. 2003, 23, 110–112. [Google Scholar]
- Chen, M.; Bai, C.; Li, J. Simulation on Initial Velocity and Structure Dynamic Response for Fuel Dispersion. Chin. J. Energetic Mater. 2015, 23, 323–329. [Google Scholar]
- Bai, C.; Wang, Y.; Xue, K.; Wang, F. Experimental Study of Detonation of Large-Scale Powder–Droplet–Vapor Mixtures. Shock Waves 2018, 28, 599–611. [Google Scholar] [CrossRef]
- Liu, L. Transient Detonation Characteristics and Propagation Law of Multiphase Cloud. Ph.D. Thesis, Beijing Institute of Technology, Beijing, China, 2019. [Google Scholar]
- Ye, C.; Zhang, Q. Optimal Falling Track Design for Twice-detonating Fuze of Double-event Fuel-air Explosive with High Speed. Def. Sci. J. 2020, 70, 366–373. [Google Scholar] [CrossRef]
- Ye, C.; Zhang, Q. Systematic Analysis on Gas-Liquid-Solid Three-Phase Flow and Initiation Structure for Fuel-Air Explosive Weapon Reliability. Propellants Explos. Pyrotech. 2022, 47, e202100202. [Google Scholar] [CrossRef]
- Zhou, T.; He, C.; Chen, H.; Shi, C.; Li, X.; Wang, S. A Twice-Detonating Fuel-Air Explosive Warhead Suitable for 300 m/s Fall Velocity. CN111457794B, 19 November 2021. [Google Scholar]
- Zhao, C.; Li, J.; Jia, X.; Zhang, P. Design and Characteristic Study of Ejection Mechanism of Twice-detonating Device. J. Proj. Rocket. Missiles Guid. 2022, 42, 111–116. [Google Scholar]
- Liu, Y.; Huang, Q. Numerical Simulation Study of the Chaff Dispersed by Black Powder Explosion. Shipboard Electron. Countermeas. 2019, 42, 33–36. [Google Scholar]
- Cui, Q.; Zhang, F.; Li, M. Study on the Performance of a New Kind of Ignition Powder. Initiat. Pyrotech. 1999, 2, 14–16. [Google Scholar]
- Lee, E.L.; Hornig, H.C.; Kury, J.W. Adiabatic Expansion of High Explosive Detonation Products; University of California Radiation Lab: Livermore, CA, USA, 1968. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).