Numerical Analysis of Restrained Continuous Steel Columns under Standard Fire
Abstract
:1. Introduction
- Exploring the structural fire performance of restrained continuous steel columns;
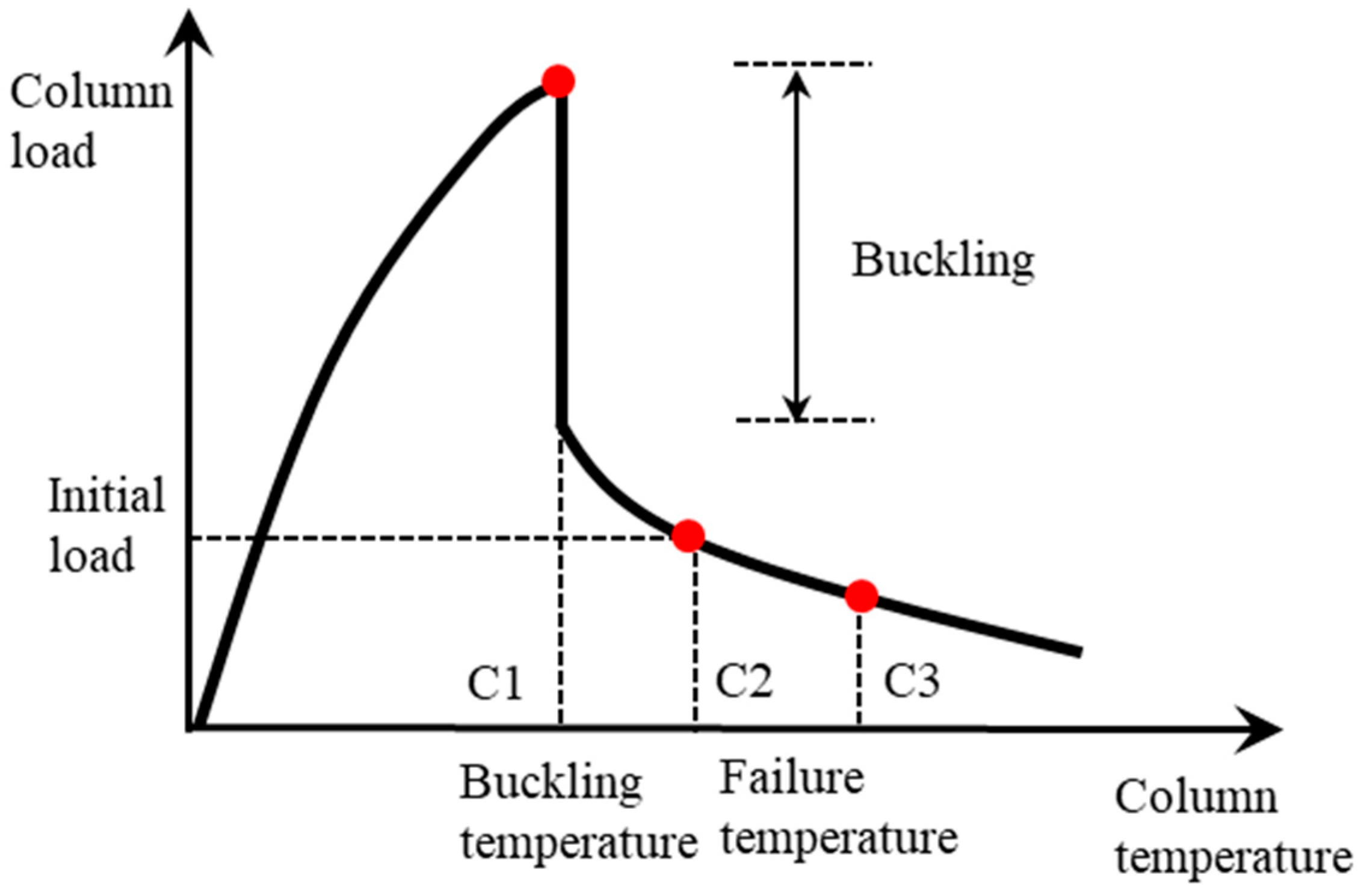
- Discussing the fire resistance of continuous columns using the deflection limit or deflection rate as the failure criteria instead of the point of internal force returning back to the initial value;
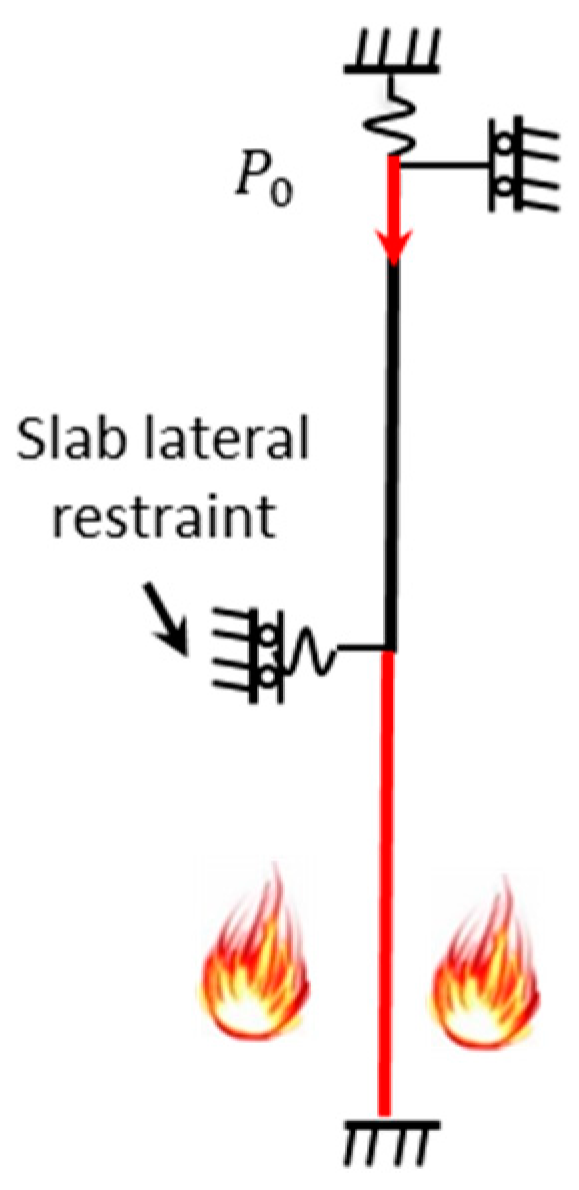
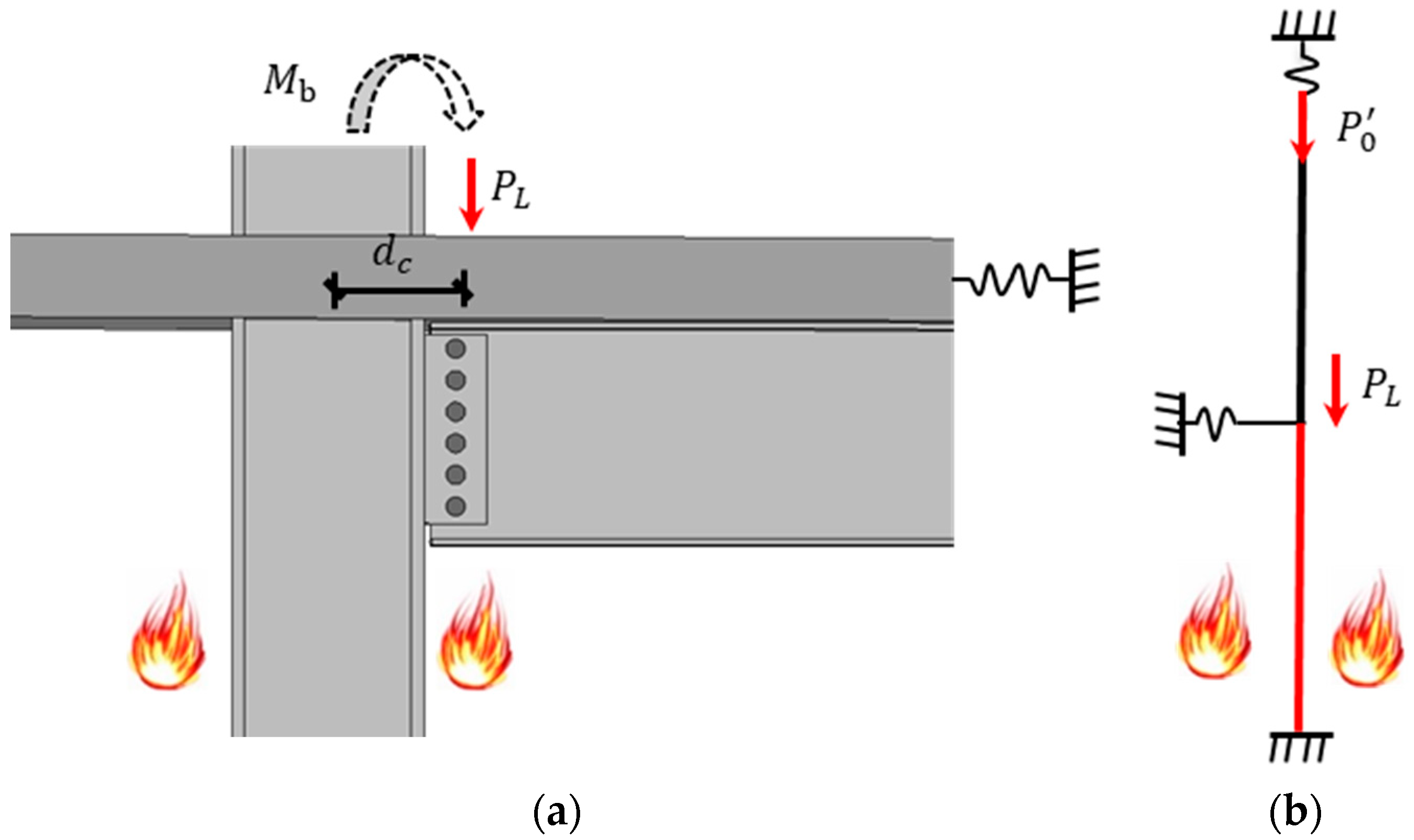
- Investigating the single-sided lateral moments from the connected steel beam on restrained continuous steel columns;
- Assessing the reliability of current structural fire design procedures considering the restraint effect on steel columns.
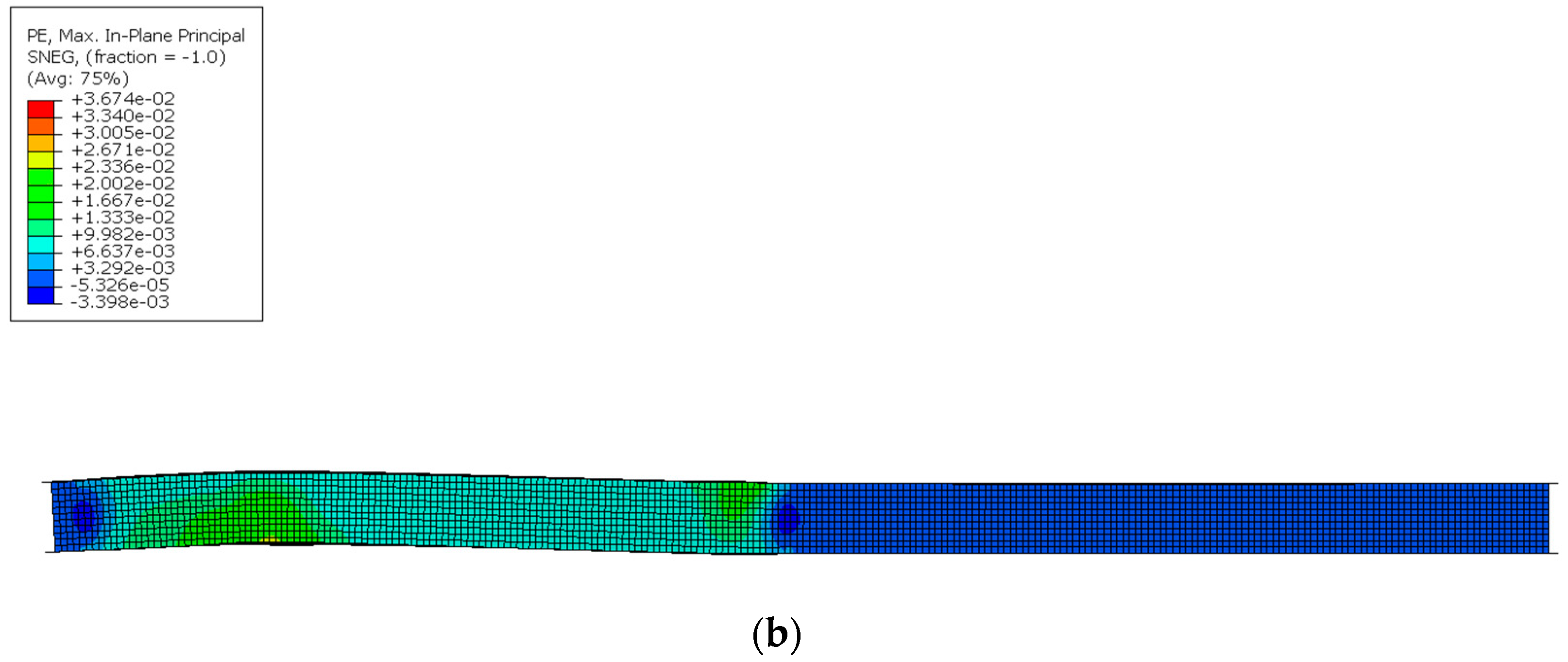
2. Development of Finite Element Models
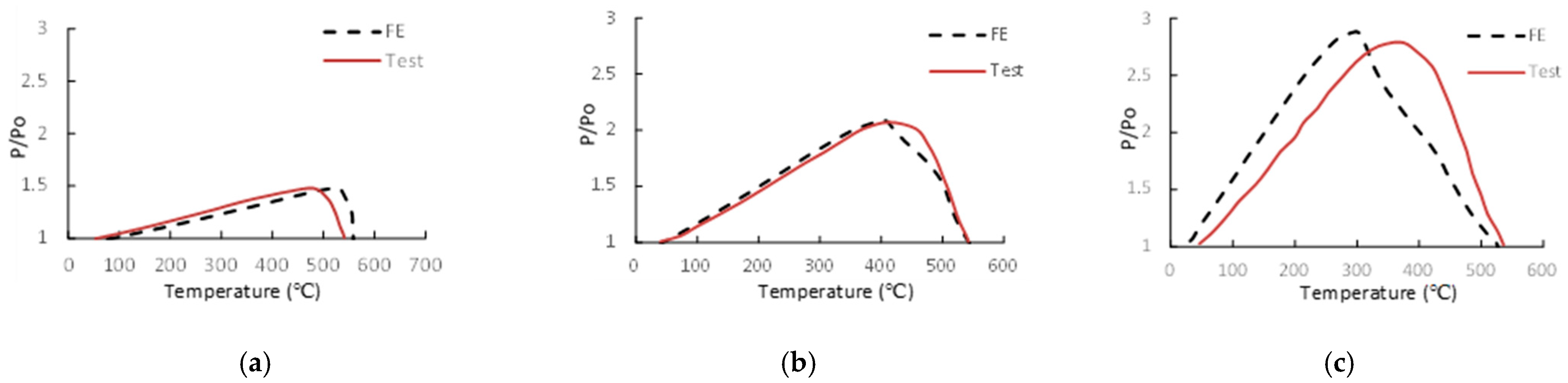
3. Numerical Validation against Experimental Results
4. Parametric Studies of Compact Steel Columns
5. Analysis and Discussion
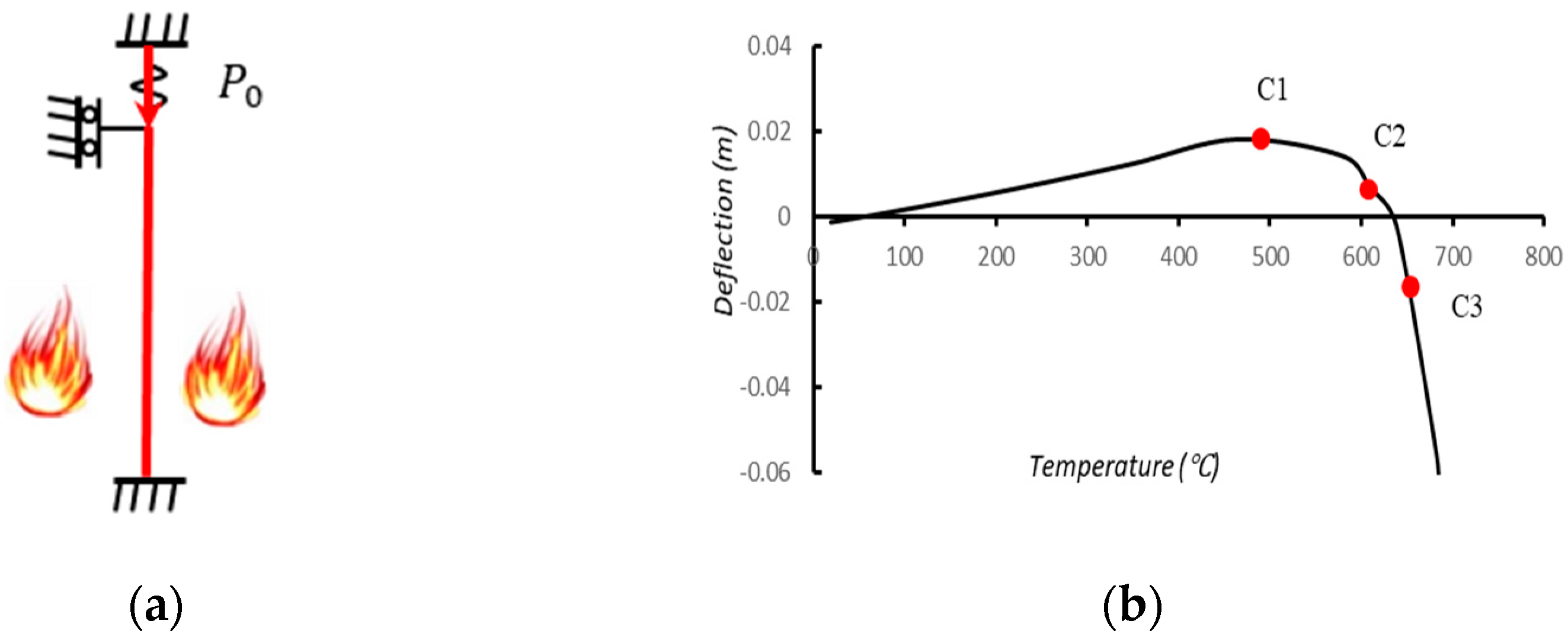
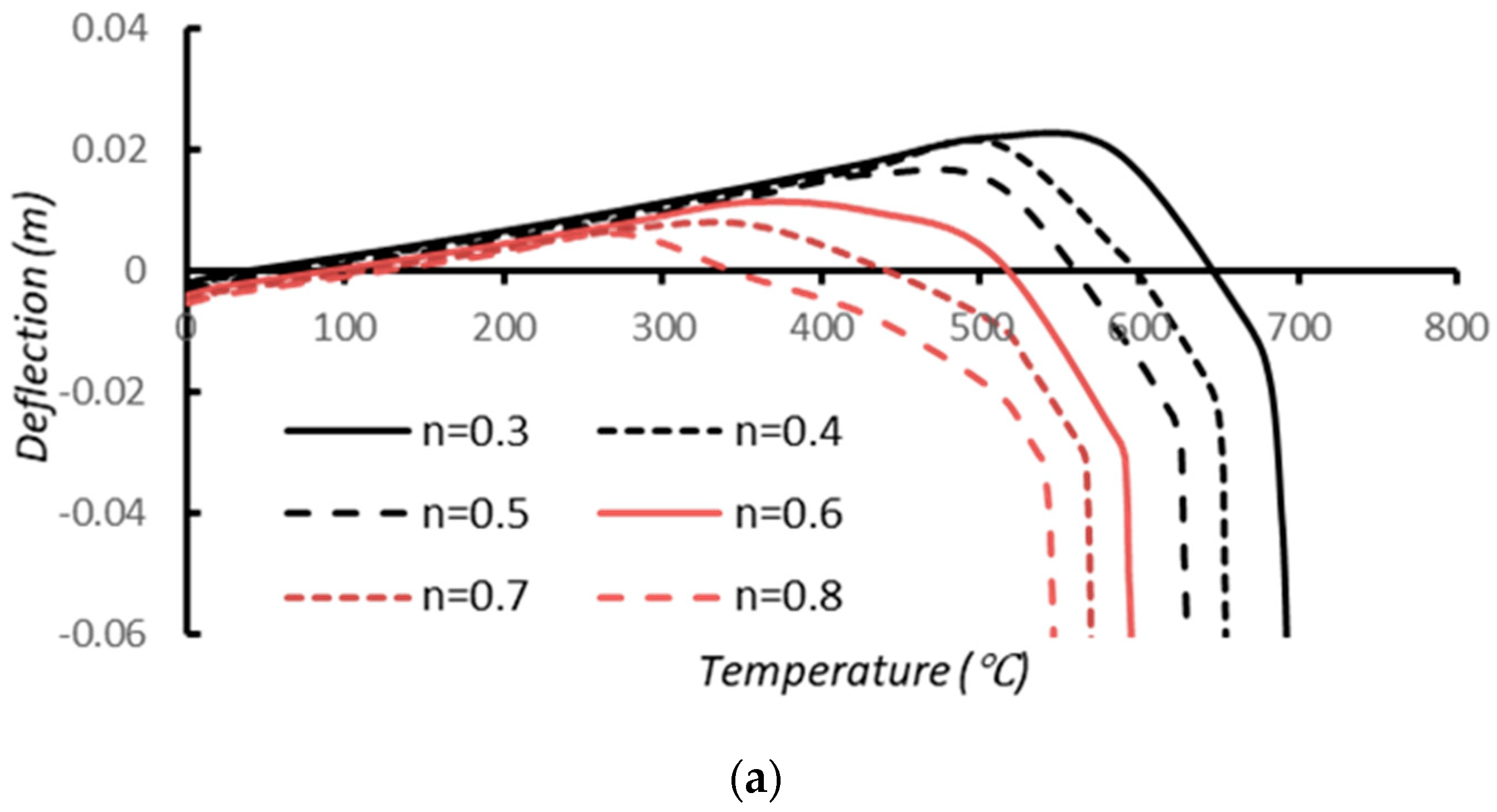
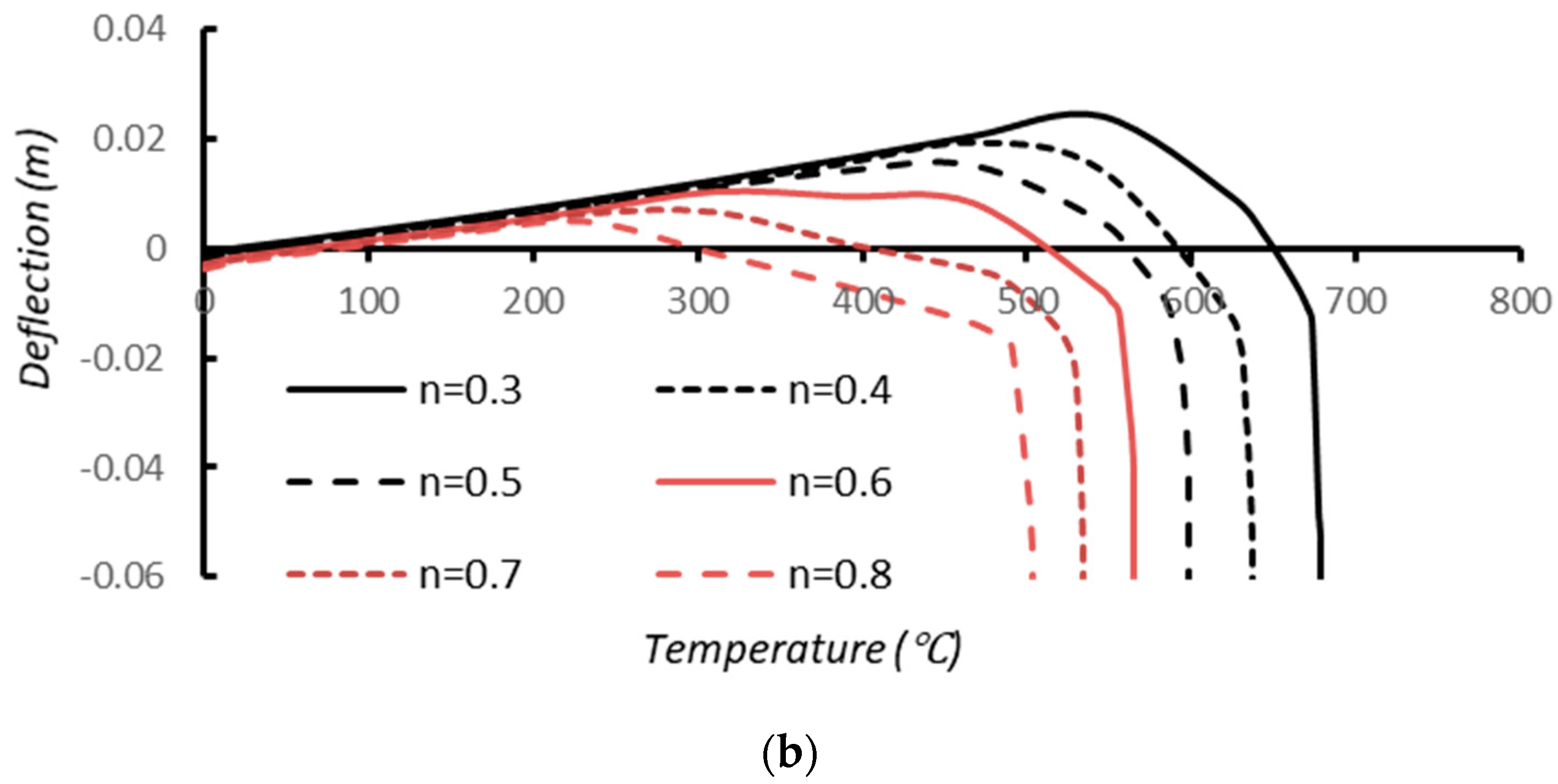
5.1. Failure Criteria of Restrained Columns
5.2. Axial Load and Restraint Ratios
5.3. Continuity of Steel Columns
5.4. Single-Sided Lateral Moment
6. Conclusions
- The results from the parametric studies indicated that the column retained a substantial loading capacity when the internal axial force of the columns returned to the applied value ();
- The increasing axial restraint stiffness ratio () did not have a detrimental effect on the fire performance of the steel columns investigated. This was primarily due to the restraint stiffness suppressing the column contraction as well;
- Although the single-sided bending moment from the connected steel beam resulted in an accelerated deflection of the columns in fire, the results demonstrated that steel columns still had sufficient fire resistance when compared to the designed limiting temperature;
- The comparison of the simulation against the design standard showed that the current design approach in EN 1993-1-2: 2005 was conservative in predicting the limiting temperature of internal and edge columns.In light of these findings, it is recommended that prospective investigations be undertaken to formulate an innovative design methodology that systematically incorporates the restraint effects from interconnected elements.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kelly, F.; Sha, W. A comparison of the mechanical properties of fire-resistant and S275 structural steels. J. Constr. Steel Res. 1999, 50, 223–233. [Google Scholar] [CrossRef]
- Meng, F.; Zhu, M.-C.; Mou, B.; He, B. Residual strength of steel-reinforced concrete-filled square steel tubular (SRCFST) stub columns after exposure to ISO-834 standard fire. Int. J. Steel Struct. 2019, 19, 850–866. [Google Scholar] [CrossRef]
- Meng, F.-Q.; Zhu, M.-C.; Clifton, G.C.; Ukanwa, K.U.; Lim, J.B. Performance of square steel-reinforced concrete-filled steel tubular columns subject to non-uniform fire. J. Constr. Steel Res. 2020, 166, 105909. [Google Scholar] [CrossRef]
- Meng, F.-Q.; Zhu, M.-C.; Clifton, G.C.; Ukanwa, K.U.; Lim, J.B. Fire performance of edge and interior circular steel-reinforced concrete-filled steel tubular stub columns. Steel Compos. Struct. 2021, 41, 115–122. [Google Scholar]
- Rodrigues, J.C.; Neves, I.C.; Valente, J. Experimental research on the critical temperature of compressed steel elements with restrained thermal elongation. Fire Saf. J. 2000, 35, 77–98. [Google Scholar] [CrossRef]
- Li, G.-Q.; Wang, P.; Wang, Y. Behaviour and design of restrained steel column in fire, Part 1: Fire test. J. Constr. Steel Res. 2010, 66, 1138–1147. [Google Scholar] [CrossRef]
- Wang, P.; Wang, Y.; Li, G.-Q. Behaviour and design of restrained steel column in fire: Part 2. Parameter study. J. Constr. Steel Res. 2010, 66, 1148–1154. [Google Scholar] [CrossRef]
- Pournaghshband, A.; Afshan, S.; Foster, A. Structural fire performance of axially and rotationally restrained stainless steel columns. Thin-Walled Struct. 2019, 137, 561–572. [Google Scholar] [CrossRef]
- Rodrigues, J.P.C.; Laim, L. Fire response of restrained composite columns made with concrete filled hollow sections under different end-support conditions. Eng. Struct. 2017, 141, 83–96. [Google Scholar] [CrossRef]
- Correia, A.J.P.M.; Rodrigues, J.P.C. Fire resistance of steel columns with restrained thermal elongation. Fire Saf. J. 2012, 50, 1–11. [Google Scholar] [CrossRef]
- Correia, A.J.M.; Rodrigues, J.P.C.; Gomes, F.C. A simplified calculation method for fire design of steel columns with restrained thermal elongation. Comput. Struct. 2013, 116, 20–34. [Google Scholar] [CrossRef]
- Wang, Y. Postbuckling behavior of axially restrained and axially loaded steel columns under fire conditions. J. Struct. Eng. 2004, 130, 371–380. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, L.; Ge, Y.; Xu, L. Behaviour of restrained high strength steel columns at elevated temperature. J. Constr. Steel Res. 2018, 148, 251–264. [Google Scholar] [CrossRef]
- Zhang, C.; Gross, J.L.; McAllister, T.P.; Li, G.-Q. Behavior of unrestrained and restrained bare steel columns subjected to localized fire. J. Struct. Eng. 2015, 141, 04014239. [Google Scholar] [CrossRef]
- Yang, J.; Xia, Y.; Wang, W.; Al-azzani, H. Fire resistance of axially restrained Q690 H-shaped welded steel columns: Test, simulation and design. J. Constr. Steel Res. 2021, 177, 106413. [Google Scholar] [CrossRef]
- Jiang, B.; Li, G.-Q.; Li, L.; Izzuddin, B. Experimental studies on progressive collapse resistance of steel moment frames under localized furnace loading. J. Struct. Eng. 2018, 144, 04017190. [Google Scholar] [CrossRef]
- Feng, R.; Huang, Z.; Chen, Z.; Roy, K.; Chen, B.; Lim, J.B. Finite-element analysis and design of stainless-steel CHS-to-SHS hybrid tubular joints under axial compression. Thin-Walled Struct. 2020, 151, 106728. [Google Scholar] [CrossRef]
- Maraveas, C. Local buckling of steel members under fire conditions: A review. Fire Technol. 2019, 55, 51–80. [Google Scholar] [CrossRef]
- Huang, Z.-F.; Tan, K.-H. Structural response of restrained steel columns at elevated temperatures. Part 2: FE simulation with focus on experimental secondary effects. Eng. Struct. 2007, 29, 2036–2047. [Google Scholar] [CrossRef]
- Tan, K.-H.; Toh, W.-S.; Huang, Z.-F.; Phng, G.-H. Structural responses of restrained steel columns at elevated temperatures. Part 1: Experiments. Eng. Struct. 2007, 29, 1641–1652. [Google Scholar] [CrossRef]
- Dassault Systèmes Simulia. ABAQUS Analysis User’s Manual (Version 6.14); Dassault Systèmes Simulia: Providence, RI, USA, 2016. [Google Scholar]
- Mago, N.; Hicks, S.J. Fire behaviour of slender, highly utilized, eccentrically loaded concrete filled tubular columns. J. Constr. Steel Res. 2016, 119, 123–132. [Google Scholar] [CrossRef]
- Cai, J.-M.; Pan, J.-L.; Wu, Y.-F. Performance of steel-reinforced square concrete-filled steel hollow section (SRSCFSHS) columns under uniaxial compression. Adv. Steel Constr. 2016, 12, 410–427. [Google Scholar] [CrossRef]
- Kyvelou, P.; Gardner, L.; Nethercot, D.A. Finite element modelling of composite cold-formed steel flooring systems. Eng. Struct. 2018, 158, 28–42. [Google Scholar] [CrossRef]
- Meng, F.; Mago, N.; Andisheh, K.; Clifton, G.C. Numerical validation of structural fire design for steel framed car park buildings. Fire Saf. J. 2023, 139, 103819. [Google Scholar] [CrossRef]
- Ali, F.; O’Connor, D. Structural performance of rotationally restrained steel columns in fire. Fire Saf. J. 2001, 36, 679–691. [Google Scholar] [CrossRef]
- EN 1993-1-2; Eurocode 3: Design of Steel Structures-Part 1-2: General Rules-Structural Fire Design. European Committee for Standardization: Brueeels, Belgium, 2005.
- Mago, N. Influence of Slab Panel Edge Sagging in Fire–Stage 2 of the SPM: Concise Summary; Rep. No. R4-118.1; New Zealand Heavy Engineering Research Association: Manukau City, Auckland, 2004. [Google Scholar]



| Test Reference | (%) | (°C) | (°C) | |||
|---|---|---|---|---|---|---|
| HEA200-K13-L30 | 50.6 | 30 | 370 | 541 | 568 | 1.05 |
| HEA200-K45-L30 | 50.6 | 30 | 364 | 542 | 560 | 1.03 |
| HEA200-K128-L30 | 50.6 | 30 | 412 | 532 | 560 | 1.06 |
| HEA160-K13-L30 | 50.6 | 30 | 399 | 544 | 543 | 0.99 |
| HEA160-K45-L30 | 50.6 | 30 | 385 | 511 | 540 | 1.06 |
| HEA160-K128-L30 | 50.6 | 30 | 395 | 499 | 538 | 1.08 |
| Average | 1.04 |
| Column Length (L) | Load Ratio ) | Design Temperature Limits | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Full-length heat L = 3 m | 0.3 | 664 °C | 695 °C | 695 °C | 695 °C | 695 °C | 695 °C | 710 °C | 710 °C | 710 °C |
| 0.4 | 620 °C | 656 °C | 656 °C | 656 °C | 656 °C | 656 °C | 655 °C | 659 °C | 663 °C | |
| 0.5 | 585 °C | 620 °C | 620 °C | 618 °C | 618 °C | 618 °C | 625 °C | 627 °C | 631 °C | |
| 0.6 | 554 °C | 591 °C | 591 °C | 591 °C | 591 °C | 591 °C | 591 °C | 591 °C | 591 °C | |
| 0.7 | 526 °C | 547 °C | 547 °C | 546 °C | 546 °C | 532 °C | 532 °C | 563 °C | 563 °C | |
| 0.8 | 496 °C | 532 °C | 532 °C | 532 °C | 532 °C | 532 °C | 532 °C | 532 °C | 532 °C | |
| Full-length heat L = 6 m | 0.3 | 664 °C | 697 °C | 697 °C | 697 °C | 697 °C | 697 °C | 697 °C | 697 °C | 697 °C |
| 0.5 | 585 °C | 618 °C | 618 °C | 618 °C | 618 °C | 618 °C | 618 °C | 617 °C | 617 °C | |
| 0.8 | 496 °C | 546 °C | 546 °C | 546 °C | 546 °C | 546 °C | 545 °C | 545 °C | 540 °C | |
| Full-length heatL = 9 m | 0.3 | 664 °C | 725 °C | 725 °C | 728 °C | 728 °C | 724 °C | 724 °C | 724 °C | 727 °C |
| 0.5 | 585 °C | 660 °C | 660 °C | 660 °C | 660 °C | 660 °C | 660 °C | 660 °C | 657 °C | |
| 0.8 | 496 °C | 572 °C | 572 °C | 572 °C | 572 °C | 572 °C | 572 °C | 572 °C | 572 °C | |
| Half-length heatL = 6 m (Lateral restraint) | 0.3 | 664 °C | 711 °C | 711 °C | 711 °C | 711 °C | 711 °C | 711 °C | 711 °C | 711 °C |
| 0.4 | 620 °C | 667 °C | 667 °C | 667 °C | 667 °C | 667 °C | 667 °C | 667 °C | 667 °C | |
| 0.5 | 585 °C | 638 °C | 638 °C | 638 °C | 638 °C | 638 °C | 638 °C | 638 °C | 638 °C | |
| 0.6 | 554 °C | 607 °C | 607 °C | 607 °C | 607 °C | 607 °C | 607 °C | 607 °C | 607 °C | |
| 0.7 | 526 °C | 581 °C | 581 °C | 581 °C | 581 °C | 581 °C | 581 °C | 581 °C | 581 °C | |
| 0.8 | 496 °C | 557 °C | 557 °C | 557 °C | 557 °C | 557 °C | 557 °C | 557 °C | 557 °C | |
| Half-length heat L = 6 m (No lateral restraint) | 0.3 | 664 °C | 711 °C | 711 °C | 711 °C | 711 °C | 711 °C | 711 °C | 711 °C | 712 °C |
| 0.4 | 620 °C | 667 °C | 667 °C | 667 °C | 667 °C | 667 °C | 667 °C | 667 °C | 667 °C | |
| 0.5 | 585 °C | 638 °C | 638 °C | 638 °C | 638 °C | 638 °C | 638 °C | 638 °C | 639 °C | |
| 0.6 | 554 °C | 608 °C | 608 °C | 607 °C | 607 °C | 607 °C | 607 °C | 607 °C | 607 °C | |
| 0.7 | 526 °C | 580 °C | 580 °C | 580 °C | 580 °C | 580 °C | 580 °C | 580 °C | 581 °C | |
| 0.8 | 496 °C | 557 °C | 557 °C | 557 °C | 557 °C | 557 °C | 557 °C | 557 °C | 558 °C | |
| Load Ratios ) | Design Temp Limits | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.3 | 664 °C | 692 °C | 692 °C | 692 °C | 692 °C | 692 °C | 694 °C | 694 °C | 694 °C |
| 0.4 | 620 °C | 648 °C | 648 °C | 648 °C | 648 °C | 648 °C | 647 °C | 647 °C | 647 °C |
| 0.5 | 585 °C | 610 °C | 610 °C | 610 °C | 610 °C | 610 °C | 610 °C | 610 °C | 610 °C |
| 0.6 | 554 °C | 576 °C | 576 °C | 576 °C | 576 °C | 576 °C | 576 °C | 576 °C | 576 °C |
| 0.7 | 526 °C | 545 °C | 545 °C | 545 °C | 545 °C | 545 °C | 545 °C | 545 °C | 545 °C |
| 0.8 | 496 °C | 513 °C | 513 °C | 513 °C | 513 °C | 513 °C | 513 °C | 514 °C | 514 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Meng, F.; Andisheh, K.; Clifton, G.C. Numerical Analysis of Restrained Continuous Steel Columns under Standard Fire. Fire 2023, 6, 330. https://doi.org/10.3390/fire6090330
Sun J, Meng F, Andisheh K, Clifton GC. Numerical Analysis of Restrained Continuous Steel Columns under Standard Fire. Fire. 2023; 6(9):330. https://doi.org/10.3390/fire6090330
Chicago/Turabian StyleSun, Jinhua, Fanqin Meng, Kaveh Andisheh, and George Charles Clifton. 2023. "Numerical Analysis of Restrained Continuous Steel Columns under Standard Fire" Fire 6, no. 9: 330. https://doi.org/10.3390/fire6090330
APA StyleSun, J., Meng, F., Andisheh, K., & Clifton, G. C. (2023). Numerical Analysis of Restrained Continuous Steel Columns under Standard Fire. Fire, 6(9), 330. https://doi.org/10.3390/fire6090330








