Experimental and Numerical Studies on the Explosion Characteristics of Ethanol–Air Mixtures under Aviation Conditions

Abstract

As a representative renewable biofuel, ethanol can reduce mankind’s dependence on petroleum resources and the emission of greenhouse gases and other pollutants. In recent years, the application of ethanol in the aviation field has begun to be a concern of scholars. As ethanol is a flammable liquid, it is significant to study its explosion characteristics in aviation conditions from a safety perspective. In this work, at 20 kPa, the explosion characteristics of ethanol–air mixtures (concentration 6~12%) were experimentally and numerically studied under an initial temperature range of 303 K~363 K. The effects of the initial temperature and concentration on the maximum explosion pressure, maximum rate of pressure rise, explosion time, and fast burning time were analyzed. In addition, the heat loss fraction and sensitivity analysis were examined and discussed. The main conclusions are as follows: A linear relationship exists between the maximum explosion pressure and the reciprocal of the initial temperature. The maximum rate of a pressure rise appears to decrease or at least approach a constant value as the initial temperature increases. The explosion time is significantly dependent on the concentration. At a constant concentration, the proportions of heat loss are approximately constant except for 12%. In our sensitivity analysis, R1 (H + O₂ <=> O + OH) was the dominant elementary reaction.

1. Introduction

Oil security has always been an important issue in the energy field. In recent years, the reserves of traditional fossil fuels have decreased, and it is imperative to vigorously produce and use renewable energy. The development and use of renewable energy can not only effectively alleviate the energy crisis, but also reduce the emission of greenhouse gases and reduce their impact on the global climate. As a representative renewable biofuel, ethanol has been widely used in medical and food industries as well as other fields. It can reduce mankind’s dependence on petroleum resources and the emission of greenhouse gases and other pollutants. Therefore, ethanol has great potential as an alternative fuel or as an additive to gasoline and diesel. As spark-ignition or compression-ignition engine fuels, the research and application of ethanol or its blend with gasoline and diesel have received extensive attention [1,2,3,4,5], and the results of such studies have proven that ethanol has great application potential as an important renewable fuel.

In recent years, the application of ethanol in the aviation field has begun to be a concern of scholars. For example, in Brazil, ethanol has been used as a land transportation fuel for more than 30 years, and in the near future, the government is expected to approve ethanol as an aviation fuel [6]. In China, Liu et al. [7] studied ethanol/RP-3 aviation kerosene blended fuel and focused on the effect of ethanol addition on the laminar burning velocity (LBV) of RP-3. What is more, they point out that the use of ethanol or ethanol/kerosene blends in aero-engines is still rare at present. However, while studying the combustion characteristics of ethanol/aviation kerosene blends, safety problems regarding the use of ethanol cannot be neglected, especially in the prevention of ethanol explosion accidents. Otherwise, it is easy for it to cause casualties and the loss of property. For example, in 2018, an ethanol explosion occurred in the workshop of a pharmaceutical company in Tianjin city, resulting in three deaths, two serious injuries, and a direct economic loss of about 17.408 million yuan [8]. If an explosion occurs on a plane, the consequences could be even more severe. Therefore, it is significant to study the explosion characteristics of ethanol in aviation conditions. In terms of ethanol explosion characteristics, researchers are mainly concerned with two aspects: the flammability limits and the explosion parameters. For flammability limits, the influences of pressure and temperature on the flammability limits and the prediction methods of flammability limits are the main interests of scholars [6,9,10,11,12]. For example, Coronado et al. [6] investigated the flammability limit of ethanol for aeronautical applications and found that temperature, pressure, and water content all affect the flammability limit of ethanol. Velasquez et al. [12] developed a model that can predict flammability limits for ethanol–air blends in various ambient environments, taking into account the influence of temperature, pressure, and moisture concentration. For the explosion parameters, the main research contents include the maximum explosion pressure, maximum rate of pressure rise, deflagration index, explosion time, and burning velocity, and the influencing factors considered include the initial pressure, initial temperature, oxygen concentration, explosion vessel, diluent, explosion location, and so forth [13,14,15,16,17,18,19,20]. For example, Mitu et al. [16,17] investigated the influence of pressure, temperature, and vessel volume on the explosion characteristics of ethanol–air mixtures, and examined the mitigation effects of different diluents as well. Cammarota et al. [14] studied the effect of hydrogen addition on the explosion of ethanol–air mixtures. As can be seen from the above literature, although many scholars have studied the explosion characteristics of ethanol under different experimental conditions, due to the serious consequences of ethanol explosions on aircraft, it is still necessary to study the explosion characteristics of ethanol in the aviation environment.

Hence, in this study, experimental and numerical studies were carried out to study the explosion characteristics of ethanol–air gaseous mixtures in aviation conditions (initial temperature range: 303 K–363 K and initial pressure: 20 kPa). The volume concentration of ethanol varies from 6% to 12% for it can cover the range from the lean side to the rich side. The effects of the initial temperature and ethanol concentration on the maximum explosion pressure, maximum rate of pressure rise, explosion time, and fast burning time were analyzed. In addition, the heat loss fraction and sensitivity analysis were examined and discussed. The research results enrich the database of ethanol–air mixture explosion characteristics and could also be used as a basis for hazard assessment and safety design in aviation conditions.

2. Experiment

2.1. Experimental Setup

In this study, the experimental apparatus was built according to ASTM E681-04 “Standard Test Method for Concentration Limits of Flammability of Chemicals (Vapors and Gases)” [21]. A schematic diagram of the experimental system is shown in Figure 1. The main component of the system is a 5 L spherical vessel made of stainless steel. Four parts are equipped, including the ignition source, heater, detection unit, and gas distribution unit. The ignition source is an electric spark generator that can provide enough energy to ignite the fuel–air gaseous mixture. It can produce electric sparks between two electrodes through a 15 kV voltage and 20 mA current. The heater is used to raise the temperature inside the vessel by means of infrared radiation and hot air circulation. The detection unit is composed of a pressure sensor and temperature sensor, which are responsible for detecting the pressure and temperature data inside the vessel and transferring these data to the data acquisition unit, respectively. The measuring range of the pressure sensor is 0~2 MPa, with a resolution of 0.1 kPa, and the measuring range of the temperature sensor is 0~1350 °C, with a resolution of 0.1 °C. The gas distribution unit is composed of a magnetic stirrer, vacuum pump, fuel feed line, and gas feed line. This unit is responsible for preparing a homogeneous fuel–air gaseous mixture through the partial pressure method. In addition to the four parts, a data acquisition unit was used to record the pressure and temperature data and transmit them to a computer. It can record data every 0.2 ms, with an acquisition time of 2 s. A computer, as a controller, is used to operate the experiment and store the data.

Before the experiment, the airtightness of the vessel was strictly controlled at no more than 0.1 kPa/min. At the outset of each test, the vessel was heated to the test temperature. Then, the vacuum pump cleaned the gas in the vessel, making the pressure below 1.3 kPa. After the vessel was evacuated, the fuel was injected first, and then the air was filled into the vessel, forming the fuel–air gaseous mixture. Next, the stirrer was run for 5 min at a rotating speed of 400 r/min, ensuring that the fuel vapor and the air were mixed homogeneously. Finally, the ignition source was triggered, and the discharge time was set as 200 ms to release 12 J ignition energy. After each ignition, the pressure history was recorded and stored in the computer. At the end of each test, the pressure in the vessel was pumped below 2 kPa two consecutive times to remove the residual gas.

2.2. Experimental Conditions

In this paper, ethanol with purity greater than or equal to 99.7% was used as the experimental fuel without further purification. Generally, the cruising altitude of an aircraft can usually reach 10,000 m and above. At this altitude, the external atmospheric pressure can be reduced to 20 kPa or less. For the temperature, the internal temperature of the fuel tank rarely exceeds 90 °C. Therefore, all explosion experiments were carried out at the initial pressure of 20 kPa. The experimental temperatures varied from 303 K to 363 K, and the ethanol concentrations varied from 6% to 12%. The test conditions are listed in

Table 1. Test conditions.

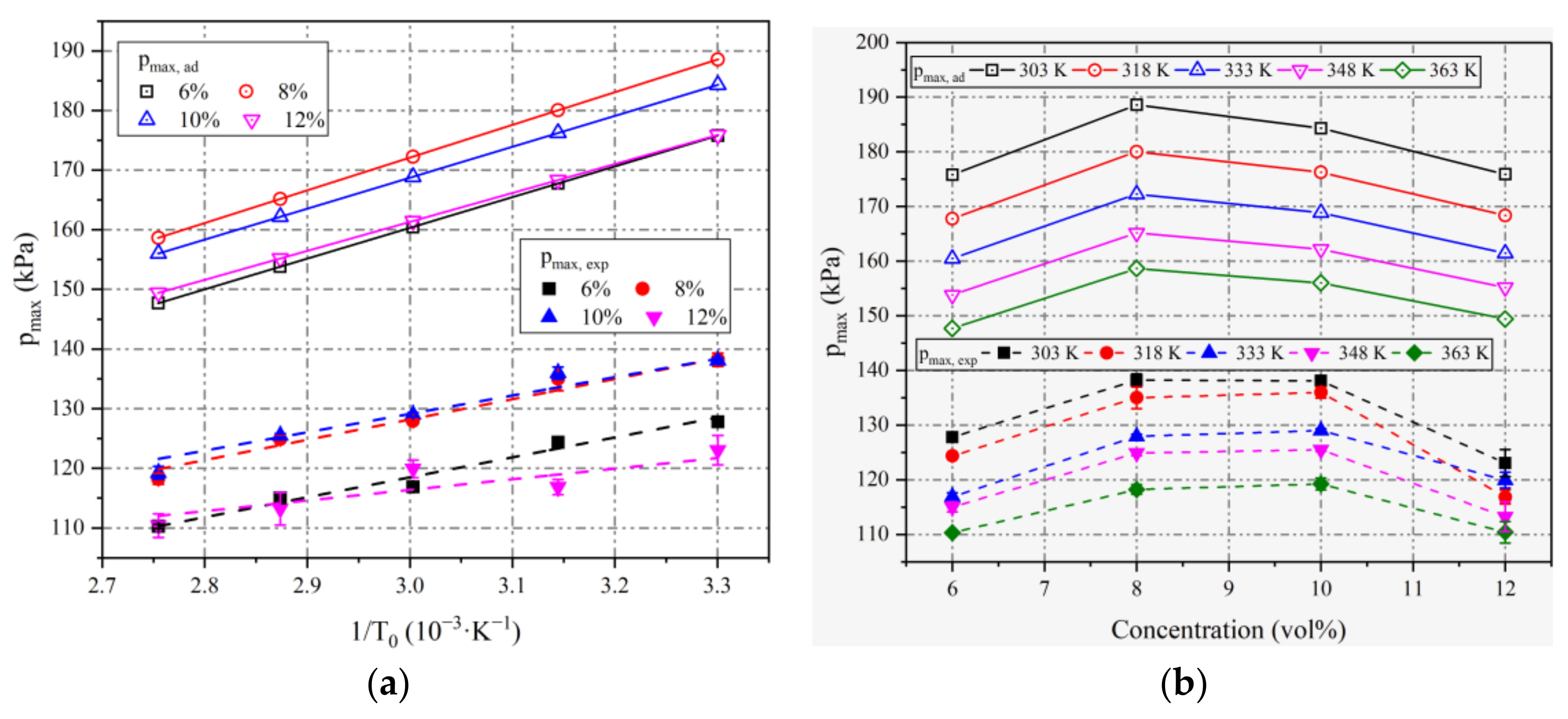
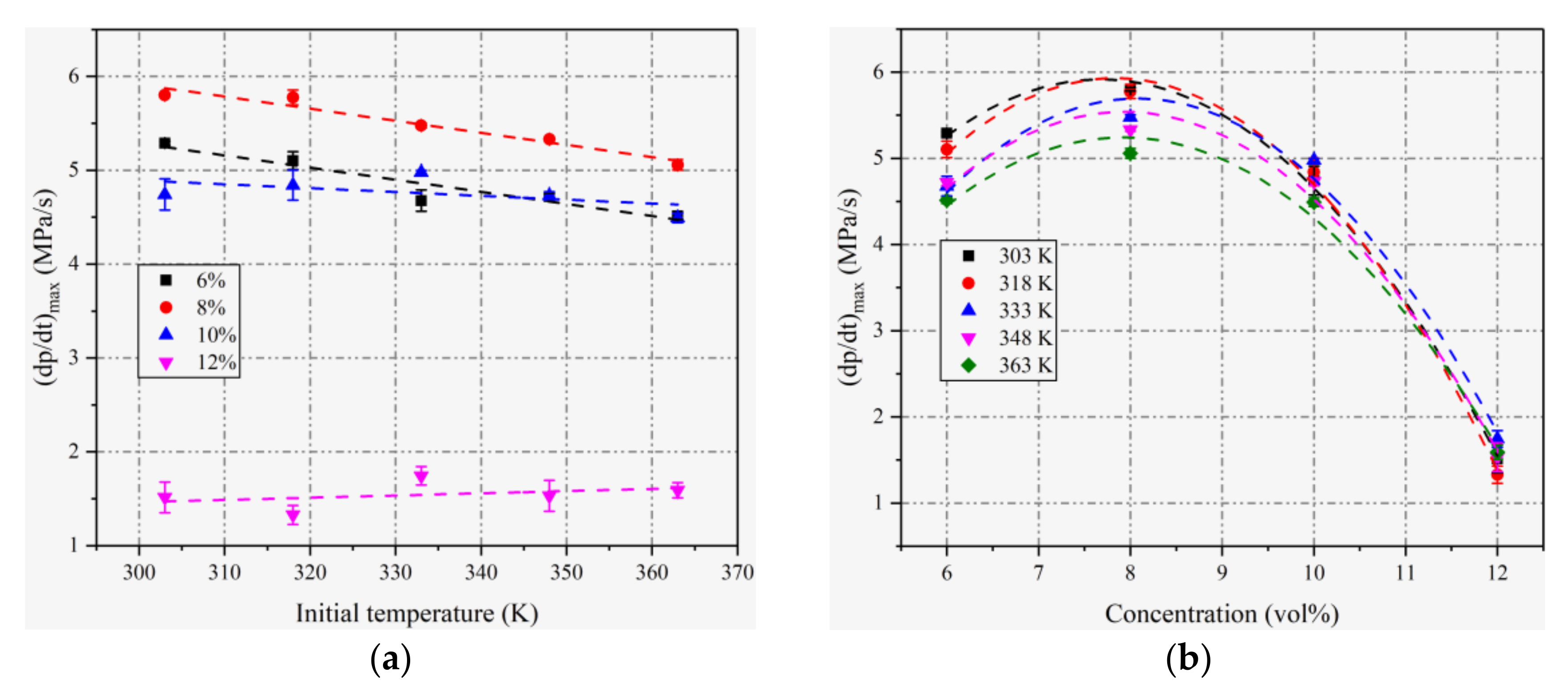
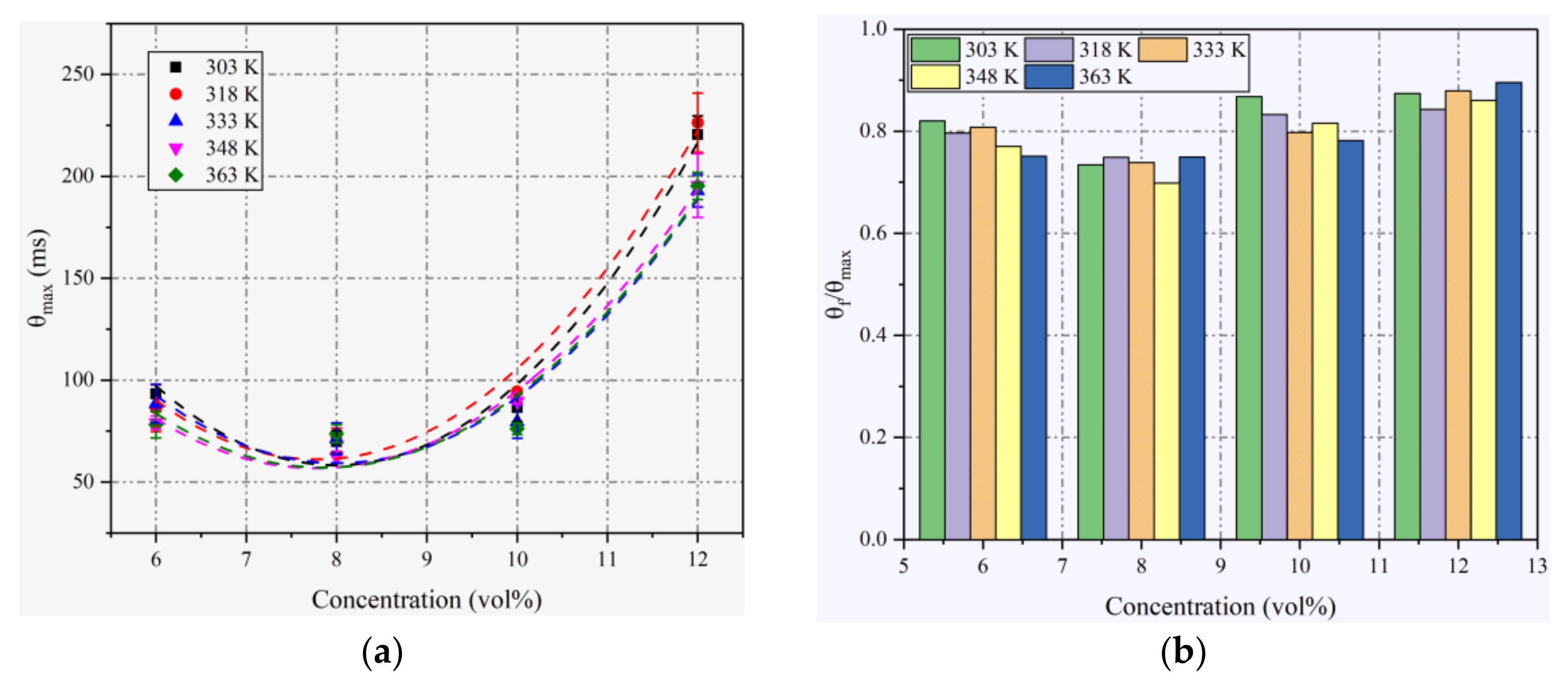
Initial Pressure	Initial Temperatures	Concentration (vol%)
20 kPa	303 K, 318 K, 333 K, 348 K, 363 K	6%, 8%, 10%, 12%

.

2.3. Experimental Data Processing

To guarantee the reliability of the data, tests for each condition were repeated at least three times. A test value with a large deviation was discarded. The mean of the remaining repeated tests was calculated as the final value of each parameter. The standard deviations in the measured maximum explosion pressures were <2.5% in all conditions.

To obtain smooth first derivative curves from the pressure-time curves, the Savitzky–Golay smoothing method was adopted based on least squares quartic polynomial fitting across a moving window within the data [22].

3. Numerical Simulations

The numerical simulations were performed by the program Chemkin-Pro 18.0, which is a powerful tool for solving complex chemical reaction problems and is often used to simulate combustion processes and other chemical reactions. According to different simulation requirements, the software provides a variety of reaction models, which can be directly invoked by users. In this work, the maximum adiabatic explosion pressures were calculated using the “chemical and phase equilibrium calculations” model, which can calculate the physical state of the system at phase equilibrium under adiabatic conditions based on the input initial conditions, regardless of the reaction path. Due to the experiment being conducted in a closed vessel, the problem type of the calculation was selected as “constant volume energy”. The flow rate sensitivity coefficient can represent the influence of an elementary reaction on laminar burning velocity, so it can be used for sensitivity analysis. It was calculated using the “premixed laminar flame-speed calculation” model, which can calculate the laminar burning velocity and flow rate sensitivity coefficient of a premixed flame. The GRAD and CURV were set as 0.03 and 0.05, respectively, in the calculation domain of 0–10.6 cm. The numbers of the grid points were all above 495 to ensure grid independence. The detailed chemical mechanism of ethanol combustion proposed by Mittal et al. [23] was adopted for the simulation. The mechanism consists of 113 species and 710 reactions. Using this chemical mechanism, the calculated LBV of the stoichiometric mixture (φ = 1) at 453 K and 0.1 MPa was 86.0 cm/s, consistent with the experimental data of Egolfopoulos et al. [24]. Therefore, the accuracy and reliability of the simulation results can be ensured.

4. Results and Discussion

A typical explosion pressure curve in blue against time and its first derivative curve in red (after smoothing) are drawn in Figure 2. After ignition via an electric spark, the flammable mixture starts burning and releasing heat. At first, the heat generation rate of the system is greater than the heat dissipation rate, resulting in a rapid increase in system pressure. The pressure rises to the maximum when the rate of heat production is equal to the rate of heat dissipation. Finally, once the rate of heat production is less than the rate of heat dissipation, the pressure begins to decrease. The definitions of the maximum explosion pressure p_max, the explosion time θ_max, the maximum rate of pressure rise (dp/dt)_max, and the fast burning time θ_f are illustrated in the graph.

4.1. Maximum Explosion Pressures

The correlation between the initial temperature and p_max has been studied and discussed in many works, such as methane–air mixtures [25], synthetic biogas–air mixtures [26], LPG–air mixtures [27], and propane–air mixtures [28]. All of the studies found that there is a linear relationship between p_max and the reciprocal of the initial temperature. Based on a study on the heat balance of the gaseous fuel–air mixture in constant volume combustion [29], a correlation between p_max, p₀, and T₀ was proposed by Razus et al. [28]:

$$p_{\mathit{max}}=\left(\xi +\frac{r_l}{{\nu }_l}·\frac{{\Delta }^c{U}^{\prime }}{T_0·\overline{C_{e,V}}}\right)p_0-q_{\mathit{tr}}\frac{{\gamma }_e-1}{V_0},$$

(1)

The meaning of each physical quantity in Equation (1) is explained in detail in the nomenclature.

In Equation (1), the third term results from the heat dissipation of the system. By rearranging Equation (1), an intuitive equation for p_max and 1/T₀ can be obtained:

$$p_{\mathit{max}}=\frac{r_l{\Delta }^c{U}^{\prime }{p}_0}{{\nu }_l\overline{C_{e,V}}}·\frac{1}{T_0}+\xi p_0-q_{\mathit{tr}}\frac{{\gamma }_e-1}{V_0}$$

(2)

Assuming a = $\frac{r_l{\Delta }^c{U}^{\prime }{p}_0}{{\nu }_l\overline{C_{e,V}}}$ and b = $\xi p_0-q_{\mathit{tr}}\frac{{\gamma }_e-1}{V_0}$, Equation (2) can be expressed as:

$$p_{\mathit{max}}=a\frac{1}{T_0}+b$$

(3)

It is obvious that a linear correlation exists between p_max and 1/T₀.

Define φ as the equivalence ratio of the ethanol–air mixture, φ = ([fuel]/[O₂])_real/([fuel]/[O₂])_stoich, and x as the volume concentration of ethanol in the mixture. When fuel is the limiting component (φ ≤ 1), the reaction is located on the lean side. According to the chemical reaction equation of oxygen-rich combustion, $r_l$ = x and ${\nu }_l$ = 1. Substitute them into Equation (2):

$$a=x\frac{{\Delta }^c{U}^{\prime }{p}_0}{\overline{C_{e,V}}}$$

(4)

When oxygen is the limiting component (φ > 1), the reaction is located on the rich side. According to the chemical reaction equation of fuel-rich combustion, $r_l$ = 0.21 (1 − x) and ${\nu }_l$ = 1. Since oxygen is the limiting component, according to the stoichiometric ratio of oxygen and ethanol in the combustion reaction, ${\Delta }^c{U}^{\prime }$ is reduced to $\frac{1}{3}{\Delta }^c{U}^{\prime }$. Equation (4) can be written as:

$$a=0.07\left(1-x\right)\frac{{\Delta }^c{U}^{\prime }{p}_0}{\overline{C_{e,V}}}$$

(5)

Comparing Equations (4) and (5), the value of a varies slightly because x varies from 0.06 to 0.12 in this paper.

Figure 3a shows the variation in p_max with 1/T₀ at different ethanol concentrations, where the simulation data p_max,ad are illustrated by hollow points and the measured data p_max,exp are illustrated by solid points and error bars. Due to the heat loss in practical circumstances, p_max,ad is much greater than p_max,exp for all conditions. However, it has the same variation trend as the initial temperature.

The data in Figure 3a are fitted by Equation (3). The fitted lines of p_max,ad and p_max,exp are shown as solid lines and dashed lines, respectively. The slope, intercept, and coefficient of determination of all the fitted lines are listed in

Table 2. Parameters of the fitted lines of p_max − 1/T₀.

Equation		${\mathit{p}}_{\mathit{max}}=\mathit{a}\frac{1}{{\mathit{T}}_0}$ + b
Data Source	Concentration	Slope (a)	Intercept (b)	Coefficient of Determination (R2)
Simulation (pmax,ad)	6%	51.50 ± 0.01	5.80 ± 0.02	1
	8%	54.83 ± 0.00	7.62 ± 0.00	1
	10%	51.84 ± 0.01	13.20 ± 0.02	1
	12%	48.53 ± 0.02	15.73 ± 0.05	1
Experiment (pmax,exp)	6%	33.44 ± 1.25	18.17 ± 3.67	0.9853
	8%	34.00 ± 2.26	26.19 ± 6.70	0.9610
	10%	30.80 ± 1.18	36.72 ± 3.54	0.9834
	12%	17.79 ± 4.83	63.01 ± 14.69	0.5913

.

From the simulation data section in Table 2, p_max,ad for all concentrations agrees with Equation (3) perfectly. The R² values and the slight changes in the slope imply the correctness of the aforementioned theoretical analysis. It is also verified by the values of R² and the slight changes in the slope at 6%, 8%, and 10% in the experimental data section. However, the fluctuation in the experimental data at 12% results in a poor linear relationship, which is probably caused by the instability in flame propagation at concentrations far from the stoichiometric mixture. This is because when the concentration of ethanol is too high, the oxygen in the mixture is seriously insufficient. In this case, ethanol cannot be completely consumed by oxygen, resulting in insufficient combustion and the poor stability of flame propagation. The larger standard deviations in 12% compared to other concentrations support this viewpoint.

From Figure 3b, p_max,ad and p_max,exp both increase first and then decrease as the concentration increases, as determined by examining the simulation and experimental data. The peak values of them for all initial temperatures appear at 8~10% (φ = 1.24~1.59), which is higher than the stoichiometric mixture and consistent with other works, such as propane–air mixtures [28] and ethanol–air mixtures [16]. This is because due to the reversible reaction limit, oxygen cannot be completely consumed at φ = 1. In order to completely consume oxygen, an equivalent ratio slightly greater than 1 is needed.

4.2. Maximum Rates of Pressure Rise

For all concentrations in this work, the maximum rates of pressure rise appear to decrease or at least approach a constant value as the initial temperature increases, as seen in Figure 4a. Similar results were observed for an ethane–air mixture [30]. For a spherical flame with adiabatic propagation, the rate of pressure rise depends on both the laminar combustion velocity and the maximum explosion pressure [31,32,33]. With the increase in the initial temperature, the laminar combustion velocity increases and the maximum explosion pressure decreases. The balance of these two effects determines the overall effect of the initial temperature on the maximum rate of pressure rise [22,34,35].

The plots of (dp/dt)_max at various T₀ of ethanol–air mixtures with various concentrations are given in Figure 4b. A similar variation trend against concentration is observed for (dp/dt)_max compared with p_max. At different T₀, the (dp/dt)_max reaches peak values, approximately at 8% concentration, slightly greater than the stoichiometric mixture. The obtained results of the maximum explosion pressures and the maximum rates of a pressure rise can both help in the design and safety prevention of a relevant pressure container for ethanol–air mixture explosions.

4.3. Explosion Times and Fast Burning Times

From Figure 5a, the variation trend of θ_max against concentration is exactly contrary to that of p_max and (dp/dt)_max. As observed in Figure 5a, θ_max is significantly dependent on the initial concentration. It is almost unaffected by the variation in the initial temperature within the experimental temperature range. Higher explosion times can be measured in the near-limit mixtures due to the combined effect of lower burning velocities and enhanced heat losses at the vessel’s wall in these mixtures [28]. The minimums of θ_max appear at approximately 8% concentration (φ = 1.24) for all initial temperatures, which is the same as (dp/dt)_max.

The fast burning time θ_f is the time from ignition to (dp/dt)_max. It is a useful index for designing explosion suppression measures because the difference between the heat generation rate and the heat dissipation rate reaches a maximum at this moment. The ratios from θ_max to θ_f are listed in Figure 5b. At a constant concentration, θ_f/θ_max varies slightly due to the variation in T₀. At a constant temperature, θ_f/θ_max varies notably with the concentration. It can be seen that the ratio is generally smaller at concentrations close to the stoichiometric mixture, which is caused by the combustion reaction being more intense at these concentrations. The minimum of θ_f/θ_max is approximately 0.7, occurring at 8% concentration. The explosion times and fast burning times have practical implications for the timing of the release of the explosion suppressant.

4.4. Heat Loss

During the process of flame propagation from ignition to the end of an explosion in a practical case, part of the heat is transferred to the vessel wall rather than absorbed by the gas, which is defined as the heat loss in the explosion process. The proportion of heat loss for each condition can be calculated by the following equation [36]:

$$F_{\mathit{loss}}=\frac{p_{\mathit{max},\mathit{ad}}-p_{\mathit{max},\mathit{exp}}}{p_{\mathit{max},\mathit{ad}}-p_0}$$

(6)

Figure 6 shows the proportions of heat loss for all conditions. By comparing different concentrations, it was found that the proportions of heat loss at 12% were notably larger than those at other concentrations due to the longer explosion times at this concentration. At a constant concentration, the proportions of heat loss are approximately constant for the whole examined temperature range except for 12%, which may be attributed to the instability in the flame propagation at this concentration.

4.5. Sensitivity Analysis

Sensitivity analysis is used to find key elementary reactions and analyze their influence on the reactivity of a premixed flame [37]. The elementary reaction with a positive coefficient can enhance reactivity [38].

Table 3. Main reactions with the greatest influence on the LBVs.

R1	H + O2 <=> O + OH	R135	CH3 + OH <=> CH2OH + H
R9	H + O2(+M) <=> HO2(+M)	R145	CH3 + HO2 <=> CH3O + OH
R12	HO2 + H <=> OH + OH	R146	CH3 + HO2 <=> CH4 + O2
R13	H2 + O2 <=> H + HO2	R189	CH3 + CH3(+M) <=> C2H6(+M)
R15	HO2 + OH <=> H2O + O2	R327	C2H2 + H(+M) <=> C2H3(+M)
R27	CO + OH <=> CO2 + H	R332	C2H3 + H <=> C2H2 + H2
R30	HCO + M <=> H + CO + M	R363	C2H5OH + H <=> SC2H4OH + H2
R32	HCO + H <=> CO + H2	R383	SC2H4OH <=> CH3CHO + H
R127	CH3 + H(+M) <=> CH4(+M)

summarizes the main reactions with the greatest influence on the LBVs for the whole examined concentration range.

Figure 7 shows the sensitivity coefficients of the main reactions for all concentrations. In Figure 7a–d, R1, R27, R30, R32, R127, R145, and R189 show the greatest influence on the LBVs for all examined concentrations. Among them, R1, R27, R30, and R145 have positive influences on the LBV because these elementary reactions are the primary sources of O, OH, and H radicals, and R27 is the main reaction with CO2 as the product. R32, R127, and R189 inhibit the LBV. In all the elementary reactions, R1 is the dominant reaction, and this position becomes more obvious as the concentration increases. For negative reactions, R32 is dominant at 6% and 8%, while R127 is dominant at 10% and 12%. Both of them are the primary consumers of H radicals. The above analysis can help to screen and analyze the main elementary reactions, find out the active free radicals that have the greatest influence on the combustion reaction, and conduct further research accordingly. As shown in Figure 7, the increasing temperature accelerates positive reactions and inhibits negative reactions. Therefore, the LBV increases with the increasing temperature.

5. Conclusions

In this paper, experimental and numerical studies were conducted to study the explosion characteristics of ethanol–air gaseous mixtures under aviation conditions. The initial temperature varied from 303 K to 363 K, the ethanol volume concentration varied from 6% to 12%, and the initial pressure was set at 20 kPa. The influences of the initial temperature and ethanol concentration on the maximum explosion pressure, maximum rate of pressure rise, explosion time, and fast burning time were analyzed. In addition, the heat loss fraction was examined and a sensitivity analysis was conducted.

According to theoretical derivation, a linear relationship exists between p_max and 1/T₀ at a constant concentration, and the correctness of the above analysis was confirmed by the simulation and experimental data. At a constant initial temperature, p_max increases first and then decreases as the concentration increases, and the peak values for all initial temperatures appear at 8~10% (φ = 1.24~1.59), higher than the stoichiometric mixture. The p_max,ad is greater than the p_max,exp in all conditions due to the heat loss in practical circumstances.

For all concentrations in this paper, (dp/dt)_max appears to decrease or at least approach a constant value as the initial temperature increases, which results from the overall influence of the initial temperature on (dp/dt)_max. A similar variation trend against concentration is observed for (dp/dt)_max compared with p_max.

θ_max and θ_f/θ_max are significantly dependent on the initial concentration and almost unaffected by the variation in the initial temperature. The variation trend of θ_max against concentration is exactly contrary to that of p_max and (dp/dt)_max. The minimum of θ_f/θ_max is approximately 0.7, occurring at 8% concentration.

At a constant concentration, the proportions of heat loss are approximately constant except for 12%. Moreover, the proportions of heat loss at 12% are notably larger.

In the sensitivity analysis, R1, R27, R30, R32, R127, R145, and R189 showed the greatest influence on the LBVs. Among them, R1 is the dominant reaction in all the elementary reactions, and this position becomes more obvious as the concentration increases. R1, R27, R30, and R145 have positive influences on the LBV because these elementary reactions are the primary sources of O, OH, and H radicals. R32, R127, and R189 are the main negative reactions, in which R32 and R127 are the primary consumers of H radicals. Moreover, the LBV increases with the increasing temperature.

This work can enrich the test and simulation data for the study of ethanol explosion characteristics in the aviation environment and provide references for the safety design of ethanol–air explosion containers and the hazard assessment of explosion accidents. In view of the application prospect of ethanol in the aviation field, the study of the explosion characteristics of ethanol/aviation kerosene blended fuel in the aviation environment should be carried out systematically in the near future.