Examining the Effectiveness of Aerial Firefighting with the Components of Firebreak Requirements and Footprint Geometry—Critics of the Present Practice

Abstract

The negative impact of climate change is increasingly evident in the severity of forest fires. Fires are becoming more intense and can often only be controlled by aerial means. Aerial firefighting is known as a very effective method—in some cases, it is the only option—of suppressing fire, but it is a very expensive solution. Recently, the effectiveness of this method has received a lot of criticism, with some studies showing a loss of between 60 and 95%, so it is worth approaching this issue in a different way. The aim of this study is to estimate losses using a new method that has not been used before. For this purpose, this study focuses on two components: the requirements of the firebreak and the geometry of the footprint. For the first, the rules of thumb of the practice were applied depending on the fireline intensity. One is the required coverage level of the surface with suppressant, and the other is the required wetted bandwidth, which is the firebreak. In practice, the firebreak should be 2–2.5 times wider than the length of the flame. For the footprint geometry, the author used the results of previous studies dealing with footprint formation. At the end, the design of the required firebreak and the simplified design of the footprint, which is an ellipsoid, were compared to each other. The results show that, in the case of a fireline intensity of 3 MWm⁻¹ and a coverage level of 2.4 kgm⁻², the loss is approximately 36.4–44.6% for the ellipsoidal footprint alone and 86–87.8% for the total amount of extinguishing agent. The conclusion is that future work should focus not on a more accurate description and understanding of emissions but on developing a technology that can change the shape of the footprint from an elliptical to a rectangular shape.

1. Introduction

One manifestation of extreme weather events caused by climate change is that the severity of forest fires during periods of drought increases [1,2,3]. Xanthophoulos et al. have shown that although the number of forest fires is decreasing globally, the area burned is increasing, meaning that on average, one fire results in a larger burn area than before [4]. While there have been significant successes in some areas, there are always difficult situations in extreme cases. The complexity and temporal dynamics of the task are well illustrated in a summary by Pyne et al. [5], which mainly focuses on the challenges faced by the United States, while Castro Rego et al. present the drastic changes needed and future possibilities of the European continent [6]. Moreover, the statistics of Xanthophoulos et al. [4] and Ingalsbee et al. [7] show that even the cost of extinguishment is increasing at a faster rate than the increase in burnt area. In other words, the specific costs of extinguishment are increasing faster than the increase in a specific burnt area. Furthermore, the problem of climate change and burnt areas does not only apply to forests; it also affects many other areas that affect the quality of life, such as agricultural production [8], animal husbandry [9], and our environment [10].

Aeiral fighting often makes up a very significant proportion of the total cost of extinguishment [11,12,13]. Therefore, by increasing the effectiveness of this method, it is expected that not only will the efficiency be increased, but even the specific cost of extinguishing will be reduced.

During aerial firefighting, the effectiveness of suppression is determined by the amount of extinguishing agent and the form it takes on the surface (footprint). Experiments to determine the effective amount of extinguishing agent have been ongoing for decades. Initially, water [14,15], and later more effective retardants, were tested for their effectiveness under different conditions [16,17]. The importance of the subject is demonstrated by the fact that experiments have continued ever since, with the obvious aim of optimizing suppressant use [18].

The formation of the applied suppressant has been the subject of several studies; e.g., George and Blakely investigated the footprints of different types of suppressants in complex experiments [19], and Hardy investigated the rheological curves formed after the release [20]. Moreover, Plucinsky and Pastor focused on the efficiency of the lines of defense against burn-through [21], and Qureshi and Altman drew conclusions from the flow of liquids [22,23]. The high cost of aerial firefighting often raises questions about its true effectiveness [24,25], as well as criticisms of the current practice [26,27]. Therefore, it is certainly worth re-examining the causes of losses to find new ways to create a more efficient spray pattern.

Most open containers and closed tanks are discharged naturally by gravity, such as in the case of the Canadian CL-415 [28] or the Russian Be-200 [29], but there are also pressurized tank systems, such as the MAFFS tanks [30] or the B-747 Global Supertanker [31]. For the latter two (MAFFS and B-747), the cross-sections of the release openings using gravity alone—relating to the flight speed and altitude—would not provide enough flow rate. In other words, the amount of extinguishing agent on the surface would not reach the acceptable coverage level to stop the spread of the fire [32,33]. Therefore, pressure is applied to empty the extinguishing agent tank faster so that the amount of extinguishing agent discharged (the extinguishing agent stream or flow rate) is sufficient to provide the correct coverage level. This coverage level is required to extinguish the fire per unit area according to the flight speed (approx. 260 kmh⁻¹) and altitude (approx. 120–240 m) of the discharge [30,31,33]. For safety reasons, large air tankers (LAT) and very large air tankers (VLAT) cannot reduce the flight speed and altitude below the limit of the aircraft used.

After the discharge, the extinguishing agent mechanically collides with the air, causing it to break up and form a spray pattern of different shapes depending on the conditions [19,20]. The latter has also been addressed in a number of studies, including numerical modelling [34,35,36,37], laboratory testing [38], field experiments [22,39], empirical descriptions [19,40], and complex approaches [20,41,42,43,44].

Based on an analysis of the above research, it can be clearly concluded that the formation of the spray pattern is very complex and influenced by many factors. These factors are mainly the type and characteristics of the extinguishing agent, the volume of the release, flight speed, and altitude, but also the wind direction and speed, which are external factors.

The author further concludes that the analysis of the spray patterns significantly facilitated an understanding of their formation, but this did not fundamentally change the emission technology or effectiveness. The result of this is that, although the effectiveness of aerial firefighting has undoubtedly improved over the past few decades, a radical breakthrough in this area is not visible according to the analysis of the footprints.

The author aims to examine the current effectiveness of aerial firefighting using two components: the width of the firebreak required to successfully extinguish the fire and the geometry of the footprint. The result of the analysis points to the effectiveness of the current procedure on the one hand and the necessary direction of future developments on the other.

The article is structured as follows: The first section provides a discussion on how wide the firebreak needs to be in relation to the intensity of the fire front in order to be safe against burn-through. Then, the characteristics of the footprint under current technologies, such as its very uneven distribution both transversely and longitudinally and its very irregular footprint shape, which is best approximated in practice as an ellipse, are presented. The next section determines how much of the footprint, which is simplified as an ellipse, can be adequately covered by the suppressant and considered an effective part, i.e., the part where the width is neither more nor less than what is required. Finally, by means of a geometric analysis, it is shown how the width of the effective part can be increased by converting the inefficient area of the ellipse.

In the next chapter, specific calculations are carried out to determine the effective part of the released suppressant using the suggested method from the previous chapter, geometric analysis, and simple mathematical calculations. The calculations are made using four different values of firebreak width. The most accurate value is 2.5 times the flame length (7.5 m), followed by three different rounded values (8, 9, and 10 m) adapted to practice. Each of the four values is used to calculate the effective amount of the suppressant relating both to the adequately covered ellipse and to the total transported suppressant.

The conclusion confirms that the results are consistent with critical findings on effectiveness by other authors. However, the methodology used by the author also has the potential to guide future research. It is suggested that future work should focus not on a more accurate description and understanding of emissions but on developing a technology that can change the shape of the footprint from an elliptical to a rectangular shape.

2. Materials and Methods

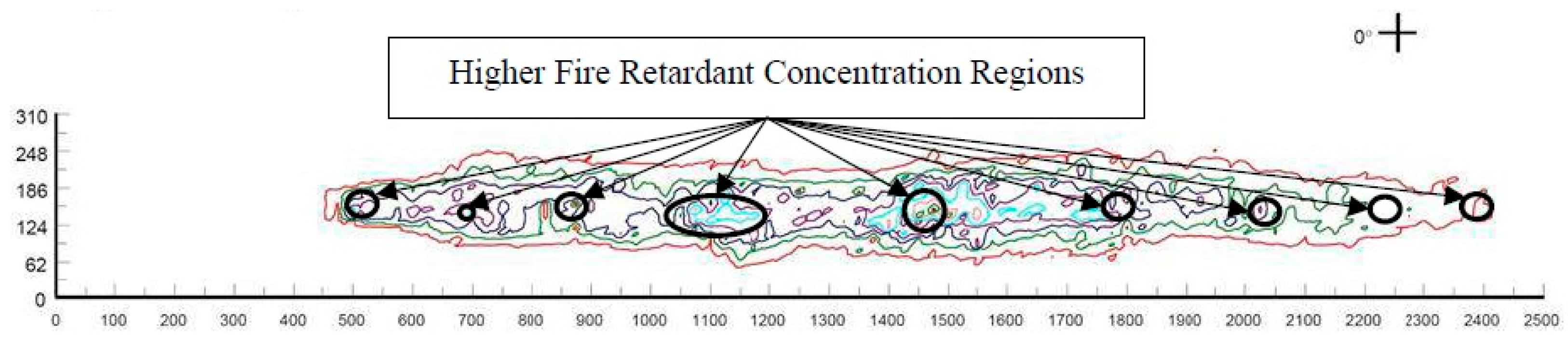
2.1. Footprint Characteristics and Protection against Burn Through

The released suppressant forms a so-called spray pattern, or footprint, on the surface. This is characterized by various parameters besides its shape, mostly the amount of suppressant on a unit surface, which experience has shown varies considerably at different points of the wetted surface [19,20]. By connecting the points of the same value, they give the so-called quantitative distribution curves, which are collectively referred to as spray patterns or footprint.

Experience shows that, despite an adequate amount of suppressant, an insufficiently wide wetted surface can burn through, and, conversely, if the amount of suppressant is inadequate, even a wider wetted surface can burn through [23,41,42,43,44]. That is, two conditions must be met simultaneously to create a safe firebreak. On the one hand, there must be a sufficient amount of suppressant per unit area, and on the other hand, the wetted surface must reach a suitable width.

The firebreak width is one of the main elements of effective suppression. There are many calculations regarding the effective break width but there is no overarching consensus. To stop fire in different conditions (e.g., humidity, wind) means that the effective width is also different. Escrig et al. [45] summarized the results of several relevant studies in which the scale was found to vary from 2 to 160 m. Loane and Gould [16] state that 1 m is the minimum width of the effective firebreak, although this is in the context of low intensity fires. For the effective firebreak, Simon et al. [46], based on rule of thumb, used a width that was 2–3 times wider than the flame length. In the work of Brou, in which the rule of thumb is that a width 2–3 times the flame length already gives a minimal risk of through burn (2.93–0.2% at 3–12 MWm⁻¹ fireline intensity), a probability (%) was found of the fire breaking through the firebreak [47]. Murgatroyd also suggests a 2.5 wider break width than the flame length, although, as in the work of Loane and Gould, this study focuses on prescribed fires and low fireline intensity [48].

Even though there is a difference between fire intensity and fireline intensity, in the case of wildfires, most authors use them as synonyms [49]. Fireline intensity was first defined by Byram as the rate of heat output per length of fireline and expressed as kilowatts per meter of fire edge [50]. The fireline intensity is one of the most important parameters to predict fire severity and behavior; therefore, there is a significant amount of research that focuses on its description and understanding [51,52,53,54,55]. There is a complex but clear correlation between the fireline intensity and the length of the flame column. The length of the flame naturally depends on many factors, such as the type of vegetation, its moisture content, temperature, humidity, etc. [51,54,55,56,57]. According to the above, in this study, the author preferred the value of the practice of rule of thumb and the probability approaches, which suggest a width of approximately 2–3 wider than the flame lengths for an effective firebreak.

The amount of extinguishing agent per unit area required to prevent fire from spreading further, based on empirical and laboratory tests, is tabulated [20,58,59]. The values in the literature may differ due to different conditions and geography, but the values are appropriate as a guideline.

Summarizing the above, it can be seen that two conditions must be met simultaneously for effective suppression. One is the presence of the right amount of suppressant per unit area for the type of vegetation. The other is that the width of the surface treated with the extinguishing agent must be 2 to 2.5 times the flame length of the burning vegetation. If either the wetted strip is not wide enough [21,42] or the amount of extinguishing agent is insufficient [44], the area can burn through, and extinguishing will only temporarily slow down the spread of the fire. Insufficient extinguishing agent or insufficient width of the wetted strip means that the fire will eventually pass through it, and, thus, the extinguishing process is not sufficiently effective.

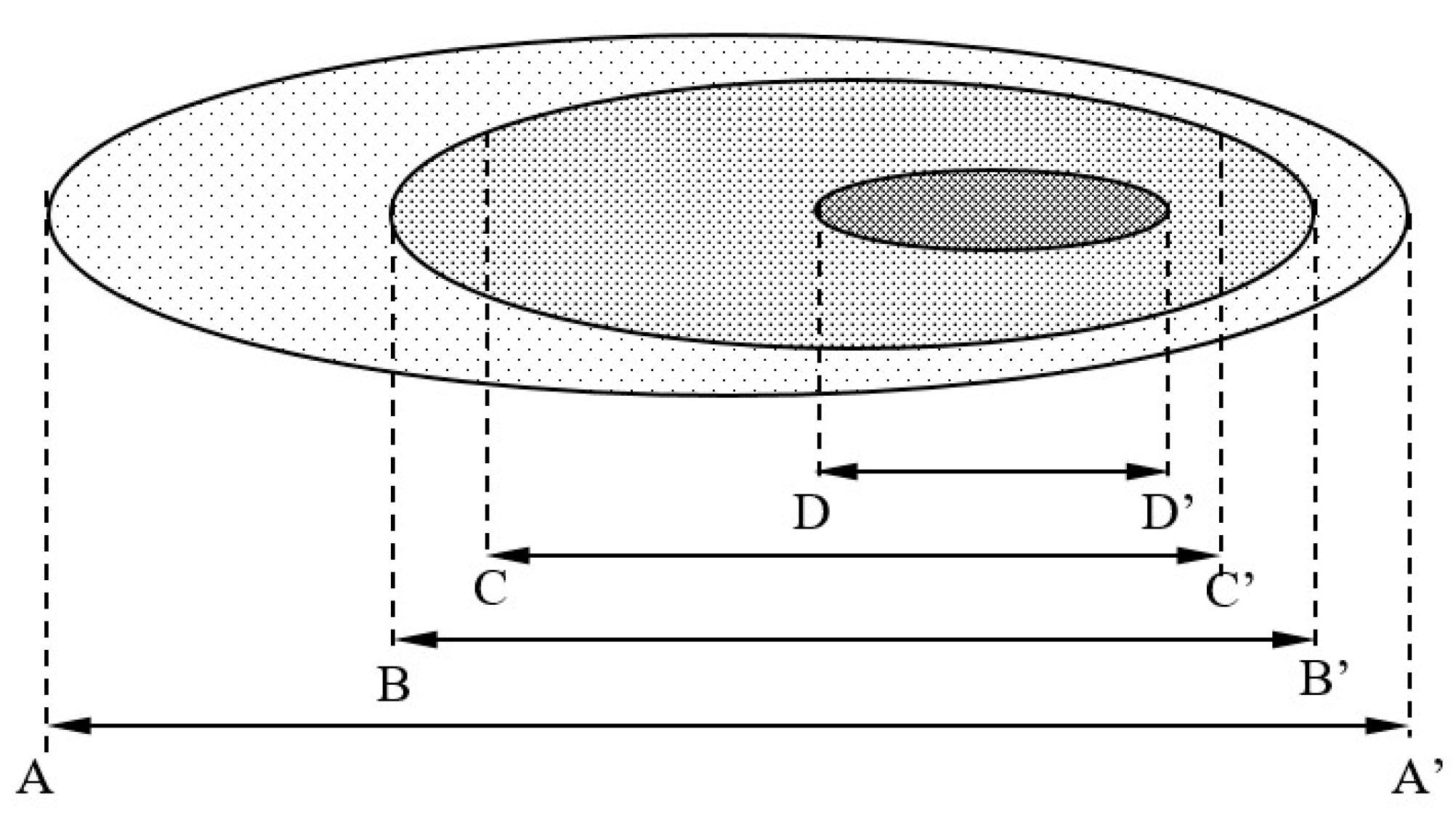
2.2. Simplifying the Footprint Geometry to an Ellipse Form

According to studies on the formation of the spray pattern, it is easy to draw the conclusion that the shape of the wetted area observed on the surface (vegetation) is mostly irregular but resembles an “egg shape” or ellipse in a graphical approximation, as shown in Figure 1 [60,61].

It can be observed that the spray pattern becomes more elongated as the amount of suppressant released increases. For very large aircraft (VLAT), such as the B-747, DC-10, or those using MAFFS tanks (C-130 Hercules), where the discharge volume reaches or exceeds approx. 10 m³, instead of an ellipse, the footprint resembles an irregular rectangle or band with rounded ends [22,23,33]. Of course, the length of the footprint is also significantly affected by the flight speed, so releasing the same amount of suppressant at a higher speed can result in a longer and therefore more elongated footprint [62]. According to the work of Qureshi and Altman, shown in Figure 2, it can also be concluded that the unevenness and hecticness of the distribution of the suppressant are not changed by a longer footprint, even if the aerial services provide a uniform spreading pattern by assuming an average calculation in the case of elongated footprints [22].

From the above, it can be concluded that the spray pattern, the footprint, is formed through an extremely complex process influenced by the characteristics of the suppressant, flight speed, and altitude as well as other environmental factors. Very simply, a higher altitude with the same flight speed results in a lower coverage level; however, the wetted width can be wider. A higher flight speed with the same altitude results in a lower coverage level; however, the wetted band can be longer. If both the flight speed and the altitude are the same, however, the flow rate of the suppressant is higher, which means that the coverage level will also be higher. Naturally, there are other factors in addition to the flight related parameters, e.g., wind and topography, which influence the shape of the footprint [63].

In order to simplify practical use [64], presumably in search of the simplest form, there are ellipses within which additional concentric ellipses can be drawn in such a way as to separate the discrete values of different amounts of suppression material measured per unit area [41,58,64]. The use of the ellipse model is also acceptable because the exact spray pattern of a release can probably never be predicted in advance—the law of small numbers [65]—but considering the average of a sufficiently large number of repetitions—the law of large numbers [66]—the distribution should already show an elliptical shape [67].

In both the ellipse [64] and the rounded-end rectangle [33,41] models, the quantity curves of the suppressant distribution are determined by discrete values; however, based on the real tests shown in Figure 3, it can be established that its vertical distribution is just as uneven or hectic as the horizontal [20,22,23,68].

The amount of suppressant measured per unit area is not uniform either longitudinally or transversely. Simplifying the distribution, a Gaussian curve can be found in most cases, with a longitudinal peak shifting towards the start or end point of the release [41].

Furthermore, it can be concluded that the formation of footprints is influenced by a number of circumstances. These different circumstances are each unique, so they are almost unrepeatable. Nevertheless, the transverse and longitudinal distribution of the suppressant has patterns that can be modeled in a simplified form that can be used in practice. For smaller amounts of suppressant, the practice is to use the ellipse model [64], but in the case of larger amounts, a long and narrow, rounded shape is used, usually resembling a rectangle [33,41].

Moreover, depending on the conditions, it is obvious that the burn intensity of the vegetation will vary [69]. As referred to above, for safe extinguishing, following the next principle, the wetted bandwidth is required to be 2 to 2.5 times wider than the flame length [46,47,48]. Based on practical experience and measurements [50,70], different vegetation types require different amounts of suppressant. These correlations, used in practice, are known in tabular form [48,64,71]. As an example, according to Delforge’s Aerial Firefighting Handbook [64], low grass fire requires 0.4 kgm⁻² of water to be suppressed, tall and lush shrubs 1.6 kgm⁻², and the same shrubs with dead biomass fuel require 2.4 kgm⁻² of water.

In addition to the above, the choice of firefighting tactics is a very important factor, as it has a major impact on the effectiveness of the intervention. In aerial firefighting, a basic distinction is made between direct and indirect attacks. In this article, the distinction is not relevant since the basic characteristics of the footprint formed, such as irregular shape and uneven distribution, are present in both cases. Likewise, there is no doubt that the effectiveness of firefighting is significantly influenced by the distribution of combustible material [72] as well as the rate of extinguishing agent evaporation and drying [73]. However, these are also irrelevant for the purpose of this study since the author focuses on footprint geometry. This footprint geometry is optimized for fire safety requirements, but in this case, the firefighting tactics (direct or indirect attack), fire behavior (e.g., fire breaching), or change in extinguishing agent efficiency over time (e.g., evaporation or drying) are obviously not relevant. Still, one of the fire characteristics, fireline intensity, is used in the calculations.

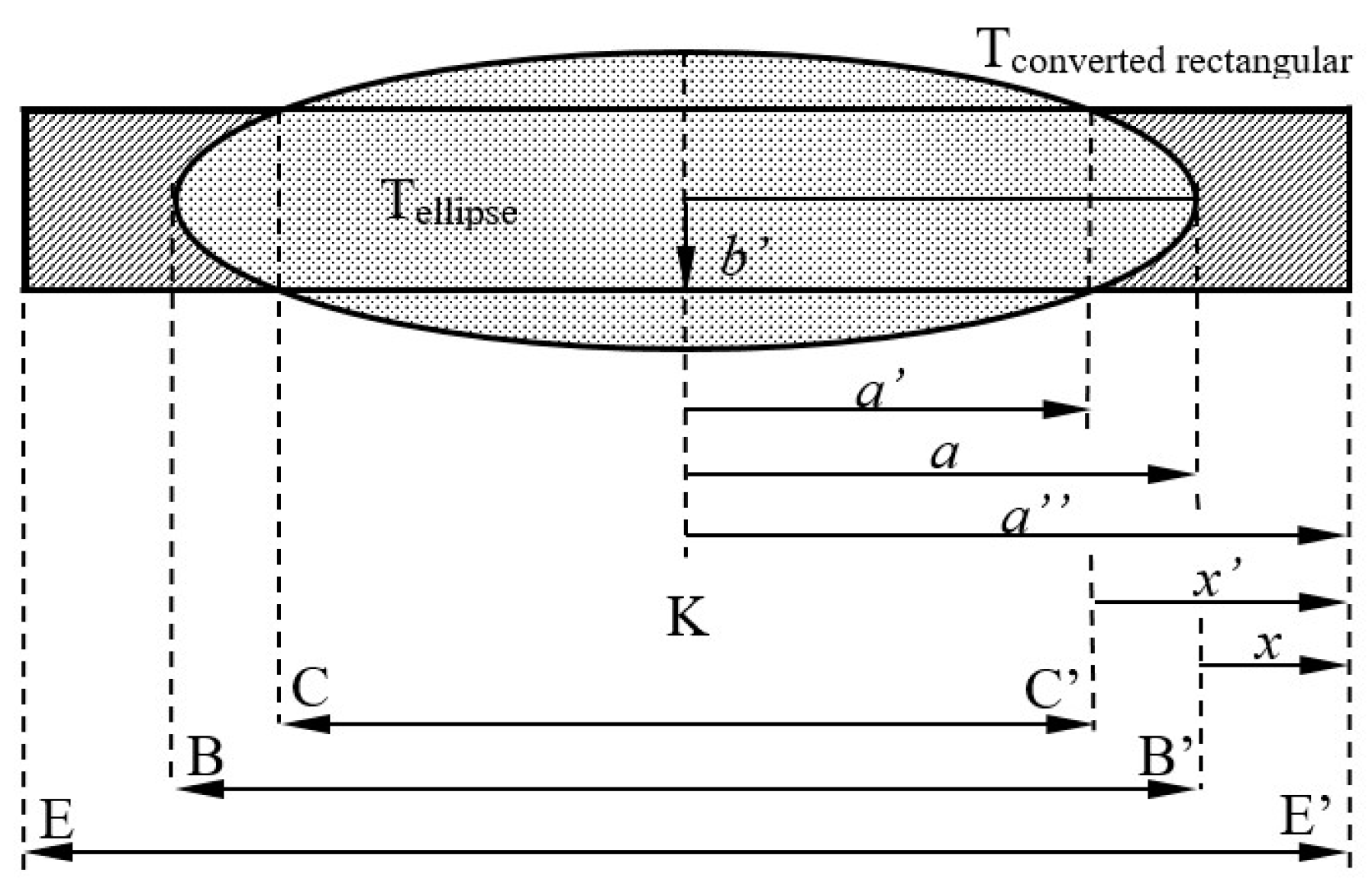
2.3. Footprint Loss and Theoretical Compensation along the Transverse Axis

Thus, according to the above, the basic characteristic of the surface footprints is that the suppressant is not homogeneously distributed along either the longitudinal or transverse axes. A simplified cross-section of the distribution shows a mostly symmetric distribution similar to a Gaussian curve [41]. Looking along the longitudinal axis, the distribution may also be symmetric; in this case, a true resemblance to the Gaussian curve is also present; however, it is more typical that the distribution peaks near the initial or endpoint [58,59,60,64].

According to the above, it can be concluded that the areas between the intersections at points AB and A′B′ are ineffective due to the insufficient amount of suppressant per unit area, while the areas between the intersections at points DD′ are ineffective due to the excess suppressant (Figure 4). In the area between the intersections at points BB′, the amount of extinguishing agent per unit surface area would be sufficient to prevent the spread of the fire under the given conditions; however, the width of the wetted surface between points BC and B′C′ is not sufficient, and between points CC′, the area is wider than necessary (Figure 5). In the graphical model, there is a deficit in the first case and a surplus in the second; both can be considered losses in terms of efficiency (Figure 5).

In the area between points AA′, the conditions for effective suppression exist between points CC′ in such a way that the value of the width over the entire length between points DD′, with the exception of the starting and end points, is more than required (Figure 4), i.e., there is a loss.

The author notes or does not rule out that the area between points BC and B′C′ may also be effective in preventing the spread of fire, provided that it is considered that the insufficient amount of extinguishing agent in the area between points AA′ may compensate for the lack of sufficient extinguishing agent due to the insufficient width of the area. By the same logic, taking into account the amount of suppressant on the surface typical between points AA′, points CC′ can also be shifted outwards, assuming a narrower wetted strip where the amount of suppressant per unit surface is adequate. Since the prevention of burn-through or the effectiveness of the firebreak is influenced by a number of factors, it is appropriate to express it in terms of empirical values [21,45,74] or probabilities [47]. For the sake of simplicity, these possibilities are ignored here, as they do not affect the evaluation of the solution proposed later.

The logical question is how to eliminate the losses, i.e., increase the amount of suppressant to the extent necessary in areas with shortages and reduce it to the extent necessary in areas with surpluses.

2.4. Interpreting the Effective Part in the Ellipse Model

In aerial firefighting, the extinguishing agent is mostly released perpendicular to the spread of the fire, parallel to the fire line [64]. The intervention is successful if the further spread of the fire is completely prevented or slowed down to a point where other methods or tactics such as ground forces can be used [21]. In the first case, aerial firefighting contributes directly to the overall success, while in the second case, it contributes indirectly. It has already been shown that, in order to have an effective intervention, the wetted surface must be adequate in terms of both the quantity of extinguishing agent per unit area and the width of the area wetted by the appropriate quantity of extinguishing agent, depending on the characteristics of the burn [21,58,59]. Of course, the above must also take into account the limitations of firefighting. Firefighting by ground forces is assumed to be effective up to 4 MWm⁻¹, whereas firefighting by aerial means is assumed to be effective up to 7 MWm⁻¹ fireline intensity [75,76,77]. For the latter case, some authors give even lower values [20,64].

Depending on the characteristics of the fire and, most importantly, the intensity of the fire, both conditions will vary, so a higher fireline intensity will require not only more extinguishing agents per unit surface but also a wider wetted surface. In practice, the maximum value of the first is approx. 5 kgm⁻² [20,58,64,73,78] for a mature forest due to the water retention capacity of the vegetation surface, while the second, based on empirical values, is about 2–2.5 times the flame length [46,47,48]. Focusing on the latter, the author follows Hardy’s work and assumes, as an example, the technically accepted limit between high and very high fireline intensity, which corresponds with a flame length of 3.5 m (I = approx. 3 MWm⁻¹) [20]. To suppress this, empirical examples show that a suppressant quantity of about 2.4 kgm⁻² is required [16,64]. The width of the required wetted surface can be taken as 7 m for a flame length of twice the flame length and 8.75 m for a flame length of two and a half times the flame length.

The area of the elliptical footprint, for which the amount of suppressant per unit area is adequate by marking the notable points in Figure 6, can be written in form (1) or in simpler form (2) and is given as follows:

T_{ellipse; k = 2.4 kgm⁻²} = πa_BB′b_BB′

(1)

T_{e; k = 2.4 kgm⁻²} = πab

(2)

where T_{ellipse; k = 2.4 kgm⁻²} and T_{e; k = 2.4 kgm⁻²} represent the area of the ellipse shown in Figure 6, where the value of the coverage level reaches 2.4 kgm⁻². Moreover, a_BB′ and a represent the semi-major axis, b_BB′ and b represents the semi-minor axis of the above ellipse.

The effective width of the area fitted to the ellipse, by marking the notable points (3), or in a simpler form (4), is given as follows:

T_{rectangular; k = 2.4 kgm⁻²} = 4a′_CC′b′_CC′

(3)

T_{r; k = 2.4 kgm⁻²} = 4a′b′,

(4)

where T_{rectangular; k = 2.4 kgm⁻²} and T_{r; k = 2.4 kgm⁻²} represent the area of the rectangle shown on Figure 6 and Figure 7, where the value of the coverage level reaches 2.4 kgm⁻² but the width of the wetted zone is not wider then required to sufficiently control the spread of the fire. Moreover, a′_CC″ and a′ represent the semi-major axis and b′cc and b′ represent the semi-minor axis of the above rectangle.

A comparison between the area of the ellipse obtained by the conventional method and the area of the loss-free solution is shown in Figure 7, where the area given by Formulae (1) and (2) is larger than the area given by Formulae (3) and (4). In other words, the amount of extinguishing material of the conventional footprint on the same discharge axis can, theoretically, be converted to a lossless one. A graphical representation of this is shown in Figure 7. The spatial correspondence between the conventional footprint and the converted rectangle is expressed by the full (5), and simple Formula (6), respectively:

T_{ellipse; k= 2.4 kgm⁻²} = T_{converted rectangular; k = 2.4 kgm⁻²},

(5)

T_{e; k= 2.4 kgm⁻²} = T_{con r; k = 2.4 kgm⁻²}

(6)

where T_{converted rectangular; k = 2.4 kgm⁻²} and T_{con r; k = 2.4 kgm⁻²} represent a rectangular shape that is converted from the same size area of the T_{ellipse; k = 2.4 kgm⁻²} and T_{e; k = 2.4 kgm⁻²} shown in Figure 7, where the value of the coverage level reaches 2.4 kgm⁻² but the width of the wetted zone is not wider then required to sufficiently control the spread of the fire.

The formula for the converted rectangle can be given in several ways by continuing the simplicity of Formulas (2), (4), and (6) to obtain (7), (8) and (9) as follows:

T_{con r; k = 2.4 kgm⁻²} = 4a″b′

(7)

T_{con r; k = 2.4 kgm⁻²} = 4(a + x)b′,

(8)

T_{con r; k = 2.4 kgm⁻²} = 4(a′ + x′) b′

(9)

where a″ and b′ represent the semi-major and the semi-minor axes of the converted rectangular shape where the value of the coverage level reaches 2.4 kgm⁻² but the width of the wetted zone is neither wider nor narrower than required to sufficiently control the spread of the fire. Moreover, x represents the difference between the semi-major axis of the ellipse and the semi-major axis of the converted rectangular area, while x′ represents the difference between the semi-major axis of the effective rectangular shape of the ellipse and the semi-major axis of the converted rectangle. These are shown in Figure 7.

Using the Formulas (2) and (7)–(9), Equations (10), (11) or (12) can be obtained as follows:

πab = 4a″b′

(10)

πab = 4(a + x)b′,

(11)

πab = 4(a′ + x′) b′

(12)

Equation (10) expresses a simple equality of the area sizes, while Equation (11) shows how much shorter the ellipse wetted with the appropriate amount of suppressant is compared to the longitudinal axis of the converted area. Equation (12) shows the change in the length of the part of the ellipse with the corresponding width and the corresponding amount of suppressant. While it is easiest to focus on the former (as this is what it is known so far), it is the latter Equation (12) that reveals the real change in efficiency.

By rearranging Equation (11) and looking for ratios, firstly, the term (13) can be obtained and then (14). The values of a and b are known empirically, and the value of b′ can be calculated from the fireline intensity or flame length. From these, the value of x, i.e., the increase in the length of the converted area, can be determined.

$$\frac{1}{4}\pi \frac{b }{b^{\prime } }=1+\frac{x}{a}$$

(13)

$$x=\frac{1}{4}\frac{\pi ab }{b^{\prime } }-a$$

(14)

3. Results and Discussion

In a given case, both the intensity of the fire and the corresponding amount of extinguishing agent required to stop it can be determined on the basis of the length of the flame. In the example above, a fireline intensity of approx. 3 MWm⁻¹ is given, which implies a flame length of approx. 3.5 m [20]. Thus, using the more stringent empirical rule of 2.5 times the width of the wetted surface [46,47,48], a strip of 8.75 m wide is required, where the amount of suppressant reaches approx. 2.4 kgm⁻². The rounded value for the properly wetted strip is 9 m, which is relatively easy to use in practice for firefighters using imperial units (about 10 yards). For firefighters who use the standard system (SI), rounding to 10 m may be useful in practice. Obviously, different basic data will lead to different results, so a significant difference between the two extreme values in the example, 7 m (twice the flame length) and 10 m (2.5 times the flame length rounded), is to be expected. Although the differences are mathematically significant, it must be taken into account that firefighters are unlikely to be able to accurately assess differences of this magnitude during firefighting, if only because firefighters are more likely to apply satisfactory decision-making procedures, so-called rules of thumb, rather than the most precise solutions [79,80,81]. The author will hereafter use the rounded value of the more stringent condition (the width of the wetted surface being 2.5 times the flame length) (2b′ = 9 m).

The empirical footprint ellipses of each aircraft type are known, as are their length and width data [20,41,64]. Taking an example, there is a footprint where the area covered with 2.4 kgm⁻² of suppressant is about 550 m², which, approximately, is an ellipse with a length of (2a) 50 m and whose widest part (2b) is 14 m [64]. Using these data and formula (15), converting 550 m² into a rectangle (2a″ and 2b′), the length of the wetted surface for a 9 m wide strip (2a″) is approx. 61 m, which is effectively 11 m longer (x = 5.5 m, 2x = 11 m) than the axis of the ellipse, which, in this case, represents about a 20% gain in favor of the converted rectangle (50 m to 61 m).

$$x=\frac{1}{4}\frac{\pi ab }{b^{\prime } }-a= \frac{1}{4} \frac{550 {\mathrm{m}}^2 }{9 \mathrm{m}}-25 \mathrm{m}=5.5 \mathrm{m}$$

(15)

By determining the intersections of the rectangle bounding the converted area and the ellipse, it is also possible to calculate how much longer the converted area (EE′ → 2a″) is than the part of the ellipse where not only the quantity of the suppressant but also the width of the wetted surface is sufficient (CC′ → 2a′), that is, the effective part of the ellipse. This is what actually determines the difference in efficiency and is therefore a more important indicator than a comparison with the longitudinal axis of the ellipse and rectangle.

If given Equation (16) for any point xy on the curve of the ellipse, finding the value of x gives Formula (17).

$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$

(16)

$$x=a \sqrt{1-\frac{y^2}{b^2}}$$

(17)

Transferring the notations used in Figure 7 (x = a′; y = b′), Formula (18) can be written, where, taking into account the 9 m wide safety strip (b_{I = 3 MWm}⁻¹ = 4.5 m) and using 550 m² (a = 25 m, b = 7 m) ellipse data of the footprint for the 2.4 kgm⁻² of suppressant [16,64], the following Formula (19) is obtained:

$$a^{\prime }=a \sqrt{1-\frac{{b^{\prime }}^2}{b^2}}$$

(18)

$$a^{\prime }= 25 \sqrt{1-\frac{20.25}{49}}=19.25$$

(19)

According to the above, the length of the effective area of the 50-m-long ellipse is 38.5 m (2a′ = 38.5 m), but the length of the converted area is 61.1 m. The difference is 22.6 m, which represents a 58.7% increase in effectiveness in the rounded width band of acceptable safety (9 m) and only in the range of k = 2.4 kgm⁻² suppressant amount.

In

Table 1. Physical parameters of a 550 m² ellipse in case of 10–9–8.75–7 m (B1–B4) width firebreak.

Characteristics of A 550 m2 Ellipse (a = 25 m; b = 7 m)	B1	B2	B3	B4
Required width of the fire brake (2b) [m]	10	9	8.75	7
Length of the effective part of the ellipse (2a′) [m]	35.0	38.5	39.0	43.5
Length of the converted strip ˙(2a′ + 2x′) [m]	55.0	61.1	62.9	78.6
Difference in the length effectiveness (x′) [m]	20.0	22.6	23.9	35.1
Difference in the length effectiveness in percentage (x′) [%]	57.1	58.7	61.3	80.7
Effective area size of the ellipse (4a′b′) [m2]	350.0	346.5	341.3	304.5
Ineffective area size of the ellipse (πab-4a′b′) [m2]	200.0	203.5	208.7	245.5
Ineffective part of the ellipse [%]	36.4	37.0	37.9	44.6

, by sorting the values in descending order of magnitude and using the notation B1–B4, the author has defined the values for the 10 m wide strip (B1), 2.5 times the flame length (B3), and 2 times the flame length (B4), in addition to the values for the 9 m wide strip (B2). The table also includes the areas, ratios, and percentages of the ellipses of the values given for the effective and loss areas. It can be seen that between the two extreme values (B1 and B4), the part of the original ellipse that can be considered efficient is only between 35 and 43.5 m compared to the original 50 m length, while the increase in length for the converted area is between 20 and 35.1 m, which would result in an increase in efficiency from 57.1 to 80.7%. With these values, it can also be calculated that the effective area of the ellipse is only between 350 and 304.5 m⁻² instead of 550 m⁻², with a loss rate of 200–245.5 m⁻², which represents a loss of 36.4–44.6%.

It is natural that by increasing the axes of the ellipse and reducing the effectively wetted strip, as well as changing their ratios within the ellipse, the length of the effectively wetted rectangle becomes closer and closer to the longitudinal axis, so this type of loss becomes less and less significant. The latter is already evident in the cases of LAT (large air tanker) and VLAT (very large air tanker).

The above takes into account the ellipse or wetted area resulting from the conversion of the ellipse, where the amount of the suppressant reaches the desired value of 2.4 kgm⁻². Due to the identity of the area, the amount of the effectively used suppressant is also the same, i.e., a total of 550 m² × 2.4 kgm⁻² = 1320 kg. This means that for an airplane carrying about 6000 kg of extinguishing agent, less than a quarter of the suppressant, approx. 22%, is used effectively, while more than three-quarters (approx. 78%) can be considered a loss in some form. The difference can be considered a loss because the amount of extinguishing agent per unit area in the wetted area beyond the ellipse does not reach a level sufficient to prevent the fire from spreading.

It should be noted that this utilization rate is only a theoretical possibility since only that part of the elliptical shape formed on the surface after the discharge is accepted as the utilized part where the width of the wetted surface is neither less nor more than required. The values of the losses calculated in this way for the previous nominal strip widths (B1–B4) are shown in

Table 2. Characteristics of the effectiveness of a 550 m² ellipse in the case of 10–9–8.75–7 m (B1–B4) width fire brake.

Characteristics of the 550 m2 Ellipse	B1	B2	B3	B4
Amount of the useful extinguishing material [kg]	840	832	819	731
Amount of the useless extinguishing material [kg]	480	488	501	589
Useless ratio of the extinguishing material in the ellipse [%]	36.4	37.0	37.9	44.6
Useless ratio of the whole amount of the tank [%]	86.0	86.2	86.3	87.8
Useful ratio of the whole amount of tank [%]	14.0	13.8	13.7	12.2

.

According to the above, it can be concluded that the losses are shockingly high, ranging from 36.4% to 44.6% for the ellipsis footprint alone and from 86% to 87.8% for the total amount of extinguishing agent.

At the beginning of the article, it was presented that there are many studies that deal with the effectiveness of aerial firefighting; however, they focus mostly on a better understanding of the release of the extinguishing agent or the problems of burn-through, and none of them deal with calculating or estimating losses. Regarding the losses of the delivered suppressant, the author examined two relevant studies, of which Satoh et al. mention a 60% loss [36], while Pekić states up to 95% [82]. The author did not find any studies that disputed them. The first study explains the losses based on numerical modeling, while the latter examines the drop pattern concentration after the release of the water. On the one hand, the results of this article confirm the high rate of losses, and on the other hand, they highlight a different but easy-to-follow methodology. In addition to being simple and easy to follow, the different methodology has two advantages. On the one hand, by contrasting the losses, we can also say how long the front line could potentially be extinguished with the available suppressant. On the other hand, it also points out how technological development can be used to increase efficiency. According to the author’s view, even if we understand the physics of traditional emissions even better, the efficiency cannot be significantly increased. Instead, researchers should focus on developing a technology that can be used to create a rectangular spray pattern (footprint) on the surface, the parameters of which can be derived from the characteristics of the fireline intensity.

4. Conclusions

This study examined the effectiveness of the presently used aerial firefighting practices, focusing on two key components required to stop a fire: the required surface coverage level and the wetted bandwidth. It can be concluded that present practice creates a footprint on the surface that is neither uniform in shape nor homogeneous in coverage. The footprint depends on a number of factors, e.g., the type of extinguishing agent, the flow rate, or the flight-related parameters (flight speed or altitude). Although systematic research into the study of release and footprint has been observed since the 1950s [83], the efficiency indicators do not appear to have increased drastically since then and are assumed to be a loss of between 60 and 95%.

The footprint used in present practice is very varied; with simplification, it looks like an elliptical shape, which has the problem that in some places the area with the right level of coverage is not wide enough, while in others it is too wide. The ellipsoidal model is also characterized by uneven coverage, with insufficient extinguishing agent in some places and too much in others. Where it is not wide enough, the area will burn through, and it is applied unnecessarily. Where far more suppressant is used than necessary, it is also a loss due to wastage. Since current practice can only produce the elliptical form, this model is considered practically set in stone, even if its losses are obvious.

In this paper, a model is presented in which the shape of the footprint is rectangular. In this model, both the coverage level of the surface and the width of the rectangle are such that present practice considers them to be effective. This is an idealized shape, but it is able to show how present practice works with losses, and it is also good for showing the direction of future improvements.

The article has taken as a basis a coverage of 2.4 kgm⁻², where the bandwidth to be wetted has been defined as 7.5–8–9 and 10 m, due to simplifications required in practice. The calculations show that the losses are shockingly high, ranging from 36.4 to 44.6% for the ellipsoidal footprint alone and from 86% to 87.8% for the total amount of suppressant.

In the future, new research should focus on footprint formation rather than modelling and on understanding the physics of suppressant release. Furthermore, the current research results help to determine the potential extinguishing capability of the delivered suppressant as a function of the parameters of the fire. Although it may seem like a distant future, the use of extinguishing agents adjusted to the parameters of the fire can open the way for the implementation of precision firefighting.