Effect of Surface Reaction on the Distribution Characteristics of Temperature and OH Radicals in Microchannel Combustion
Abstract
1. Introduction
2. Materials and Methods
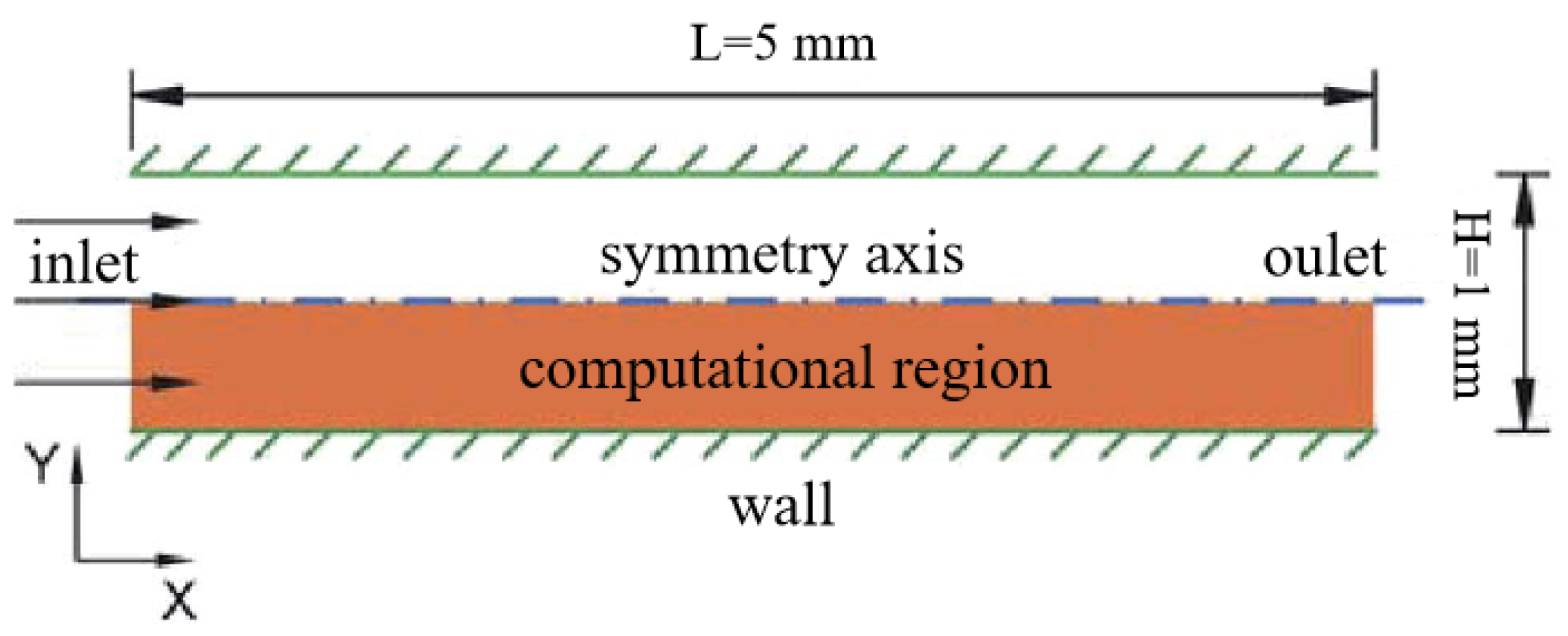
2.1. Physical Model
2.2. Mathematical Model
2.3. Reaction Mechanism
| NO | Reactions | S0 or A (s−1) | β | E (kJ·mol−1) |
|---|---|---|---|---|
| 1 | CH3 + * ⇒ CH3* | 1 | — | — |
| 2 | H + * ⇒ H* | 1 | — | — |
| 3 | O + * ⇒ O* | 1 | — | — |
| 4 | OH + * ⇒ OH* | 1 | — | — |
| 5 | 2CH3* ⇒ C2H6 + 2* | 1013 | 0 | 0 |
| 6 | CH3* + H* ⇒ CH4 + 2* | 1013 | 0 | 0 |
| 7 | 2H* ⇒ H2 + 2* | 1013 | 0 | 0 |
| 8 | 2OH* ⇒ H2O + O* + * | 1013 | 0 | 0 |
| 9 | 2O* ⇒ O2 + 2* | 1013 | 0 | 0 |
| 10 | OH* + H* ⇒ H2O + 2* | 1013 | 0 | 0 |
2.4. Calculation Method
2.5. Method Validation
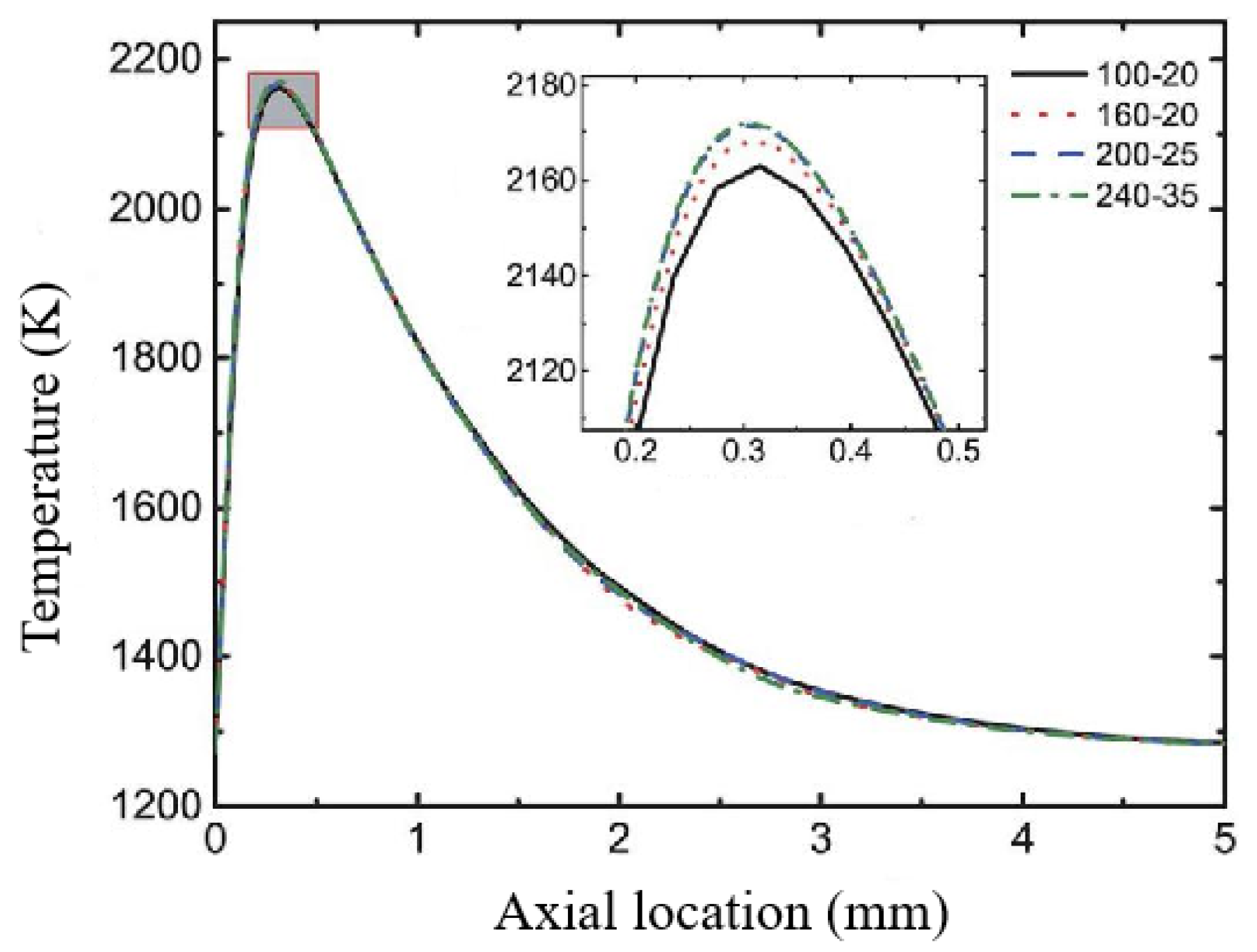
2.5.1. Grid Independence Verification
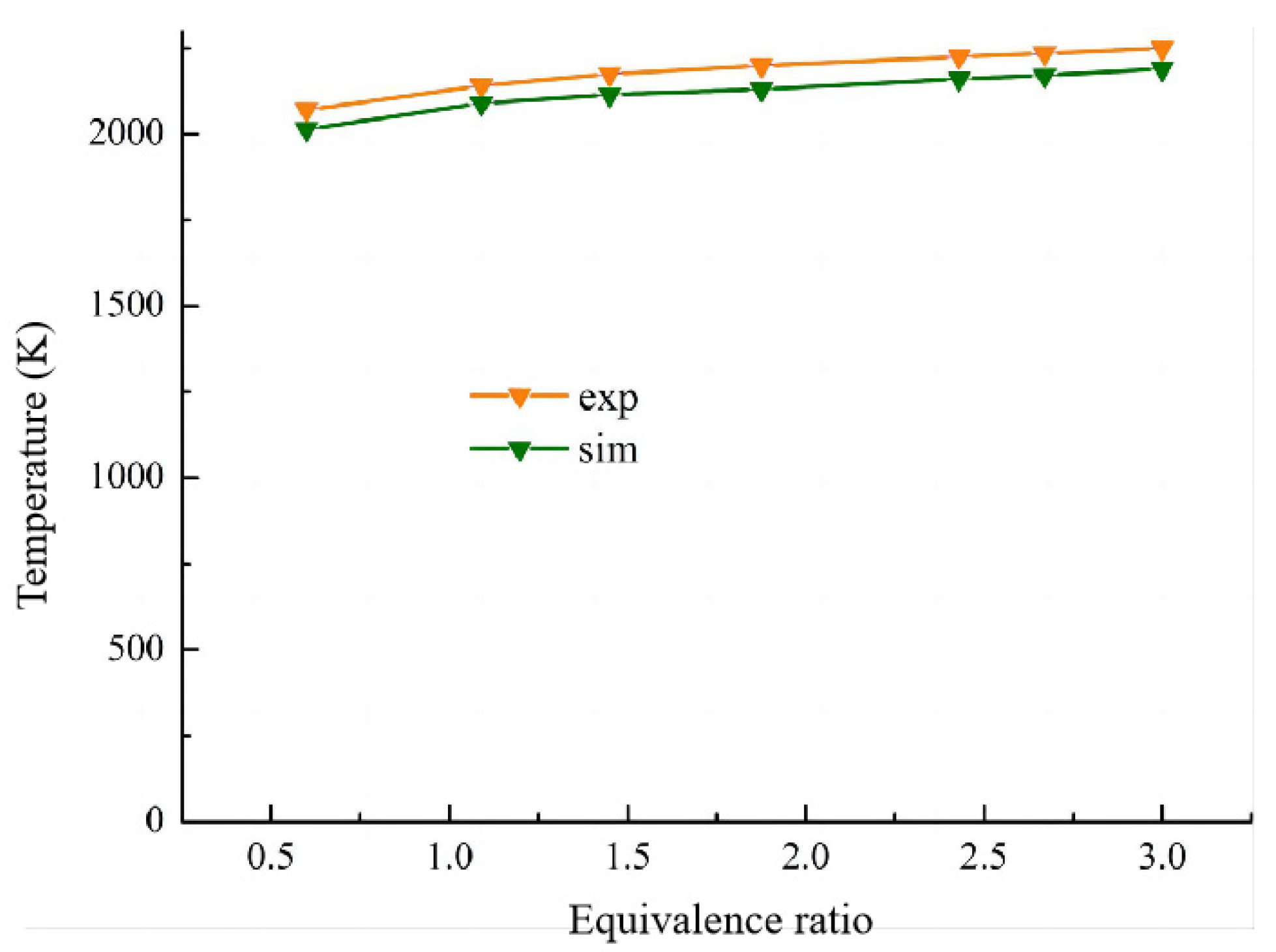
2.5.2. Feasibility Analysis of Calculation Method
3. Result and Discussion
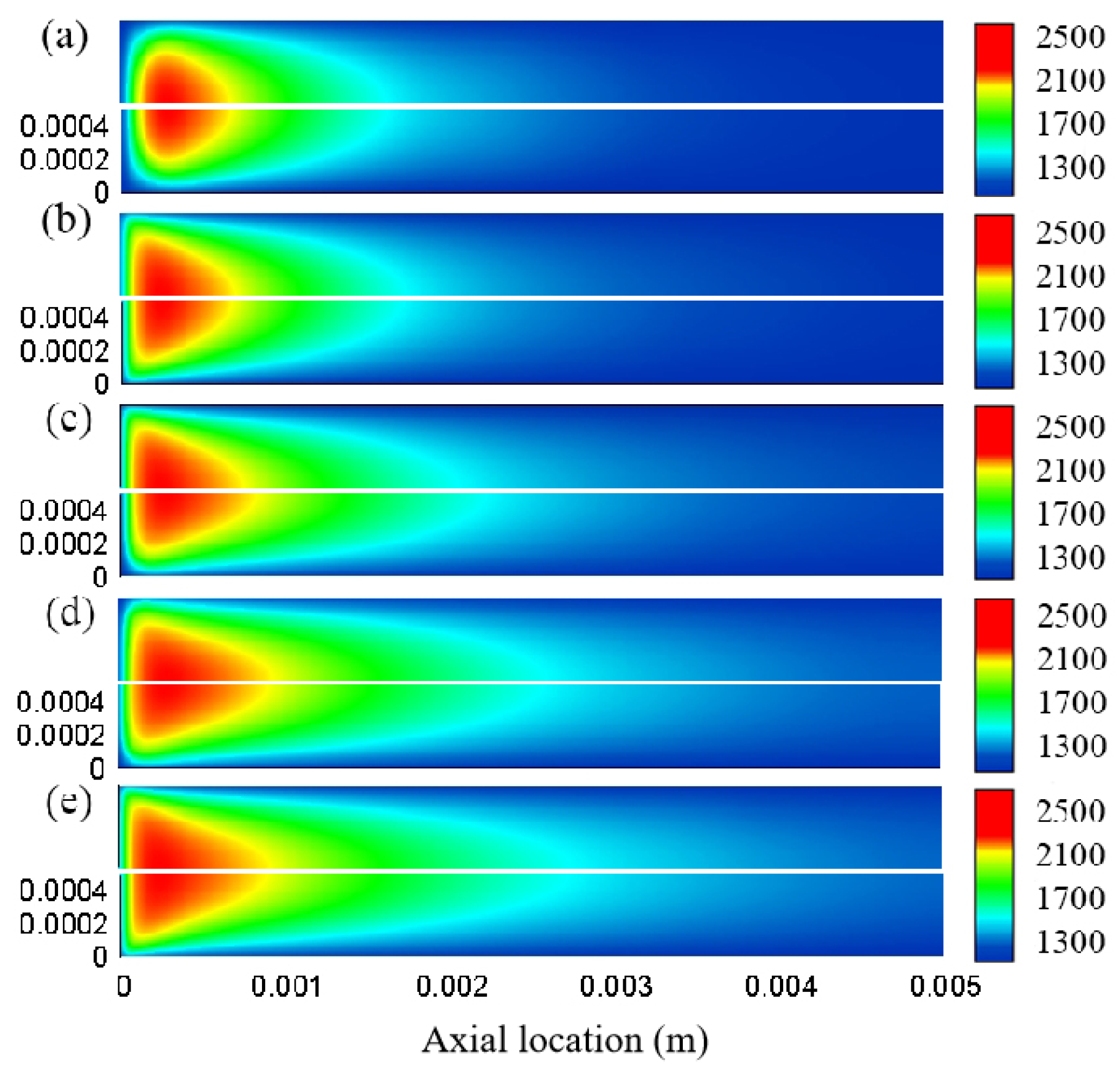
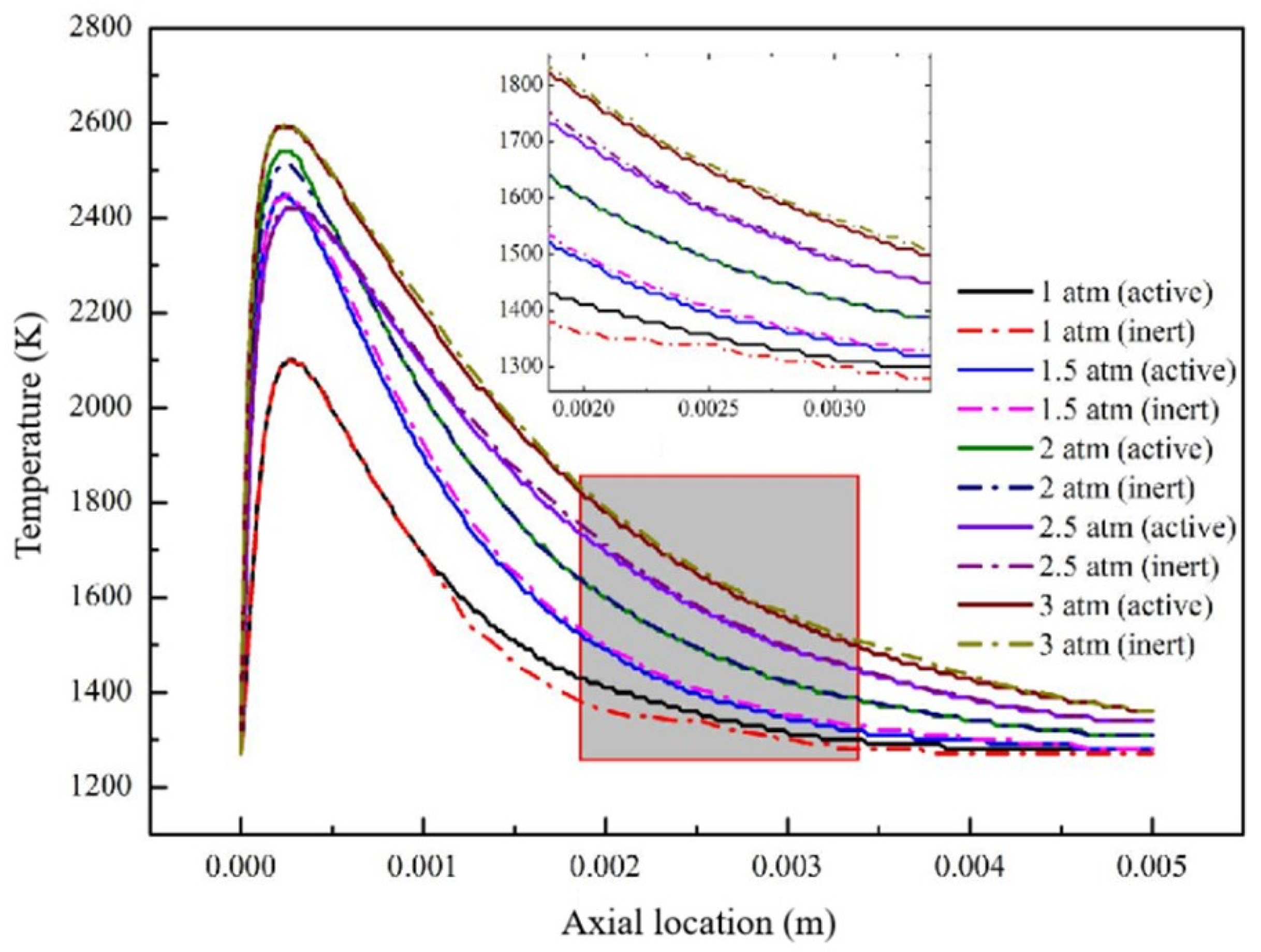
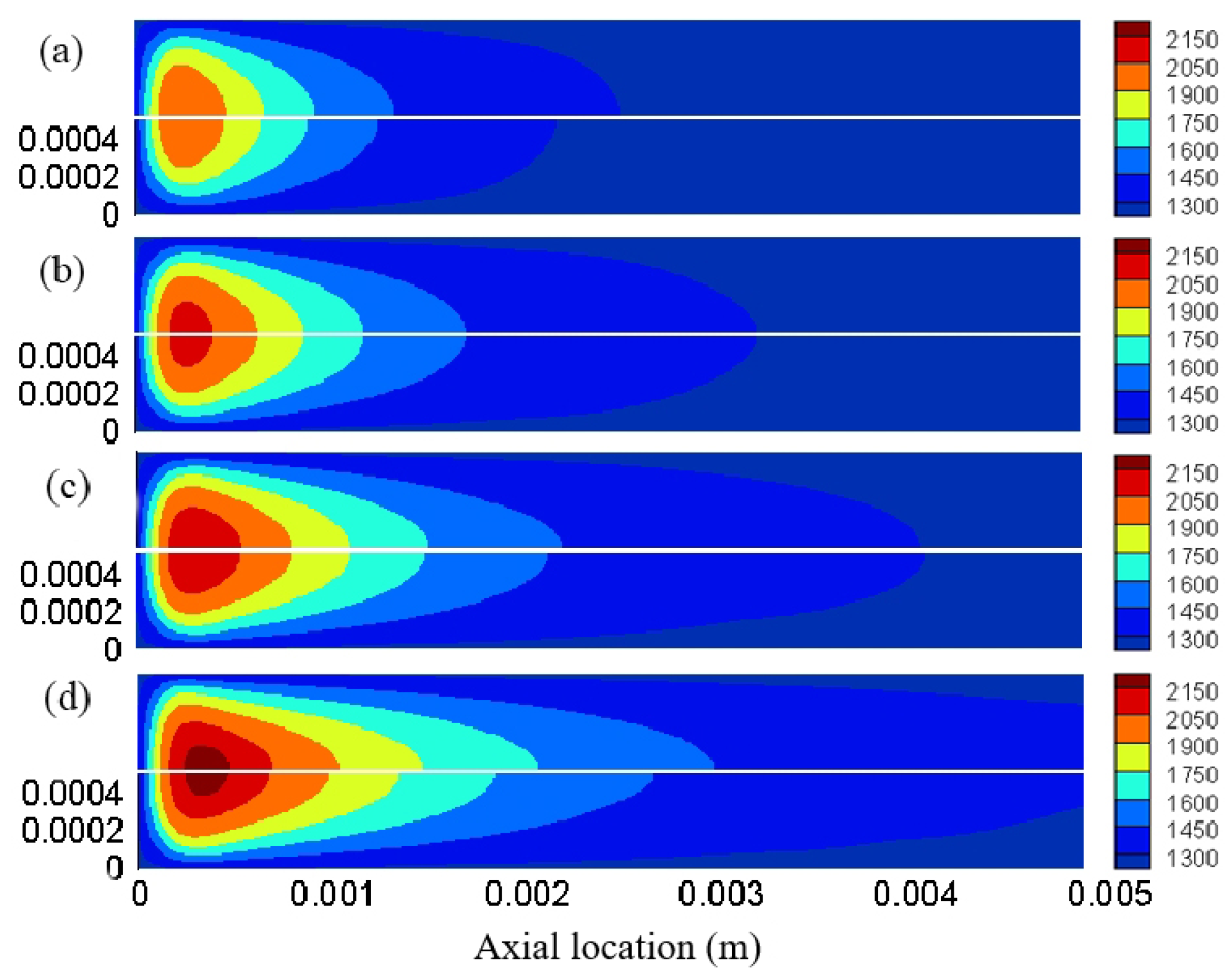
3.1. Effect of Different Reaction Pressures
3.2. Effect of Different Equivalence Ratios
3.3. The Effect of Different Inlet Velocity
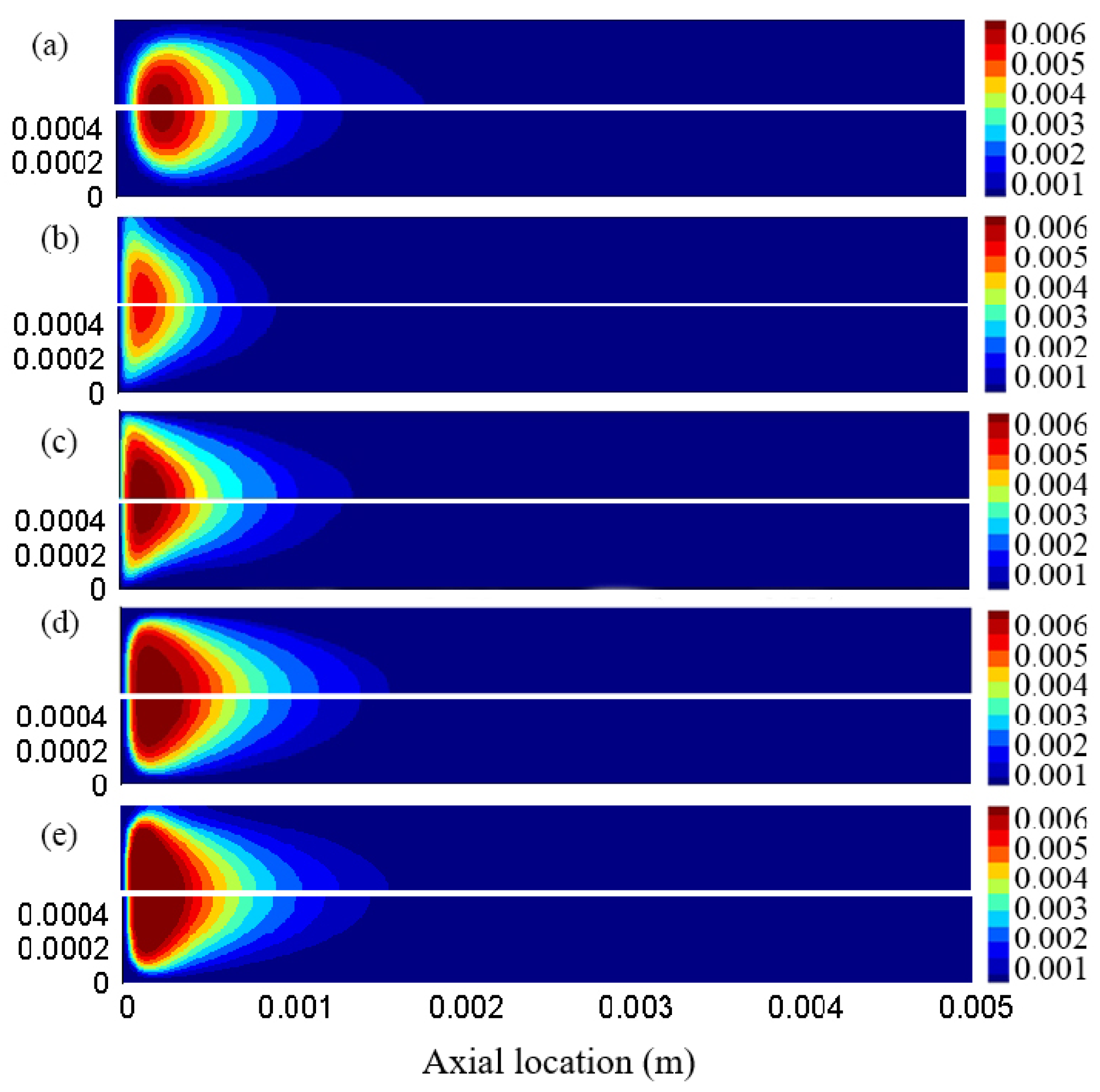
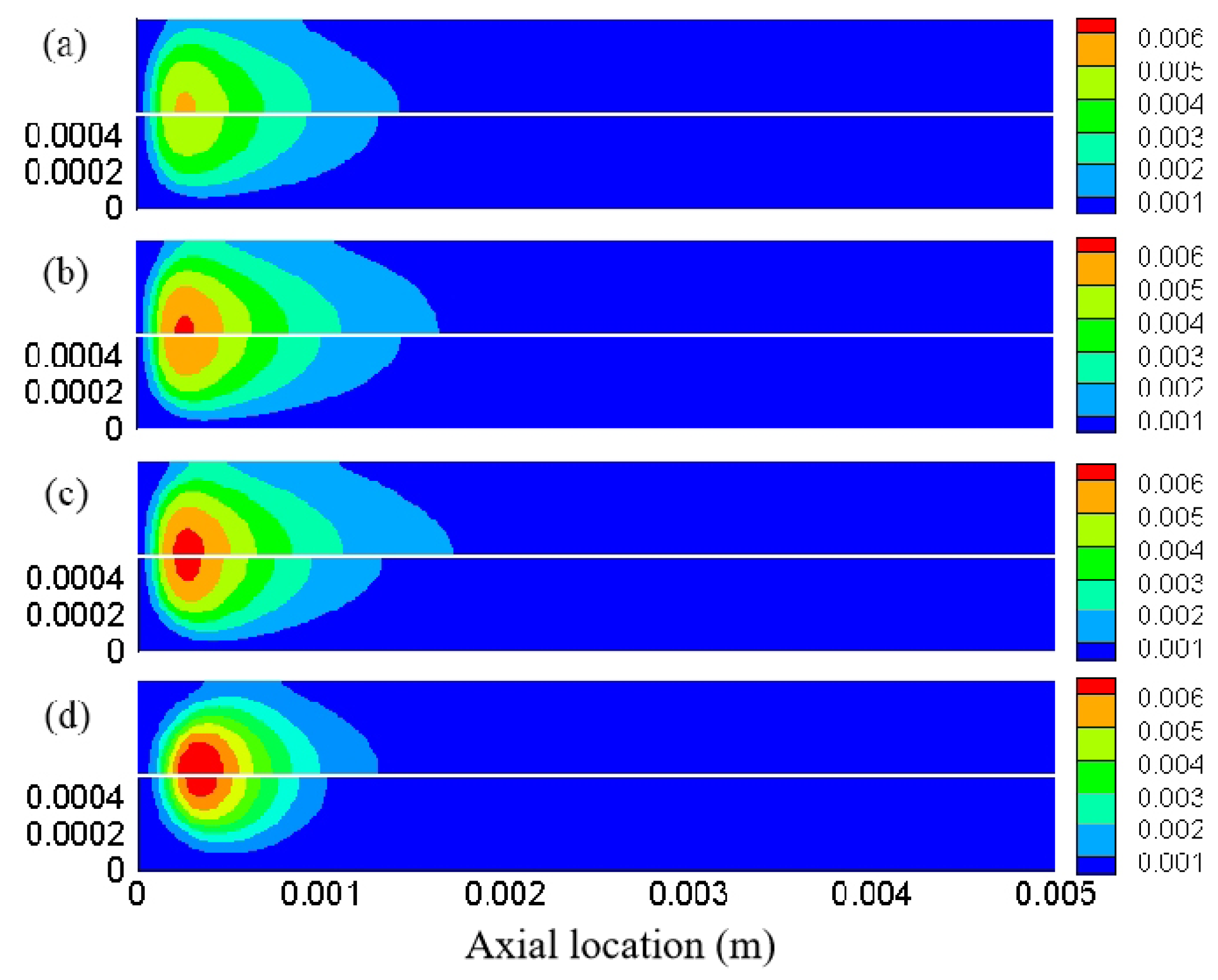
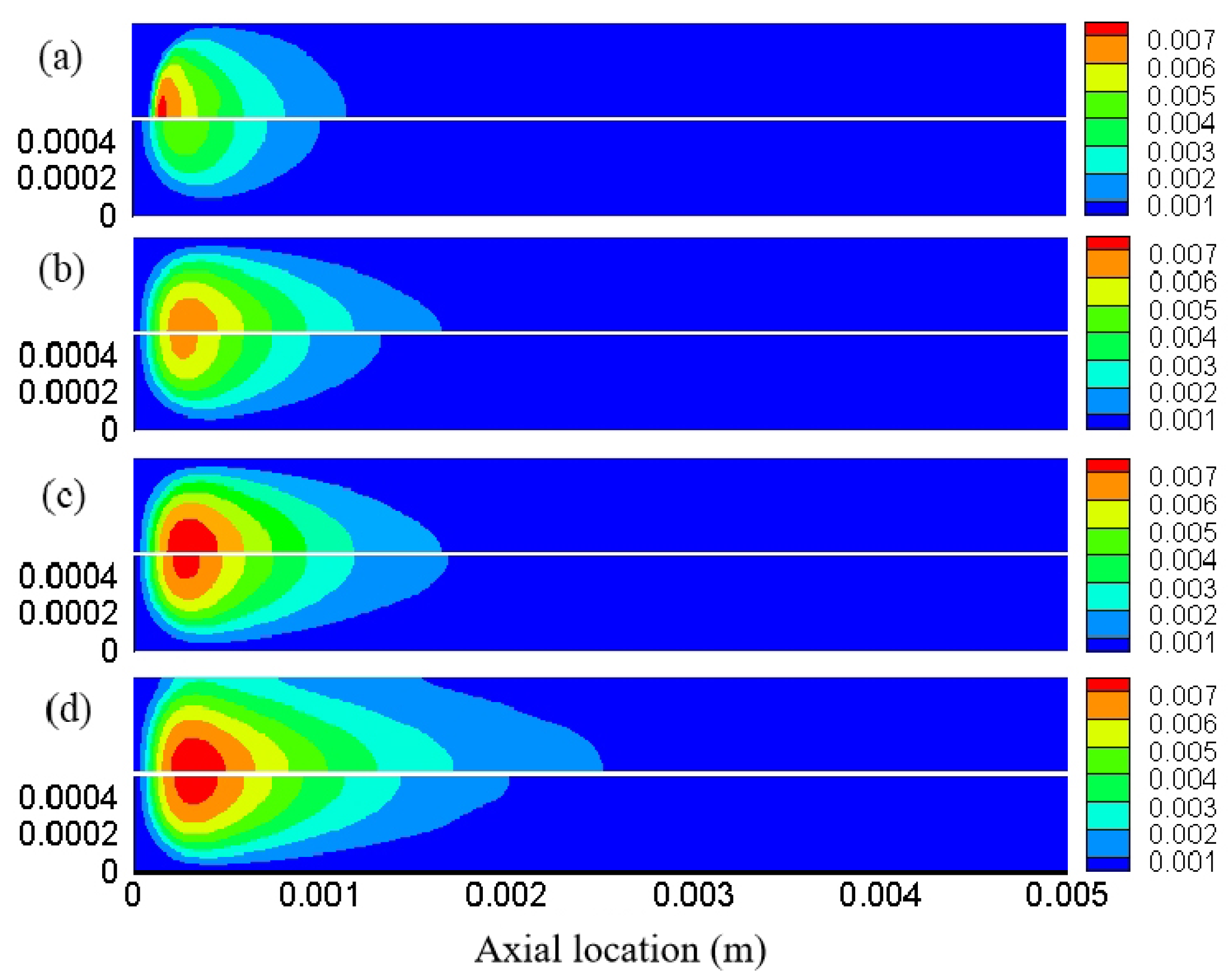
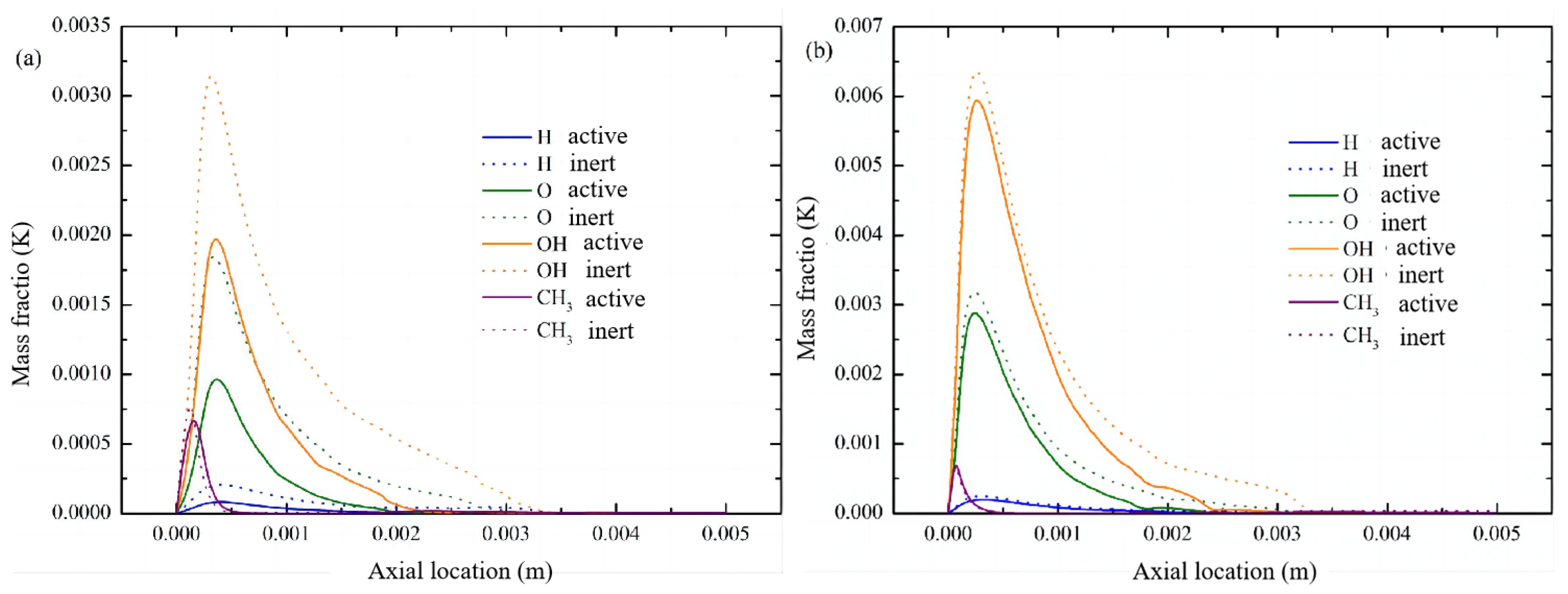
3.4. Distribution Characteristics of Other Free Radicals
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, M.; Hu, T. Research status and development trend of MEMS S&A devices: A review. Def. Technol. 2021, 17, 450–456. [Google Scholar]
- Faudzi AA, M.; Sabzehmeidani, Y.; Suzumori, K. Application of micro-electro-mechanical systems (MEMS) as sensors: A review. J. Robot. Mechatron. 2020, 32, 281–288. [Google Scholar] [CrossRef]
- Bogue, R. Recent developments in MEMS sensors: A review of applications, markets and technologies. Sens. Rev. 2013, 33, 300–304. [Google Scholar] [CrossRef]
- Mahalik, N.P. Principle and applications of MEMS: A review. Int. J. Manuf. Technol. Manag. 2008, 13, 324–343. [Google Scholar] [CrossRef]
- Roos, M.M.; Winkler, A.; Nilsen, M.; Menzel, S.B.; Strehle, S. Towards green 3D-microfabrication of Bio-MEMS devices using ADEX dry film photoresists. Int. J. Precis. Eng. Manuf. Green Technol. 2022, 9, 43–57. [Google Scholar] [CrossRef]
- Baranski, M.; Bargiel, S.; Passilly, N.; Gorecki, C.; Jia, C.; Frömel, J.; Wiemer, M. Micro-optical design of a three-dimensional microlens scanner for vertically integrated micro-opto-electro-mechanical systems. Appl. Opt. 2015, 54, 6924–6934. [Google Scholar] [CrossRef]
- Wang, D.; Xie, H.; Thomas, L.; Koppal, S.J. A miniature LiDAR with a detached MEMS scanner for micro-robotics. IEEE Sens. J. 2021, 21, 21941–21946. [Google Scholar] [CrossRef]
- Zhang, C.; Yan, Y.; Shen, K.; Xue, Z.; You, J.; Wu, Y.; He, Z. Study on synergistic heat transfer enhancement and adaptive control behavior of baffle under sudden change of inlet velocity in a micro combustor. J. Clean. Prod. 2023, 434, 139856. [Google Scholar] [CrossRef]
- He, Z.; Zhang, L.; Li, X.; You, J.; Xue, Z.; Yan, Y. Heat transfer enhancement and pressure loss analysis of hydrogen-fueled microcombustor with slinky projection shape channel for micro-thermophotovoltaic system. Energy 2023, 283, 129119. [Google Scholar] [CrossRef]
- Nakamura, Y.; Gao, J.; Matsuoka, T. Progress in small-scale combustion. J. Therm. Sci. Technol. 2017, 12, 243–256. [Google Scholar] [CrossRef][Green Version]
- Yu, X.; Sandhu, N.S.; Yang, Z.; Zheng, M. Suitability of energy sources for automotive application-A review. Appl. Energy 2020, 271, 115169. [Google Scholar] [CrossRef]
- Forsberg, C. What is the long-term demand for liquid hydrocarbon fuels and feedstocks? Appl. Energy 2023, 341, 121104. [Google Scholar] [CrossRef]
- Zengin, F.; Okumuş, E.; Ateş, M.N.; Tunaboylu, B. Applications and Expectations of Fuel Cells and Lithium Ion Batteries. In Digitizing Production Systems: Selected Papers from ISPR2021, Online, Turkey, 7–9 October 2021; Springer International Publishing: Berlin/Heidelberg, Germany, 2022; pp. 91–106. [Google Scholar]
- Aichlmayr, H.T.; Kittelson, D.B.; Zachariah, M.R. Miniature free-piston homogeneous charge compression ignition engine-compressor concept–Part I: Performance estimation and design considerations unique to small dimensions. Chem. Eng. Sci. 2015, 57, 4161–4171. [Google Scholar] [CrossRef]
- Kim, N.I.; Aizumi, S.; Yokomori, T.; Kato, S.; Fujimori, T.; Maruta, K. Development and scale effects of small Swiss-roll combustors. Proc. Combust. Inst. 2007, 31, 3243–3250. [Google Scholar] [CrossRef]
- Zuo, W.; Wang, Z.; Jiaqiang, E.; Li, Q.; Cheng, Q.; Wu, Y.; Zhou, K. Numerical investigations on the performance of a hydrogen-fueled micro planar combustor with tube outlet for thermophotovoltaic applications. Energy 2023, 263, 125957. [Google Scholar] [CrossRef]
- Zuo, W.; Li, D.; Jiaqiang, E.; Xia, Y.; Li, Q.; Quan, Y.; Zhang, G. Parametric study of cavity on the performance of a hydrogen-fueled micro planar combustor for thermophotovoltaic applications. Energy 2023, 263, 126028. [Google Scholar] [CrossRef]
- Zuo, W.; Chen, Z.; Jiaqiang, E.; Li, Q.; Zhang, G.; Huang, Y. Effects of structure parameters of tube outlet on the performance of a hydrogen-fueled micro planar combustor for thermophotovoltaic applications. Energy 2023, 266, 126434. [Google Scholar] [CrossRef]
- Chen, Z.; Zuo, W.; Zhou, K.; Li, Q.; Yi, Z.; Huang, Y. Numerical investigation on the performance enhancement of PEMFC with gradient sinusoidal-wave fins in cathode channel. Energy 2023, 288, 129894. [Google Scholar] [CrossRef]
- Yue, L.; Li, G.; He, G.; Guo, Y.; Xu, L.; Fang, W. Impacts of hydrogen to carbon ratio (H/C) on fundamental properties and supercritical cracking performance of hydrocarbon fuels. Chem. Eng. J. 2016, 283, 1216–1223. [Google Scholar] [CrossRef]
- Feng, Y.; Qin, J.; Zhang, S.; Bao, W.; Cao, Y.; Huang, H. Modeling and analysis of heat and mass transfers of supercritical hydrocarbon fuel with pyrolysis in mini-channel. Int. J. Heat Mass Transf. 2015, 91, 520–531. [Google Scholar] [CrossRef]
- Ju, Y.; Maruta, K. Microscale combustion: Technology development and fundamental research. Prog. Energy Combust. Sci. 2011, 37, 669–715. [Google Scholar] [CrossRef]
- You, J.; Xue, Z.; He, Z.; Yan, Y.; Zhang, Z. Hydrogel use in burn therapy, thermal management, wastewater treatment and fire fighting: A review. Environ. Chem. Lett. 2023, 21, 3273–3328. [Google Scholar] [CrossRef]
- Yang, X.; Li, S.; Yu, B.; Lyu, F.; Ma, X. Improving the thermophotovoltaic performance of a hydrogen-fueled planar combustor with four-corner inlets via partially inserting porous medium. Fuel 2023, 339, 126926. [Google Scholar] [CrossRef]
- Thapa, S.; Borquist, E.; Baniya, A.; Weiss, L. Experimental and computational investigation of a MEMS-based boiler for waste heat recovery. Energy Convers. Manag. 2015, 100, 403–413. [Google Scholar] [CrossRef]
- Mathew, B.; Jakub-Wood, B.; Ogbonnaya, E.; Weiss, L. Investigation of a MEMS-based capillary heat exchanger for thermal harvesting. Int. J. Heat Mass Transf. 2013, 58, 492–502. [Google Scholar] [CrossRef]
- Yang, M.; Li, C.; Tang, Y.; Wu, W.; Zhang, X. A collaborative resequencing approach enabled by multi-core PREA for a multi-stage automotive flow shop. Expert Syst. Appl. 2024, 237, 121825. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, J.; Lu, Q.; Wang, Y.; Li, J.; Quaye, E.K.; Weng, J. Numerical investigation on the self-ignition and combustion characteristics of H2/air in catalytic micro channel. Int. J. Hydrogen Energy 2022, 47, 1965–1978. [Google Scholar] [CrossRef]
- Raimondeau, S.; Norton, D.; Vlachos, D.G.; Masel, R.I. Modeling of high-temperature microburners. Proc. Combust. Inst. 2002, 29, 901–907. [Google Scholar] [CrossRef]
- Peng, Q.; Yang, W.; Jiaqiang, E.; Li, S.; Li, Z.; Xu, H.; Fu, G. Effects of propane addition and burner scale on the combustion characteristics and working performance. Appl. Energy 2021, 285, 116484. [Google Scholar] [CrossRef]
- Maruta, K.; Kataoka, T.; Kim, N.I.; Minaev, S.; Fursenko, R. Characteristics of combustion in a narrow channel with a temperature gradient. Proc. Combust. Inst. 2005, 30, 2429–2436. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, Q.; Fan, B.; Long, L.; Quaye, E.K.; Pan, J. Effect of multiple bluff bodies on hydrogen/air combustion characteristics and thermal properties in micro combustor. Int. J. Hydrogen Energy 2023, 48, 4064–4072. [Google Scholar] [CrossRef]
- Kamada, T.; Nakamura, H.; Tezuka, T.; Hasegawa, S.; Maruta, K. Study on combustion and ignition characteristics of natural gas components in a micro flow reactor with a controlled temperature profile. Combust. Flame 2014, 161, 37–48. [Google Scholar] [CrossRef]
- Jiaqiang, E.; Luo, B.; Han, D.; Chen, J.; Liao, G.; Zhang, F.; Ding, J. A comprehensive review on performance improvement of micro energy mechanical system: Heat transfer, micro combustion and energy conversion. Energy 2022, 239, 122509. [Google Scholar]
- Pan, J.; Zhang, C.; Pan, Z.; Wu, D.; Zhu, Y.; Lu, Q.; Zhang, Y. Investigation on the effect of bluff body ball on the combustion characteristics for methane/oxygen in micro combustor. Energy 2020, 190, 116465. [Google Scholar] [CrossRef]
- Okuno, T.; Nakamura, H.; Tezuka, T.; Hasegawa, S.; Maruta, K. Ultra-lean combustion characteristics of premixed methane flames in a micro flow reactor with a controlled temperature profile. Proc. Combust. Inst. 2017, 36, 4227–4233. [Google Scholar] [CrossRef]
- Guo, L.; Zhai, M.; Xu, S.; Shen, Q.; Dong, P.; Bai, X.S. Flame characteristics of methane/air with hydrogen addition in the micro confined combustion space. Int. J. Hydrogen Energy 2022, 47, 19319–19337. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, J.; Wang, J.; Lu, Q.; Zhang, Y.; Quaye, E.K. Study on repetitive extinction-ignition characteristics of methane/oxygen combustion in micro tube combustor. Fuel 2023, 334, 126597. [Google Scholar] [CrossRef]
- Baigmohammadi, M.; Sadeghi, S.S.; Tabejamaat, S.; Zarvandi, J. Numerical study of the effects of wire insertion on CH4 (methane)/AIR pre-mixed flame in a micro combustor. Energy 2013, 54, 271–284. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, Y.; Wu, F.; Bai, J. Study on the combustion characteristics and ignition limits of the methane homogeneous charge compression ignition with hydrogen addition in micro-power devices. Fuel 2019, 236, 354–364. [Google Scholar] [CrossRef]
- Kim, K.T.; Lee, D.H.; Kwon, S. Effects of thermal and chemical surface-flame interaction on flame quenching. Combust. Flame 2006, 146, 19–28. [Google Scholar] [CrossRef]
- Fan, Y.; Suzuki, Y.; Kasagi, N. Experimental study of micro-scale premixed flame in quartz channels. Proc. Combust. Inst. 2009, 32, 3083–3090. [Google Scholar] [CrossRef]
- Fan, Y.; Suzuki, Y.; Kasagi, N. Quenching mechanism study of oscillating flame in micro channels using phase-locked OH-PLIF. Proc. Combust. Inst. 2011, 33, 3267–3273. [Google Scholar] [CrossRef]
- Fan, Y.; Suzuki, Y.; Kasagi, N. Flame Propagation and Quenching in Ultra-Thin Quartz Combustors. In Proceedings of the 7th International Workshop on Micro and Nanotechnology for Power Generation and Energy Conversion Applications (PowerMEMS 2007), Freiburg, Germany, 28–29 November 2007. [Google Scholar]
- Fan, Y.; Lin, W.; Wan, S.; Suzuki, Y. Investigation of wall chemical effect using PLIF measurement of OH radical generated by pulsed electric discharge. Combust. Flame 2018, 196, 255–264. [Google Scholar] [CrossRef]
- Johe, P.; Zentgraf, F.; Greifenstein, M.; Steinhausen, M.; Hasse, C.; Dreizler, A. Characterization of flow field and combustion dynamics in a novel pressurized side-wall quenching burner using high-speed PIV/OH-PLIF measurements. Int. J. Heat Fluid Flow 2022, 94, 108921. [Google Scholar] [CrossRef]
- Prakash, S.; Glumac, N.G.; Shankar, N.; Shannon, M.A. OH concentration profiles over alumina, quartz, and platinum surfaces using laser-induced fluorescence spectroscopy in low-pressure hydrogen/oxygen flames. Combust. Sci. Technol. 2005, 177, 793–817. [Google Scholar] [CrossRef]
- Davis, M.B.; Pawson, M.D.; Veser, G.; Schmidt, L.D. Methane oxidation over noble metal gauzes: An LIF study. Combust. Flame 2000, 123, 159–174. [Google Scholar] [CrossRef]
- Vlachos, D.G.; Schmidt, L.D.; Aris, R. Ignition and extinction of flames near surfaces: Combustion of CH4 in air. AIChE J. 1994, 40, 1005–1017. [Google Scholar] [CrossRef]
- Saiki, Y.; Suzuki, Y. Effect of wall surface reaction on a methane-air premixed flame in narrow channels with different wall materials. Proc. Combust. Inst. 2013, 34, 3395–3402. [Google Scholar] [CrossRef]
- Jens, K.N.; Studt, F.; Abild-Pedersen, F.; Bligaard, T. Fundamental Concepts in Heterogeneous Catalysis; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Kuo, C.H.; Ronney, P.D. Numerical modeling of non-adiabatic heat-recirculating combustors. Proc. Combust. Inst. 2007, 31, 3277–3284. [Google Scholar] [CrossRef]
- Chen, P.; Sun, Y.; Li, Y.; Luo, G. Experimental and LES investigation of premixed methane/air flame propagating in an obstructed chamber with two slits. J. Loss Prev. Process Ind. 2017, 49, 711–721. [Google Scholar] [CrossRef]
- Tingas, E.A.; Wang, Z.; Sarathy, S.M.; Im, H.G.; Goussis, D.A. Chemical kinetic insights into the ignition dynamics of n-hexane. Combust. Flame 2018, 188, 28–40. [Google Scholar] [CrossRef]
- Guan, L.; Tang, C.; Yang, K.; Mo, J.; Huang, Z. Experimental and kinetic study on ignition delay times of di-n-butyl ether at high temperatures. Energy Fuels 2014, 28, 5489–5496. [Google Scholar] [CrossRef]
- Wu, R.; Beutler, J.; Price, C.; Baxter, L.L. Biomass char particle surface area and porosity dynamics during gasification. Fuel 2020, 264, 116833. [Google Scholar] [CrossRef]
- Badawy, T.; Hamza, M.; Mansour, M.S.; Elbaz, A.M.; Turner, J.W.; Fayad, M.A.; Wang, C. Flame stability and equivalence ratio assessment of turbulent partially premixed flames. Fuel 2022, 326, 125107. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, J.; Tang, A.; Lu, Q.; Zha, Z.; Bani, S. Effects of inlet parameters on combustion characteristics of premixed CH4/Air in micro channels. J. Energy Inst. 2019, 92, 824–834. [Google Scholar] [CrossRef]
- Zhou, B.; Yang, S.; Jiang, X.; Cai, J.; Xu, Q.; Song, W.; Zhou, Q. The reaction of free radicals and functional groups during coal oxidation at low temperature under different oxygen concentrations. Process Saf. Environ. Prot. 2021, 150, 148–156. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Kang, D.; Zhang, L.; Chen, J.; Huang, S.; Zou, Q.; He, Z. Effect of Surface Reaction on the Distribution Characteristics of Temperature and OH Radicals in Microchannel Combustion. Fire 2024, 7, 71. https://doi.org/10.3390/fire7030071
Li X, Kang D, Zhang L, Chen J, Huang S, Zou Q, He Z. Effect of Surface Reaction on the Distribution Characteristics of Temperature and OH Radicals in Microchannel Combustion. Fire. 2024; 7(3):71. https://doi.org/10.3390/fire7030071
Chicago/Turabian StyleLi, Xiuquan, Dugang Kang, Lei Zhang, Jie Chen, Song Huang, Qunfeng Zou, and Ziqiang He. 2024. "Effect of Surface Reaction on the Distribution Characteristics of Temperature and OH Radicals in Microchannel Combustion" Fire 7, no. 3: 71. https://doi.org/10.3390/fire7030071
APA StyleLi, X., Kang, D., Zhang, L., Chen, J., Huang, S., Zou, Q., & He, Z. (2024). Effect of Surface Reaction on the Distribution Characteristics of Temperature and OH Radicals in Microchannel Combustion. Fire, 7(3), 71. https://doi.org/10.3390/fire7030071












