The Influence of Confined Space Size on the Temperature Distribution Characteristics of Internal Window Plume from Well-Ventilated Compartment Fires
Abstract
1. Introduction
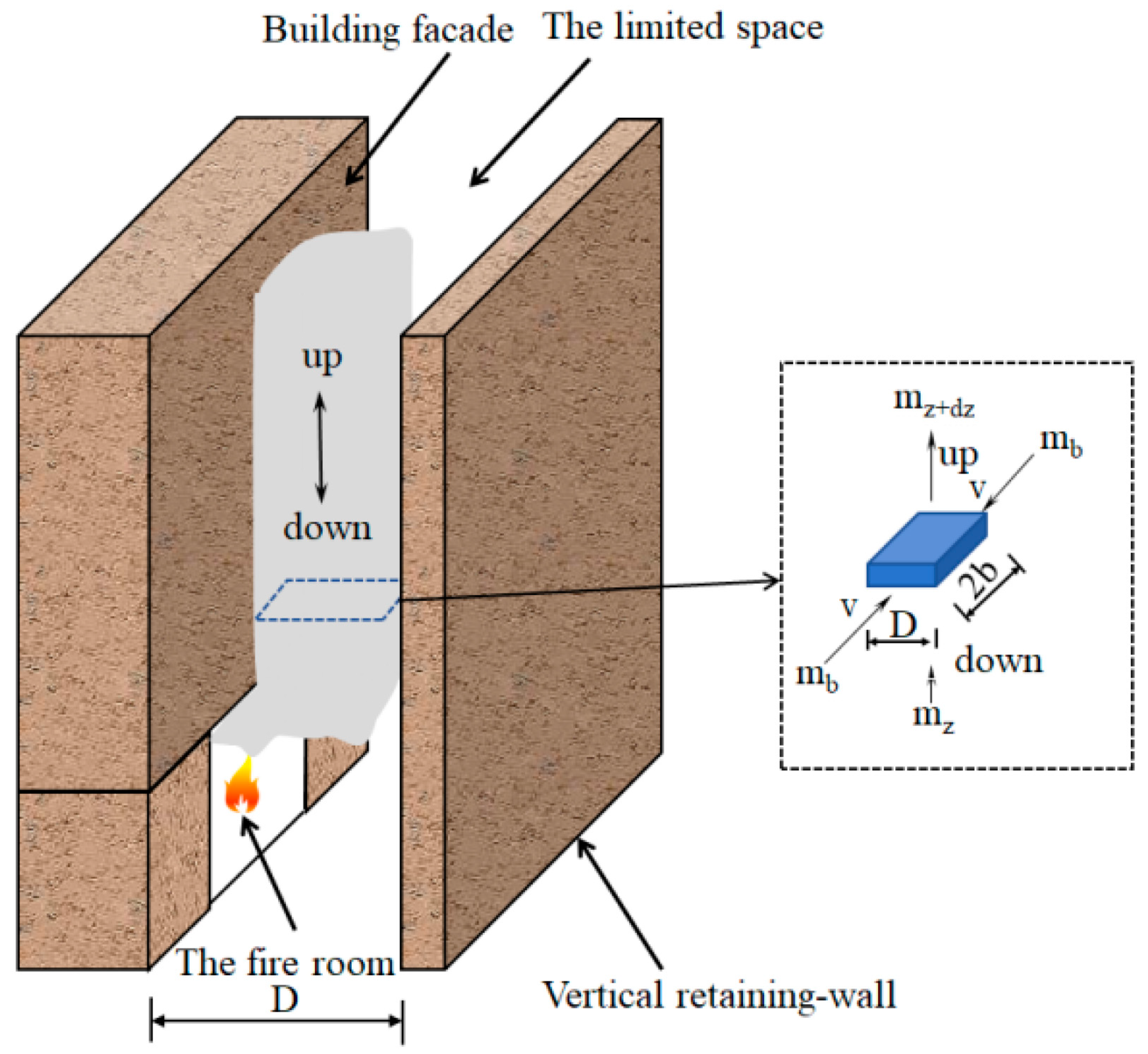
2. Theoretical Analysis
3. Experiments
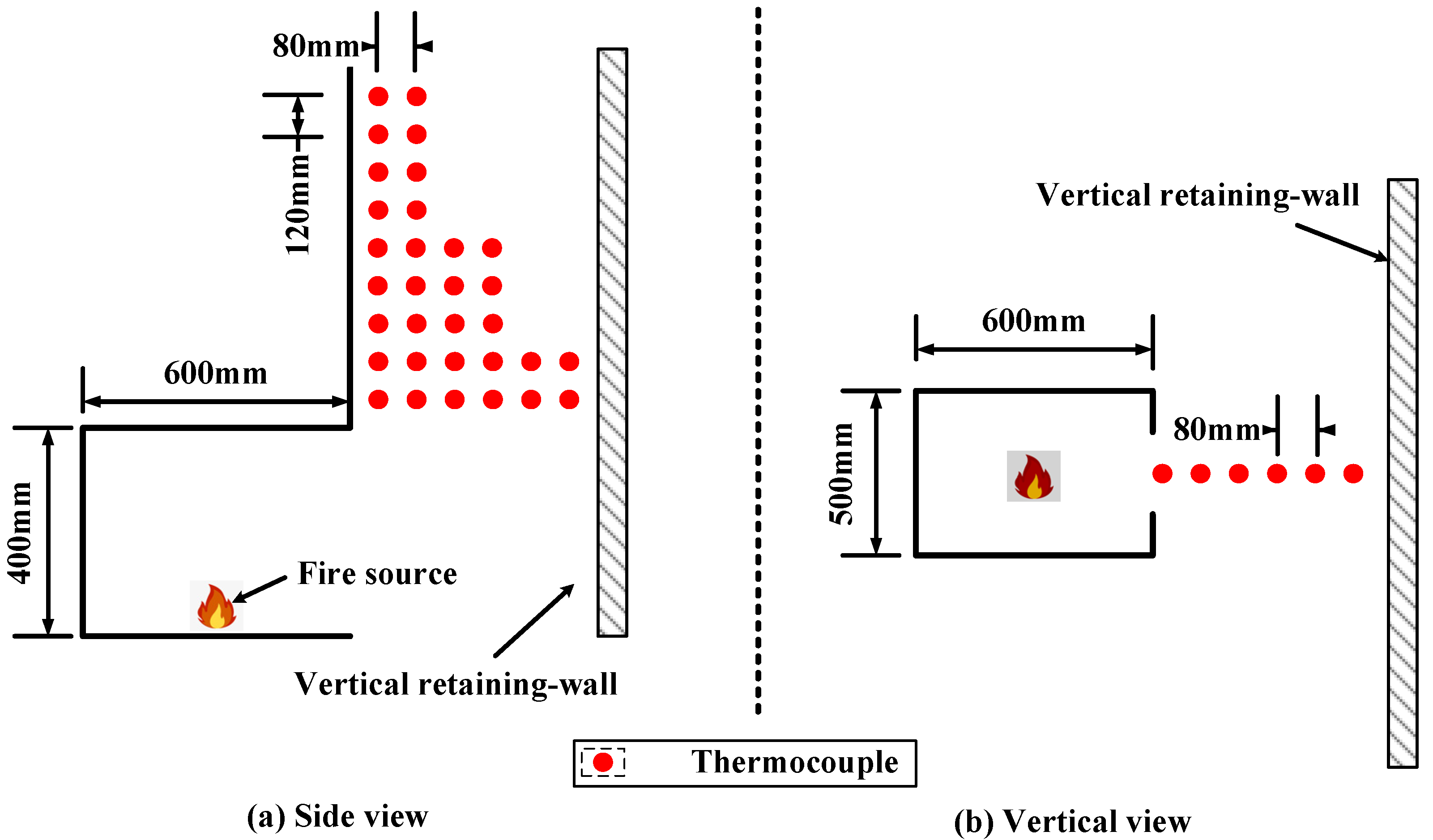
3.1. Experimental Setup
3.2. Experimental Results
4. Numerical Simulation
4.1. Fire Scenarios
4.2. Grid Analysis
4.3. Validation of Modelling
5. Results
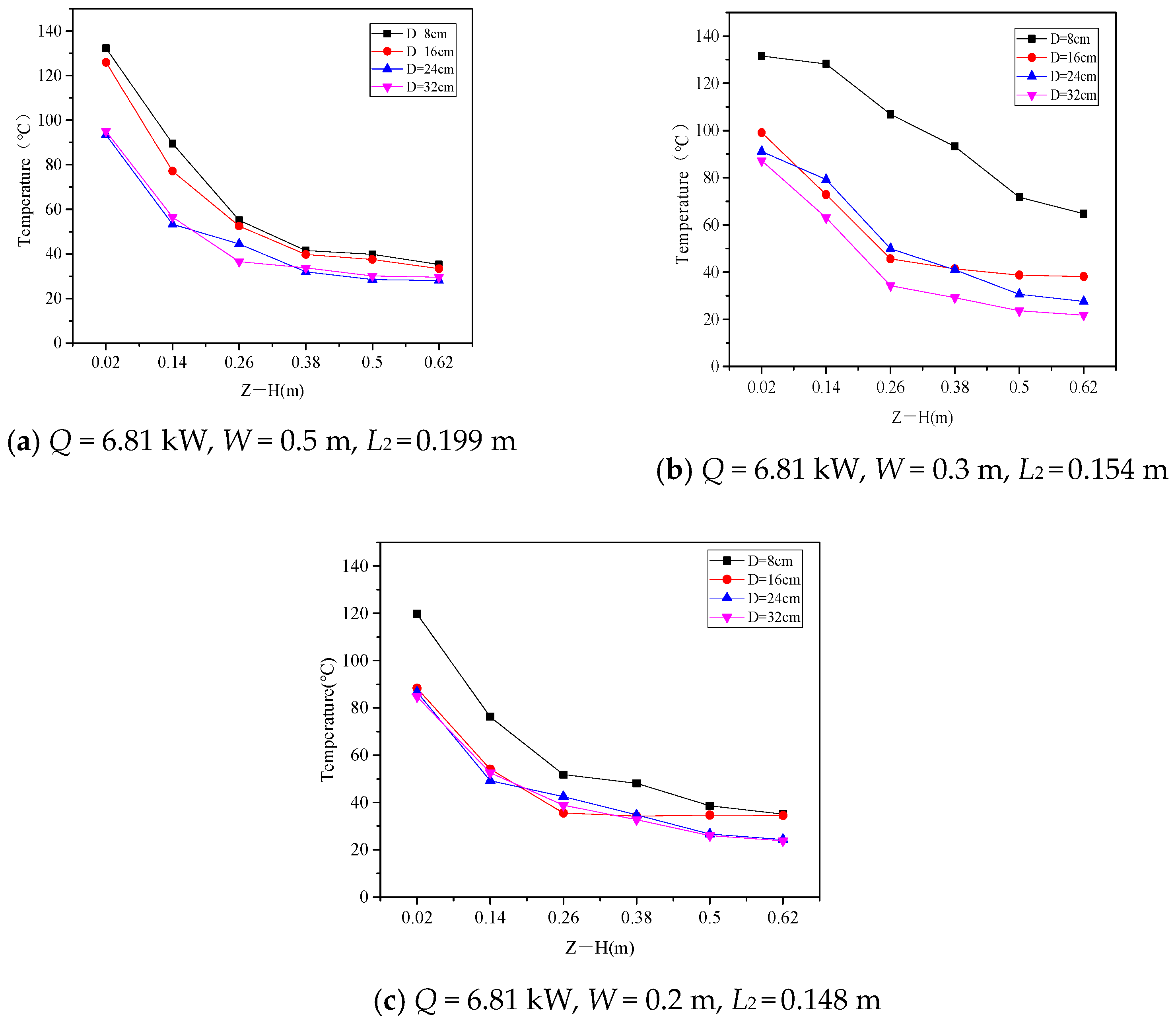
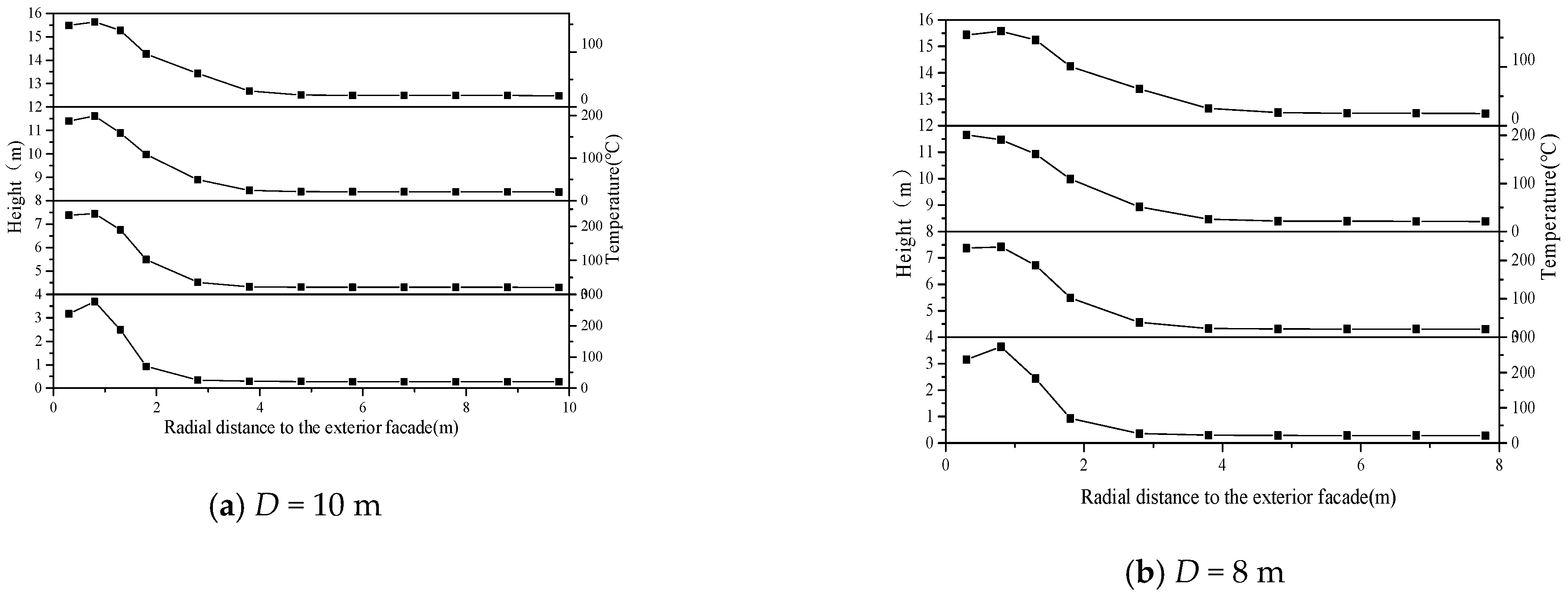
5.1. Radial (Perpendicular to the Building Facade) Temperature Distribution
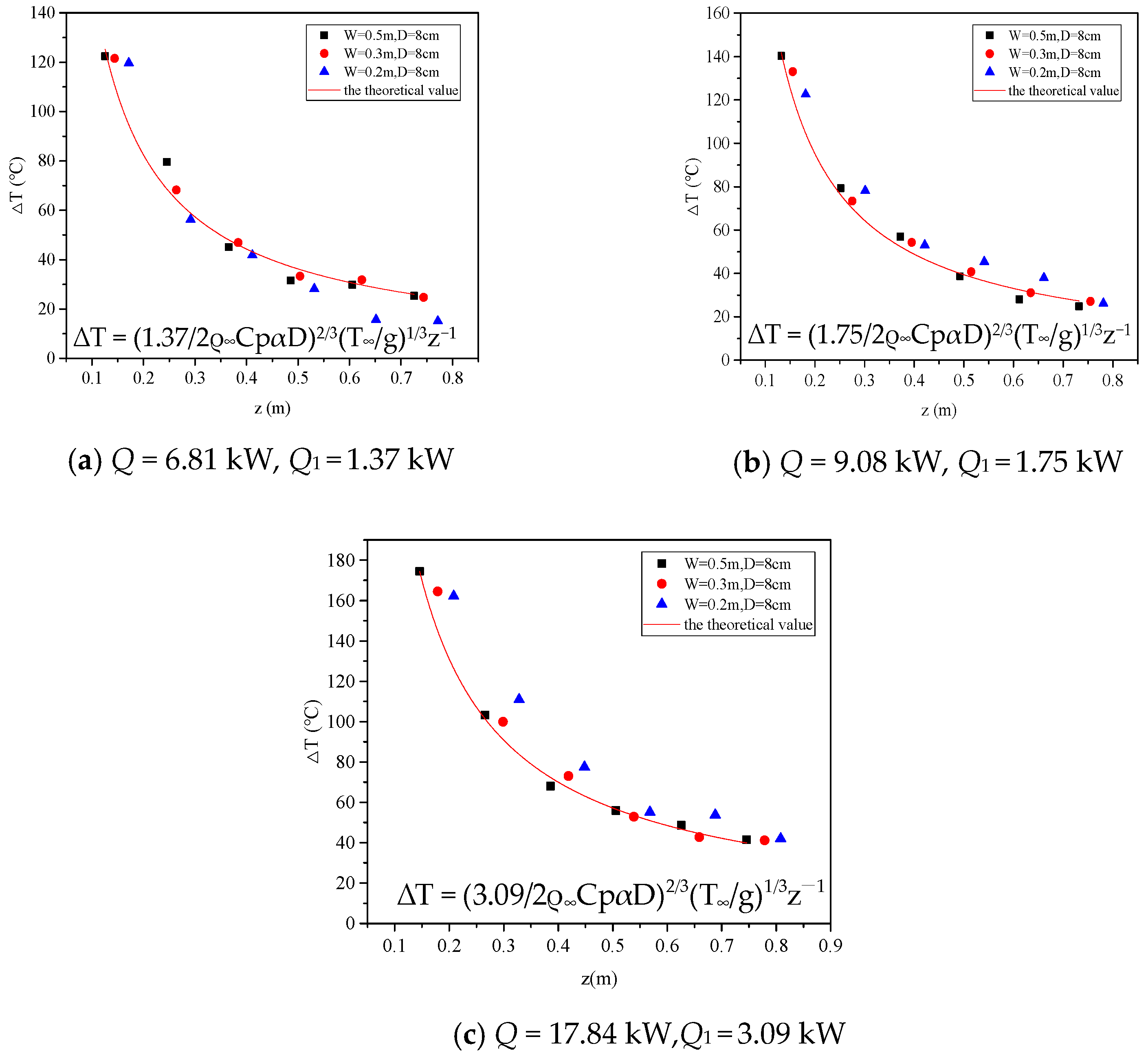
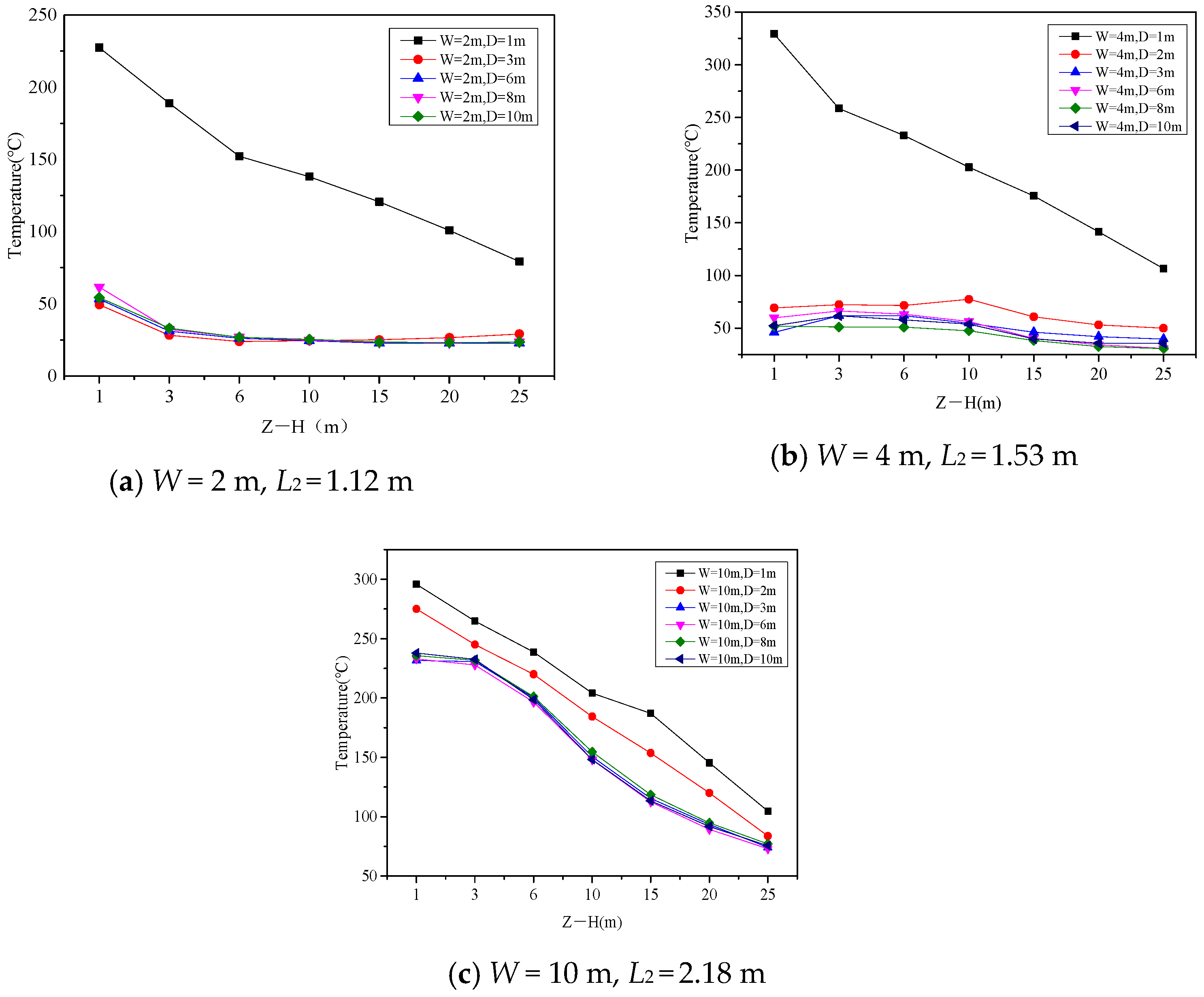
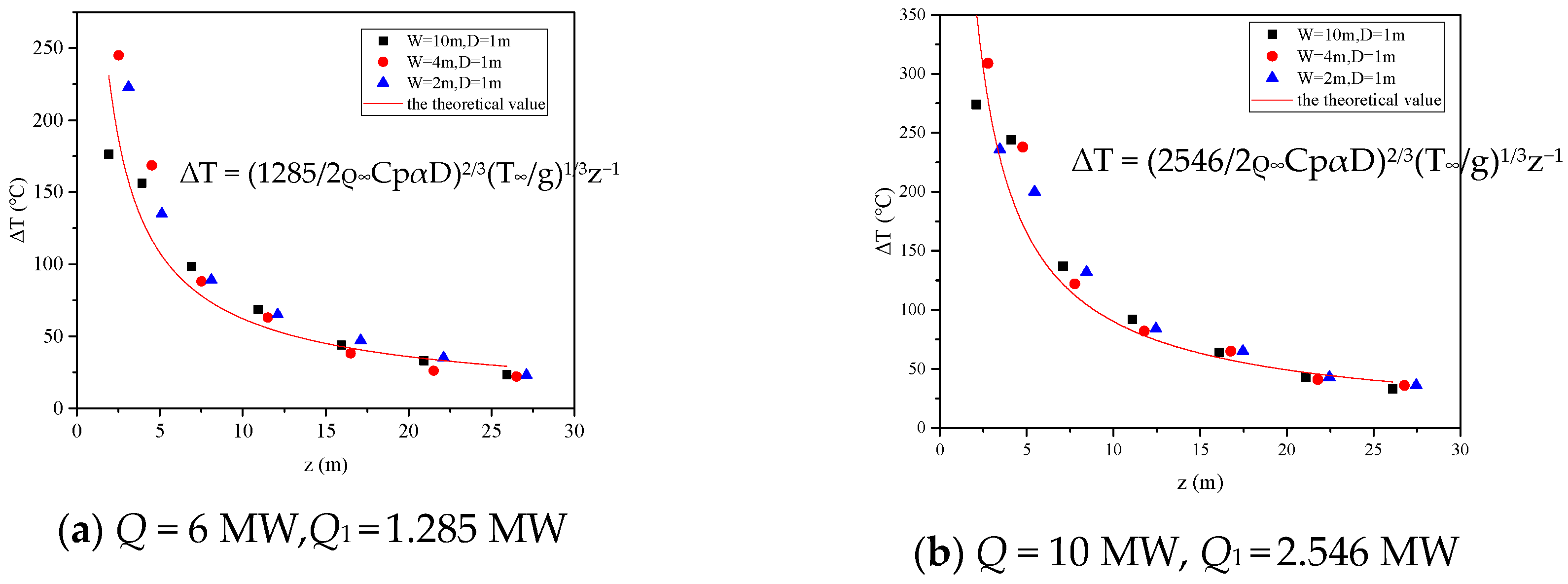
5.2. Vertical Temperature Distribution
6. Conclusions and Discussion
- There is also a critical distance L2 in confined spaces under well-ventilated compartment fires, which can provide a basis for the width of confined spaces. When the distance D is greater than L2, the radial temperature inside the confined space can approximate a Gaussian distribution. As the distance D decreases, the radial temperature change of the plume is not significant, and the temperature increase at each point is relatively slow. When D is less than L2, the radial temperature distribution inside the confined space will tend to be consistent, and the temperature at each point in the confined space will sharply increase as D decreases.
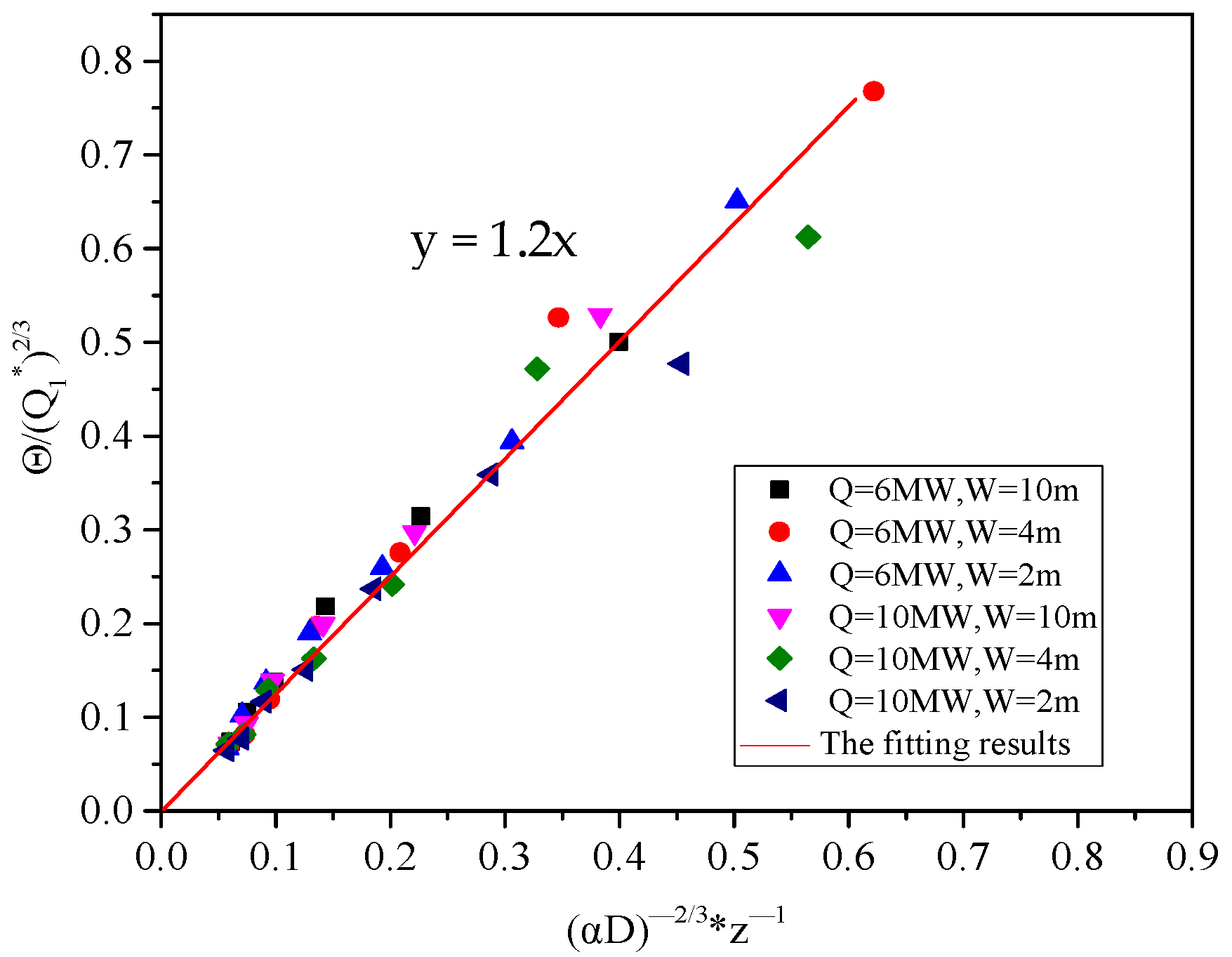
- When the distance D is less than L2, based on the internal ignition source plume model of the confined space, the relationship between dimensionless temperature rise and vertical height can be obtained. The acquisition of this relationship can provide guidance for determining the vertical spread of similar building fire hazards.
- The above conclusion can provide a basis for the fire prevention design of glass curtain wall buildings and narrow street valleys. However, this paper did not consider the influence of the location of the fire source in the room on the temperature distribution characteristics of the internal window plume in the confined space. Further research can be conducted on the impact of the fire source location on the subsequent window plume in larger office buildings.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ding, Y.; Zhang, Y.; Huang, X. Intelligent emergency digital twin system for monitoring building fire evacuation. J. Build. Eng. 2023, 77, 107416. [Google Scholar] [CrossRef]
- Garcia-Castillo, E.; Paya-Zaforteza, I.; Hospitaler, A. Fire in heritage and historic buildings, a major challenge for the 21st century. Dev. Built. Environ. 2023, 13, 100102. [Google Scholar] [CrossRef]
- Omar, M.; Mahmoud, A.; Aziz, S.B.A. Fire safety index for high-rise buildings in the Emirate of Sharjah, UAE. Fire 2023, 6, 51. [Google Scholar] [CrossRef]
- Ma, Y.; Hu, L.; Huang, Y.; Zhua, N.; Fujita, O. Effect of sample thickness on concurrent steady spread behavior of floor- and ceiling flames. Combust. Flame 2021, 233, 111600. [Google Scholar] [CrossRef]
- Sun, X.; Hu, L.; Zhang, X.; Yang, Y.; Ren, F.; Fang, X.; Wang, K.; Lu, H. Temperature evolution and external flame height through the opening of fire compartment: Scale effect on heat/mass transfer and revisited models. Int. J. Therm. Sci. 2021, 164, 106849. [Google Scholar] [CrossRef]
- Sun, X.; Hu, L.; Zhang, X.; Yang, Y.; Ren, F.; Fang, X.; Wang, K. Experimental study of flame extinction with fuel diffusion combustion inside a wall-opening compartment under reduced ventilation conditions. Fuel 2021, 289, 119781. [Google Scholar] [CrossRef]
- Naddaf, M.S.; Baper, S.Y. The role of double-skin facade configurations in optimizing building energy performance in Erbil city. Sci. Rep. 2023, 13, 8394. [Google Scholar] [CrossRef] [PubMed]
- Jankovic, A.; Goia, F. Impact of double skin facade constructional features on heat transfer and fluid dynamic behaviour. Build. Environ. 2021, 196, 107796. [Google Scholar] [CrossRef]
- Chow, W.K.; Hung, W. Effect of cavity depth on smoke spreading of double-skin facade. Build. Environ. 2006, 41, 970–979. [Google Scholar] [CrossRef]
- Oleszkiewicz, I. Fire exposure to exterior walls and flame spread on combustible cladding. Fire Technol. 1990, 26, 357–375. [Google Scholar] [CrossRef]
- Oleszkiewicz, I. Fire and combustible Exterior Walls. Natl. Res. Counc. Can. 1990, 32, 339–341. [Google Scholar] [CrossRef]
- Oleszkiewicz, I. Vertical separation of windows using Spandrel walls and horizontal projections. Fire Technol. 1991, 27, 334–340. [Google Scholar] [CrossRef]
- Lee, Y.P. Heat Fluxes and Flame Heights in External Facade Fires. Ph.D. Thesis, University of Ulster, Coleraine, UK, 2006. [Google Scholar]
- Delichatsios, M.A.; Lee, Y.P.; Tofilo, P. A new correlation for gas temperature inside a burning enclosure. Fire Saf. J. 2009, 44, 1003–1009. [Google Scholar] [CrossRef]
- Tang, F.; Hu, L.; Lu, K.; Zhang, X.; Shi, Q. Heat flux profile upon building facade due to ejected thermal plume from window in a sub atmospheric pressure at high altitude. Energy Build. 2015, 92, 331–337. [Google Scholar] [CrossRef]
- Tang, F.; Hu, L.; Wang, Q.; Lu, K.; Yang, L. An experimental investigation on temperature profile of buoyant spill plume from under-ventilated compartment fires in a reduced pressure atmosphere at high altitude. Int. J. Heat. Mass. Tran. 2012, 55, 5642–5649. [Google Scholar] [CrossRef]
- Lu, K.; Wang, J.; Hu, L. Vertical temperature profile of fire-induced facade thermal plume ejected from a fire compartment window with two adjacent side walls. Appl. Therm. Eng. 2017, 113, 70–78. [Google Scholar] [CrossRef]
- Nakao, T.; Yanagisawa, A.; Jo, A.; Wakatsuki, K.; Ohmiya, Y. Fire Plume Ejected from an Opening in Unconfined Space Part 1 Experimental Outline. Fire Sci. Technol. 2007, 26, 497–503. [Google Scholar] [CrossRef]
- Yanagisawa, A.; Jo, A.; Nakao, T.; Wakatsuki, K.; Ohmiya, Y. Fire plume Ejected from an opening in unconfmed space, Part 2 generation limit of the external flame. Fire Sci. Technol. 2007, 26, 505–510. [Google Scholar] [CrossRef][Green Version]
- Sun, X.; Tang, F.; Lu, K.; Ren, F.; Shi, C.; Merci, B.; Hu, L. Fundamentals of window-ejected fire plumes from under-ventilated compartment fires: Recent progresses and perspectives. Prog. Energy Combust. Sci. 2023, 94, 101039. [Google Scholar] [CrossRef]
- Torero, J.L.; Majdalani, A.H.; Abecassis-Empis, C.; Cowlard, A. Revisiting the compartment fire. Fire Saf. Sci. 2014, 11, 28–45. [Google Scholar] [CrossRef]
- Miao, L.; Chow, C. A study on window plume from a room fire to the cavity of a double-skin façade. Appl. Therm. Eng. 2018, 129, 230–241. [Google Scholar] [CrossRef]
- Li, J.; Zhao, Y.; Chow, W.; Yue, T. Side Wind Effect on the Flow Behavior of the Window Plume. In Proceedings of the 11th Asia-Oceania Symposium on Fire Science and Technology, Taipei, Taiwan, 21–25 October 2018. [Google Scholar]
- Bai, Z.; Li, Y.; Zhao, Y. Study on characteristics of fire plume in building facade window under lateral blow. PLoS ONE 2019, 14, e0225120. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.P.; Delichatsios, M.A.; Silcock, G.W.H. Heat fluxes and flame heights in facades in enclosures of varying geometry. Proc. Combust. Inst. 2007, 31, 2521–2528. [Google Scholar] [CrossRef]
- Lee, Y.P.; Delichatsios, M.A.; Ohmiya, Y.; Wakatsuki, K.; Yanagisawa, A.; Goto, D. Heat fluxes on opposite building wall by flames emerging from an enclosure. Proc. Combust. Inst. 2009, 32, 2551–2558. [Google Scholar] [CrossRef]
- Lee, Y.P.; Delichatsios, M.A.; Ohmiya, Y. The study for the physics of the outflow from the opening of a burning enclosure. In Proceedings of the 5th International Seminar on Fire and Explosion Hazards, Edinburgh, UK, 23–27 April 2007. [Google Scholar]
- Poreh, M.; Marshall, N.R.; Regev, A. Entrainment by adhered two-dimensional plumes. Fire Saf. J. 2008, 43, 344–350. [Google Scholar] [CrossRef]
- Shi, C.L.; Lu, W.Z.; Chow, W.K.; Huo, R. An investigation on spill plume development and natural filling in large full-scale atrium under retail shop fire. Int. J. Heat. Mass. Tran. 2007, 50, 513–529. [Google Scholar] [CrossRef]
- ISO.1990; Fire Tests–Full-Scale Room Test for Surface Products. International Organization for Standardization: Geneva, Switzerland, 1990.
- Ji, J.; Guo, F.; Gao, Z.; Zhu, J. Effects of ambient pressure on transport characteristics of thermal-driven smoke flow in a tunnel. Int. J. Therm. Sci. 2018, 125, 210–217. [Google Scholar] [CrossRef]
- McDermott, R.; McGrattan, K.; Hostikka, S. Fire dynamics simulator (version 5) technical reference guide. NIST Spec. Publ. 2008, 1018, 3–4. [Google Scholar]
- Morgan, H.P.; Ghosh, B.K.; Garrad, G.; Pamlitschka, R.; De Smedt, J.C.; Schoonbaert, L.R. Design Methodologies for Smoke and Heat Exhaust Ventilation; Construction Research Communications Limited by permission of Building Research Establishment Limited: Garston, UK, 1999. [Google Scholar]
- Harrison, R. Smoke Control in Atrium Buildings: A Study of the Thermal Spill Plume. Master’s Thesis, University of Canterbury, Christchurch, New Zealand, 2004. [Google Scholar]
- Harrison, R.; Spearpoint, M.J. A review of simple entrainment calculation methods for the thermal spill plume. Int. J. Eng. Performanced-Based Fire Codes, 2009; accepted for publication. [Google Scholar]
- Harrison, R. Entrainment of Air Into Thermal Spill Plumes. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2009. [Google Scholar]


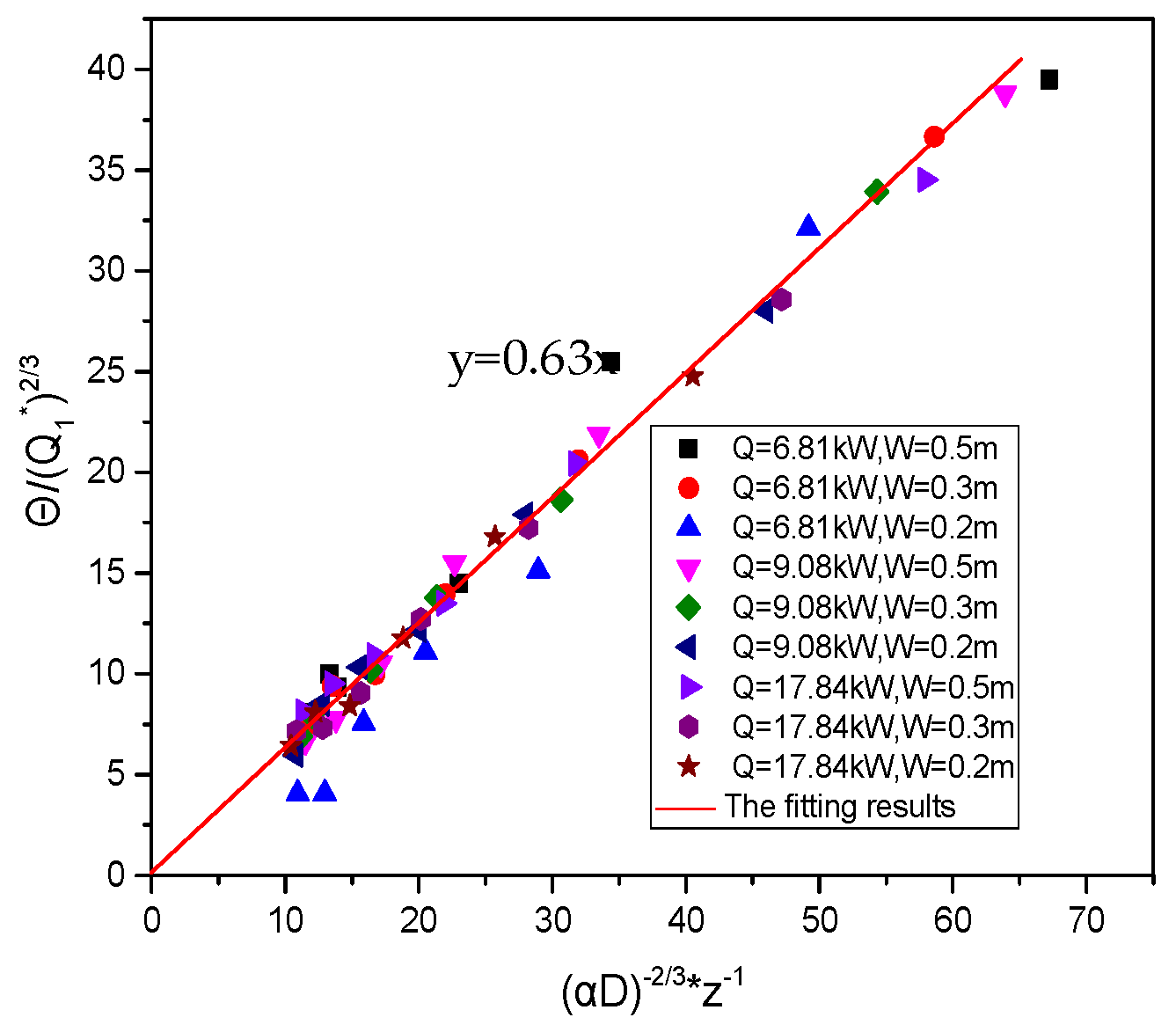
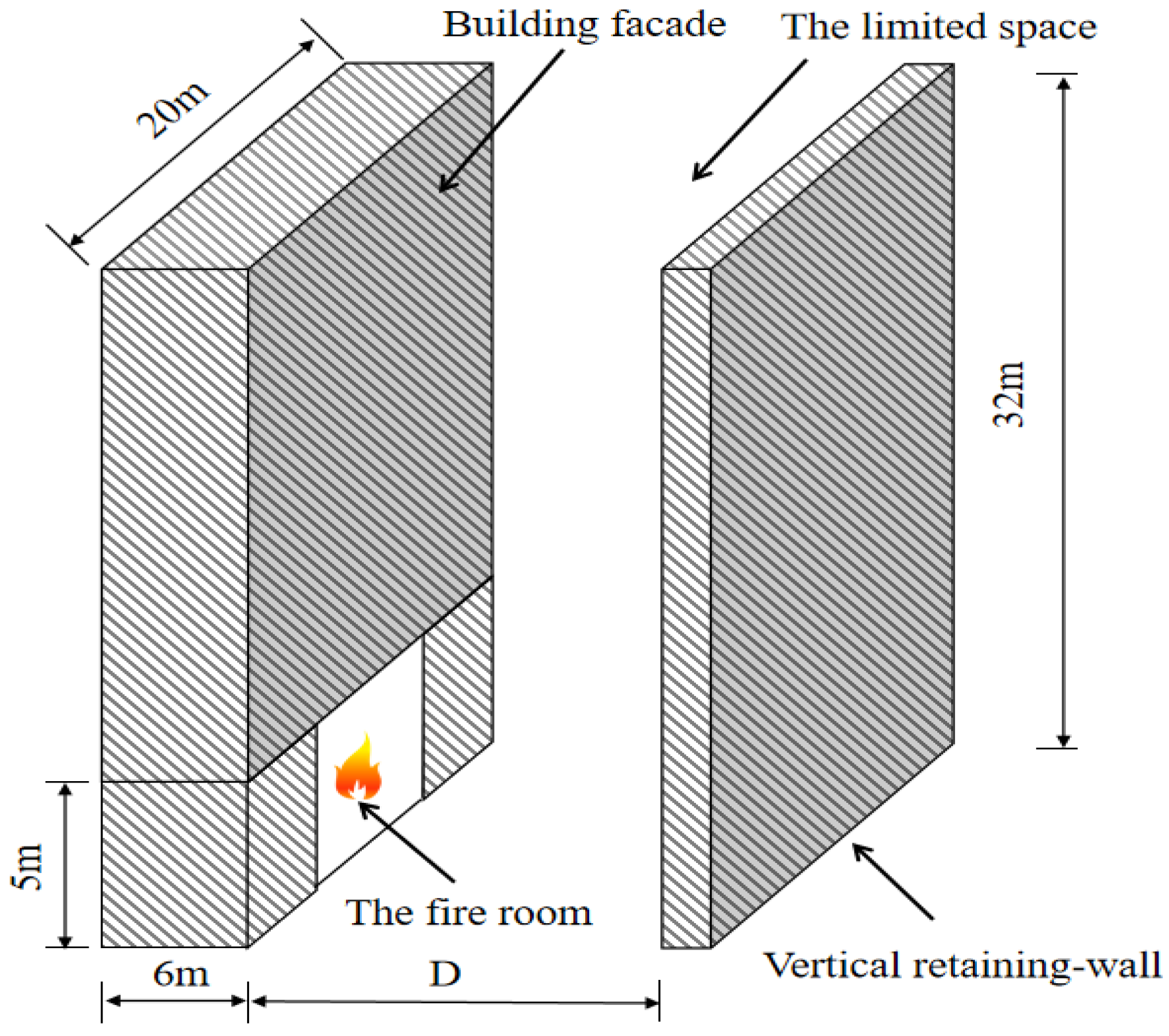
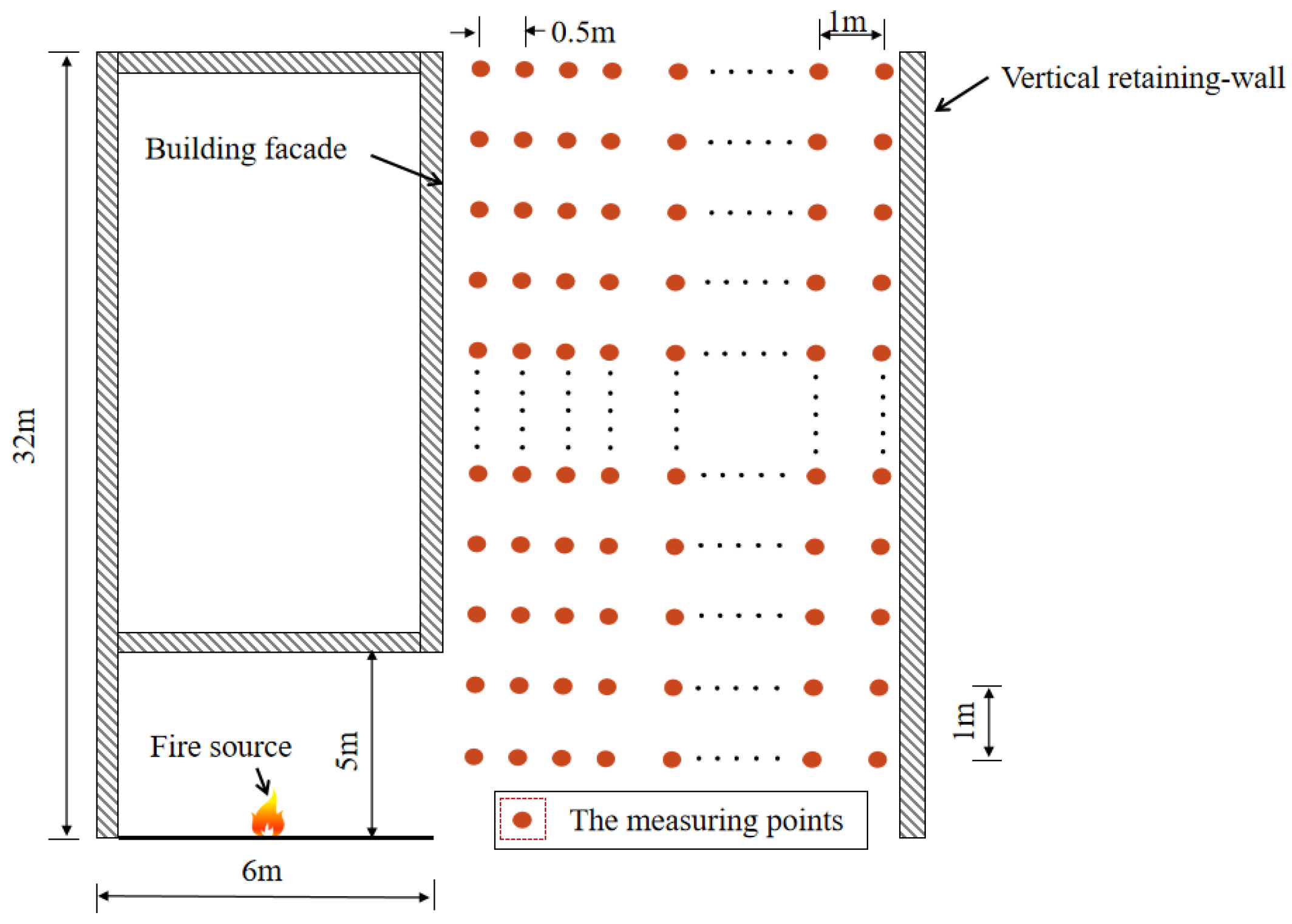
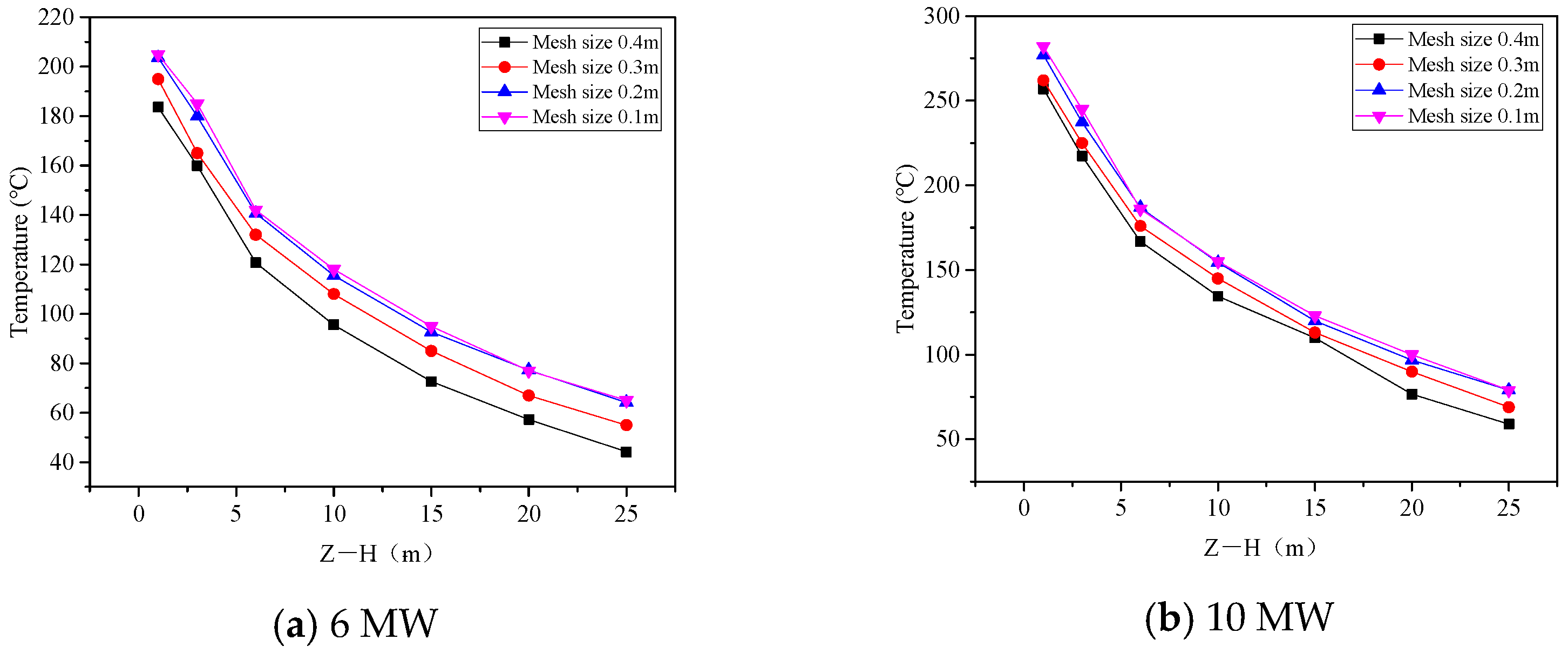




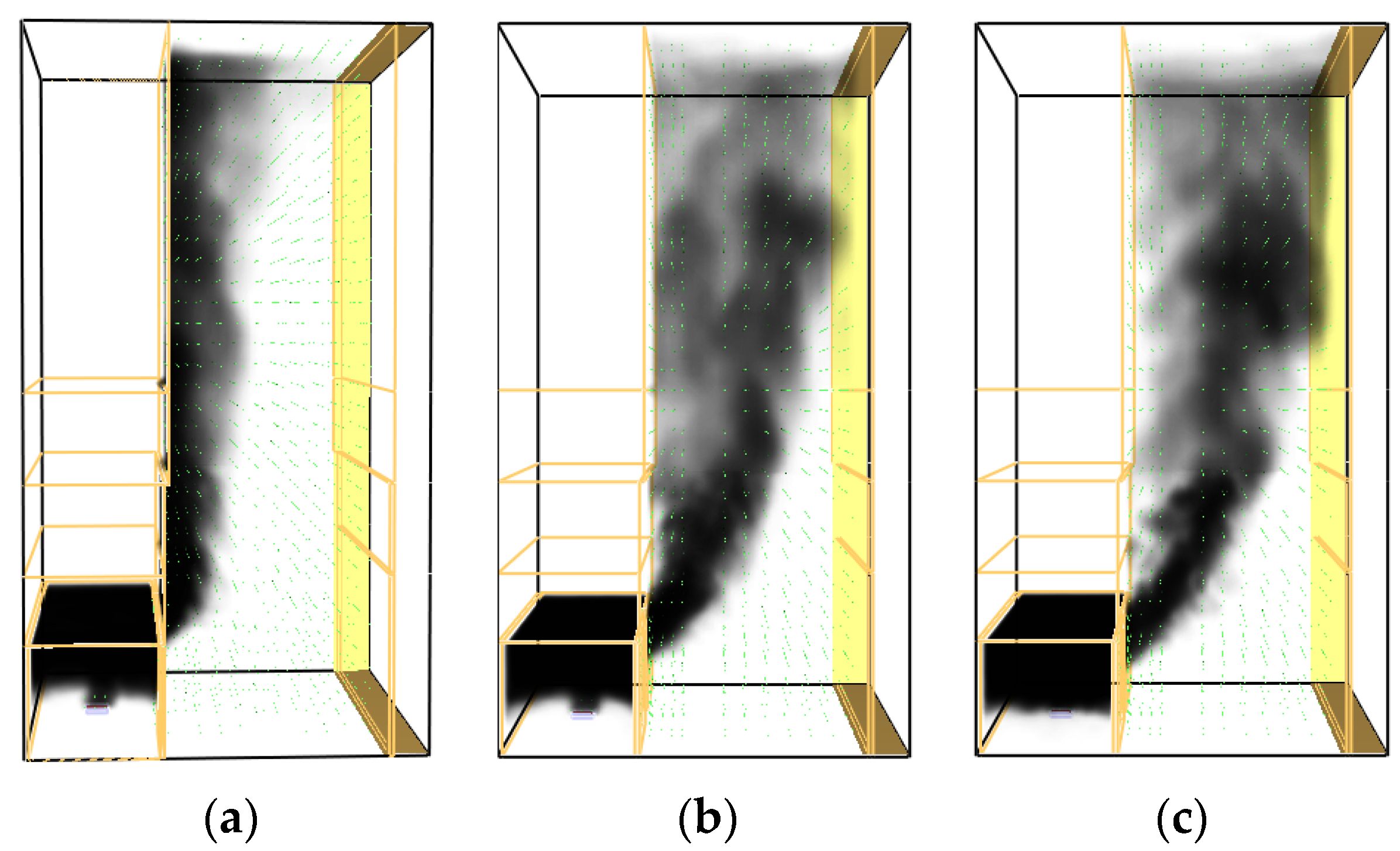




| Working Condition | Fuel | Fuel Pool Size (m2) | Mass Combustion Rate (kg/s·m2) | Fire HRR Q (kW) |
|---|---|---|---|---|
| SF1 | methanol | 0.1 0.1 | 0.03 | 6.81 |
| SF2 | methanol | 0.1 0.2 | 0.02 | 9.08 |
| SF3 | n-heptane | 0.1 0.1 | 0.04 | 17.84 |
| Working Condition | The Fire HRR Q (Kw) | Opening Size | The Distance D (cm) | |
|---|---|---|---|---|
| Height H (m) | Width W (m) | |||
| EGK1 | 6.81 | 0.4 | 0.5 | 32 |
| EGK2 | 0.3 | 32 | ||
| EGK3 | 0.2 | 32 | ||
| EGK4 | 0.4 | 0.5 | 24 | |
| EGK5 | 0.3 | 24 | ||
| EGK6 | 0.2 | 24 | ||
| EGK7 | 0.4 | 0.5 | 16 | |
| EGK8 | 0.3 | 16 | ||
| EGK9 | 0.2 | 16 | ||
| EGK10 | 0.4 | 0.5 | 8 | |
| EGK11 | 0.3 | 8 | ||
| EGK12 | 0.2 | 8 | ||
| EGK13 | 9.08 | 0.4 | 0.5 | 32 |
| EGK14 | 0.3 | 32 | ||
| EGK15 | 0.2 | 32 | ||
| EGK16 | 0.4 | 0.5 | 24 | |
| EGK17 | 0.3 | 24 | ||
| EGK18 | 0.2 | 24 | ||
| EGK19 | 0.4 | 0.5 | 16 | |
| EGK20 | 0.3 | 16 | ||
| EGK21 | 0.2 | 16 | ||
| EGK22 | 0.4 | 0.5 | 8 | |
| EGK23 | 0.3 | 8 | ||
| EGK24 | 0.2 | 8 | ||
| EGK25 | 17.84 | 0.4 | 0.5 | 32 |
| EGK26 | 0.3 | 32 | ||
| EGK27 | 0.2 | 32 | ||
| EGK28 | 0.4 | 0.5 | 24 | |
| EGK29 | 0.3 | 24 | ||
| EGK30 | 0.2 | 24 | ||
| EGK31 | 0.4 | 0.5 | 16 | |
| EGK32 | 0.3 | 16 | ||
| EGK33 | 0.2 | 16 | ||
| EGK34 | 0.4 | 0.5 | 8 | |
| EGK35 | 0.3 | 8 | ||
| EGK36 | 0.2 | 8 | ||
| The fire HRR Q (kW) | 6.81 | 9.08 | 17.84 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Opening width W (m) | 0.5 | 0.3 | 0.2 | 0.5 | 0.3 | 0.2 | 0.5 | 0.3 | 0.2 |
| L2 (m) | 0.199 | 0.154 | 0.148 | 0.190 | 0.159 | 0.136 | 0.163 | 0.129 | 0.109 |
| Working Condition | Fire HRR Q (MW) | Window Height W (m) | The Distance D (m) | Working Condition | Fire HRR Q (MW) | Window Height W (m) | The Distance D (m) |
|---|---|---|---|---|---|---|---|
| SGK1 | 10 | 10 | 1 | SGK19 | 6 | 10 | 1 |
| SGK2 | 2 | SGK20 | 2 | ||||
| SGK3 | 3 | SGK21 | 3 | ||||
| SGK4 | 6 | SGK22 | 6 | ||||
| SGK5 | 8 | SGK23 | 8 | ||||
| SGK6 | 10 | SGK24 | 10 | ||||
| SGK7 | 4 | 1 | SGK25 | 4 | 1 | ||
| SGK8 | 2 | SGK26 | 2 | ||||
| SGK9 | 3 | SGK27 | 3 | ||||
| SGK10 | 6 | SGK28 | 6 | ||||
| SGK11 | 8 | SGK29 | 8 | ||||
| SGK12 | 10 | SGK30 | 10 | ||||
| SGK13 | 2 | 1 | SGK31 | 2 | 1 | ||
| SGK14 | 2 | SGK32 | 2 | ||||
| SGK15 | 3 | SGK33 | 3 | ||||
| SGK16 | 6 | SGK34 | 6 | ||||
| SGK17 | 8 | SGK35 | 8 | ||||
| SGK18 | 10 | SGK36 | 10 |
| Fire HRR (MW) | 10 | 6 | ||||
|---|---|---|---|---|---|---|
| Window Width W (m) | 10 | 4 | 2 | 10 | 4 | 2 |
| L2 (m) | 2.18 | 1.53 | 1.12 | 1.97 | 1.45 | 1.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Q.; Li, Y.; Li, J.; Xie, F.; Xu, D.; Su, Z. The Influence of Confined Space Size on the Temperature Distribution Characteristics of Internal Window Plume from Well-Ventilated Compartment Fires. Fire 2024, 7, 158. https://doi.org/10.3390/fire7050158
Dong Q, Li Y, Li J, Xie F, Xu D, Su Z. The Influence of Confined Space Size on the Temperature Distribution Characteristics of Internal Window Plume from Well-Ventilated Compartment Fires. Fire. 2024; 7(5):158. https://doi.org/10.3390/fire7050158
Chicago/Turabian StyleDong, Qiwei, Yanfeng Li, Junmei Li, Fei Xie, Desheng Xu, and Zhihe Su. 2024. "The Influence of Confined Space Size on the Temperature Distribution Characteristics of Internal Window Plume from Well-Ventilated Compartment Fires" Fire 7, no. 5: 158. https://doi.org/10.3390/fire7050158
APA StyleDong, Q., Li, Y., Li, J., Xie, F., Xu, D., & Su, Z. (2024). The Influence of Confined Space Size on the Temperature Distribution Characteristics of Internal Window Plume from Well-Ventilated Compartment Fires. Fire, 7(5), 158. https://doi.org/10.3390/fire7050158







