A Social Force-Based Model for Pedestrian Evacuation with Static Guidance in Emergency Situations
Abstract
:1. Introduction
2. Model Construction
2.1. Introduction to the Social Force Model
2.2. Static Guided Evacuation Model
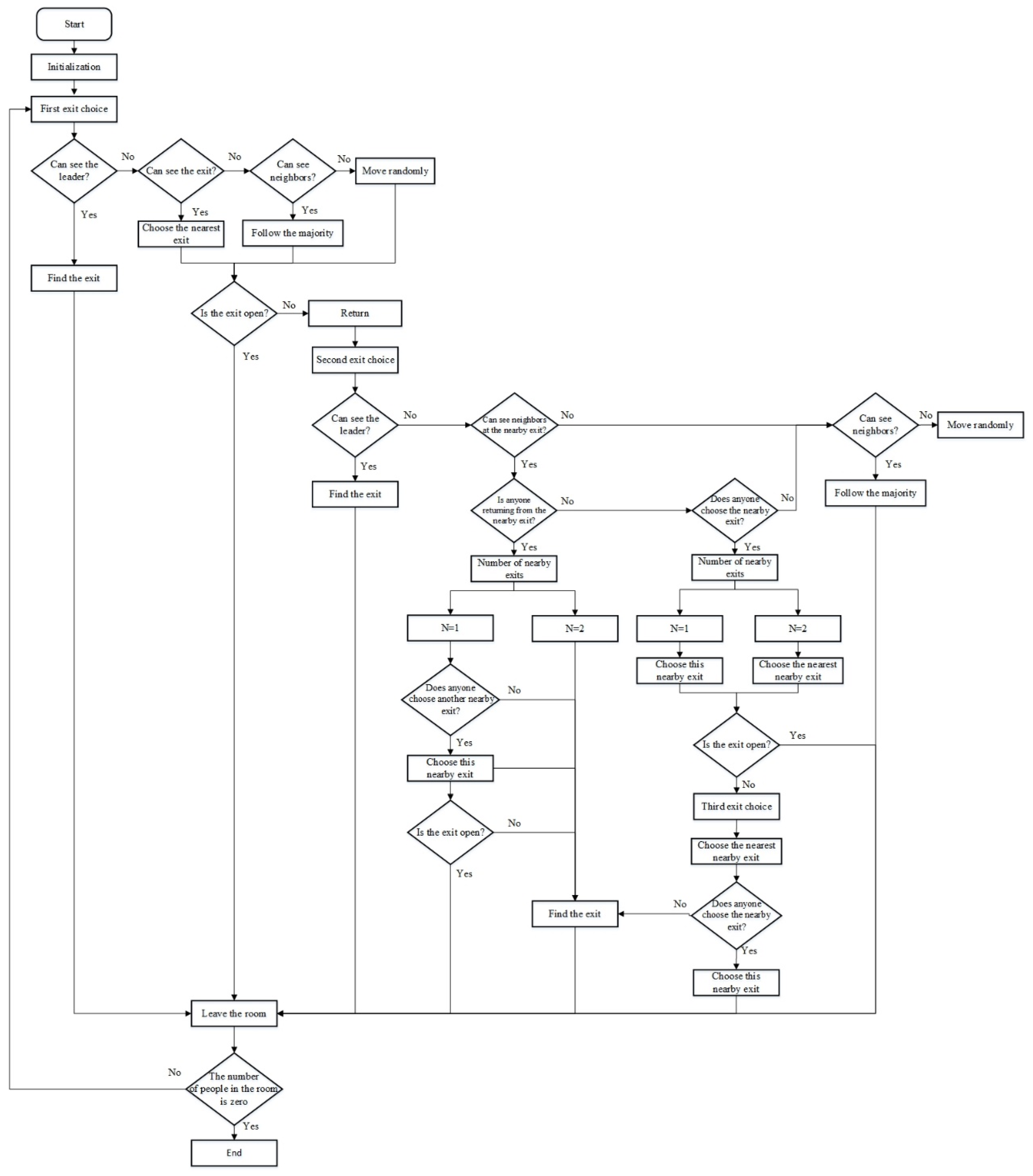
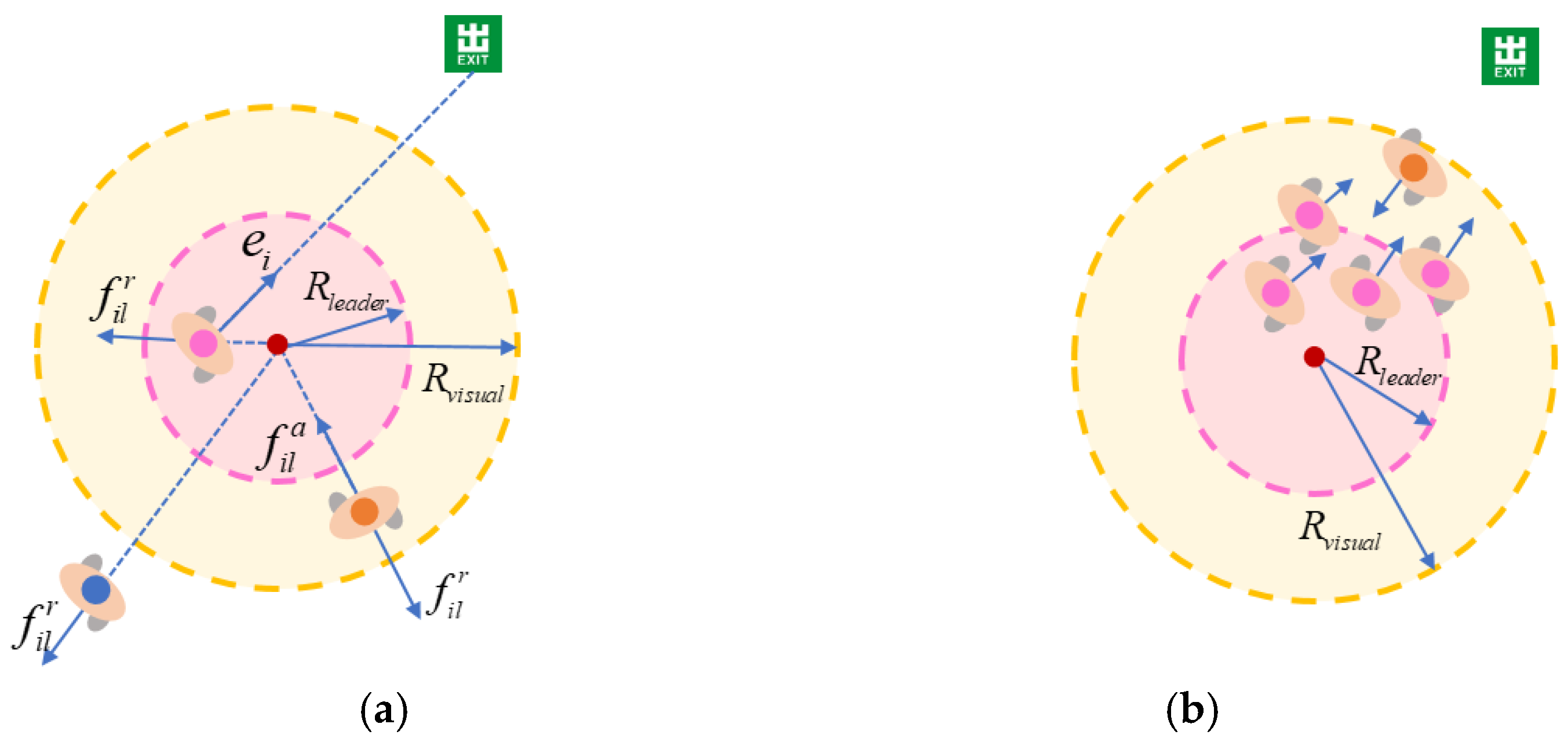
2.2.1. Model Description
2.2.2. Model Rules
2.2.3. Scenarios and Parameters
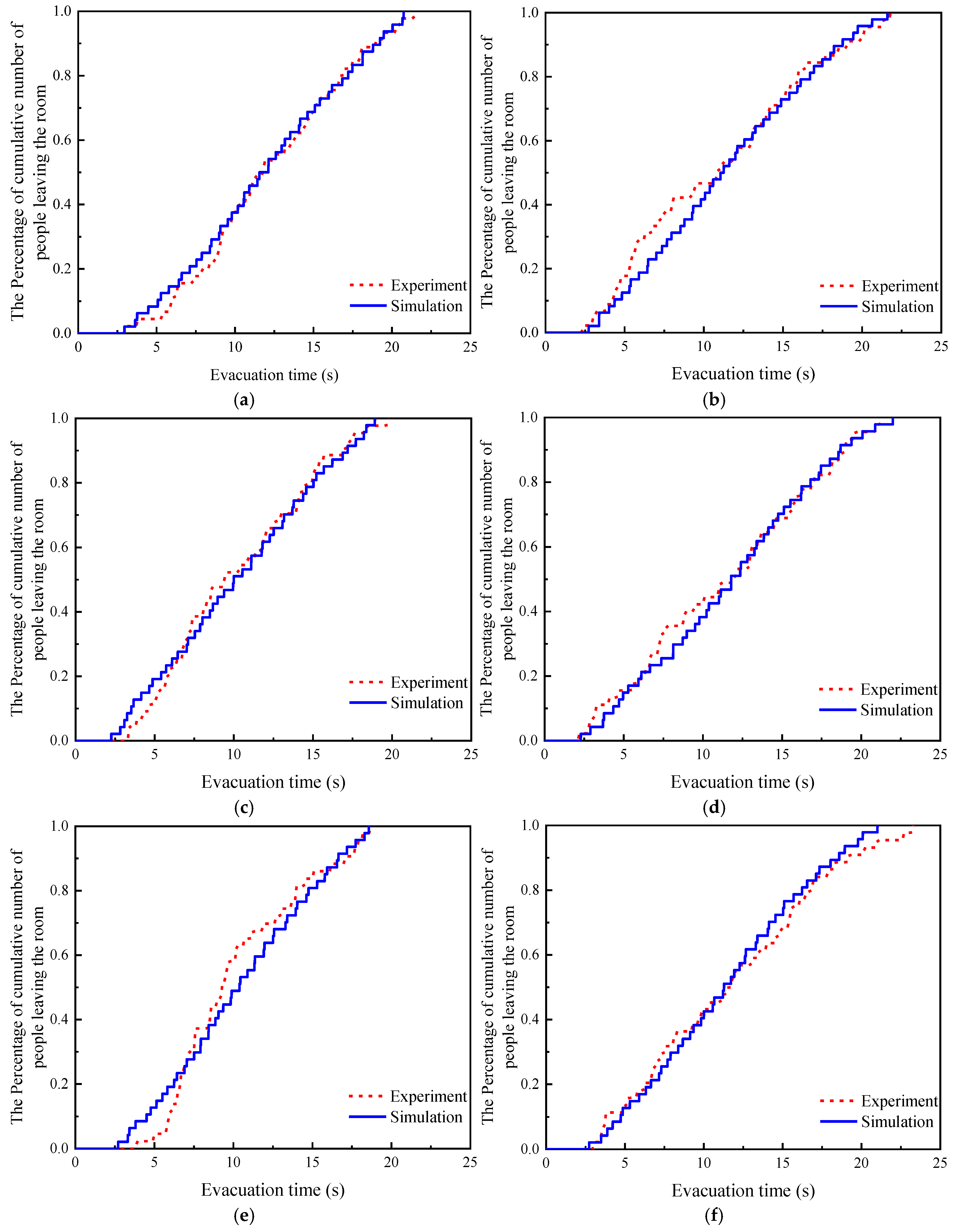
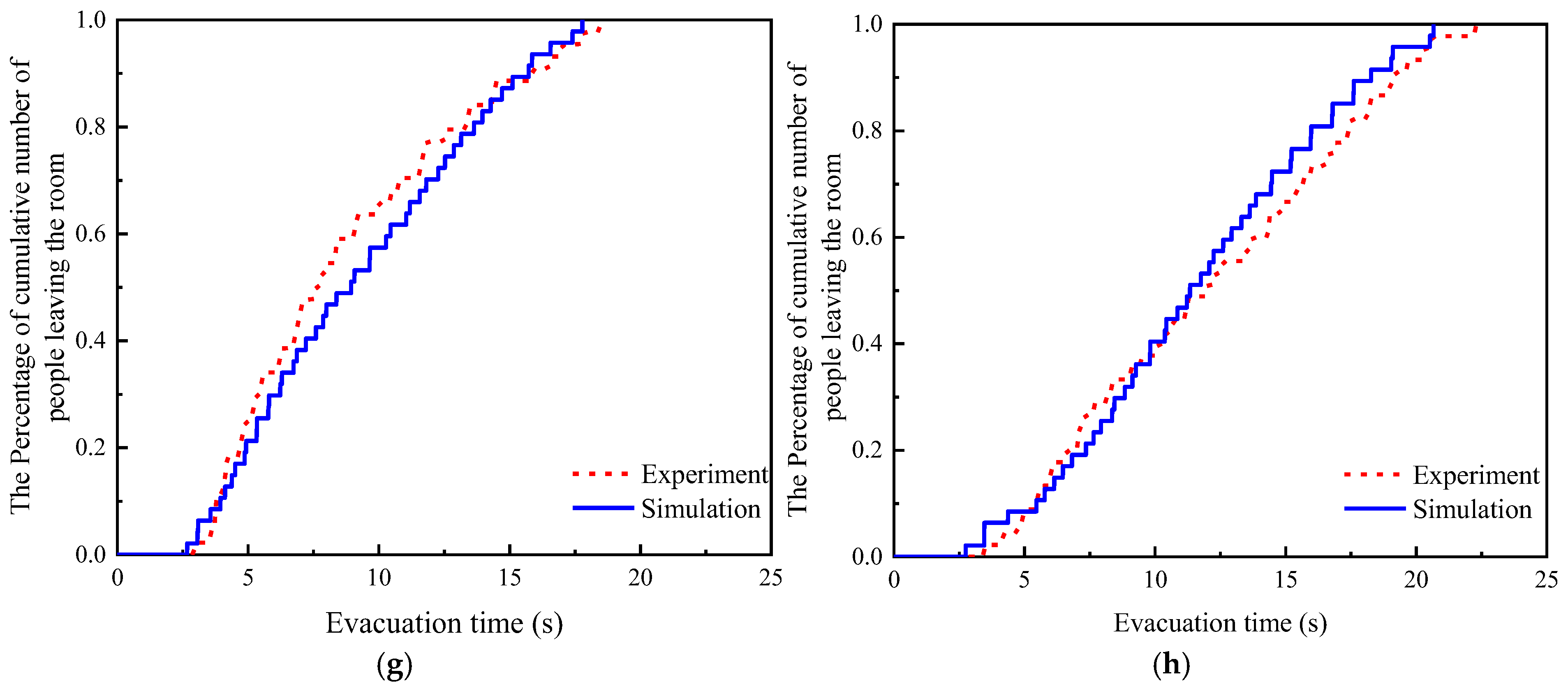
3. Model Validation
4. Results and Discussion
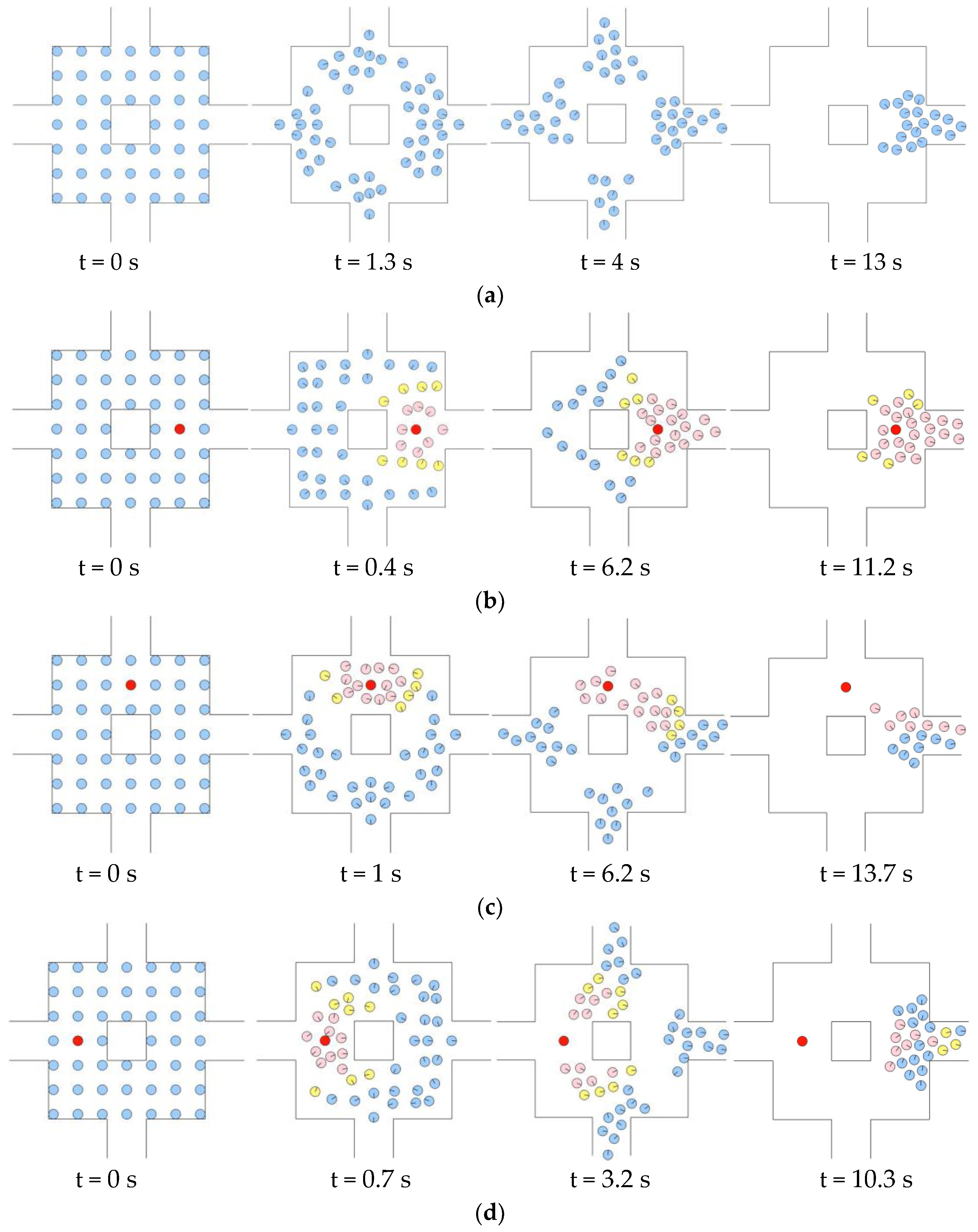
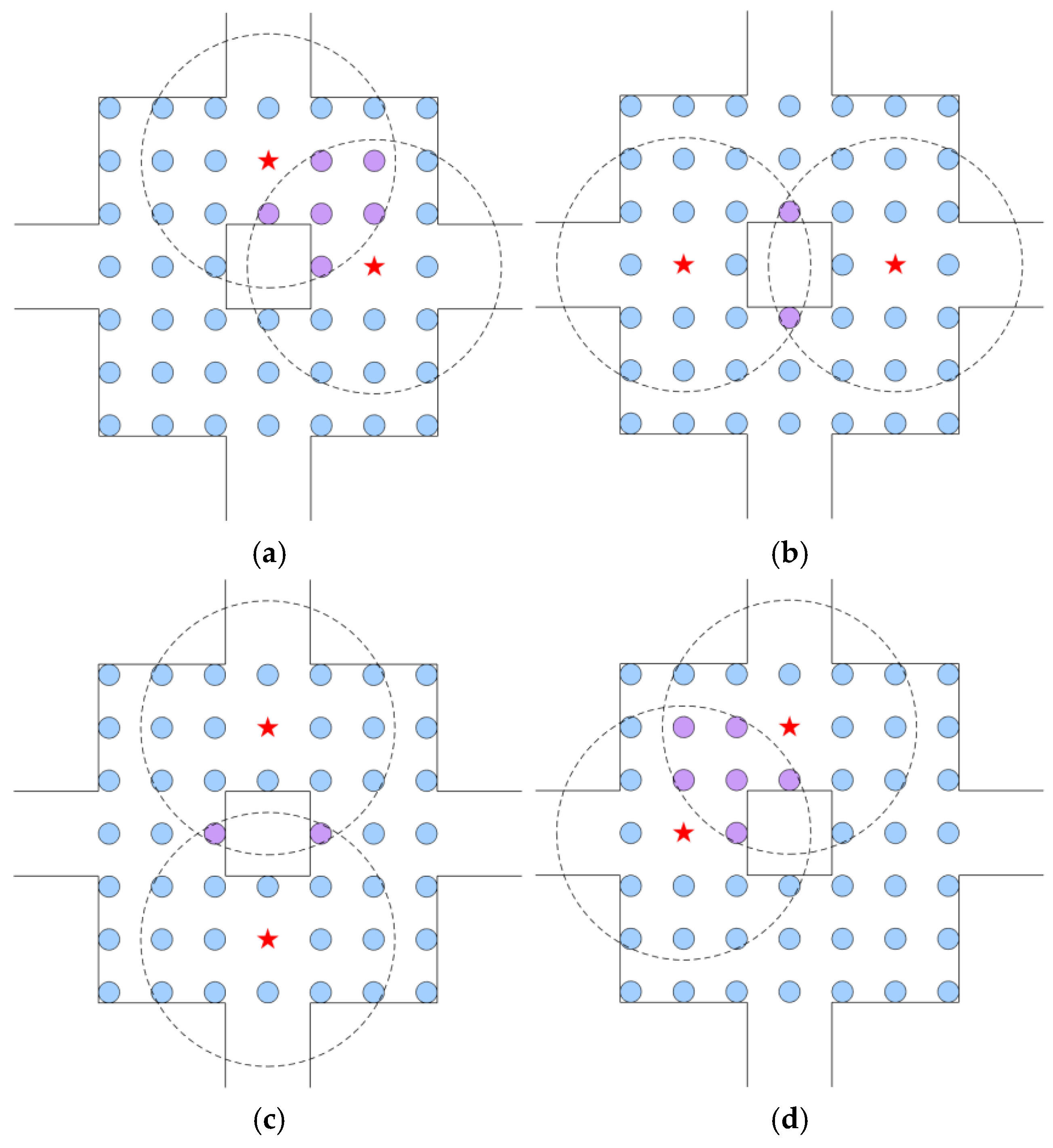
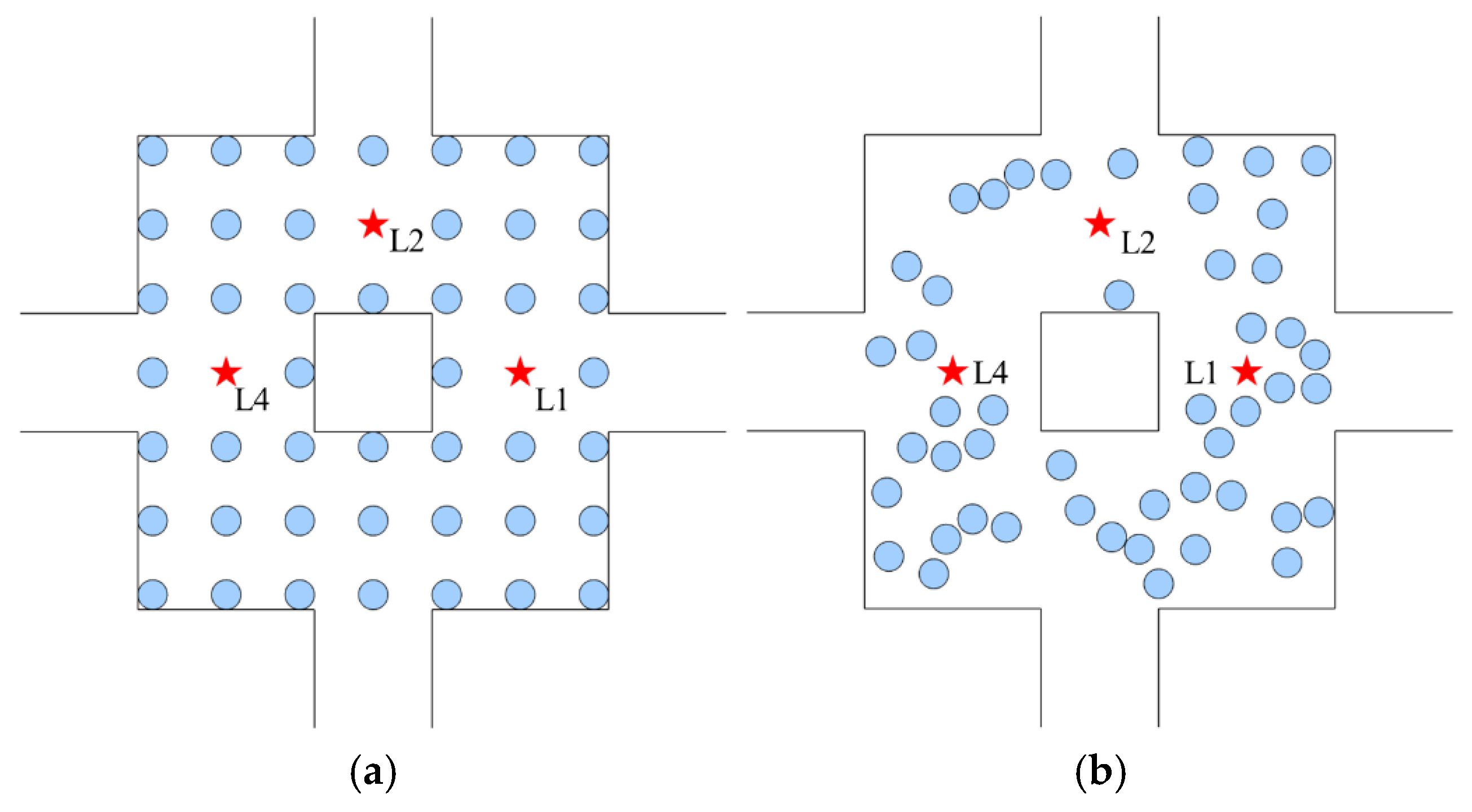
4.1. Leader Location
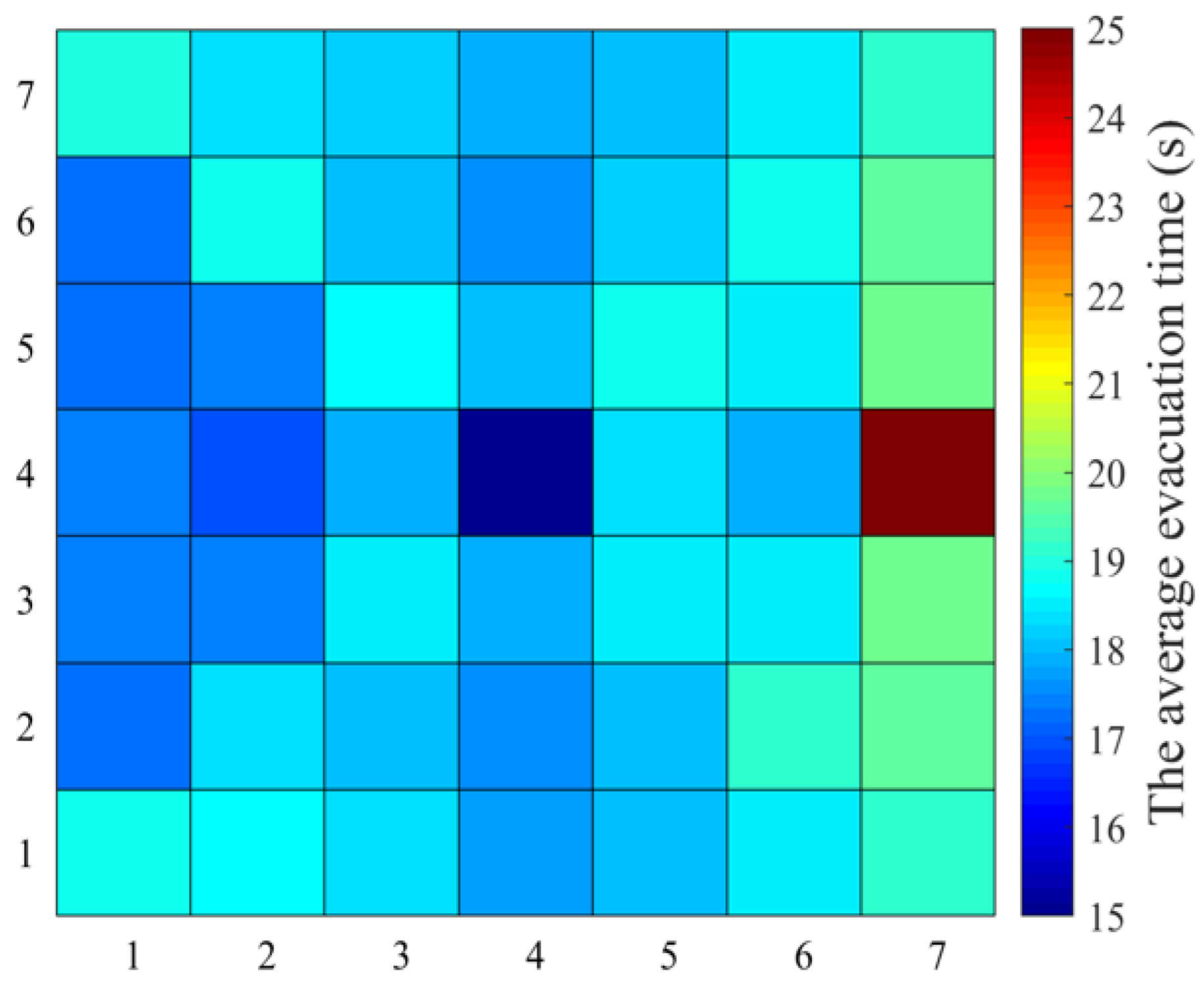
4.2. Number of Leaders
4.3. Pedestrian Distribution
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mou, H. Study on the Emergency Evacuation Efficiency of Personnel in Typical Building Areas. Ph.D. Thesis, University of Science and Technology of China, Hefei, China, 2015. [Google Scholar]
- Larusdottir, A.R.; Dederichs, A.S. Evacuation of Children: Movement on Stairs and on Horizontal Plane. Fire Technol. 2012, 48, 43–53. [Google Scholar] [CrossRef]
- Wang, F. Research on Emergency Rescue and Safe Evacuation of Personnel in Metro Fire Accidents. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2015. [Google Scholar]
- Shi, R. Research on Smoke Control Strategies and Personnel Evacuation in Metro Station Platforms Fire. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2016. [Google Scholar]
- Ma, Y.; Yuen, R.K.K.; Lee, E.W.M. Effective leadership for crowd evacuation. Phys. A Stat. Mech. Its Appl. 2016, 450, 333–341. [Google Scholar] [CrossRef]
- Cao, S.; Song, W.; Lv, W. Modeling pedestrian evacuation with guiders based on a multi-grid model. Phys. Lett. A 2016, 380, 540–547. [Google Scholar] [CrossRef]
- Hou, L.; Liu, J.-G.; Pan, X.; Wang, B.-H. A social force evacuation model with the leadership effect. Phys. A Stat. Mech. Its Appl. 2014, 400, 93–99. [Google Scholar] [CrossRef]
- Yuan, W.; Tan, K.H. Cellular automata model for simulation of effect of guiders and visibility range. Curr. Appl. Phys. 2009, 9, 1014–1023. [Google Scholar] [CrossRef]
- Yang, X.; Dong, H.; Yao, X.; Sun, X.; Wang, Q.; Zhou, M. Necessity of guides in pedestrian emergency evacuation. Phys. A Stat. Mech. Its Appl. 2016, 442, 397–408. [Google Scholar] [CrossRef]
- Zhou, X.; Lin, X.; Ji, X. Pedestrian Evacuation Simulation Considering the Guidance Information. In CICTP 2021; American Society of Civil Engineers: Reston, VA, USA, 2021; pp. 996–1007. [Google Scholar]
- Aubé, F.; Shield, R. Modeling the effect of leadership on crowd flow dynamics. In Proceedings of the International Conference on Cellular Automata, Amsterdam, The Netherlands, 25–27 October 2004; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Yang, X.; Yang, X.; Wang, Q.; Pan, F. Guide optimization in pedestrian emergency evacuation. Appl. Math. Comput. 2020, 365, 124711. [Google Scholar] [CrossRef]
- Jiang, Q.; Zhou, Y.; Zhang, L.; Li, K.; Li, H. Influence of pedestrian psychology on evacuation dynamics with the guide of emergency signage. Europhys. Lett. 2022, 137, 41001. [Google Scholar] [CrossRef]
- Cai, Z.-Y.; Zhou, R.; Cui, Y.-K.; Wang, Y.; Jiang, J.-C. Simulation based on a modified social force model for sensitivity to emergency signs in subway stations. Chin. Phys. B 2022, 32, 020507. [Google Scholar] [CrossRef]
- Faria, J.J.; Dyer JR, G.; Tosh, C.R.; Krause, J. Leadership and social information use in human crowds. Anim. Behav. 2010, 79, 895–901. [Google Scholar] [CrossRef]
- Li, L.; Ma, Y.; Ding, N.; Zhang, H.; Ma, Y. Changes in social relation networks and leader–follower behavior in emergency evacuations. J. Tsinghua Univ. (Sci. Technol.) 2016, 56, 334–340. [Google Scholar]
- Li, J.; Tang, J.; Wang, D. Dynamic spreading model of passenger group panic considering official guidance information in subway emergencies. Math. Probl. Eng. 2019, 2019, 4691641. [Google Scholar] [CrossRef]
- Peng, Y.-C.; Chou, C.-I. Simulation of pedestrian flow through a “T” intersection: A multi-floor field cellular automata approach. Comput. Phys. Commun. 2011, 182, 205–208. [Google Scholar] [CrossRef]
- Zhang, P.; Yang, L.; Lo, S.; Wang, D.; Li, M.; Jiang, J.; Jiang, N. Experimental study on evacuation behavior with guidance under high and low urgency conditions. Saf. Sci. 2022, 154, 105865. [Google Scholar] [CrossRef]
- Helbing, D.; Molnar, P. Social force model for pedestrian dynamics. Phys. Rev. E 1995, 51, 4282. [Google Scholar] [CrossRef]
- Ma, Y.; Lee, M.W.E.; Shi, M. Dual Effects of Guide-based Guidance on Pedestrian Evacuation. Phys. Lett. A 2017, 381, 1837–1844. [Google Scholar] [CrossRef]
- Helbing, D.; Farkas, I.; Vicsek, T. Simulating dynamical features of escape panic. Nature 2000, 407, 487–490. [Google Scholar] [CrossRef]
- Helbing, D.; Farkas, I.J.; Vicsek, T. Freezing by heating in a driven mesoscopic system. Phys. Rev. Lett. 2000, 84, 1240. [Google Scholar] [CrossRef]
- Lakoba, T.I.; Kaup, D.J.; Finkelstein, N.M. Modifications of the Helbing-Molnar-Farkas-Vicsek social force model for pedestrian evolution. Simulation 2005, 81, 339–352. [Google Scholar] [CrossRef]
- Mehran, R.; Oyama, A.; Shah, M. Abnormal crowd behavior detection using social force model. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- Li, Q.; Gao, Y.; Chen, L.; Kang, Z. Emergency evacuation with incomplete information in the presence of obstacles. Phys. A Stat. Mech. Its Appl. 2019, 533, 122068. [Google Scholar] [CrossRef]
- Yuan, Z.; Jia, H.; Zhang, L.; Bian, L. A social force evacuation model considering the effect of emergency signs. Simulation 2018, 94, 723–737. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Q.; Cai, Y.; Zhang, J.; Ma, Q. Simulation study of pedestrian flow in a station hall during the Spring Festival travel rush. Phys. A Stat. Mech. Its Appl. 2013, 392, 2470–2478. [Google Scholar] [CrossRef]
- Wang, L.; Zheng, J.-H.; Zhang, X.-S.; Zhang, J.-L.; Wang, Q.-Z.; Zhang, Q. Pedestrians’ behavior in emergency evacuation: Modeling and simulation. Chin. Phys. B 2016, 25, 118901. [Google Scholar] [CrossRef]
- Ding, N.; Liu, T.; Liu, Z.; Wang, Y.; Chai, Y.; Jiang, L. Analysis and improvement of panic concept in social force model. J. Comput. Appl. 2021, 41, 2460. [Google Scholar]
- Zhang, Q. Simulation Research on the Multi-Exit Emergency Evacuation. Master’s Thesis, Zhejiang University, Hangzhou, China, 2014. (In Chinese). [Google Scholar]
- Purser, D. Dependence of modelled evacuation times on key parameters and interactions. In Pedestrian and Evacuation Dynamics 2008; Springer: Berlin/Heidelberg, Germany, 2010; pp. 667–675. [Google Scholar]





| Parameters | Significance | Values |
|---|---|---|
| Pedestrian mass | 80 kg | |
| Pedestrian shoulder width | 0.6 m | |
| Strength of social repulsive force | 2000 N | |
| Characteristic distance of social repulsive force | 0.08 m | |
| Body compression coefficient | 1.2 × 105 kg s−2 | |
| Coefficient of sliding friction | 2.4 × 105 kg m−1s−1 | |
| Pedestrian reaction time | 0.5 s | |
| Information dissemination distance | 2 m | |
| Leader repulsive force parameter | 2000 N | |
| Leader repulsive force parameter | 0.08 m | |
| Leader attractive force parameter | 0.1 |
| Evacuation Conditions | Evacuation Time in Experiments (s) | Evacuation Time in Simulations (s) |
|---|---|---|
| No guidance, high stress level | 21.5 | 19.39 0.46 |
| P-R, high stress level | 19.8 | 18.34 0.49 |
| P-N-R, high stress level | 18.7 | 18.10 0.44 |
| P-O-R, high stress level | 18.5 | 17.21 0.39 |
| No guidance, low stress level | 21.8 | 20.73 0.34 |
| P-R, low stress level | 21.3 | 21.47 0.44 |
| P-N-R, low stress level | 23.3 | 21.45 0.65 |
| P-O-R, low stress level | 20.6 | 20.72 0.51 |
| Source of Variation | Sum of Squares (SS) | Degrees of Freedom (df) | Mean Square (MS) | F-Value | p-Value |
|---|---|---|---|---|---|
| Between Groups | 33.13 | 1 | 33.13 | 33.615 | 0.000125 |
| Within Groups | 3.25 | 6 | 0.542 | ||
| Total | 36.38 | 7 |
| Leaders’ Location Assignment | Evacuation Time (s) |
|---|---|
| No guidance | 19.39 0.46 |
| L1 | 18.34 0.49 |
| L2 | 18.10 0.44 |
| L4 | 17.21 0.39 |
| L1, L2 | 17.19 0.55 |
| L1, L4 | 16.91 0.49 |
| L2, L3 | 17.12 0.52 |
| L2, L4 | 17.15 0.56 |
| L1, L2, L3 | 16.52 0.53 |
| L1, L2, L4 | 16.49 0.55 |
| L2, L3, L4 | 16.46 0.51 |
| L1, L2, L3, L4 | 16.22 0.47 |
| Evac | Estimates | Standard Error | t | p > |t| | 95% Confidence Interval | |
|---|---|---|---|---|---|---|
| Dist | −0.109 ** | 0.045 | −2.42 | 0.016 | −0.198 | −0.020 |
| Dist*N | 0.013 ** | 0.005 | 2.48 | 0.014 | 0.002 | 0.024 |
| Constant | 17.279 | 0.121 | 142.81 | 0.000 | 17.041 | 17.518 |
| No. of observations | 200 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Liu, W.; Yang, L.; Wu, J.; Wang, K.; Cui, Y. A Social Force-Based Model for Pedestrian Evacuation with Static Guidance in Emergency Situations. Fire 2025, 8, 30. https://doi.org/10.3390/fire8010030
Zhang P, Liu W, Yang L, Wu J, Wang K, Cui Y. A Social Force-Based Model for Pedestrian Evacuation with Static Guidance in Emergency Situations. Fire. 2025; 8(1):30. https://doi.org/10.3390/fire8010030
Chicago/Turabian StyleZhang, Ping, Wenjun Liu, Lizhong Yang, Jinzhong Wu, Kaixuan Wang, and Yujie Cui. 2025. "A Social Force-Based Model for Pedestrian Evacuation with Static Guidance in Emergency Situations" Fire 8, no. 1: 30. https://doi.org/10.3390/fire8010030
APA StyleZhang, P., Liu, W., Yang, L., Wu, J., Wang, K., & Cui, Y. (2025). A Social Force-Based Model for Pedestrian Evacuation with Static Guidance in Emergency Situations. Fire, 8(1), 30. https://doi.org/10.3390/fire8010030







