The Influence of Different Concentrations of Methane in Ditches on the Propagation Characteristics of Explosions
Abstract
1. Introduction
2. Mathematical Model of Methane Gas Explosion
3. Modeling and Verification of Ditch Model
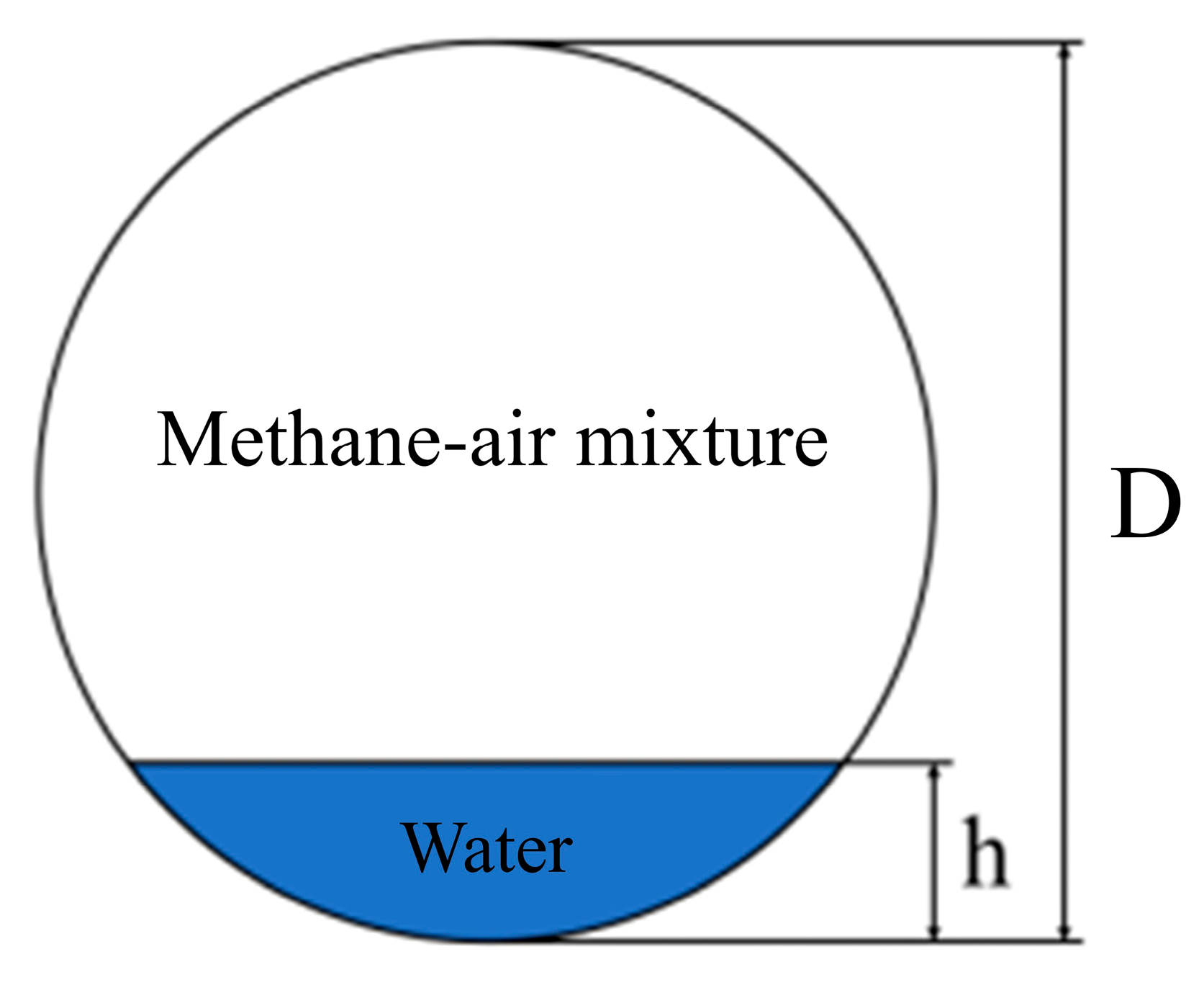
3.1. Modeling of Ditch Model
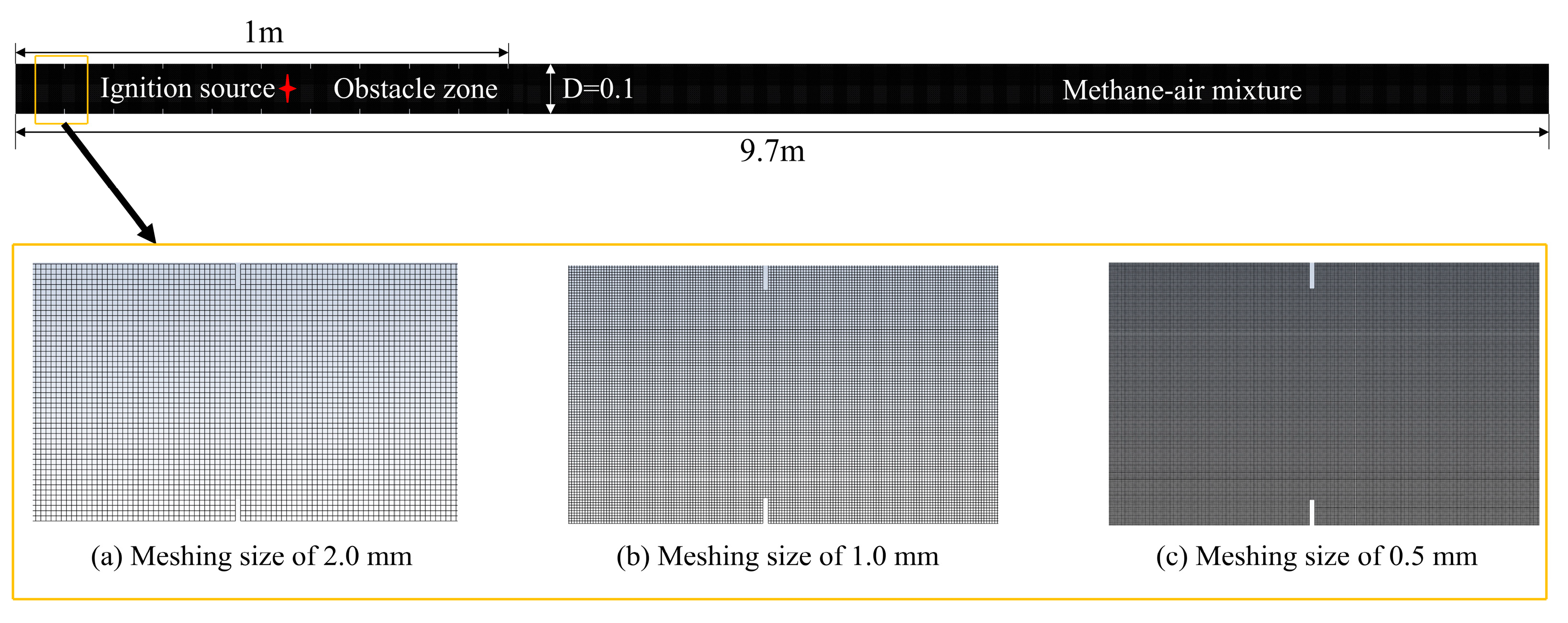
3.2. Mesh Independence Test
3.3. Basic Assumptions and Initialization of Numerical Simulation
- (1)
- Thermodynamic and Mechanical Boundary Conditions: The model assumes no heat exchange between the enclosed system and the external environment (adiabatic boundary). Structural displacement of the ditch model during the explosion event is neglected, and the gas velocity at the wall surface is set to zero (no-slip boundary condition).
- (2)
- Chemical Reaction Kinetics: The methane–air reaction is modeled as a one-step irreversible process, with the reaction rate constant governed by the Arrhenius equation, as specified in Equation (10).
- (3)
- Pre-Ignition State Parameters: Prior to ignition, methane–air mixtures at specified concentrations (10%, 11%, 13%, 16%) are assumed to be fully premixed and uniformly distributed throughout the computational domain. Initial conditions are defined as follows: temperature 288.15 K, pressure 1 atm, initial time t = 0, and initial velocity v = 0.
- (4)
- Phase Interaction Simplification: Given the disparity in time scales between interphase heat transfer and explosive reaction dynamics—where heat transfer rates between the gas and liquid phases are significantly slower than the combustion process—water evaporation is excluded from the model formulation.
- (5)
- Thermophysical Property Assumptions: The gas phase is treated as an ideal gas, with density governed by the ideal gas state equation. The dynamic viscosity and thermal conductivity of individual species are assumed to be constant throughout the computational domain. The compressibility of water is neglected, and its thermophysical properties—including density and specific heat capacity—are considered invariant under the modeled conditions.
- (6)
- Diffusion Term Simplifications: In the species transport equation, thermal diffusion and pressure diffusion effects are not accounted for. The mass diffusion coefficient is assumed to adhere to Fick’s law of diffusion, which describes molecular diffusion based on concentration gradients [27].
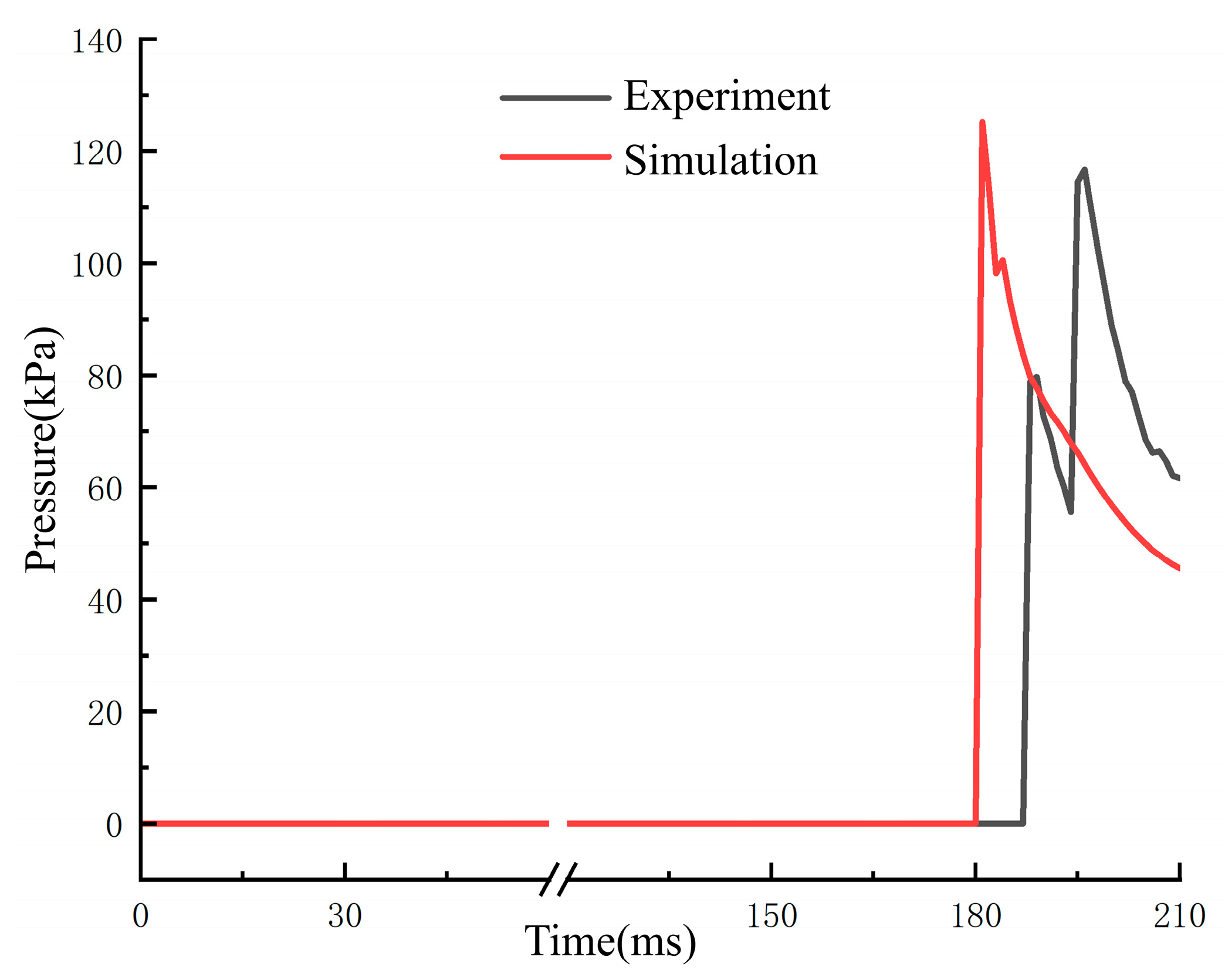
3.4. Validation Results of Numerical Simulation
4. Analysis of the Influence of Methane Concentration Variations on Explosion Propagation
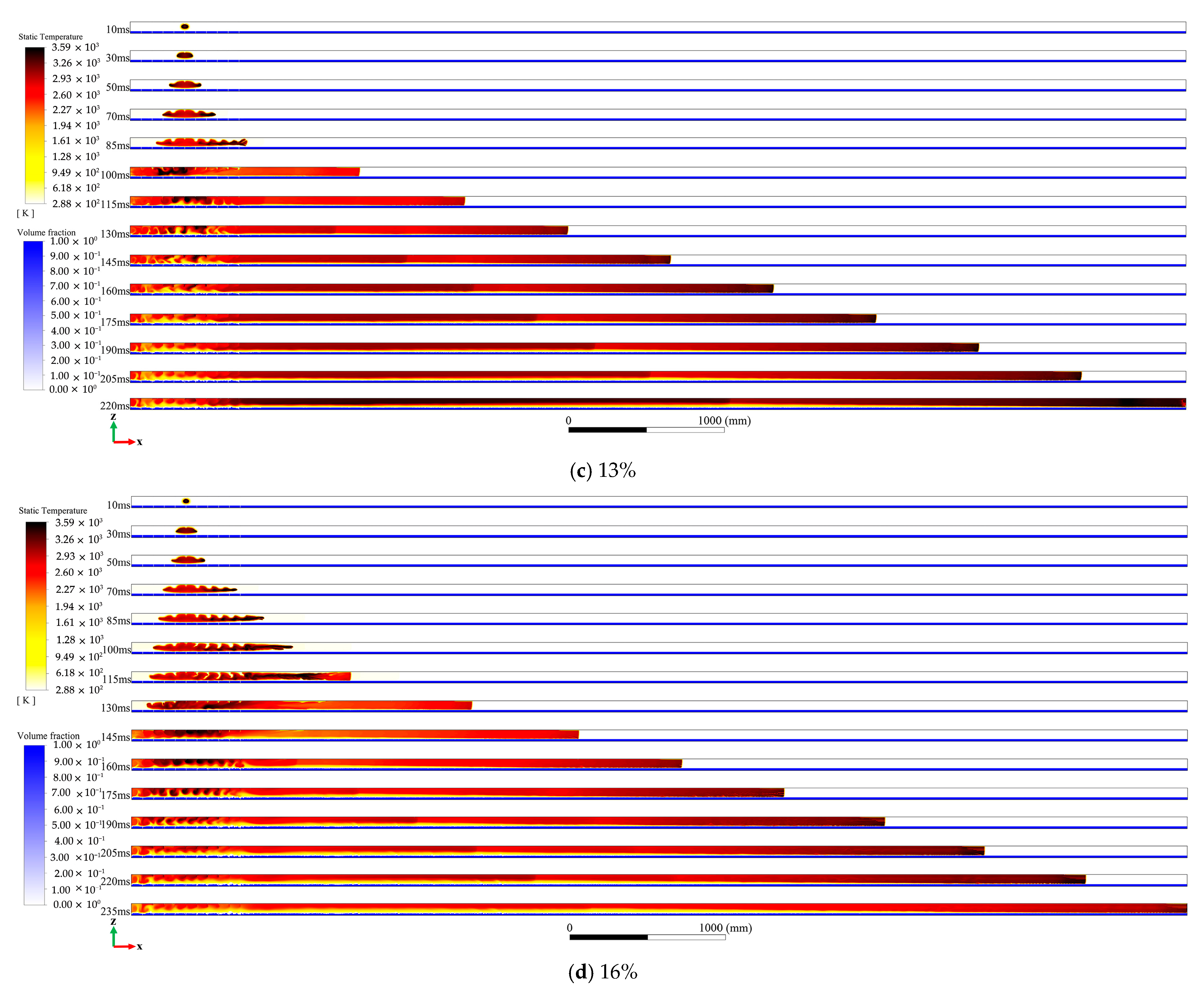
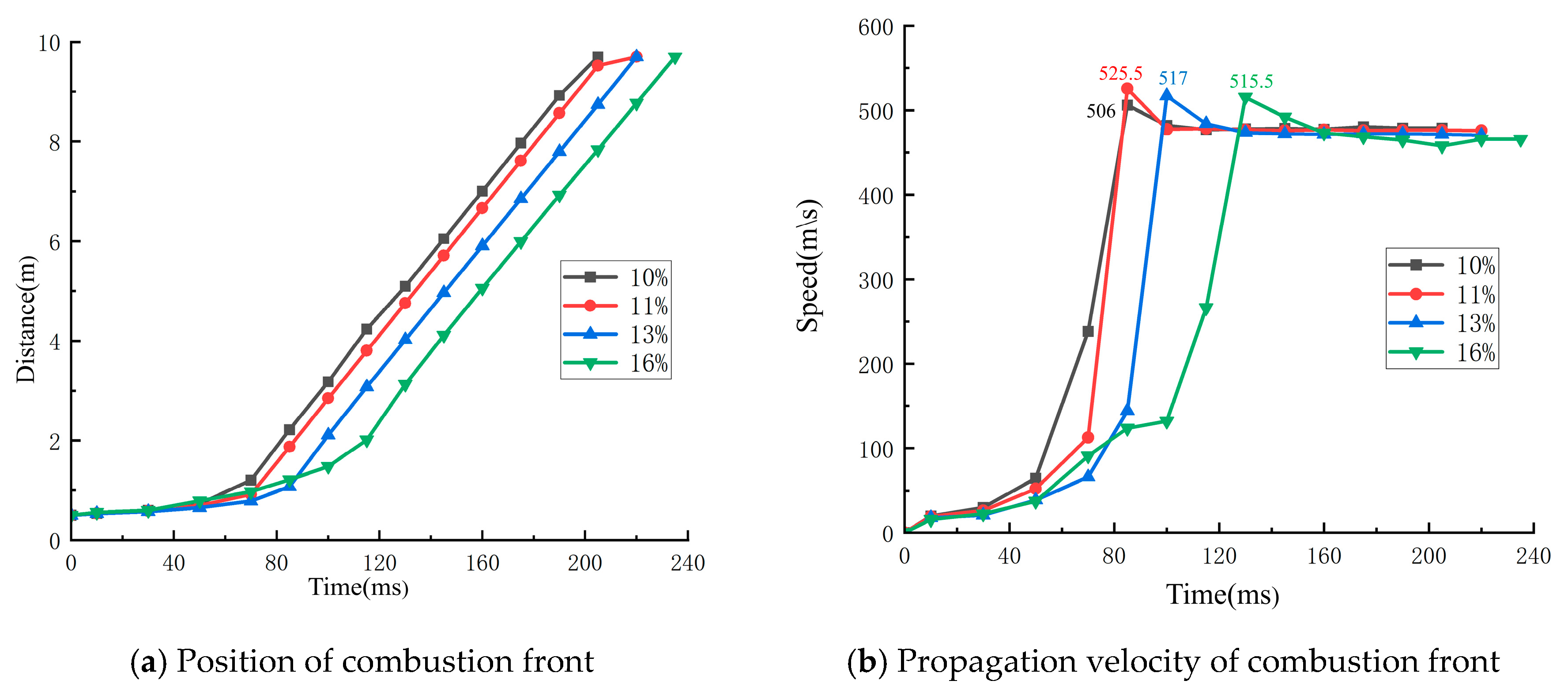
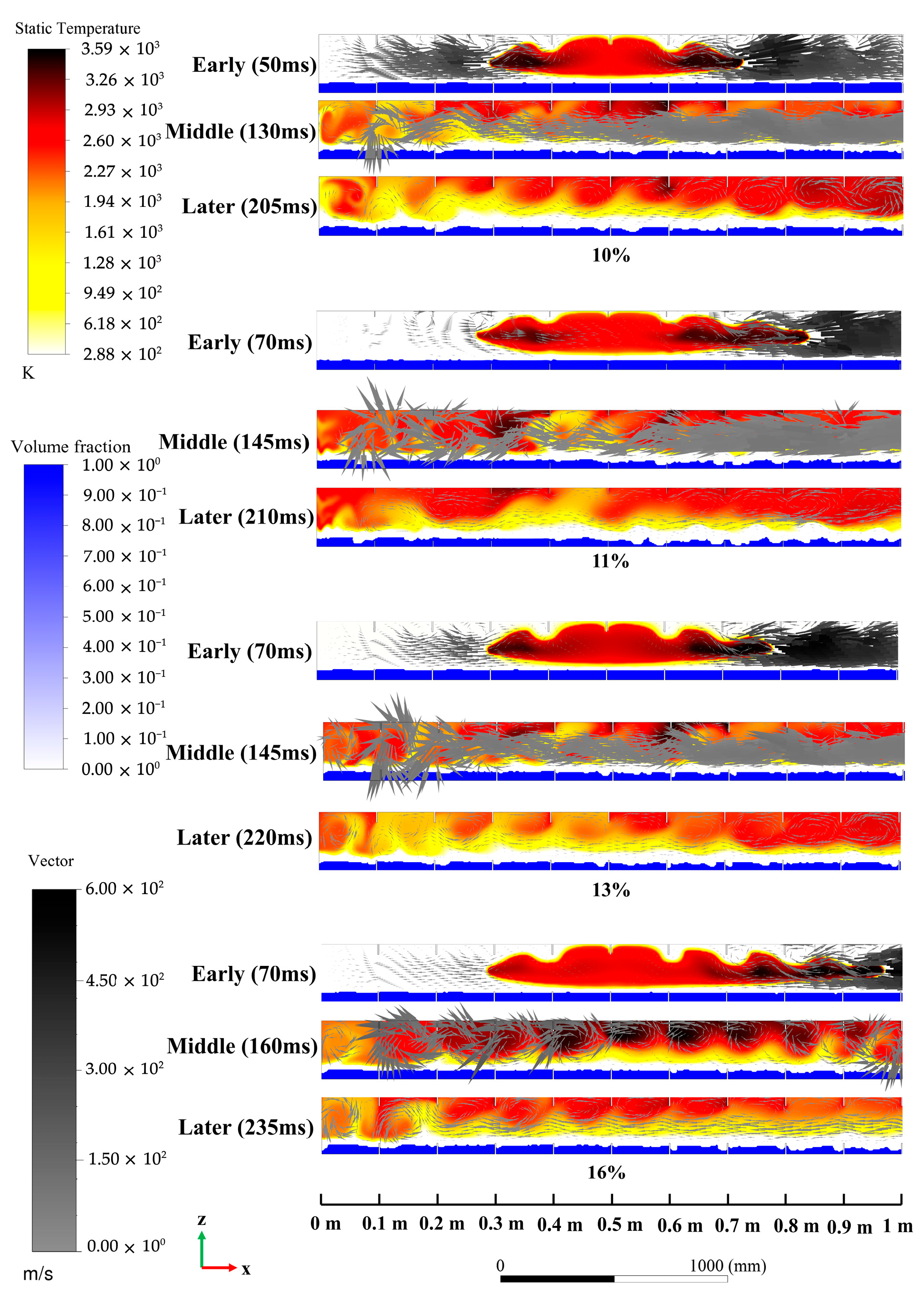
4.1. Analysis of the Influence of Explosion Flame Propagation
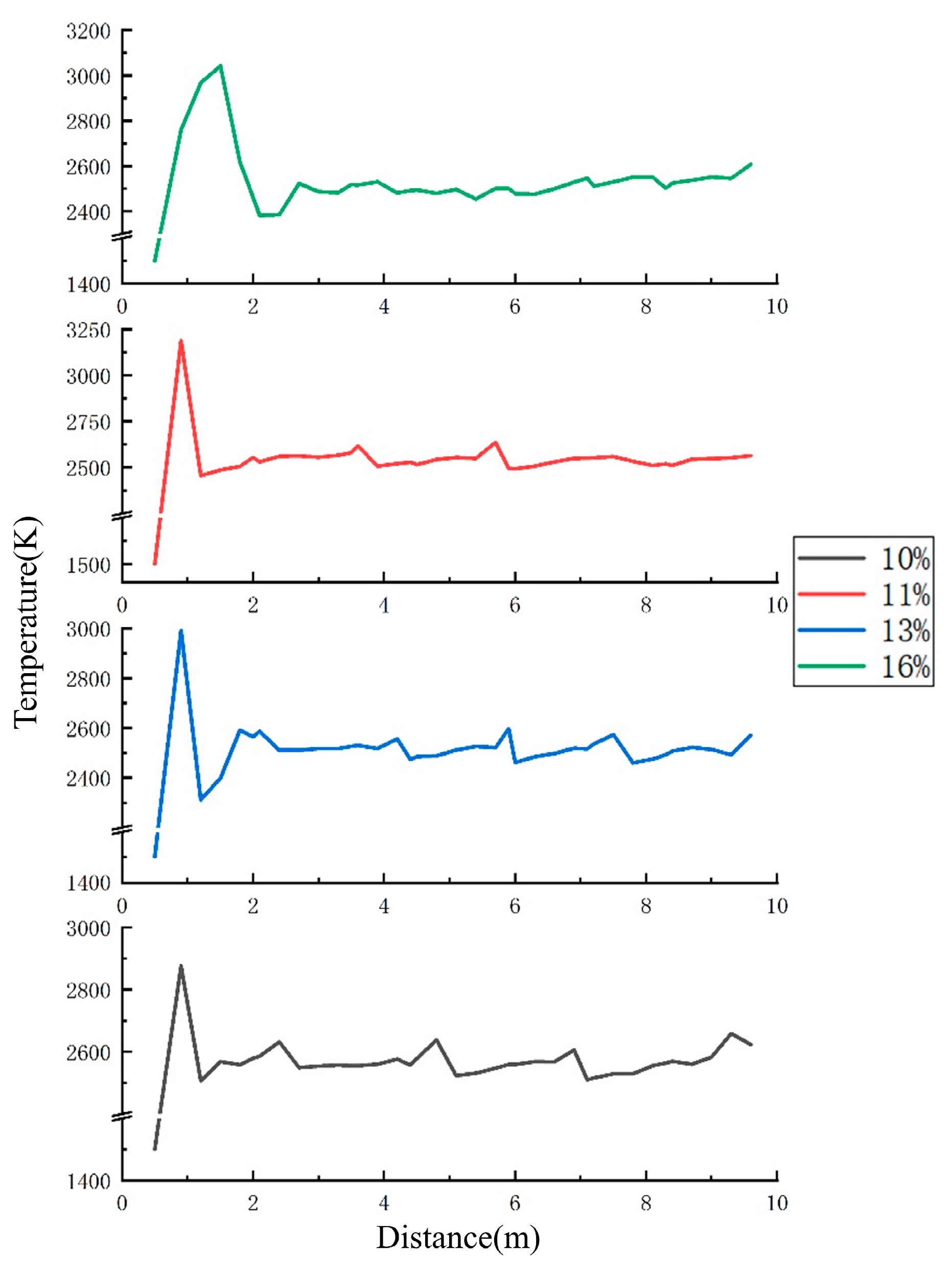
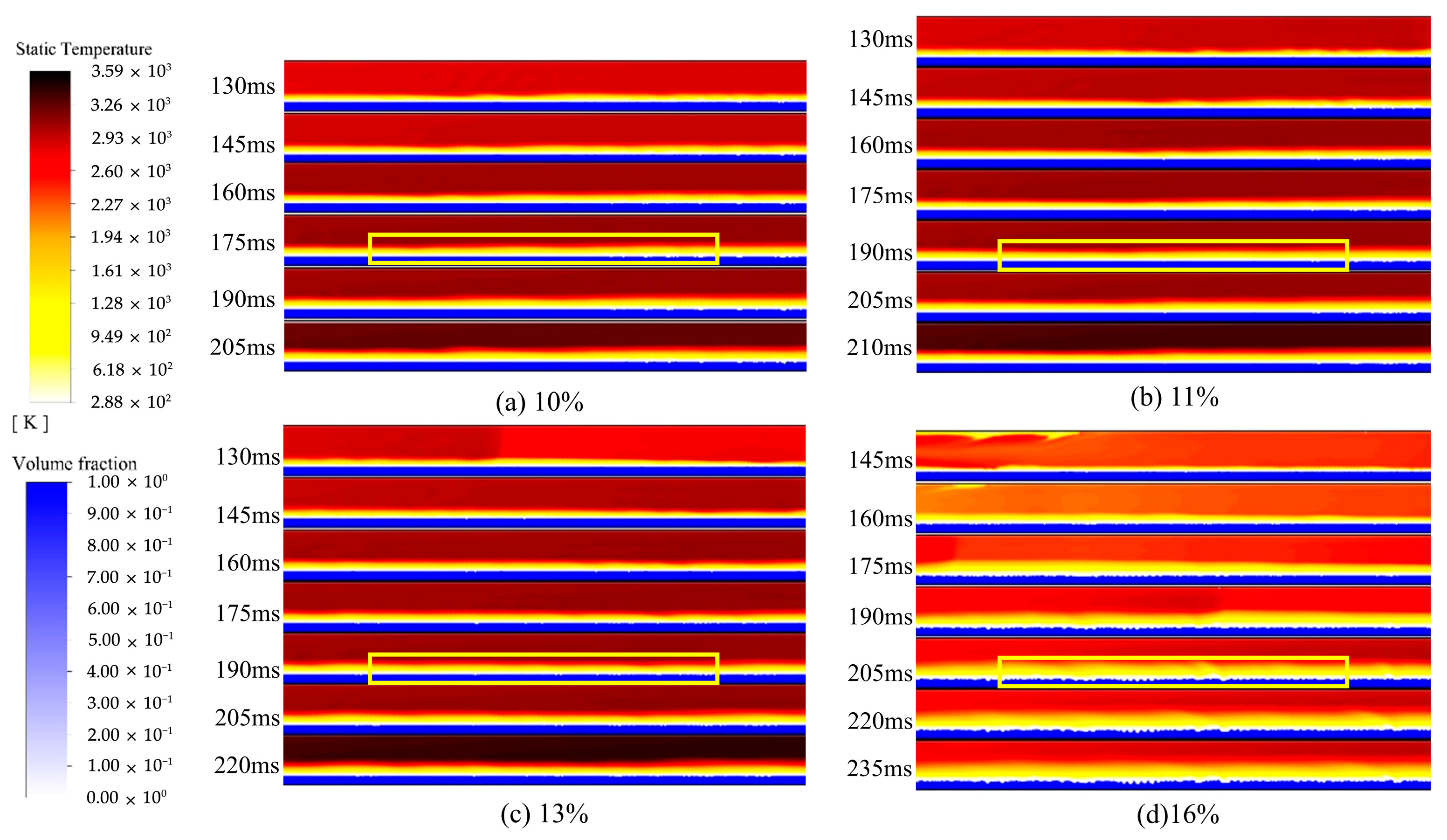
4.2. Analysis of the Influence of Explosion Temperature Propagation
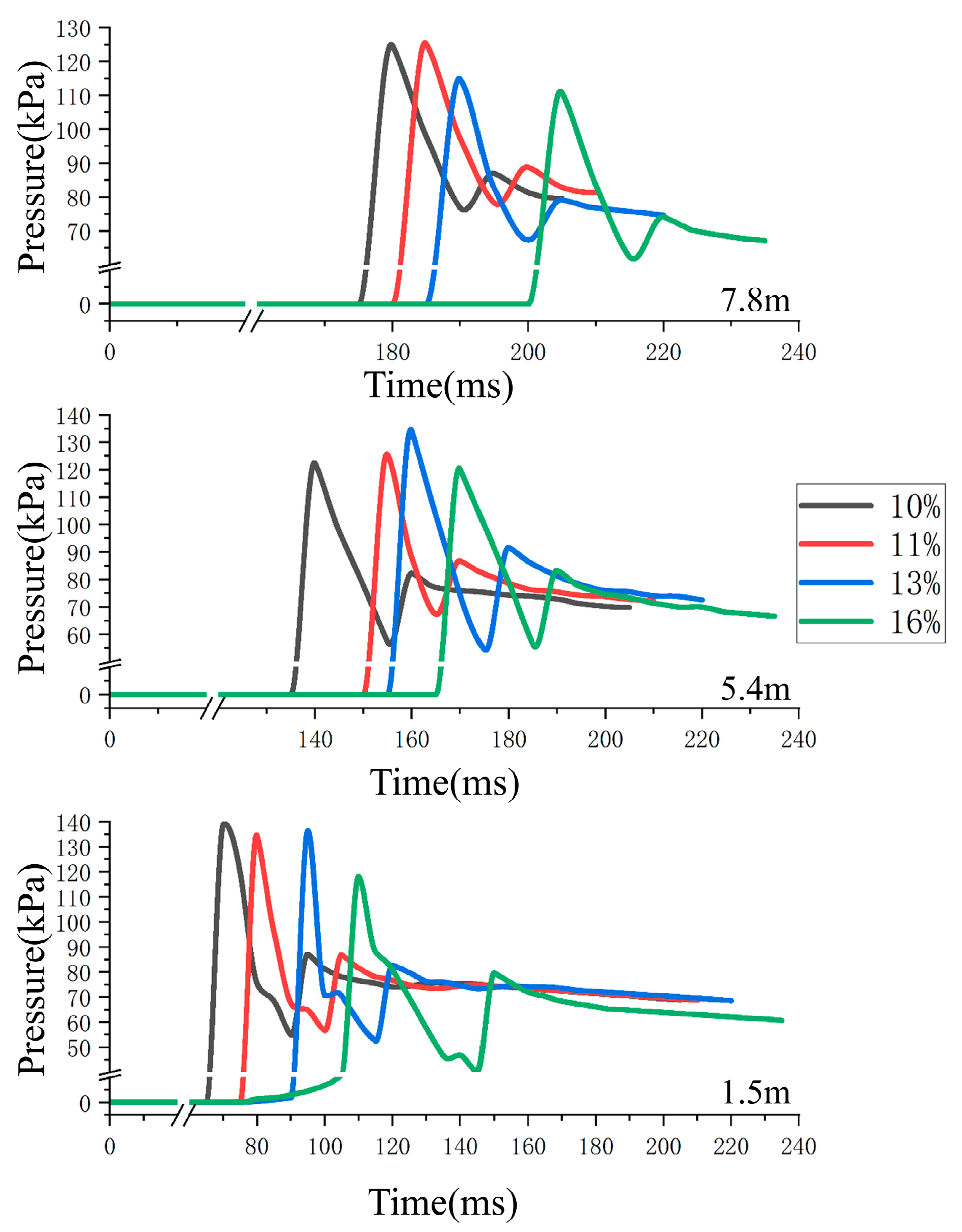
4.3. Analysis of the Influence of Explosion Pressure Propagation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, X.M.; Tan, Y.F.; Zhang, T.T. Numerical study on the diffusion process of pinhole leakage of natural gas from underground pipelines to the soil. J. Nat. Gas Sci. Eng. 2021, 87, 103792. [Google Scholar] [CrossRef]
- Gao, J.F.; He, X.D.; Qiu, Y.Q. Experiment and numerical simulation on oil vapor explosion in oil pipelines. Oil Gas Storage Transp. 2019, 38, 71–75. [Google Scholar] [CrossRef]
- Zhang, S.C.; Mou, S.J.; Zhao, Y. Discussion into Safety Risk Evaluation and Accident Investigation Methods—Reflections on Oil Pipe Explosion Accident in Qingdao on Nov. 22. Saf. Health Environ. 2015, 15, 7–10+27. [Google Scholar]
- Blanchard, R.; Arndt, D.; Grätz, R. Explosions in closed pipes containing baffles and 90 degree bends. J. Loss Prev. Process Ind. 2010, 23, 253–259. [Google Scholar] [CrossRef]
- Zhu, P.K. Study on Influence of Ambient Factors on Methane Explosive Limit Concentration. Coal Technol. 2019, 38, 108–111. [Google Scholar] [CrossRef]
- Jiao, F.Y.; Huo, Y.J.; Liu, J.B. Experimental study on influence of mixing uniformity on methane explosion characteristics. China Saf. Sci. J. 2018, 28, 38–42. [Google Scholar] [CrossRef]
- Liu, K.X.; Liu, W.; Sun, Y.S. Influence of multi-factor coupling on methane explosion characteristics. Explos. Shock. Waves 2023, 43, 032101. [Google Scholar] [CrossRef]
- Movileanu, C.; Gosa, V.; Razus, D. Propagation of ethylene–air flames in closed cylindrical vessels with asymmetrical ignition. Process Saf. Environ. Prot. 2015, 96, 167–176. [Google Scholar] [CrossRef]
- Zeng, W.P.; Li, Z.; Li, H.B. Experimental Study on the Explosion Limits of Methane at Elevated Temperature and Pressure. Oil-Gas-Fleld Surf. Eng. 2017, 36, 16–19. [Google Scholar] [CrossRef]
- Jiang, B.Y.; Liu, Z.G.; Shi, S.L.; Cai, F.; Liu, J.; Tang, M.Y.; Lin, B.Q. Influences of fuel concentration, fuel volume, initial temperature, and initial pressure on flame propagation and flameproof distance of methane-air deflagrations. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 1710–1728. [Google Scholar] [CrossRef]
- Su, B.; Luo, Z.; Wang, T. Experimental and numerical evaluations on characteristics of vented methane explosion. J. Cent. South Univ. 2020, 27, 2382–2393. [Google Scholar] [CrossRef]
- Yu, R.Z.; Qiu, Y.Y.; Xing, H.D. Experimental investigation on initiation mechanism, overpressure, and flame propagation characteristics of methane-air mixtures explosion induced by hexogen in a closed pipeline. Energy 2024, 288, 129746. [Google Scholar] [CrossRef]
- Liang, X.X.; Liao, Y.L.; Wang, Z.Q. Explosion Load Characteristics of Fuel—Air Mixture in a Vented Chamber: Analysis and New Insights. Energies 2024, 17, 5649. [Google Scholar] [CrossRef]
- Wan, H.; Wen, Y.; Zhang, Q. Flame behaviors and explosion characteristics of two-phase propylene oxide/air mixture under different ambient pressures. Process Saf. Prog. 2022, 42, 126–140. [Google Scholar] [CrossRef]
- Shi, G.Q.; Zhou, T.; Liu, M.X. Numerical analysis on methane explosion hazard during the process of fire zone sealing 1ncoal mine. J. China Univ. Min. Technol. 2017, 46, 10. [Google Scholar]
- Wang, S.; Xiao, G.; Mi, H. Experimental and numerical study on flame fusion behavior of premixed hydrogen/methane explosion with two-channel obstacles. Fuel 2023, 333, 126530. [Google Scholar] [CrossRef]
- Jiao, W.; Song, B.; Cen, K.; Zhang, H.; Liu, G.; Tian, X. Experimental and numerical study on explosion characteristics and hazards of methane-air mixtures in a chamber. Energy Sources Part A Recovery Util. Environ. Eff. 2021, 1–19. [Google Scholar] [CrossRef]
- RNG k-Epsilon Model. Available online: https://www.cfd-online.com/Wiki/RNG_k-epsilon_model (accessed on 3 October 2024).
- Bakker, A. Lecture 10-Turbulence Models. Available online: http://www.bakker.org/dartmouth06/engs150/10-rans.pdf (accessed on 21 October 2024).
- K-Epsilon Turbulence Model. Available online: https://en.wikipedia.org/wiki/K-epsilon_turbulence_model#cite_note-fvmethod-2 (accessed on 8 November 2024).
- Zhang, Q.; Qian, X.; Fu, L.; Yuan, M.; Chen, Y. Shock wave evolution and overpressure hazards in partly premixed gas deflagration of DME/LPG blended multi-clean fuel. Fuel 2020, 268, 117368. [Google Scholar] [CrossRef]
- Ansys. (n.d.). Reactions. Available online: https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v221/en/flu_ug/flu_ug_Reactions.html%23flu_ug_Reactions (accessed on 28 November 2024).
- Vaishnavi, G.; Ramarajan, J.; Jayavel, S. Numerical studies of bubble formation dynamics in gas-liquid interaction using Volume of Fluid (VOF) method. Therm. Sci. Eng. Prog. 2023, 39, 101718. [Google Scholar] [CrossRef]
- Wu, J.; Li, Y.; Wang, Y. Three-dimension simulation of two-phase flows in a thin gas flow channel of PEM fuel cell using a volume of fluid method. Int. J. Hydrogen Energy 2020, 45, 29730–29737. [Google Scholar] [CrossRef]
- Ji, T.C. Experimental Study of Methane Explosion Under Gas Liquid Coexistence Condition in a Confined Space; School of Mechatronical Engineering, Beijing Institute of Technology: Beijing, China, 2019. [Google Scholar]
- Huang, Z.; Liu, Z.; Chen, S.; Zhang, Y.; Zhang, Y. Numerical simulation and study on the transmission law of flame and pressure wave of pipeline gas explosion. Saf. Sci. 2012, 50, 806–810. [Google Scholar] [CrossRef]
- Zhang, Q.; Fu, L.; Li, Z.; Fan, T.; Ma, Y.; Cai, P.; Qian, X.; Zhang, R.; Chen, Y. Coupling mechanism of natural gas deflagration flame and continuous water in closed pipeline. Process Saf. Environ. Prot. 2020, 143, 177–185. [Google Scholar] [CrossRef]
- Zhou, G.; Kong, Y.; Cui, Y.; Qian, X. The law of gas explosion and gas-liquid coupling in urban underground drainage pipelines. Explos. Shock Waves 2024, 44, 032101. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2016; pp. 108–111. [Google Scholar]
- Zhang, P. Numerical Simulation and Experimental Research on Explosion Process of Pressure Vessel Based on Fluentd; Jiangxi University of Science and Technology: Ganzhou, China, 2021. [Google Scholar]
- Kessler, D.A.; Gamezo, R.N.; Oran, R.S. Simulations of flame acceleration and deflagration-to-detonation transitions in methane–air systems. Combust. Flame 2010, 157, 2063–2077. [Google Scholar] [CrossRef]
- Zhao, H.Y. The Principles of Gas and Dust Explosions. Beijing Institute of Technology Press: Beijing, China, 1996; pp. 72–89. [Google Scholar]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, X.; Cheng, J.; Zhang, Y.; Wang, Z. The Influence of Different Concentrations of Methane in Ditches on the Propagation Characteristics of Explosions. Fire 2025, 8, 275. https://doi.org/10.3390/fire8070275
Liang X, Cheng J, Zhang Y, Wang Z. The Influence of Different Concentrations of Methane in Ditches on the Propagation Characteristics of Explosions. Fire. 2025; 8(7):275. https://doi.org/10.3390/fire8070275
Chicago/Turabian StyleLiang, Xingxing, Junjie Cheng, Yibo Zhang, and Zhongqi Wang. 2025. "The Influence of Different Concentrations of Methane in Ditches on the Propagation Characteristics of Explosions" Fire 8, no. 7: 275. https://doi.org/10.3390/fire8070275
APA StyleLiang, X., Cheng, J., Zhang, Y., & Wang, Z. (2025). The Influence of Different Concentrations of Methane in Ditches on the Propagation Characteristics of Explosions. Fire, 8(7), 275. https://doi.org/10.3390/fire8070275





