Multimessenger Studies with the Pierre Auger Observatory †
Abstract
1. Introduction
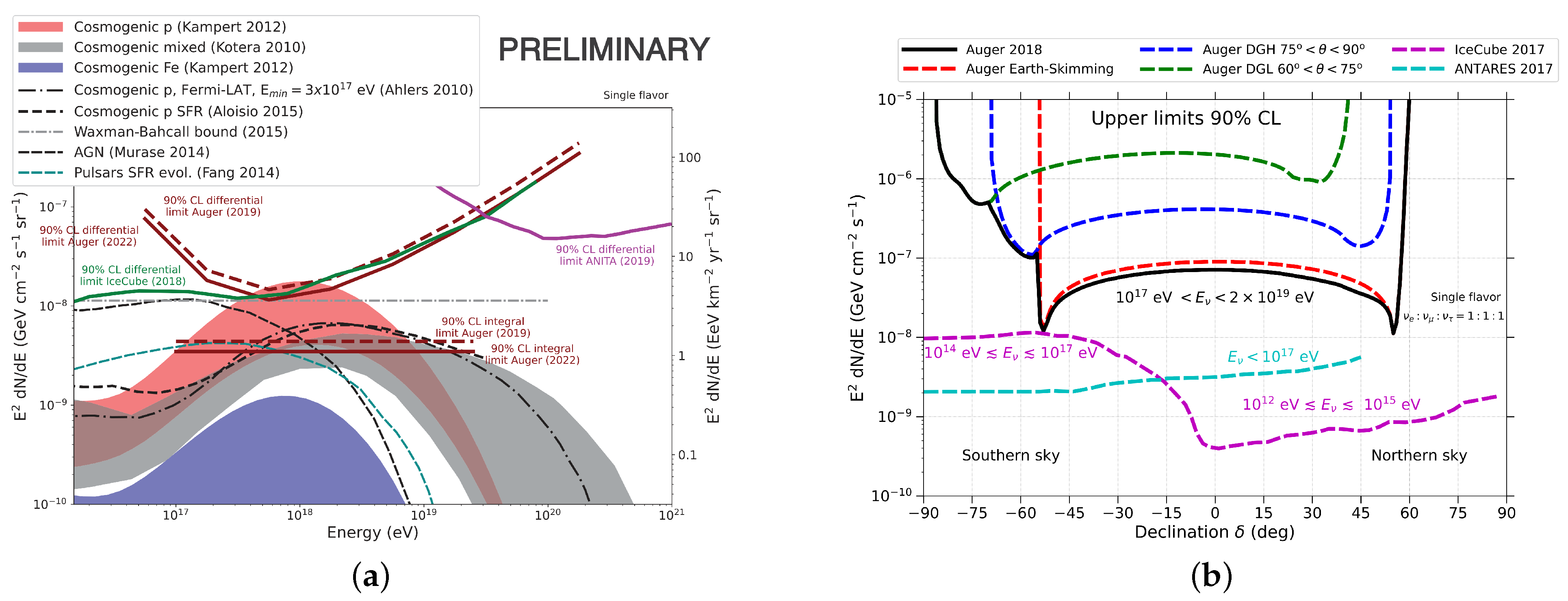
2. Neutrino Search
3. Neutrinos and Gravitational Waves
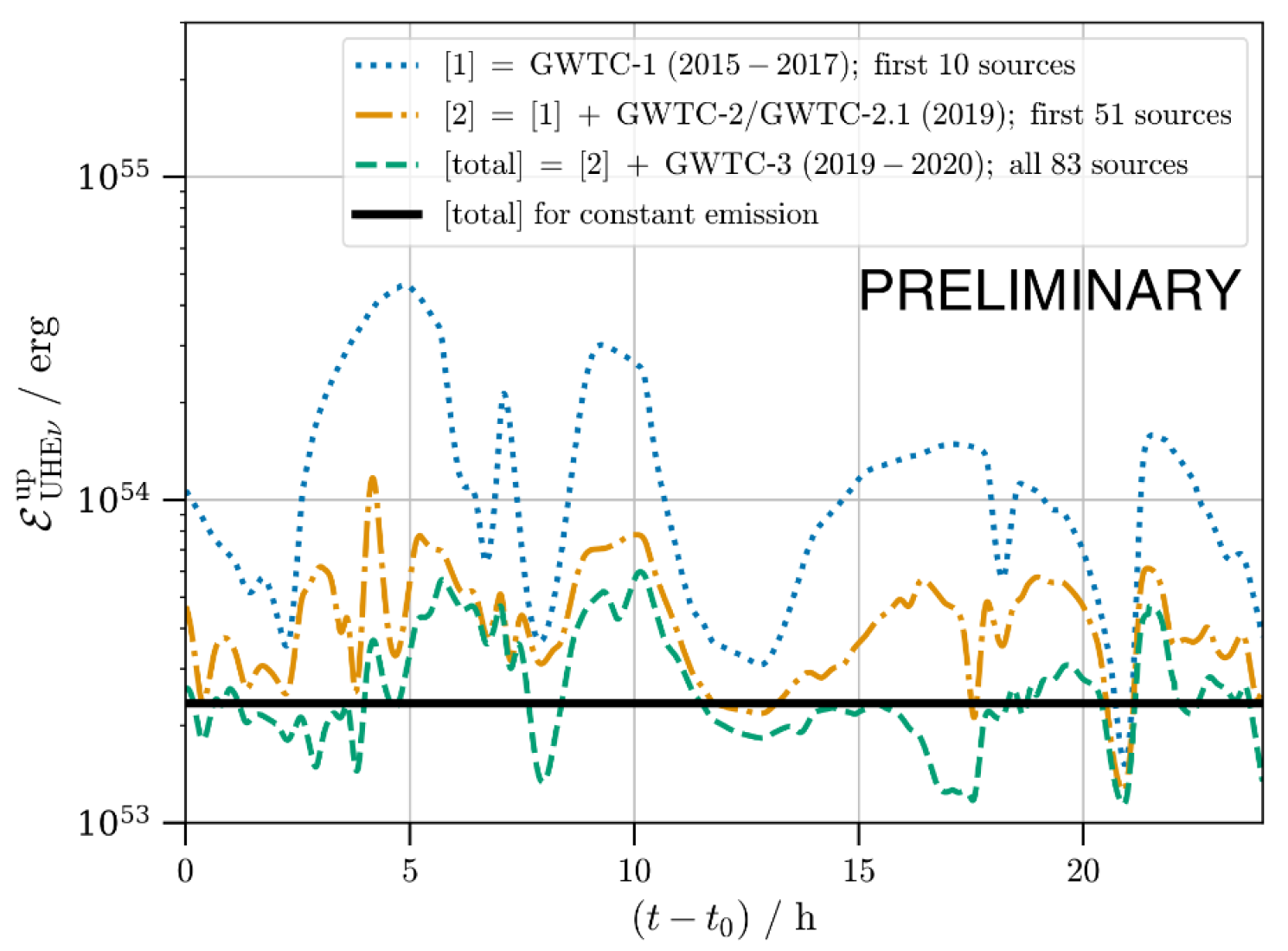
3.1. Binary Black Hole Merger Neutrinos
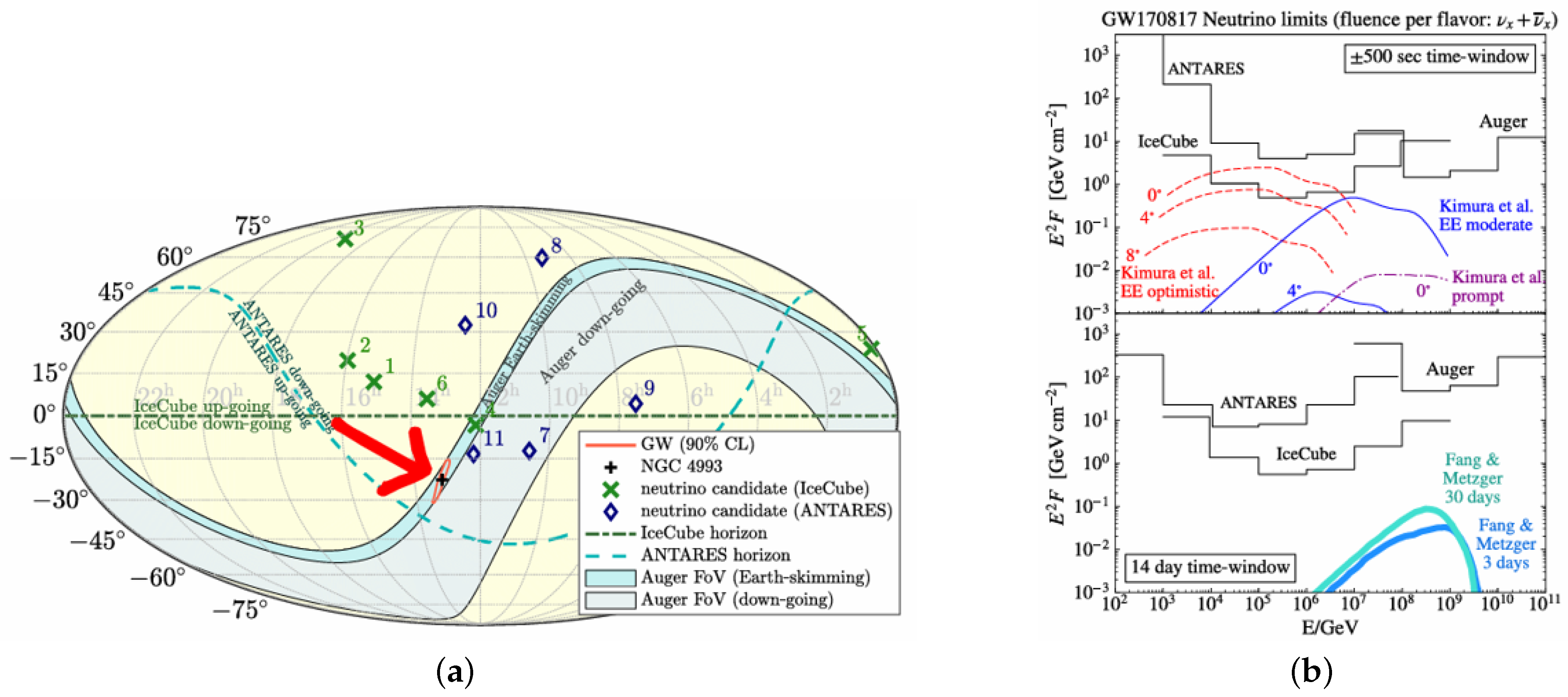
3.2. Binary Neutron Star Merger Neutrinos
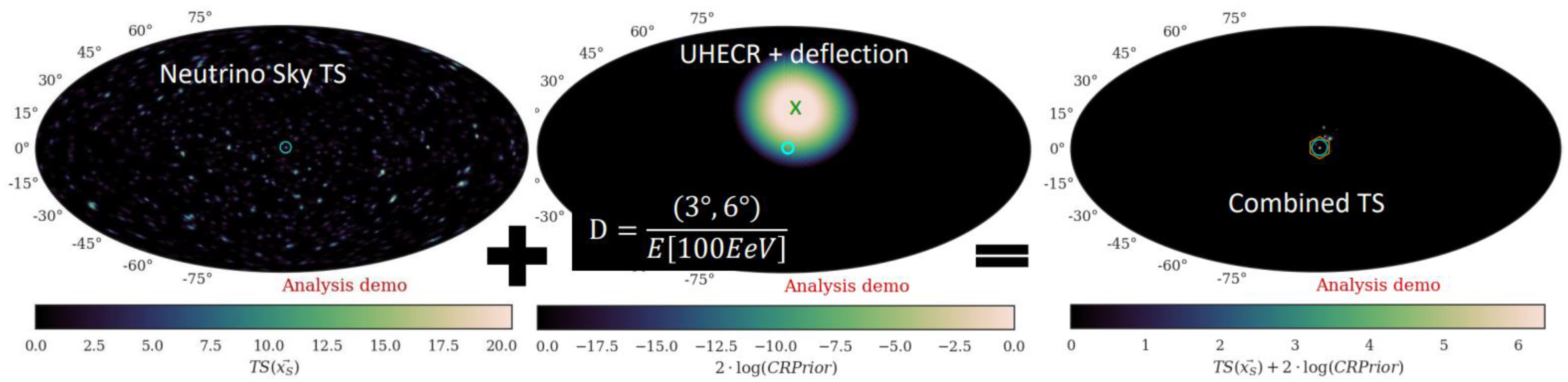
4. UHECR and Neutrinos
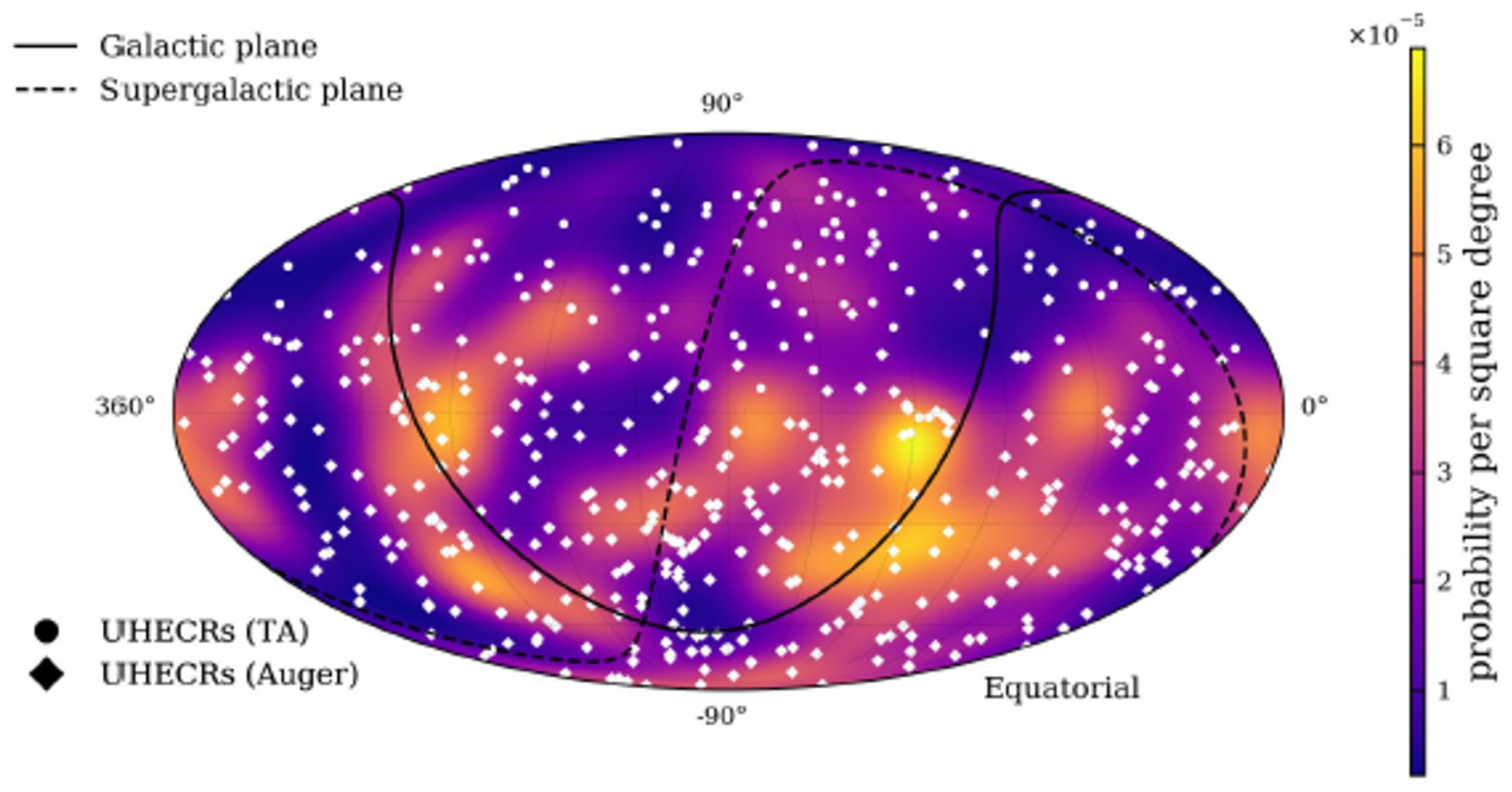
4.1. Arrival Direction Cross-Correlation
4.2. UHECR Excess Around High-Energy Neutrinos
4.3. Neutrino Excess Around Extreme UHECR
5. Neutrons and Galactic Gamma-Rays
6. Outlook
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aab, A.; Aminaei, A.; Buitink, S.; Coppens, J.M.S.; de Jong, S.J.; De Mauro, G.; Dolron, P.; Falcke, H.; Grebe, S.; Grillo, A.F.; et al. The Pierre Auger Cosmic Ray Observatory. Nucl. Instrum. Methods Phys. Res. Sect. A 2015, 798, 172–213. [Google Scholar] [CrossRef]
- Abdul Halim, A.; Abreu, P.; Aglietta, M.; Allekotte, I.; Cheminant, K.A.; Almela, A.; Aloisio, R.; Alvarez-Muñiz, J.; Yebra, J.A.; Anastasi, G.A.; et al. Latest results from the searches for ultra-high-energy photons and neutrinos at the Pierre Auger Observatory. In Proceedings of the 38th International Cosmic Ray Conference—PoS(ICRC2023), Nagoya, Japan, 26 July–3 August 2023; Volume 444, p. 1488. [Google Scholar] [CrossRef]
- Niechciol, M. Searching for neutral particles at the highest energies at the Pierre Auger Observatory. In Proceedings of the 6th International Symposium on Ultra-High Energy Cosmic Rays (UHECR2022), L’Aquila, Italy, 3–7 October 2022; Volume 283, p. 04003. [Google Scholar] [CrossRef]
- Abdul Halim, A.; Abreu, P.; Aglietta, M.; Allekotte, I.; Cheminant, K.A.; Almela, A.; Aloisio, R.; Alvarez-Muñiz, J.; Yebra, J.A.; Anastasi, G.A.; et al. Investigating the UHECR characteristics from cosmogenic neutrino limits with the measurements of the Pierre Auger Observatory. In Proceedings of the 38th International Cosmic Ray Conference—PoS(ICRC2023), Nagoya, Japan, 26 July–3 August 2023; Volume 444, p. 1520. [Google Scholar] [CrossRef]
- Aab, A.; Abreu, P.; Aglietta, M.; Albuquerque, I.F.M.; Albury, J.M.; Allekotte, I.; Almela, A.; Castillo, J.A.; Alvarez-Muñiz, J.; Anastasi, G.A.; et al. Limits on point-like sources of ultra-high-energy neutrinos with the Pierre Auger Observatory. J. Cosmol. Astropart. Phys. 2019, 2019, 004. [Google Scholar] [CrossRef]
- Schimp, M.; Abreu, P.; Aglietta, M.; Albury, J.M.; Allekotte, I.; Almela, A.; Alvarez-Muniz, J.; Batista, R.A.; Anastasi, G.A.; Anchordoqui, L.A.; et al. Combined Search for UHE Neutrinos from Binary Black Hole Mergers with the Pierre Auger Observatory. In Proceedings of the 37th International Cosmic Ray Conference—PoS(ICRC2021), Berlin, Germany, 12–23 July 2021; Volume 395, p. 968. [Google Scholar] [CrossRef]
- Albert, A.; Andre, M.; Anghinolfi, M.; Ardid, M.; Aubert, J.-J.; Aublin, J.; Avgitas, T.; Baret, B.; Barrios-Marti, J.; Basa, S.; et al. Search for High-energy Neutrinos from Binary Neutron Star Merger GW170817 with ANTARES, IceCube, and the Pierre Auger Observatory. Astrophys. J. Lett. 2017, 850, L35. [Google Scholar] [CrossRef]
- Albert, A.; Alves, S.; André, M.; Anghinolfi, M.; Ardid, S.; Aubert, J.-J.; Aublin, J.; Baret, B.; Basa, S.; Belhorma, B.; et al. Search for Spatial Correlations of Neutrinos with Ultra-high-energy Cosmic Rays. Astrophys. J. 2022, 934, 164. [Google Scholar] [CrossRef]
- Schumacher, L. Search for correlations of high-energy neutrinos and ultrahigh- energy cosmic rays. In Proceedings of the VLVnT-2018 Conference, Dubna, Russia, 1–4 October 2018; Volume 207, p. 02010. [Google Scholar] [CrossRef]
- Abdul Halim, A.; Abreu, P.; Aglietta, M.; Allekotte, I.; Cheminant, K.A.; Almela, A.; Aloisio, R.; Alvarez-Muñiz, J.; Yebra, J.A.; Anastasi, G.A.; et al. Search for evidence of neutron fluxes using Pierre Auger Observatory data. In Proceedings of the 38th International Cosmic Ray Conference—PoS(ICRC2023), Nagoya, Japan, 26 July–3 August 2023; Volume 444, p. 246. [Google Scholar] [CrossRef]
- Aab, A.; Abreu, P.; Aglietta, M.; Ahlers, M.; Ahn, E.J.; Samarai, I.A.; Albuquerque, I.F.M.; Allekotte, I.; Allen, J.; Allison, P.; et al. A Targeted Search for Point Sources of EeV Neutrons. Astrophys. J. Lett. 2014, 789, L34. [Google Scholar] [CrossRef]
- Castellina, A. AugerPrime: The Pierre Auger Observatory Upgrade. In Proceedings of the 2018 International Symposium on Ultra-High-Energy Cosmic Rays-UHECR-2018, Paris, France, 8–12 October 2018; Volume 210, p. 06002. [Google Scholar] [CrossRef]

| Parameter Definitions for Equation (1) | |
|---|---|
| Indices s: BBH Merger, p: Healpix Pixel Locations | : Non-observation 90% CL (Section 2) |
| Neutrino Emission Time Window | : Pixels inside 90% CL Solid Angle of Source s |
| : GW Source Probability (PDF) at Pointing Direction | : GW Luminosity Distance PDF |
| : Redshift | : Integrated Effective Detector Area. Function of Zenith Angle and Time. |
| Parameter Definitions for Equations (3a)–(3c) | |
|---|---|
| : # of Signal UHECR (Free Parameter) | : Total UHECR Number |
| : UHECR Event i Signal Probability | : UHECR i Background Probability (Exposure) |
| Declination of UHECR Event i | : Relative Exposure at |
| : 2-d Gaussian Around Source j | : UHECR Event Pointing-direction |
| Combined Angular Uncertainty. Gaussian STD. | : Detector Angular Resolution |
| Magnetic Deflection as a Function of Energy | |
| Parameter Definitions for Equation (4) | |
|---|---|
| : Number of Signal Events (Free Parameter) | : Source Spectrum Index (Free Parameter) |
| : UHECR and Neutrino Event Counts | : Event i Signal Probability |
| : Event i Background Probability | : Healpix Grid Point Pointing-direction |
| : UHECR Pointing-direction | : Combined Angular Uncertainty |
| Most Significant Source | Total Source Class | |||||||
|---|---|---|---|---|---|---|---|---|
| Class | R.A. | Dec. | p-Val | p∗ | Flux U.L. | E-Flux U.L. | p-Val | p-Val (Weighted) |
| msec PSRs | 286.2 | 2.1 | 0.0075 | 0.88 | 0.026 | 0.19 | 0.90 | 0.50 |
| -ray PSRs | 296.6 | −54.1 | 0.013 | 0.023 | 0.17 | 0.16 | 0.020 | |
| LMXB | 237.0 | −62.6 | 0.0069 | 0.51 | 0.017 | 0.12 | 0.62 | 0.25 |
| HMXB | 308.1 | 41.0 | 0.014 | 0.57 | 0.13 | 0.97 | 0.49 | 0.34 |
| H.E.S.S. PWN | 128.8 | −45.6 | 0.0070 | 0.18 | 0.016 | 0.12 | 0.24 | 0.0052 |
| H.E.S.S. other | 128.8 | −45.2 | 0.022 | 0.63 | 0.014 | 0.11 | 0.52 | 0.22 |
| H.E.S.S. UNID | 305.0 | 40.8 | 0.0066 | 0.31 | 0.15 | 1.1 | 0.61 | 0.75 |
| Microquasars | 308.1 | 41.0 | 0.014 | 0.19 | 0.13 | 0.95 | 0.39 | 0.81 |
| Magnetars | 249.0 | −47.6 | 0.15 | 0.99 | 0.011 | 0.079 | 0.99 | 0.98 |
| LHAASO | 292.3 | 17.8 | 0.024 | 0.20 | 0.038 | 0.28 | 0.22 | 0.42 |
| Crab | 83.6 | 22.0 | 0.71 | … | 0.22 | 0.15 | 0.71 | … |
| Gal. Center | 266.4 | −29.0 | 0.86 | … | 0.0053 | 0.039 | 0.86 | … |
| Most Significant Source | Total Source Class | |||||||
|---|---|---|---|---|---|---|---|---|
| Class | R.A. | Dec. | p-Val | p∗ | Flux U.L. | E-Flux U.L. | p-Val | p-Val (Weighted) |
| H.E.S.S. other | 288.2 | 10.2 | 0.0033 | 0.036 | 5.5 | 40.2 | 0.074 | 0.58 |
| Magnetars | 274.7 | −16.0 | 0.13 | 0.44 | 1.6 | 11.8 | 0.31 | 0.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lundquist, J.P.; the Pierre Auger Collaboration. Multimessenger Studies with the Pierre Auger Observatory. Particles 2025, 8, 45. https://doi.org/10.3390/particles8020045
Lundquist JP, the Pierre Auger Collaboration. Multimessenger Studies with the Pierre Auger Observatory. Particles. 2025; 8(2):45. https://doi.org/10.3390/particles8020045
Chicago/Turabian StyleLundquist, Jon Paul, and the Pierre Auger Collaboration. 2025. "Multimessenger Studies with the Pierre Auger Observatory" Particles 8, no. 2: 45. https://doi.org/10.3390/particles8020045
APA StyleLundquist, J. P., & the Pierre Auger Collaboration. (2025). Multimessenger Studies with the Pierre Auger Observatory. Particles, 8(2), 45. https://doi.org/10.3390/particles8020045








