A Review of the Science and Logic Associated with Approach Used in the Universal Soil Loss Equation Family of Models
Abstract
1. Introduction
2. The USLE/RUSLE Model Factors
2.1. The R Factor
2.2. The K Factor
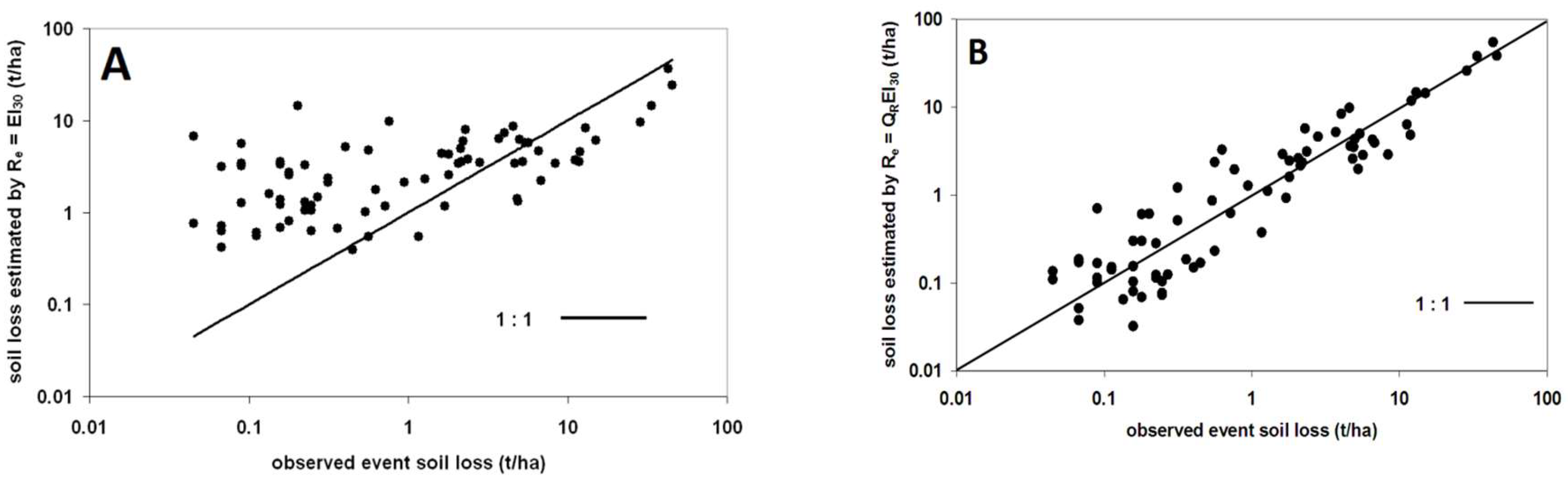
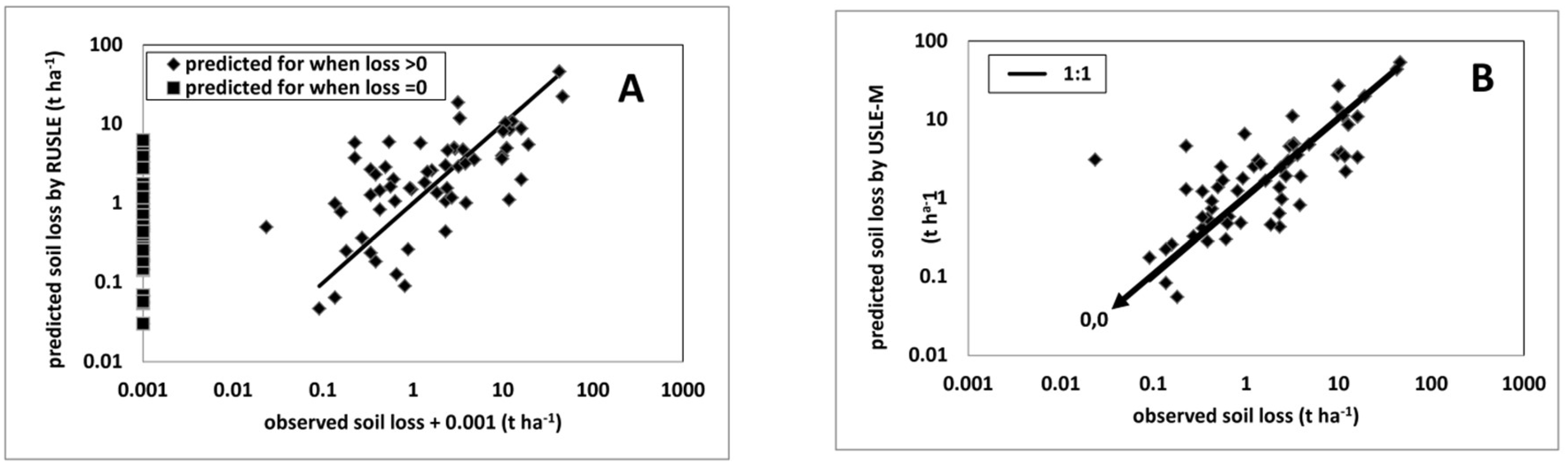
2.3. Alternatives to EI30
2.4. The L Factor
2.5. The S Factor
2.6. The C Factor
2.7. The P Factor
3. Accounting for Deposition through Changes in Slope Gradient and Vegetation
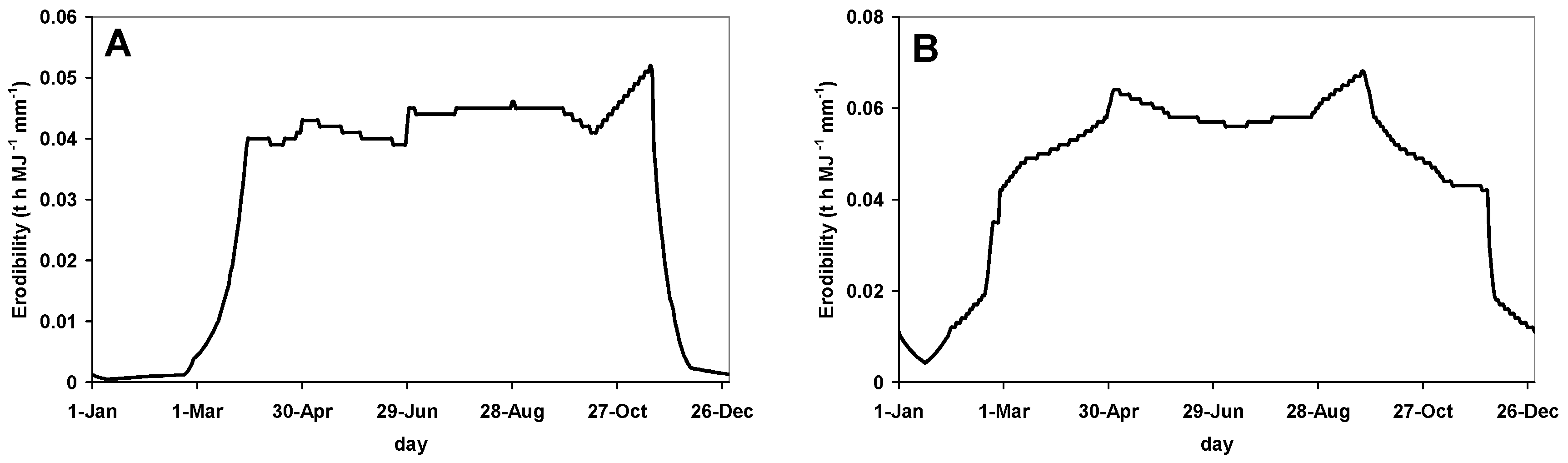
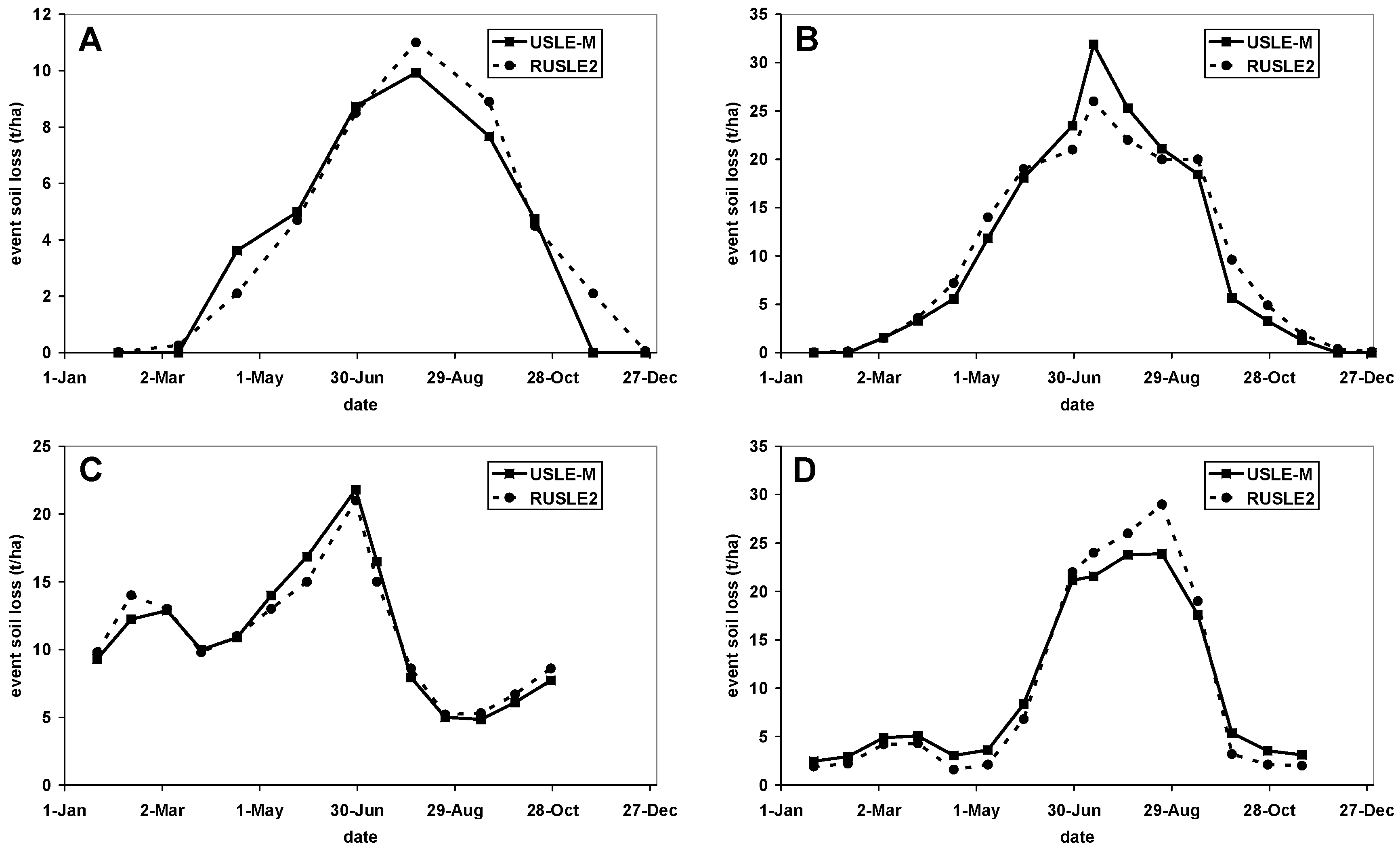
4. Dealing with the Effect of How Soil Loss Varies during the Year
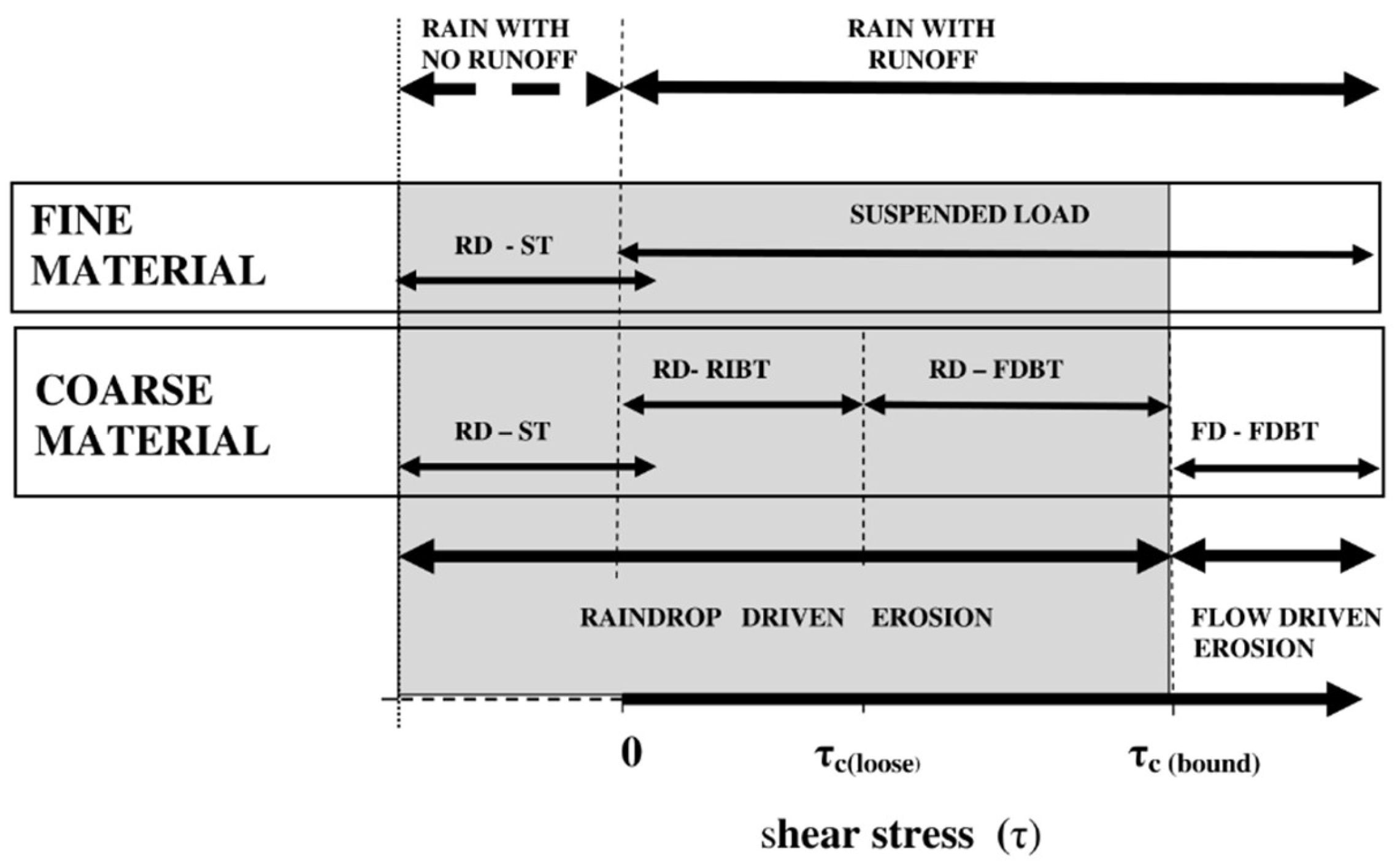
5. Accounting for the Effects of Rill Erosion
6. The Unit Plot as the Physical Model
7. What Next?
Funding
Conflicts of Interest
References
- Wischmeier, W.; Smith, D. Rainfall-erosion losses from cropland east of the Rocky Mountains, guide for selection of practices for soil and water conservation. In Agriculture Handbook; United States Department of Agriculture: Washington, DC, USA, 1965; p. 282. [Google Scholar]
- Wischmeier, W.H.; Smith, D.D. Predicting rainfall erosion losses—A guide to conservation planning. In USDA Agricultural Handbook; United States Department of Agriculture: Washington, DC, USA, 1978; p. 537. [Google Scholar]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting soil erosion by water: A guide to conservation planning with the revised universal soil loss equation (RUSLE). In U.S. Department of Agriculture Agricultural Handbook. No. 703; US Department of Agriculture: Washington, DC, USA, 1997. [Google Scholar]
- Flanagan, D.; Nearing, M. USDA-Water Erosion Prediction Project: Hillslope Profile and Watershed Model Documentation; NSERL Report; Flanagan, D., Nearing, M., Eds.; United States Department of Agriculture: Washington, DC, USA, 1995.
- Zingg, A.W. Degree and length of land slope as it affects soil loss in run-off. Agric. Eng. 1940, 21, 59–64. [Google Scholar]
- Wischmeier, W.H.; Smith, D.D. Rainfall energy and its relationship to soil loss. Trans. Am. Geophys. Union 1958, 39, 285–291. [Google Scholar] [CrossRef]
- Laws, J.O.; Parsons, D.A. The relation of raindrop-size to intensity. Trans. Am. Geophys. Union 1943, 24, 452–460. [Google Scholar] [CrossRef]
- USDA, Draft User’s Reference Guide Revised Universal Soil Loss Equation Veraion 2; USDA-Agricultural Research Service: Washington, DC, USA, 2008.
- Nearing, M.A.; Yin, S.Q.; Borrelli, P.; Polyakov, V.O. Rainfall erosivity: An historical review. Catena 2017, 157, 357–362. [Google Scholar] [CrossRef]
- Kinnell, P. The Problem of Assessing the Erosive Power of Rainfall from Meteorological Observations 1. Soil Sci. Soc. Am. J. 1973, 37, 617–621. [Google Scholar] [CrossRef]
- Yang, X.; Yu, B. Modelling and mapping rainfall esosivity in New South Wales Australia. Soil Res. 2015, 53, 178–189. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K.; Yu, B.; Klik, A.; Lim, K.J.; Yang, J.E.; Ni, J.; Miao, C.; Chattopadhyay, N.; et al. Global rainfall erosivity assessment based on high-temporal resolution rainfall records. Sci. Rep. 2017, 7, 4175. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Mannering, J. Relation of soil properties to its erodibility. Soil Sci. Soc. Am. J. 1969, 33, 131–137. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Johnson, V.; Cross, C. Soil erodibility nomograph for farmland and construction sites. Soil Water Conserv. J. 1971, 5, 189–193. [Google Scholar]
- Auerswald, K.; Fiener, P.; Martin, W.; Elhaus, D. Use and misuse of the K factor equation in soil erosion modeling: An alternative equation for determining USLE nomograph soil erodibility values. Catena 2014, 118, 220–225. [Google Scholar] [CrossRef]
- Dabney, S.M.; Wilson, G.V.; McGregor, K.C.; Foster, G.R. History, residue, and tillage effects on erosion of loessial soil. Trans. ASAE 2004, 47, 767. [Google Scholar] [CrossRef]
- Romkens, M. The soil erodibility factor: A perspective. In Soil Erosion and Conservation; El-Swaify, S.A., Moldenhauer, W.C., Eds.; Soil and Water Conservation Society of America: Ankeny, IA, USA, 1985; pp. 445–461. [Google Scholar]
- Kinnell, P.I.A. Accounting for the influence of runoff on event soil erodibilities associated with the EI30 index in RUSLE2. Hydrol. Process. 2015, 29, 1397–1405. [Google Scholar] [CrossRef]
- El-Swaify, S.A.; Dangler, E.W. Erodibilities of selected tropical soils in relation to structural and hydrologic parameters. In Soil Erosion: Prediction and Control; Soil and Water Conservation Society of America: Ankeny, IA, USA, 1977; pp. 105–114. [Google Scholar]
- Loch, R.; Slater, B.; Devoil, C. Soil erodibility (Km) values for some Australian soils. Soil Res. 1998, 36, 1045–1056. [Google Scholar] [CrossRef]
- Bagarello, V.; Di Stefano, C.; Ferro, V.; Giordano, G.; Iovino, M.; Pampalone, V. Estimating the USLE soil erodibility factor in Sicily, south Italy. Appl. Eng. Agric. 2012, 28, 199–206. [Google Scholar] [CrossRef]
- Panagos, P.; Meusburger, K.; Ballabio, C.; Borrelli, P.; Alewell, C. Soil erodibility in Europe: A high-resolution dataset based on LUCAS. Sci. Total Environ. 2014, 479, 189–200. [Google Scholar] [CrossRef]
- Tiwari, A.; Risse, L.; Nearing, M. Evaluation of WEPP and its comparison with USLE and RUSLE. Trans. ASAE 2000, 43, 1129. [Google Scholar] [CrossRef]
- Foster, G.; Meyer, L.; Onstad, C. A runoff erosivity factor and variable slope length exponents for soil loss estimates. Trans. ASAE 1977, 20, 683–687. [Google Scholar] [CrossRef]
- Williams, J.R. Sediment-yield prediction with universal equation using runoff energy factor. In Present and Prospective Technology for Predicting Sediment Yield and Sources; Volume ARS-S-40; Agricultural Research Service: New Orleans, LA, USA, 1975; pp. 244–252. [Google Scholar]
- Onstad, C.; Foster, G. Erosion modeling on a watershed. Trans. ASAE 1975, 18, 288–292. [Google Scholar] [CrossRef]
- Williams, J.W.; Izaurralde, R.C.; Steglich, E. Agricultural Policy/Environmental Extender Model Theoretical Documantation; Blackland Research and Extension Center: Temple, TX, USA, 2008.
- Williams, J.; Jones, C.; Dyke, P. The EPIC Model. In An Erosion/Productivity Impact Calculator: Model Documentation; Sharply, A.N., Williams, J.R., Eds.; USDA Tech Bulletin; USDA: Washington, DC, USA, 1990. [Google Scholar]
- Kinnell, P.I.A.; McGregor, K.C.; Rosewell, C.J. The IXEA Index as an Alternative to the El30 Erosivity Index. Trans. ASAE 1994, 37, 1449–1456. [Google Scholar] [CrossRef]
- Kinnell, P.I.A.; Risse, L.M. USLE-M: empirical modeling rainfall erosion through runoff and sediment concentration. Soil Sci. Soc. Am. J. 1998, 62, 1667–1672. [Google Scholar] [CrossRef]
- Kinnell, P.I.A. Event soil loss, runoff and the Universal Soil Loss Equation family of models: A review. J. Hydrol. 2010, 385, 384–397. [Google Scholar] [CrossRef]
- Hawkins, R.H.; Ward, T.J.; Woodward, D.E.; Van Mullem, J.A. (Eds.) Curve Number Hydrology: State of the Practice; American Society of Civil Engineers: Reston, VI, USA, 2008.
- Dabney, S.M.; Yoder, D.C.; Vieira, D.A.; Bingner, R.L. Enhancing RUSLE to include runoff-driven phenomena. Hydrol. Process. 2011, 25, 1373–1390. [Google Scholar] [CrossRef]
- Bagarello, V.; Di Piazza, G.V.; Ferro, V.; Giordano, G. Predicting unit plot soil loss in Sicily, south Italy. Hydrol. Process. 2008, 22, 586–595. [Google Scholar] [CrossRef]
- Bagarello, V.; Ferro, V.; Giordano, G. Testing alternative erosivity indices to predict event soil loss from bare plots in Southern Italy. Hydrol. Process. 2010, 24, 789–797. [Google Scholar] [CrossRef]
- Bagarello, V.; Ferro, V.; Giordano, G.; Mannocchi, F.; Todisco, F.; Vergni, L. Predicting event soil loss from bare plots at two Italian sites. Catena 2013, 109, 96–102. [Google Scholar] [CrossRef]
- Kinnell, P.I.A. Determining soil erodibilities for the USLE-MM rainfall erosion model. Catena 2018, 163, 424–426. [Google Scholar] [CrossRef]
- Bagarello, V.; Di Stefano, C.; Ferro, V.; Pampalone, V. Comparing theoretically suppored rainfall-runoff erosivity factors at Sparacia (Southern Italy) experimental site. Hydrol. Process. 2018, 32, 507–515. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Di Stefano, C.; Ferro, V.; Pampalone, V. Applying the USLE family of models at the Sparacia (south Italy) experimental site. Land Degrad. Dev. 2017, 28, 994–1004. [Google Scholar] [CrossRef]
- Moore, I.D.; Burch, G.J. Physical basis of the length-slope factor in the Universal Soil Loss Equation. Soil Sci. Soc. Am. J. 1986, 50, 1294–1298. [Google Scholar] [CrossRef]
- Foster, G.; Wischmeier, W. Evaluating irregular slopes for soil loss prediction. Trans. ASAE 1974, 17, 305–309. [Google Scholar] [CrossRef]
- Desmet, P.; Govers, G. A GIS procedure for automatically calculating the USLE LS factor on topographically complex landscape units. J. Soil Water Conserv. 1996, 51, 427–433. [Google Scholar]
- Yu, B.; Rosewell, C. Evaluation of WEPP for runoff and soil loss prediction at Gunnedah, NSW, Australia. Soil Res. 2001, 39, 1131–1145. [Google Scholar] [CrossRef]
- Moore, I.D.; Wilson, J.P. Length-slope factors for the Revised Universal Soil Loss Equation: Simplified method of estimation. J. Soil Water Conserv. 1992, 47, 423–428. [Google Scholar]
- Mutchler, C.; Murphree, C.; McGregor, K. Subfactor method for computing C factors for continuous cotton. Trans. ASAE 1982, 25, 327–332. [Google Scholar] [CrossRef]
- Borrelli, P.; Meusburger, K.; Ballabio, C.; Panagos, P.; Alewell, C. Object-oriented soil erosion modelling: A possible paradigm shift from potential to actual risk assessments in agricultural environments. Land Degrad. Dev. 2018, 29, 1270–1281. [Google Scholar] [CrossRef]
- Foster, G.R.; Lane, L.J.; Nowlin, J.D.; Laflen, J.M.; Young, R.A. Estimating erosion and sediment yield on field-sized areas. Trans. ASAE 1981, 24, 1253–1262. [Google Scholar] [CrossRef]
- Walling, D.E. The sediment delivery problem. J. Hydrol. 1983, 65, 209–237. [Google Scholar] [CrossRef]
- Meyer, L.; Wischmeier, W. Mathematical simulation of the process of soil erosion by water. Trans. ASAE 1969, 12, 754–758. [Google Scholar]
- Dabney, S.; Yoder, D.; Vieira, D. The application of the Revised Universal Soil Loss Equation, Version 2, to evaluate the impacts of alternative climate change scenarios on runoff and sediment yield. J. Soil Water Conserv. 2012, 67, 343–353. [Google Scholar] [CrossRef]
- Pandey, A.; Himanshu, S.K.; Mishra, S.K.; Singh, V.P. Physically based soil erosion and sediment yield models revisited. Catena 2016, 147, 595–620. [Google Scholar] [CrossRef]
- Kinnell, P.I.A. A comparison of the abilities of the USLE-M, RUSLE2 and WEPP to model event erosion from bare fallow areas. Sci. Total Environ. 2017, 596, 32–42. [Google Scholar] [CrossRef] [PubMed]
- Nicks, A.; Lane, L.; Gander, G. Weather generator, Chapter 2. USDA-Water Erosion Prediction Project Hillslope Profile and Watershed Model Documentation. NSERL Rep. 1995, 10, 1–123. [Google Scholar]
- Kinnell, P.I.A. CLIGEN as a weather generator for RUSLE2. Catena 2019, 172, 877–880. [Google Scholar] [CrossRef]
- Yu, B. Using CLIGEN to generate RUSLE climate inputs. Trans. ASAE 2002, 45, 993. [Google Scholar]
- Kinnell, P.I.A.; Yu, B. CLIGEN as a weather generator for predicting rainfall erosion using USLE based modelling systems. Land Degred. Dev. 2018. in review. [Google Scholar]
- Richardson, C.; Foster, G.; Wright, D. Estimation of erosion index from daily rainfall amount. Trans. ASAE 1983, 26, 153–156. [Google Scholar] [CrossRef]
- Moss, A.; Green, P. Movement of solids in air and water by raindrop impact. Effects of drop-size and water-depth variations. Soil Res. 1983, 21, 257–269. [Google Scholar] [CrossRef]
- Brazier, R.E.; Beven, K.J.; Freer, J.; Rowan, J.S. Equifinality and uncertainty in physically based soil erosion models: Application of the GLUE methodology to WEPP—The Water Erosion Prediction Project—For sites in the UK and USA. Earth Surface Process. Landf. 2000, 25, 825–845. [Google Scholar] [CrossRef]
- Nearing, M.; Hairsine, P. The future of soil erosion modelling. In Handbook of Erosion Modelling; John and Wiley and Sons: Hoboken, NJ, USA, 2011; pp. 387–397. [Google Scholar]
- Nearing, M.A.; Govers, G.; Norton, L.D. Variability in soil erosion data from replicated plots. Soil Sci. Soc. Am. J. 1999, 63, 1829–1835. [Google Scholar] [CrossRef]
- Kinnell, P.I.A. Comparison between the USLE, the USLE-M and replicate plots to model rainfall erosion on bare fallow areas. Catena 2016, 145, 39–46. [Google Scholar] [CrossRef]
- Wendt, R.; Alberts, E.; Hjelmfelt, A. Variability of runoff and soil loss from fallow experimental plots. Soil Sci. Soc. Am. J. 1986, 50, 730–736. [Google Scholar] [CrossRef]
- Gómez, J.A.; Nearing, M.A.; Giráldez, J.V.; Alberts, E.E. Analysis of sources of variability of runoff volume in a 40 plot experiment using a numerical model. J. Hydrol. 2001, 248, 183–197. [Google Scholar] [CrossRef]
- Baoyuan, L.; Keli, Z.; Yun, X. An empirical soil loss equation. In Proceedings 12th International Soil Conservation Organization Conference; Tsinghua University Press: Beijing, China, 2002. [Google Scholar]
- Laflen, J.M.; Flanagan, D.C. The development of US soil erosion prediction and modeling. Int. Soil Water Conserv. Res. 2013, 1, 1–11. [Google Scholar] [CrossRef]
- Nearing, M.A. Comments and Letters to the Editor-Comments on USLE-M: Empirical Modeling Rainfall Erosion through Runoff and Sediment Concentration. Soil Sci. Soc. Am. J. 2000, 64, 1137. [Google Scholar]
- Foster, G.R.; Yoder, D.C.; Weesies, G.A.; Toy, T.J. The design philosophy behind RUSLE2: Evolution of an empirical model. In Soil Erosion; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2001. [Google Scholar]
- Wang, B.; Zheng, F.; Guan, Y. Improved USLE-K factor prediction: A case study on water erosion areas in China. Int. Soil Water Conserv. Res. 2016, 4, 168–176. [Google Scholar] [CrossRef]
- Sánchez, Y.; Martínez-Graña, A.; Santos-Francés, F.; Yenes, M. Influence of the sediment delivery ratio index on the analysis of silting and break risk in the Plasencia reservoir (Central System, Spain). Nat. Hazards 2018, 91, 1–15. [Google Scholar] [CrossRef]
- Nwakor, E.; Mbajiorgu, C.; Ogbu, K. Assessment of Soil Erosion Using Rusle2 Model and GIS in Upper Ebonyi River Watershed, Enugu State, Nigeria. Int. J. Geosci. Remote Sens. 2015, 4, 7–17. [Google Scholar]
- Khaleghpanah, N.; Shorafa, M.; Asadi, H.; Gorji, M.; Davari, M. Modeling soil loss at plot scale with EUROSEM and RUSLE2 at stony soils of Khamesan watershed, Iran. Catena 2016, 147, 773–788. [Google Scholar] [CrossRef]
- Nearing, M.A. Soil erosion and conservation. In Environmental Modelling: Finding Simplicity in Complexity, 2nd ed.; John Wainwright, M.M., Ed.; John Wiley and Sons: Hoboken, NJ, USA, 2013; pp. 365–378. [Google Scholar]
- Flanagan, D.; Frankenberger, J. Ascough II, WEPP: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1463–1477. [Google Scholar] [CrossRef]
- Laflen, J.M.; Elliot, W.J.; Simanton, J.R.; Holzhey, C.S.; Kohl, K.D. WEPP: Soil erodibility experiments for rangeland and cropland soils. J. Soil Water Conserv. 1991, 46, 39–44. [Google Scholar]
- Kinnell, P.I.A. Interrill erodibilities based on the rainfall intensity flow discharge erosivity factor. Soil Res. 1993, 31, 319–332. [Google Scholar] [CrossRef]


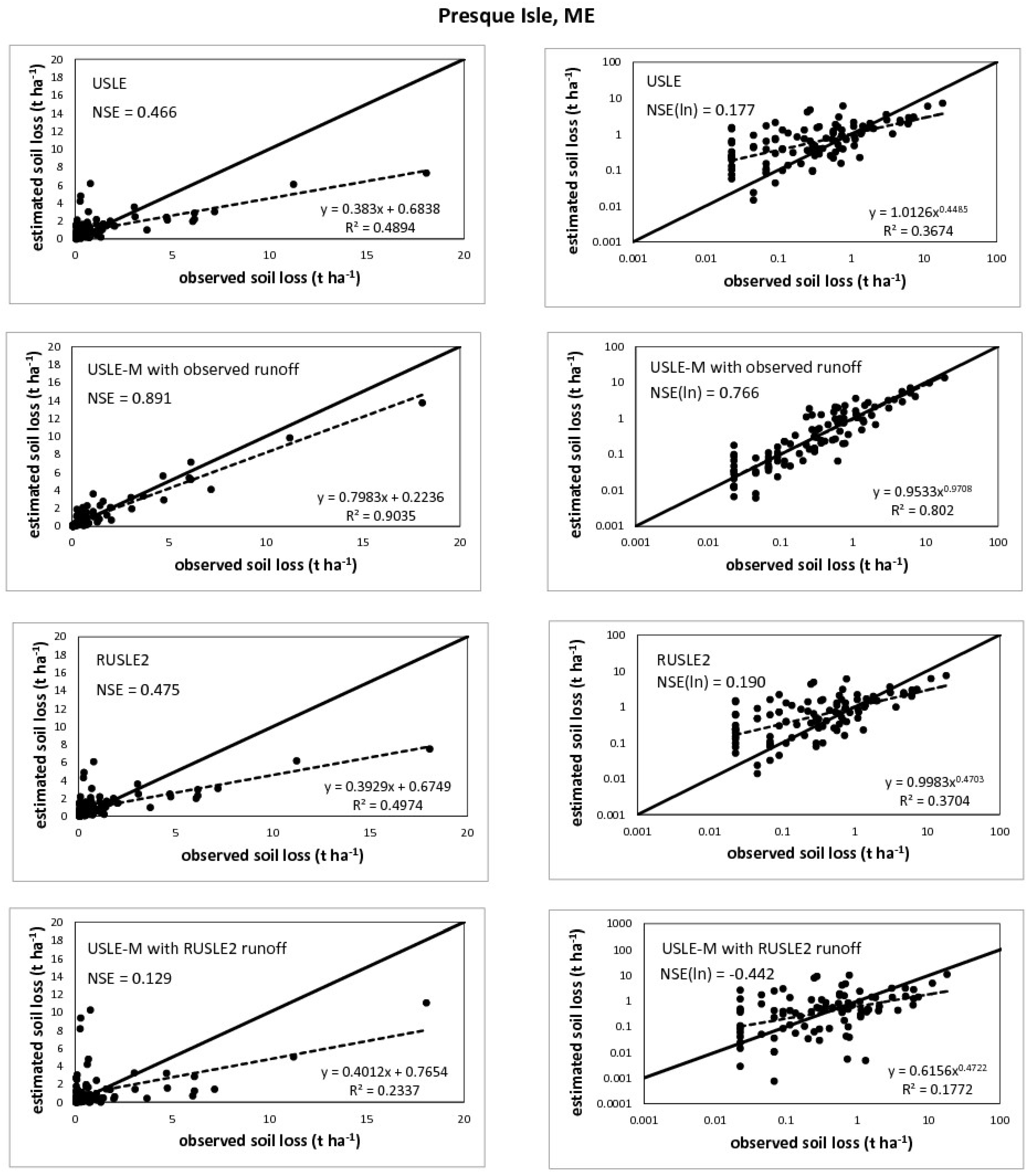
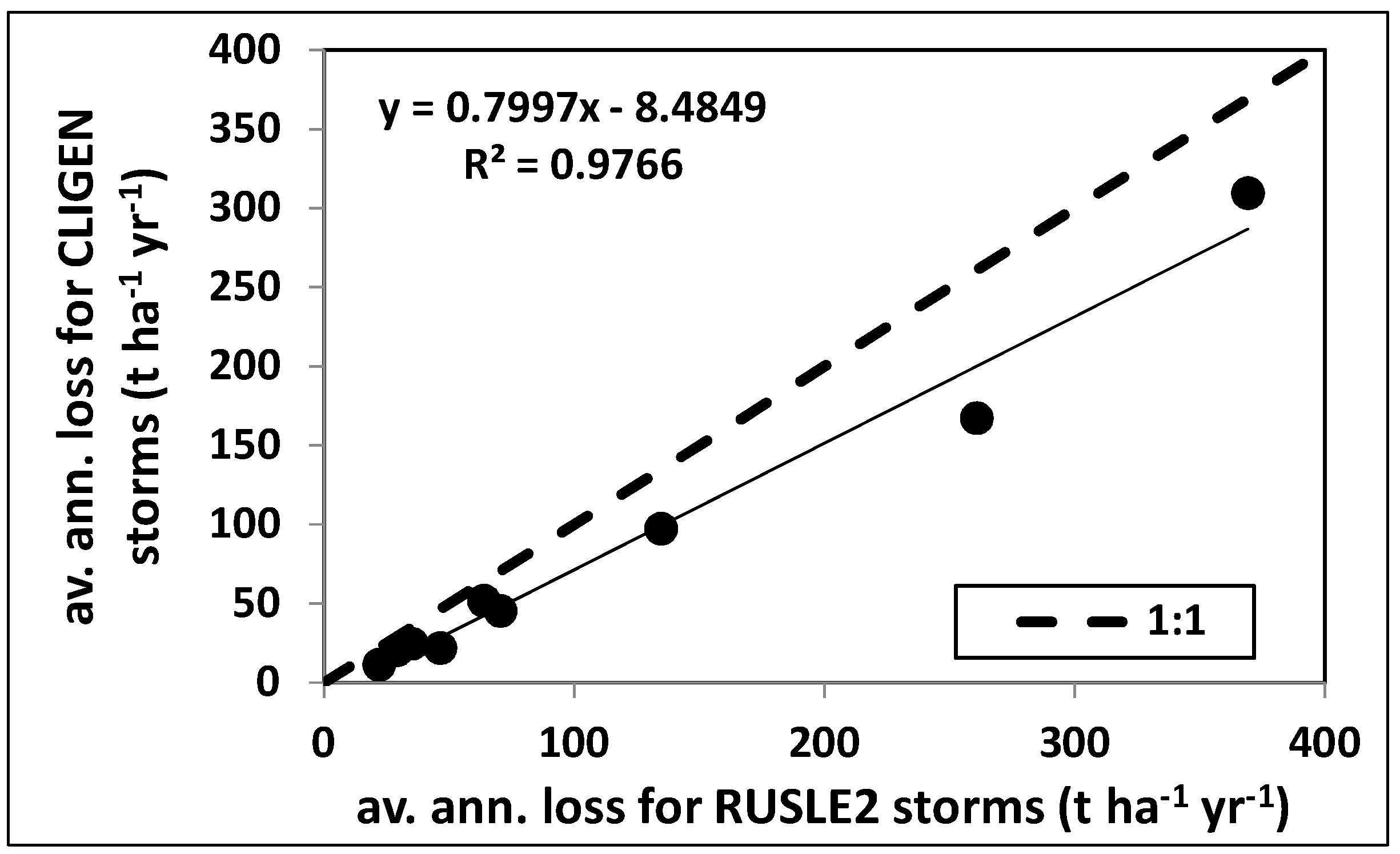

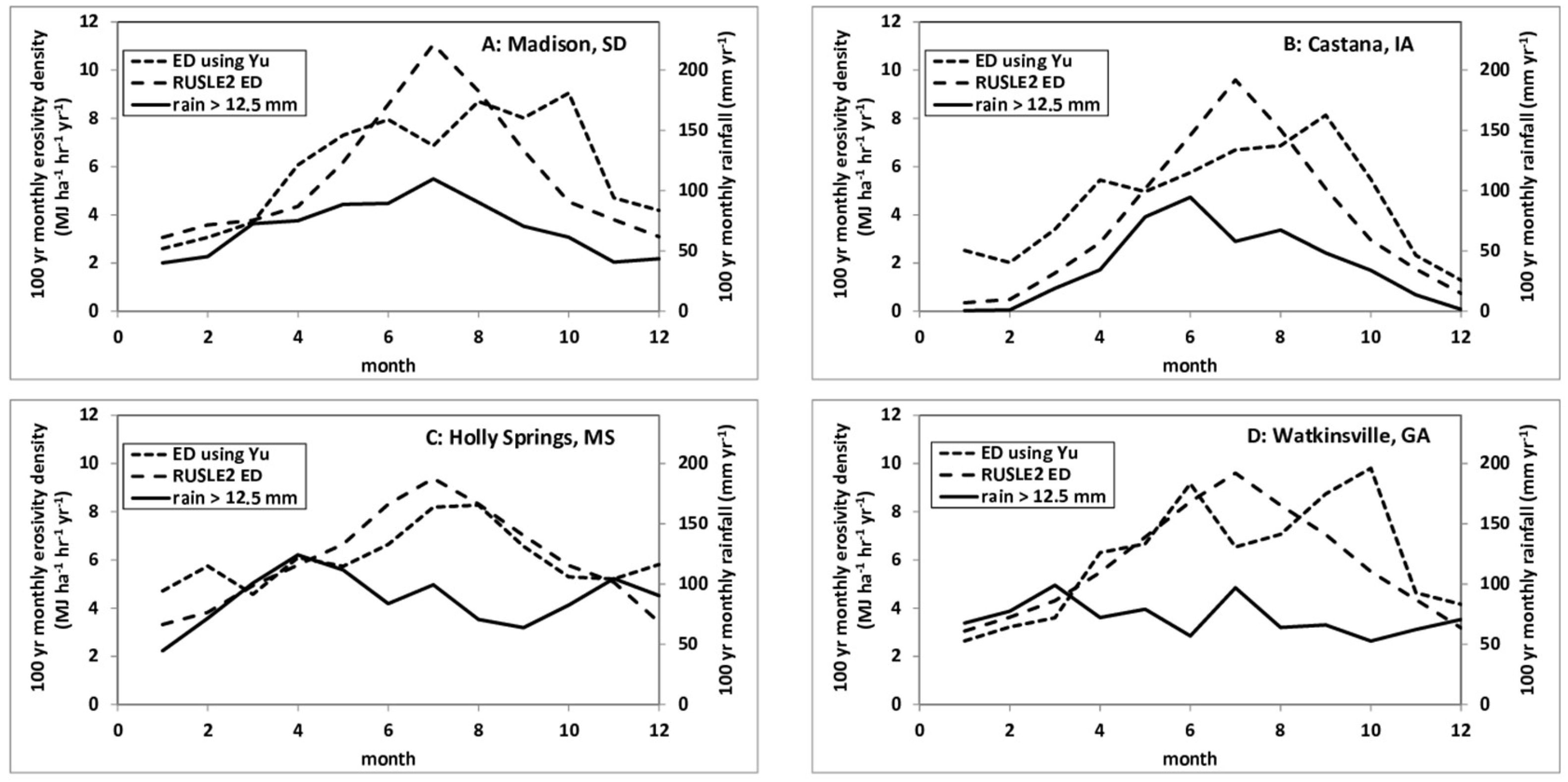
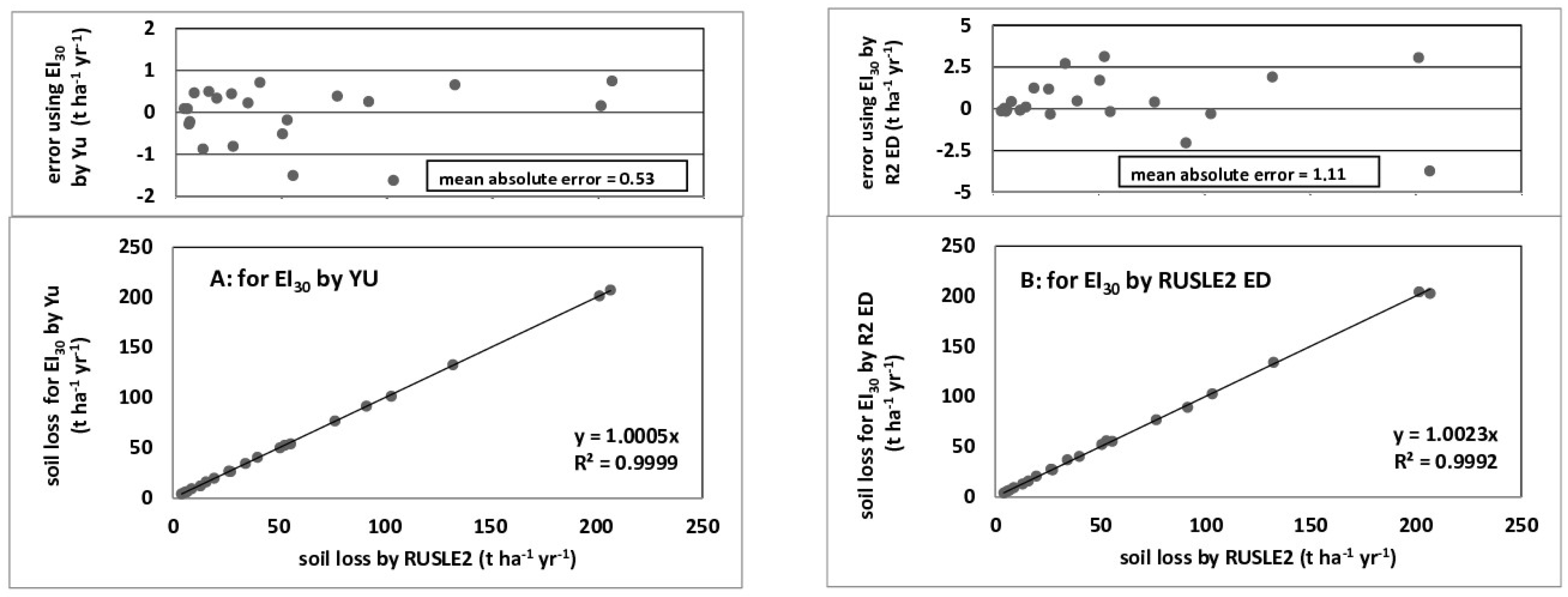
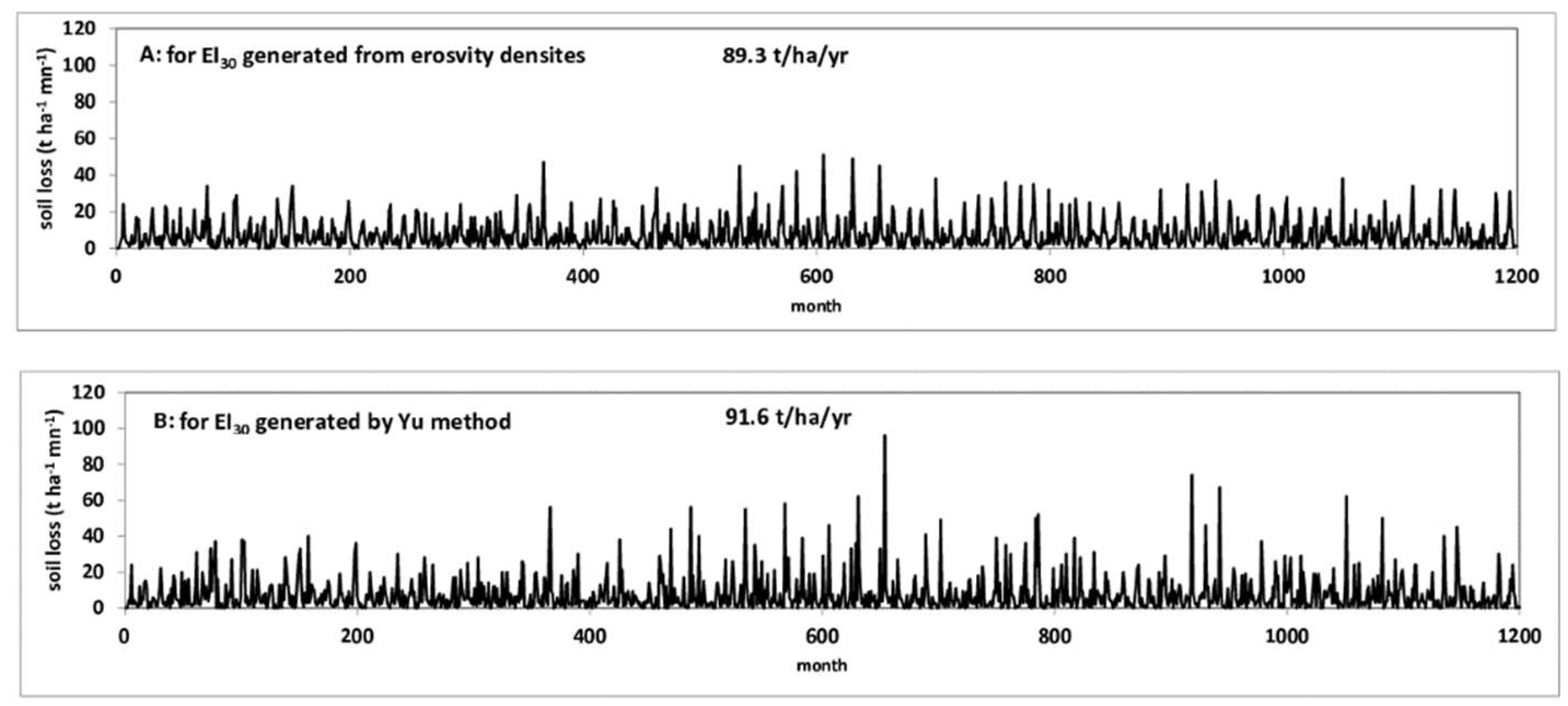


| NSE(ln) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Location | Plot No | Gradient % | QR.rope | No of Obs | USLE | RUSLE2 | USLE-M with Obs Runoff | USLE-M with RUSLE2 Runoff |
| Holly Springs, MS | 3–7 | 5.0 | 0.64 | 166 | 0.528 | 0.563 | 0.703 | 0.376 |
| Zanesville, OH | 1–8 | 12.0 | 0.59 | 287 | 0.646 | 0.644 | 0.728 | 0.469 |
| Tyler, TX | 1–9 | 8.8 | 0.30 | 192 | 0.342 | 0.372 | 0.696 | 0.358 |
| Presque Isle, ME | 1–3 | 8.0 | 0.29 | 102 | 0.177 | 0.190 | 0.766 | −0.442 |
| Location | State | County | Soil | RRUSLE2 |
|---|---|---|---|---|
| Bethany | MO | Brooke | Selby (sl) | 3330 |
| Castana | IA | Monona | Monona (l) | 2650 |
| Holly Springs | MI | Marshall | Providence (sil) | 6360 |
| Madison | SD | Lake | Egan (sicl) | 1330 |
| Presque Isle | ME | Aroostook | Caribou (Gr-l) | 1230 |
| Tifton | GA | Tilt | Tifton (sl) | 7110 |
| Watkinsville | GA | Oconee | Cecil (scl) | 5050 |
| Guthrie | OK | Logan | Stephensville (fsl) | 3800 |
| Geneva | NY | Ontario | Ontario (l) | 1380 |
| Location | RUSLE2 R | Length | Slope | RUSLE2 K | Treatment | Average Annual Soil Loss | ||
|---|---|---|---|---|---|---|---|---|
| std RUSLE2 | EI30 by Yu | EI30 by R2 ED | ||||||
| MJ mm/(ha hr yr) | m | % | t hr/(MJ mm) | t/ha/yr | t/ha/yr | t/ha/yr | ||
| Bethany | 3330 | 22.3 | 7.0 | 0.085 | continous bare fallow | 201.4 | 201.6 | 204.5 |
| 112 bu corn | 52.7 | 52.5 | 55.8 | |||||
| NT-corn soybeans NT-wheat | 15.6 | 16.1 | 15.7 | |||||
| Castana | 2650 | 22.1 | 14.0 | 0.030 | continous bare fallow | 132.2 | 132.9 | 134.1 |
| 112 bu corn | 34.2 | 34.4 | 36.9 | |||||
| corn soybeans | 19.4 | 19.7 | 20.6 | |||||
| Geneva | 1380 | 22.1 | 7.7 | 0.042 | continous bare fallow | 39.8 | 40.5 | 40.3 |
| 112 bu corn | 8.7 | 9.2 | 9.1 | |||||
| Winter Wheat | 4.0 | 4.1 | 3.8 | |||||
| Guthrie | 3800 | 22.1 | 8.0 | 0.011 | continous bare fallow | 76.4 | 76.8 | 76.9 |
| 112 bu corn | 26.4 | 26.8 | 27.5 | |||||
| wheat soybeans | 5.4 | 5.5 | 5.5 | |||||
| Holly Springs | 6360 | 22.1 | 5.0 | 0.044 | continous bare fallow | 206.6 | 207.4 | 202.9 |
| 112 bu corn | 50.5 | 50.0 | 52.2 | |||||
| cotton (fall chisel) | 91.3 | 91.6 | 89.3 | |||||
| Madison | 1670 | 22.1 | 5.6 | 0.071 | continous bare fallow | 55.5 | 54.0 | 55.3 |
| 112 bu corn | 12.9 | 12.0 | 12.8 | |||||
| corn soybeans | 6.6 | 6.4 | 6.5 | |||||
| Watkinsville | 5050 | 22.1 | 7.0 | 0.027 | continous bare fallow | 103.1 | 101.4 | 102.8 |
| 112 bu corn | 27.1 | 26.3 | 26.8 | |||||
| Model | ARUSLE2 = b ACLIGEN | ||
|---|---|---|---|
| CLIGEN EI30 by | b | r2 | Mean abs Error |
| Yu method | 1.0005 | 0.9999 | 0.528 |
| RUSLE2 ED | 1.0023 | 0.9993 | 1.113 |
| Rain2 | 1.014 | 0.9985 | 1.629 |
| Random number | 0.9928 | 0.9983 | 2.183 |
| NSE(ln) | ||||||
|---|---|---|---|---|---|---|
| Location | Plot No | Gradient % | Runoff | WEPP | USLE-M with WEPP Runoff | Mode |
| Bethany, MO | 1–9 | 7.0 | 0.123 | −0.394 | 0.300 | validation |
| 0.153 | −0.258 | 0.317 | calibration | |||
| Holly Springs, MI | C5 | 5.0 | 0.656 | 0.239 | 0.538 | validation |
| 0.689 | 0.375 | 0.605 | calibration | |||
| Presque Isle, ME | 1–3 | 8.0 | −0.125 | −0.440 | 0.214 | validation |
| 0.156 | −0.115 | 0.296 | calibration | |||
| Tifton, GA | 1–2 | 3.0 | 0.319 | −1.231 | −0.283 | validation |
| calibration | ||||||
| Watkinsville, GA | 2–47 | 7.0 | 0.281 | −0.888 | 0.280 | validation |
| 0.320 | −0.797 | 0.362 | calibration | |||
| NSLE(ln) | ||||||
|---|---|---|---|---|---|---|
| Location | Obs | Principal | Replicate | REPLICATE | USLE | USLE-M |
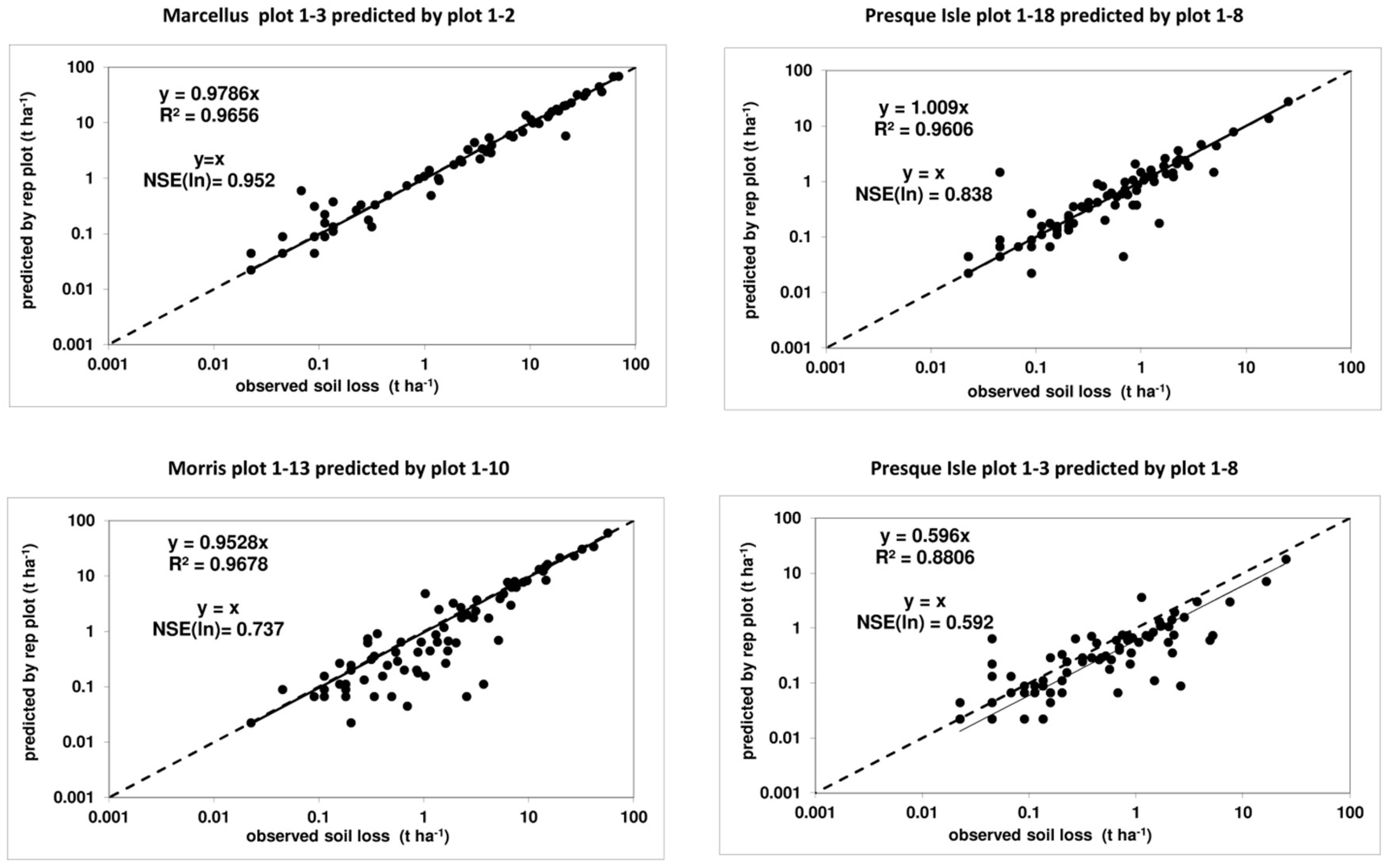
| Presque Isle | 82 | plot 1–3 | plot 1–8 | 0.592 | 0.091 | 0.693 |
| Presque Isle | 85 | plot 1–8 | plot 1–18 | 0.838 | 0.137 | 0.772 |
| Marcellus | 65 | plot 1–2 | plot 1–3 | 0.957 | 0.365 | 0.786 |
| Marcellus | 65 | plot 1–3 | plot 1–2 | 0.952 | 0.366 | 0.771 |
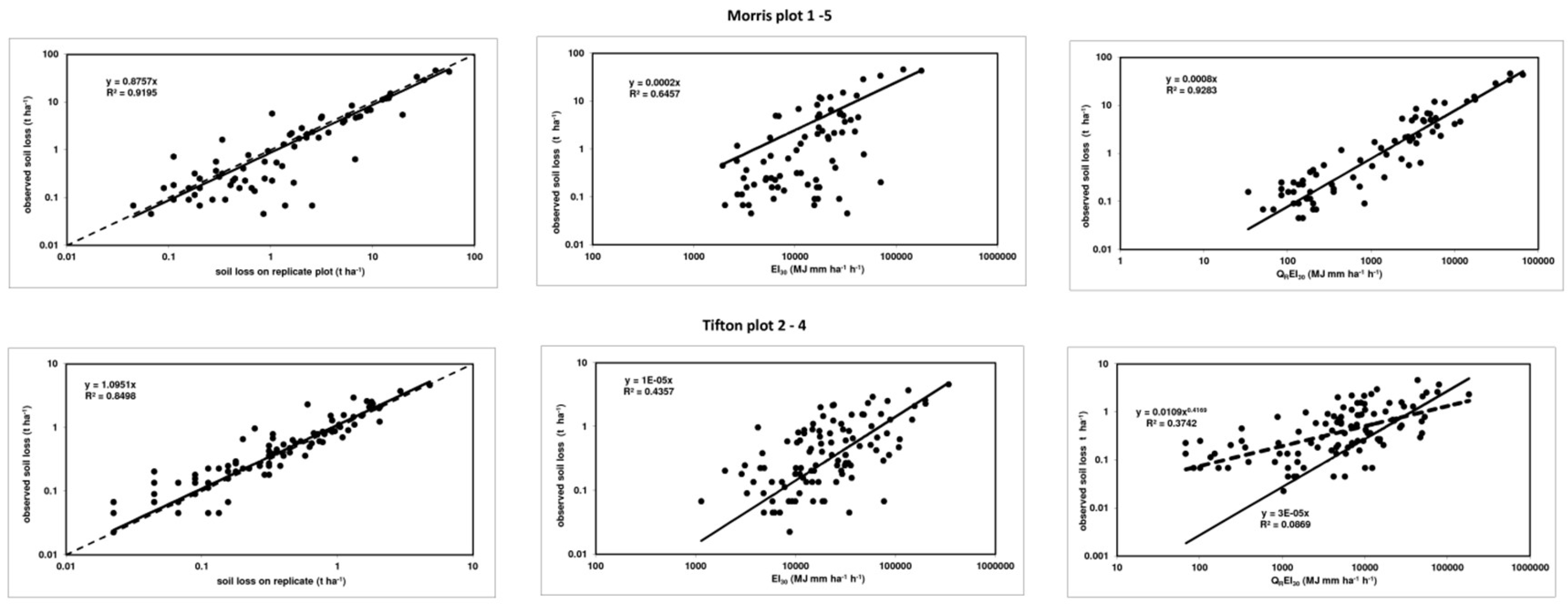
| Morris | 74 | plot 1–5 | plot 1–10 | 0.706 | 0.015 | 0.838 |
| Morris | 74 | plot 1–10 | plot 1–13 | 0.636 | 0.133 | 0.784 |
| Morris | 74 | plot 1–13 | plot 1–5 | 0.737 | −0.078 | 0.758 |
| Castana | 116 | Plot 1–3 | plot 1–4 | 0.829 | 0.396 | 0.777 |
| Castana | 116 | plot 1–4 | plot 1–3 | 0.878 | 0.307 | 0.809 |
| Bethnay | 135 | plot 1–9 | plot 1–10 | 0.772 | 0.498 | 0.761 |
| Bethnay | 135 | plot 1–10 | plot 1–9 | 0.765 | 0.396 | 0.716 |
| McCredie | 124 | plot 2–1 | plot 2–18 | 0.763 | 0.332 | 0.842 |
| McCredie | 124 | plot 2–18 | plot 2–1 | 0.742 | 0.058 | 0.548 |
| LaCrosse | 97 | plot 1–8 | plot 1–9 | 0.828 | 0.566 | 0.854 |
| LaCrosse | 97 | plot 1–9 | plot 1–8 | 0.832 | 0.547 | 0.853 |
| Holly Springs | 187 | plot 3–5 | plot 3–7 | 0.826 | 0.520 | 0.645 |
| Holly Springs | 187 | plot 3–7 | plot 3–5 | 0.843 | 0.491 | 0.704 |
| Watkinsville | 111 | plot 2–47 | plot 2–64 | 0.722 | 0.443 | 0.594 |
| Watkinsville | 111 | plot 2–64 | plot 2–47 | 0.765 | 0.354 | 0.453 |
| Madison | 66 | plot 1–5 | plot 1–12 | 0.893 | 0.024 | 0.781 |
| Madison | 66 | plot 1–12 | plot 1–5 | 0.886 | 0.058 | 0.751 |
| Tifton | 103 | plot 1–2 | plot 2–4 | 0.820 | 0.263 | −0.511 |
| Tifton | 103 | plot 2–4 | plot 1–2 | 0.838 | 0.157 | −0.346 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kinnell, P.I.A. A Review of the Science and Logic Associated with Approach Used in the Universal Soil Loss Equation Family of Models. Soil Syst. 2019, 3, 62. https://doi.org/10.3390/soilsystems3040062
Kinnell PIA. A Review of the Science and Logic Associated with Approach Used in the Universal Soil Loss Equation Family of Models. Soil Systems. 2019; 3(4):62. https://doi.org/10.3390/soilsystems3040062
Chicago/Turabian StyleKinnell, P. I. A. 2019. "A Review of the Science and Logic Associated with Approach Used in the Universal Soil Loss Equation Family of Models" Soil Systems 3, no. 4: 62. https://doi.org/10.3390/soilsystems3040062
APA StyleKinnell, P. I. A. (2019). A Review of the Science and Logic Associated with Approach Used in the Universal Soil Loss Equation Family of Models. Soil Systems, 3(4), 62. https://doi.org/10.3390/soilsystems3040062




