Context, Development, and Intent: An Introduction to the IPI Preservation Metrics
Abstract
:1. Introduction
2. Aims and Applications of the IPI Preservation Metrics
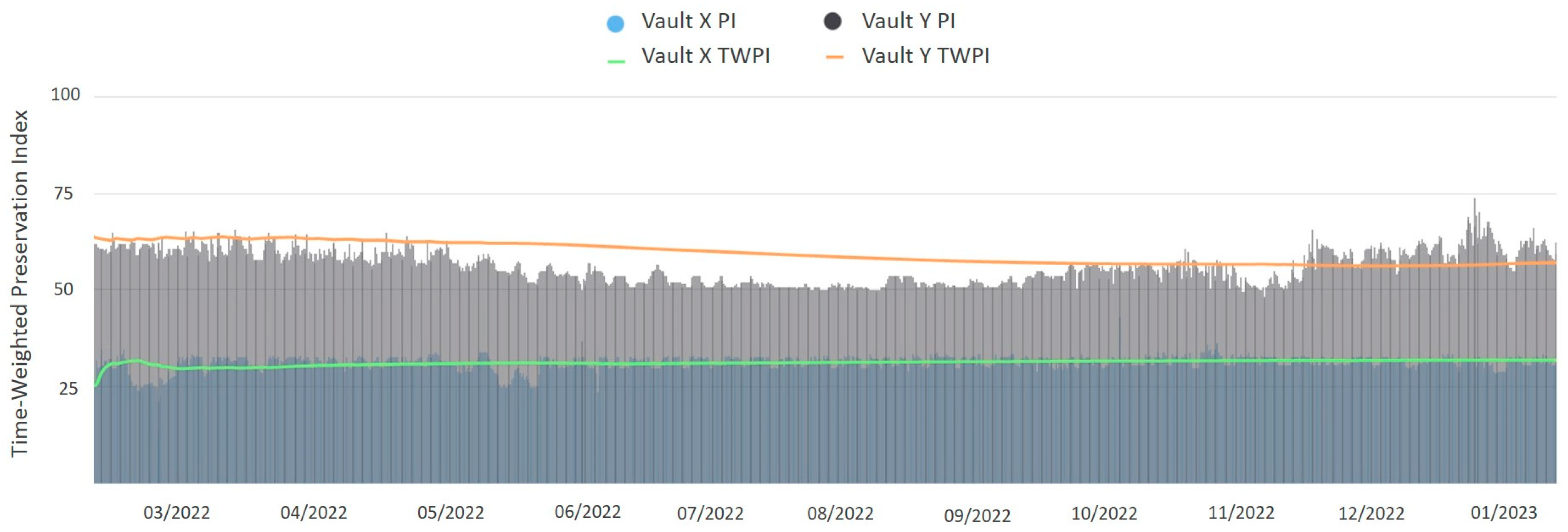
2.1. Preservation Index and the Time-Weighted Preservation Index
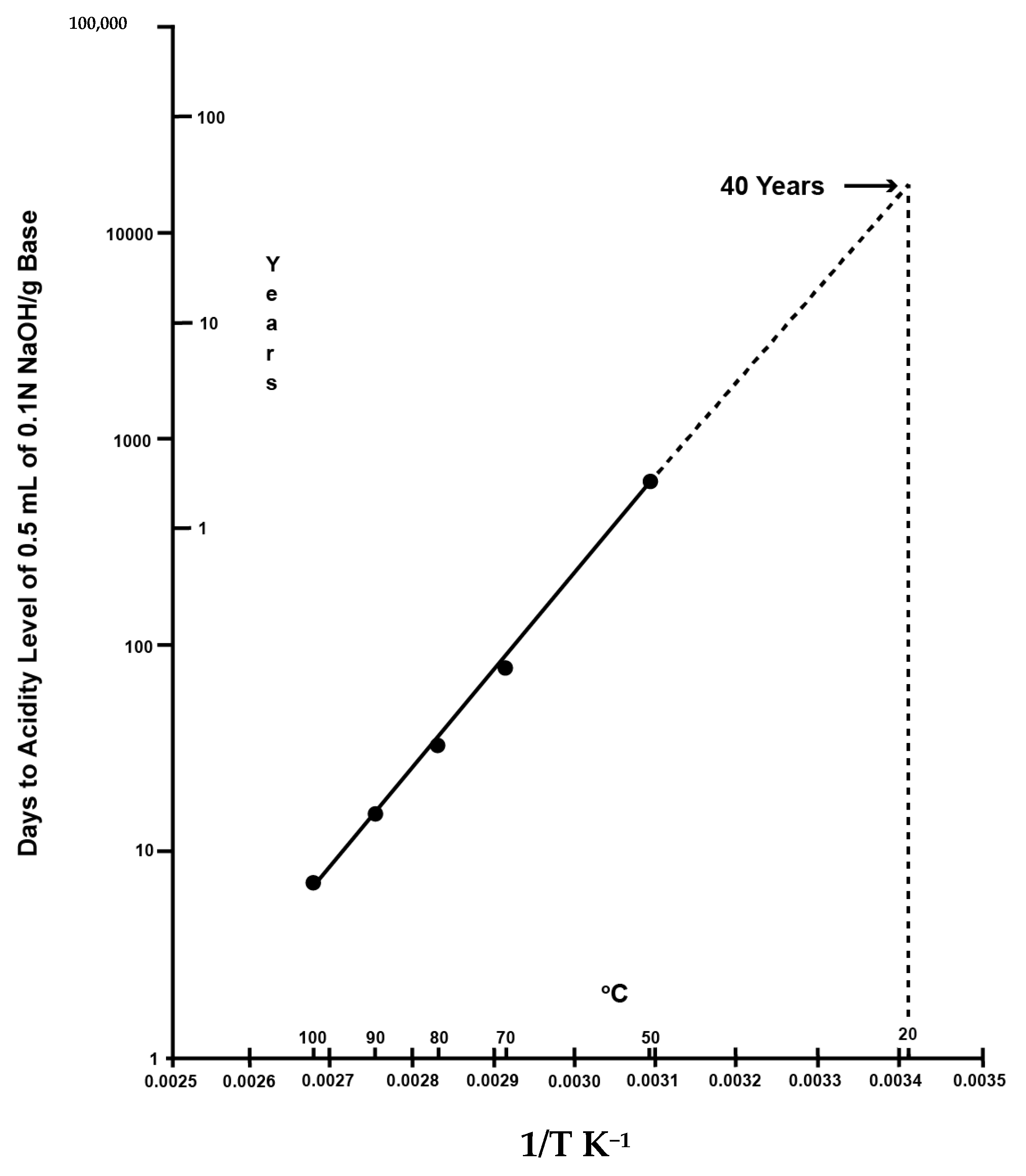
2.1.1. Fundamentals of the Preservation Index
2.1.2. Fundamentals of the Time-Weighted Preservation Index
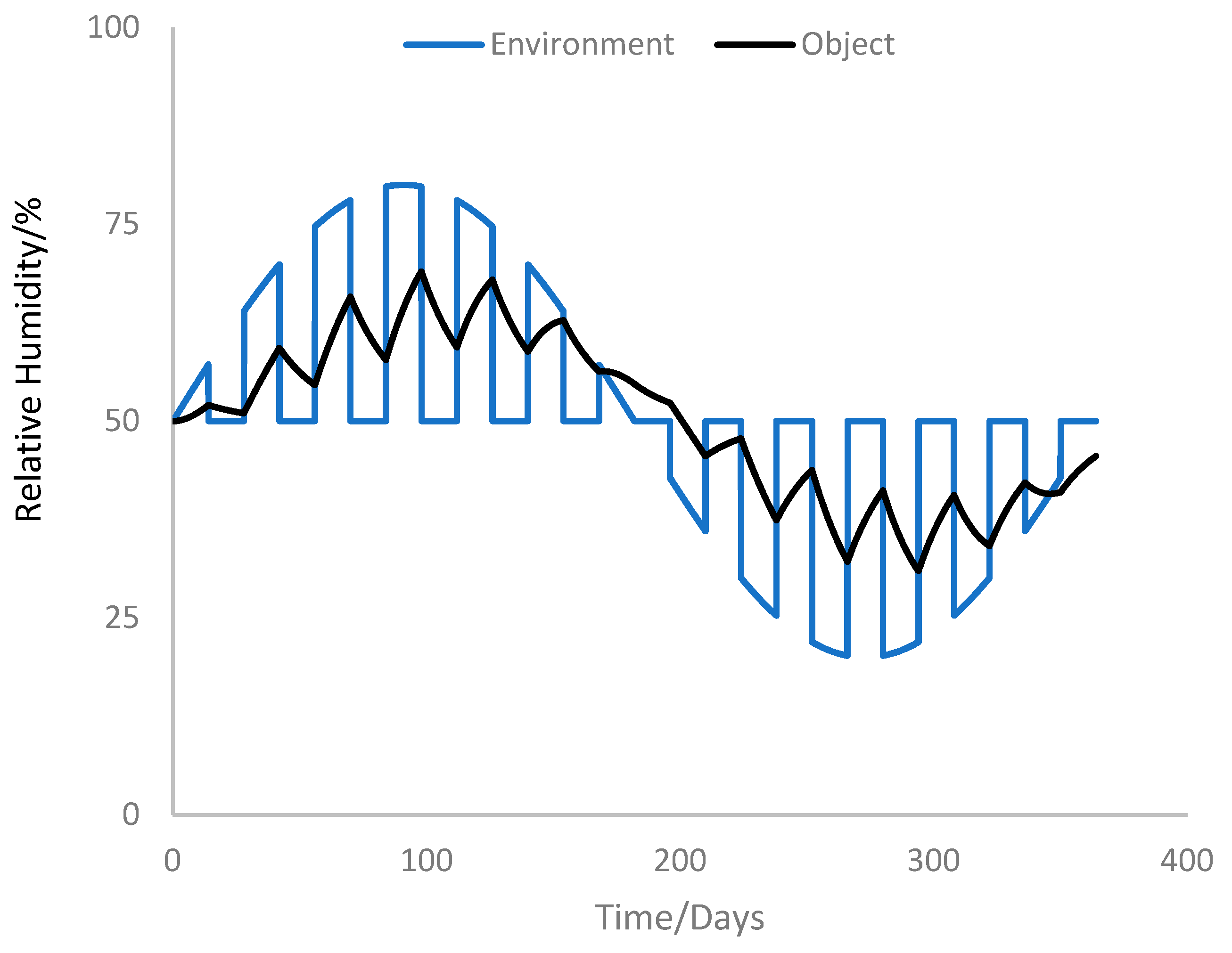
2.1.3. Limitations of the Preservation Index and Time-Weighted Preservation Index
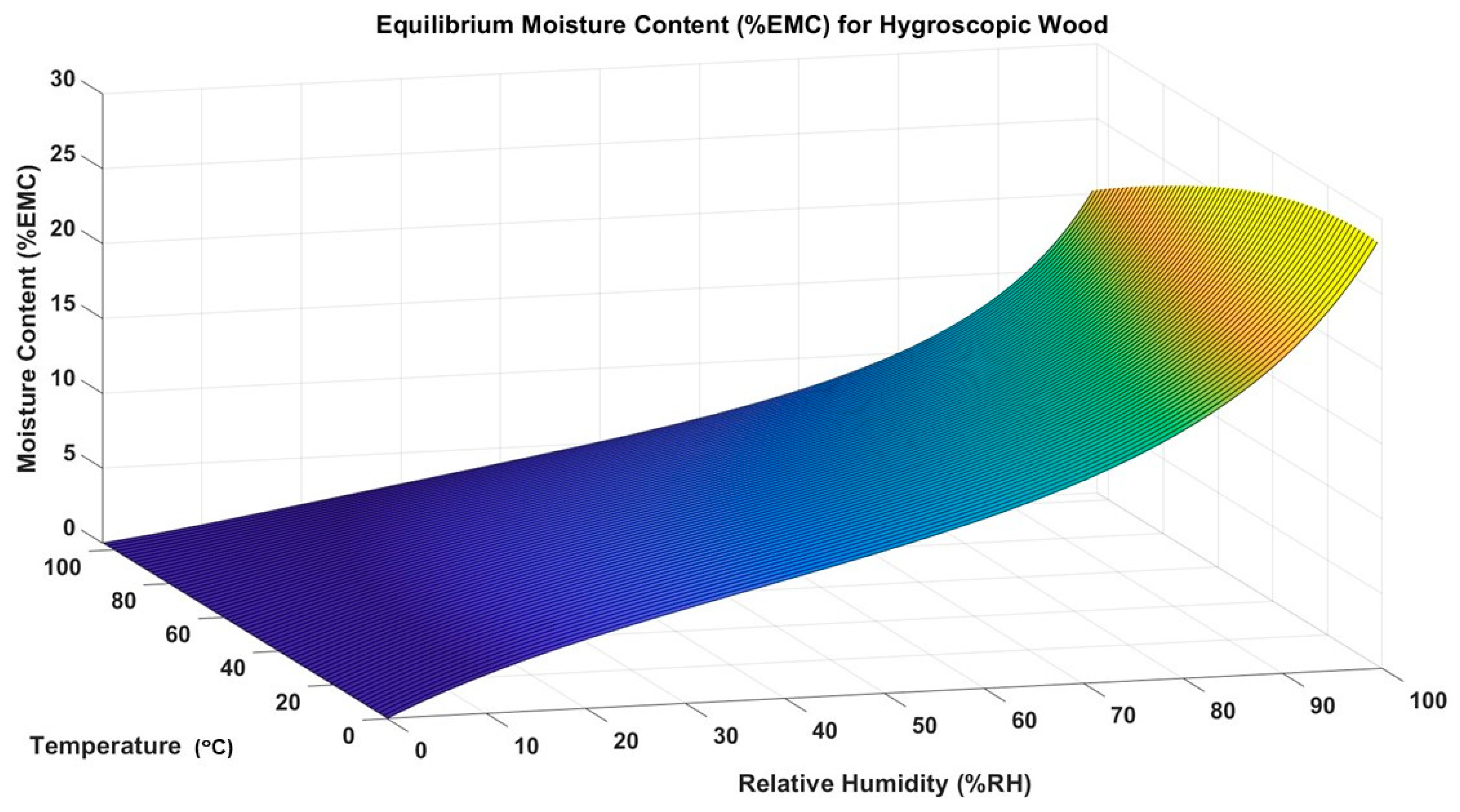
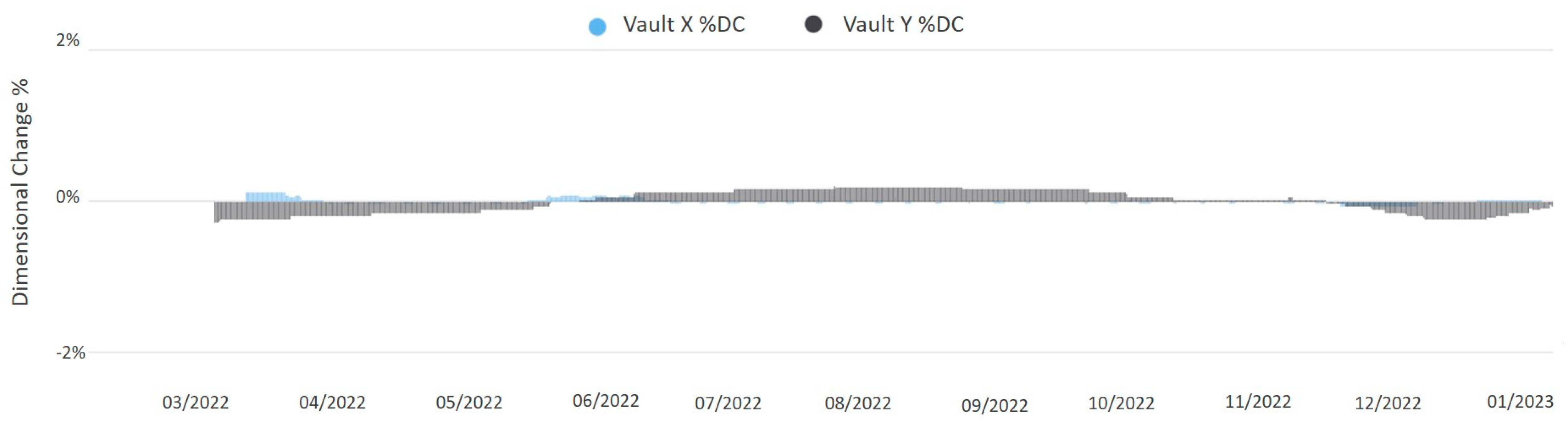
2.2. Percent Equilibrium Moisture Content and the Percent Dimensional Change
2.2.1. Fundamentals of the Percentage Equilibrium Moisture Content
2.2.2. Fundamentals of the Percentage Dimensional Change
2.2.3. Limitations of the Percentage Equilibrium Moisture Content and Percentage Dimensional Change
3. Future IPI Preservation Metrics
3.1. Sustainable Humidity Control Modeling
3.2. Dimensional Change for Composite Plastics
4. Conclusions and Summary of the IPI Preservation Metrics
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tools for the Analysis of Collection Environments: Lessons Learned and Future Developments; Getty Conservation Institute: Los Angeles, CA, USA, 2022.
- Arends, T.; Pel, L.; Schellen, H.L.; Smeulders, D.M.J. Relating Relative Humidity Fluctuations to Damage in Oak Panel Paintings by a Simple Experiment. Stud. Conserv. 2018, 64, 101–114. [Google Scholar] [CrossRef]
- Janas, A.; Mecklenburg, M.F.; Fuster-López, L.; Kozłowski, R.; Kékicheff, P.; Favier, D.; Andersen, C.K.; Scharff, M.; Bratasz, Ł. Shrinkage and Mechanical Properties of Drying Oil Paints. Herit. Sci. 2022, 10, 181. [Google Scholar] [CrossRef]
- Krzemień, L.; Czyżewska, A.; Soboń, M.; Kozłowski, R.; Bratasz, Ł. Risk of Climate-Induced Damage in Historic Parchment. Herit. Sci. 2020, 8, 17. [Google Scholar] [CrossRef]
- Berger, L.; Strojecki, M. HERIe; herie.pl: 2020. Available online: https://www.herie.pl (accessed on 10 January 2023).
- HORIZON 2020 IPERION HS: Integrating Platforms for the European Research Infrastructure ON Heritage Science. European Commission, H2020-INFRAIA-2014-2015, under Grant No. 654028, n.d. Available online: http://www.iperionch.eu/iperion-hs-a-new-horizon-2020-project-was-born/ (accessed on 10 January 2023).
- Michalski, S.; Pedersoli, J.-L. The ABC Method: A Risk Management Approach to the Preservation of Cultural Heritage; Canadian Conservation Institute (CCI): Ottawa, ON, Canada; International Centre for the Study of the Preservation and Restoration of Cultural Property (ICCROM): Rome, Italy, 2016; Available online: https://www.canada.ca/en/conservation-institute/services/risk-management-heritage-collections/abc-method-risk-management-approach.html (accessed on 10 January 2023).
- Kupczak, A.; Jędrychowski, M.; Bratasz, Ł.; Łukomski, M.; Kozłowski, R. Processing Relative Humidity Data Using Discrete Fourier Transform to Control Strain in Art Objects. Strain 2019, 55, e12311. [Google Scholar] [CrossRef]
- Strlič, M.; Grossi, C.M.; Dillon, C.; Bell, N.; Fouseki, K.; Brimblecombe, P.; Menart, E.; Ntanos, K.; Lindsay, W.; Thickett, D.; et al. Damage Function for Historic Paper. Part III: Isochrones and Demography of Collections. Herit. Sci. 2015, 3, 40. [Google Scholar] [CrossRef]
- Michalski, S. CCI Light Damage Calculator. Canadian Conservation Institute (CCI). 2012. Available online: https://app.pch.gc.ca/application/cdl-ldc/description-about.app?lang=en (accessed on 10 January 2023).
- Sebera, D.K. Isoperms: An Environmental Management Tool; The Commission on Preservation and Access: Washington, DC, USA, 1994. [Google Scholar]
- Strlič, M.; Grossi, C.M.; Dillon, C.; Bell, N.; Fouseki, K.; Brimblecombe, P.; Menart, E.; Ntanos, K.; Lindsay, W.; Thickett, D.; et al. Damage Function for Historic Paper. Part II: Wear and Tear. Herit. Sci. 2015, 3, 36. [Google Scholar] [CrossRef]
- Menart, E.; de Bruin, G.; Strlič, M. Effects of NO2 and Acetic Acid on the Stability of Historic Paper. Cellulose 2014, 21, 3701–3713. [Google Scholar] [CrossRef]
- Reilly, J.M.; Nishimura, D.; Zinn, E. New Tools for Preservation: Assessing Long-Term Environmental Effects on Library and Archives Collections; The Commission on Preservation and Access: Washington DC, USA, 1995. [Google Scholar]
- Adelstein, P.Z.; Reilly, J.M.; Nishimura, D.W.; Erbland, C.J. Stability of Cellulose Ester Base Photographic Film: Part I—Laboratory Testing Procedures. Soc. Motion Pict. Telev. Eng. J. 1992, 101, 336–346. [Google Scholar] [CrossRef]
- Adelstein, P.Z.; Reilly, J.M.; Nishimura, D.W.; Erbland, C.J. Stability of Cellulose Ester Base Photographic Film: Part II—Practical Storage Considerations. Soc. Motion Pict. Telev. Eng. J. 1992, 101, 347–353. [Google Scholar] [CrossRef]
- Adelstein, P.Z.; Reilly, J.M.; Nishimura, D.W.; Erbland, C.J. Stability of Cellulose Ester Base Photographic Film: Part III—Measurement of Film Degradation. Soc. Motion Pict. Telev. Eng. J. 1995, 104, 281–291. [Google Scholar] [CrossRef]
- Ahmad, I.R.; Cane, D.; Townsend, J.H.; Triana, C.; Mazzei, L.; Curran, K. Are We Overestimating the Permanence of Cellulose Triacetate Cinematographic Films? A Mathematical Model for the Vinegar Syndrome. Polym. Degrad. Stab. 2020, 172, 109050. [Google Scholar] [CrossRef]
- Bigourdan, J.-L. Stability of Acetate Film Base: Accelerated-Aging Data Revisited. J. Imaging Sci. Technol. 2006, 50, 495–501. [Google Scholar] [CrossRef]
- McCormick-Goodhart, M.; Mecklenburg, M.F. Cold Storage Environments for Photographic Materials. In Final Program and Advance Printing of Paper Summaries, IS&T’s 46th Annual Conference; Society for Imaging Science and Technology: Boston, MA, USA, 1993; pp. 277–280. [Google Scholar]
- Vos, M. Heat and Moisture Diffusion in Magnetic Tape Packs. IEEE Trans. Magn. 1994, 30, 237–242. [Google Scholar] [CrossRef]
- Bigourdan, J.-L.; Reilly, J.M.; Adelstein, P.Z. Moisture and Temperature Equilibration: Behavior and Practical Significance in Photographic Film Preservation. In Proceedings of the La Conservation: Une Science en Evolution, Bilans et Perspectives, Actes des Troisièmes Journées Internationales d’Études de l’ARSAG, Paris, France, 21–25 April 1997; pp. 154–164. [Google Scholar]
- Padfield, T. The Preservation Index and the Time Weighted Preservation Index: Fundamentals. Conservation Physics 2004. Available online: https://www.conservationphysics.org/twpi/twpi_01.html (accessed on 11 January 2023).
- Strlič, M.; Kolar, J. Ageing and Stabilisation of Paper; National and University Library: Ljubljana, Slovenia, 2005. [Google Scholar]
- Myung-Joon, J.; Potthast, A. Improving the Accuracy of Estimating Paper Permanence for Accelerated Degradation in Closed Vials. Cellulose 2021, 28, 4053–4068. [Google Scholar] [CrossRef]
- Browning, B.L.; Wink, W.A. Studies on the Permanence and Durability of Paper: 1 Prediction of Paper Permanence. TAPPI 1968, 51, 156–163. [Google Scholar]
- Luxford, N.; Thickett, D. Designing Accelerated Ageing Experiments to Study Silk Deterioration in Historic Houses. J. Inst. Conserv. 2011, 34, 115–127. [Google Scholar] [CrossRef]
- Bertram, H.; Cuddihy, E. Kinetics of the Humid Aging of Magnetic Recording Tape. IEEE Trans. Magn. 1982, 18, 993–999. [Google Scholar] [CrossRef]
- Wood Handbook: Wood as an Engineering Material; Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2010.
- Hailwood, J.; Horrobin, S. Absorption of Water by Polymers: Analysis in Terms of a Simple Mode. Trans. Faraday Soc. 1946, 42, B084–B092. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Richardson, E.J.; Cummings, M.; Bigourdan, J.-L. Context, Development, and Intent: An Introduction to the IPI Preservation Metrics. Heritage 2023, 6, 4202-4213. https://doi.org/10.3390/heritage6050221
Richardson EJ, Cummings M, Bigourdan J-L. Context, Development, and Intent: An Introduction to the IPI Preservation Metrics. Heritage. 2023; 6(5):4202-4213. https://doi.org/10.3390/heritage6050221
Chicago/Turabian StyleRichardson, Emma J., Marvin Cummings, and Jean-Louis Bigourdan. 2023. "Context, Development, and Intent: An Introduction to the IPI Preservation Metrics" Heritage 6, no. 5: 4202-4213. https://doi.org/10.3390/heritage6050221
APA StyleRichardson, E. J., Cummings, M., & Bigourdan, J.-L. (2023). Context, Development, and Intent: An Introduction to the IPI Preservation Metrics. Heritage, 6(5), 4202-4213. https://doi.org/10.3390/heritage6050221





