Binaural Synthetic Aperture Imaging of the Field of Audition as the Head Rotates and Localisation Perception of Monophonic Sound Listened to through Headphones

Abstract

A human listening to monophonic sound through headphones perceives the sound to emanate from a point inside the head at the auditory centre at effectively zero range. The extent to which this is predicted by synthetic-aperture calculation performed in response to head rotation is explored. The instantaneous angle between the auditory axis and the acoustic source, lambda, for the zero inter-aural time delay imposed by headphones is 90°. The lambda hyperbolic cone simplifies to the auditory median plane, which intersects a spherical surface centred on the auditory centre, along a prime meridian lambda circle. In a two-dimensional (2-D) synthetic-aperture computation, points of intersection of all lambda circles as the head rotates constitute solutions to the directions to acoustic sources. Geometrically, lambda circles cannot intersect at a point representing the auditory centre; nevertheless, 2-D synthetic aperture images for a pure turn of the head and for a pure lateral tilt yield solutions as pairs of points on opposite sides of the head. These can reasonably be interpreted to be perceived at the sums of the position vectors of the pairs of points on the acoustic image, i.e., at the auditory centre. But, a turn of the head on which a fixed lateral tilt of the auditory axis is concomitant (as in species of owl) yields a 2-D synthetic-aperture image without solution. However, extending a 2-D synthetic aperture calculation to a three-dimensional (3-D) calculation will generate a 3-D acoustic image of the field of audition that robustly yields the expected solution.

1. Introduction

A notable event in the lives of many of us was the first time we heard high fidelity reproduction music through headphones and experienced the shock and the “wow” of perceiving sound to apparently emanate from a single point at the centre of our head, even though a pair of headphones constitutes two sources of sound albeit in very close proximity to our ears. Stereo effects would typically also be located between our ears inside our head (e.g., [1]).

In this paper, only monophonic sound is considered. Also avoided is the complication of the more recent innovation of “binaural” recordings listened to through headphones.

Another situation in which we expect to perceive sound to emanate from inside our head is when listening to the sound of our own voice. This, however, is a different experience from listening to monophonic sound through headphones, because resonances within our head and upper body lead to our not identifying a confined single point within our body as the location of the source of sound.

It has previously been described how acoustic source localisation can be achieved in a binaural system by synthetic-aperture calculation as an image-processing-based operation performed in a virtual acoustic image of the field of audition [2,3,4,5]. This suggestion first arose as a cross-fertilisation from the field of applied geophysics to that of binaural audition [2] in a consideration of how a synthetic-aperture process, familiar to geophysicists as that of “migration” applied in seismic reflection image processing [6], and in synthetic aperture sonar and radar systems [6], may be applied to localise far-field acoustic sources (having an effectively infinite range) to yield visualised solutions to the binaural localisation problem in two-dimensional (2-D) images of the field of audition. The process was subsequently extended to three dimensions, to not only to find the directions, but also to estimate the ranges to near-field acoustic sources (appropriate for ranges extending to several times the distance between the ears or listening antennae) [3]. In this paper, an exploration is focused on the extent to which a synthetic-aperture approach to binaural localisation can predict the experience of sound apparently emanating from our auditory centre (i.e., an effective zero range) when listening to monophonic sound through headphones.

There is not a unique way in which a human direction-finds or localises sound incident at the ears. There are several that appear to work concurrently, and the effectiveness of each depends on the nature of the signal incident on the ears. One involves interpreting inter-aural arrival time differences. This has been found to apply principally to acoustic signals having frequencies below circa 1500 Hz [7,8,9,10]. A second process involves interpreting differences in the intensity or level of the signal entering the ears, and this applies to acoustic signals having higher frequencies, greater than approximately 1500 Hz [8]. A third process involves unconsciously interpreting features (principally notches) in the spectra of sound entering the ear canals, which is an effect of the shape of the head and the pinnae, as incoming sound interacts with them, the so-called head- or pinnae-related transfer function [11,12,13,14,15]. It is with the first of these that this article is exclusively concerned.

An instantaneous arrival time difference of an acoustic signal between the ears inferred from a short-time-based cross-correlation process [16] would enable the direction from which an acoustic signal emanates to be disambiguated to a cone having an apex at the auditory centre and an axis geometrically congruent with the auditory axis. The angle between the auditory axis and the surface of the cone, lambda, is determined from the inter-aural time difference using a mapping relationship (by whatever means that is inferred) between the inter-aural time difference and lambda. The three-dimensional (3-D) cone (strictly speaking, a hyperbolic cone) may be conveniently represented in two dimensions by a circle at the intersection of the cone with a spherical shell centred on the auditory centre.

As additional instantaneous arrival time differences are mapped to lambda cones/circles in response to further rotation of the head, the auditory system is hypothesised to perform a wonder of image processing whereby a collection of lambda cones/circles stored previously during the head rotation, in a virtual image of the field of audition, is rotated back relative to the head, so that the collection is perceived to be at rest relative to the real world, in much the same way that our visual system maintains our perception of the visual world to be at rest relative to the real world, even when we rotate our head and eyes in their sockets in as wild a fashion as we can. Thus, acoustic data are distended over lambda cones (3-D) or circles (2-D), and as we rotate our heads, data for a collection of cones or circles are integrated into an acoustic image of our acoustic environment. The points in the acoustic image at which all lambda cones or circles intersect each other constitute solutions to the acoustic source direction-finding or localisation process. This is the essence of the synthetic aperture process [2].

An equation for computing a value of lambda (the angle between the auditory axis and the direction to the acoustic source) from the direction to the acoustic source, is derived in Appendix A of reference [2]. The equations for rotating a circle of colatitude into position to represent a lambda circle on the surface of a sphere using a spherical geometry are given in Appendix B of reference [2], together with the equations for displaying curved spherical surfaces as flat images in a Mercator projection. In addition, the essential similarity between the synthetic aperture process applied to binaural localisation and the anthropogenic synthetic aperture process employed in seismic reflection image processing (migration), and in synthetic-aperture sonar and radar systems [6], is described and illustrated in Appendix C of reference [2].

No matter whether humans or other animals unconsciously perform a synthetic aperture process for sound localisation, it might nevertheless, be applied as an elegant image-processing-based solution to acoustic localisation in a binaural robotic system [2,3,4,5] readily affording a full visualisation of both processing workings and solutions.

The synthetic aperture computation approach to localisation has hitherto been based on lambda circles and has been principally employed for direction-finding far field acoustic sources [2,4,5]. In an exploration of the potential for estimating the range (for short ranges) as well as the direction to an acoustic source, the method was effectively extended to three dimensions, despite this being presented in the form of collections of 2-D images [3].

In listening to monophonic sound through headphones, the inter-aural time difference is at all times zero. All instantaneous values of the angle between the auditory axis and the surface of the cone, lambda, are 90° (π/2 radians). The cone, therefore, simplifies to a plane surface, specifically the auditory median plane. The median plane intersects a spherical shell having a centre shared with the auditory centre on a lambda circle that is the prime meridian of the spherical shell relative the direction the head is facing.

A flaw that might be anticipated in an attempt to use intersecting lambda circles in a 2-D acoustic image to find the direction to an acoustic source expected to be located at the auditory centre is that this is the one location in space for which a direction to the source (from the auditory centre) is not defined. Nevertheless, the potential of intersecting lambda circles in a 2-D acoustic image for acoustic source localisation will be explored. In addition, the need to distend data over planes intersecting in a 3-D acoustic image to adequately locate an acoustic source at the auditory centre will be considered.

In this paper, the effects of head rotation about orthogonal axes on a synthetic-aperture-based approach to acoustic source localisation, when listening to monophonic sound through headphones, is explored by simulated experiment. Three kinds of pure head rotation about a single axis are considered: (1) a turn (yaw); (2) a lateral tilt (roll); and (3) a nod (pitch). A fourth is a turn (yaw) combined with a constant or fixed concomitant lateral tilt (roll) 20° downslope to the right across the head. Information pertaining to these is presented in

Table 1. Colour coding and indexing for seven discrete angles for which lambda circles are generated (see Table 2) and shown in the skeletonised two-dimensional images of the field of audition in Figure 1, Figure 2, Figure 3 and Figure 4.

Rotation Angle (°)	Colour	Index
−67.5	Red	1
−45	Orange	2
−22.5	Yellow	3
0	Grey	4
22.5	Green	5
45	Blue	6
67.5	Violet	7

and

Table 2. Meanings of the rotation angles (Table 1) in three orthogonal head rotations for which acoustic images are generated (Figure 1, Figure 2 and Figure 3) and for a fourth rotation in which a turn (yaw) incorporates a constant lateral tilt (roll) downslope to the right across the head (Figure 4).

Type of Head Rotation	Rotation Angle Description	Section	Figure
Turn (yaw)	Bearing of the direction the head is facing	Section 2.1	Figure 1a,b
Lateral tilt (roll)	Negative to left (port) and positive to right (starboard)	Section 2.2	Figure 2
Nod (pitch)	Negative facing upwards and positive facing downwards	Section 2.3	Figure 3
Turn (with a 20° tilt)	Bearing of the direction the head is facing	Section 2.4	Figure 4

.

2. Synthetic-Aperture Images

A real synthetic-aperture calculation, either in nature or in a robotic system emulating a natural binaural system, rather than a simulated one, would be expected to generate numerous lambda cones or circles in response to a head rotation. The ensuing acoustic image would then be subjected to a search process looking for bright-spots-indicating points where many lambda cones/circles intersect, these representing solutions to directions to acoustic sources. In this paper, to produce figures that are not overcharged with information, lambda circles were generated for only seven instantaneous angles corresponding to the orientations of the head during head rotation (Table 1 and Table 2).

2.1. Head Turn (Yaw)

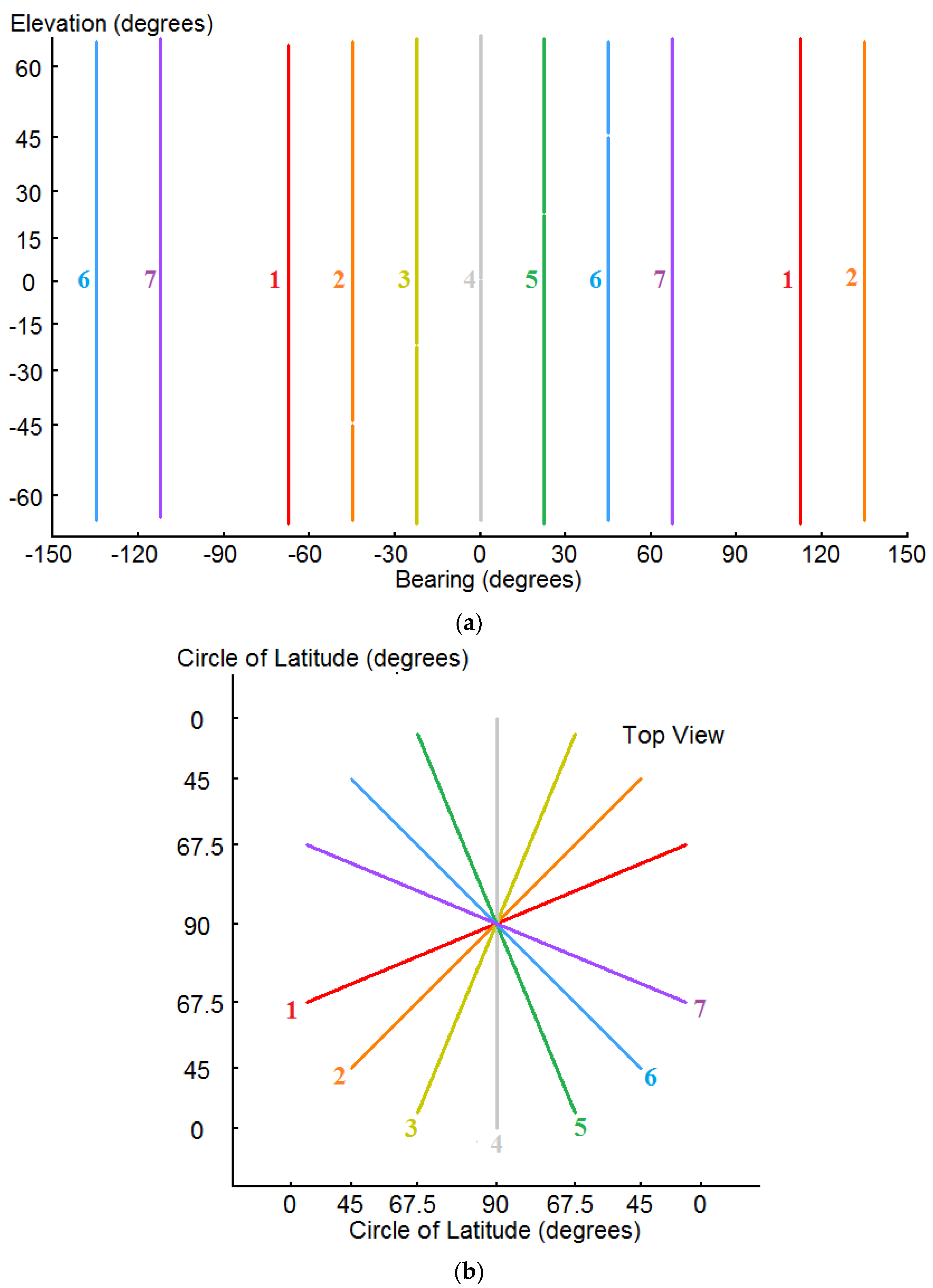
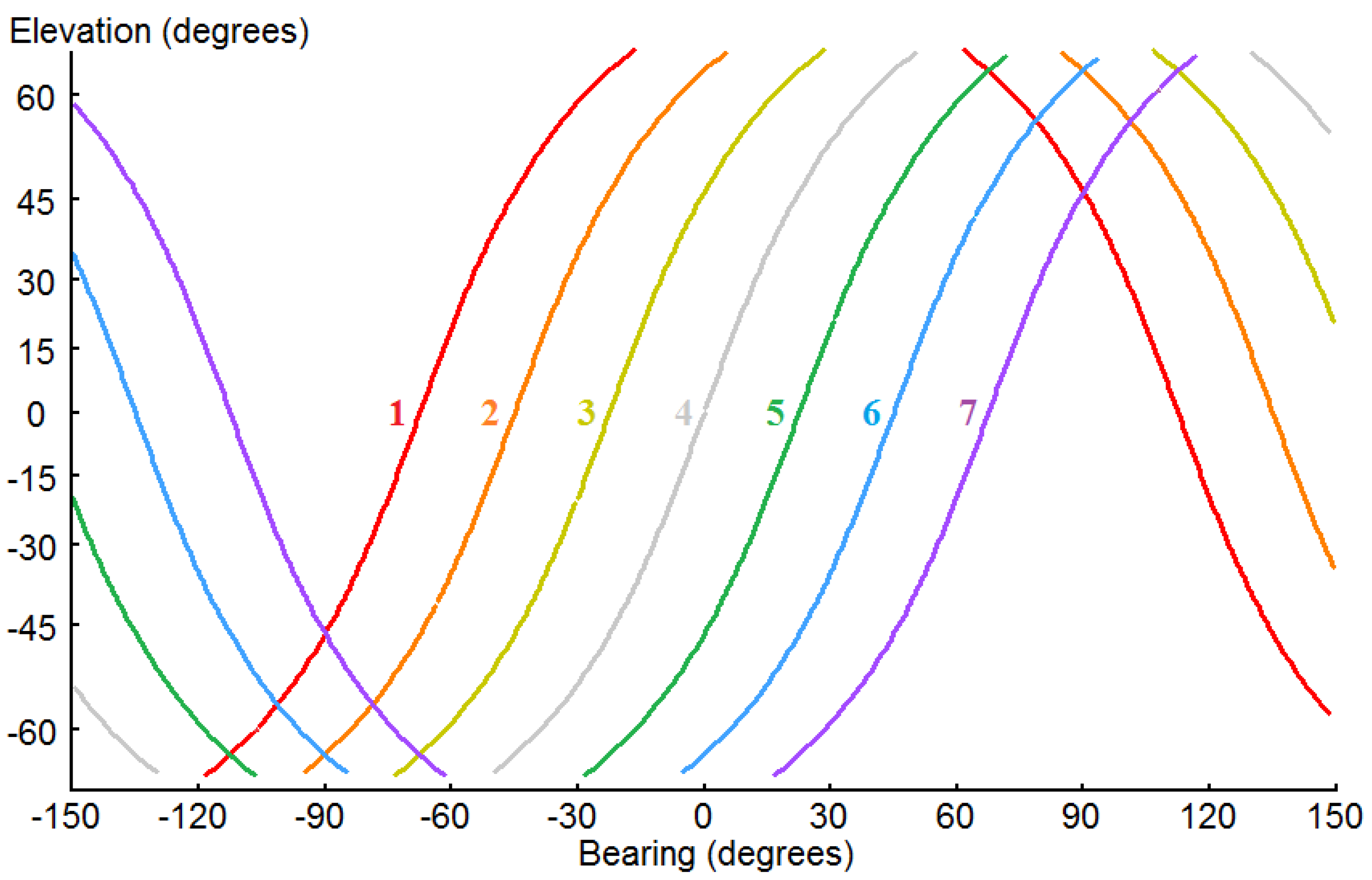
Lambda circles for a synthetic-aperture acoustic image of the field of audition generated as the head turns from facing 67.5° to the left to 67.5° to the right (in 22.5° increments) are shown in Mercator projection in Figure 1.

For all of the lambda circles throughout this paper, the inter-aural time delays between the left and right ears are zero for all orientations of the head. Thus, the value for lambda is always 90° (π/2 radians), and each circle defines a plane (a special case of a cone), specifically the median plane, i.e., the plane orthogonal to the auditory axis containing the auditory centre. The lambda circles shown in the synthetic-aperture acoustic image are, thus, the prime meridian circles of a spherical surface intersecting the median planes as the head turns, for the purpose of representing the planes by circles in a 2-D image.

One of the generally useful properties of the Mercator projection is that the true azimuth is preserved; thus, the lines having a constant azimuth of zero with respect to the vertical are all vertical in Figure 1a. One of the unfortunate properties of the Mercator projection however, is that the “poles” are located at an infinite distance from the “equator”, and therefore these cannot be shown in Figure 1a. However, the lambda circles are shown in top view in Figure 1b, and they are seen to intersect at the poles. Thus, the points of intersection of the lambda circles in the 2-D image indicate two directions to acoustic sources, one vertically upwards from the auditory centre, and the other vertically downwards.

In listening to monophonic sound through a pair of loud speakers placed separated in front of us, rather than through headphones, we perceive the sound to emanate from a point mid-way between the speakers rather than from two points corresponding to the locations of the two speakers. Acoustic intensity is a vector quantity; thus, identical sounds from two sources seem to us to emanate from the direction of the vector sum of the separate intensities, i.e., from the point mid-way between the sources. Thus, it seems likely that the pair of sources apparent in Figure 1 and Figure 2 would be perceived as emanating from the vector sum of the two position vectors, i.e., from the middle of the head between the ears at the auditory centre. Certainly, a robotic system could relatively straightforwardly be programmed to recognise the condition of a pair of solutions on the opposite sides of the auditory centre and the solution for the location of the acoustic source assigned to be at the auditory centre.

Figure 1. (a) Skeletonised synthetic-aperture image of the field of audition in a Mercator projection. Lambda circles are shown for seven discrete bearings, in which the head faces as it turns (or yaws) from 67.5° to the left (port) (index 1; coloured red), through 22.5° increments, to 67.5° to the right (starboard) (index 7; coloured violet) with respect to the mean position (0°, index 4; coloured grey). (b) The same lambda circles presented in (a), but shown in a top view.

Figure 1. (a) Skeletonised synthetic-aperture image of the field of audition in a Mercator projection. Lambda circles are shown for seven discrete bearings, in which the head faces as it turns (or yaws) from 67.5° to the left (port) (index 1; coloured red), through 22.5° increments, to 67.5° to the right (starboard) (index 7; coloured violet) with respect to the mean position (0°, index 4; coloured grey). (b) The same lambda circles presented in (a), but shown in a top view.

If instead of considering the intersections of the lambda circles in two dimensions, the intersection of the median planes on which the circles lie is considered in three dimensions, the planes all intersect on the vertical line passing through the auditory centre. The source of sound is then no better disambiguated than to be somewhere on this polar axis. In forcing a solution, the mean position of all positions on the polar axis is the auditory centre.

2.2. Head Lateral Tilt (Roll)

Lambda circles for a synthetic-aperture acoustic image of the field of audition generated as the head tilts or rolls from a lateral tilt of the head of 67.5° to the left to 67.5° to the right (in 22.5° increments) are shown in Figure 2.

Figure 2. Skeletonised synthetic-aperture image of the field of audition in a Mercator projection. Lambda circles are shown for seven discrete angles, as the head laterally tilts (or rolls) from 67.5° to the left (port) (index 1; coloured red), through 22.5° increments, to 67.5° to the right (starboard) (index 7; coloured violet) with respect to the mean upright un-tilted position (0°, index 4; coloured grey).

Figure 2. Skeletonised synthetic-aperture image of the field of audition in a Mercator projection. Lambda circles are shown for seven discrete angles, as the head laterally tilts (or rolls) from 67.5° to the left (port) (index 1; coloured red), through 22.5° increments, to 67.5° to the right (starboard) (index 7; coloured violet) with respect to the mean upright un-tilted position (0°, index 4; coloured grey).

Again, the values of lambda for all orientations of the head are constant at 90° (π/2 radians), and the lambda circles of colatitude are prime meridian circles on a spherical surface relative to the head, onto which the median planes are projected as the head rolls from left to right. They intersect at points represented by zero elevation and a bearing of 0° and also at ±180°. Although only a single point of intersection of lambda circles is seen in Figure 2, the second is vis-a-vis on the opposite sides of the field of audition, i.e., directly behind the direction the head is facing which lies out with the range of bearings, shown in Figure 2. Its presence is indicated by the plane mirror symmetry of the lambda circles with respect to the ±90° bearings.

The source of sound could reasonably be expected to be perceived to be located at the vector sum (or mean position) of the two intersection positions, i.e., at the auditory centre. The condition and the solution could readily enough be recognised and programmed in a robotic system.

In considering the intersections of the median planes rather than those of the lambda circles on the planes, the median planes all intersect along the line extending directly in front of and directly behind the head. In forcing a completely disambiguated solution, the mean position on this line is the auditory centre.

2.3. Head Nod (Pitch)

Lambda circles for a synthetic-aperture acoustic image of the field of audition generated as the head undergoes a nodding or pitching motion, from facing upwards at an angle of 67.5° above the horizontal to 67.5° below the horizontal (in 22.5° increments) are shown in Figure 3.

Figure 3. Skeletonised synthetic-aperture image of the field of audition in a Mercator projection. Lambda circles are shown for seven discrete angles as the head nods (or pitches) from 67.5° facing upwards (index 1), in 22.5° increments, to 67.5° facing downwards (index 7,) with respect to the mean forward facing position (0°, index 4). Since all lambda circles are coincident, they are represented by the colour black.

Figure 3. Skeletonised synthetic-aperture image of the field of audition in a Mercator projection. Lambda circles are shown for seven discrete angles as the head nods (or pitches) from 67.5° facing upwards (index 1), in 22.5° increments, to 67.5° facing downwards (index 7,) with respect to the mean forward facing position (0°, index 4). Since all lambda circles are coincident, they are represented by the colour black.

The median planes for all of the angles of pitch are in perfect geometrical congruence. The line representing the lambda circles is shown coloured black; the colour that ensues when pigments having the colours of the rainbow are mixed.

Wallach [17] mentioned that in human subjects a nodding rotation of the head was found to not disambiguate directions to an acoustic source. For the sake of completeness, Figure 3 is included to illustrate explicitly by example how a synthetic aperture calculation predicts this. Thus, for the value of lambda of 90° (π/2 radians), a pure nodding or pitching rotation of the head does no better than to locate the source of sound to be somewhere on the median plane. Perhaps it could be argued that forcing a solution to the localisation of an acoustic source, that is no better disambiguated than somewhere on the median plane, might lead to the perception that the acoustic source is located at the auditory centre. However, it would seem unwise to force further disambiguation in programming a robotic system when this condition is recognised.

2.4. Head Turn (with a Fixed 20° Tilt)

The effect is considered of a turn of the head from facing 67.5° to the left to 67.5° to the right (in 22.5° increments), concomitant with a superimposed constant tilt of the head (in emulation of owls [18,19,20]) which has proved in previous calculations [2,3,4,5] to be very effective in uniquely disambiguating directions to acoustic sources in synthetic-aperture images. Whilst it is not expected that owls should for any imaginable purpose don headphones, lambda circles for a synthetic-aperture image for a turn of the head, concomitant with a fixed lateral tilt of the head of 20° downslope to the right across the head, for a fixed lambda value of 90° (π/2 radians), are shown in Figure 4.

Figure 4. Skeletonised synthetic-aperture image of the field of audition in a Mercator projection. Lambda circles are shown for seven discrete bearings, in which the head faces as it turns (or yaws) from 67.5° to the left (port) (index 1; coloured red), through 22.5° increments, to 67.5° to the right (starboard) (index 7; coloured violet) with respect to the mean position (0°, index 4; coloured grey). For all of the lambda circles, the auditory axis has imposed on it a constant lateral tilt (or roll) of 20° downslope to the right across the head.

Figure 4. Skeletonised synthetic-aperture image of the field of audition in a Mercator projection. Lambda circles are shown for seven discrete bearings, in which the head faces as it turns (or yaws) from 67.5° to the left (port) (index 1; coloured red), through 22.5° increments, to 67.5° to the right (starboard) (index 7; coloured violet) with respect to the mean position (0°, index 4; coloured grey). For all of the lambda circles, the auditory axis has imposed on it a constant lateral tilt (or roll) of 20° downslope to the right across the head.

This shows that there are no points at which all lambda circles intersect, indicating that there is no solution evident in the 2-D representation of the problem, as shown in Figure 4. However, the median planes on which the lambda circles are located, robustly and unambiguously have a single point of intersection, located at the auditory centre. This can be appreciated visually from an inspection of Figure 4 by considering that each of the median planes represented by a lambda circle, is tilted 20° to the right. In addition, bearing in mind that the circles on the median planes are equidistant from the centre of the field of audition, it can readily be envisaged that the tilted median planes, as the head executes the turn, are arranged precession-like about the point located at the auditory centre, this point being shared by all of the median planes represented by the lambda circles in Figure 4. Thus, the auditory centre falls out robustly as the solution to the localisation problem, when the problem is considered in three dimensions.

This however, begs an important question regarding the applicability of the synthetic aperture computation process to animals, more specifically humans, and in a robotic emulation of a human-like, at the very least a binaural, experience. The localisation of acoustic sources based on finding points of intersection of lambda circles, which has been demonstrated to be elegantly successful in a number of simulation experiments [2,3,4,5], especially when incorporating a 20° lateral tilt to the right in the emulation of some species of owls’ auditory systems, has proved unsuccessful in disambiguating monophonic sound heard through headphones in this (the fourth) simulation experiment, and only marginally convincingly in the first and second simulation experiments. At least for the first and second experiments (a pure turn and tilt, respectively), it would be readily relatively straightforward to write computer code for a robotic system to recognise the condition pertaining to each of the experiments and then appropriately localise the acoustic source in each case. However, for the fourth simulation experiment (a turn with a fixed tilt), the condition would be difficult to identify, unless it were stipulated that “no solution” should indicate the acoustic source to be located at the auditory centre, which should be regarded, at best, as inadequate. For a more rigorous and robust handling of the situation encountered in simulation experiment four, it would be necessary to extend the 2-D acoustic image of the field of audition, in which data (e.g., the short-time-base cross-correlation functions of the signals received at the left and right ears) are first mapped to angles and then distended over circles, to one in which data are distended over surfaces in a 3-D acoustic image of the field of audition. This would yield a robust and unambiguous solution to acoustic source localisation for the situation illustrated in two dimensions in Figure 4.

Of course, the wearing of headphones and the ensuing acoustic illusion of a source of sound located at our auditory centre, is not something nature via a process of evolution has prepared us for. There is no other circumstance in nature that would yield the same solution (excluding the less well defined solution to the location of the sound of our own voice). This is the reason why the effect of hearing Pink Floyd’s Dark Side of the Moon through headphones for the first time when it was first released all those years ago made such a big impression (and I am sure many other people with a scientific bent will have been likewise similarly impressed by, and remember, their own first experience of this kind).

3. Discussion

In considering the effect of turning the head (a pure turn), followed by a pure roll of the head, as separate but sequentially connected motions of the head, the intersection of the line running the length of the pole of the field of audition as the solution generated when the head undergoes a pure turn, with the line directed forwards and backwards from the direction the head is facing as the solution generated when the head undergoes a pure roll, in combination in three dimensions unambiguously locates the source of sound to be at the auditory centre. Regarding this, it is of some interest that Wallach [17] noted that human subjects when exploring sounds were often observed to first execute a turn rotation of the head and immediately follow this with a tilt rotation of the head.

It would certainly be interesting to explore experimentally whether a human being, when listening to monophonic sound through headphones and turning their head while concomitantly having a constant lateral tilt imposed on the head orientation, strongly perceives the source of sound to be located at the auditory centre, or whether a separated and sequential pure turn followed by a pure tilt is found to be better at strongly locating the acoustic source at the auditory centre. If the former is found to be the case, then any synthetic-aperture calculation that humans perform would be expected to involve distending data over surfaces (generally hyperbolic cones) in a 3-D field of audition, and if the latter, then a synthetic-aperture calculation would be expected to involve distending data over lambda circles in a 2-D field of audition.

Clearly, the generation of data in a 3-D image is very much more computationally intensive than in a 2-D image. A compromise can be imagined in which data found to reside off the median plane are distended over lambda circles in a 2-D field of audition, but for data found to reside on the median plane (the acoustic equivalent of the visual fovea after all), an acoustic image is extended to three dimensions. Certainly, it seems unsatisfactory to invoke the need to process aural data within a 3-D acoustic image of the field of audition solely for the purpose of wearing headphones, for which generally there is little utility and certainly no evolutionary basis, when processing within a 2-D acoustic image would appear to elegantly generate solutions to directions to acoustic sources from the head for situations in which headphones are not worn.

It is obvious that lambda circles at the intersections of cones and a spherical surface at an unspecified but certainly finite distance from the auditory axis will not mathematically be able to intersect at a unique point that could represent the auditory centre. It is similarly obvious that a plane surface representing the auditory median plane, generally rotating about a fixed point representing the auditory centre, will have only a single common point, specifically the auditory centre, which it permanently occupies. However, humans do perceive the source of monophonic sound listened to through headphones to emanate from the auditory centre, and therefore, it would seem that if the human auditory system does employ a synthetic-aperture process for disambiguating acoustic source localisation as the head rotates, then it operates on lambda hyperbolic cone surfaces rotating in a 3-D acoustic image rather than on lambda circles in a 2-D acoustic image.

In an implementation of a synthetic-aperture auditory process in a binaural robot, it would seem sensible in the first instance to explore the utility of images on a 2-D surface before embarking on the big jump in programming effort required and computing power needed to implement an operation in a 3-D acoustic image for possibly a small gain in performance and utility.

Most of the synthetic-aperture images generated for the binaural localisation problem presented previously [2,4,5] have been for the case of signals arriving from far range representing the special case for an extremity (effectively infinite range) which is appropriate for most of the sounds incident at the ears, because sound emanating from a range greater than a relatively small factor of the distance between the ears is, so far as the arrival time difference between the ears is concerned, effectively from sources at an infinite range. Near-field effects have also been explored appropriate for non-zero ranges extending to a few times the distance between the ears [3], and this required a 3-D consideration of the problem. In the present paper, the case for the other extreme, i.e., a source at an effectively zero range, has been explored. As one might hope and expect in an exploration of an extreme case, it has provided new insight. Specifically, it has challenged the notion that if human acoustic source localisation deploys synthetic-aperture calculation as the head rotates, it does so over a 2-D virtual acoustic image of the field of audition, and rather suggests it might do so in a 3-D virtual image within which acoustic data distended over hyperbolic cones (planes for zero inter-aural time differences) are integrated. Perhaps a pragmatic compromise is realised, in which near-field sources are dealt with in a 3-D acoustic image extending to an effective maximum range limited by the inability to satisfactorily infer non-infinite distances beyond a certain distance, and effectively far-field sources consequently being localised over a 2-D image at the periphery of the 3-D one.

4. Conclusions

Humans, when listening to monophonic sound through headphones, perceive the sound to emanate from the auditory centre between the ears inside the head. In an exploration of the extent to which this observation is predicted by a 2-D synthetic-aperture computation as the head rotates, it was found that a pure turning (yawing) rotation of the head generates two solutions on opposite sides of the auditory centre directly above and below the head. This can reasonably be interpreted as being likely to be perceived by a human as a single solution at the vector sum of these two positions, i.e., at the auditory centre. A binaural robotic system could readily be programmed to recognise a pair of solutions such as this and interpret them as a single solution at the vector sum of the position vectors, i.e., at the auditory centre.

Similarly, it was found that a pure tilting (rolling) rotation of the head generates two solutions in a 2-D synthetic-aperture computation on opposite sides of the auditory centre directly in front of and behind the direction the head is facing. Again, this can be interpreted as being likely to be perceived by a human, and be readily perceivable by a binaural robot, as a single solution at the auditory centre.

A nodding (pitching) rotation of the head has no effect on source location disambiguation. This has been found to be true for all synthetic-aperture simulation experiments undertaken for a horizontal auditory axis for which headphones are not worn [2,3,4,5]. However, for a permanent and fixed laterally tilted auditory axis as occurs in nature in species of owl, acoustic source locations are generally uniquely disambiguated in response to, not only turns of the head, but also nods (pitches) of the head.

It was shown that when wearing headphones, a turn of the head for which there is a concomitant fixed laterally tilted auditory axis, yields no solution in a 2-D synthetic-aperture image. It would be informative to explore by experiment whether humans have difficulty disambiguating sound through headphones when the head turns with a concomitant permanent tilt of the auditory axis imposed.

A synthetic-aperture computation that distends acoustic data over surfaces (hyperbolic cones; planes in the special case of wearing headphones) and stores/integrates the result in a 3-D acoustic image, would robustly locate the common point on the median plane rotated any-which-way about the auditory centre, to be at the auditory centre. Thus, it might be that humans, if they deploy a synthetic-aperture process, perform the calculation using surfaces within a 3-D acoustic image. This is the basis of the anthropogenic process of “migration” (a synthetic-aperture calculation) applied to 3-D seismic reflection data volumes (e.g., [21]).

It might naively be expected that a source of monophonic sound listened to through headphones will be located by a human to reside at an ill-defined position somewhere on the median plane. The fact that we so distinctly and emphatically locate the sound to emanate from a point at the auditory centre demands an explanation that the synthetic-aperture hypothesis provides which, in so doing, constitutes evidence that humans include a synthetic-aperture computation in a 3-D virtual field of audition, operating as the head rotates, to locate sources of acoustic signal.