1. Introduction
According to Békésy’s traveling wave theory [
1], the basilar membrane (BM) in the cochlea plays an important role in analyzing the frequency spectrum of sound waves. The BM has a long trapezoid shape, and becomes narrower and thicker near the base of the cochlea. In approaching the apex, it becomes wider and thinner, and increases in flexibility. As a result, higher frequency sounds cause a displacement of the BM near the base, and lower frequency sounds cause a displacement near the apex. These displacements are detected by the outer hair cells, which are regularly arranged on the BM [
2]. By using such an auditory system, humans hear sounds in an audible frequency range from 20 Hz to 20,000 Hz and in a huge dynamic range of about 120 dB [
3]. Even after Békésy’s proposal of the traveling wave theory, considerable progress and great discoveries have continued, including the active process of a cochlear amplifier [
4]. However, there are still many questions regarding the auditory mechanism.
In looking at the cochlear models reported in recent years, the finite element method (FEM) based on fluid dynamics is primarily used due to its design flexibility for three–dimensional cochlea models [
5,
6,
7,
8,
9,
10,
11,
12,
13]. In fact, some models include the scala vestibuli (SV), scala tympani (ST), BM, oval window (OW), round window (RW), and even the cochlear aqueduct. These models can be classified using the following two aspects. One is the shape of the cochlea models, that is, a simplified straight–type cochlear model and a realistic spiral–shaped cochlear model. Though there might be a small difference between their simulation results, both models are considered to be useful to study the basic mechanisms of the cochlea. The other aspect is the settings of the perilymph, which fills the SV and ST. When the perilymph is set as a compressible medium, compression waves (that is, sound waves) are allowed to propagate in the SV and ST, and their wavelengths and phases are precisely processed in the cochlear simulation. However, if the perilymph is set as an incompressible medium, the perilymph is not compressed at all, and the wavelength in the medium would be infinity. Though such an approximation might be useful at a lower audible frequency, errors can be more significant at a higher frequency.
This paper designs a cochlear model assuming that the perilymph in the SV and ST is compressible, and explains the excitation mechanism of a traveling wave based on even and odd mode analysis [
14]. This is a basic technique that has been used for a long time in microwave engineering for designing parallel couplers and explaining the principle of undesired crosstalk on analog phones. We explain this technique briefly in
Section 3. By applying the even and odd mode analysis technique to FEM–based simulations, we explain that an even sound wave mode and an odd sound wave mode are excited simultaneously in the cochlea, and the odd mode contributes to generating Békésy’s traveling waves on the BM and the even mode forms a standing wave in the cochlea. Though these modes show different behaviors, both modes cannot exist independently and are deeply related to each other so as to meet the boundary conditions of the cochlea, such as the reflection conditions at the round window and the apex of the cochlea. In addition to this brand–new approach, we also develop a new cochlear–equivalent circuit, based on the transmission line theory [
14]. From these simulation results, we conclude that the input impedance of the cochlea is defined by the parallel connection of the input impedance of the even mode and the odd mode, which means that the overall performance of the cochlea is determined by a combination of the even and odd mode sound waves. Finally, we would like to emphasize that it is indispensable to define the perilymph as a compressible medium to discuss the even and odd mode approach.
3. Even/Odd Mode Analysis
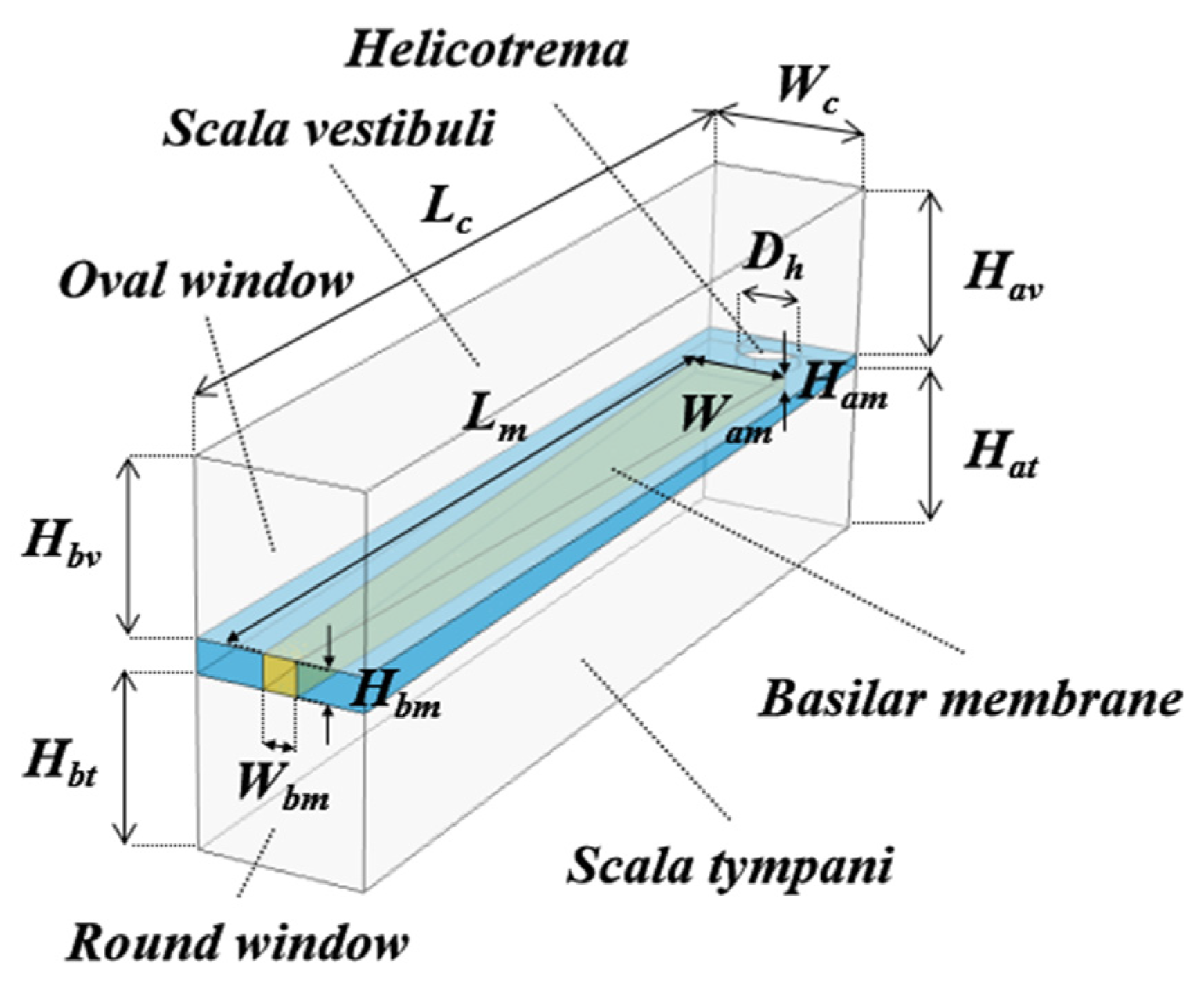
The cochlea model shown in
Figure 1 has an architecture in which the SM is symmetrically sandwiched by the same–shaped SV and ST. This means that even and odd mode analyses can be applied to the model. Even and odd mode analyses are basic techniques that have been used for a long time in microwave engineering for designing couplers using parallel transmission lines and for explaining the principle of the crosstalk often seen in analog telephones [
14]. As shown in
Figure 5a, two transmission lines, A and B, were placed in parallel, and the terminals were numbered from Port 1 to Port 4. Then, when a signal was input from Port 1, it was transmitted along transmission line A and output from Port 3. However, depending on the degree of coupling between the lines, the signal in transmission line A leaked somewhat into transmission line B. This problem is expressed by the sum of two transmission line modes. One is an even symmetric mode (even mode) that was generated by exciting Port 1 and Port 2 with the same amplitude and in–phase signals, as shown in
Figure 5b. The other one is an odd symmetric mode (odd mode) that was generated by exciting Port 1 and Port 2 with the same amplitude, but with anti–phase signals, as shown in
Figure 5c. Simply through the superposition of these modes, the excitation at Port 1 in
Figure 5a could be treated as the sum of the even and odd mode excitations [
14].
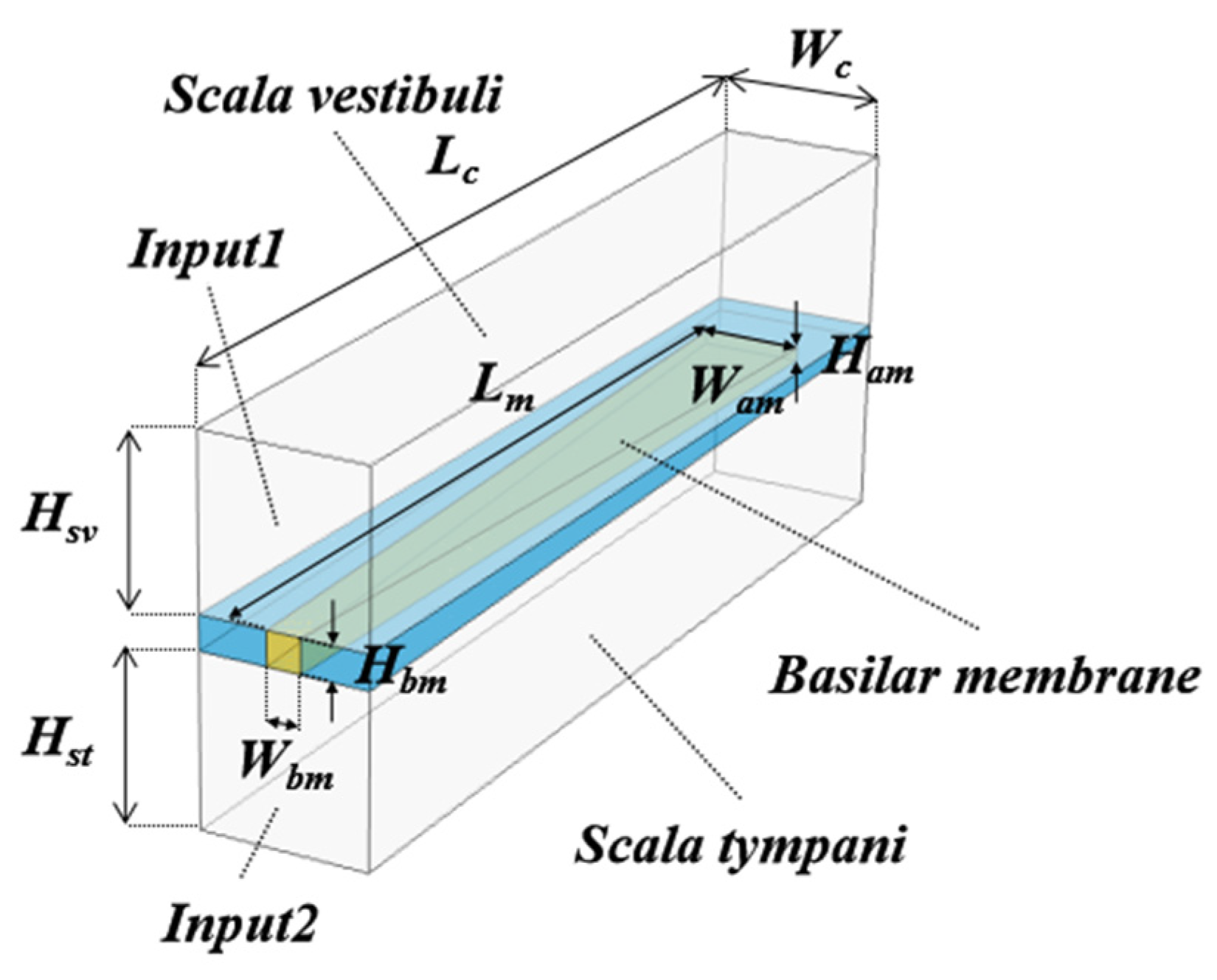
In this section, in order to evaluate how the even and odd modes of the sound wave (fast wave) contribute to generating the traveling wave (slow wave), a symmetric model (
Figure 6) was designed based on the cochlear architecture shown in
Figure 1. This model has two input planes, designated as “input 1” and “input 2” in the figure. In the even mode, these planes were excited by the same in–phase amplitude sound waves, while in the odd mode, they were excited by the same anti–phase amplitude sound waves. To avoid undesired coupling between the odd mode sound waves in the SV and ST, the helicotrema was removed from the original cochlear model, and only the BM remained as it was. Other physical and structural parameters were completely the same as the original model in
Figure 1.
The simulation results are summarized in
Figure 7 when a 1 Pa, 5000 Hz sound wave was applied for both input planes. The SPLs in the SV and ST and the displacement of the BM, which was generated by the even or odd symmetric sound waves, are presented. As shown in
Figure 7a, in the odd mode, odd symmetric SPLs could be observed in the SV and ST at the internal cochlear position from 0 mm to 12 mm. However, the odd mode response disappeared beyond 12 mm. This means that the odd mode sound wave plays an important role in generating the traveling wave. The color bar also presents this phenomenon visually. It should be noted that the energy of the odd mode sound wave was perfectly transformed into that of the traveling wave on the BM.
On the other hand, in the even mode, as shown in
Figure 7b, the SPL graphs of the SV and ST completely overlapped with each other and formed an even symmetric sound wave in the cochlea. However, the displacement of the BM was not seen at all. This can be confirmed visually with the color bar. This means that the even mode sound wave does not generate the traveling wave. Though only the demonstration result at 5000 Hz is shown here, the same can be said for other frequencies.
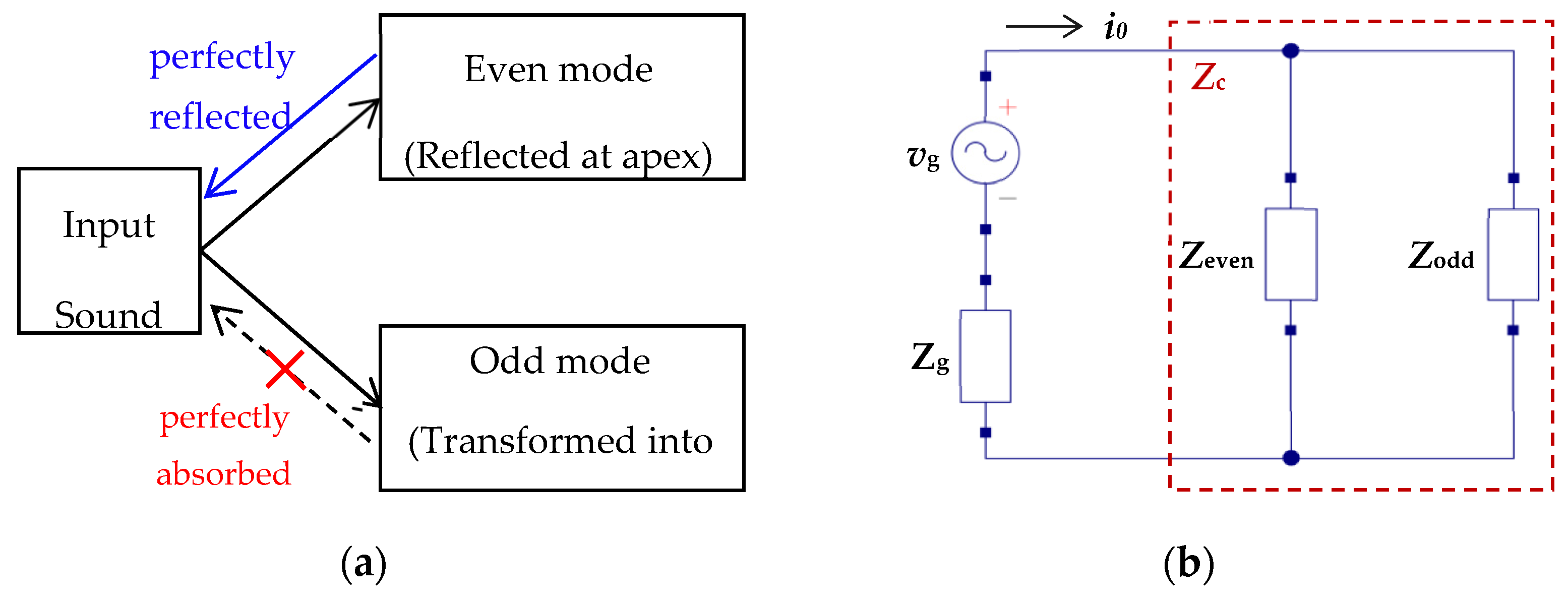
The results mentioned above are summarized in
Figure 8a; namely, the sound wave excited at the OW generated two symmetric sound modes, an even mode and an odd mode. Focusing on the wave phenomena in the SV, the even mode traveled in the SV, and was reflected at the cochlear apex with the maximum sound pressure level and zero fluid velocity, and finally, it came back to the OW without power dissipation, while in the odd mode, since the sound wave was completely transformed into the traveling wave and absorbed in the BM, the odd mode sound did not come back to the OW. These phenomena can be simply expressed by an equivalent circuit based on transmission line theory, as shown in
Figure 8b.
In this circuit, an alternative voltage source,
vg, and the inner impedance of the source,
Zg, were connected in series to design an excitation circuit, and the input impedance of the cochlea,
Zc, wa expressed by a parallel connection of an even mode impedance,
Zeven, and an odd mode impedance,
Zodd. Since the even and odd modes behave independently in the SV and ST, the coupling of both modes was ignored. Then,
Zeven and
Zodd were written as (see
Appendix A):
where
j is the imaginary unit (
j2 = −1),
Z0 is the acoustic characteristic impedance of the perilymph,
ρ is the mass density,
κ is the bulk modulus,
f is the sound wave frequency,
β is the phase constant, and
Lc is the cochlear length, respectively.
From these, the total input impedance of the cochlea
Zc was expressed by the parallel connection of the
Zeven and
Zodd as follows:
Circuit current
i0 was calculated as:
Then, the applied voltage (
vc) to the
Zeven and
Zodd were estimated by:
and currents on the
Zeven and
Zodd were given by:
Finally, the power dissipation on the even and odd modes,
PDeven and
PDodd, and the total power dissipation by the cochlea,
PDc, were expressed as:
In the circuit simulations, parameters vg = 1.0 V (corresponding to a 1 Pa sound wave excitation), Z0 = 1.5 MPa s/m3, ρ = 994.6 kg/m3, κ = 2.30e9 Pa, f = 5000 Hz, and Lc = 35 mm were used.
The circuit simulation results are shown in
Figure 9. The frequency dependence of the even and odd mode impedance,
Zeven and
Zodd, are shown in
Figure 9a,b. Blue solid curves and red dashed curves denote the real part and imaginary part of the impedance, respectively. As shown by
Zeven, the real part of
Zeven became zero for all frequencies because the even mode sound wave was perfectly reflected at the apex and went back to the voltage source again without power dissipation. On the other hand, at lower frequencies, below 10,600 Hz, the imaginary part of the
Zeven became negative, which meant that the cochlea became capacitive. Contrarily, at higher frequencies beyond 10,600 Hz, it became positive, and the cochlea became inductive. This result tells us an important fact in that the
Zeven reached zero at around 10,600 Hz. In this case, since
Zeven was connected to
Zodd in parallel, as shown in
Figure 8b, the input impedance of the cochlea,
Zc, also reached zero, and sound stimuli could not enter the cochlea. As a result, hearing loss will occur at this frequency. In fact, the displacement of the BM shown in
Figure 2f was also confined around there. Furthermore, note that hearing deterioration is confirmed at the measured equal–loudness contours around 10,000 Hz [
22]. We need to compare both results carefully because the equal loudness contours include psychological effects on the test subjects. However, our simulation result implies that the hearing deterioration at this frequency might occur due to the structure of the cochlea.
Next, the frequency dependence of the even and odd mode power dissipation,
PDeven and
PDodd, are presented in
Figure 9c,d. The graph of the
PDeven indicates that only the reactive power was stored in the cochlea and there was no power dissipation at any frequency. In contrast, the graph of the
PDodd shows that the cochlea dissipated active power to displace the BM and generate the traveling waves. However, the power dissipation was reduced around 10,600 Hz, because the even mode impedance,
Zeven = 0, affected the odd mode properties.
The input impedance of the cochlea,
Zc, is expressed by Equation (6), and the frequency dependence of
Zc is summarized in
Figure 9e. As pointed out, the zero impedance of the even mode
Zeven = 0 at 10,600 Hz affected the whole hearing performance of the cochlea; namely, the input impedance of the cochlea also became zero, and a significant impedance mismatch between the source and the cochlea occurred. As a result, although the cochlea as excited by the 1 Pa (
vg = 1.0 V) sound source, the actual pressure applied to the cochlea became smaller. The red point shows an applied pressure at 5000 Hz, calculated by the FEM–based structural simulation of the even and odd mode sound waves in
Figure 4. Although there are some errors between the results obtained by the structural analysis and the equivalent circuit analysis, we consider that they are within an acceptable range.
4. Conclusions
The wavelengths of the sound wave propagating in the perilymph at a speed of 1520 m/s were estimated as λ = 15.2 m at 100 Hz and λ = 1.52 m at 1000 Hz, respectively. These wavelengths were long enough compared to the size of the cochlea. However, at 10,000 Hz, the wavelength was only λ = 152 mm, and the 35 mm cochlea corresponded to about a quarter wavelength of the sound wave. Since the total length of the SV and ST was about 70 mm, the OW and RW were located at a half wavelength distance at this frequency. This means that, when the OW was pushed in, the RW moved toward the inside simultaneously. In reality, the physics of the cochlea are not so easy to understand because it includes elastic media such as the BM, OW, and RW. However, considering the wavelength of the sound waves at the higher audible frequency, we need to define the perilymph as a compressible medium to treat the phenomena caused by the sound waves in the cochlea more precisely.
Due to these reasons, we treated the perilymph of the SV and ST as a compressible medium, and fluid dynamics simulations were carried out using the Navier–Stokes equation for compressible media. From the time domain simulations, we observed that the sound wave (first wave) started to propagate in the cochlea first, and then the traveling wave (slow wave) as generated on the BM after a delay. This indicates that sound waves play an important role in exciting the traveling wave in the cochlea. From the frequency domain simulations, we observed that (1) the odd mode sound waves contributed to exciting the traveling wave; (2) the even mode sound waves did not generate the traveling wave; and (3) both modes did not couple in the cochlea. However, as indicated by the equivalent circuit simulations based on the transmission line theory, the even and odd modes are deeply related in terms of the impedance of the cochlea. For example, the cochlea is expected to lose hearing capability at 10,600 Hz due to the zero impedance of the even mode. Finally, we hope that many new discoveries will be made by assuming the compressible perilymph when the acoustic aspects of the cochlea are studied.