Ultrasonic Study of Longitudinal Critically Refracted and Bulk Waves of the Heat-Affected Zone of a Low-Carbon Steel Welded Joint under Fatigue
Abstract
:1. Introduction
2. Theoretical Background
2.1. Bulk Waves
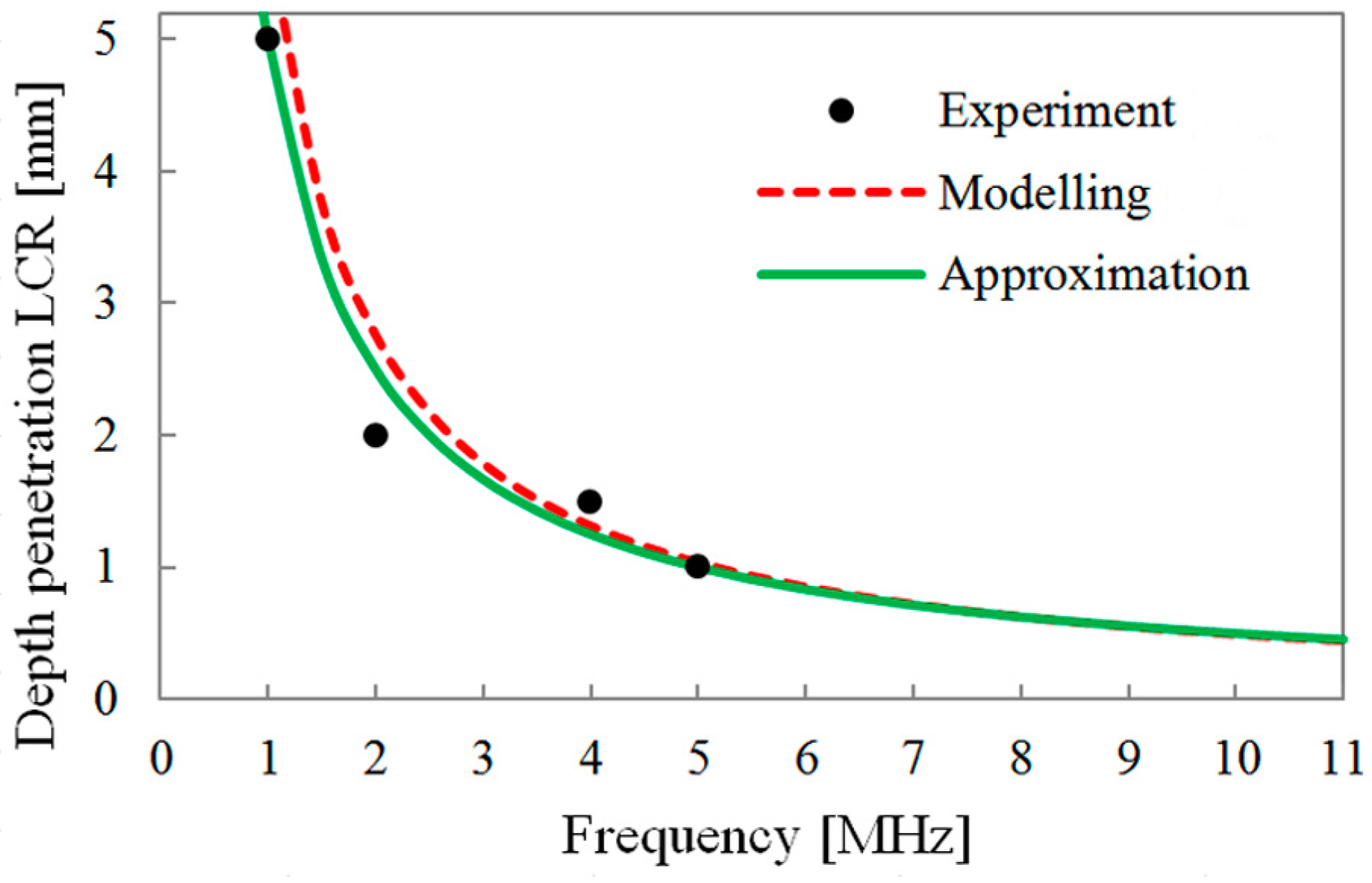
2.2. Longitudinal Critically Refracted Wave
3. Materials and Methods
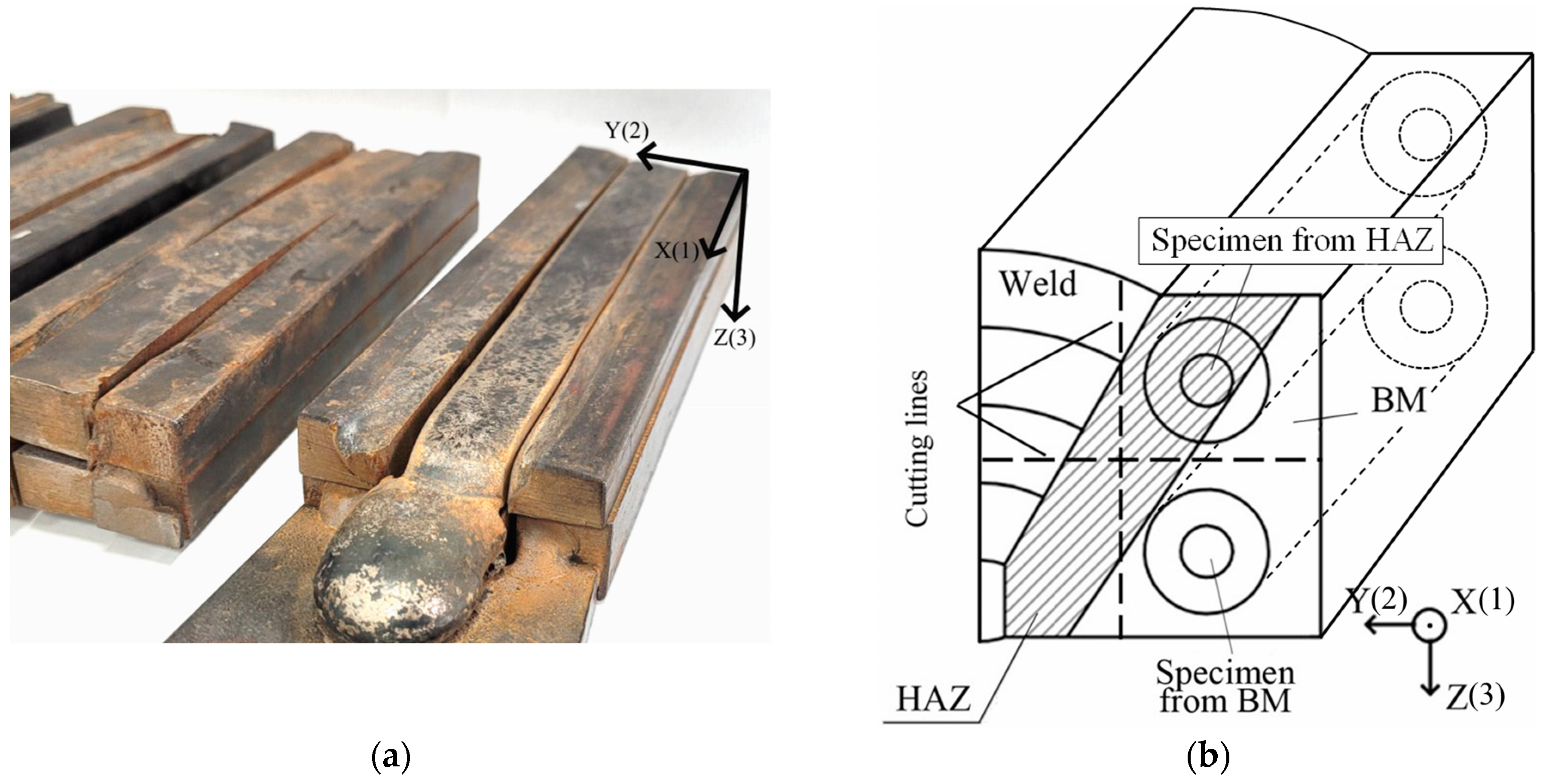
3.1. Material and Specimens
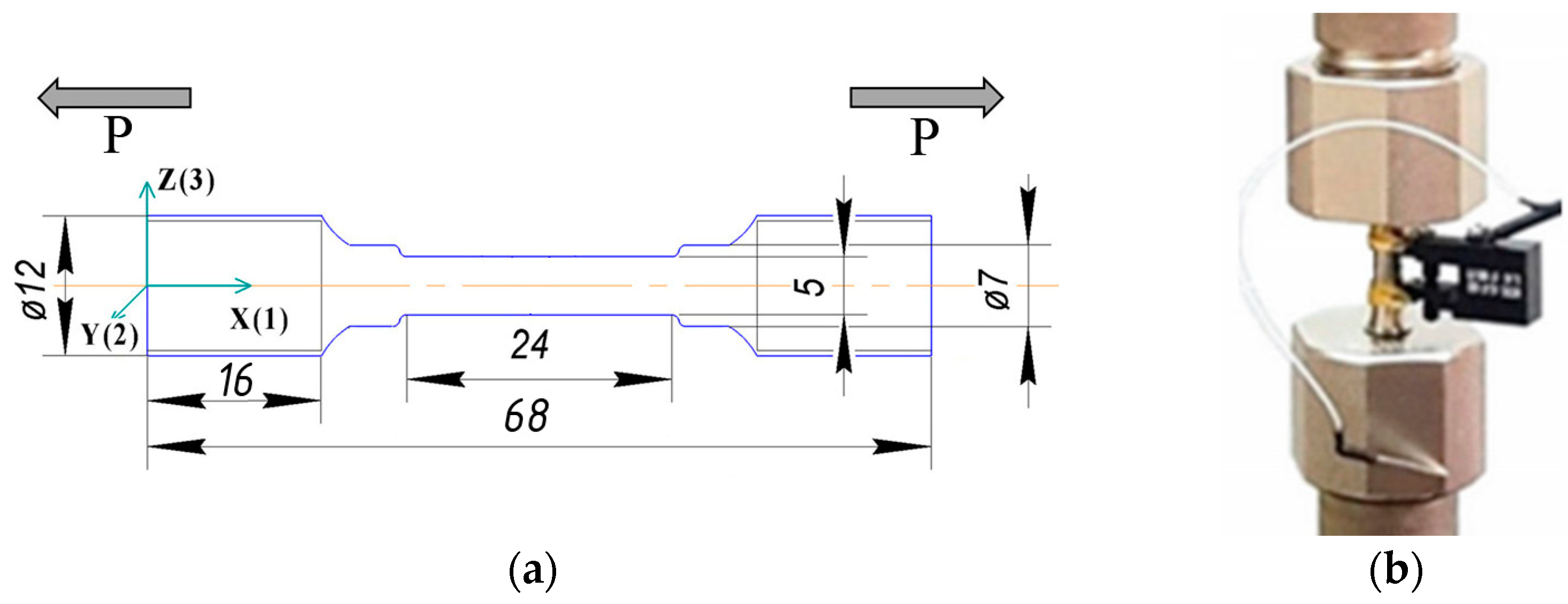
3.2. Low-Cycle Fatigue Tests
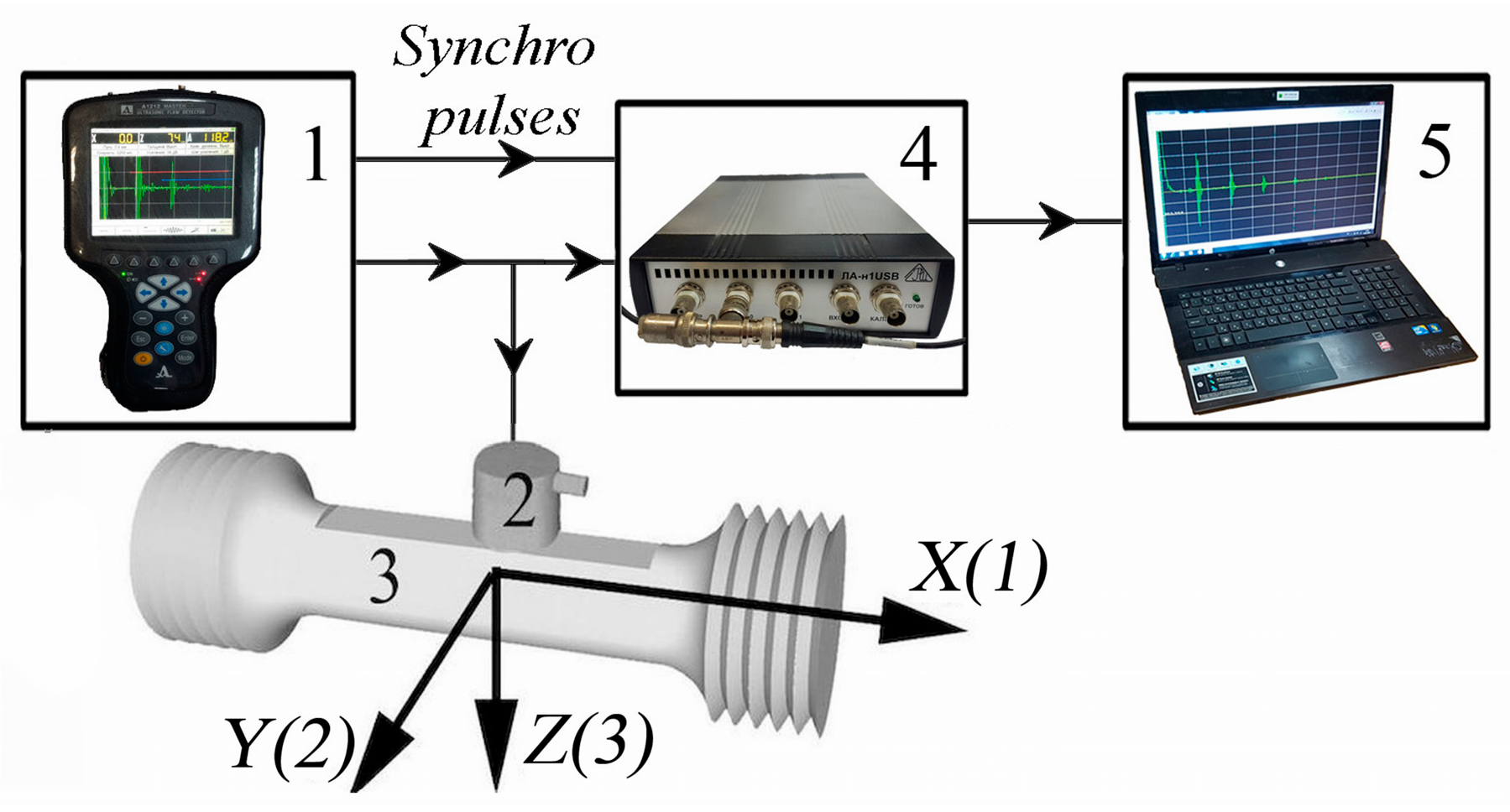
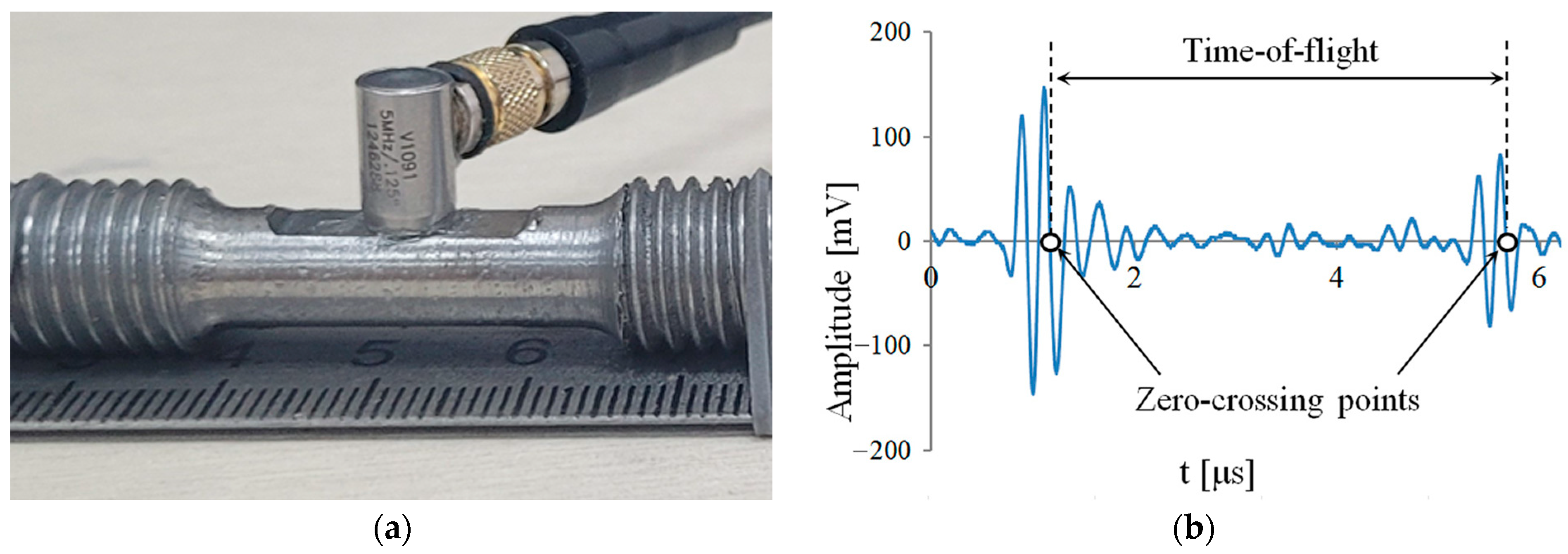
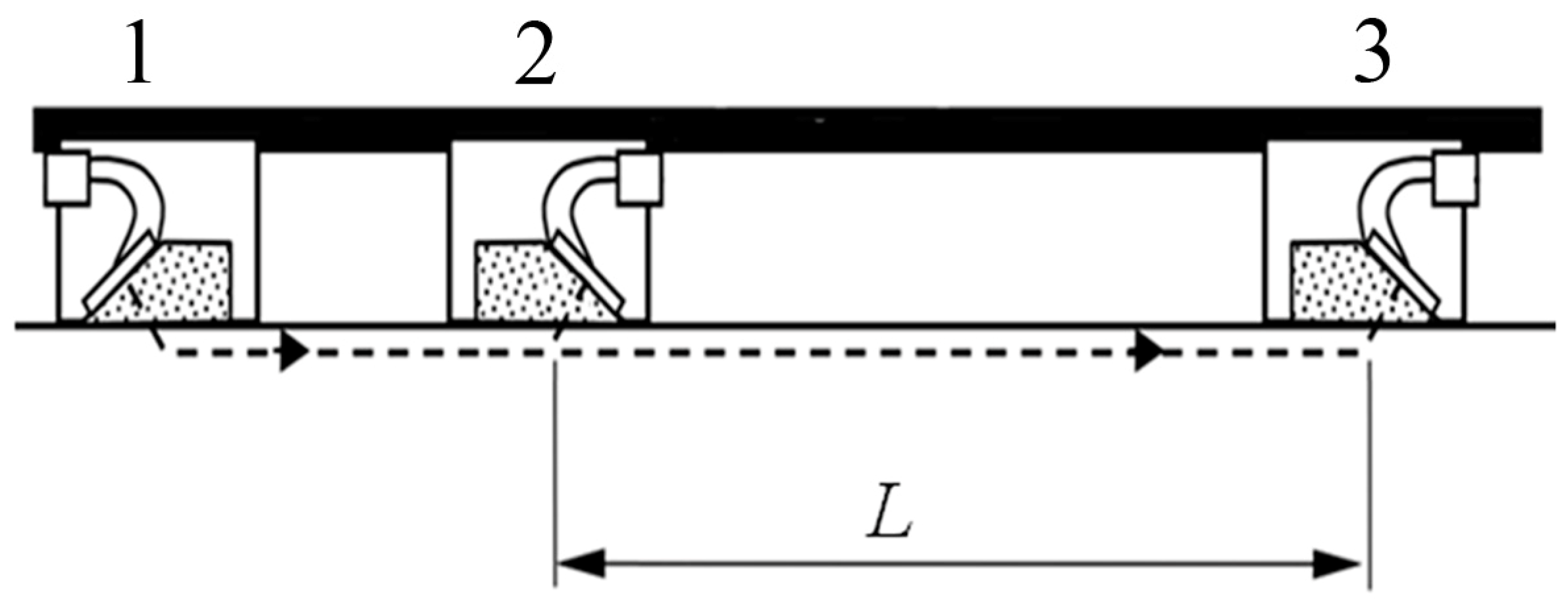
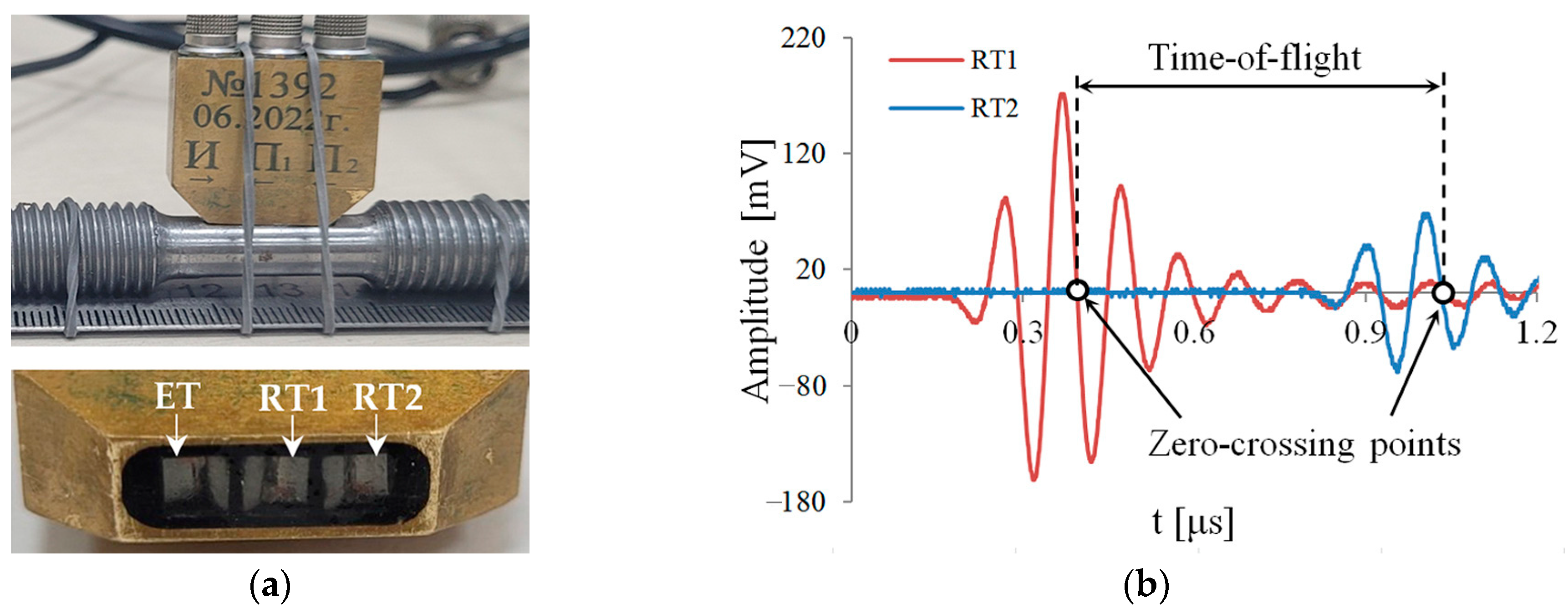
3.3. Ultrasonic Investigations
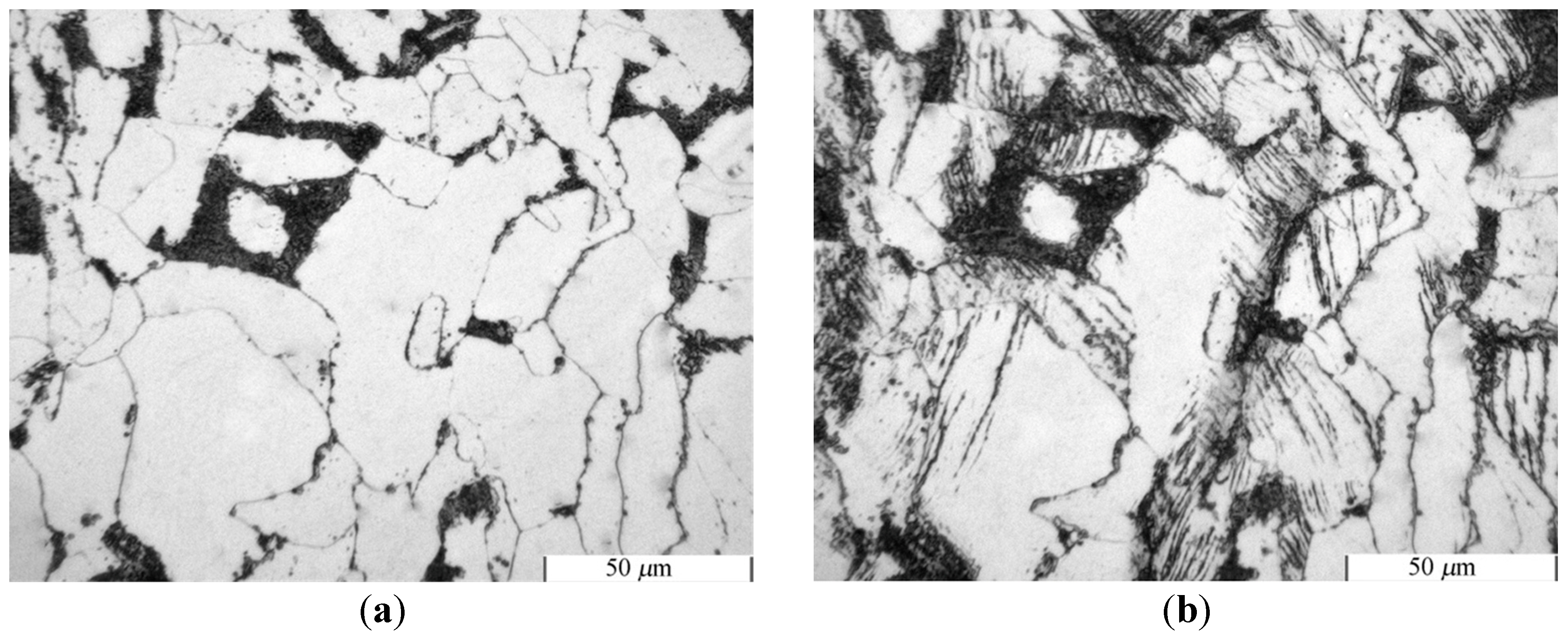
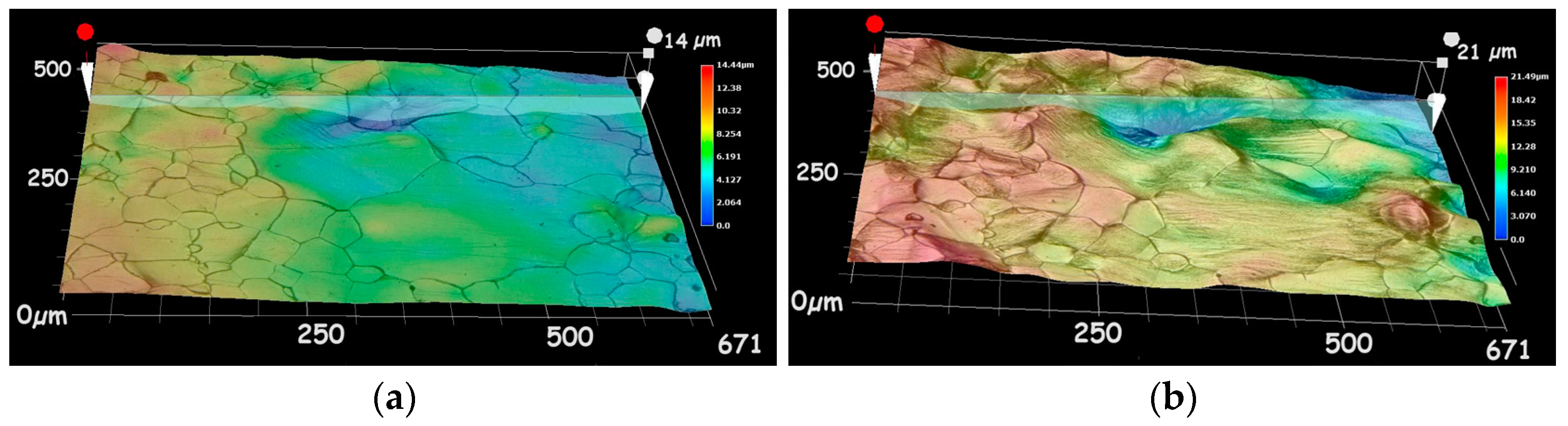
3.4. Metallographic Investigations
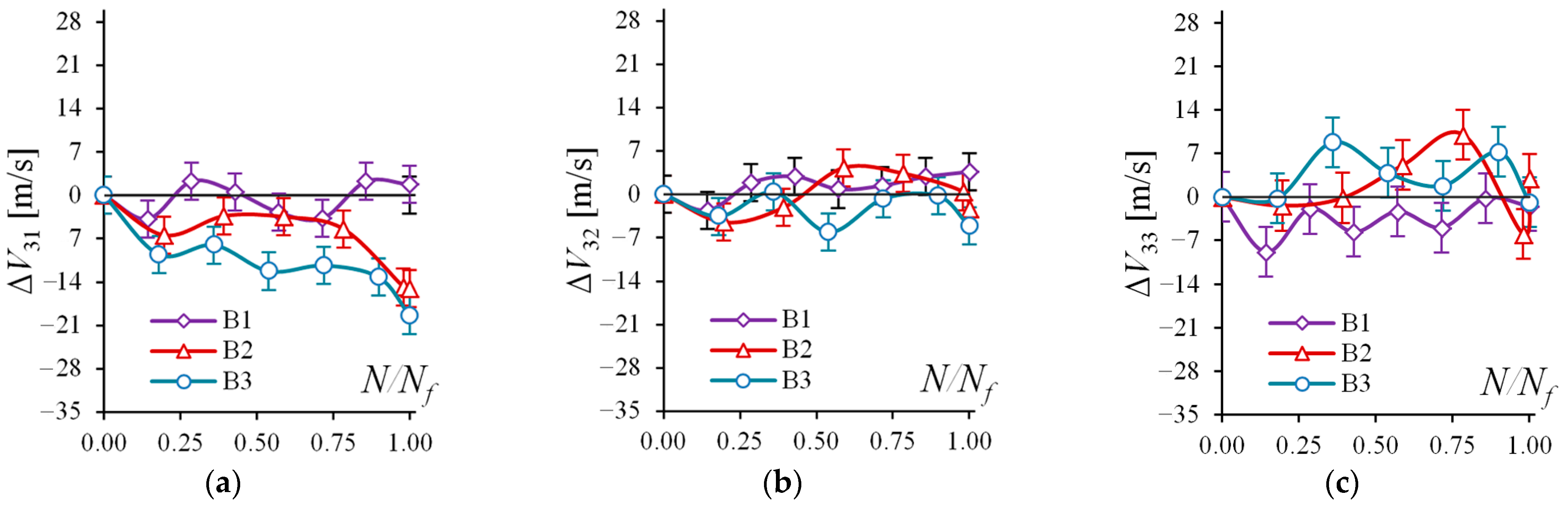
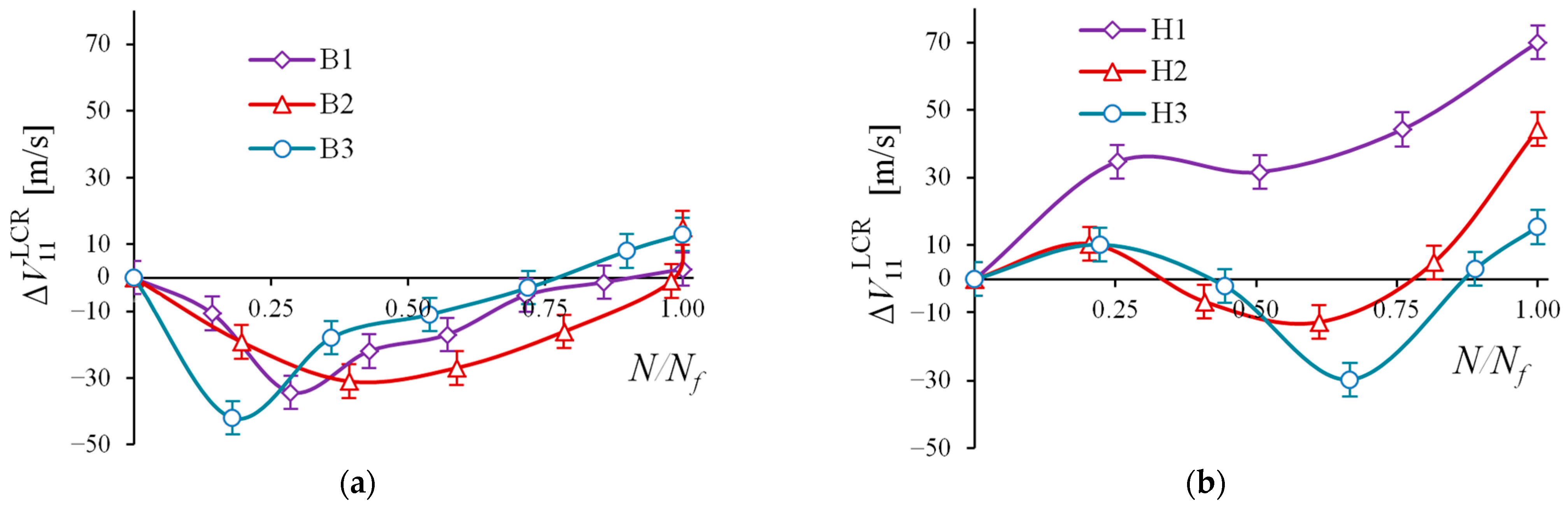
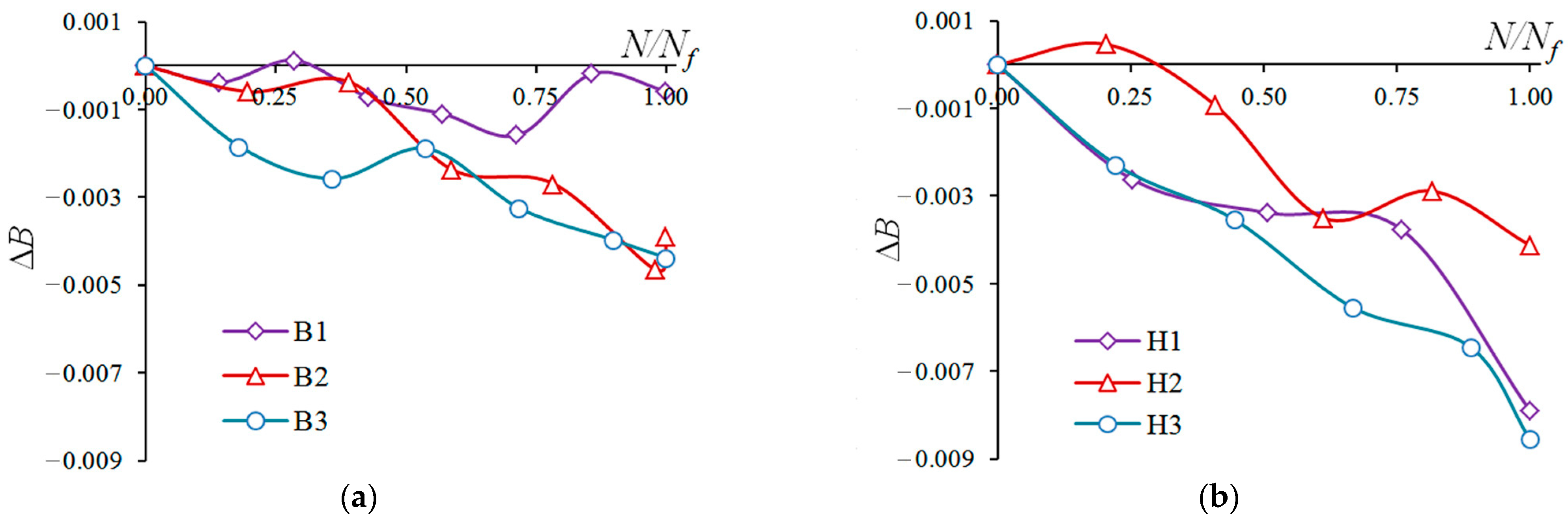
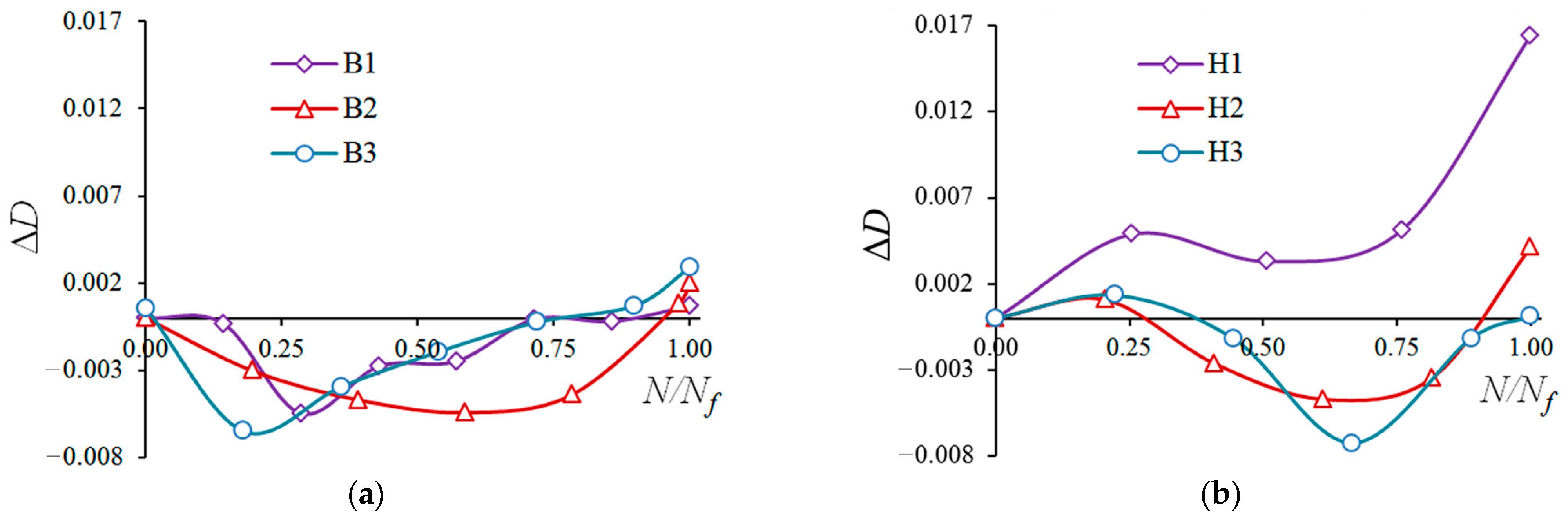
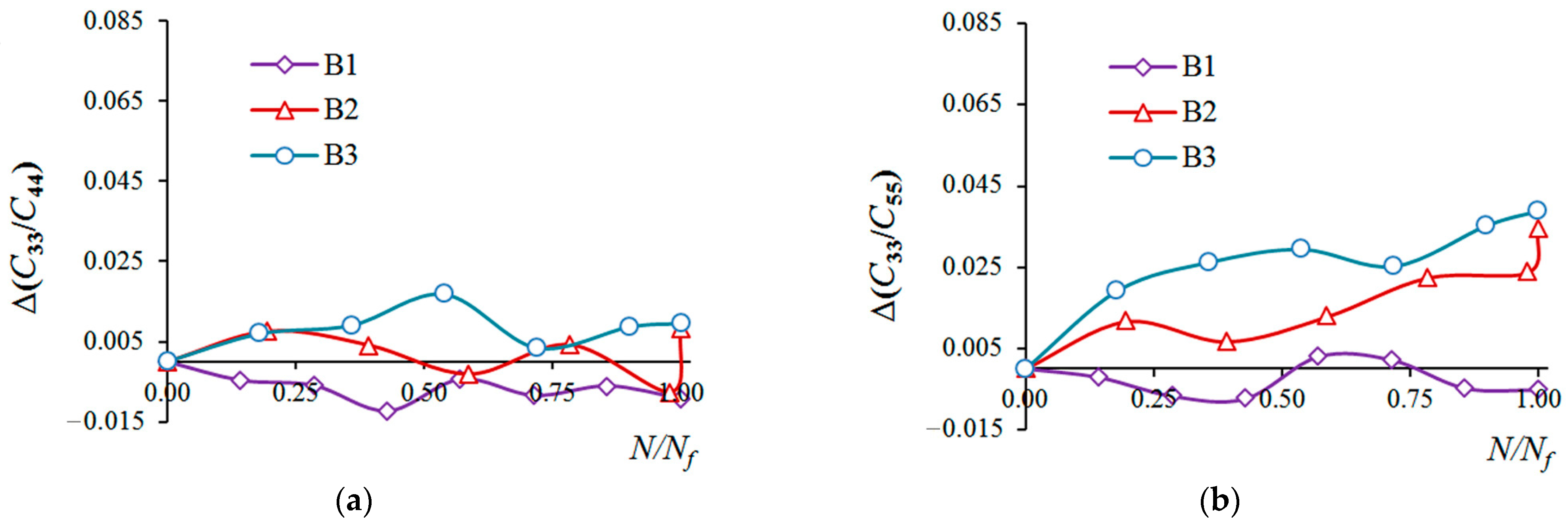
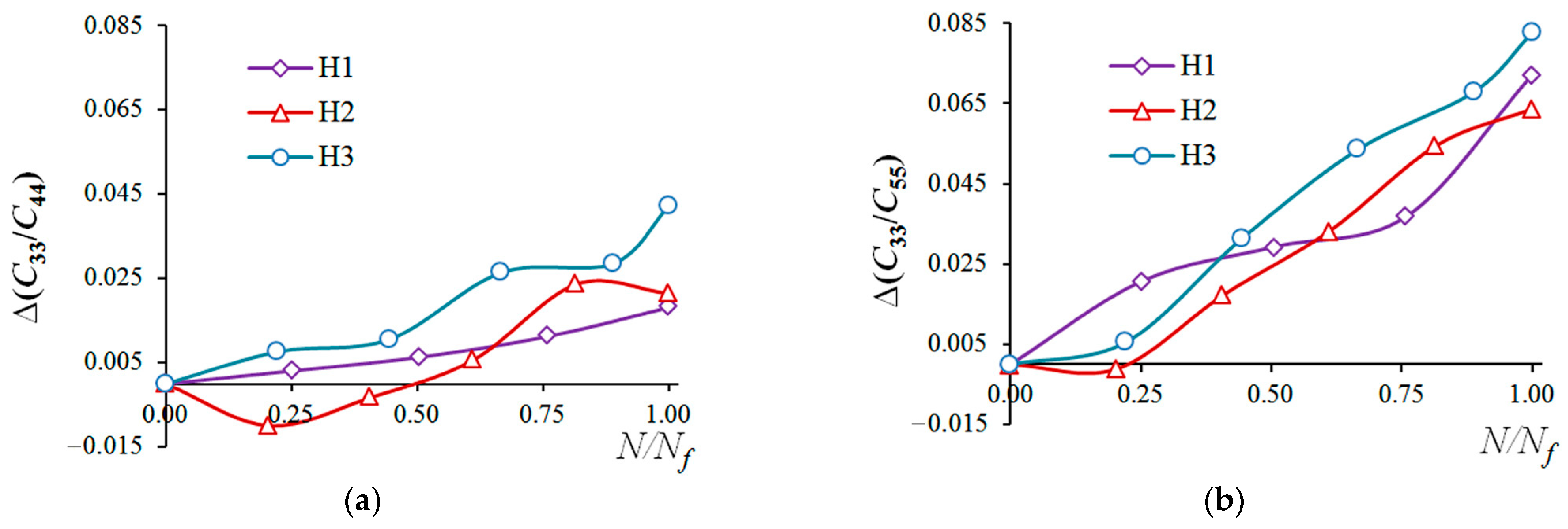
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wolfgang, F. Fatigue Analysis of Welded Joints: State of Development. Marine Struct. 2003, 16, 185–200. [Google Scholar] [CrossRef]
- Veerababu, J.; Goyal, S.; Atikukke, N. Studies on creep-fatigue interaction behavior of Grade 92 steel and its weld joints. Int. J. Fatigue 2021, 149, 106307. [Google Scholar] [CrossRef]
- Nishikawa, H.-a.; Furuya, Y.; Igi, S.; Goto, S.; Briffod, F.; Shiraiwa, T.; Enoki, M.; Kasuya, T. Effect of microstructure of simulated heat-affected zone on low-to high-cycle fatigue properties of low-carbon steels. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 1239–1249. [Google Scholar] [CrossRef]
- Wisner, B.; Mazur, K.; Kontsos, A. The use of nondestructive evaluation methods in fatigue: A rewiew. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 859–878. [Google Scholar] [CrossRef]
- Ensminger, D.; Bond, L.J. Ultrasonics: Fundamentals, Technologies, and Applications, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Vanniamparambil, P.A.; Bartoli, I.; Hazeli, K.; Cuadra, J.; Schwartz, E.; Saralaya, R.; Kontsos, A. An integrated structural health monitoring approach for crack growth monitoring. J. Int. Mat. Syst. Struct. 2012, 23, 1563–1573. [Google Scholar] [CrossRef]
- Pan, S.; Yu, G.; He, X.; Li, S.; Zhang, Y.; Li, Q. Collective evolution of surface microcrack for compacted graphite iron under thermal fatigue with variable amplitude. Int. J. Fatigue 2019, 118, 139–149. [Google Scholar] [CrossRef]
- Chen, E.Y.; Sauer, S.; Meshii, M.; Tucker, W.T. Fatigue microcrack distributions and the reability of a nickel base superalloy. Int. J. Fatigue 1997, 19, 75–82. [Google Scholar] [CrossRef]
- Besel, M.; Brueckner-Foit, A. Surface damage evolution of engineering steel. Fatigue Fract. Eng. Mater. Struct. 2008, 31, 885–891. [Google Scholar] [CrossRef]
- Mishakin, V.V.; Klyushnikov, V.A.; Gonchar, A.V.; Kachanov, M. On assessing damage in austenitic steel based on combination of the acoustic and eddy current monitoring. Int. J. Eng. Sci. 2019, 135, 17–22. [Google Scholar] [CrossRef]
- Cantrell, J.H.; Yost, W.T. Nonlinear ultrasonic characterization of fatigue microstructures. Int. J. Fatigue 2001, 23, 487–490. [Google Scholar] [CrossRef]
- Gupta, S.; Ray, A.; Keller, E. Online fatigue damage monitoring by ultrasonic measurements: A symbolic dynamics approach. Int. J. Fatigue 2007, 29, 1100–1114. [Google Scholar] [CrossRef]
- Gonchar, A.V.; Solovyov, A.A. Ultrasonic and metallographic study of the heat-affected zone of a carbon steel welded joint under plastic deformation and fatigue. J. Appl. Mech. Tech. Phys. 2023, 64, 921–928. [Google Scholar] [CrossRef]
- Makowska, K.; Piotrowski, L.; Kowalewski, Z.L. Prediction of the Mechanical Properties of P91 Steel by Means of Magneto-acoustic Emission and Acoustic Birefringence. J. Nondestruct. Eval. 2017, 36, 43. [Google Scholar] [CrossRef]
- Piotrowski, L.; Augustyniak, B.; Chmielewski, M. On the possibility of the application of magnetoacoustic emission intensity measurements for the diagnosis of thick-walled objects in the industrial environment. Meas. Sci. Technol. 2010, 21, 035702. [Google Scholar] [CrossRef]
- Gonchar, A.V.; Mishakin, V.V.; Klyushnikov, V.A. The effect of phase transformations induced by cyclic loading on the elastic properties and plastic hysteresis of austenitic stainless steel. Int. J. Fatigue 2018, 106, 153–158. [Google Scholar] [CrossRef]
- Hirsekorn, S.; Andel, P.; Netzelmann, U. Ultrasonic methods to detect and evaluate damage in steel. Nondestruct. Test. Eval. 2000, 15, 373–393. [Google Scholar] [CrossRef]
- Pei, N.; Zhao, B.; Zhao, X.; Liu, Z.; Bond, L.J. Analysis of the directivity of Longitudinal Critically Refracted (LCR) waves. Ultrasonics 2021, 113, 106359. [Google Scholar] [CrossRef]
- Javadi, Y.; Pirzaman, H.M.; Raeisi, M.H.; Najafabadi, M.A. Ultrasonic Evaluation of Welding Residual Stresses in Stainless Steel Pressure Vessel. J. Press. Vessel. Technol. 2013, 135, 041502. [Google Scholar] [CrossRef]
- Buenos, A.A.; Jr, P.P.; Mei, P.R.; Santos, A.A. Influence of Grain Size on the Propagation of LCR Waves in Low Carbon Steel. J. Nondestruct. Eval. 2014, 33, 562–570. [Google Scholar] [CrossRef]
- Ferrand, A.; Darmon, V.; Chatillon, S.; Deschamps, M. Modeling of ray paths of head waves on irregular interfaces in TOFD inspection for NDE. Ultrasonics 2014, 54, 1851–1860. [Google Scholar] [CrossRef]
- Zernov, V.; Fradkin, L.; Gautesen, A.; Darmon, M.; Calmon, P. Wedge diffraction of a critically incident Gaussian beam. Wave Motion 2013, 50, 708–722. [Google Scholar] [CrossRef]
- Huet, G.; Darmon, M.; Lhéemery, A.; Mahaut, S. Modeling of corner echo ultrasonic inspection with bulk and creeping waves. In Ultrasonic Wave Propagation in Non Homogeneous Media; Leger, A., Deschamps, M., Eds.; Springer Proceedings in Physics, 128; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Darmon, M.; Ferrand, A.; Dorval, V.; Chatillon, S.; Lonné, S. Recent modelling advances for ultrasonic TOFD inspections. AIP Conf. Proc. 2015, 1650, 1757–1765. [Google Scholar] [CrossRef]
- Ermolov, I.N. Progress in the theory of ultrasonic flaw detection. Problems and prospects. Russ. J. Nondestruct. Test. 2004, 40, 655–678. [Google Scholar] [CrossRef]
- Fedorov, F.I. Theory of Elastic Waves in Crystals; Springer: New York, NY, USA, 1968. [Google Scholar]
- Gonchar, A.V.; Mishakin, V.V.; Klyushnikov, V.A.; Kurashkin, K.V. Variation of Elastic Characteristics of Metastable Austenite Steel under Cycling Straining. Tech. Phys. 2017, 62, 537–541. [Google Scholar] [CrossRef]
- Bray, D.E. Ultrasonic Stress Measurement and Material Characterization in Pressure Vessels, Piping and Welds. J. Press. Vessel. Technol. 2002, 124, 326–335. [Google Scholar] [CrossRef]
- Bray, D.E.; Griffin, R.B. Monitoring Hydrogen Release from 4140 Steel Using the LCR Ultrasonic Technique. In Nondestructive Testing of Materials and Structures; Springer: Dordrecht, The Netherlands, 2011; pp. 689–694. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, E.; Chen, Y.; Wang, X.; Sun, C.; Tan, J. Study on Propagation Depth of Ultrasonic Longitudinal Critically Refracted (LCR) Wave. Sensors 2020, 20, 5724. [Google Scholar] [CrossRef] [PubMed]
- ASTM E8/E8M-11; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2011.
- ASTM E1823-13; Standard Terminology Relating to Fatigue and Fracture Testing. ASTM International: West Conshohocken, PA, USA, 2013.
- Szelążek, J. Sets of Piezoelectric Probeheads for Stress Evaluation with Subsurface Waves. J. Nondestruct. Eval. 2013, 32, 188–199. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.; Li, T.; Zhang, X.; Liu, Y.; Liu, K.; Wang, Y. Influence factors analysis and accuracy improvement for stress measurement using ultrasonic longitudinal critically refracted (LCR) wave. App. Acoust. 2018, 141, 178–187. [Google Scholar] [CrossRef]
- Gonchar, A.V.; Kurashkin, K.V.; Andreeva, O.V.; Anosov, M.S.; Klyushnikov, V.A. Fatigue life prediction of structural steel using acoustic birefringence and characteristics of persistent slip bands. Fatigue Fract. Eng. Mat. Struct. 2021, 45, 101–112. [Google Scholar] [CrossRef]
- Truell, R.; Elbaum, C.; Chick, B.B. Ultrasonic Methods in Solid State Physics; Academic Press: New York, NY, USA; London, UK, 1969. [Google Scholar]
- Mishakin, V.V.; Gonchar, A.V.; Kirikov, S.V.; Klyushnikov, V.A. Evaluation of condition of low-carbon steels experiencing plastic deformation using the effect of acoustic birefringence. Nondestruct. Test. Eval. 2021, 36, 225–235. [Google Scholar] [CrossRef]
- Viktorov, I.A. Rayleigh and Lamb Waves: Physical Theory and Applications; Plenum Press: New York, NY, USA, 1967. [Google Scholar]
- Sarpün, İ.H.; Kılıçkaya, M.S.; Tuncel, S. Mean grain size determination in marbles by ultrasonic velocity techniques. NDT E Int. 2005, 38, 21–25. [Google Scholar] [CrossRef]
- Petch, N.J. The cleavage strength of polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
- Sylwestrowicz, W.; Hall, E.O. The Deformation and Ageing of Mild Steel. Proc. Phys. Soc. B. 1951, 64, 495–502. [Google Scholar] [CrossRef]
- Yan, X.; Wang, H.; Fan, X. Research Progress in Nonlinear Ultrasonic Testing for Early Damage in Metal Materials. Materials 2023, 16, 2161. [Google Scholar] [CrossRef] [PubMed]



| Fe | C | Si | Mn | Ni | Cr | Cu | As | S | P |
|---|---|---|---|---|---|---|---|---|---|
| >98.7 | 0.18 | 0.21 | 0.56 | 0.08 | 0.11 | 0.08 | 0.04 | <0.01 | <0.02 |
| Yield Tensile Strength, MPa | Ultimate Tensile Strength, MPa | Elongation at Break, % |
|---|---|---|
| 270 ± 10 | 450 ± 10 | 28 ± 2 |
| Test No. | Type | Δε, % | Δσ, MPa | Nf |
|---|---|---|---|---|
| B1 | Base Metal | 0.3 | 306 | 10,500 |
| B2 | 0.4 | 347 | 5100 | |
| B3 | 0.5 | 379 | 2780 | |
| H1 | Heat-affected zone | 0.3 | 308 | 5900 |
| H2 | 0.4 | 314 | 4900 | |
| H3 | 0.5 | 348 | 2250 |
| Test No. | N, Cycles | , m/s | , m/s | , m/s | , m/s |
|---|---|---|---|---|---|
| B1 | 0 | 3272 | 3268 | 5984 | 5941 |
| 1500 | 3268 | 3266 | 5975 | 5931 | |
| 3000 | 3274 | 3270 | 5982 | 5907 | |
| 4500 | 3272 | 3271 | 5978 | 5919 | |
| 6000 | 3269 | 3269 | 5982 | 5924 | |
| 7500 | 3268 | 3270 | 5979 | 5936 | |
| 9000 | 3274 | 3271 | 5984 | 5940 | |
| 10,500 | 3273 | 3272 | 5983 | 5944 | |
| B2 | 0 | 3279 | 3277 | 6001 | 5930 |
| 1000 | 3273 | 3273 | 6000 | 5911 | |
| 2000 | 3276 | 3275 | 6001 | 5902 | |
| 3000 | 3276 | 3281 | 6006 | 5903 | |
| 4000 | 3274 | 3281 | 6011 | 5914 | |
| 5000 | 3265 | 3278 | 5995 | 5929 | |
| 5100 | 3264 | 3275 | 6004 | 5945 | |
| B3 | 0 | 3275 | 3272 | 5978 | 5939 |
| 500 | 3265 | 3268 | 5978 | 5897 | |
| 1000 | 3267 | 3272 | 5987 | 5921 | |
| 1500 | 3262 | 3265 | 5982 | 5928 | |
| 2000 | 3263 | 3271 | 5980 | 5936 | |
| 2500 | 3261 | 3271 | 5986 | 5947 | |
| 2780 | 3255 | 3266 | 5978 | 5952 | |
| H1 | 0 | 3259 | 3274 | 5984 | 5869 |
| 1500 | 3252 | 3275 | 5990 | 5904 | |
| 3000 | 3252 | 3277 | 5997 | 5901 | |
| 4500 | 3249 | 3276 | 5998 | 5914 | |
| 5900 | 3238 | 3278 | 6009 | 5992 | |
| H2 | 0 | 3258 | 3270 | 5990 | 5853 |
| 1000 | 3253 | 3263 | 5994 | 5863 | |
| 2000 | 3248 | 3262 | 5999 | 5846 | |
| 3000 | 3245 | 3268 | 6005 | 5840 | |
| 4000 | 3244 | 3265 | 6016 | 5858 | |
| 4900 | 3240 | 3265 | 6010 | 5897 | |
| H3 | 0 | 3255 | 3271 | 5972 | 5874 |
| 500 | 3254 | 3277 | 5974 | 5884 | |
| 1000 | 3241 | 3269 | 5977 | 5872 | |
| 1500 | 3236 | 3271 | 5985 | 5832 | |
| 2000 | 3226 | 3263 | 5982 | 5877 | |
| 2250 | 3224 | 3268 | 5987 | 5889 |
| Test No | N, Cycles | B | D | C33/C44 | C33/C55 |
|---|---|---|---|---|---|
| B1 | 0 | 0.0011 | −0.007 | 3.353 | 3.345 |
| 1500 | 0.0007 | −0.008 | 3.348 | 3.343 | |
| 3000 | 0.0012 | −0.013 | 3.347 | 3.339 | |
| 4500 | 0.0004 | −0.010 | 3.340 | 3.338 | |
| 6000 | 0.0000 | −0.010 | 3.348 | 3.348 | |
| 7500 | −0.0005 | −0.007 | 3.344 | 3.347 | |
| 9000 | 0.0009 | −0.007 | 3.347 | 3.341 | |
| 10,500 | 0.0005 | −0.006 | 3.344 | 3.340 | |
| B2 | 0 | 0.0007 | −0.012 | 3.354 | 3.349 |
| 1000 | 0.0001 | −0.015 | 3.361 | 3.361 | |
| 2000 | 0.0003 | −0.017 | 3.358 | 3.356 | |
| 3000 | −0.0017 | −0.017 | 3.350 | 3.362 | |
| 4000 | −0.0020 | −0.016 | 3.358 | 3.371 | |
| 5000 | −0.0040 | −0.011 | 3.346 | 3.373 | |
| 5100 | −0.0032 | −0.010 | 3.362 | 3.383 | |
| B3 | 0 | 0.0009 | −0.007 | 3.339 | 3.333 |
| 500 | −0.0009 | −0.014 | 3.346 | 3.353 | |
| 1000 | −0.0016 | −0.011 | 3.348 | 3.360 | |
| 1500 | −0.0010 | −0.009 | 3.356 | 3.363 | |
| 2000 | −0.0023 | −0.007 | 3.343 | 3.358 | |
| 2500 | −0.0030 | −0.006 | 3.348 | 3.369 | |
| 2780 | −0.0035 | −0.004 | 3.349 | 3.372 | |
| H1 | 0 | −0.0045 | −0.019 | 3.342 | 3.372 |
| 1500 | −0.0071 | −0.014 | 3.345 | 3.393 | |
| 3000 | −0.0079 | −0.016 | 3.348 | 3.401 | |
| 4500 | −0.0083 | −0.014 | 3.353 | 3.409 | |
| 5900 | −0.0124 | −0.003 | 3.360 | 3.444 | |
| H2 | 0 | −0.0036 | −0.023 | 3.362 | 3.386 |
| 1000 | −0.0032 | −0.022 | 3.352 | 3.385 | |
| 2000 | −0.0045 | −0.026 | 3.359 | 3.404 | |
| 3000 | −0.0071 | −0.028 | 3.367 | 3.419 | |
| 4000 | −0.0065 | −0.027 | 3.385 | 3.441 | |
| 4900 | −0.0078 | −0.019 | 3.383 | 3.450 | |
| H3 | 0 | −0.0050 | −0.017 | 3.333 | 3.366 |
| 500 | −0.0073 | −0.015 | 3.341 | 3.372 | |
| 1000 | −0.0085 | −0.017 | 3.343 | 3.398 | |
| 1500 | −0.0105 | −0.024 | 3.359 | 3.420 | |
| 2000 | −0.0114 | −0.017 | 3.361 | 3.434 | |
| 2250 | −0.0135 | −0.016 | 3.375 | 3.449 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonchar, A.; Solovyov, A.; Klyushnikov, V. Ultrasonic Study of Longitudinal Critically Refracted and Bulk Waves of the Heat-Affected Zone of a Low-Carbon Steel Welded Joint under Fatigue. Acoustics 2024, 6, 593-609. https://doi.org/10.3390/acoustics6030032
Gonchar A, Solovyov A, Klyushnikov V. Ultrasonic Study of Longitudinal Critically Refracted and Bulk Waves of the Heat-Affected Zone of a Low-Carbon Steel Welded Joint under Fatigue. Acoustics. 2024; 6(3):593-609. https://doi.org/10.3390/acoustics6030032
Chicago/Turabian StyleGonchar, Alexander, Alexander Solovyov, and Vyacheslav Klyushnikov. 2024. "Ultrasonic Study of Longitudinal Critically Refracted and Bulk Waves of the Heat-Affected Zone of a Low-Carbon Steel Welded Joint under Fatigue" Acoustics 6, no. 3: 593-609. https://doi.org/10.3390/acoustics6030032
APA StyleGonchar, A., Solovyov, A., & Klyushnikov, V. (2024). Ultrasonic Study of Longitudinal Critically Refracted and Bulk Waves of the Heat-Affected Zone of a Low-Carbon Steel Welded Joint under Fatigue. Acoustics, 6(3), 593-609. https://doi.org/10.3390/acoustics6030032







