A Power Law Reconstruction of Ultrasound Backscatter Images
Abstract
:1. Introduction
2. Theory
- ;
- a power law function of discrete frequency in the expected value of the ensemble average;
- a power law distribution of amplitudes, i.e., Burr distribution;
- a Lomax distribution of the intensity;
- the spatial autocorrelation function of approaches a power law function of lag.
3. Methods
- (i)
- Initial conditions: From the received echo , calculate the analytical envelope and intensity ; optionally check the histogram of within a region of interest in tissue.
- (ii)
- Generate a random uncorrelated noise distribution from Gaussian or uniform zero-mean white noise adjusted locally such that the mean is equal to and where is a scale factor adjusted such that has approximately the same energy as . In two dimensions, is formed as a discrete and whitened version of .
- (iii)
- Filter with a two dimensional, isotropic filter in the frequency domain (or by convolution with the equivalent filter in the sampled time domain) to produce , which then would have an ensemble-averaged power law spectrum approaching .
- (iv)
- The magnitude of serves as the first iteration estimate of the local scattering density and can be used as an initial image. The above steps can be repeated and averaged, to obtain an ensemble average estimate of the inherent scattering distributions, and, optionally, further iterations can be taken as follows.
- (v)
- Calculate the new image lines as , and the new intensity .
- (vi)
- Adjust the local amplitudes of so that the convolution with the pulse yields a better match to the original envelope: .
- (vii)
- Optionally enforce any of the constraints on the intensity, autocorrelation, and power spectra listed in Section 2.
- (viii)
- Repeat steps (v)–(vii) until a convergence criteria is met.
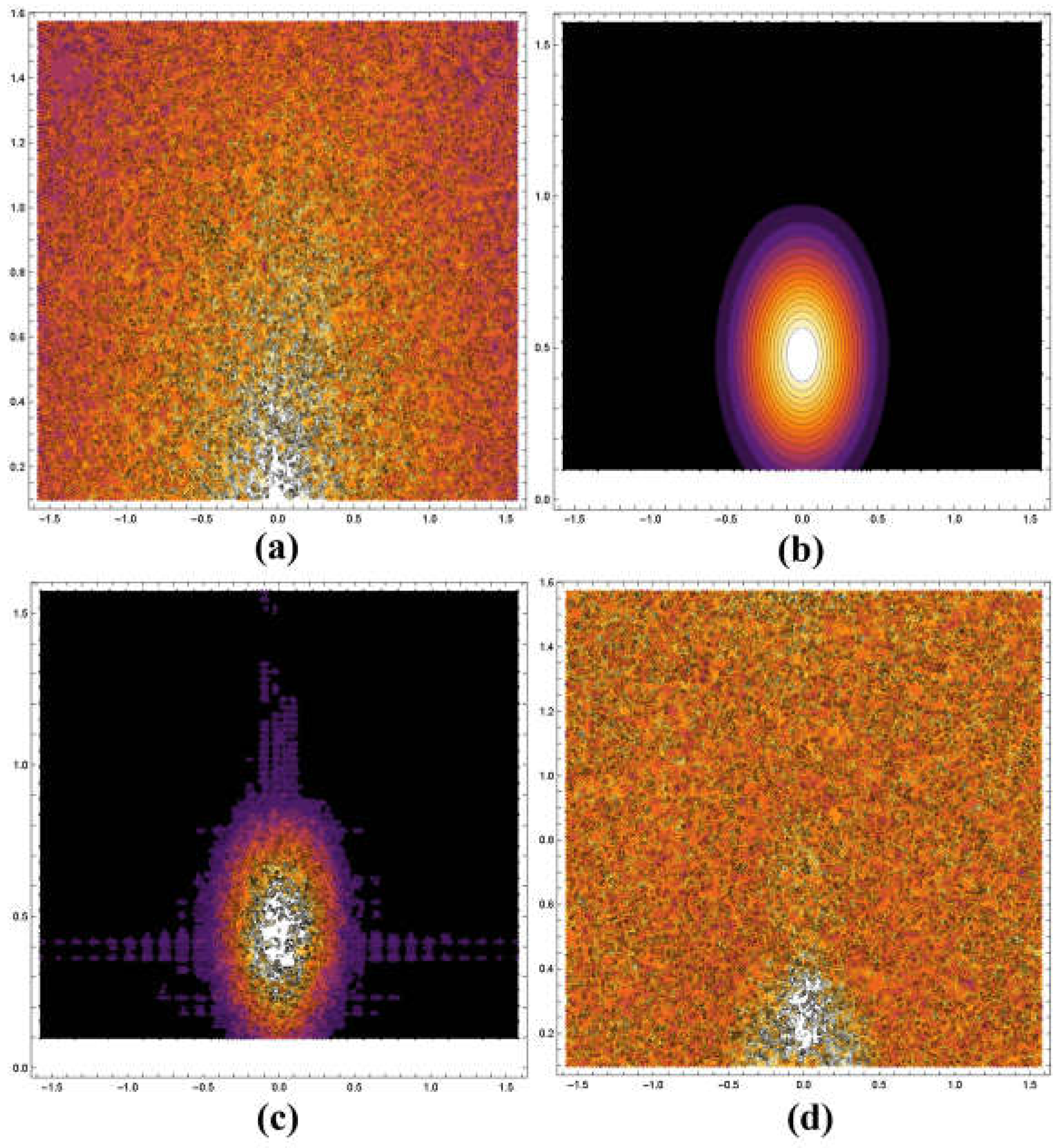
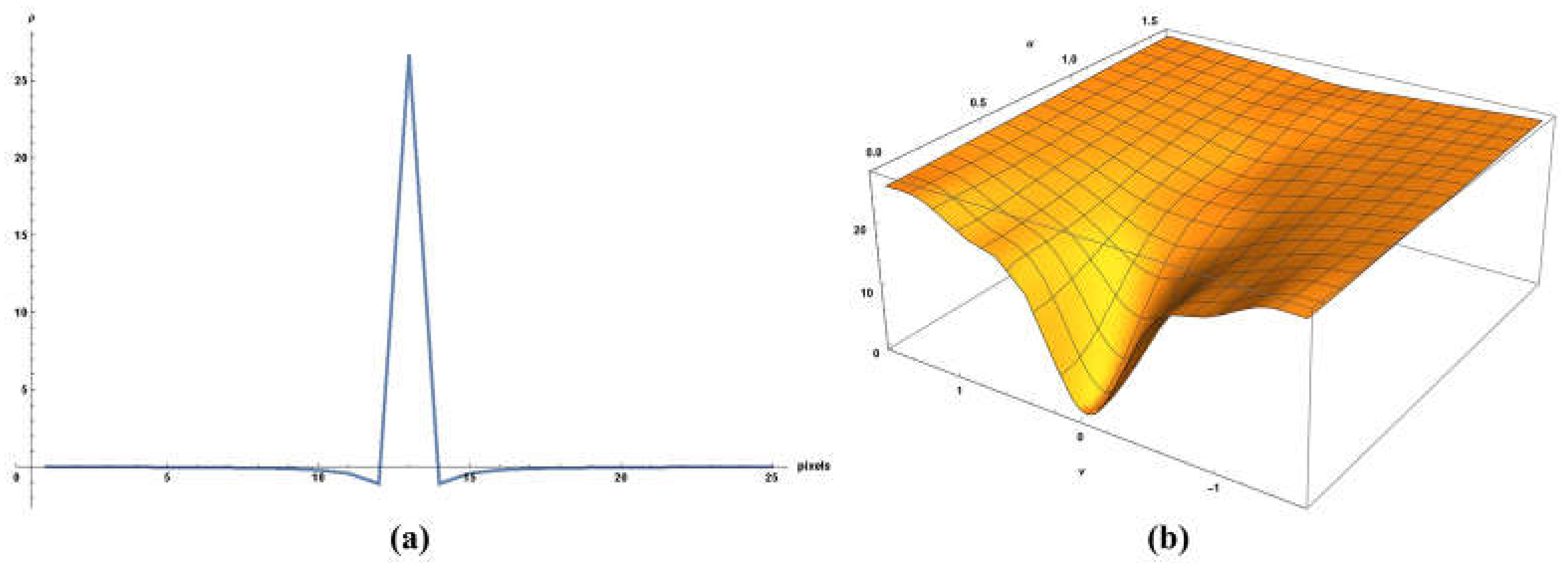
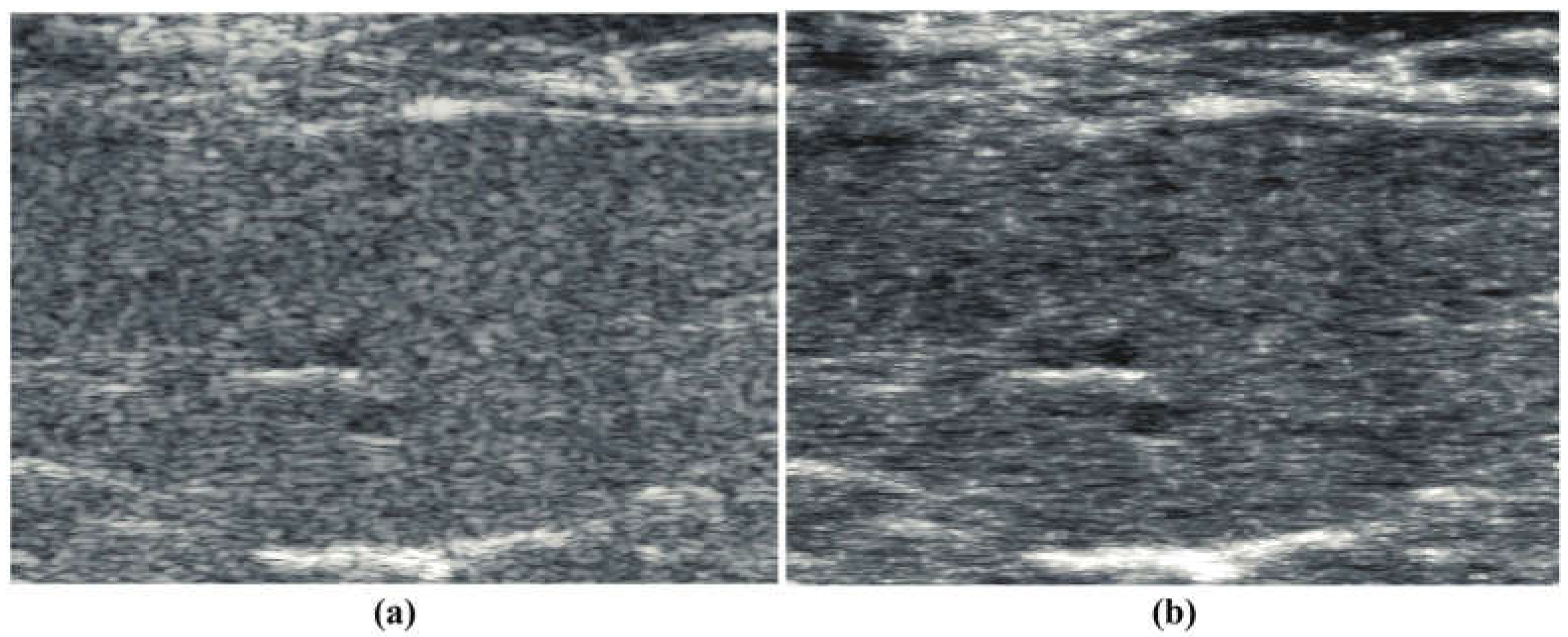
4. Results
5. Discussion and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Burckhardt, C.B. Speckle in ultrasound b-mode scans. IEEE Trans. Sonics Ultrason. 1978, 25, 1–6. [Google Scholar] [CrossRef]
- Shin, H.C.; Prager, R.; Ng, J.; Gomersall, H.; Kingsbury, N.; Treece, G.; Gee, A. Sensitivity to point-spread function parameters in medical ultrasound image deconvolution. Ultrasonics 2009, 49, 344–357. [Google Scholar] [CrossRef] [PubMed]
- Jensen, J.A. Real time deconvolution of in-vivo ultrasound images. In Proceedings of the 2013 IEEE International Ultrasonics Symposium (IUS), Prague, Czech Republic, 21–25 July 2013; pp. 29–32. [Google Scholar]
- Chen, S.; Parker, K.J. Enhanced resolution pulse-echo imaging with stabilized pulses. J. Med. Imaging 2016, 3, 027003. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Parker, K.J. Enhanced axial and lateral resolution using stabilized pulses. J. Med. Imaging 2017, 4, 027001. [Google Scholar] [CrossRef] [PubMed]
- Duarte-Salazar, C.A.; Castro-Ospina, A.E.; Becerra, M.A.; Delgado-Trejos, E. Speckle noise reduction in ultrasound images for improving the metrological evaluation of biomedical applications: An overview. IEEE Access 2020, 8, 15983–15999. [Google Scholar] [CrossRef]
- Kassab, G.S. Scaling laws of vascular trees: Of form and function. Am. J. Physiol. Heart Circ. Physiol. 2006, 290, H894–903. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar] [CrossRef]
- Parker, K.J. Power laws prevail in medical ultrasound. Phys. Med. Biol. 2022, 67, 09TR02. [Google Scholar] [CrossRef] [PubMed]
- Parker, K.J.; Poul, S.S. Burr, Lomax, Pareto, and logistic distributions from ultrasound speckle. Ultrason. Imaging 2020, 42, 203–212. [Google Scholar] [CrossRef] [PubMed]
- Waag, R.C.; Lee, P.P.K.; Persson, H.W.; Schenk, E.A.; Gramiak, R. Frequency-dependent angle scattering of ultrasound by liver. J. Acoust. Soc. Am. 1982, 72, 343–352. [Google Scholar] [CrossRef] [PubMed]
- Campbell, J.A.; Waag, R.C. Measurements of calf liver ultrasonic differential and total scattering cross sections. J. Acoust. Soc. Am. 1984, 75, 603–611. [Google Scholar] [CrossRef]
- Parker, K.J. Shapes and distributions of soft tissue scatterers. Phys. Med. Biol. 2019, 64, 175022. [Google Scholar] [CrossRef] [PubMed]
- Doyley, M.M. Model-based elastography: A survey of approaches to the inverse elasticity problem. Phys. Med. Biol. 2012, 57, R35–R73. [Google Scholar] [CrossRef] [PubMed]
- Szabo, T.L. Diagnostic Ultrasound Imaging: Inside Out, 2nd ed.; Academic Press: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Macovski, A. Basic Ultrasonic Imaging; Prentice-Hall: Englewood Cliffs, NJ, USA, 1983. [Google Scholar]
- Prince, J.L.; Links, J.M. Medical Imaging Signals and Systems; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2006; p. xvi. 480p. [Google Scholar]
- Basavarajappa, L.; Li, J.; Tai, H.; Song, J.; Parker, K.J.; Hoyt, K. Early detection of liver steatosis using multiparametric ultrasound imaging. In Proceedings of the 2021 IEEE International Ultrasonics Symposium (IUS), Virtual, 11–16 September 2021; pp. 1–4. [Google Scholar]
- Baek, J.; Basavarajappa, L.; Margolis, R.; Arthur, L.; Li, J.; Hoyt, K.; Parker, K.J. Multiparametric ultrasound imaging for early-stage steatosis: Comparison with magnetic resonance imaging-based proton density fat fraction. Med. Phys. 2024, 51, 1313–1325. [Google Scholar] [CrossRef] [PubMed]
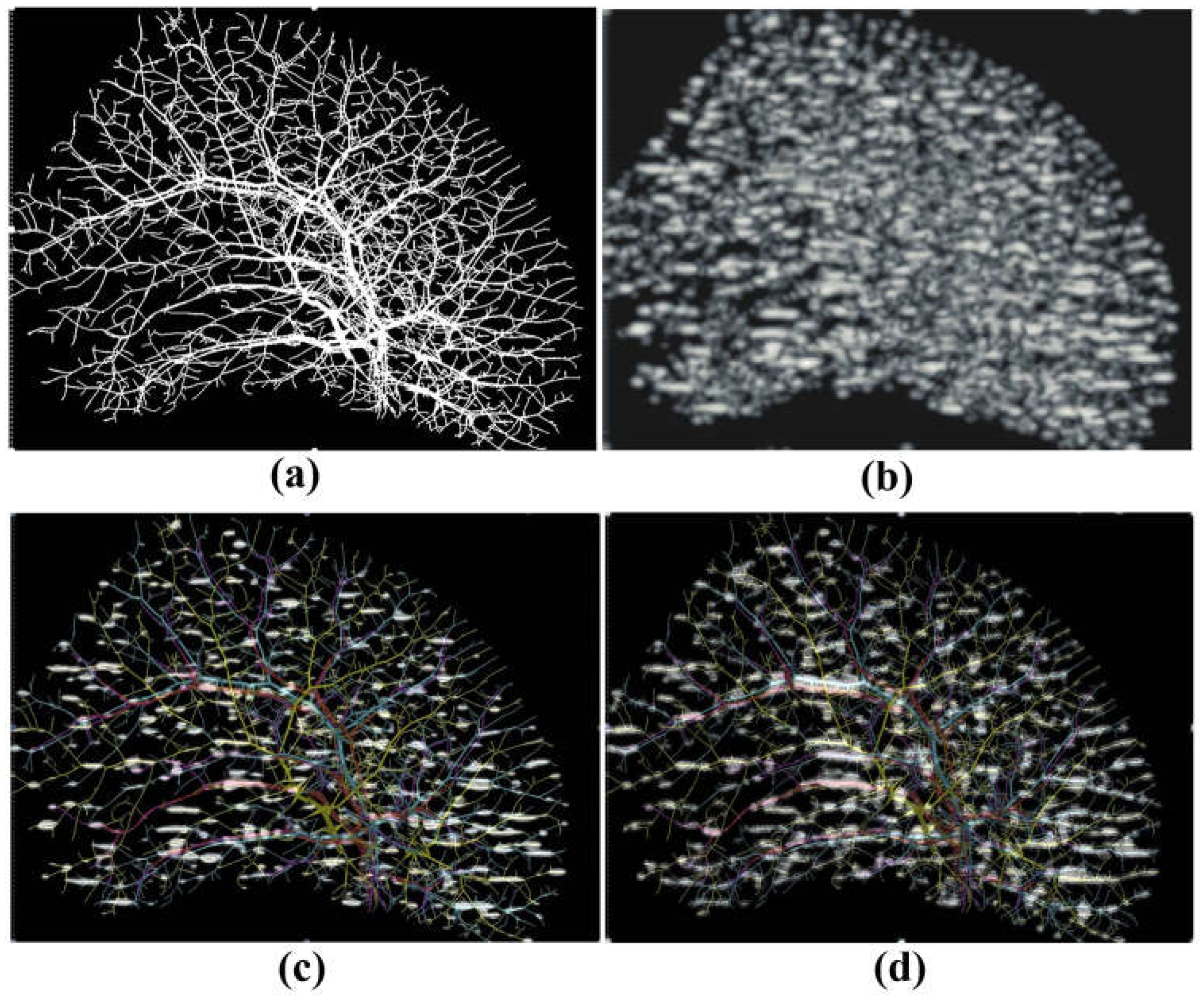
- Carroll-Nellenback, J.J.; White, R.J.; Wood, R.W.; Parker, K.J. Liver backscatter and the hepatic vasculature’s autocorrelation function. Acoustics 2020, 2, 3–12. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, A.; Chen, S.; Yuan, J.; Jiang, T.; Li, X.; Luo, Q.; Feng, Z.; Gong, H. Multiscale reconstruction of various vessels in the intact murine liver lobe. Commun. Biol. 2022, 5, 260. [Google Scholar] [CrossRef] [PubMed]
- Faran, J.J., Jr. Sound scattering by solid cylinders and spheres. J. Acoust. Soc. Am. 1951, 23, 405–418. [Google Scholar] [CrossRef]
- Stanton, T.K. Sound scattering by cylinders of finite length. II. Elastic cylinders. J. Acoust. Soc. Am. 1988, 83, 64–67. [Google Scholar] [CrossRef]

| Parameter | Definition | Additional Information |
|---|---|---|
| Analytic envelope of the received signal | ||
| Intensity | Specified here as the square of the analytic envelope. | |
| Power spectrum of | Specified here as , where is the Fourier transform operator. | |
| Reflection coefficient | Unknown at high resolution and is the object of our constrained reconstruction. In the theory of multiscale weak scattering, is distributed as a zero-mean random variable with a magnitude described by the power law (Pareto) distribution, so the ultrasound pulse will encounter few strong scatterers and many smaller weaker scatterers according to a power law. | |
| Histogram of intensity of the echoes | In theory approaching a Lomax distribution, or concurrently, a Burr distribution for amplitude. | |
| Autocorrelation function of the reflections | In theory approaching a power law function. | |
| Power spectrum of the scatterers | In theory and from scattering experiments the ensemble average approaches a power law function of frequency. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parker, K.J. A Power Law Reconstruction of Ultrasound Backscatter Images. Acoustics 2024, 6, 782-791. https://doi.org/10.3390/acoustics6030043
Parker KJ. A Power Law Reconstruction of Ultrasound Backscatter Images. Acoustics. 2024; 6(3):782-791. https://doi.org/10.3390/acoustics6030043
Chicago/Turabian StyleParker, Kevin J. 2024. "A Power Law Reconstruction of Ultrasound Backscatter Images" Acoustics 6, no. 3: 782-791. https://doi.org/10.3390/acoustics6030043
APA StyleParker, K. J. (2024). A Power Law Reconstruction of Ultrasound Backscatter Images. Acoustics, 6(3), 782-791. https://doi.org/10.3390/acoustics6030043







