Wavelet-Based Estimation of Damping from Multi-Sensor, Multi-Impact Data
Abstract
1. Introduction
2. Problem Formulation
2.1. Model of Mechanical System
2.2. Model of Observation
2.3. Problem Setting
3. Damping Extraction Methods
3.1. Frequency-Domain Damping Extraction Methods
3.1.1. Peak-Picking
3.1.2. Least-Square Rational Function Estimation
3.1.3. Poly-Reference Least Squares Complex Frequency
3.1.4. Bertocco–Yoshida
3.2. Wavelet-Based Damping Extraction
3.2.1. Introduction to Wavelet
3.2.2. Wavelet-Based Energy Estimation
3.2.3. Damping Extraction Using Wavelet
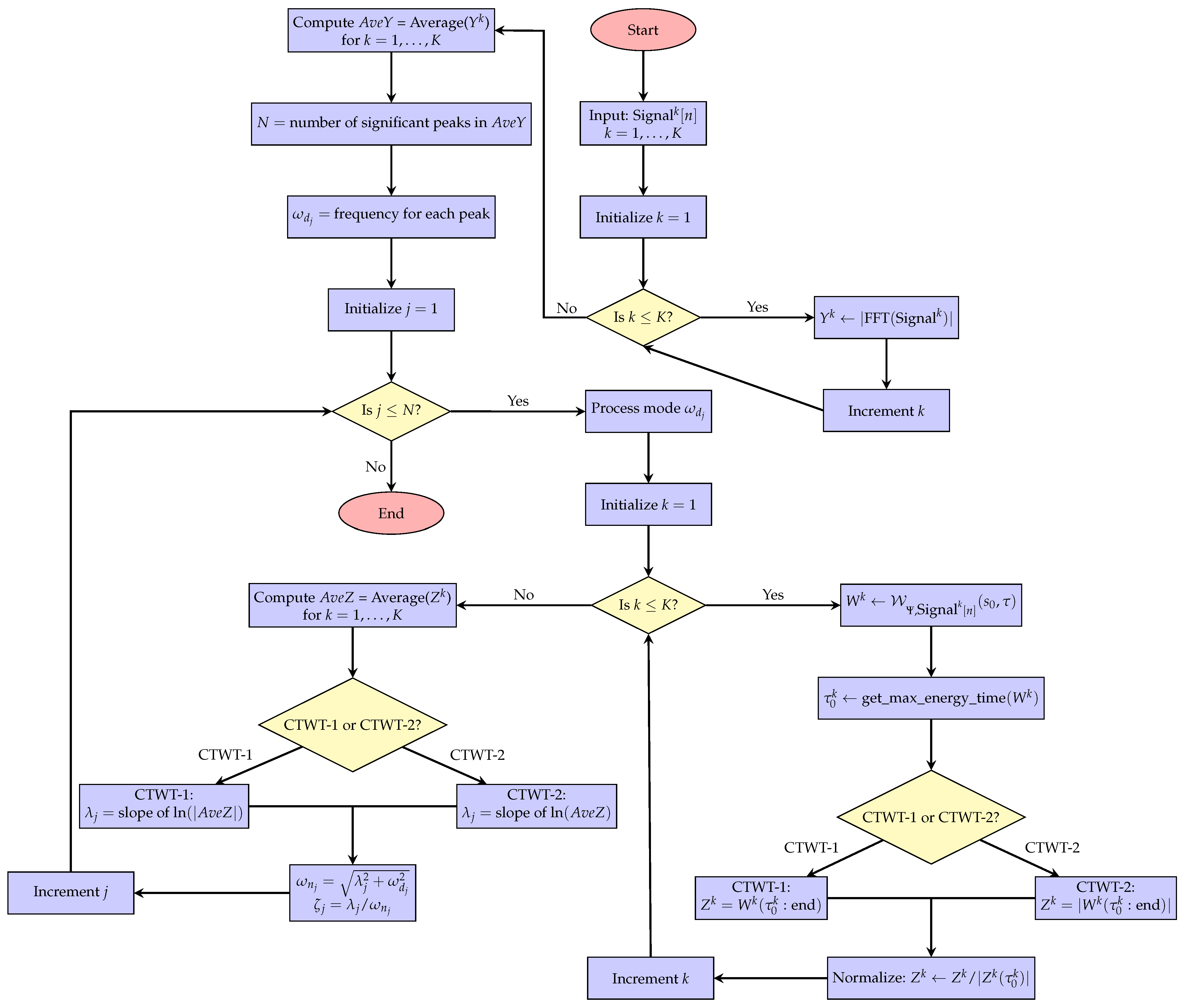
4. Proposed Algorithms
| Algorithm 1: CTWT-1 and CTWT-2 Methods |
|
- 1.
- Estimation of Damping Frequencies: The initial phase of the algorithm focuses on the analysis of the FFT for each sample. By evaluating the FFT’s magnitude, represented by , we identify significant peaks. These peaks are indicative of the system’s modes, with the damping frequencies, , corresponding to these peaks. Since individual samples might provide varying results, we average out the damping frequencies using the mean of all s.
- 2.
- CTWT and Sample Alignment: Assuming that the system behaves similarly to an SDOF dynamic around each damped frequency, we determine the corresponding scale. At this designated scale, the CTWT is computed for every sample, denoted by . A fundamental step in this phase involves the alignment of samples. Due to the variability in impact times across repeated measurements, we use the maximum energy point as an alignment reference. This reference point, which is an estimate of the time of impact, is obtained from the get_max_energy_time function. This function finds the maximum point after applying a Savitzky–Golay finite impulse response (FIR) smoothing filter to the input data. Data recorded prior to this point are disregarded. To account for the varying magnitudes of each impact, a normalization factor is incorporated before the averaging step.
- 3.
- Averaging and Extraction of Damping Ratio: As the wavelet transform is linear, it retains the additive characteristics of Gaussian noise. The CTWT-1 approach involves averaging the complex-valued values directly in the wavelet domain. This method aims to reduce noise while preserving the full complex signal information before further processing. Conversely, in the CTWT-2 approach, the averaging is performed after converting the complex values to real values by taking their absolute values. This distinction underscores the importance of the location where averaging occurs within the process, affecting the accuracy and reliability of the resulting damping ratio estimates. By employing Equations (3) and (31), the damping coefficient and damping ratio are obtained.
5. Results and Discussion
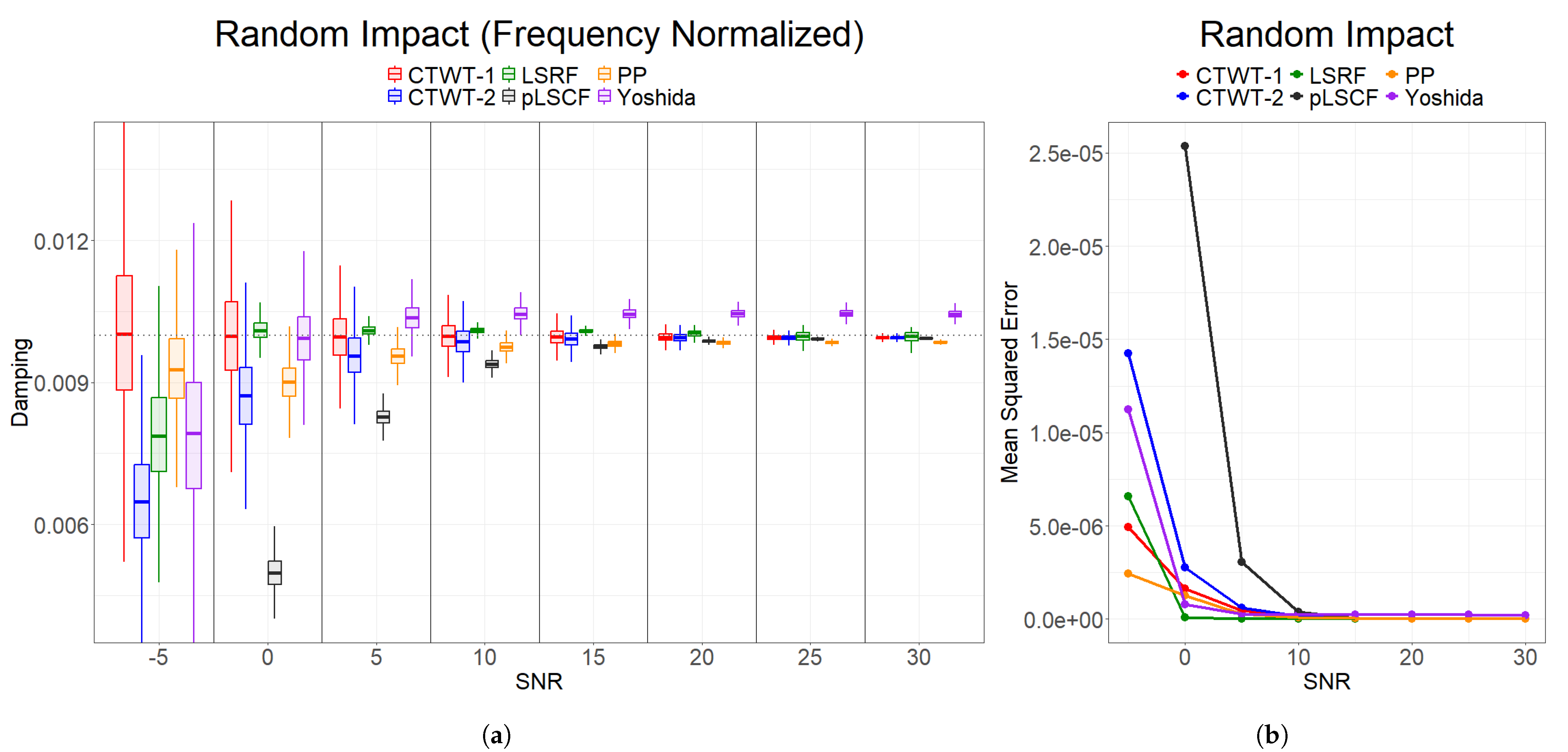
5.1. Numerical Simulation
- The CTWT-2 method shows a significant effect of the number of samples on damping ratio estimates, with a relatively low p-value (0.015), indicating a notable influence of the number of recordings on its performance.
- The CTWT-1 method shows a moderate effect with a p-value of 0.079, suggesting some influence of the number of recordings, though less pronounced compared to CTWT-2.
- The LSRF method demonstrates a limited impact with a p-value of 0.377, suggesting lower sensitivity to the number of recordings compared to CTWT methods.
- The pLSCF method demonstrates a lower relative effect with a higher p-value of 0.831, indicating the least influence of the number of recordings on its performance.
- The PP and Yoshida methods also show limited effectiveness with p-values of 0.429 and 0.493, similar to the LSRF method.
- The PP method shows a highly significant effect of the number of samples on damping ratio estimates, with an extremely low p-value (), indicating a strong influence of the number of recordings on its performance.
- The pLSCF method also shows a significant effect with a p-value of , although the influence is less pronounced compared to the PP method.
- The CTWT-1, CTWT-2, LSRF, and Yoshida methods do not show significant effects of the number of samples on damping ratio estimates, as indicated by their high p-values.
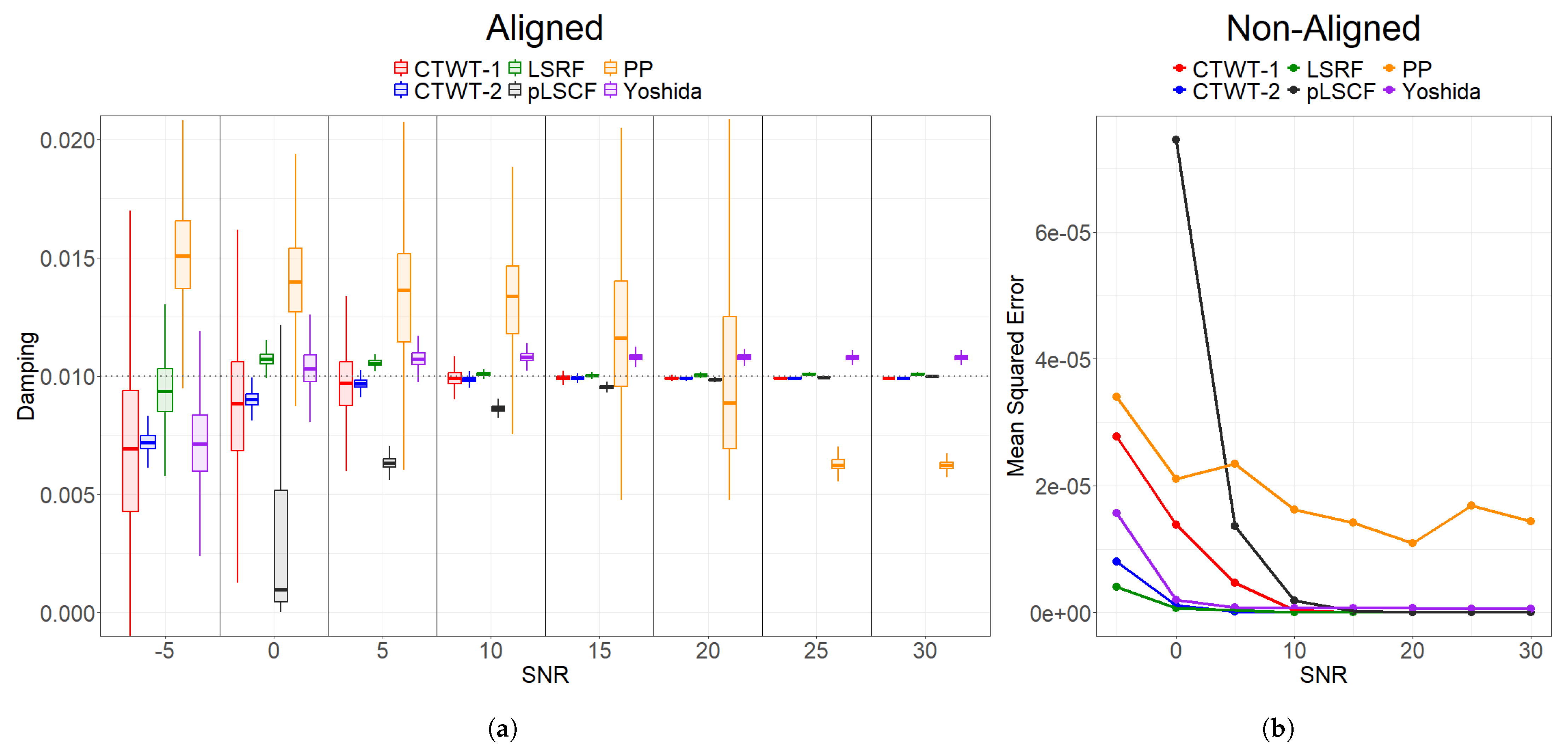
5.2. Experimental Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Ewins, D.J. Modal Testing: Theory, Practice and Application; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Chopra, A.K. Dynamics of Structures; Pearson Education India: Tamil Nadu, India, 2007. [Google Scholar]
- Inman, D.J.; Singh, R.C. Engineering Vibration; Prentice Hall Englewood Cliffs: Englewood Cliffs, NJ, USA, 1994; Volume 3. [Google Scholar]
- Rao, S.S.; Yap, F.F. Mechanical Vibrations; Addison-Wesley: New York, NY, USA, 1995. [Google Scholar]
- Barattini, C.; Dimauro, L.; Vella, A.D.; Vigliani, A. Dynamic Analysis of a High-Performance Prosthetic Leg: Experimental Characterisation and Numerical Modelling. Appl. Sci. 2023, 13, 11566. [Google Scholar] [CrossRef]
- Liu, D.; Tang, Z.; Bao, Y.; Li, H. Machine-learning-based methods for output-only structural modal identification. Struct. Control. Health Monit. 2021, 28, e2843. [Google Scholar] [CrossRef]
- Santos, J.; Crémona, C.; Silveira, P. Automatic operational modal analysis of complex civil infrastructures. Struct. Eng. Int. 2020, 30, 365–380. [Google Scholar] [CrossRef]
- Wang, C.; Huang, H.; Lai, X.; Chen, J. A New Online Operational Modal Analysis Method for Vibration Control for Linear Time-Varying Structure. Appl. Sci. 2020, 10, 48. [Google Scholar] [CrossRef]
- Soria, L.; Peeters, B.; Anthonis, J. Operational modal analysis and the performance assessment of vehicle suspension systems. Shock Vib. 2012, 19, 1099–1113. [Google Scholar] [CrossRef]
- Feng, Z.; Liang, M.; Chu, F. Recent advances in time–frequency analysis methods for machinery fault diagnosis: A review with application examples. Mech. Syst. Signal Process. 2013, 38, 165–205. [Google Scholar] [CrossRef]
- Zhang, Y.; Randall, R. Rolling element bearing fault diagnosis based on the combination of genetic algorithms and fast kurtogram. Mech. Syst. Signal Process. 2009, 23, 1509–1517. [Google Scholar] [CrossRef]
- He, J.; Fu, Z.F. 1—Overview of modal analysis. In Modal Analysis; He, J., Fu, Z.F., Eds.; Butterworth-Heinemann: Oxford, UK, 2001; pp. 1–11. [Google Scholar] [CrossRef]
- Slavič, J.; Simonovski, I.; Boltežar, M. Damping identification using a continuous wavelet transform: Application to real data. J. Sound Vib. 2003, 262, 291–307. [Google Scholar] [CrossRef]
- Staszewski, W. Identification of damping in MDOF systems using time-scale decomposition. J. Sound Vib. 1997, 203, 283–305. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification of output-only systems using frequency domain decomposition. Smart Mater. Struct. 2001, 10, 441. [Google Scholar] [CrossRef]
- Wang, Y.; Egner, F.S.; Willems, T.; Kirchner, M.; Desmet, W. Camera-based experimental modal analysis with impact excitation: Reaching high frequencies thanks to one accelerometer and random sampling in time. Mech. Syst. Signal Process. 2022, 170, 108879. [Google Scholar] [CrossRef]
- Nadkarni, I.; Bhardwaj, R.; Ninan, S.; Chippa, S. Experimental modal parameter identification and validation of cantilever beam. Mater. Today Proc. 2021, 38, 319–324. [Google Scholar] [CrossRef]
- Li, M.; Lu, Z.; Cao, Q.; Gao, J.; Hu, B. Automatic assessment method and device for depression symptom severity based on emotional facial expression and pupil-wave. IEEE Trans. Instrum. Meas. 2024, 73, 1–15. [Google Scholar] [CrossRef]
- Zhang, S.; Qu, N.; Zheng, T.; Hu, C. Series arc fault detection based on wavelet compression reconstruction data enhancement and deep residual network. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Albaqami, H.; Hassan, G.M.; Subasi, A.; Datta, A. Automatic detection of abnormal EEG signals using wavelet feature extraction and gradient boosting decision tree. Biomed. Signal Process. Control. 2021, 70, 102957. [Google Scholar] [CrossRef]
- Boltežar, M.; Slavič, J. Enhancements to the continuous wavelet transform for damping identifications on short signals. Mech. Syst. Signal Process. 2004, 18, 1065–1076. [Google Scholar] [CrossRef]
- Tomac, I.; Slavič, J. Damping identification based on a high-speed camera. Mech. Syst. Signal Process. 2022, 166, 108485. [Google Scholar] [CrossRef]
- Zieliński, T.P.; Duda, K. Frequency and damping estimation methods-an overview. Metrol. Meas. Syst. 2011, 18, 505–528. [Google Scholar] [CrossRef]
- Slavič, J.; Boltežar, M. Damping identification with the Morlet-wave. Mech. Syst. Signal Process. 2011, 25, 1632–1645. [Google Scholar] [CrossRef]
- Tomac, I.; Lozina, Ž.; Sedlar, D. Extended Morlet-Wave damping identification method. Int. J. Mech. Sci. 2017, 127, 31–40. [Google Scholar] [CrossRef]
- Zrayka, A.K.; Mucchi, E. A comparison among modal parameter extraction methods. SN Appl. Sci. 2019, 1, 781. [Google Scholar] [CrossRef]
- Tomac, I.; Slavič, J. Morlet-wave-based modal identification in the time domain. Mech. Syst. Signal Process. 2023, 192, 110243. [Google Scholar] [CrossRef]
- Xu, H.; Liu, Y.; Chen, J.; Yang, D.; Yang, Y. Novel formula for determining bridge damping ratio from two wheels of a scanning vehicle by wavelet transform. Mech. Syst. Signal Process. 2024, 208, 111026. [Google Scholar] [CrossRef]
- Janeliukstis, R. Continuous wavelet transform-based method for enhancing estimation of wind turbine blade natural frequencies and damping for machine learning purposes. Measurement 2021, 172, 108897. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, W.; Zhang, G.; Xu, H.; Du, Y. Identification of structural parameters from free vibration data using Gabor wavelet transform. Mech. Syst. Signal Process. 2021, 147, 107122. [Google Scholar] [CrossRef]
- Silva-Navarro, G.; Beltran-Carbajal, F.; Trujillo-Franco, L.G.; Peza-Solis, J.F.; Garcia-Perez, O.A. Online estimation techniques for natural and excitation frequencies on MDOF vibrating mechanical systems. Actuators 2021, 10, 41. [Google Scholar] [CrossRef]
- Meirovitch, L. Fundamentals of Vibrations; Waveland Press: Long Grove, IL, USA, 2010. [Google Scholar]
- Liu, M.; Gorman, D.G. Formulation of Rayleigh damping and its extensions. Comput. Struct. 1995, 57, 277–285. [Google Scholar] [CrossRef]
- A Hasan, M.D.; Ahmad, Z.; Salman Leong, M.; Hee, L. Enhanced frequency domain decomposition algorithm: A review of a recent development for unbiased damping ratio estimates. J. Vibroeng. 2018, 20, 1919–1936. [Google Scholar] [CrossRef]
- Døssing, O. Structural testing. Brüel Kjær (Ed.) 1988, 2, 1–54. [Google Scholar]
- Sanchez, H.; Nova, F.; González-Estrada, O. Implementation of the Operational Modal Analysis technique in a power transmission shaft. Phys. Conf. Ser. 2019, 1247, 012032. [Google Scholar] [CrossRef]
- Ozdemir, A.A.; Gumussoy, S. Transfer function estimation in system identification toolbox via vector fitting. IFAC-PapersOnLine 2017, 50, 6232–6237. [Google Scholar] [CrossRef]
- Sanathanan, C.; Koerner, J. Transfer function synthesis as a ratio of two complex polynomials. IEEE Trans. Autom. Control. 1963, 8, 56–58. [Google Scholar] [CrossRef]
- El-kafafy, M.; De Troyer, T.; Peeters, B.; Guillaume, P. Fast maximum-likelihood identification of modal parameters with uncertainty intervals: A modal model-based formulation. Mech. Syst. Signal Process. 2013, 37, 422–439. [Google Scholar] [CrossRef]
- Trumpp, R.F. Implementierung des Poly-reference Least Square Complex Frequency (p-LSCF) Algorithmus zur Operational Modal Analysis (OMA). Bachelor’s Thesis, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany, 2017. [Google Scholar]
- Guillaume, P.; Verboven, P.; Vanlanduit, S.; Van Der Auweraer, H.; Peeters, B. A poly-reference implementation of the least-squares complex frequency-domain estimator. In Proceedings of the IMAC; A Conference & Exposition on Structural Dynamics, Society for Experimental, Kissimmee, FL, USA, 3–6 February 2003; Volume 21. [Google Scholar]
- Junsheng, C.; Dejie, Y.; Yu, Y. Time–energy density analysis based on wavelet transform. Ndt E Int. 2005, 38, 569–572. [Google Scholar] [CrossRef]
- Chen, S.L.; Liu, J.J.; Lai, H.C. Wavelet analysis for identification of damping ratios and natural frequencies. J. Sound Vib. 2009, 323, 130–147. [Google Scholar] [CrossRef]



| Method | F | p-Value |
|---|---|---|
| CTWT-1 | 3.09 | 0.079 |
| CTWT-2 | 5.91 | 0.015 |
| LSRF | 0.78 | 0.377 |
| pLSCF | 0.045 | 0.831 |
| PP | 0.625 | 0.429 |
| Yoshida | 0.47 | 0.493 |
| Method | F | p-Value |
|---|---|---|
| CTWT-1 | 2.49 | 0.114 |
| CTWT-2 | 1.52 | 0.217 |
| LSRF | 1.16 | 0.282 |
| pLSCF | 64.0 | 1.27 × 10−15 |
| PP | 889.0 | 2.21 × 10−194 |
| Yoshida | 0.002 | 0.969 |
| Method | 4.71 Hz | 17.81 Hz | 27.68 Hz | |||
|---|---|---|---|---|---|---|
| Damping Ratio | Variance | Damping Ratio | Variance | Damping Ratio | Variance | |
| CTWT-1 | 0.0308 | 2.72 × 10−4 | 0.0086 | 1.52 × 10−6 | 0.0093 | 2.14 × 10−6 |
| CTWT-2 | 0.0482 | 1.58 × 10−6 | 0.0084 | 2.11 × 10−9 | 0.0092 | 1.20 × 10−9 |
| LSRF | 0.0411 | 2.09 × 10−4 | 0.0090 | 2.32 × 10−5 | 0.0088 | 7.85 × 10−7 |
| pLSCF | 0.0210 | 1.17 × 10−4 | 0.0034 | 1.02 × 10−7 | 0.0032 | 5.48 × 10−6 |
| PP | 0.0521 | 1.09 × 10−3 | 0.0074 | 4.98 × 10−6 | 0.0094 | 4.13 × 10−6 |
| Yoshida | 0.0150 | 2.03 × 10−4 | 0.0058 | 7.03 × 10−6 | 0.0040 | 2.17 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daniali, H.M.; Mohrenschildt, M.v. Wavelet-Based Estimation of Damping from Multi-Sensor, Multi-Impact Data. Signals 2025, 6, 13. https://doi.org/10.3390/signals6010013
Daniali HM, Mohrenschildt Mv. Wavelet-Based Estimation of Damping from Multi-Sensor, Multi-Impact Data. Signals. 2025; 6(1):13. https://doi.org/10.3390/signals6010013
Chicago/Turabian StyleDaniali, Hadi M., and Martin v. Mohrenschildt. 2025. "Wavelet-Based Estimation of Damping from Multi-Sensor, Multi-Impact Data" Signals 6, no. 1: 13. https://doi.org/10.3390/signals6010013
APA StyleDaniali, H. M., & Mohrenschildt, M. v. (2025). Wavelet-Based Estimation of Damping from Multi-Sensor, Multi-Impact Data. Signals, 6(1), 13. https://doi.org/10.3390/signals6010013






