Harmonic and Supraharmonic Emissions of Plug-In Electric Vehicle Chargers
Abstract
:1. Introduction
- Ecologically friendly with negligible direct polluting emissions;
- Indirect emissions are also lower, if more efficient generation at the source and the possibility of exploiting renewables are considered;
- Higher energy efficiency and better performance than conventional fossil-fuel vehicles;
- Reduced noise, especially at low speed amid cities.
- Voltage unbalance, troublesome in the case of numerous, albeit low-power, single-phase charging loads;
- Verification of suitability of LV distribution elements, such as MV/LV cabin transformers and feeders;
- Balancing power demand by economic incentives and regulations to push the peaks of exploitation to more attractive times of the day.
- On-board chargers may differ significantly among EV models, especially considering the span of fabrication date and of power levels, from small vehicles to sport cars and to public transportation means;
- Distortion patterns may change during the charging process as a function of the state of charge, of the absorbed current intensity and the charging mode;
- For the widespread use of power converters and smart conversion methods to enhance flexibility and efficiency, distortion patterns are not only various, but extend significantly in the supraharmonic range (namely, 9–150 kHz), where switching components and their harmonics are easily visible;
- Superposition of low- and high-frequency distortion and secondary emissions (distortion caused by a converter subject to network voltage distortion, such as caused by other converters) are more important as the mix of connected EV chargers becomes more complex.
2. EV Charging Modes and Architectures
- Different charging power levels may be negotiated during one charge session thanks to the communication channel between the intelligent socket and the on-board logic; it is observed that, for example, fast charging may be allowed only when grid conditions are suitable, such as when there is no risk of abnormal voltage fluctuations and grid instability;
- Communication supports also the V2G (vehicle-to-grid) mode [24], particularly useful when the EV is available connected for long times (such as a work day or an entire night at office and home, respectively); the V2G operation, however, reduces expected battery life;
- Higher efficiency compared to, e.g., wireless power transfer at the cost of a direct injection of distortion into the grid.
- Single-phase diode rectifiers are followed by a full-rated boost converter (DC–DC step-up converter);
- The solution is not directly suitable for three-phase bridges (so for higher power levels), although three interleaved PFC boost converters may be used;
- The active rectifier solution can control voltage and current vectors over a wide range of conditions and is equally applicable to single- and three-phase connections; however, being usually decoupled with series inductors to the grid, necessitates a compensating inner current loop to improve speed of response [27];
- An attractive solution that allows downrating the PFC circuit is the use of a shunt connected active power filter, which is sized for approximately 40% of the rated power of the diode rectifier [28].
- Zero dead-time PWM that improves the THD by about a factor of two [32] without exposing the converter to the shoot-through risk, since the implemented switching pattern does not allow to activate consecutively two switches of the same leg;
- Random PWM, which avoids the peaks of emission at the switching frequency harmonics, but increases the remaining spectrum significantly, de facto providing only a partial solution.
- Buck, buck–boost, Cuk, Sepic for non-isolated architectures;
- Single or dual active bridge (SAB and DAB), or even dual half bridge (DHB), providing galvanic isolation.
3. Distortion Limits and Assessment
- Propagation or attenuation of emissions from the respective connection points along the network;
- Characteristics of phase angle distribution and degree of superposition and compensation;
- Network impedance transforming current emissions of loads into network voltage distortion.
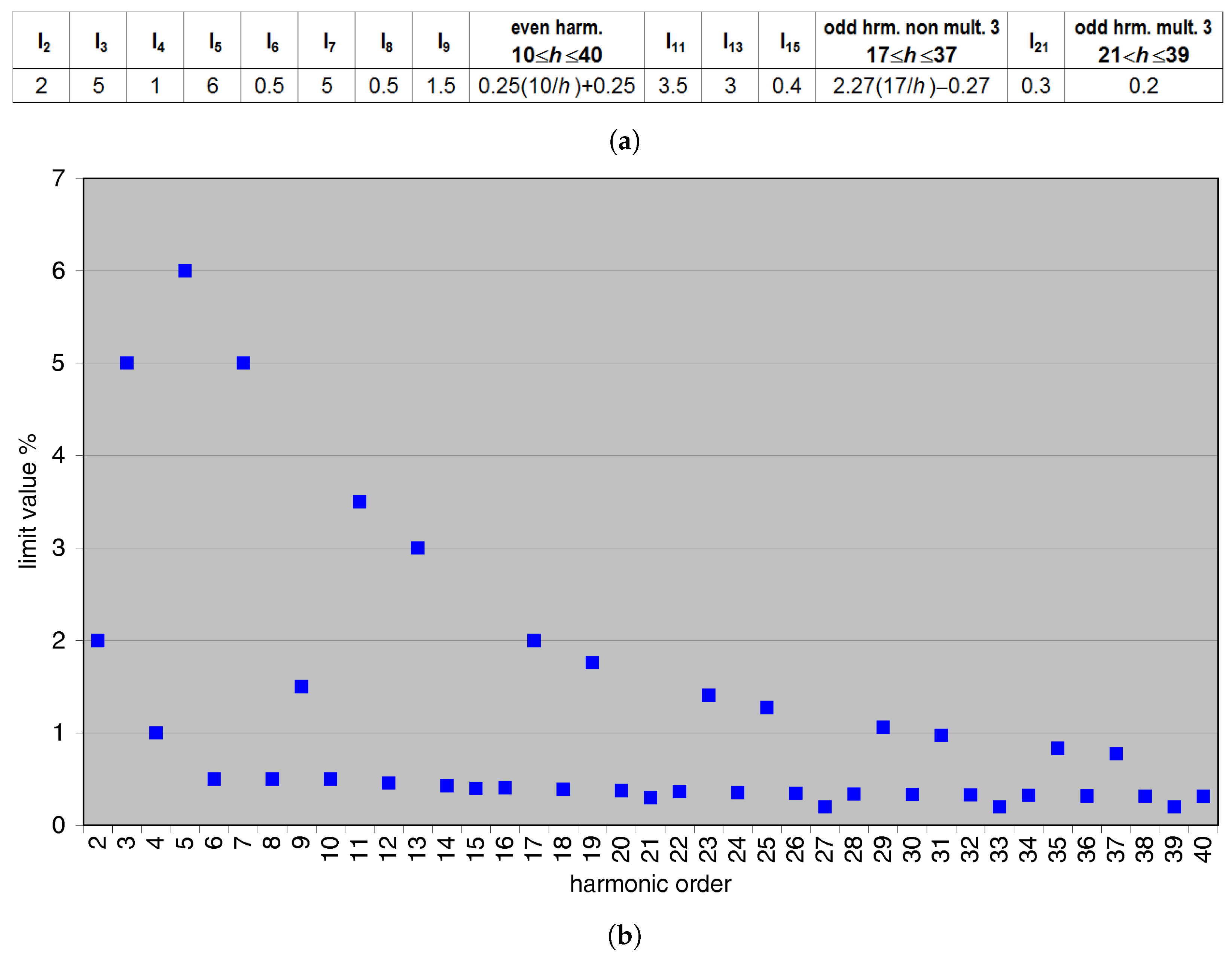
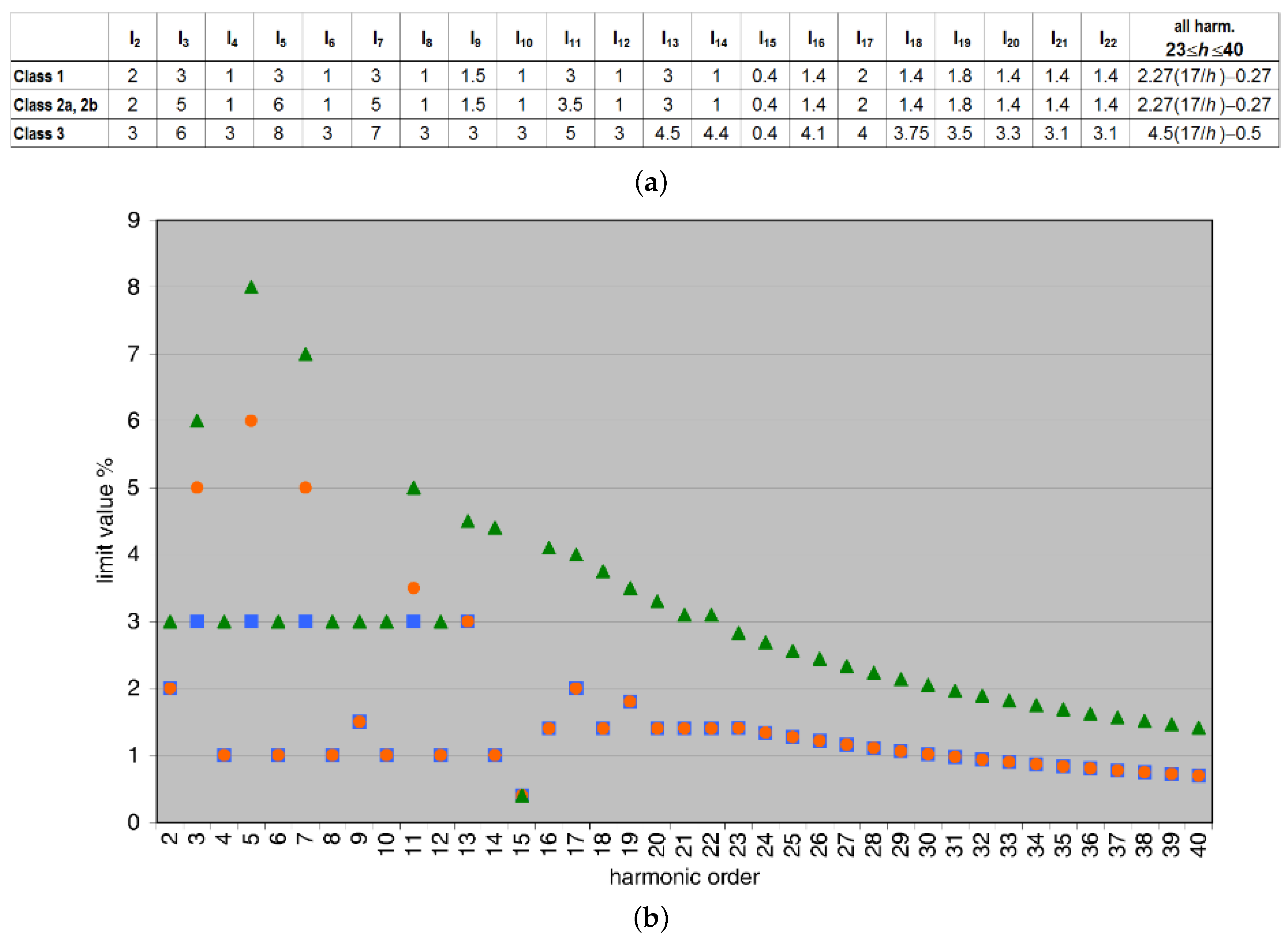
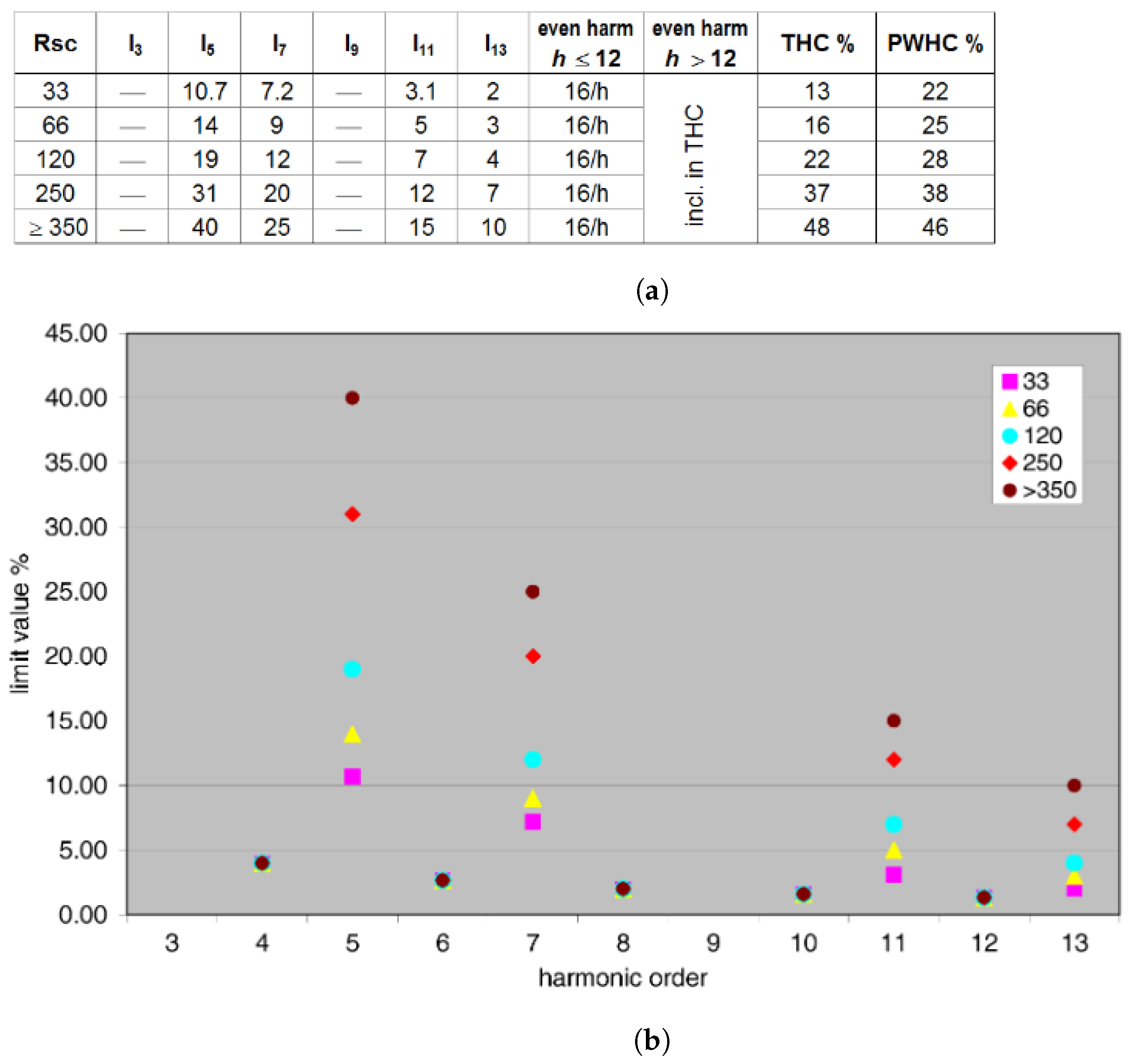
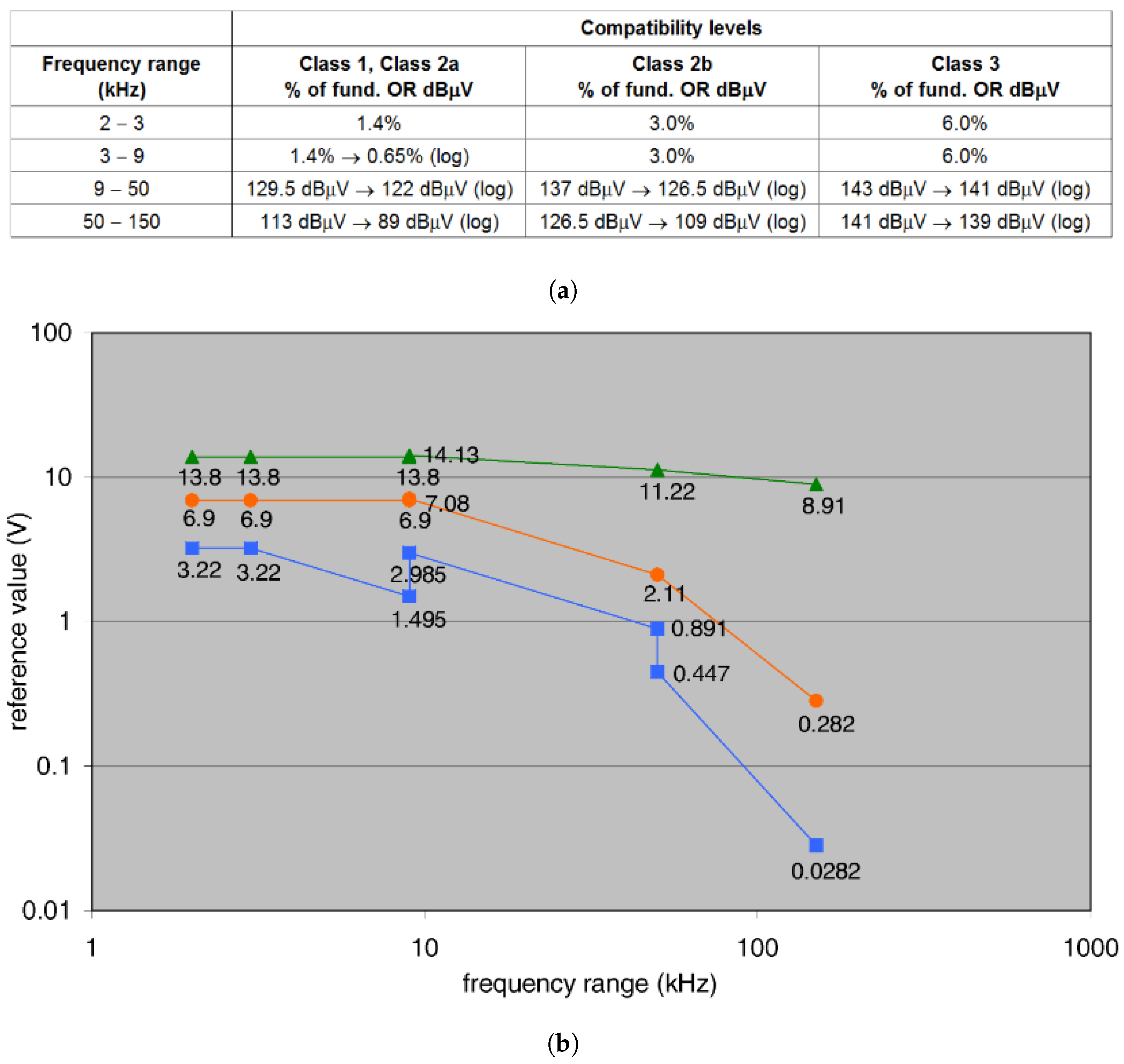
3.1. Harmonics and Supraharmonics Limits
3.1.1. Harmonic Frequency Interval
- Class 1: protected supplies with compatibility levels lower than public networks, representing, e.g., laboratories with measurement and scientific equipment;
- Class 2: light industrial environment that may be without (class 2a, office) or with (class 2b, office + light industry) industrial power electronic equipment; in case of class 2b, there is no separation by a supply transformer between the office-like and the light industrial parts of the network;
- Class 3: heavy industrial environment with power converters, welding machines, motors starting and stopping frequently.
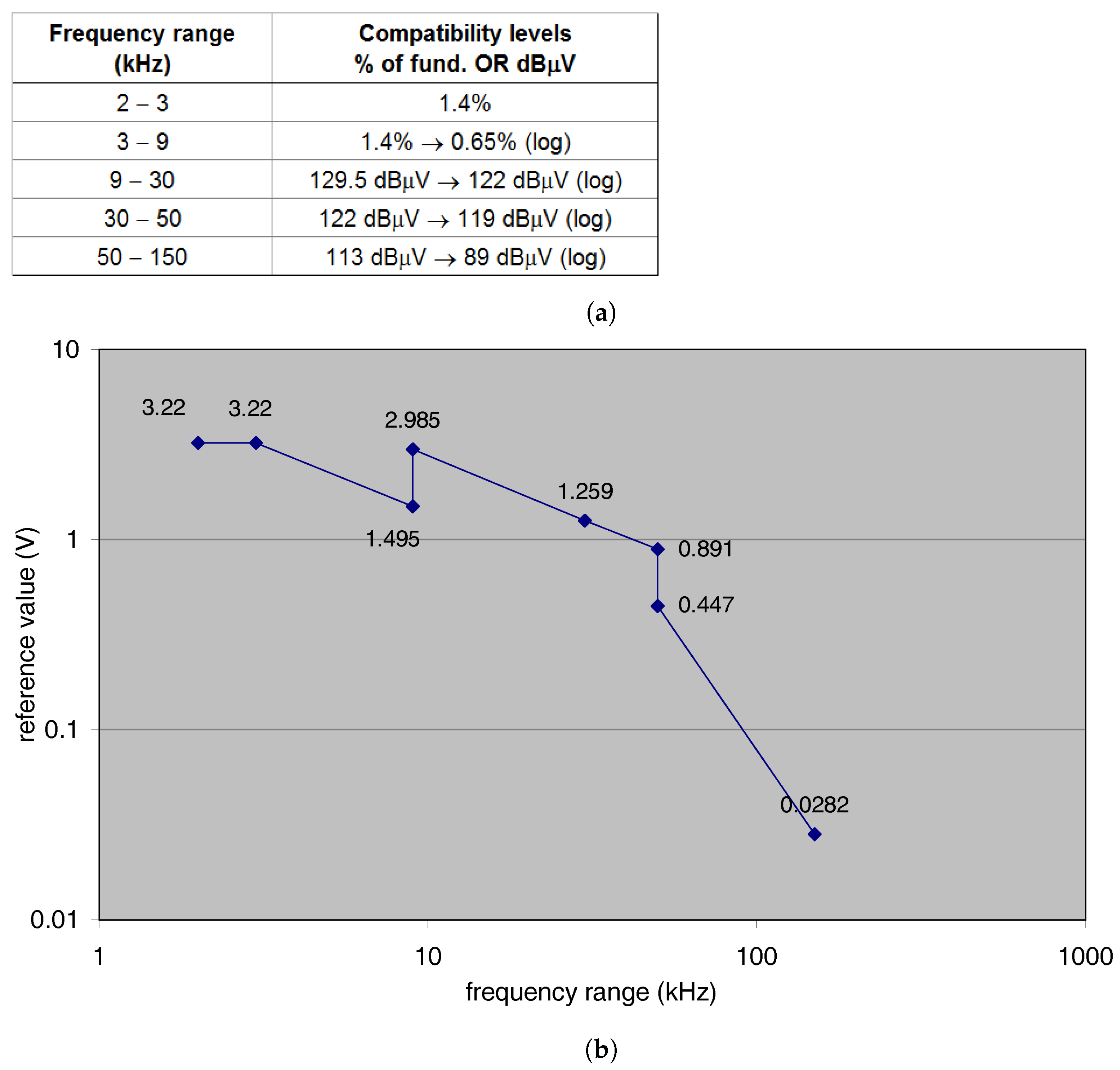
3.1.2. Supraharmonic Frequency Interval
- Large penetration in supply networks, undergoing marginal attenuation similar to high-order harmonics;
- Potential disturbance to metering and control equipment, as well as to power line carrier (PLC) devices;
- Possible excitation of network resonances, in particular considering the small LV grids of limited extension.
- The concept of location should be better defined, as for LV distribution, it may mean the same part of the LV grid, or the entire LV grid that is fed from the same MV/LV transformer, representing a decoupling point; in both cases, it is easy to see that several EVs can be plugged at the same time (during the day at the office, during the night at home) in a small portion of the LV network;
- The “same bandwidth interval of 200 Hz” could exclude the combination of different sources of emission, but in a real scenario the number of different EV models is not so large (9 BEVs were considered in [51] and a few had similar emissions).
3.2. Extrapolation of Supraharmonic Limits
3.3. Distortion Measurement and Assessment
3.3.1. Time Window, Frequency Resolution and Grouping
- First, whatever the uncertainty of the measuring equipment and probes and having even minimized background noise sources, a significant deal of variability of emissions is expected both with respect to time and while ideally sweeping the frequency axis, passing from one spectral component to the adjacent one.
- Second, the amount of data, if stored unaltered as time-domain samples, is huge since the required sampling rate is in the order of 500 kHz or larger for the supraharmonic range. Data compression, when going beyond simple lossless algorithms, unavoidably requires a choice for results representation, namely what should be included and what left out. Examples of condensed indexes are average values and maxima, percentiles, etc., over given time intervals.
- As most supraharmonic emission sources are switching power converters with emissions mostly of the pulse-width-modulated (PWM) type, attention must be paid to the width of each PWM carrier (or switching frequency multiple ) and the side bands, spaced by even multiples of the modulation frequency . Each switching+modulation PWM group of components is characterized by some amount of power that spectral grouping should try to capture and preserve in the resulting representation [62]. From this, the exigency to set B to a value bracketing most of such side-band components belonging to the same PWM group. However, such justification should be accompanied by the determination of the switching carriers and their harmonics, so as to align the grouping bandwidth B [62], which complicates spectrum evaluation;
- In a scenario of several EV chargers of the same type, whose emissions overlap with plausible shifts of the switching frequency due to normal tolerance of components and settings and related drift over time, a sufficient bandwidth value should be set to correctly compose alike spectral components and observe the expected compensation, if phase displacement occurs. This is demonstrated in [63], where a 1 kHz bandwidth puts together slightly different peaks around the nominal 10 kHz switching frequency, resulting in mutual compensation, although beating phenomena also take place.
- In view of evaluating supraharmonic emissions to compare with limits and to limit disturbance to connected devices, B should be interpreted as the bandwidth of the victim equipment, as all spectral components falling within the same bandwidth B will contribute to the same disturbance term. For a uniform approach, however, the bandwidth B should not be changed depending on victim devices, but unified to a standard value (as the proposed 2 kHz), from which disturbance occurring with larger bandwidth may be simply estimated by, e.g., rms summation. Authors in [59] are cautious on the interpretation of the potential interference effect of grouped components over, in that case, a 4 kHz bandwidth, stating that the impact will not be that of a single component of same intensity; on this, it is possible to object that interference is to be weighted with the concept of victim bandwidth and also that spectrum components quite close to each other may give rise to modulation and beating effects that one single component is not able to. This is confirmed by [22], who report unwanted tripping of residual current devices due to disturbance occurring when many EVs of the same type (but not switching exactly at the same frequency) were plugged in.
- Tested bandwidths were 5 Hz, 200 Hz and 2 kHz, in line with the discussed standards, representing well a narrow, medium and large bandwidth for the supraharmonic frequency range;
- Effects of bandwidth on the amplitude estimate of spectral components can be divided, as known, between narrowband and broadband components: the influence is larger for broadband components, where the increase of amplitude follows ideally the square root of the ratio of the bandwidth, namely, 16 dB passing from 5 Hz to 200 Hz, and 10 dB from 200 Hz to 2 kHz. Even apparently narrowband components subjected to some frequency instability or modulation undergo variability of amplitude estimate, as it was shown in Figure 10 of [64]. In that figure, curves at 5 Hz and 200 Hz have a difference of about 7 dB, reduced to about 1 dB passing from 200 Hz to 2 kHz: this confirms the inadequacy of too-narrow bandwidth values (namely 5 Hz or so), when dealing with real emissions, which seem stably evaluated by bandwidth values of hundreds of Hz or few kHz;
- When facing transient components for which a larger bandwidth allows tracking a fast-changing spectrum, the attention is drawn in [35] on the worsening of the amplitude estimate accuracy, due to the increased superposed background noise, and widening of spectral lines (visible in the same Figure 10 of [64]).
3.3.2. Supply Voltage, Grid Distortion and Superposition of Emissions
- Two EVs (EV1 and EV2) show a completely different behavior of their , with very constant values in one case and a change of about ± A around a mean value of about 14 A for an excursion of the supply voltage of 230 V ±10%;
- Individual harmonics feature a wide range of values for the same supply voltage excursion: EV1 has the fifth spreading +200% and −60% around the reference amplitude of 11 A, whereas the most variable harmonic for EV2 is the ninth varying by +110% and −10%; in both cases, the increase of harmonic amplitude is observed at the largest power supply levels ( 241 V and 253 V);
- Phase angle variations are also dramatic with both harmonics considered above spanning 120.
- Superposition of spectral components from different sources occurring at the same frequency or, better, with a difference less than the resolution bandwidth. Examples are not only multiple EV chargers, but also for coexistence with other power converters, such as photovoltaic inverters and various types of power drives. Superposition, depending on the specific phase relationship, may have the positive effect of the reduction of the overall distortion components. This in general is more likely to occur for harmonics, whose frequency is fixed by the grid fundamental, rather than supraharmonics; quite interestingly in [63] the intensity of the 10 kHz switching component at the feeding point reduces significantly with the number of vehicles n, more than the expected assuming random phase and identical frequency. The amount of harmonic cancellation may be expressed simply by the coefficient , calculated for a variable number of sources N. Combined emissions of EVs and household loads were evaluated in [68], showing a non-obvious relationship between low-order harmonics and the amount of connected EVs (see Section 4);
- The influence of low-frequency harmonic distortion on higher-frequency emissions, such as in the supraharmonic range. Such influence was observed for various types of converters, where, in general, supraharmonic emissions depend on both the AC supply voltage level and low-order distortion (affecting the local wave shape and thus high-frequency emissions localized along the fundamental waveform). This is discussed further in Section 4;
- The so-called secondary emissions, where the charger is passively subject to grid distortion components, letting flow a corresponding current at the same frequency of the said components. This is particularly evident when small distortion voltages can cause a significant current intensity to flow through the low EMI (electromagnetic interference) filter impedance at such frequencies; in such cases, minimizing the amount of capacitance at the grid side is a necessity, not only used to prevent zero-sequence current leakage. Figure 2 in [64] demonstrates that three supraharmonics spectra taken at two field locations and one laboratory are quite different with broadband and narrowband components occurring at 35 and 100 kHz for the two field measurements, respectively.
4. Experimental Data
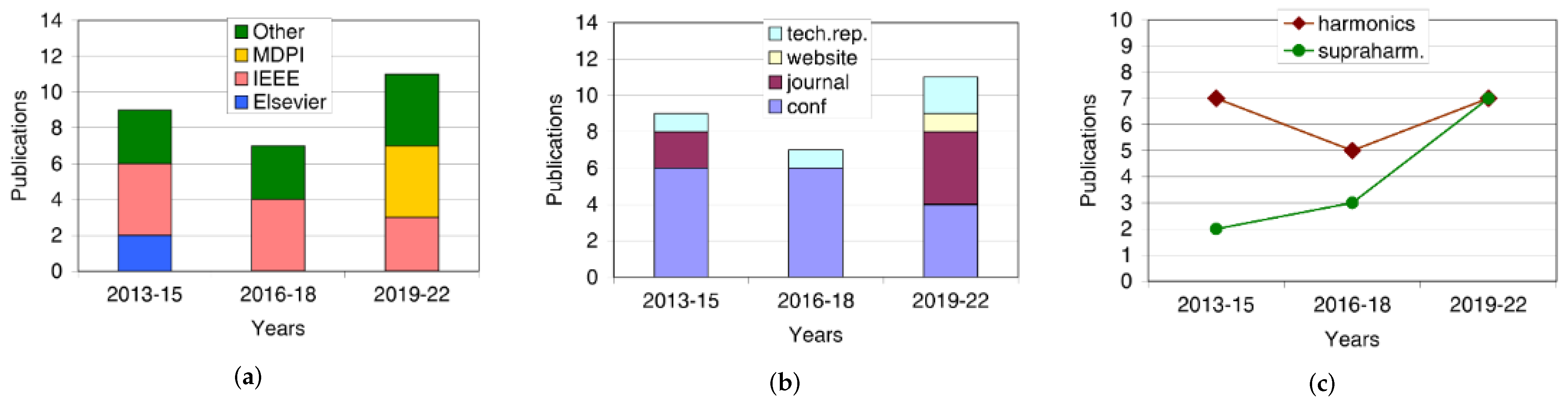
4.1. Arrangement and Results of the Systematic Review
4.2. Discussion of Publications and Experimental Data
- Beating takes place when harmonic or supraharmonic emissions exist with a small frequency difference and they mix within the grid to which the EV chargers are connected. The small frequency difference may be justified by normal tolerance, drift and ageing of two otherwise identical chargers. The result is a low-frequency pulsation after superposition of individual emission signals as difference of the two frequency values, thus, mathematically identical to a second-order intermodulation discussed below. The example provided in [22] indicates a pulsation of 10% amplitude, resulting from two “identical” EVs with a frequency difference of 2.4 Hz out of the two respective 10 kHz switching frequencies;
- Intermodulation distortion instead occurs even with spectral components of emission that are located farther apart and is in general caused by nonlinear elements, such as the power converters themselves. The example in [22] clarifies the extent to which such a phenomenon can occur: taking two components at and of a measured spectrum, in the spectrum itself a second-order intermodulation term () and two third-order intermodulation terms ( and ) are clearly visible.
5. Conclusions
- Harmonic distortion is still quite variable between EV models, above IEC limits in some conditions, although PFC should be extensively applied;
- Superposition of harmonics can occur with a wide range of distorting loads, such as home and office appliances and equipment, characterized by a significant penetration into the AC grid;
- Some major low-order harmonics may be quite dependent on the waveshape of the grid voltage, in particular for cases of flat-top voltage affected thus by third harmonic pollution; this exemplifies the necessity of testing reflecting the real conditions of use;
- The supraharmonic interval contains emissions from the PFC stage and power converters downstream inside the EV, in the form of a main switching component and its harmonics; broadband emissions may occur in the lowest frequency interval, below, e.g., 10 kHz, excited by the PFC impulses;
- A significant mutual influence between different chargers connected to the same grid was observed, pointing out the influence of field conditions contrasted with laboratory qualification results of single standalone EV; such influence materializes in a significant deal of beating and intermodulation phenomena;
- At a different level, mutual influence was also reported, consisting of the reciprocal interference between EVs passing through different charging conditions and switching on and off the charging process abruptly, causing changes of grid response and transient disturbance; interference resulted in EV charger disconnection, repeated charging attempts and the necessity of manual intervention.
- Modeling and accounting for superposition of components and resulting intermodulation;
- Consistent test of emissions to reflect real conditions of use for grid impedance (including the effect of other loads) and pre-existing distortion;
- Immunity test of EVs to supraharmonics, zero-crossing oscillatory signals and transient events caused by EV interactions and concomitant charging.
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Energy Technology Policy (ETP) Division. Nordic EV Outlook 2018, Directorate of Sustainability, Technology and Outlooks (STO) of the International Energy Agency (IEA); Technical Report; International Energy Agency (IEA): Paris, France, 2018. [Google Scholar]
- Energy Technology Policy (ETP) Division. Global EV Outlook 2019, Directorate of Sustainability, Technology and Outlooks (STO) of the International Energy Agency (IEA); Technical Report; International Energy Agency (IEA): Paris, France, 2019. [Google Scholar]
- European Union. European Green Deal: Commission Proposes Transformation of EU Economy and Society to Meet Climate Ambitions. 2021. Available online: https://ec.europa.eu/commission/presscorner/detail/en/IP_21_3541 (accessed on 28 January 2022).
- Sanguesa, J.A.; Torres-Sanz, V.; Garrido, P.; Martinez, F.J.; Marquez-Barja, J.M. A Review on Electric Vehicles: Technologies and Challenges. Smart Cities 2021, 4, 372–404. [Google Scholar] [CrossRef]
- Dharmakeerthi, C.; Mithulananthan, N.; Saha, T. Impact of electric vehicle fast charging on power system voltage stability. Int. J. Electr. Power Energy Syst. 2014, 57, 241–249. [Google Scholar] [CrossRef]
- Auer, M.; Kaffe, E.; La Fauci, R. Impact of fast charging and home charging infrastructure for electric vehicles on the power quality of the distribution grid. In Proceedings of the 25th International Conference on Electricity Distribution, Madrid, Spain, 3–6 June 2019. [Google Scholar]
- Liu, L.; Kong, F.; Liu, X.; Peng, Y.; Wang, Q. A review on electric vehicles interacting with renewable energy in smart grid. Renew. Sustain. Energy Rev. 2015, 51, 648–661. [Google Scholar] [CrossRef]
- Fernández-Rodriguez, A.; Fernández-Cardador, A.; Cucala, A.; Falvo, M. Energy Efficiency and Integration of Urban Electrical Transport Systems: EVs and Metro-Trains of Two Real European Lines. Energies 2019, 12, 366. [Google Scholar] [CrossRef] [Green Version]
- Smith, K.; Hunter, L.; Galloway, S.; Booth, C.; Kerr, C.; Kellett, M. Integrated Charging of EVs Using Existing LVDC Light Rail Infrastructure: A Case Study. In Proceedings of the 2019 IEEE Third International Conference on DC Microgrids (ICDCM), Matsue, Japan, 20–23 May 2019. [Google Scholar]
- Akhavan-Hejazi, H.; Mohsenian-Rad, H.; Nejat, A. Developing a Test Data Set for Electric Vehicle Applications in Smart Grid Research. In Proceedings of the 2014 IEEE 80th Vehicular Technology Conference (VTC2014-Fall), Vancouver, QC, Canada, 14–17 September 2014. [Google Scholar]
- Gaete-Morales, C.; Kramer, H.; Schill, W.P.; Zerrahn, A. An open tool for creating battery-electric vehicle time series from empirical data, emobpy. Sci. Data 2021, 8, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Haben, S.; Arora, S.; Giasemidis, G.; Voss, M.; Greetham, D.V. Review of low voltage load forecasting: Methods, applications, and recommendations. Applied Energy 2021, 304, 117798. [Google Scholar] [CrossRef]
- Arif, S.M.; Lie, T.T.; Seet, B.C.; Ayyadi, S.; Jensen, K. Review of Electric Vehicle Technologies, Charging Methods, Standards and Optimization Techniques. Electronics 2021, 10, 1910. [Google Scholar] [CrossRef]
- Mies, J.; Helmus, J.; van den Hoed, R. Estimating the Charging Profile of Individual Charge Sessions of Electric Vehicles in The Netherlands. World Electr. Veh. J. 2018, 9, 17. [Google Scholar] [CrossRef] [Green Version]
- Amara-Ouali, Y.; Goude, Y.; Massart, P.; Poggi, J.M.; Yan, H. A Review of Electric Vehicle Load Open Data and Models. Energies 2021, 14, 2233. [Google Scholar] [CrossRef]
- Gruosso, G. Analysis of impact of electrical vehicle charging on low voltage power grid. In Proceedings of the 2016 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Toulouse, France, 2–4 November 2016. [Google Scholar]
- Abraham, D.S.; Verma, R.; Kanagaraj, L.; Raman, S.R.G.T.; Rajamanickam, N.; Chokkalingam, B.; Sekar, K.M.; Mihet-Popa, L. Electric Vehicles Charging Stations’ Architectures, Criteria, Power Converters, and Control Strategies in Microgrids. Electronics 2021, 10, 1895. [Google Scholar] [CrossRef]
- Mariscotti, A. Power Quality Phenomena, Standards, and Proposed Metrics for DC Grids. Energies 2021, 14, 6453. [Google Scholar] [CrossRef]
- Rafi, M.A.H.; Bauman, J. A Comprehensive Review of DC Fast-Charging Stations with Energy Storage: Architectures, Power Converters, and Analysis. IEEE Trans. Transp. Electrif. 2021, 7, 345–368. [Google Scholar] [CrossRef]
- Rönnberg, S.K.; Castro, A.G.; Bollen, M.H.J.; Moreno-Munoz, A.; Romero-Cadaval, E. Supraharmonics from power electronics converters. In Proceedings of the 9th International Conference on Compatibility and Power Electronics (CPE), Costa da Caparica, Portugal, 24–26 June 2015; pp. 539–544. [Google Scholar]
- Meyer, J.; Mueller, S.; Ungethuem, S.; Xiao, X.; Collin, A.; Djokic, S. Harmonic and supraharmonic emission of on-board electric vehicle chargers. In Proceedings of the IEEE PES Transmission & Distribution Conference and Exposition-Latin America (PES T&D-LA), Morelia, Mexico, 21–24 September 2016. [Google Scholar]
- Slangen, T.; van Wijk, T.; Ćuk, V.; Cobben, S. The Propagation and Interaction of Supraharmonics from Electric Vehicle Chargers in a Low-Voltage Grid. Energies 2020, 13, 3865. [Google Scholar] [CrossRef]
- Blum, J. Evaluating Supraharmonics Up to 150 kHz in Electric Vehicles at the University of Applied Sciences Bingen; Technical Report; 2021; Available online: https://powerquality.blog/2021/11/05/evaluating-supraharmonics-up-to-150-khz-in-electric-vehicles-at-the-university-of-applied-sciences-bingen (accessed on 28 January 2022).
- Lee, B.K.; Kim, J.P.; Kim, S.G.; Lee, J.Y. An Isolated/Bidirectional PWM Resonant Converter for V2G(H) EV On-Board Charger. IEEE Trans. Veh. Technol. 2017, 66, 7741–7750. [Google Scholar] [CrossRef]
- IEC 61851-1; Electric Vehicle Conductive Charging System—Part 1: General Requirements. IEC: Geneva, Switzerland, 2017.
- Triviño, A.; González-González, J.M.; Aguado, J.A. Wireless Power Transfer Technologies Applied to Electric Vehicles: A Review. Energies 2021, 14, 1547. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, H.; Shi, L.; Li, D.; Han, Y. A unit power factor DC fast charger for electric vehicle charging station. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012. [Google Scholar]
- Kuperman, A.; Levy, U.; Goren, J.; Zafranski, A.; Savernin, A. Modeling and Control of the PFC Stage for a 50 kW EV Fast Battery Charger. Proc. World Congr. Eng. 2011, 2, 5–9. [Google Scholar]
- Ramakrishnan, H.; Rangaraju, J. Power Topology Considerations for Electric Vehicle Charging Stations; Technical Report; Texas Instruments: Dallas, TX, USA, 2020. [Google Scholar]
- Piasecki, S.; Zaleski, J.; Jasinski, M.; Bachman, S.; Turzyński, M. Analysis of AC/DC/DC Converter Modules for Direct Current Fast-Charging Applications. Energies 2021, 14, 6369. [Google Scholar] [CrossRef]
- Das, S.; Narayanan, G. Analytical Closed-Form Expressions for Harmonic Distortion Corresponding to Novel Switching Sequences for Neutral-Point-Clamped Inverters. IEEE Trans. Ind. Electron. 2014, 61, 4485–4497. [Google Scholar] [CrossRef]
- Kan, Y.; Hyun, S.W.; Hong, S.J.; Won, C.Y. Zero dead-time PWM implementation method for reducing total harmonic distortion in 3-level NPC inverter. In Proceedings of the 2015 18th International Conference on Electrical Machines and Systems (ICEMS), Pattaya City, Thailand, 25–28 October 2015. [Google Scholar]
- Feng, Z.; Zhang, X.; Wang, J.; Yu, S. A High-Efficiency Three-Level ANPC Inverter Based on Hybrid SiC and Si Devices. Energies 2020, 13, 1159. [Google Scholar] [CrossRef] [Green Version]
- Zambra, D.A.B.; Rech, C.; Pinheiro, J.R. Comparison of Neutral-Point-Clamped, Symmetrical, and Hybrid Asymmetrical Multilevel Inverters. IEEE Trans. Ind. Electron. 2010, 57, 2297–2306. [Google Scholar] [CrossRef]
- Mariscotti, A. Experimental characterisation of active and non-active harmonic power flow of AC rolling stock and interaction with the supply network. Electr. Syst. Transp. 2021, 11, 109–120. [Google Scholar] [CrossRef]
- Streubel, T.; Kattmann, C.; Eisenmann, A.; Rudion, K. Characterization of Supraharmonic Emission from Three Different Electric Vehicle Charging Infrastructures in Time and Frequency Domain. Energies 2022, 15, 394. [Google Scholar] [CrossRef]
- Sandrolini, L.; Mariscotti, A. Signal Transformations for Analysis of Supraharmonic EMI Caused by Switched-Mode Power Supplies. Electronics 2020, 9, 2088. [Google Scholar] [CrossRef]
- Sandrolini, L.; Mariscotti, A. Waveform and Spectral Characteristics of Supraharmonic Unsymmetrical Conducted EMI of Switched-Mode Power Supplies. Electronics 2022, 11, 591. [Google Scholar] [CrossRef]
- ISO 6469-3; Electrically Propelled Road Vehicles—Safety Specifications. Part 3: Electrical Safety. ISO: Geneva, Switzerland, 2017.
- Liu, C. Analysis, Design and Control of DC-DC Resonant Converter for On-Board Bidirectional Battery Charger in Electric Vehicles. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 2017. Available online: https://etheses.whiterose.ac.uk/17528/1/ChaohuiLiu_Thesis_Final_2017-05-30.pdf (accessed on 28 January 2022).
- Liu, K.; Yang, Z.; Tang, X.; Cao, W. Automotive Battery Equalizers Based on Joint Switched-Capacitor and Buck-Boost Converters. IEEE Trans. Veh. Technol. 2020, 69, 12716–12724. [Google Scholar] [CrossRef]
- IEC 61000-2-2; Electromagnetic Compatibility (EMC)—Part 2-2: Environmen—Compatibility Levels for Low-Frequency Conducted Disturbances and Signalling in Public Low-Voltage Power Supply Systems. IEC: Geneva, Switzerland, 2019.
- IEC 61000-2-4; Electromagnetic Compatibility (EMC)—Part 2-4: Environment—Compatibility Levels In Industrial Plants for Low-Frequency Conducted Disturbances. IEC: Geneva, Switzerland, 2020.
- IEC 61000-3-2; Electromagnetic Compatibility (EMC)—Part 3-2: Limits – Limits for Harmonic Current Emissions (Equipment Input Current ≤ 16 A Per Phase). IEC: Geneva, Switzerland, 2019.
- IEC 61851-21-1; Electric Vehicle Conductive Charging System—Part 21-1: Electric Vehicle on-Board Charger EMC Requirements for Conductive Connection to an AC/DC Supply. IEC: Geneva, Switzerland, 2017.
- IEC 61000-3-12; Electromagnetic Compatibility (EMC)—Part 3-12: Limits–Limits for Harmonic Currents Producedby Equipment Connected to Public Low-Voltage Systems with Input Current >16 A and ≤ 75 A per Phase. IEC: Geneva, Switzerland, 2011.
- IEC 61000-4-7; Electromagnetic Compatibility (EMC)—Part 4-7: Testing and Measurement Techniques—General Guide on Harmonics and Interharmonics Measurements and Instrumentation, for Power Supply Systems and Equipment Connected Thereto. IEC: Geneva, Switzerland, 2002.
- CISPR 16-1-1; Specification for Radio Disturbance and Immunity Measuring Apparatus and Methods—Part 1-1: Radio Disturbance and Immunity Measuring Apparatus—Measuring Apparatus. IEC: Geneva, Switzerland, 2019.
- Sandrolini, L.; Mariscotti, A. Impact of short-time Fourier transform parameters on the accuracy of EMI spectra estimates in the 2–150 kHz supraharmonic interval. Electr. Power Syst. Res. 2021, 195, 107130. [Google Scholar] [CrossRef]
- Klatt, M.; Meyer, J.; Schegner, P. Comparison of measurement methods for the frequency range of 2 kHz to 150 kHz. In Proceedings of the International Conference on Harmonics and Quality of Power, Bucharest, Romania, 25–28 May 2014; pp. 818–822. [Google Scholar]
- Slangen, T.M.H.; van Wijk, T.; Cuk, V.; Cobben, J.F.G. The Harmonic and Supraharmonic Emission of Battery Electric Vehicles in The Netherlands. In Proceedings of the 2020 International Conference on Smart Energy Systems and Technologies (SEST), Istanbul, Turkey, 7–9 September 2020. [Google Scholar]
- CISPR 16-2-1; Specification for Radio Disturbance and Immunity Measuring Apparatus and Methods—Part 2-1: Methods of Measurement of Disturbances and Immunity—Conducted Disturbance Measurements. IEC: Geneva, Switzerland, 2014.
- EN 50065-1; Signalling on Low-Voltage Electrical Installations in the Frequency Range 3 kHz to 148,5 kHz Part 1: General Requirements, Frequency Bands and Electromagnetic Disturbances. CENELEC: Brussels, Belgium, 2012.
- CISPR 16-1-2; Specification for Radio Disturbance and Immunity Measuring Apparatus and Methods—Part 1-2: Radio Disturbance and Immunity Measuring Apparatus—Coupling Devices for Conducted Disturbance Measurements. IEC: Geneva, Switzerland, 2014.
- IEC 61000-3-11; Electromagnetic Compatibility (EMC)—Part 3-11: Part 3-11: Limits—Limitation of Voltage Changes, Voltage Fluctuationsand Flicker in Public Low-Voltage Supply Systems—Equipment with rated Current ≤ 75 A and Subject to Conditional Connection. IEC: Geneva, Switzerland, 2019.
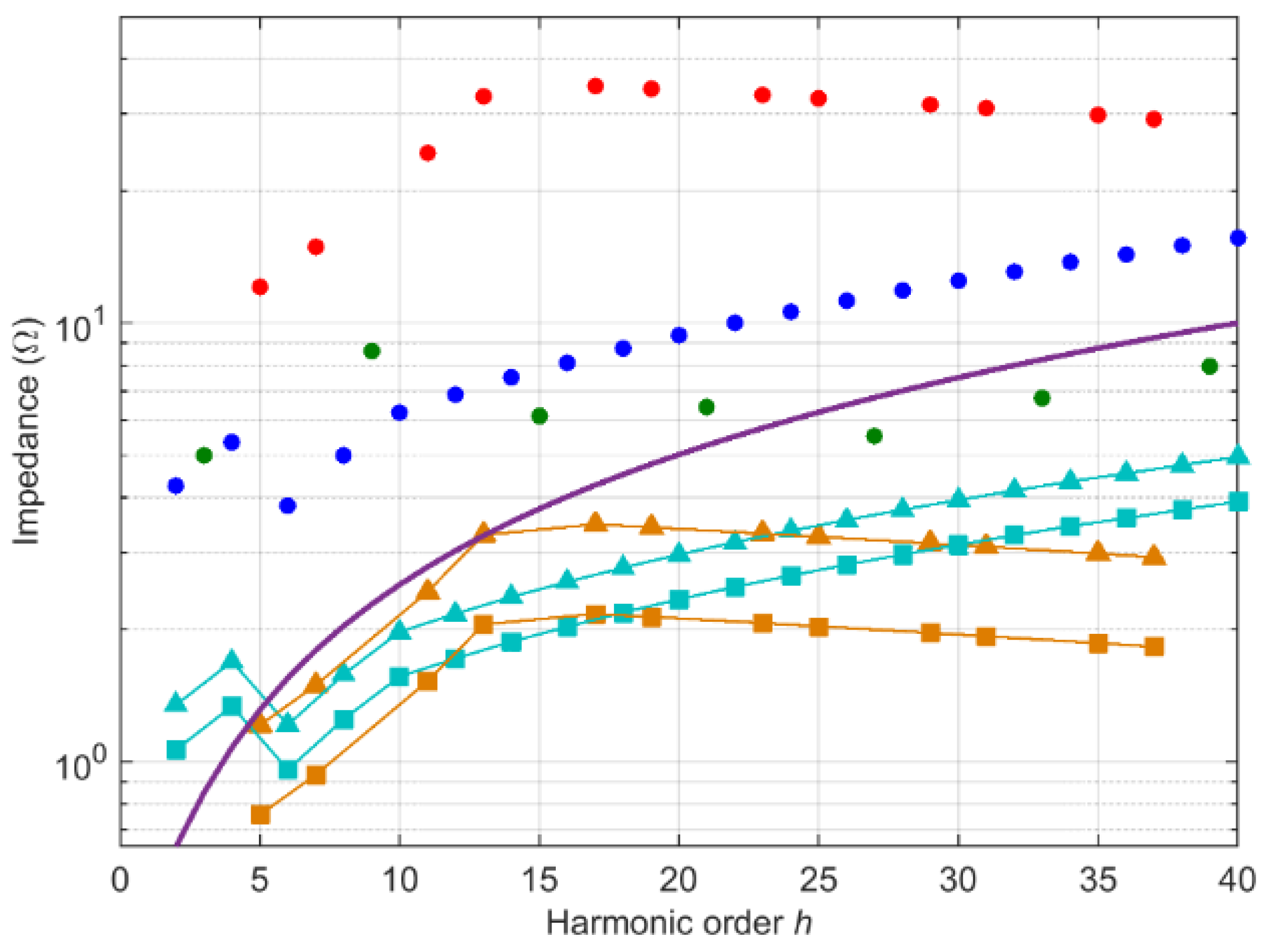
- Busatto, T.; Larsson, A.; Ronnberg, S.K.; Bollen, M.H.J. Including Uncertainties From Customer Connections in Calculating Low-Voltage Harmonic Impedance. IEEE Trans. Power Deliv. 2019, 34, 606–615. [Google Scholar] [CrossRef]
- Stiegler, R.; Meyer, J.; Schori, S.; Höckel, M.; Scheida, K.; Drápela, J.; Hanžlík, T. Survey of network impedance in the frequency range 2–9 kHz in public low voltage networks in AT/CH/CZ/GE. In Proceedings of the 25th International Conference and Exhibition on Electricity Distribution (CIRED), Madrid, Spain, 3–6 June 2019. [Google Scholar]
- Harris, F.J. On the use of windows for harmonic analysis with the discrete Fourier transform. Proc. IEEE 1978, 66, 51–83. [Google Scholar] [CrossRef]
- Darmawardana, D.; David, J.; Perera, S.; Robinson, D.; Meyer, J.; Jayatunga, U. Analysis of High Frequency (Supraharmonics) Emissions Caused by Electric Vehicle Charging. In Proceedings of the 2020 19th International Conference on Harmonics and Quality of Power (ICHQP), Dubai, United Arab Emirates, 6–7 July 2020. [Google Scholar]
- Streubel, T.; Kattmann, C.; Eisenmann, A.; Rudion, K. Detection and Monitoring of Supraharmonic Anomalies of an Electric Vehicle Charging Station. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 27 June 2017. [Google Scholar]
- IEC 61000-4-30; Electromagnetic Compatibility (EMC)—Part 4-30: Testing and Measurement Techniques—Power Quality Measurement Methods. IEC: Geneva, Switzerland, 2015.
- Wang, Y.; Xu, Y.; Tao, S.; Siddique, A.; Dong, X. A Flexible Supraharmonic Group Method Based on Switching Frequency Identification. IEEE Access 2020, 8, 39491–39501. [Google Scholar] [CrossRef]
- Möller, F.; Müller, S.; Meyer, J. Impact of Electric Vehicles on Power Quality in Central Charging Infrastructures. In Proceedings of the 1st E-Mobility Power System Integration Symposium, Berlin, Germany, 23 October 2017. [Google Scholar]
- Meyer, J.; Bollen, M.; Amaris, H.; Blanco, A.M.; Gil De Castro, A.; Desmet, J.; Klatt, M.; Kocewiak, L.; Ronnberg, S.; Yang, K. Future work on harmonics—Some expert opinions Part II —Supraharmonics, standards and measurements. In Proceedings of the International Conference on Harmonics and Quality of Power, ICHQP, Bucharest, Romania, 25–28 May 2014; pp. 909–913. [Google Scholar]
- Gil-De-Castro, A.; Medina-Gracia, R.; Ronnberg, S.; Blanco, A.; Meyer, J. Differences in the performance between CFL and LED lamps under different voltage distortions. In Proceedings of the 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13–16 May 2018. [Google Scholar]
- Mariscotti, A.; Sandrolini, L.; Pasini, G. Variability caused by Setup and Operating Conditions for Conducted EMI of Switched Mode Power Supplies over the 2–1000 kHz Interval. IEEE Trans. Instrum. Meas. 2022. [Google Scholar] [CrossRef]
- Kutt, L.; Saarijarvi, E.; Lehtonen, M.; Molder, H.; Niitsoo, J. Electric vehicle charger load current harmonics variations due to supply voltage level differences—Case examples. In Proceedings of the 2014 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Ischia, Italy, 18–20 June 2014. [Google Scholar]
- Möller, F.; Müller, S.; Wald, C.; Isensee, S. Impact of electric vehicle charging on unbalance and harmonic distortion—Field study in an urban residential area. In Proceedings of the 23rd International Conference on Electricity Distribution, Lyon, Franc, 15–18 June 2015. [Google Scholar]
- Collin, A.J.; Djokic, S.Z.; Thomas, H.F.; Meyer, J. Modelling of electric vehicle chargers for power system analysis. In Proceedings of the 11th International Conference on Electrical Power Quality and Utilisation, Lisbon, Portugal, 17–19 October 2011. [Google Scholar]
- Malano, A.A.; Muller, S.; Meyer, J.; Bachmann, S. Harmonic interaction of electric vehicle chargers in a central charging infrastructure. In Proceedings of the 2016 17th International Conference on Harmonics and Quality of Power (ICHQP), Belo Horizonte, Brazil, 16–19 October 2016. [Google Scholar]
- Iqbal, M.N.; Kütt, L.; Daniel, K.; Asad, B.; Ghahfarokhi, P.S. Estimation of Harmonic Emission of Electric Vehicles and Their Impact on Low Voltage Residential Network. Sustainability 2021, 13, 8551. [Google Scholar] [CrossRef]


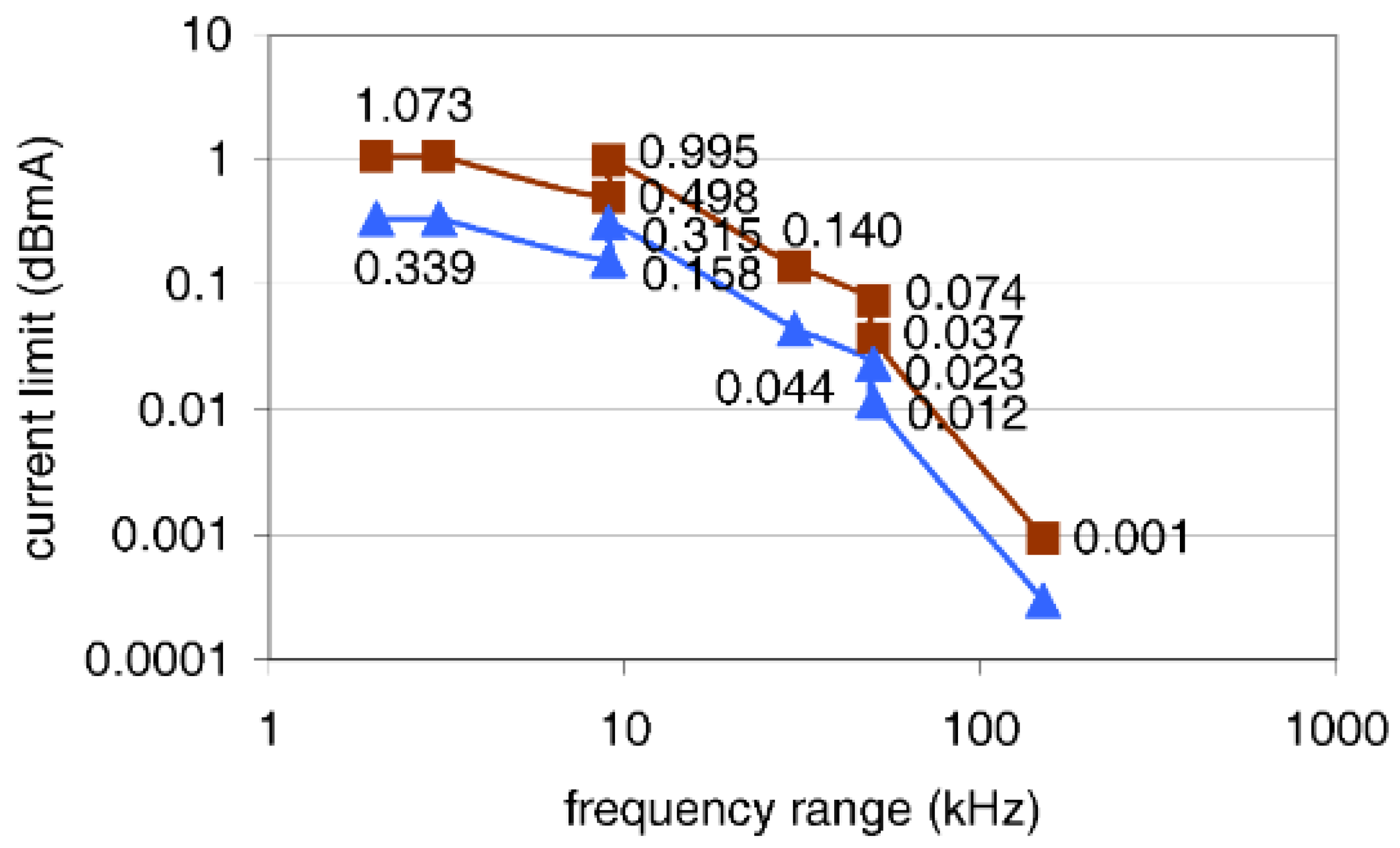
| Harmonic Order h | Limit (A) |
|---|---|
| 2 | 1.08 |
| 3 | 2.30 |
| 4 | 0.43 |
| 5 | 1.14 |
| 6 | 0.30 |
| 7 | 0.77 |
| 9 | 0.40 |
| 11 | 0.33 |
| 13 | 0.21 |
| Publisher/Search Engine | “Supraharmonic” | “Harmonic” | Ratio |
|---|---|---|---|
| Elsevier | 24 | 1511 | 1.6% |
| IEEE | 78 | 12,910 | 0.6% |
| MDPI | 15 | 1072 | 1.4% |
| 5440 | 1,050,000 | 0.5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mariscotti, A. Harmonic and Supraharmonic Emissions of Plug-In Electric Vehicle Chargers. Smart Cities 2022, 5, 496-521. https://doi.org/10.3390/smartcities5020027
Mariscotti A. Harmonic and Supraharmonic Emissions of Plug-In Electric Vehicle Chargers. Smart Cities. 2022; 5(2):496-521. https://doi.org/10.3390/smartcities5020027
Chicago/Turabian StyleMariscotti, Andrea. 2022. "Harmonic and Supraharmonic Emissions of Plug-In Electric Vehicle Chargers" Smart Cities 5, no. 2: 496-521. https://doi.org/10.3390/smartcities5020027
APA StyleMariscotti, A. (2022). Harmonic and Supraharmonic Emissions of Plug-In Electric Vehicle Chargers. Smart Cities, 5(2), 496-521. https://doi.org/10.3390/smartcities5020027






