Intersection Sight Distance in Mixed Automated and Conventional Vehicle Environments with Yield Control on Minor Roads
Abstract
:Highlights
- A surrogate safety measure, which is the probability of unresolved conflicts (PUC), is developed to account for the reliability of intersection sight distance (ISD) at intersections with yield control on a minor road and is applied for conventional, driver-operated vehicles (DVs), and automated vehicles (AVs).
- The results show mixed DV-AV and AV-only traffic to have higher PUC values than those of DV-only traffic.
- The scenarios of mixed vehicle traffic with high PUC values indicate lower safety performances.
- A reduction in the speed limit for AVs on the minor road would lead to lowering the PUC values, improving the safety at the intersection.
Abstract
1. Introduction
- An established relationship for estimating conflicts at intersections that accounts for AV penetration rates.
- Defined models for computing the ISD along the intersecting roads of a yield-controlled intersection based on the mixed vehicle traffic of DVs and AVs.
- A developed surrogate safety measure, which is the probability of unresolved conflict (PUC), to account for the probability of the demand ISD exceeding the supply ISD and the expected number of conflicts at the intersection.
- Corrective countermeasures for mitigating the ISD issues of existing designs being inconsistent with a mixed traffic environment and addressing new intersection designs.
2. Research Methodology
2.1. Vehicle Interactions
- DVN/DVM.
- DVN/AVM.
- AVN/DVM.
- AVN/AVM.
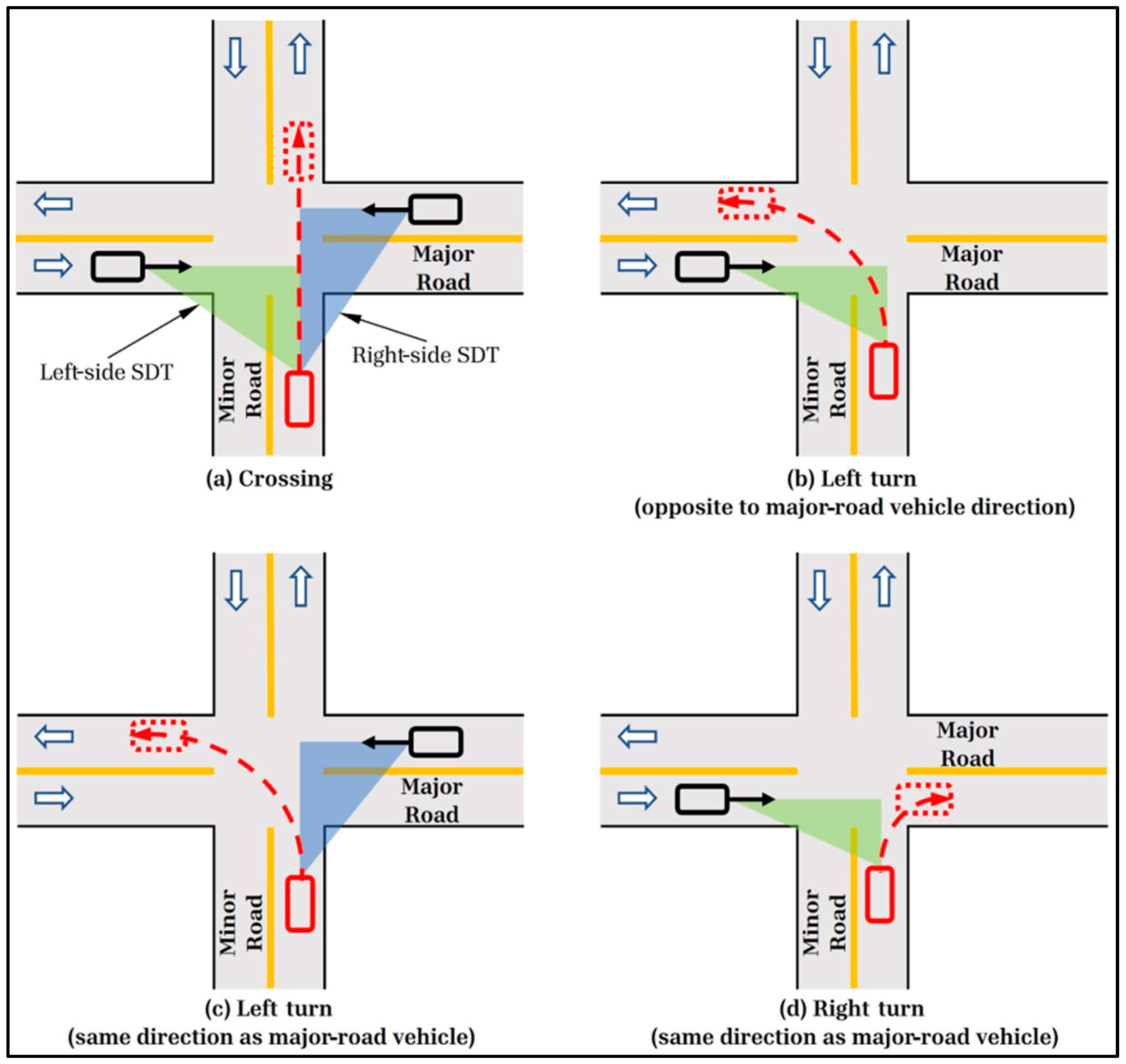
2.2. Conflict Analysis
- The crossing-right side (CRS) involves a-minor-road vehicle and a major-road vehicle approaching from the right side.
- The crossing-left side (CLS) involves a minor-road vehicle and a major-road vehicle approaching from the left side.
- The left turn-left side (LTLS) involves a left-turning minor-road vehicle and a major-road vehicle approaching from the left side.
- The left turn-right side (LTRS) involves a left-turning minor-road vehicle and a major-road vehicle approaching from the right side.
- The right turn-left side (RTLS) involves a right-turning minor-road vehicle and a major-road vehicle approaching from the left side.
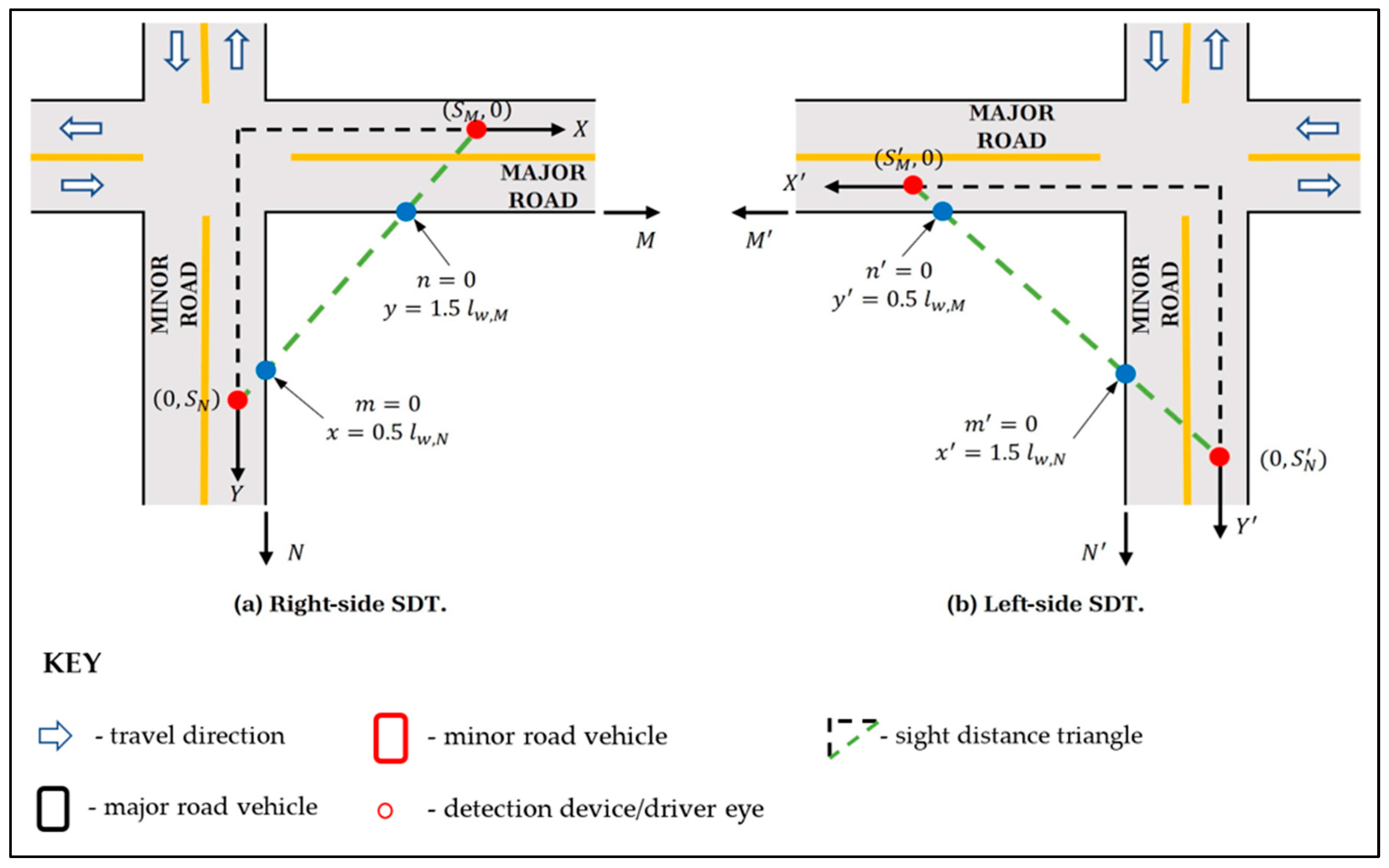
2.3. SDT Properties
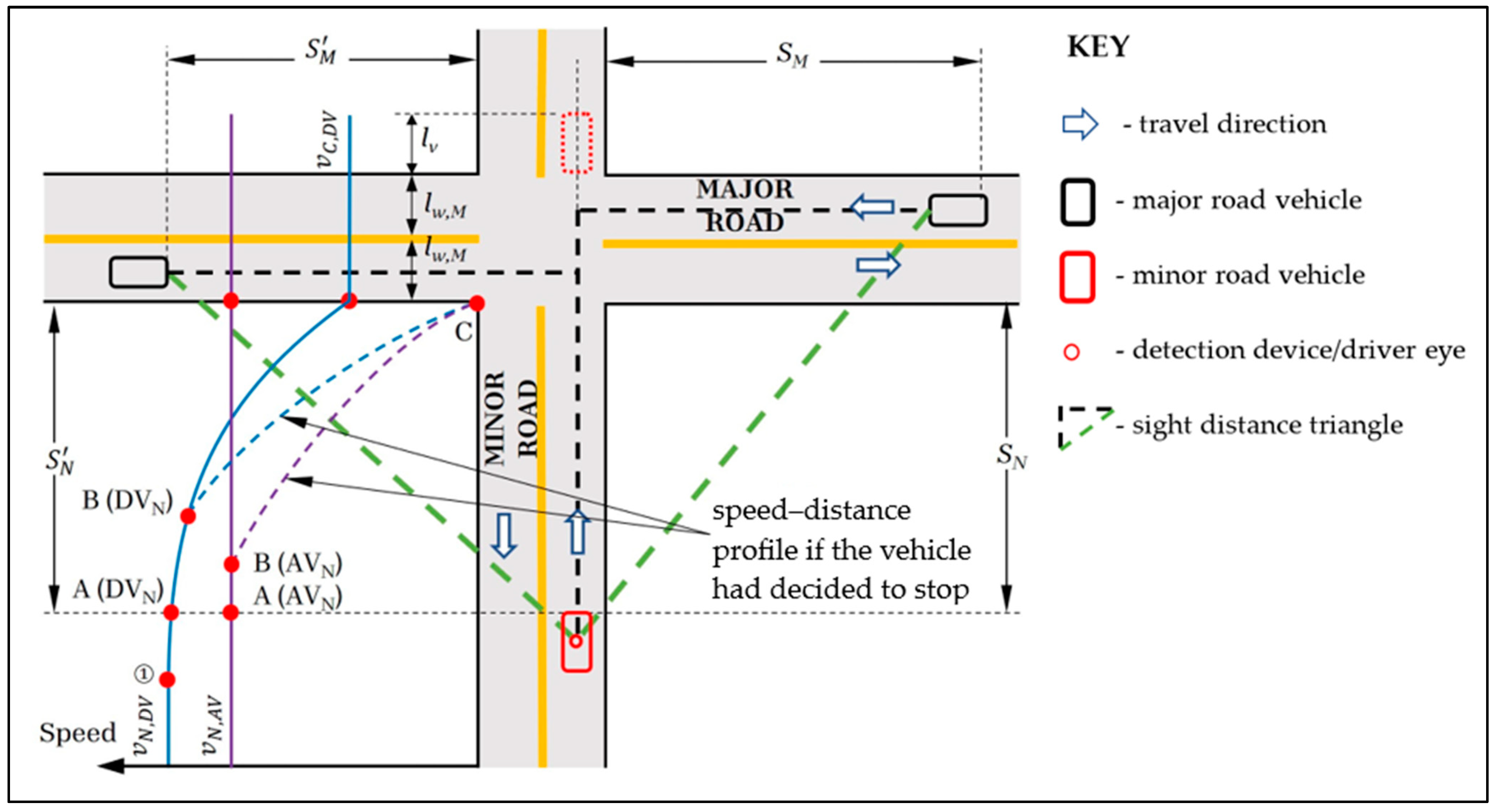
2.4. ISD Models
2.4.1. Minor-Road Models
- Point A: the decision point and beginning of the PRT.
- Point B: the end of the PRT and the beginning of the braking distance.
- Point C: the end of the braking distance and the beginning of the intersection. The location of Point C coincides with Point ➁, with both points coinciding with the beginning of the intersection.
2.4.2. Major-Road Models
Crossing Maneuver (CRS and CLS)
- The travel time between Points A and B () is equal to the PRT or DRT ( or ) for the DVN or AVN, respectively.
- The travel time between Point B and the beginning of the intersection (Point ➁ or C) follows the original speed profile with no stopping ().
- The travel time to cross the major road: for the CLS and two-lane major roads, the minor-road vehicle needs to clear only one major-road lane, while it has to clear both lanes for the CRS.
- The travel time is shown for a distance equivalent to the vehicle length ().
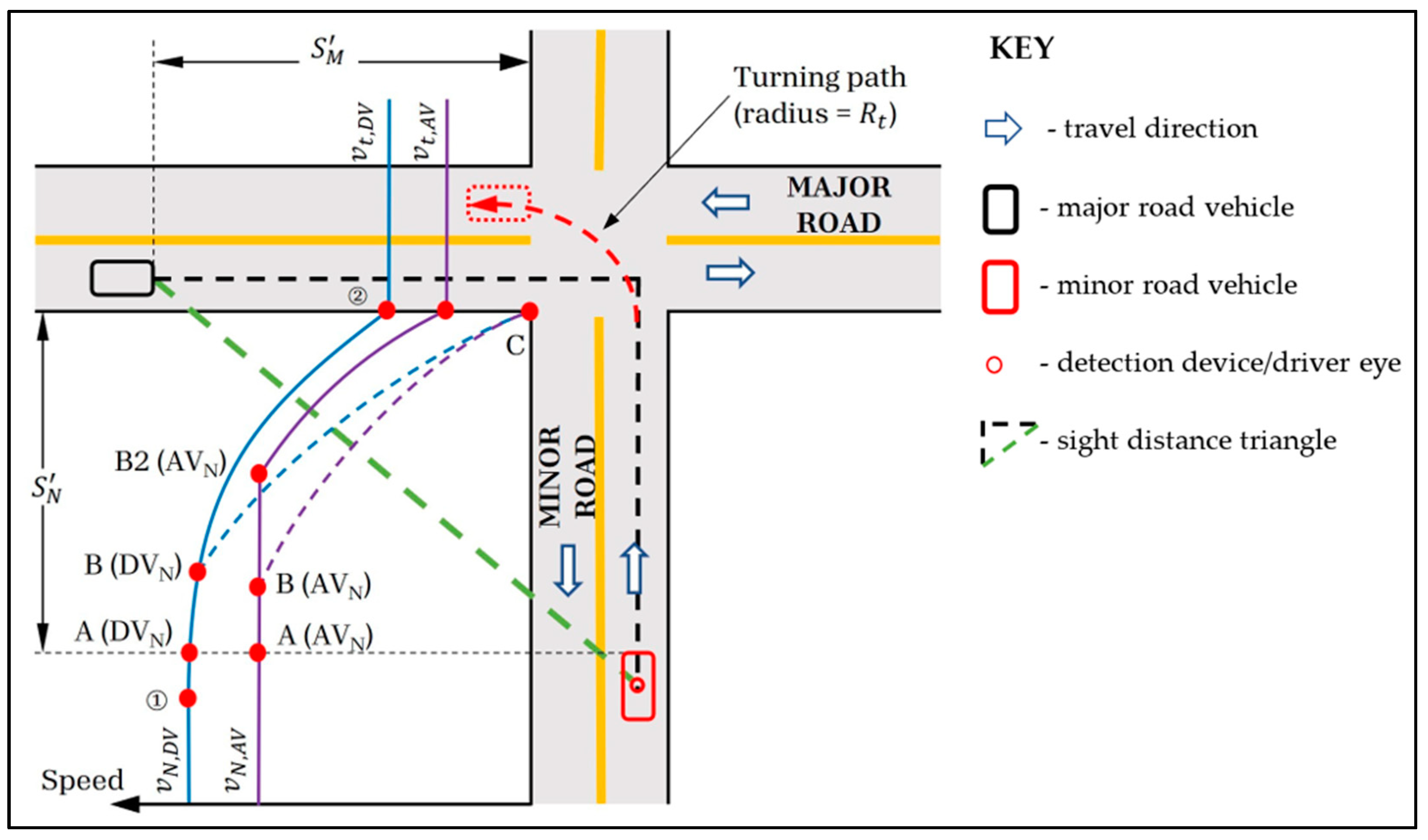
Turning Opposite to Major-Road Traffic (LTLS)
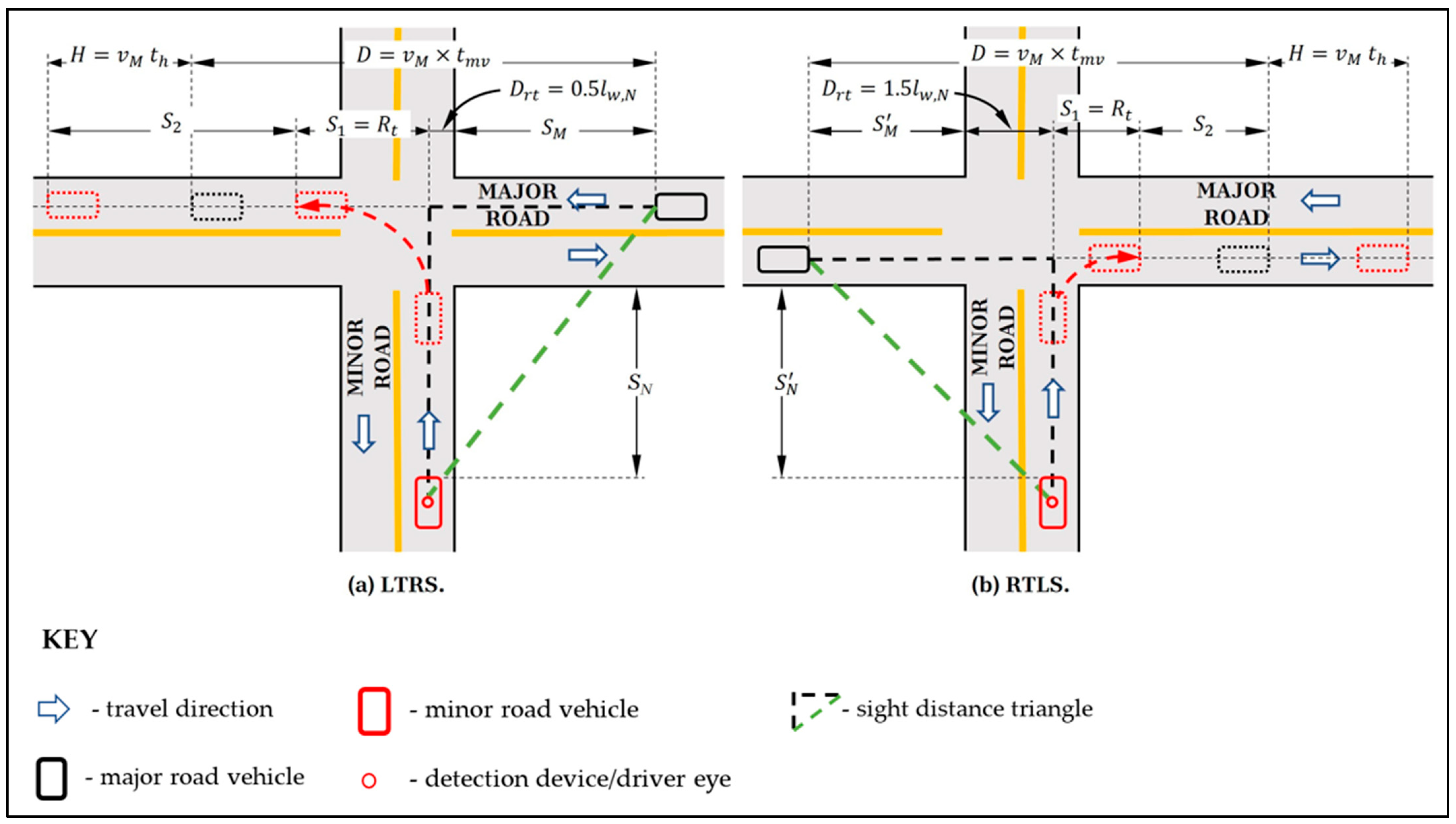
Turning in the Same Direction as Major-Road Traffic (LTRS and RTLS)
2.5. System Models
2.6. Probabilistic Assessment
2.7. Target PUC
3. Statistical Distributions of Model Parameters
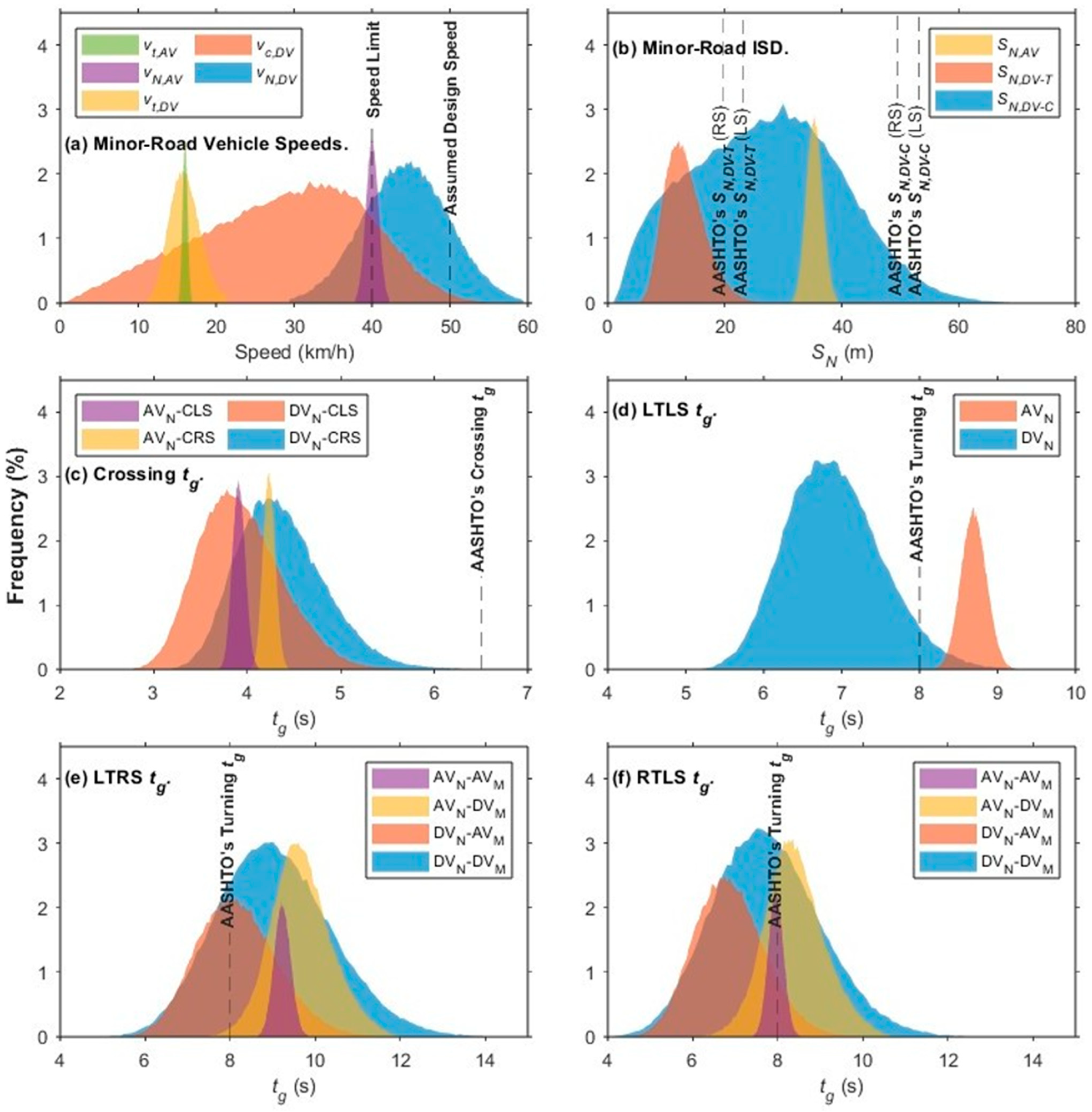
3.1. Driver and Vehicle Parameters
3.2. Parameter Correlation
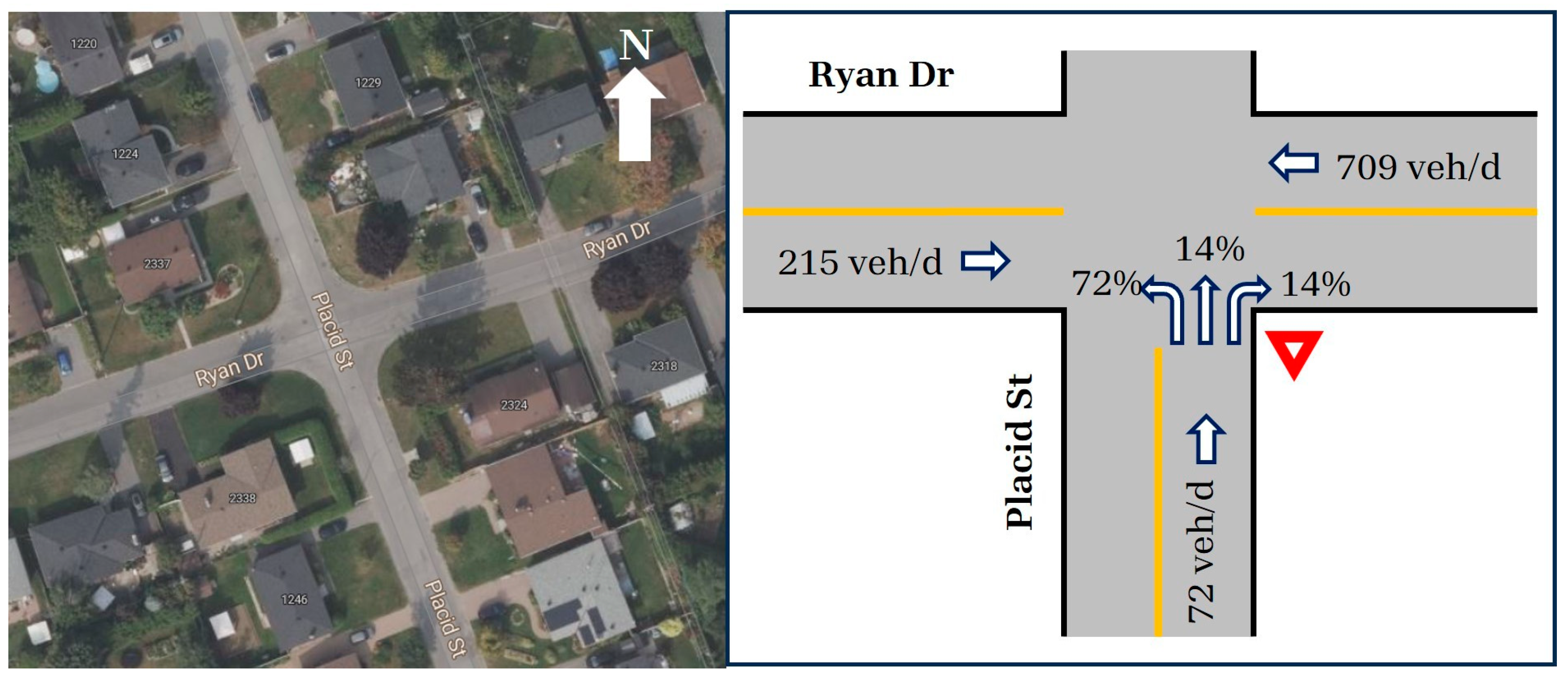
4. Case Study
- Lane width (both roads): 3.6 m.
- Speed limit (both roads): 40 km/h. The design speed of both roads was assumed as 50 km/h or 10 km/h above the speed limit.
- Curb radius: 7.5 m.
- Road shoulders: none.
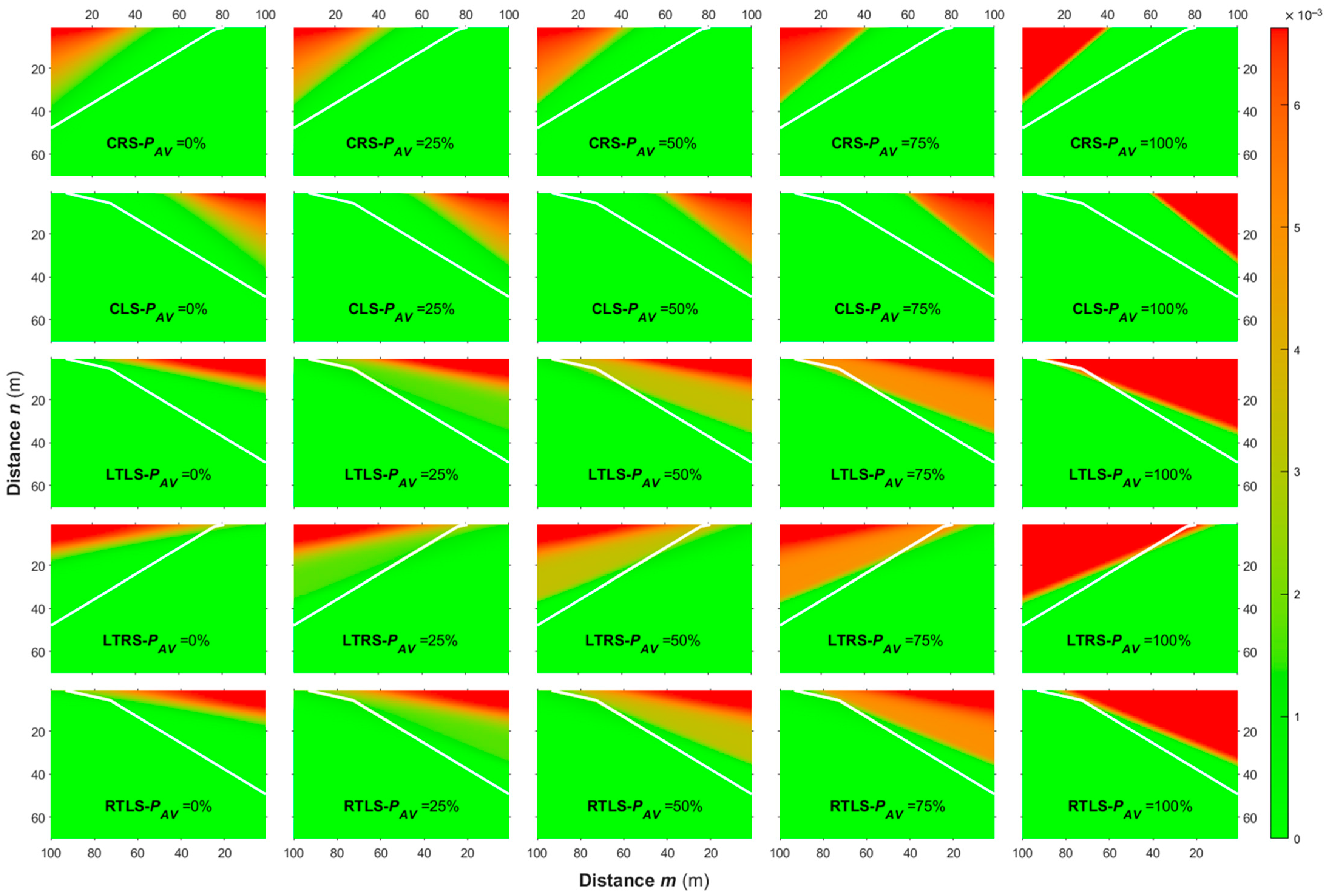
4.1. Results of Conflict Analysis
4.2. PUC Results
4.2.1. Target PUC
4.2.2. Effect of AVs
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AASHTO | American Association of State and Highway Officials |
| ADT | Average Daily Traffic |
| AV | Autonomous vehicle |
| CAV | Connected, Automated Vehicles |
| CLS | Crossing-left side |
| CoV | Coefficient of variation |
| CRS | Crossing-right side |
| DRT | Detection and reaction time |
| DT | Decision tree |
| DV | Driver-operated vehicle |
| FORM | First-order reliability method |
| FOSM | First-order second-moment method |
| ISD | Intersection sight distance |
| LT | Left turn |
| LTLS | Left turn-left side |
| LTRS | Left turn-right side |
| MCS | Monte Carlo Simulation |
| NCHRP | National Cooperative Highway Research Program |
| PNC | Probability of non-compliance |
| PRT | Perception and reaction time |
| PUC | Probability of unresolved conflicts |
| RT | Right turn |
| RTLS | Right turn-left side |
| RTRS | Right Turn-Right Side |
| SDT | Sight distance triangle |
| SSD | Stopping sight distance |
| TAC | Transportation Association of Canada |
References
- AASHTO. A Policy on Geometric Design of Highway and Streets, 7th ed.; The American Association of State Highway and Transportation Officials: Washington, DC, USA, 2018. [Google Scholar]
- TAC. Geometric Design Guide for Canadian Roads; Technical Report; Transportation Association of Canada: Ottawa, ON, Canada, 2017. [Google Scholar]
- Harwood, D.; Mason, J.; Brydia, R.; Pietrucha, M.; Gittings, G. Report 383: Intersection Sight Distance; Transportation Research Board (TRB): Washington, DC, USA, 1996. [Google Scholar]
- Easa, S.M. Reliability Approach to Intersection Sight Distance Design. Transp. Res. Rec. 2000, 1701, 42–52. [Google Scholar] [CrossRef]
- Easa, S.M.; Ma, Y.; Liu, S.; Yang, Y.; Arkatkar, S. Reliability Analysis of Intersection Sight Distance at Roundabouts. Infrastructures 2020, 5, 67. [Google Scholar] [CrossRef]
- Easa, S.M.; Hussain, A. Reliability of Sight Distance at Stop-Control Intersections. Proc. Inst. Civ. Eng.—Transp. 2016, 169, 138–147. [Google Scholar] [CrossRef]
- Hussain, A.; Easa, S.M. Reliability Analysis of Left-Turn Sight Distance at Signalized Intersections. J. Transp. Eng. 2016, 142, 04015048. [Google Scholar] [CrossRef]
- Osama, A.; Sayed, T.; Easa, S. Framework for Evaluating Risk of Limited Sight Distance for Permitted Left-Turn Movements: Case Study. Can. J. Civ. Eng. 2016, 43, 369–377. [Google Scholar] [CrossRef]
- Sarran, S.; Hassan, Y. Impacts of Automated Vehicles in a Mixed Environment on Intersection Sight Distance at Uncontrolled Intersections. J. Transp. Eng. A Syst. 2025, 151, 04024016. [Google Scholar] [CrossRef]
- Rengaraju, V.R.; Rao, V.T. Vehicle-Arrival Characteristics at Urban Uncontrolled Intersections. J. Transp. Eng. 1995, 121, 317–323. [Google Scholar] [CrossRef]
- Yin, W.; Zou, Q.; Lv, C.; Wu, Z.; Tan, G. A Quantitative Model of Conflict Risk Degree at Non-Signalized Intersections. Procedia Eng. 2016, 137, 171–179. [Google Scholar] [CrossRef]
- MathWorks, R2024b, Triangular Distribution—MATLAB & Simulink; MathWork: Natick, MA, USA, 2024. Available online: https://www.mathworks.com/help/stats/triangular-distribution.html (accessed on 4 April 2024).
- Dabbour, E. Design Gap Acceptance for Right-Turning Vehicles Based on Vehicle Acceleration Capabilities. Transp. Res. Record. 2015, 2521, 12–21. [Google Scholar] [CrossRef]
- Dabbour, E.; Easa, S. Sight-Distance Requirements for Left-Turning Vehicles at Two-Way Stop-Controlled Intersections. J. Transp. Eng. Part A Syst. 2017, 143, 04016004. [Google Scholar] [CrossRef]
- Abdelnaby, A.; Hassan, Y. Probabilistic Analysis of Freeway Deceleration Speed-Change Lanes. Transp. Res. Rec. 2014, 2404, 27–37. [Google Scholar] [CrossRef]
- Huang, C.; El Hami, A.; Radi, B. Overview of structural reliability analysis methods—Part I: Local reliability methods. Incertitudes et fiabilité des systèmes multiphysiques. Engineering 2017, 17, 1–10. [Google Scholar] [CrossRef]
- Andrade-Catano, F.; De Santos-Berbel, C.; Castro, M. Reliability-Based Safety Evaluation of Headlight Sight Distance Applied to Road Sag Curve Standards. IEEE Access 2020, 8, 43606–43617. [Google Scholar] [CrossRef]
- Singh, V.P.; Jain, S.K.; Tyagi, A. Risk and Reliability Analysis: A Handbook for Civil and Environmental Engineers; American Society of Civil Engineers: Reston, VA, USA, 2007. [Google Scholar] [CrossRef]
- Sarhan, M.; Hassan, Y. Three-dimensional, Probabilistic Highway Design: Sight Distance Application. Transp. Res. Rec. 2008, 2060, 10–18. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Stone, M. Comments on Model Selection Criteria of Akaike and Schwartz. J. R. Stat. Soc. B 1979, 41, 276–278. [Google Scholar] [CrossRef]
- Kuha, J. AIC and BIC: Comparisons of Assumptions and Performance. Sociol. Methods Res. 2004, 33, 188–229. [Google Scholar] [CrossRef]
- Sukennik, P. Deliverable 2.5: Microsimulation Guide for Automated Vehicles; Technical Report. CoEXist; PTV Group: Karlsruhe, Germany, 2018. [Google Scholar]
- Fambro, D.; Fitzpatrick, K.; Koppa, R. National Cooperative Highway Research Program Report (NCHRP) 400: Determination of Stopping Sight Distances; Transportation Research Board (TRB): Washington, DC, USA, 1997. [Google Scholar]
- Peng, H. Driving Etiquette; Technical Report; Transportation Research Institute: Ann Arbor, MI, USA, 2020. [Google Scholar]
- Ismail, K.; Sayed, T. Risk-Based Framework for Accommodating Uncertainty in Highway Geometric Design. Can. J. Civ. Eng. 2009, 36, 743–753. [Google Scholar] [CrossRef]
- Moon, S.; Yi, K. Human Driving Data-Based Design of a Vehicle Adaptive Cruise Control Algorithm. Veh. Syst. Dyn. 2008, 46, 661–690. [Google Scholar] [CrossRef]
- Urmson, C. Driving Beyond Stopping Distance Constraints. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 1189–1194. [Google Scholar] [CrossRef]
- Sukennik, P.; Kautzsch, L. Deliverable 2.3: Default Behavioral Parameter Sets for Automated Vehicles (AV). CoEXist; PTV Group: Karlsruhe, Germany, 2018. [Google Scholar]
- Weber, Y.; Kanarachos, S. CUPAC—The Coventry University public road dataset for automated cars. Data Brief 2020, 28, 104950. [Google Scholar] [CrossRef]
- Tesla. Model 3 Owner’s Manual: About Auto Pilot; Tesla, Inc.: Austin, TX, USA, 2025. [Google Scholar]
- Wortman, R.H.; Matthias, J.S. An Evaluation of Driver Behavior at Signalized Intersections. Transp. Res. Rec. 1983, 904, 10–20. [Google Scholar]
- Wang, J.; Dixon, K.K.; Li, H.; Ogle, J. Normal Acceleration Behavior of Passenger Vehicles Starting from Rest at All-Way Stop-Controlled Intersections. Transp. Res. Rec. 2004, 1883, 158–166. [Google Scholar] [CrossRef]
- Wood, J.S.; Zhang, S. Evaluating Relationships Between Perception-Reaction Times, Emergency Deceleration Rates, and Crash Outcomes Using Naturalistic Driving Data. Transp. Res. Rec. 2021, 2675, 213–223. [Google Scholar] [CrossRef]
- Siebert, F.W.; Oehl, M.; Pfister, H.R. The Influence of Time Headway on Subjective Driver States in Adaptive Cruise Control. Transp. Res. Part F Traffic Psychol. Behav. 2014, 25, 65–73. [Google Scholar] [CrossRef]
- Siebert, F.W.; Oehl, M.; Bersch, F.; Pfister, H.R. The Exact Determination of Subjective Risk and Comfort Thresholds in Car Following. Transp. Res. Part F Traffic Psychol. Behav. 2017, 46, 1–13. [Google Scholar] [CrossRef]
- Winsum, W.V.; Heino, A. Choice of Time-Headway in Car-Following and the Role of Time-to-Collision Information in Braking. Ergonomic 1996, 39, 579–592. [Google Scholar] [CrossRef]
- Grubbs, F.E. Procedures for Detecting Outlying Observations in Samples. Technometrics 1969, 11, 1–21. [Google Scholar] [CrossRef]
- Demuynck, V. Driving Safely with ADAS Map Speed Limits. TomTom 2020. Available online: https://www.tomtom.com/newsroom/product-focus/adas-map-speed-limits/ (accessed on 18 March 2025).




| Interaction | Right-Side SDT | Left-Side SDT |
|---|---|---|
| DVN/DVM | ||
| DVN/AVM | ||
| AVN/DVM | ||
| AVN/AVM |
| Design Speed (km/h) | (m) | (s) |
|---|---|---|
| 20 | 20 | 7.1 |
| 30 | 30 | 6.5 |
| 40 | 40 | 6.5 |
| 50 | 55 | 6.5 |
| 60 | 65 | 6.5 |
| 70 | 80 | 6.5 |
| 80 | 100 | 6.5 |
| 90 | 115 | 6.8 |
| 100 | 135 | 7.1 |
| 110 | 155 | 7.4 |
| 120 | 180 | 7.7 |
| 130 | 205 | 8.0 |
| Design Parameter | Distribution | Statistical Parameters | Source |
|---|---|---|---|
| , : speed at 40 km/h posted speed limit | Normal | = 44.20 km/h = 5.58 km/h | Data |
| , : speed at 50 km/h posted speed limit | Normal | = 53.90 km/h = 5.85 km/h | Data |
| , : speed at 60 km/h posted speed limit | Normal | = 62.74 km/h = 7.26 km/h | Data |
| : intersection turning speed | Normal * | = 16.00 km/h = 2.02 km/h ** | [3] |
| speed reduction factor | Triangular * | = 0.0 = 0.095 = 1.0 | [3] |
| : braking rate | Normal | = 3.92 m/s2 = 0.41 m/s2 | [24] |
| : initial deceleration rate | Normal * | = 1.21 m/s2 = 0.13 m/s2 | [3] |
| : acceleration rate | Generalized Extreme Value | = 0.1426 m/s2 = 0.1930 m/s2 = 1.0457 m/s2 | [25] |
| : perception–reaction time | Lognormal | = 1.5 s = 0.4 s | [26] |
| : time headway | Lognormal | = 1.156 s = 0.756 s | Data |
| , : distance from the left side of the vehicle to the lane edge | Gamma | = 6.54 m = 0.10 | [9] |
| : distance from driver eye to the left side of the vehicle | Normal | = 0.45 m = 0.04 m | [9] |
| : distance from the driver eye to the front of the vehicle | Normal | = 2.45 m = 0.17 m | [9] |
| : vehicle length | Lognormal | = 4.813 m = 0.45 m | Data |
| : vehicle width | Logistic | = 1.891 m = 0.061 m | Data |
| Design Parameter | Distribution | Statistical Parameters | Source |
|---|---|---|---|
| , : speed at 40 km/h posted speed limit | Normal | = 40 km/h = 0.8 km/h | Equations (27) and (28) |
| , : speed at 50 km/h posted speed limit | Normal | = 50 km/h = 1.0 km/h | Equations (27) and (28) |
| , : speed at 60 km/h posted speed limit | Normal | = 60 km/h = 1.2 km/h | Equations (27) and (28) |
| : intersection turning speed | Normal | = 16 km/h = 0.32 km/h | [23] |
| : braking rate | Normal | = 2.10 m/s2 = 0.04 m/s2 | [27] |
| : acceleration rate | Normal | = 2.10 m/s2 = 0.04 m/s2 | [27] |
| : detection–reaction time | Normal | = 0.53 s = 0.01 s | [28] |
| : time headway | Normal | = 0.90 s = 0.018 s | [29] |
| : vehicle length | Uniform | Minimum = 3.969 m Maximum = 5.057 m | [30,31] |
| : distance from the detection device to the front of the vehicle | Uniform | Minimum = 1.66 m Maximum = 2.64 m | [30,31] |
| Interaction Type | PAV (%) | CRS | CLS | LTLS | LTRS | RTLS |
|---|---|---|---|---|---|---|
| 0 | 0.2188 | 0.0663 | 0.3445 | 1.1361 | 0.0663 | |
| 25 | 0.1231 | 0.0373 | 0.1939 | 0.6393 | 0.0373 | |
| DVN-DVM | 50 | 0.0547 | 0.0166 | 0.0862 | 0.2842 | 0.0166 |
| 75 | 0.0137 | 0.0041 | 0.0216 | 0.0711 | 0.0041 | |
| 100 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | |
| 25 | 0.0410 | 0.0124 | 0.0647 | 0.2133 | 0.0124 | |
| DVN-AVM | 50 | 0.0547 | 0.0166 | 0.0862 | 0.2842 | 0.0166 |
| 75 | 0.0410 | 0.0124 | 0.0646 | 0.2131 | 0.0124 | |
| 100 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | |
| 25 | 0.0410 | 0.0124 | 0.0646 | 0.2131 | 0.0124 | |
| AVN-DVM | 50 | 0.0547 | 0.0166 | 0.0862 | 0.2842 | 0.0166 |
| 75 | 0.0410 | 0.0124 | 0.0647 | 0.2133 | 0.0124 | |
| 100 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | |
| 25 | 0.0137 | 0.0041 | 0.0216 | 0.0711 | 0.0041 | |
| AVN-AVM | 50 | 0.0547 | 0.0166 | 0.0862 | 0.2842 | 0.0166 |
| 75 | 0.1231 | 0.0373 | 0.1939 | 0.6393 | 0.0373 | |
| 100 | 0.2188 | 0.0663 | 0.3445 | 1.1361 | 0.0663 |
| PAV | Original PUC | Reduced AV Speed Limit (km/h) | Reduced PUC |
|---|---|---|---|
| 25 | 7.89 × 10−3 | 36 | 6.62 × 10−3 |
| 50 | 9.53 × 10−3 | 36 | 5.93 × 10−3 |
| 75 | 1.17 × 10−2 | 37 | 6.44 × 10−3 |
| 100 | 1.43 × 10−2 | 37 | 5.73 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarran, S.; Hassan, Y. Intersection Sight Distance in Mixed Automated and Conventional Vehicle Environments with Yield Control on Minor Roads. Smart Cities 2025, 8, 73. https://doi.org/10.3390/smartcities8030073
Sarran S, Hassan Y. Intersection Sight Distance in Mixed Automated and Conventional Vehicle Environments with Yield Control on Minor Roads. Smart Cities. 2025; 8(3):73. https://doi.org/10.3390/smartcities8030073
Chicago/Turabian StyleSarran, Sean, and Yasser Hassan. 2025. "Intersection Sight Distance in Mixed Automated and Conventional Vehicle Environments with Yield Control on Minor Roads" Smart Cities 8, no. 3: 73. https://doi.org/10.3390/smartcities8030073
APA StyleSarran, S., & Hassan, Y. (2025). Intersection Sight Distance in Mixed Automated and Conventional Vehicle Environments with Yield Control on Minor Roads. Smart Cities, 8(3), 73. https://doi.org/10.3390/smartcities8030073







