Study on Parameterization of Vortex-Induced Vibration Energy Harvester in Agricultural Environment
Abstract
1. Introduction
2. Mathematical Model
2.1. Mathematical Model of VIV of Cylinder
2.2. Efficiency
3. Experimental Equipment
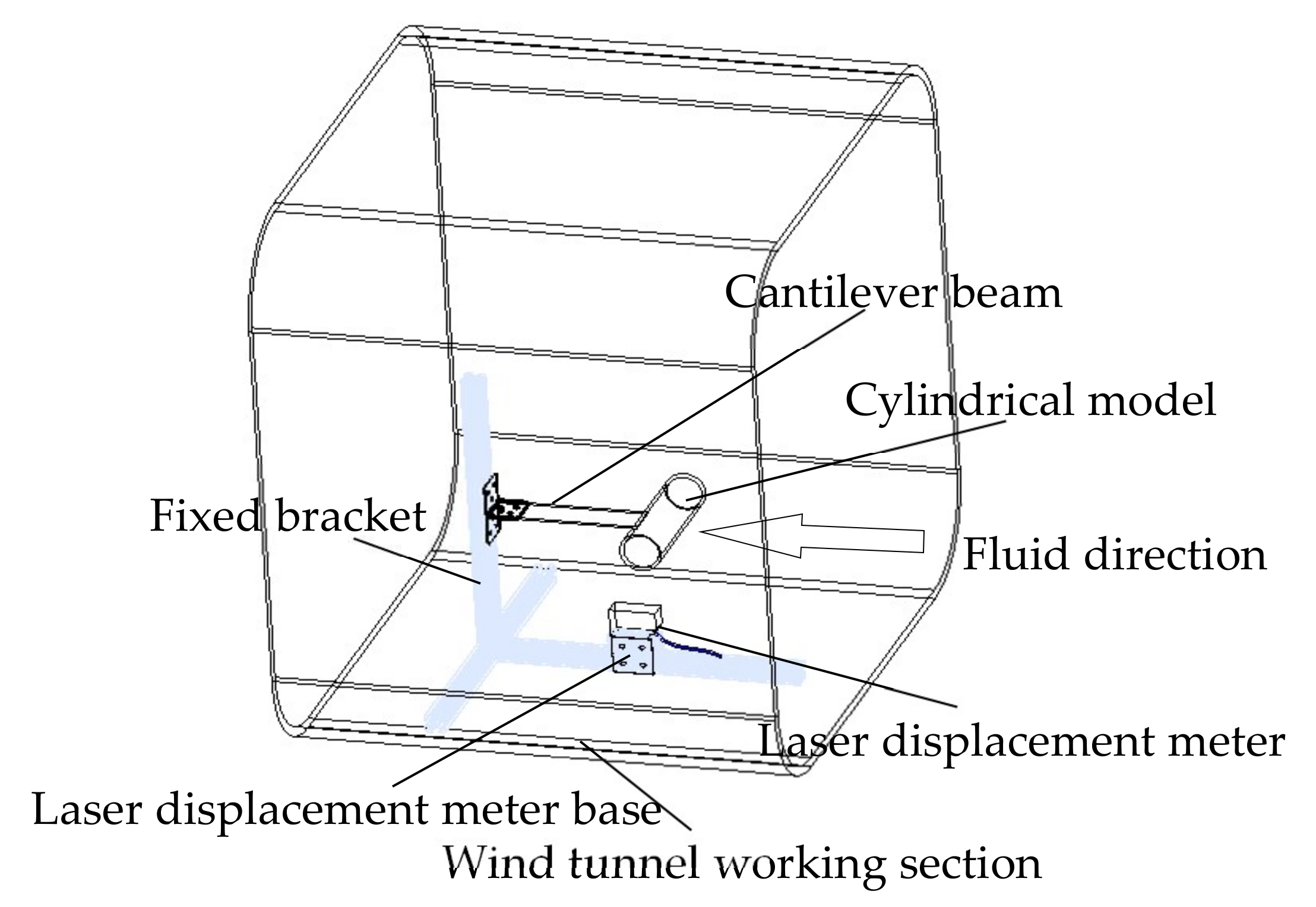
3.1. Annular Wind Tunnel
3.2. Experimental Model and Experimental System
3.3. Experimental Content
4. Experimental Results and Discussion
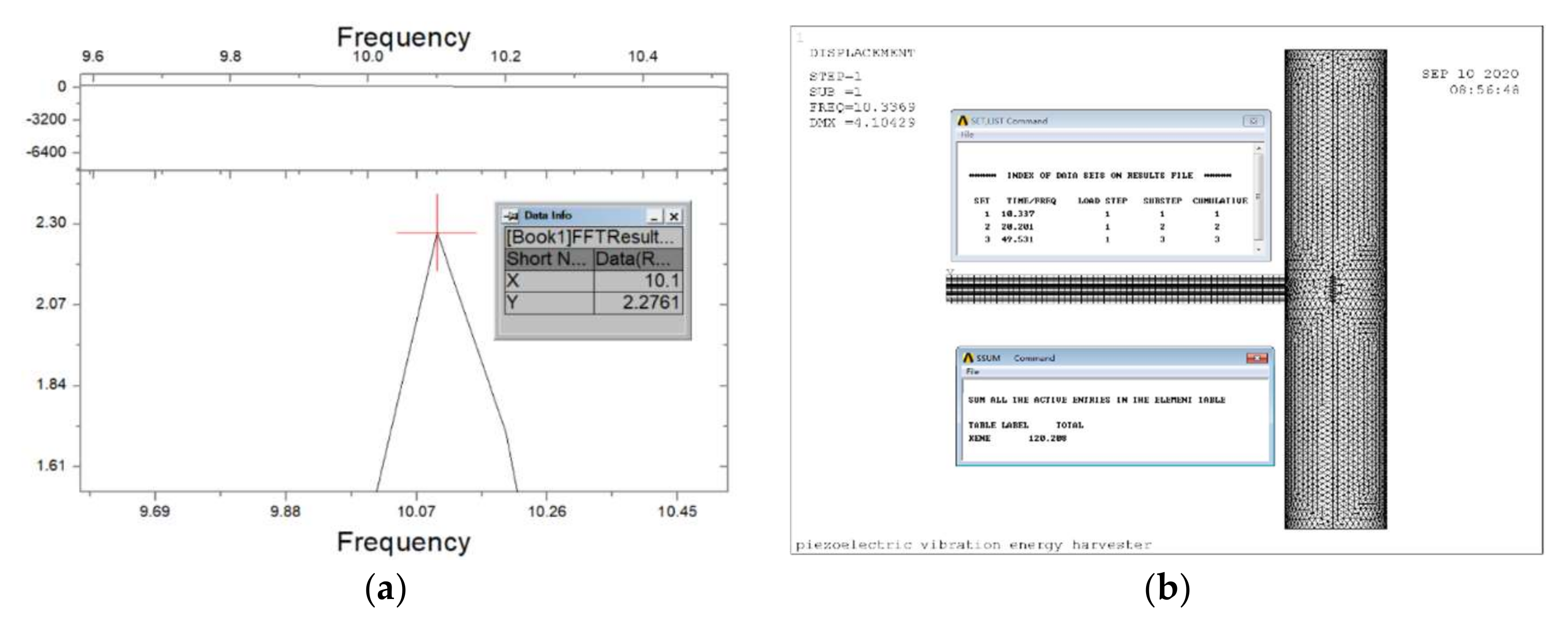
4.1. Experimental Model Parameter Calculation and Reliability Analysis
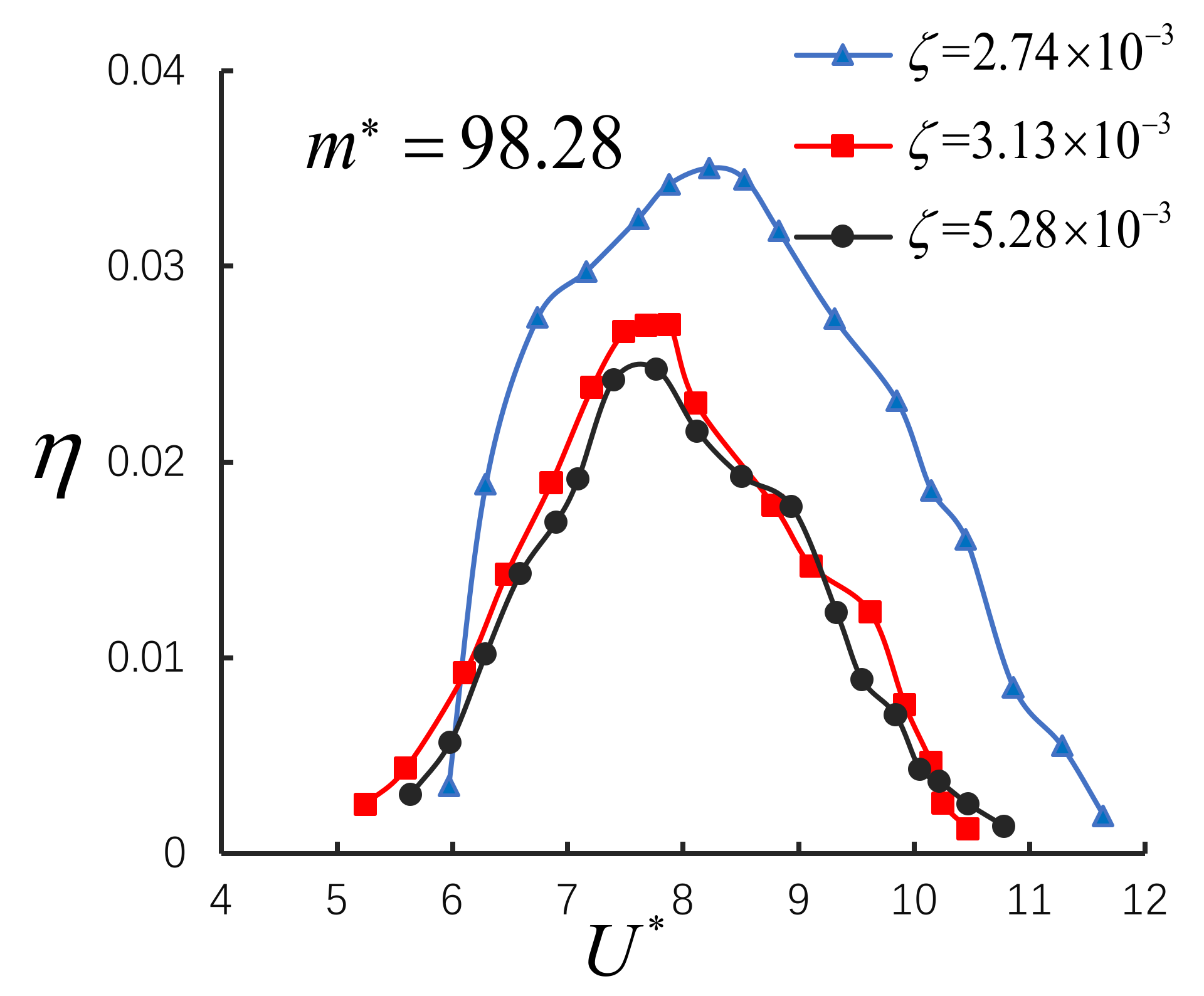
4.2. The Effect of on VIV Conversion Efficiency
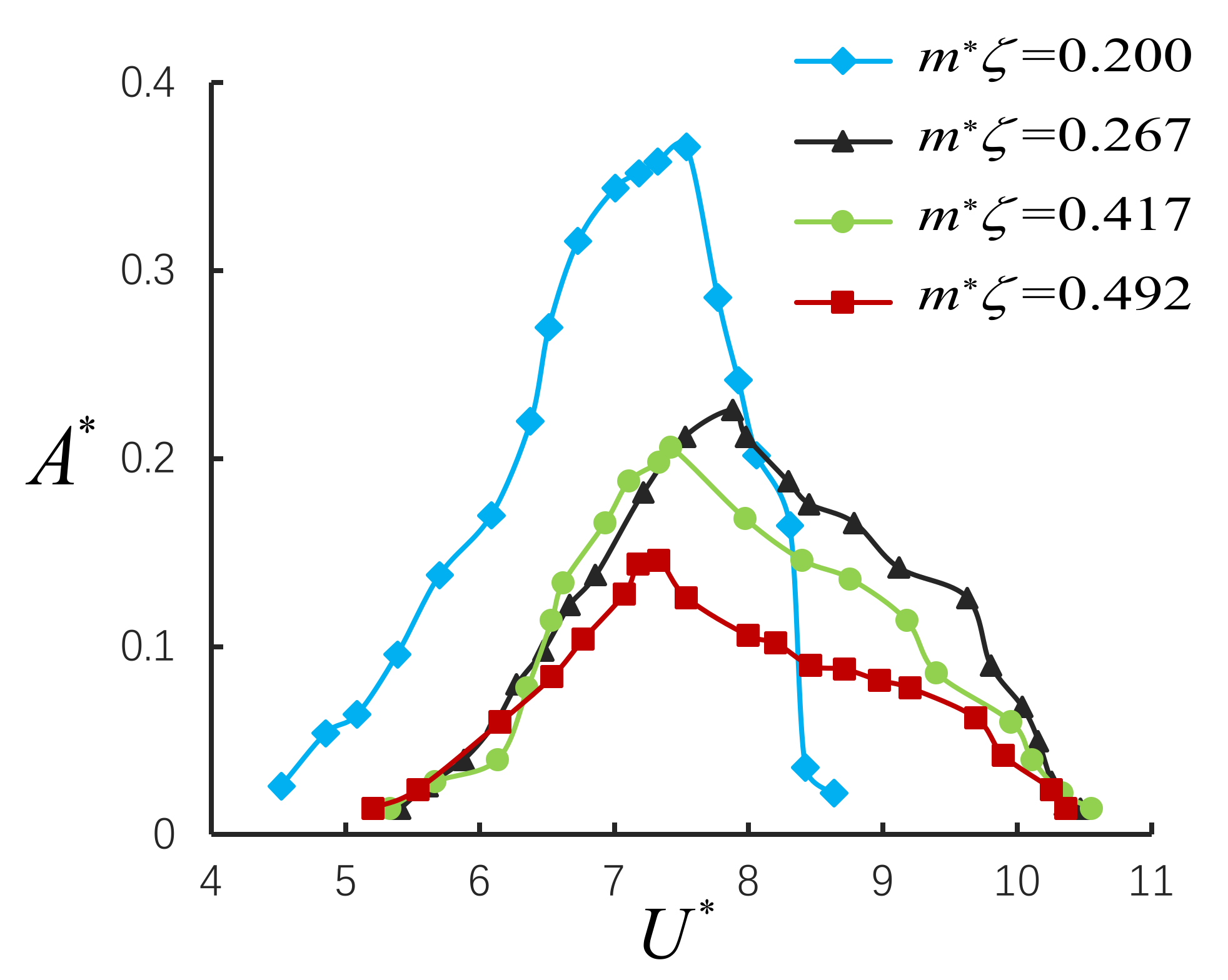
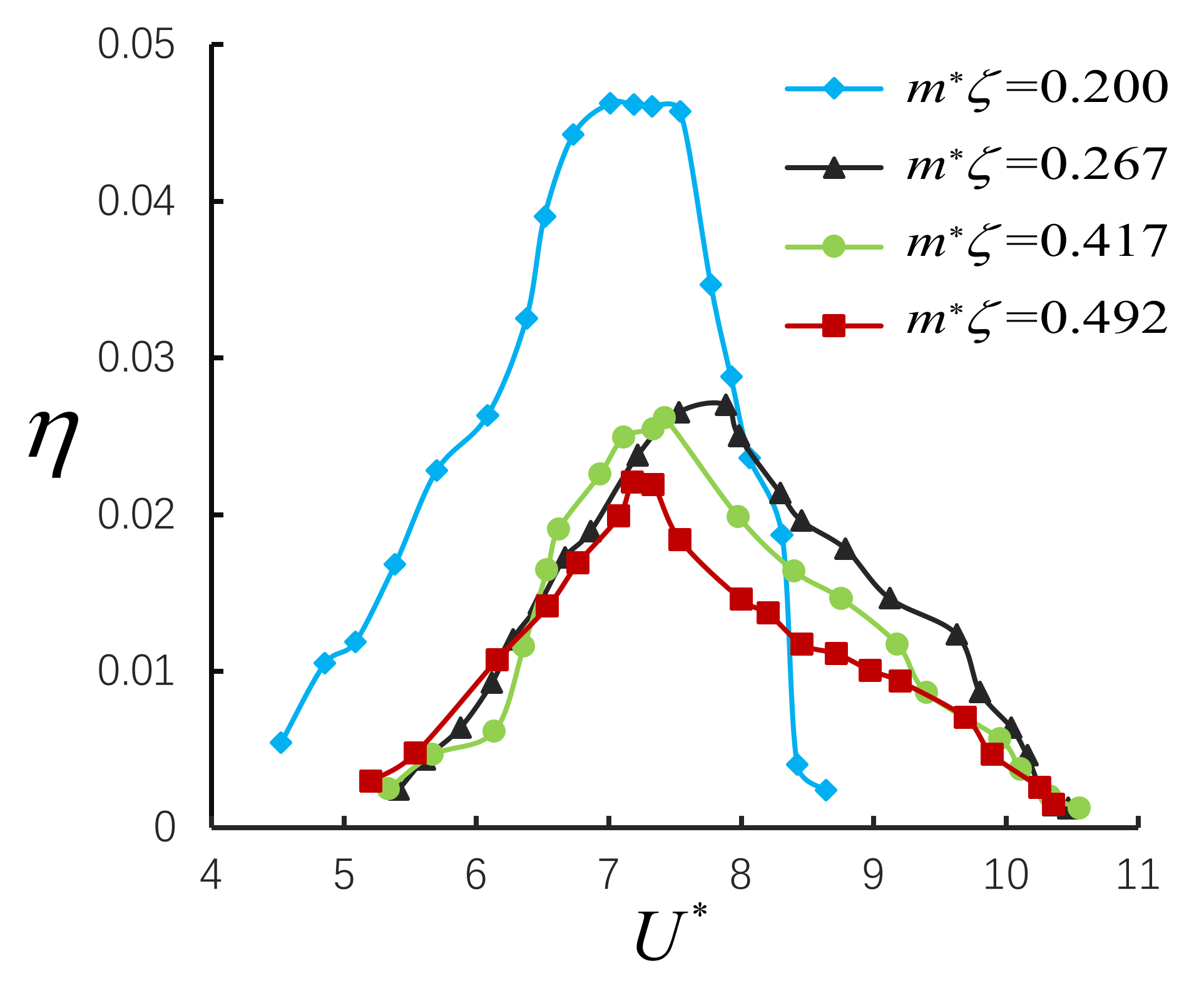
4.3. The Effect of on VIV Conversion Efficiency
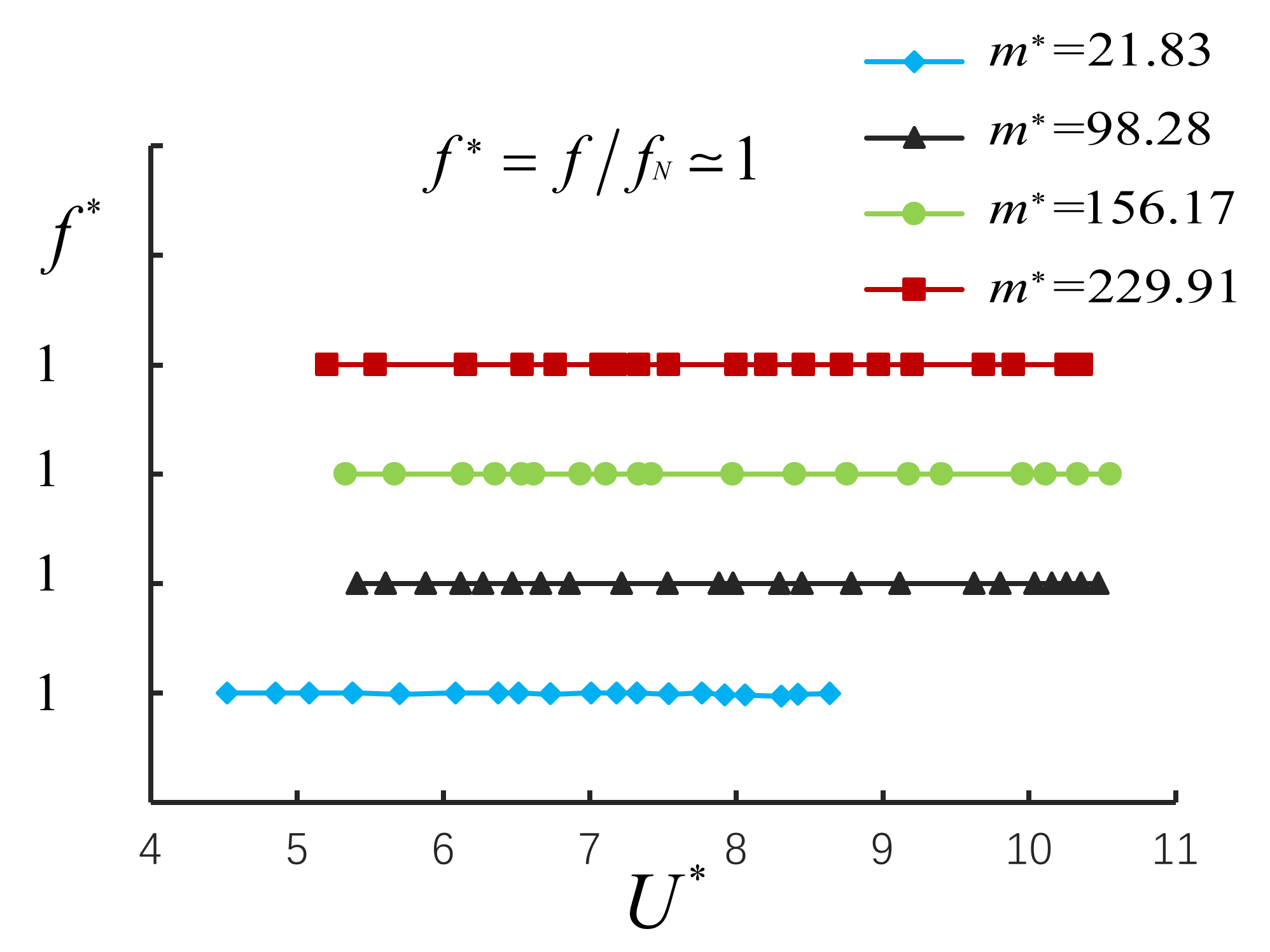
4.4. Normalized Frequency Changes with
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chatterjea, S.; Havinga, P. Improving Temporal Coverage of an Energy-Efficient Data Extraction Algorithm for Environmental Monitoring Using Wireless Sensor Networks. Sensors 2009, 9, 4941–4954. [Google Scholar] [CrossRef] [PubMed]
- Farooq, M.S.; Riaz, S.; Abid, A.; Umer, T.; Zikria, Y.B. Role of IoT Technology in Agriculture: A Systematic Literature Review. Electronics 2020, 9, 319. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Hajj, M.R.; Nayfeh, A.H. Phenomena and modeling of piezoelectric energy harvesting from freely oscillating cylinders. Nonlinear Dyn. 2012, 70, 1377–1388. [Google Scholar] [CrossRef]
- Bearman, P.W. Circular cylinder wakes and vortex-induced vibrations. J. Fluids Struct. 2011, 27, 648–658. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L.; An, H. Numerical investigation of vortex-induced vibration of a circular cylinder in transverse direction in oscillatory flow. Ocean Eng. 2012, 41, 39–52. [Google Scholar] [CrossRef]
- Mehmood, A.; Abdelkefi, A.; Hajj, M.R.; Nayfeh, A.H.; Akhtar, I.; Nuhait, A.O. Piezoelectric energy harvesting from vortex-induced vibrations of circular cylinder. J. Sound Vib. 2013, 332, 4656–4667. [Google Scholar] [CrossRef]
- Ran, J.Y.; Wang, J.L.; Wang, R.R. A Model for Energy Harvesting from Vortex-Induced Vibration of Circular Cylinder. Adv. Mater. Res. 2014, 3248, 877–881. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Ye, Z.; Jiang, Y. Mechanism of frequency lock-in in vortex-induced vibrations at low Reynolds numbers. J. Fluid Mech. 2015, 783, 72–102. [Google Scholar] [CrossRef]
- Soti, A.K.; Zhao, J.; Thompson, M.C.; Sheridan, J.; Bhardwaj, R. Damping effects on vortex-induced vibration of a circular cylinder and implications for power extraction. J. Fluids Struct. 2018, 81, 289–308. [Google Scholar] [CrossRef]
- Chang, T.J.; Lua, K.B. Simulation on Vortex Induced Vibration of Circular Cylinder. J. Phys. Conf. Ser. 2020, 1509, 12–24. [Google Scholar] [CrossRef]
- Rodríguez-Robles, J.; Martin, Á.; Martin, S.; Ruipérez-Valiente, J.A.; Castro, M. Autonomous Sensor Network for Rural Agriculture Environments, Low Cost, and Energy Self-Charge. Sustainability 2020, 12, 5913. [Google Scholar] [CrossRef]
- Haseeb, K.; Ud Din, I.; Almogren, A.; Islam, N. An Energy Efficient and Secure IoT-Based WSN Framework: An Application to Smart Agriculture. Sensors 2020, 20, 2081. [Google Scholar] [CrossRef] [PubMed]
- Zhimin, C.; Xun, R.; Guangzhong, C. Design of a self-powered power based on piezoelectric energy harvesting technology. Electron. Des. Eng. 2016, 10, 1674–6236. [Google Scholar]
- Xinghao, L.; Kaiyi, Z.; Lihua, Y.; Xiantao, Q. Design of Intelligent Water Quality Wireless Online Monitoring System Based on Zigbee. Think Tank Times 2019, 189, 234–235. [Google Scholar]
- Bearman, P.W. Vortex shedding from oscillating bluff bodies. Ann. Rev. Fluid Mech. 1984, 16, 195–222. [Google Scholar] [CrossRef]
- Sarpkaya, T. A critical review of the intrinsic nature of vortex-induced vibrations. Fluids Struct. 2004, 19, 389–447. [Google Scholar] [CrossRef]
- Williamson, C.H.K.; Govardhan, R. Vortex-induced vibrations. Ann. Rev. Fluid Mech. 2004, 36, 413–455. [Google Scholar] [CrossRef]
- Khalak, A.; Williamson, C.H.K. Fluid forces and dynamics of hydroelastic structure with very low mass and damping. J. Fluids Struct. 1997, 11, 973–982. [Google Scholar] [CrossRef]
- Khalak, A.; Williamson, C.H.K. Motons, forces and mode transitions in vortex induced vibrations at low mass-damping. J. Fluids Struct. 1999, 13, 813–851. [Google Scholar] [CrossRef]
- Allen, J.J.; Smits, A.J. Energy Harvesting eel. J. Fluids Struct. 2001, 15, 629–640. [Google Scholar] [CrossRef]
- Bernitsas, M.; Raghawan, K.; Ben-Simon, Y.; Garcia, E.M.H. VIVACE (vortex induced vibration for aquatic clean energy): A new concept in generation of clean and renewable energy from fluid flow. J. offshore Mech. Arct. Eng. 2008, 130, 41–59. [Google Scholar] [CrossRef]
- Barrero-Gil, A.; Alonso, G.; Sanz-Andres, A. Energy harvesting from transverse galloping. Sound Vib. 2010, 329, 2873–2883. [Google Scholar] [CrossRef]
- Zhu, G.; Haase, M.; Wu, C.H. Modelling the capacity of a novel flow-energy harvester. Appl. Math. Model. 2009, 33, 2207–2217. [Google Scholar] [CrossRef]
- Barrero-Gil, A.; Pindado, S.; Avila, S. Extracting energy from Vortex-Induced Vibrations: A parametric study. Appl. Math. Model. 2012, 36, 3153–3160. [Google Scholar] [CrossRef]
- Perelli, A.; Faggioni, O.; Soldani, M.; Zunino, R. Design and performance analysis of a piezoelectric generator by Von Karman vortexes for underwater energy harvesting. J. Energy Chall. Mech. 2014, 1, 127–132. [Google Scholar]
- Gao, X.; Shih, W.H.; Wan, Y.S. Flow Energy Harvesting Using Piezoelectric Cantilevers With Cylindrical Extension. IEEE Trans. Ind. Electron. 2013, 60, 1116–1118. [Google Scholar] [CrossRef]
- Jieli, F.; Wei-Ping, H. Numerical simulation of 2-DOF vortex-induced video of a long riser. J. Vib. Shock. 2012, 31, 65–68. [Google Scholar]
- Zhumei, L.; Lixiang, Z. Study on the parameters affecting the energy obtained from vortex-induced vibration. J. Vib. Shock. 2014, 33, 12–15. [Google Scholar]




| Cylinder | D (mm) | L (mm) | L/D | m (g) |
|---|---|---|---|---|
| 1 | 50 | 252 | 5.04 | 10.8 |
| 2 | 50 | 252 | 5.04 | 59.5 |
| 3 | 50 | 252 | 5.04 | 94.6 |
| 4 | 50 | 252 | 5.04 | 139.3 |
| Number | Cylinder | ||||
|---|---|---|---|---|---|
| 1 | 2 | 98.28 | 0.00274 | 6.7 | 5.9~11.6 |
| 2 | 2 | 98.28 | 0.00313 | 10.1 | 5.2~10.4 |
| 3 | 2 | 98.28 | 0.00528 | 11.7 | 5.6~10.7 |
| Number | Cylinder | ||||
|---|---|---|---|---|---|
| 1 | 1 | 21.83 | 0.00915 | 0.200 | 4.5~8.6 |
| 2 | 2 | 98.28 | 0.00313 | 0.307 | 5.2~10.4 |
| 3 | 3 | 156.17 | 0.00267 | 0.417 | 5.3~10.5 |
| 4 | 4 | 229.91 | 0.00214 | 0.492 | 5.2~10.3 |
| Number | Error | ||
|---|---|---|---|
| I 1 | 6.7 | 7.0 | 4.28% |
| I 2 | 10.1 | 10.3 | 1.94% |
| I 3 | 11.7 | 12.4 | 5.64% |
| II 1 | 26.1 | 26.6 | 1.88% |
| II 2 | 10.1 | 10.3 | 1.94% |
| II 3 | 9 | 9.3 | 3.22% |
| II 4 | 7.8 | 8.1 | 3.70% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Z.; Xiong, A.; Liu, R. Study on Parameterization of Vortex-Induced Vibration Energy Harvester in Agricultural Environment. AgriEngineering 2020, 2, 511-522. https://doi.org/10.3390/agriengineering2040034
Liao Z, Xiong A, Liu R. Study on Parameterization of Vortex-Induced Vibration Energy Harvester in Agricultural Environment. AgriEngineering. 2020; 2(4):511-522. https://doi.org/10.3390/agriengineering2040034
Chicago/Turabian StyleLiao, Zhangyi, Anping Xiong, and Renxin Liu. 2020. "Study on Parameterization of Vortex-Induced Vibration Energy Harvester in Agricultural Environment" AgriEngineering 2, no. 4: 511-522. https://doi.org/10.3390/agriengineering2040034
APA StyleLiao, Z., Xiong, A., & Liu, R. (2020). Study on Parameterization of Vortex-Induced Vibration Energy Harvester in Agricultural Environment. AgriEngineering, 2(4), 511-522. https://doi.org/10.3390/agriengineering2040034




