Next Article in Journal
Tomato Leaf Diseases Classification Based on Leaf Images: A Comparison between Classical Machine Learning and Deep Learning Methods
Previous Article in Journal
Cotton Gin Stand Machine-Vision Inspection and Removal System for Plastic Contamination: Software Design
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
AgriEngineering
Volume 3
Issue 3
10.3390/agriengineering3030034
agriengineering-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Mathematical Programming Models for Fresh Fruit Supply Chain Optimization: A Review of the Literature and Emerging Trends

by
Tri-Dung Nguyen
1,2,
Tri Nguyen-Quang
2,*,
Uday Venkatadri
1,
Claver Diallo
1 and
Michelle Adams
3
1
Department of Industrial Engineering, Dalhousie University, P.O. Box 15000, Halifax, NS B3H 4R2, Canada
2
Biofluids and Biosystems Modeling Lab. (BBML), Department of Engineering, Faculty of Agriculture, Dalhousie University, 39 Cox Road, Truro, NS B2N 5E3, Canada
3
School for Resource and Environmental Studies, Dalhousie University, 6100 University Ave, P.O. Box 15000, Halifax, NS B3H 4R2, Canada
*
Author to whom correspondence should be addressed.
AgriEngineering 2021, 3(3), 519-541; https://doi.org/10.3390/agriengineering3030034
Submission received: 6 May 2021 / Revised: 25 June 2021 / Accepted: 6 July 2021 / Published: 8 July 2021
Browse Figures
Review Reports Versions Notes

Abstract

:
The fresh fruit agricultural and distribution sector is faced with risks and uncertainties from climate change, water scarcity, land-use increase for industrial and urban development, consumer behavior, and price volatility. The planning framework for production and distribution is highly complex as a result. Mathematical models have been developed over the decades to deal with this complexity. With improvements in both processor speed and memory, these models are becoming increasingly sophisticated. This review focuses on the recent progress in mathematically based decision making to account for uncertainties in the fresh fruit supply chain. The models in the literature are mostly based on linear and mixed integer programming and involve variants such as stochastic programming and robust optimization. The functional areas of application include planting, harvest optimization, logistics and distribution. The perishability of the fresh fruit supply chain is an important issue as is the cycle time of cultivation and harvest.

1. Introduction

The consumption of fruits and vegetables is highly recommended for everyone on a daily basis, whether in developed, underdeveloped or developing countries, because of their content of essential vitamins, dietary fibers and minerals. Like other perishable products (fish, bread, packaged salads, and fresh meals), they indispensably require corresponding supply chains that can help deliver them from the original producers to the end consumer as fast as possible and in the best condition [1].
In recent years, along with the development of the supply chain management and logistics industry, the agriproduct supply chain in general, and the fruit chain in particular, have been recognized as a very important and strategic part of the economic development of many countries [2].
Compared to other stable and nonperishable crops, fruit production can bring greater economic benefits. However, like other sectors in agriculture, perishable fruit and vegetable production faces uncertainties and risks from society and the living environment, such as climate change, water scarcity, increase in land-use for industrial and urban development, consumer behavior and price volatility. It is very complex to build a management plan for the production, distribution and pricing of fresh fruits due to their short lifetime, seasonality in production, and the volatility of price and demand.
The fruit and vegetable industry has been globalized since the 1970s [3]. Nearly 700 million tons of fruits are produced worldwide each year, the most grown being bananas and apples, followed by grapes and oranges. Asia has always been considered the largest fruit bowl of the world due to large swaths of land in the tropics and subtropics and a high population, which the sector can count on for a readily available agricultural workforce [4]. The work force converted from cultivating various cereal crops (such as rice) so that fruit and vegetable production is also increasing [5,6].
According to a report from the Food and Agriculture Organization (FAO) [7], in 2018 China took first place in the list of leading countries worldwide for fruit production, with an output of around 243.592 million tons/year, followed by India and Brazil, second and third place respectively. The yield of fruit from India is approximately 98.722 million tons/year, while for Brazil, about 40.047 million tons of fruit are produced yearly. Other large producers are listed in Table 1 below in order of their yearly quantity of production: The US, Turkey, Mexico, Indonesia, Spain, Iran and Italy [7].
A considerable number of mathematical models and algorithms have been proposed in the literature with the aim of improving the agri-food supply and fresh fruit supply chains; as well as several literature reviews related to the modeling approaches of agricultural supply chains have been done previously, and most of them just focus on the agri-food supply chain [8,9,10,11]. There are very few papers, such as those by Soto-Soto-Silva et al. [12] and Agarwal [13], which purely review the fresh fruit chain. For agriculture production models since the 1980s and earlier, a comprehensive literature review was done by Glen [8], while a revision for the crop production planning model was performed by Lowe and Preckel [9].
The review of Lowe and Preckel [9] focused on the agricultural facility allocation analysis to locate warehouses and processing plants. In addition, the complexity, challenges and uncertainties in strategic planning for production—distribution in the agricultural industry were considered in their proposed models.
Ahumada and Villalobos [11] referenced all the above-mentioned reviews but framed their review in the context of agriculture product supply chain planning. They basically took the same research approach that Lowe and Preckel [9] had adopted by considering only the production and distribution of crops. The authors covered crop production models developed for a few parties of the supply chain (including farmers and processing companies), but not for the macroeconomic models that could cover entire regions or countries.
Soto-Silva et al. [12], based on the work of Ahumada and Villalobos [11], has specifically reviewed operation research models related to the fresh fruit supply chain. The review emphasized on the rapid growth of science and technology in supply chain management to meet the challenges of increasing demand, high quality standards, and fierce competition in all aspects of production, processing and distribution for fruits and vegetables. The review shared the same opinion as Ahumada and Villalobos [11] that although numerous papers on the agri-food supply chain have been published, most of them have just focused on a part of the supply chain. Factors such as decision-making levels, problems of production, storage, processing, transportation, routing, planning and allocation have attracted more attention from researchers. Both reviews ([8,11]) showed that approaches such as linear programming and mixed integer programming are the most applicable methods in fresh fruit supply chains. Other models such as nonlinear programming, dynamic programming, stochastic programming or heuristic programming, although used less frequently, can also be relevant.
Our review focuses on the fresh fruit supply chain and looks at methodologies such as linear or stochastic programming models and their variants. We first look at various ideas leading to model formulations depending on market, environmental factors and agricultural fruit characteristics. This article is elaborated around the following points:
  • Constraints and challenges in the fresh fruit supply chain
  • The need of mathematical modeling in the fresh fruit supply chain
  • Common concepts and dominant approaches
  • Strengths and weaknesses of existing models
  • Future perspectives

2. Constraints and Challenges in the Fresh Fruit Supply Chain

2.1. Constraints and Challenges

The fresh fruit supply chain has a relatively long supply lead time, uncertain supply and demand, and a thin profit margin due to competition. These are the challenges that supply chain managers need to confront by improving the efficiency and using modern decision-making tools [12]. In developed countries, where science and technology are better leveraged and crop productivity is high, production is not able to meet demand for several reasons; some of these are a shorter growing season in the North, demand for fruits and vegetables outside their seasons, and skilled labor shortages.
To meet the year-round demand for seasonal vegetables and fruits, most rich countries resort to a high level of imports—in countries such as the US and Canada, up to 50% of fresh fruit is imported [14]. As fresh vegetables and fruits have better nutritional content and taste than preserved fruits/vegetables from past seasons, there is always sufficient demand for importing these internationally. In many developing countries, agriculture mostly follows traditional practices and uses manual labor. This brings unique challenges compared to developed countries which include difficulties in coordination between farmers, cooperatives, traders, wholesalers, distributors and retailers. Other challenges are:
  • The traditional practice of trade is still dominant. With many intermediary stages as well as complex local rules, the food supply chain is longer and logistically more complex than in developed countries.
  • Storage after harvesting and transportation is quite expensive due to a climate with high temperature and humidity.
  • Although the growth of the formal agro-industrial sector has been rapid, the practice of using low paid labor is widespread. Though labor is cheap (and often unskilled), there is a high turnaround. Companies/farms must deal with workforce shortages during busy periods at the beginning and the end of the season when planting and harvesting take place, offering opportunities for workers to quickly change employers for better pay.
  • Communication and the exchange of information between value chain partners in harvesting, preliminary processing, packing, labelling, preserving and transportation is often very poor, as is consumer awareness and the usage of agricultural products.
  • Farmers are the most important factor in the food supply chain. However, most of them cannot set a good price for their products, due to these complex elements and their lack of market information and experience. The price for their products is often determined by traders, although cooperatives and fair trade have emerged through the last 50 years.

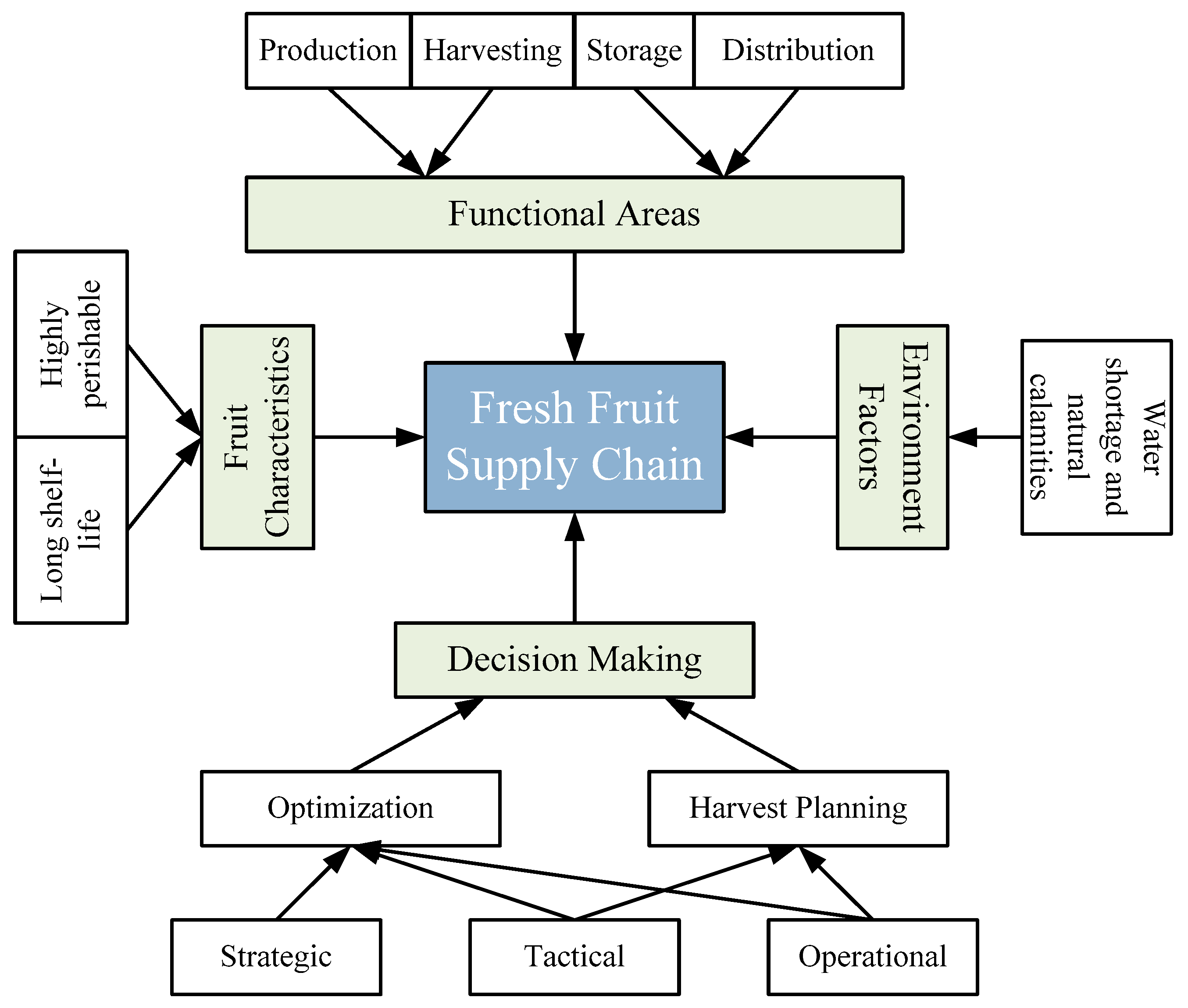
2.2. Influencing Elements

The influencing elements on the fresh fruit supply chains can be classified as follows (Figure 1):
  • Functional areas: this category comprises production, harvest, storage and distribution
  • Purpose of the chain: this category includes the scope of the decisions made: such as harvest planning and optimization.
  • Environmental factors: these include the planting environment with uncertainties and risks (countries with water shortage or natural calamities).
  • Fruit characteristics, such as (1) highly perishable and (2) long shelf life.

2.3. The Role of Mathematical Models

The decision-making strategy for fresh fruit supply chain management is a complex task, more difficult than with other supply chains [15]. This has remained a challenge for fresh fruit supply chain managers (FFSCs) over the past 40 years, especially in the context of increasing globalization and rapidly growing consumption. In the case of perennial plants that take years to grow and reach maximum yield, decisions taken today (changing the plantation portfolio, for example) have an impact on future, based on the market demands (Table 2). Therefore, we need tools to support modern data-driven decision-making strategies for medium-term and long-term production.
With new international policies in the world related to fresh fruit importation/exportation [86] and consumer needs increasing year-by-year, mathematical modelling becomes indispensable. Mathematical models can assist decision makers to logically evaluate and plan for different possible outcomes. For example, when dealing with FFS containing many uncertainties, mathematical modelling is the most effective tool to support decision makers by predicting scenario probabilities and suggesting decisions based on trade-offs [87].
Based on a literature review that covers over 70 articles linked to fresh fruit supply chains published within the last 40 years [2], there are two dominant categories of fruits that authors have focused on in their studies: (1) perennial crops, including apples [3,16,17,70,75,82,85], oranges [38], pears [37,42,62,71], cherries [44], and grapes [33,41]; and (2) annual crops including pineapple [46], strawberries [59], melon [45] tomato [24,52,53,57,58,59,81] and blueberry [83].
Although many models and simulation approaches have been suggested in the last four decades, there is always a need for robust mathematical tools to support fresh fruit supply chain planning, due in part to the many challenges and constraints such as: (1) higher exports, quality and safety, quantity, consistency, traceability, quarantine, packaging and labeling; (2) fluctuating market prices; (3) hard competition with other exporting countries; (4) while exportation has been increasing in both volume and value, the growth in value has been declining [2].

3. Common Concepts and Dominant Approaches

Several modeling approaches for the fresh fruit supply chain were conceived based on various settings, constraints, challenges and influencing elements (shown in Figure 2). Categorically, we can classify the models into four following groups: (1) models focusing on the functional areas (plantation, harvest, storage or distribution); (2) models based on the setting (decision-making scenarios for planning or optimization); (3) modelling environmental effects; and (4) modelling based on fruit characteristics.
From the modeling point of view, the classification of models falls into three main groups: (1) deterministic models and their variants; (2) stochastic models; and (3) special categories, which are neither deterministic nor stochastic (such as robust programming, which is a deterministic approach to model stochastic problems). Figure 2 shows our classification from the modeling viewpoint.
This paper aims to identify, review, and classify research works dealing with the fresh fruit supply chain. We queried relevant research databases such as Web of science, Google Scholar, Proquest with the following combination of keywords: mathematical model, fresh fruit, supply chain, agricultural supply chain and literature review. A total of 70 articles from 1976 to 2021 were collected and reviewed in this study. A brief description and the objectives to be achieved for each paper are presented in Table 2 along with a summary of the mathematical models and methods implemented by the authors. We also comment on the simplicity and outcomes of each model. From this summary, it is noticeable that linear programming (LP) and mixed integer programming (MIP) have been widely used. In addition, it is clear that the trend of using deterministic models is still popular. Although the supply chain of fresh fruit is influenced by many factors of uncertainty and risk, only a few authors have studied and applied stochastic models.

3.1. Deterministic Optimization Approach and Its Variants

It can be said that the deterministic optimization approach is very commonly used in FFSC research. There are three customary subcategories of models in this approach that researchers used: linear programming (LP), dynamic programming (DP) and mixed integer programming (MIP).
Caixeta-Filho [38] developed a case study using an LP approach for orange harvesting scheduling management in Brazil. The quality of orange fruit production is a competitive advantage of Brazil’s citrus sector. Due to the fact that the harvesting time affects fruit quality, the author linked different chemical, biological, and logistical factors to the quality of harvested oranges. An actual dataset from 320 Brazilian farms producing over seven million boxes of oranges annually was collected to verify and validate the model. The contribution of the model is the application of fruit maturation information to orange harvest scheduling.
Hamer [22] used an LP for decision-making support for planting Brussel sprouts. Information on varieties, yield, customer demand and a scheduling method were all taken into account in the system. Varieties of fruits with bad characteristics such as shape, color or weak plants were eliminated in the model. The suggested linear programming model has supported producers in selecting varieties and then in providing a planting plan to meet market demand and maximize profits. Moreover, the model can be used to evaluate cropping in a tactical plan.
Dynamic programming models may also be found in the literature for FFSC planning. Based on the characterization of agricultural products by appearance and quality, Gigler et al. [30] suggested a model to deal with the optimization of agricultural chains to involve these two aspects. According to these authors, handling actions can influence the appearance while the quality can be affected by processing, warehouse and transportation activities [30]. They optimize the “routes between components of the chain used to process products to minimize costs”. Additionally, computer software has been developed based on the dynamic programming methodology, in combination with the product quality development described as a function of the processing conditions.
Starbird [17] used dynamic programming for apple packing-plant operations. In this model, the author proposed that postharvest activities, especially storage delays, impact the quality of perishable agricultural products, which were quite similar to the model from Gigler et al. [30]. By determining the optimal order in which storage plant would be loaded, these delays were reduced. Besides, the optimal sequences depend much more on the deterioration rate of apple varieties than the storage facilities to which apples are transported to. However, this deterioration rate between two characteristics: hard and soft apples, was not reasonably determined. The optimal order did not additionally consider the difference between the capacity of warehouses and the number of apples which could be stored.
To reduce the losses of harvested fresh products, Widodo et al. [40] built a supply chain model by incorporating two important processes: plant growing and loss process into their mathematical formulation. They tried to apply the model for flowering–harvesting to maximizing the satisfied demands in every period of time and to minimizing the loss in the transportation and storage which could reach 60% of the total amount of harvested products. Their model also assumed that any on-hand inventory was not carried through more than one period, and any requirement for harvesting fresh products should be satisfied through the earliest plant maturity as possible. The model suggested by Widodo et al. [40] could lead to an optimal harvesting prototype to maximize the satisfaction of demand levels. Some numerical examples were also presented by the authors to demonstrate the feasibility of the optimization algorithm.
The family of mixed-integer linear programming models seems the most commonly used and favored optimization techniques for the fresh fruit supply chain. For example, we can cite the model by Maia et al. [23] which addressed route scheduling for fruit and vegetable crops from the fields to markets. Based on various scenarios for alternative routes and a well-set condition of crops and markets, this model was used to optimize the capital invested in food preservation facilities.
The model by Ferrer et al. [41] optimized the scheduling of wine grape harvesting operations by considering both the quality of grapes and operational costs using the mixed integer programming approach. This model includes the harvest planning, labor scheduling, and routing decisions by integrating quality loss in the objective function of the model. Their results showed the decisions which could be made at two levels, operational and tactical, to support the planning of the grape harvest at large vineyard.
Tactical level planning was also addressed by the MIP approach of Masini et al. [42], who developed the supply chain tactical optimization model in the fruit industry for a large fruit processing company in Argentina. The considerations in the model include demand from major markets, an estimate of fruit produced, capacity and availability of processing plants, a monthly storage plan for cold fruit, and final product delivery schedules. The model contains 18,000 continuous and discrete variables but does not incorporate uncertainties in demands and yield.
Ahumada and Villalobos [52] presented an operational model MIP type for planning to deal with harvesting and distribution in the fresh agricultural products industry. This model, which can generate the short-term planning decisions for perishable agricultural products, was developed to maximize farmer revenues from production and distribution during harvesting. The model, through different approximations and simplified functions, can also deal with the availability of workforce, price fluctuation, influence of weather conditions, and biological properties and varieties of plants.
Continuing to develop their MIP approach, Ahumada and Villalobos [53] integrated the tactical planning approach into another framework which can assist the decision making for harvesting, packing and distribution to maximizing profit for growers of perishable products in Mexico. Decision making was based not only on traditional conditions (such as availability of workforce and price prediction), but also on factors such as spoilage of fresh products, and transportation and inventory costs. Authors also tried to tackle the complex planning issues of the supply chain management of perishable products. A loss function integrated into the objective formulation and storage constraints was used to consider the perishability. With this model, growers could determine their planting plans, requirements of workforce and transportation throughout a crop season. In addition, the potential customers could be selected by the model via features such as the price they paid, the type of shipping they requested, conditions and quality of service they expected.
Jena and Poggi [64] applied an MIP model for sugar cane harvesting and processing for alcohol production. Their model was applied into two planning levels, tactical and operational, to maximize the total amount of sugar in the cane harvest. The tactical plan was designed for covering the entire seven-month harvesting season while the operational schedule was considered for the period from seven to thirty days.
Catalá et al. [62] presented an MIP model type for strategic planning optimization of pear and apple production. Their suggested model was used to assist a farm in optimizing its investment policy and in maximizing its net current value. The model has considered different financing scenarios to make dynamic decisions in a given period of time. Distinct constraints of their model place restrictions for risks, and integer decisions are linked to minimum planting area and the requirements for funding. Their results showed the optimal investment policy for the replacement of varieties under different scenarios, with and without external financing. In addition, a sensitivity analysis was applied for some of the mutually influencing parameters. The advantages of the model were that the modelling tool could be easily adapted to fresh fruits such as stone grape, citrus, etc., and in the explicit integration of financial considerations.
Three years later, Catalá et al. [72] extended their previous model [62]. A dual-objective model was proposed for tactical planning to maximize profit but minimize product supply shortage. A lexicographic method was developed to deal with the dual objectives. First, the inventory capacity, processing and shipping were optimized for profit, and second, the model minimized the shortage of supply.
To end this review of deterministic optimization models, Rocco and Morabito [73] developed a conceptual framework and mathematical model for production and logistics planning in the Brazilian tomato processing industry. The decision variables relate to allocating tomato areas, choosing tomato varieties, planning time for planting and harvest, routing transportation from fields to processing plants, scheduling to produce work-in-progress products (concentrated tomato pulps), final products to orders, managing inventories and shipping of these products to local warehouses.
Soto-Silva et al. [75] have developed an integrated model to optimize logistic activities for large apples in Chile. This integrated model was conceived to assist fresh produce purchase with the objective of minimizing the costs of purchasing and transportation between orchards and final destination location. This also included the varieties of apple of each producer, capacity of warehouses and the method of storage. According to these authors, their model could be applied to different fresh product processing companies using their own planting fruits in their processing [68]. However, the model did not consider uncertain factors such as weather conditions and truck fleets among producers, processing plants and warehouses.
Summary of section: Most papers dealing with FFSC in a deterministic context implement LP or MIP formulations to make tactical and/or operational decisions. Additionally, the agricultural activities such as planting, harvesting and storing are covered more than the others. Besides, almost all authors only consider one kind of fruit as a case study to evaluate their model. Diverse decision-making levels and stages of the FFSC need to be considered more. Monoculture is known to be detrimental to soil health. Thus, future models should deal with polyculture farming and its SC implications.

3.2. Stochastic Programming Approach

Traditional deterministic models using linear programming or MIP are generally unable to deal with problems that involve uncertainties or give solutions with a high level of risk. This is particularly true in agricultural with several uncertain factors starting with weather conditions. Stochastic programming and robust programming (both extensions of linear programming) can address uncertainties in the parameters of linear or MIP optimization models for production and logistics planning in agri-food industries. Typical papers of stochastic or robust programming in the industry include Bohle et al. [48] and Munhoz and Morabito [67].
Robust optimization is also a major direction in the fresh fruit supply chain. In recent years, robust optimization has been used as a methodology that allowed uncertain factors to be confronted, especially if the probabilistic knowledge on the issues was incomplete.
A robust approach to optimize the harvesting scheduling for wine grape with uncertain factors for which probabilistic knowledge may not be complete was developed by Bohle et al. [48]. The authors have considered scheduling problems for the wine grape harvesting subject to maximizing the actual yield being achieved during the harvest. The actual yield was considered as one of uncertain factors when the schedule of wine grape harvesting was planned. To illustrate the robust optimization approach which could effectively deal with the uncertainties in practice, some alternative robust models were used to solve the actual problems for the wine industry. In addition to the real yield, the labor productivity could be also an uncertain element, reflecting various variable sources.
Unlike traditional formulations, according to the standard robust optimization theory, their proposed robust programming model controlled the variation of parameters simultaneously through different constraints instead of within the same constraint to achieve feasible solutions. An aggregate constraint was added with some goals as follows: (1) to reformulate the robust model; (2) to process simultaneously uncertain factors to the original constraints; (3) to avoid the worst case and (4) to have a higher chance of obtaining feasible solutions. Although the model developed by Bohle et al. [48] was heuristic, its solutions were feasible, and it kept the values of the objective function unchanged. The authors used the Monte Carlo simulation to evaluate the solution feasibility by running various scenarios.
Munhoz and Morabito [67] introduced an optimization approach for citrus production planning in Brazil. An aggregate planning model was developed for the production of frozen concentrated orange juice by using linear programming to make production, blending, and storage decisions based on orange maturation curves. The model has also integrated a robust optimization approach for some uncertain parameters.
A two-stage stochastic programming model for Brussels sprout planting and harvesting with the utility functions was proposed by Darby-Dowman et al. [28] to minimize risks incurred by farmers. In the first stage, a planting plan for all scenarios is created and then a harvesting schedule for each scenario is developed in the second stage. The stochastic optimization model takes into account uncertainties related to the biological nature of crop production, weather and environment conditions, as well as changing demands that could impact prices. Therefore, vegetable producers can develop planting and harvesting plans that are more reliable and more robust than in a deterministic model, even though they may be less profitable on average, based on risk parametrization.
Kazaz [35] used a two-stage stochastic model for production planning in the olive oil industry under uncertainty in yield, prices and demands. Starting with studies on random yield, the author defined sale prices and purchasing costs as exogenous inputs and inversely proportional to yield. The model assumes a yield-dependent price and purchasing cost based on random yield and demand. Kazaz’s model [35] had four main contributions: (1) the objective function was concave if the planting areas were leased, therefore a globally optimal solution was provided by first-order conditions; (2) the model has illustrated how changing yield could affect the total production of olive oil; (3) the optimal farm space leased was proven to be decreasing if a second (and reliable) source of supply appeared; and finally (4) unlike in traditional maximizing yield modeling approaches, the model showed the yield would increase even if the optimal farm space leased was not expanded and even when there was a second supply source.
Distinct from the deterministic approach, the planning model by Ahumada et al. [57] for production and distribution at the tactical level of perishable products relies on the stochastic approach to model uncertainties such as weather and variability of demand. Another feature of the model is the ability to choose different risk preferences for greater robustness.
A stochastic optimization approach for harvest planning in apple orchards was developed by González-Araya et al. [70]. This model considers resource optimization as well as higher fruit quality for export purposes. The mathematical model constraints include satisfying orders generated by the fruit packing plants, plant operations with the right capacity, production at the fruit orchards, and the right harvest time for each variety of apple. A real dataset collected from three orchards in Chile during two harvest seasons were used to explain the model.
Summary of section: This section reviewed the articles using stochastic methods to deal with uncertain factors in the FFSC. The L-shaped method is considered an effective tool to solve the stochastic problem. In addition, most of the authors believed that the two-stage stochastic model was a good choice for making tactical and operational decisions. Hence, two-stage stochastic models will still be used to deal with risks and uncertainties in the FFSC. However, new developments in robustness should be considered and applied to support decision making under uncertainty.

3.3. Special Category Models

In many fresh fruit supply chains, uncertain elements include the time to harvest, quantity for packing, cost for shortage, etc. Such uncertainties can be modelled in ways other than stochastic programming. For example, Miller et al. [24] used a fuzzy mathematical program to optimize the fresh tomato packing schedule for a distributor.
Fuzzy programming was used by Zimmermann [88] to “soften” requirements by “fuzzifying” perception-based uncertainties. According to these authors, the objective function in the linear programming model could be cost minimization, while in the fuzzy model, it could be the overall satisfaction of the manager aggregated from measurements of individual satisfaction of operating costs. Although the operating costs of the fuzzy linear model were higher than in the linear programming model, they were under the budget limit. The authors summarized that their fuzzy approach had high potential to apply, to optimize, or to make general decisions, in the fuzzy environment.
A crop planning model considering uncertainties for agricultural management was presented by Itoh et al. [32] in which a linear programming model was formulated to maximize profits. However, since profit coefficients for agricultural products cannot be constant due to weather fluctuation, their linear programming model could not correctly account for environmental elements. Therefore, the authors tried to incorporate some uncertain (stochastic) parameters with fuzziness and randomness.
Mathematical models for the fresh fruit supply chain need to take perishability into account. For example, the prices of fresh fruit are at their highest during harvesting and decrease exponentially with time as products are refrigerated to reduce deterioration. Blackburn and Scudder [45] suggested a modeling framework in this category to deal with supply chain strategic problems for perishable agricultural products, such as melons and sweet corn. In their approach, the design of a supply chain for these perishable products was based on interesting questions such as: (a) how to control the timing of production including planting, harvesting and processing, (b) how to manage the ripeness time of products, and (c) how to preserve product quality through the rest of the chain. Their model separates the supply chain into two essentially independent phases: the first phase called “responsive” in which the product deterioration rate is high, and the second one is the “efficient” phase that can slow down deterioration rates. By introducing a marginal value of time (MVT) parameter, the authors showed that the appropriate method to minimize the lost value in the supply chain is a sequential combination of a responsive model for cooling fresh produce and an efficient model to reduce costs. They also pointed out there was a loose linkage between these two segments of the supply chain, and profit maximization requires close coordination throughout the chain. Their models could also be applied to the other agricultural products, such as flowers and seafood, where the time-value relationship patterns are the same as in the melon supply chain.
Another approach for perishable production is described in Amorim et al. [58] who developed multiobjective models integrating production and distribution planning with freshness considerations, such as fixed shelf-life and loose shelf-life. In each case of freshness, both integrated and decoupled models were proposed to be compared with achieving the bi-objectives of (1) minimizing total costs and (2) maximizing delivered shelf-life products. Depending on the type of shelf-life of the perishable products or the functional area decision making (production or distribution), the authors developed a multiobjective mixed-integer linear model for the fixed shelf-life, and a multiobjective mixed-integer nonlinear model for loose shelf-live because of uncertain nature of it. To compare the differences between the integrated and decoupled models for fixed and loose shelf-life, a case study was used. The results showed that the integrated models solved the problem better than the decoupled ones. In addition, the loose shelf-life models could be implemented to deal with the randomness of the spoilage process.
Hester and Cacho [31] had suggested a hybrid model with an objective of maximizing the net present value for apple orchard systems by optimizing pruning plans over a 15-year period. Their approach presented a combination of multi-approaches: dynamic optimization, genetic algorithm (GA) and nonlinear programming (NLP). A dynamic simulation was developed, based on the interactions of the complex biological and economic relationships in apple orchard networks. It can be used for the managers of the apple orchards to consider problems including how apple tree yields could be influenced by biological factors, and how to choose apple variety among a large number of apple orchards. In each apple orchard, various tasks such as selecting varieties, grafting roots, identifying intervals between trees, training planting methods can influence yield, quality of apples harvested, as well as earned profits.
Another type of model was conceived by Bezat-Jarzębowska and Rembisz [63] to support agri-food producers to maximize expected profits by optimizing production where the scale of production does not impact competitive markets. The stochastic frontier approach (SFA), which is a commonly used economic modeling primarily dealing with high randomness, had been used in their model. The SFA was the combination of two functional forms including the input(s)–output relations (the Cobb-Douglas model) [89] and a translogarithmic model to improve the efficiency of the farm production, or in other words, the profitability was increased. The model was implemented and validated by a data set collected by Farm Accountancy Data Network in Poland.
A machine repair model was modified and applied by Ampatzidis et al. [65] to optimize fruit harvesting and bin loading. Inefficient harvesting and postharvest activities that increased costs were identified and reduced, and the schedules of labor and machinery were also improved. The authors implemented the machine repair model for two harvesting fruit processes: picking and bin loading. To adapt properly, the picking workers were considered as machine breakdowns and the fruit collection points were system servers for the picking process. Similarly, transporting workers were considered as the machine breakdowns and trucks (unloading points) for the bin loading process. The model was built and solved by using Matlab to evaluate how the two-process system performed. To validate the model, two specific types of fruit were chosen as case studies: table grapes in Greece and sweet cherries in Washington State, USA. The reason why the authors chose two different fruits grown in different places is based on the difference of the size of bins and trucks.
Summary of section: Various types of mathematical models were used in the articles reviewed in this section. The authors used methods such as fuzzy logic, or heuristic algorithms or nonlinear programming models. Future works should aim at combining one or more of these methods with meta-heuristics to deal with large-scale FFSC problems.

4. Robustness and Limitations of Existing Models

In the general view, the following are the main criteria on which researchers conceive and structure their models for the planning and logistics of the fresh fruit supply chain:
  • Relationship between price and demand
  • Environmental constraints
  • Planting/harvesting times and shipping/transporting factors
  • Operational decision-making styles
The fruit species under consideration were varied but very commonly consumed on a daily basis such as tomatoes, apples, grapes, bananas, etc. However, many tropical fruits were not covered as extensively in the literature.
Figure 3 shows the coverage of the fresh fruit supply chain research in the past, focusing on several common species in the market.
It can be observed that apples, grapes and tomatoes are the most used in case studies. From the chart in Figure 3, it is noticeable that most cases covered in the literature are perennial fruit or one-year lifetime trees. Meanwhile, fast-growing perennial trees are less considered than one year trees.
Figure 4 shows that most of the papers deal with tactical decisions (17 articles) followed by the operational level (11 articles). Only six articles focused on the strategic decision level. However, the coupled models seemed the most favorite approach in dealing with the fresh fruit supply chain, including 24 articles at different levels for combined decisions, such as strategic—tactical (7 articles) and tactical—operational (17 articles).
It was observed that all models were based on the well-defined underlying factors such as links, actors, actions, and states. The product is characterized by two types of states: appearance and quality. Appearance states are affected by handling action while the quality states are affected by processing, transportation and storage.
The models in the literature can be viewed from a robustness point of view [90]. The linear programming models include crop growth characteristics, seasonality, weather data, crop growth in order to accurately model yield and the timing of the maturity of fruit. The model such as Hamer’s [22] can also be used several times during a season to update marketing strategy and early warnings of production surpluses or shortfalls. However, linear programming models are limited because they do not consider uncertain parameters. In theory, linear models can be run for a choice of parameters but organizing such sensitivity analyses in a risk/robustness/economic trade-off is a challenge.
The dynamic programming models are useful in incorporating the quality. The process of changing the quality of products was described as one function of the DP model developed by Gigler et al. [30]. In addition, the appearance of the products was also considered in their DP approach to point out the relationship between quality and appearance of the products through the supply chain from farmers to final consumers.
The “machine repair” model suggested by Ampatzidis et al. [65] could be part of a general simulation approach to integrating operation research techniques to improve the total harvest process. It can also be used to model machine harvesting with a fleet of machines to collect, pack and distribute fruits. Consequently, the queuing theory to model waiting time can be logically used for agricultural operations.
Summary of section: This section presented the distribution of papers according to the type of fruit considered and the decision planning levels. Future models should aim to incorporate biological, environmental and economic considerations such as epidemics, climate change, and price fluctuations. Furthermore, more emphasis should be put on fast-growing perennial trees and their fruit production and distribution.

5. Conclusions and Research Perspectives for Future Models

The fresh fruit supply chain, a subcategory of the fresh product supply chain, presents modelling challenges due to inherent random and uncertain factors (such as yield, demand, price). New information technologies associated with robust but affordable computers and high technologies (such as drones and sensors) could allow FFSC managers to monitor real-time crop growth information to develop better harvesting and production plans. Nevertheless, according to our review, there exist three main challenges for FFSC models: (1) the efficiency of the entire FFSC in function of the coordination between different stages; (2) the development of integrated planning models which are capable of acquisitioning data or updating parameters from such high-tech informative systems; and (3) surprisingly, a lack of standardization of all FFSC model outputs and performance metrics is observed. FFSC modelling is an interdisciplinary topic and communication between disciplines should be improved to facilitate model comparisons. These shortcomings can hinder the adoption of modelling tools by practitioners. Besides, social responsibility and changing consumer values will create an increasingly complex business planning environment. Examples of such issues are genetically modified products and organic fresh fruits. The creation of a database of FFSC models, categorized by local and regional factors, would be valuable for modelling practitioners and modelers, allowing for benchmarking to occur.
Sustainable development and sustainability criteria have become extremely controversial since international trade based on economic criteria is seen as increasing green-house gas emissions and creating waste management issues. At the same time, increasing global competition and lower prices are strongly required for efficient management, including well-organized transportation, distribution, and inventory management of fresh fruit. These are essential for profitability and provide additional research opportunities.
All models reviewed are appropriate for the specific context and problems that they deal with. Of all the papers reviewed, the following ones propose integrated models of the supply chain under:
  • deterministic conditions (Hamer, 1994 [22], Munhoz and Morabito [67])
  • stochastic contexts (Bezat-Jarzębowska and Rembisz [63], Ahumada et al. [57])
  • sustainability considerations (Foong et al. [77], Van Der Vorst et al. [46])
  • multiobjective optimization (Cittadini et al. [44], Soto-Silva et al. [75])
  • multistage and multiechelon networks (Darby-Dowman et al. [28], Trivedi et al. [85])
  • comprehensive case studies (Broekmeulen [26], Verdouw et al. [51])
For future models, there are two facts that we cannot ignore: (1) mechanization in all steps of the fresh product supply chain and (2) door-to-door service which is becoming prevalent worldwide, especially in periods of pandemic. Mechanization is a response to the combination of rising labor costs and increased opportunities for rural workers in nonfarming sectors. Information and communication technologies in association with automation systems (data-driven technologies, artificial intelligence, etc.) can replace manual decision making in the traditional farm. FFSC systems then become more complex, requiring higher investment. This creates new opportunities for mathematical modelling. Therefore, there is a strong need for models that include real-time monitoring data, uncertain information, logistics integration and product safety and quality. The extension of current models to incorporate robustness and risk reduction would be extremely useful.
Regarding the door-to-door service, it is becoming prevalent in many Asian countries and the North American market. To meet a client’s specific requirements, the retail and foodservice supply chains must evolve various services, including customs formalities, preparation of space for perishable cargo on transportation means, prioritization of storage at the places of origin and destination. Factors such as temperature, quantity, damaging degrees, sanitary inspections and quality checks are standard and need to be regularly controlled. The big question is how we could insert all these features into current optimization models.

Author Contributions

Conceptualization, T.-D.N., U.V. and T.N.-Q.; data curation, T.-D.N. and T.N.-Q.; format analysis, T.-D.N., U.V. and T.N.-Q.; funding acquisition, T.N.-Q.; investigation, T.-D.N. and U.V.; methodology, T.-D.N., U.V. and T.N.-Q.; supervision, U.V., T.N.-Q., C.D. and M.A.; validation, T.-D.N., U.V., T.N.-Q., C.D. and M.A.; visualization, C.D. and M.A.; writing—original draft, T.-D.N., U.V. and T.N.-Q.; writing—review and editing, T.-D.N., U.V., T.N.-Q., C.D. and M.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Vietnam International Education Development (VIED) via the doctoral scholarship program 911 of T-D.N.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data sharing is not applicable. No new data were created or analyzed in this review.

Acknowledgments

The first author acknowledges the Vietnam International Education Development (VIED) via the 911 research scholarship program. We would like to thank three anonymous reviewers for their very constructive comments and suggestions.

Conflicts of Interest

The authors have no conflicting financial or other interests.

Nomenclature

C&ACollecting and Analyzing data
DCDistribution Centers
DPDynamic Programming
DSSDecision Support System
FADNFarm Accountancy Data Network
FAOFood and Agriculture Organization of the United Nations
FFSCFresh Fruit Supply Chain
FLFuzzy Logic
FSCFruit Supply Chain
GAGenetic algorithm
GMOsGenetically Modified Organisms
HEUHeuristics algorithms
LPLinear Programming
MIPMixed Integer Programming
MLMachine Learning model
MOLPMultiobjective Linear Programming
MVTMarginal Value of Time
NDNetwork Designing
NLPNonlinear Programming
RORobust Optimization
SDPStochastic dynamic programming
SFAStochastic Frontier Approach
SMSimulation models
SPStochastic Programming
STAStatistical methods
THTriple Helix model
VIEDVietnam International Education Development

References

  1. O’Byrne, R. 7 Things That Matter Most to Fresh Supply Chain Leaders; Logistics Bureau Pty Ltd.: Sydney, Australia, 2016; Available online: https://www.logisticsbureau.com/7-things-that-matter-most-to-fresh-supply-chain-leaders/ (accessed on 12 March 2017).
  2. Nguyen, T.-D.; Venkatadri, U.; Nguyen-Quang, T.; Diallo, C.; Adams, M. Optimization Model for Fresh Fruit Supply Chains: Case-Study of Dragon Fruit in Vietnam. AgriEngineering 2020, 2, 1–26. [Google Scholar] [CrossRef] [Green Version]
  3. Humphrey, J.; McCulloch, N.; Ota, M. The impact of European market changes on employment in the Kenyan horticulture sector. J. Int. Dev. 2004, 16, 63–80. [Google Scholar] [CrossRef]
  4. The-Statistics-Portal. Fruit Doss. Retrieved. 2018. Available online: https://www.statista.com/study/16252/fruit-statista-dossier/ (accessed on 15 November 2019).
  5. Joshi, P.K.; Gulati, A.; Birthal, P.S.; Tewari, L. Agriculture diversification in South Asia: Patterns, determinants and policy implications. Econ. Political Wkly. 2004, 39, 2457–2467. [Google Scholar]
  6. World Bank; Food and Agriculture Organization; International Fund for Agricultural Development. Gender in Agriculture Sourcebook; World Bank Publications: Washington, DC, USA, 2009. [Google Scholar]
  7. FAO. World Food and Agriculture—Statistical Yearbook; FAO: Rome, Italy, 2020. [Google Scholar]
  8. Glen, J.J. Mathematical models in farm planning: A survey. Oper. Res. 1987, 35, 641–666. [Google Scholar] [CrossRef] [Green Version]
  9. Lowe, T.J.; Preckel, P.V. Decision technologies for agribusiness problems: A brief review of selected literature and a call for research. Manuf. Serv. Oper. Manag. 2004, 6, 201–208. [Google Scholar] [CrossRef]
  10. Lucas, M.T.; Chhajed, D. Applications of location analysis in agriculture: A survey. J. Oper. Res. Soc. 2004, 55, 561–578. [Google Scholar] [CrossRef]
  11. Ahumada, O.; Villalobos, J.R. Application of planning models in the agri-food supply chain: A review. Eur. J. Oper. Res. 2009, 196, 1–20. [Google Scholar] [CrossRef]
  12. Soto-Silva, W.E.; Nadal-Roig, E.; González-Araya, M.C.; Pla-Aragones, L.M. Operational research models applied to the fresh fruit supply chain. Eur. J. Oper. Res. 2016, 251, 345–355. [Google Scholar] [CrossRef]
  13. Agarwal, S. Issues in Supply Chain Planning of Fruits and Vegetables in Agri-Food Supply Chain: A Review of Certain Aspects. Ph.D. Thesis, IMS Business School, Kolkata, India, 2017. [Google Scholar]
  14. Karp, D. Most of America’s Fruit Is Now Imported. Is That a Bad Thing? The New York Times. 18 March 2018. Available online: https://www.nytimes.com/2018/03/13/dining/fruit-vegetables-imports.html (accessed on 15 November 2019).
  15. Shukla, M.; Jharkharia, S. Agri-fresh produce supply chain management: A state-of-the-art literature review. Int. J. Oper. Prod. Manag. 2013, 33, 114–158. [Google Scholar] [CrossRef]
  16. Willis, C.; Hanlon, W. Temporal Model for Long-Run Orchard Decisions. Can. J. Agric. Econ. 1976, 24, 17–28. [Google Scholar] [CrossRef]
  17. Starbird, S.A. Optimal loading sequences for fresh-apple storage facilities. J. Oper. Res. Soc. 1988, 39, 911–917. [Google Scholar] [CrossRef]
  18. Saedt, A.P.; Hendriks, T.H.; Smits, F.M. A transition planning method applied in a decision support system for potplant nurseries. Eur. J. Oper. Res. 1991, 52, 142–154. [Google Scholar] [CrossRef]
  19. Annevelink, E. Operational planning in horticulture: Optimal space allocation in pot-plant nurseries using heuristic techniques. J. Agric. Eng. Res. 1992, 51, 167–177. [Google Scholar] [CrossRef]
  20. Purcell, D.L.; Turner, S.C.; Houston, J.; Hall, C. A portfolio approach to landscape plant production and marketing. J. Agric. Appl. Econ. 1993, 25, 13–26. [Google Scholar] [CrossRef] [Green Version]
  21. Van Berlo, J.M. A decision support tool for the vegetable processing industry; an integrative approach of market, industry and agriculture. Agric. Syst. 1993, 43, 91–109. [Google Scholar] [CrossRef]
  22. Hamer, P.J. A decision support system for the provision of planting plans for Brussels sprouts. Comput. Electron. Agric. 1994, 11, 97–115. [Google Scholar] [CrossRef]
  23. Maia, L.O.A.; Lago, R.A.; Qassim, R.Y. Selection of postharvest technology routes by mixed-integer linear programming. Int. J. Prod. Econ. 1997, 49, 85–90. [Google Scholar] [CrossRef]
  24. Miller, W.; Leung, L.; Azhar, T.; Sargent, S. Fuzzy production planning model for fresh tomato packing. Int. J. Prod. Econ. 1997, 53, 227–238. [Google Scholar] [CrossRef]
  25. Stokes, J.R.; Mjelde, J.W.; Hall, C.R. Optimal marketing of nursery crops from container-based production systems. Am. J. Agric. Econ. 1997, 79, 235–245. [Google Scholar] [CrossRef]
  26. Broekmeulen, R.A. Operations management of distribution centers for vegetables and fruits. Int. Trans. Oper. Res. 1998, 5, 501–508. [Google Scholar] [CrossRef]
  27. Leutscher, K.J.; Renkema, J.A.; Challa, H. Modelling operational adaptations of tactical production plans on pot plant nurseries: A simulation approach. Agric. Syst. 1999, 59, 67–78. [Google Scholar] [CrossRef]
  28. Darby-Dowman, K.; Barker, S.; Audsley, E.; Parsons, D. A two-stage stochastic programming with recourse model for determining robust planting plans in horticulture. J. Oper. Res. Soc. 2000, 51, 83–89. [Google Scholar] [CrossRef]
  29. Romero, C. Risk programming for agricultural resource allocation: A multidimensional risk approach. Ann. Oper. Res. 2000, 94, 57–68. [Google Scholar] [CrossRef]
  30. Gigler, J.K.; Hendrix, E.M.; Heesen, R.A.; van den Hazelkamp, V.G.; Meerdink, G. On optimisation of agri chains by dynamic programming. Eur. J. Oper. Res. 2002, 139, 613–625. [Google Scholar] [CrossRef]
  31. Hester, S.M.; Cacho, O. Modelling apple orchard systems. Agric. Syst. 2003, 77, 137–154. [Google Scholar] [CrossRef] [Green Version]
  32. Itoh, T.; Ishii, H.; Nanseki, T. A model of crop planning under uncertainty in agricultural management. Int. J. Prod. Econ. 2003, 81, 555–558. [Google Scholar] [CrossRef]
  33. Vitoriano, B.; Ortuño, M.T.; Recio, B.; Rubio, F.; Alonso-Ayuso, A. Two alternative models for farm management: Discrete versus continuous time horizon. Eur. J. Oper. Res. 2003, 144, 613–628. [Google Scholar] [CrossRef]
  34. Allen, S.J.; Schuster, E.W. Controlling the risk for an agricultural harvest. Manuf. Serv. Oper. Manag. 2004, 6, 225–236. [Google Scholar] [CrossRef] [Green Version]
  35. Kazaz, B. Production planning under yield and demand uncertainty with yield-dependent cost and price. Manuf. Serv. Oper. Manag. 2004, 6, 209–224. [Google Scholar] [CrossRef]
  36. Rantala, J. Optimizing the supply chain strategy of a multi-unit Finnish nursery company. Silva Fenn. 2004, 38, 203–215. [Google Scholar] [CrossRef] [Green Version]
  37. Blanco, A.; Masini, G.; Petracci, N.; Bandoni, J. Operations management of a packaging plant in the fruit industry. J. Food Eng. 2005, 70, 299–307. [Google Scholar] [CrossRef]
  38. Caixeta-Filho, J.V. Orange harvesting scheduling management: A case study. J. Oper. Res. Soc. 2006, 57, 637–642. [Google Scholar] [CrossRef]
  39. Ortmann, F.G.; Van Vuuren, J.; Van Dyk, F. Modelling the South African fruit export infrastructure: A case study. Orion 2006, 22, 35–57. [Google Scholar] [CrossRef] [Green Version]
  40. Widodo, K.H.; Nagasawa, H.; Morizawa, K.; Ota, M. A periodical flowering–harvesting model for delivering agricultural fresh products. Eur. J. Oper. Res. 2006, 170, 24–43. [Google Scholar] [CrossRef]
  41. Ferrer, J.C.; Mac Cawley, A.; Maturana, S.; Toloza, S.; Vera, J. An optimization approach for scheduling wine grape harvest operations. Int. J. Prod. Econ. 2007, 112, 985–999. [Google Scholar] [CrossRef]
  42. Masini, G.L.; Blanco, A.M.; Petracci, N.; Bandoni, J.A. Supply chain tactical optimization in the fruit industry. Process Syst. Eng. Supply Chain Optim. 2007, 4, 121–172. [Google Scholar]
  43. Bai, R.; Burke, E.K.; Kendall, G. Heuristic, meta-heuristic and hyper-heuristic approaches for fresh produce inventory control and shelf space allocation. J. Oper. Res. Soc. 2008, 59, 1387–1397. [Google Scholar] [CrossRef]
  44. Cittadini, E.D.; Lubbers, M.; de Ridder, N.; Van Keulen, H.; Claassen, G. Exploring options for farm-level strategic and tactical decision-making in fruit production systems of South Patagonia, Argentina. Agric. Syst. 2008, 98, 189–198. [Google Scholar] [CrossRef]
  45. Blackburn, J.; Scudder, G. Supply chain strategies for perishable products: The case of fresh produce. Prod. Oper. Manag. 2009, 18, 129–137. [Google Scholar] [CrossRef]
  46. Van Der Vorst, J.G.; Tromp, S.O.; van der Zee, D.J. Simulation modelling for food supply chain redesign; integrated decision making on product quality, sustainability and logistics. Int. J. Prod. Res. 2009, 47, 6611–6631. [Google Scholar] [CrossRef]
  47. Arnaout, J.P.M.; Maatouk, M. Optimization of quality and operational costs through improved scheduling of harvest operations. Int. Trans. Oper. Res. 2010, 17, 595–605. [Google Scholar] [CrossRef]
  48. Bohle, C.; Maturana, S.; Vera, J. A robust optimization approach to wine grape harvesting scheduling. Eur. J. Oper. Res. 2010, 200, 245–252. [Google Scholar] [CrossRef]
  49. Morande, H.; Maturana, S. Design and validation of a decision support system for oenologists. Rev. ICHIO 2010, 1, 46–58. [Google Scholar]
  50. Arumugam, N.; Fatimah, M.A.; Chiew, E.F.; Zainalabidin, M. Supply chain analysis of fresh fruits and vegetables (FFV): Prospects of contract farming. Agric. Econ. 2010, 56, 435–442. [Google Scholar] [CrossRef] [Green Version]
  51. Verdouw, C.; Beulens, A.; Trienekens, J.; Wolfert, J. Process modelling in demand-driven supply chains: A reference model for the fruit industry. Comput. Electron. Agric. 2010, 73, 174–187. [Google Scholar] [CrossRef]
  52. Ahumada, O.; Villalobos, J.R. Operational model for planning the harvest and distribution of perishable agricultural products. Int. J. Prod. Econ. 2011, 133, 677–687. [Google Scholar] [CrossRef]
  53. Ahumada, O.; Villalobos, J.R. A tactical model for planning the production and distribution of fresh produce. Ann. Oper. Res. 2011, 190, 339–358. [Google Scholar] [CrossRef]
  54. Jang, W.; Klein, C.M. Supply chain models for small agricultural enterprises. Ann. Oper. Res. 2011, 190, 359–374. [Google Scholar] [CrossRef]
  55. Jia, X.; Huang, J. Contractual arrangements between farmer cooperatives and buyers in China. Food Policy 2011, 36, 656–666. [Google Scholar] [CrossRef]
  56. Rong, A.; Akkerman, R.; Grunow, M. An optimization approach for managing fresh food quality throughout the supply chain. Int. J. Prod. Econ. 2011, 131, 421–429. [Google Scholar] [CrossRef]
  57. Ahumada, O.; Villalobos, J.R.; Mason, A.N. Tactical planning of the production and distribution of fresh agricultural products under uncertainty. Agric. Syst. 2012, 112, 17–26. [Google Scholar] [CrossRef]
  58. Amorim, P.; Günther, H.O.; Almada-Lobo, B. Multi-objective integrated production and distribution planning of perishable products. Int. J. Prod. Econ. 2012, 138, 89–101. [Google Scholar] [CrossRef]
  59. Banaeian, N.; Omid, M.; Ahmadi, H. Greenhouse strawberry production in Iran, efficient or inefficient in energy. Energy Effic. 2012, 5, 201–209. [Google Scholar] [CrossRef]
  60. Perdana, T. The Triple Helix Model for Fruits and Vegetables Supply Chain Management Development Involving Small Farmers in Order to Fulfill the Global Market Demand: A Case Study in “Value Chain Center (VCC) Universitas Padjadjaran”. Procedia Soc. Behav. Sci. 2012, 52, 80–89. [Google Scholar] [CrossRef] [Green Version]
  61. Yu, Y.; Wang, Z.; Liang, L. A vendor managed inventory supply chain with deteriorating raw materials and products. Int. J. Prod. Econ. 2012, 136, 266–274. [Google Scholar] [CrossRef]
  62. Catalá, L.P.; Durand, G.A.; Blanco, A.M.; Bandoni, J.A. Mathematical model for strategic planning optimization in the pome fruit industry. Agric. Syst. 2013, 115, 63–71. [Google Scholar] [CrossRef]
  63. Bezat-Jarzębowska, A.; Rembisz, W. Efficiency-focused economic modeling of competitiveness in the agri-food sector. Procedia Soc. Behav. Sci. 2013, 81, 359–365. [Google Scholar] [CrossRef] [Green Version]
  64. Jena, S.D.; Poggi, M. Harvest planning in the Brazilian sugar cane industry via mixed integer programming. Eur. J. Oper. Res. 2013, 230, 374–384. [Google Scholar] [CrossRef]
  65. Ampatzidis, Y.G.; Vougioukas, S.G.; Whiting, M.D.; Zhang, Q. Applying the machine repair model to improve efficiency of harvesting fruit. Biosyst. Eng. 2014, 120, 25–33. [Google Scholar] [CrossRef]
  66. Lambert, G.F.; Lasserre, A.A.A.; Ackerman, M.M.; Sánchez, C.G.M.; Rivera, B.O.I.; Azzaro-Pantel, C. An expert system for predicting orchard yield and fruit quality and its impact on the Persian lime supply chain. Eng. Appl. Artif. Intel. 2014, 33, 21–30. [Google Scholar] [CrossRef]
  67. Munhoz, J.R.; Morabito, R. Optimization approaches to support decision making in the production planning of a citrus company: A Brazilian case study. Comput. Electron. Agric. 2014, 107, 45–57. [Google Scholar] [CrossRef]
  68. Rocco, C.D.; Morabito, R. Scheduling of production and logistics operations of steam production systems in food industries: A case study of the tomato processing industry. J. Oper. Res. Soc. 2014, 65, 1896–1904. [Google Scholar] [CrossRef]
  69. Velychko, O. Integrated modeling of solutions in the system of distributing logistics of a fruit and vegetable cooperative. Business Theory Pract (Verslas Teorija Prakt) 2014, 15, 362–370. [Google Scholar] [CrossRef]
  70. González-Araya, M.C.; Soto-Silva, W.E.; Espejo, L.G.A. Harvest Planning in Apple Orchards Using an Optimization Model. In Handbook of Operations Research in Agriculture and the Agri-Food Industry; Springer: New York, NY, USA, 2015; pp. 79–105. [Google Scholar]
  71. Nadal-Roig, E.; Plà-Aragonés, L.M. Optimal Transport Planning for the Supply to a Fruit Logistic Centre. In Handbook of Operations Research in Agriculture and the Agri-Food Industry; Springer: New York, NY, USA, 2015; pp. 163–177. [Google Scholar]
  72. Catalá, L.P.; Moreno, M.S.; Blanco, A.M.; Bandoni, J.A. A bi-objective optimization model for tactical planning in the pome fruit industry supply chain. Comput. Electron. Agric. 2016, 130, 128–141. [Google Scholar] [CrossRef]
  73. Rocco, C.D.; Morabito, R. Production and logistics planning in the tomato processing industry: A conceptual scheme and mathematical model. Comput. Electron. Agric. 2016, 127, 763–774. [Google Scholar] [CrossRef]
  74. Grillo, H.; Alemany, M.; Ortiz, A.; Fuertes-Miquel, V. Mathematical modelling of the order-promising process for fruit supply chains considering the perishability and subtypes of products. Appl. Math. Model. 2017, 49, 255–278. [Google Scholar] [CrossRef]
  75. Soto-Silva, W.E.; González-Araya, M.C.; Oliva-Fernández, M.A.; Plà-Aragonés, L.M. Optimizing fresh food logistics for processing: Application for a large Chilean apple supply chain. Comput. Electron. Agric. 2017, 136, 42–57. [Google Scholar] [CrossRef]
  76. Cheraghalipour, A.; Paydar, M.M.; Hajiaghaei-Keshteli, M. Designing and solving a bi-level model for rice supply chain using the evolutionary algorithms. Comput. Electron. Agric. 2019, 162, 651–668. [Google Scholar] [CrossRef]
  77. Foong, S.Z.; Goh, C.K.; Supramaniam, C.V.; Ng, D.K. Input–output optimisation model for sustainable oil palm plantation development. Sustain. Prod. Consum. 2019, 17, 31–46. [Google Scholar] [CrossRef]
  78. Gokarn, S.; Kuthambalayan, T.S. Creating sustainable fresh produce supply chains by managing uncertainties. J. Clean. Prod. 2019, 207, 908–919. [Google Scholar] [CrossRef]
  79. Ji, Y.; Du, J.; Han, X.; Wu, X.; Huang, R.; Wang, S.; Liu, Z. A mixed integer robust programming model for two-echelon inventory routing problem of perishable products. Phys. A Stat. Mech. Appl. 2020, 548, 124481. [Google Scholar] [CrossRef]
  80. Varas, M.; Basso, F.; Maturana, S.; Osorio, D.; Pezoa, R. A multi-objective approach for supporting wine grape harvest operations. Comput. Ind. Eng. 2020, 145, 106497. [Google Scholar] [CrossRef]
  81. Alemany, M.M.E.; Esteso, A.; Ortiz, Á.; del Pino, M. Centralized and distributed optimization models for the multi-farmer crop planning problem under uncertainty: Application to a fresh tomato Argentinean supply chain case study. Comput. Ind. Eng. 2021, 153, 107048. [Google Scholar] [CrossRef]
  82. Gómez-Lagos, J.E.; González-Araya, M.C.; Soto-Silva, W.E.; Rivera-Moraga, M.M. Optimizing tactical harvest planning for multiple fruit orchards using a metaheuristic modeling approach. Eur. J. Oper. Res. 2021, 290, 297–312. [Google Scholar] [CrossRef]
  83. Ktenioudaki, A.; O’Donnell, C.P.; Emond, J.P.; do Nascimento Nunes, M.C. Blueberry supply chain: Critical steps impacting fruit quality and application of a boosted regression tree model to predict weight loss. Postharvest Biol. Technol. 2021, 179, 111590. [Google Scholar] [CrossRef]
  84. Lim, C.H.; Cheah, Z.H.; Lee, X.H.; How, B.S.; Ng, W.P.Q.; Ngan, S.L.; Lam, H.L. Harvesting and evacuation route optimisation model for fresh fruit bunch in the oil palm plantation site. J. Clean. Prod. 2021, 307, 127238. [Google Scholar] [CrossRef]
  85. Trivedi, A.; Sohal, A.; Joshi, S.; Sharma, M. A two-stage optimization model for tactical planning in fresh fruit supply chains: A case study of Kullu, India. Int. J. Supply Oper. Manag. 2021, 8, 18–28. [Google Scholar]
  86. Diop, N.; Jaffee, S. Fruits and vegetables: Global trade and competition in fresh and processed product markets. In Global Agricultural Trade and Developing Countries; World Bank: Washington, DC, USA, 2005; pp. 237–257. [Google Scholar]
  87. Audsley, E.; Sandars, D.L. A review of the practice and achievements from 50 years of applying OR to agricultural systems in Britain. OR Insight 2009, 22, 2–18. [Google Scholar] [CrossRef]
  88. Zimmermann, H.-J. Description and optimization of fuzzy systems. Int. J. Gen. Syst. 1975, 2, 209–215. [Google Scholar] [CrossRef]
  89. Cobb, C.W.; Douglas, P.H. A theory of production. Am. Econ. Rev. 1928, 18, 139–165. [Google Scholar]
  90. Monostori, J. Supply chains robustness: Challenges and opportunities. Procedia CIRP 2018, 67, 110–115. [Google Scholar] [CrossRef]
Agriengineering 03 00034 g001 550
Figure 1. Constraints, challenges and influencing elements on the fresh fruit supply chain.
Figure 1. Constraints, challenges and influencing elements on the fresh fruit supply chain.
Agriengineering 03 00034 g001
Agriengineering 03 00034 g002 550
Figure 2. Model classification framework for fresh fruit supply chains.
Figure 2. Model classification framework for fresh fruit supply chains.
Agriengineering 03 00034 g002
Agriengineering 03 00034 g003 550
Figure 3. Statistics related to the fresh fruit supply chain research in term of fruit species from 1978–2017.
Figure 3. Statistics related to the fresh fruit supply chain research in term of fruit species from 1978–2017.
Agriengineering 03 00034 g003
Agriengineering 03 00034 g004 550
Figure 4. Number of model categories in fresh fruit supply chain optimization.
Figure 4. Number of model categories in fresh fruit supply chain optimization.
Agriengineering 03 00034 g004
Table
Table 1. Top fruit producing countries in the world in 2018 [7].
Table 1. Top fruit producing countries in the world in 2018 [7].
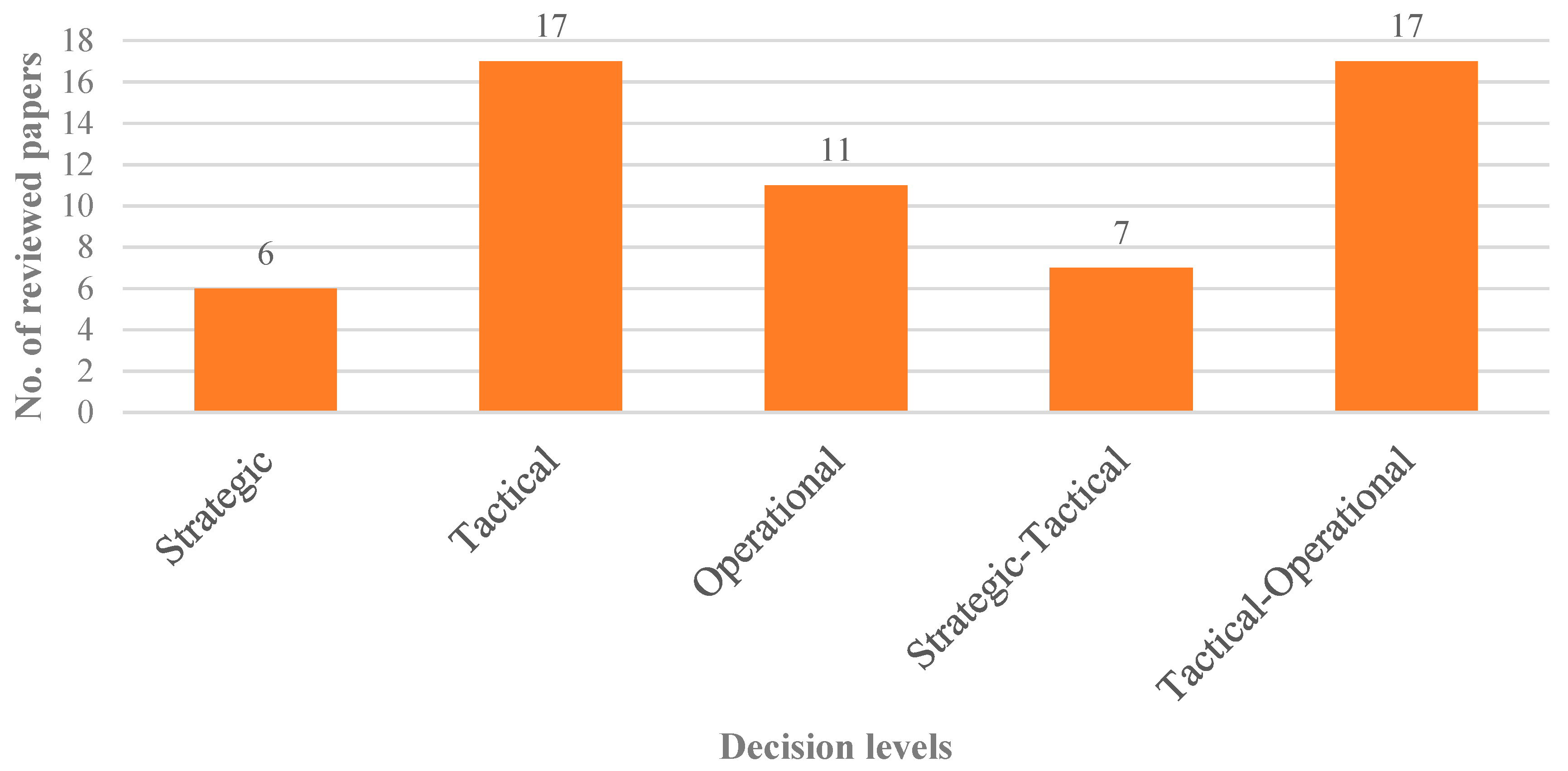
RankCountryFruits Produced (Million Tons)
1China243.592
2India98.722
3Brazil40.047
4United States26.015
5Turkey23.599
6Mexico22.768
7Indonesia20.436
8Spain19.332
9Iran18.898
10Italy18.009
Table
Table 2. Summary of mathematical models in references dealing with fresh fruit supply chain.
Table 2. Summary of mathematical models in references dealing with fresh fruit supply chain.
AuthorModel ApproachesMain ObjectiveEvaluation
Willis and Hanlon [16]DPDetermine a plan to plant a variety of kinds of apples on the farm, using dynamic programming to optimize resources neededComplex, mixed outcomes
Starbird [17]DPDetermine a loading sequence for storage facilities at an apple packing plant by using a dynamic programming modelComplex, one outcome
Saedt et al. [18]LP/MIPDevelop a plan to maximize revenue for a pot plant greenhouse with 2 models: one MIP for transition plans and one LP for future plansComplex, mixed outcomes
Annevelink [19]HEUUse heuristic techniques to optimize the location of pot plants inside a greenhouse to minimize costsComplex, mixed outcomes
Purcell et al. [20]NLPA quadratic programming model was developed for landscape land production to maximize returns for a given risk levelComplex, mixed outcomes
Van Berlo [21]LP/MIPDevelop a tactical plan using a linear goal programming to minimize costs across the logistical chainComplex, mixed outcomes
Hamer [22]LP/MIPDevelop a plan using LP to support planting and harvesting decisions for Brussel sprouts with the objective of satisfying demand and maximizing profitsComplex, mixed outcomes
Maia et al. [23]LP/MIPUsing MIP to make routing plans for fruit crops after harvesting with the objective of optimizing the capital investment under uncertaintiesSimple, mixed outcomes
Miller et al. [24]FLA fuzzy program model was developed to minimize costs of production and harvesting at a tomato packing plantComplex, mixed outcomes
Stokes et al. [25]SDPUsing stochastic dynamic programming to make production and marketing decisions for a nursery producing ornamental plants with the objective of maximizing revenueComplex, mixed outcomes
Broekmeulen [26]HEU & SMAn assignment plan was proposed to improve the operations of a distribution center for fruits and vegetables using local search techniquesComplex, mixed outcomes
Leutscher et al. [27]SMDevelop a simulation and regression metamodel to support making tactical and operational decisions for pot plant nurseries to increase profitabilityComplex, one outcome
Darby-Dowman et al. [28]SPPropose a two-stage stochastic programming model to determine the optimal planting plans involving uncertain weather factors with the objective of maximizing revenueComplex, mixed outcomes
Romero [29]MOLPA multiobjective model was built to find out an efficient cropping pattern by considering the risks for the farmersComplex, mixed outcomes
Gigler et al. [30]DPPresent a dynamic programming model as a methodology for optimization of agricultural product chains to deal with the appearance and quality of productsComplex, mixed outcomes
Hester and Cacho [31]DPDescribing a dynamic model based on the complex biological and economic relationships of apple orchards to maximize the profit over a 15-year period.Complex, mixed outcomes
Itoh et al. [32]SPA stochastic model was proposed to support crop planning dealing with uncertain factors with fuzziness and randomness to maximize revenueComplex, mixed outcomes
Vitoriano [33]LP/MIPPresenting two mathematical models to compare, one with discrete time and another with continuous time, that support planning and scheduling tasks for crop production with given time horizonComplex, mixed outcomes
Allen and Schuster [34]NLPA nonlinear model was developed to control risks of grape harvesting, to determine the optimal investing decision for harvesting and capitalComplex, mixed outcomes
Kazaz [35]SPA two-stage SP was applied for production planning under yield and demand uncertainty in olive industry, to maximize the satisfaction of customers and the profitComplex, mixed outcomes
Rantala [36]LP/MIPMIP model was presented for solving all three problem levels of SCM: operational, tactical and strategic for a nursery company to minimize costsComplex, mixed outcomes
Blanco et al. [37]LP/MIPMIP model was proposed to maximize the profit of a fruit packing plant by considering costs of raw material purchase, storage and labor.Complex, mixed outcomes
Caixeta-Filho [38]LP/MIPApply LP model to maximize the number of harvested oranges by considering quality factors.Complex, mixed outcomes
Ortmann et al. [39]LP/MIPTo optimize the export infrastructure, two models were presented: one for single product and other one for multiple productsComplex, mixed outcomes
Widodo et al. [40]DPProduction, harvest and storage of fresh product were integrated in a periodical model that developed with growth and loss functions to maximize the demandComplex, mixed outcomes
Ferrer et al. [41]LP/MIPTo optimize costs of graph harvesting operations for wine production, a mixed LP model was used.Complex, one outcome
Masini et al. [42]HEUA linear programming was presented to optimize a real fruit supply chain network to maximize profit.Complex, one outcome
Bai et al. [43]MOLPTo deal with fresh produce inventory control and shelf space allocation problem, an integration of four greedy heuristic methods was built to maximize revenueComplex, one outcome
Cittadini et al. [44]MOLPA multiobjective linear programing model was proposed to maximize total profit and to optimize working force of an Argentinian cherry farm dealing with strategic and tactical plans.Complex, mixed outcomes
Blackburn and Scudder [45]SMDeveloping a simulation model to optimize the value of marginal cost of a melon supply chain network.Complex, one outcome
Van Der Vorst et al. [46]SMIntroducing a new discrete event approach ALADIN to support decision making on redesigning a food supply chain with the objective of reducing costs and improving quality and sustainability.Complex, mixed outcomes
Arnaout and Maatouk [47]HEUDealing with scheduling problems of grape harvesting operations, some heuristic models were applied and compared with the objective of improving quality and saving costs.Complex, mixed outcomes
Bohle et al. [48]RODevelop a robust model from an extension of stochastic model to deal with uncertain factors of operations of grape wine industry.Complex, mixed outcomes
Morande and Maturana [49]SMAn introduction of DSS based on simulation model for optimizing operations from harvesting to processing within the winery.Complex, mixed outcomes
Arumugam et al. [50]C&AAn analysis was made of supply chain of fresh fruit and vegetables to help Malaysian farmers in contract farming.Simple, mixed outcomes
Verdouw et al. [51]NDDesign a framework for the fruit supply chain network to support managers.Simple, mixed outcomes
Ahumada and Villalobos [52]LP/MIPPropose an MIP model to maximize revenue from optimizing harvesting and distributing operations for bell pepper and tomatoes under uncertainty in short termsComplex, mixed outcomes
Ahumada and Villalobos [53]LP/MIPAn MIP was developed to deal with tactical operations of a vegetable supply chain for maximization of revenue.Complex, mixed outcomes
Jang and Klein [54]NLPDevelop a model to assist small farmers how to form and run a cooperative effectively, and then support them with the objective of optimizing quantity of milk production to contribute to a cooperative.Complex, mixed outcomes
Jia and Huang [55]C&AA survey was conducted to study the relationship between cooperatives and buyers in ChinaSimple, one outcome
Rong et al. [56]LP/MIPPresent an MIP model to optimize the plan of production and distribution of food supply chain with a target of increasing the food quality.Complex, one outcome
Ahumada et al. [57]SPPropose a two-stage stochastic tactical model to deal with uncertainties of weather and demand in fresh vegetable industry and to support growing and distribution planning with the objectives of increasing revenue and decreasing losses.Complex, mixed outcomes
Amorim et al. [58]MOLPA multiobjective model integrating operations of production and distribution of fresh products was built to minimize storing time.Complex, mixed outcomes
Banaeian et al. [59]C&ATo optimize energy for strawberry greenhouse and to increase strawberry yield, a nonparametric approach named data envelopment analysis was appliedSimple, one outcome
Perdana [60]THThe triple helix approach was applied to support all parties of the fresh fruit and vegetables supply chain in Indonesia to at all levels.Simple, mixed outcomes
Yu et al. [61]NLPUse non-LP model approach to optimize inventory costs of both fast deteriorating and slow deteriorating products. The results of research showed that the total costs decreased significantly.Complex, one outcome
Catalá et al. [62]LP/MIPDevelop a mixed integer linear support for making strategic decisions in planting variety and density of pears and apples with the objective of maximizing the net present value.Complex, one outcome
Bezat-Jarzębowska and Rembisz [63]SPA framework based on stochastic frontier approach was proposed to help the farmers with the objective of maximizing their profit.Complex, one outcome
Jena and Poggi [64]LP/MIPOperational planning and tactical planning were integrated in a mixed integer linear model developed for optimizing sugar production with the objective of maximizing cane yield and profit.Complex, mixed outcomes
Ampatzidis et al. [65]MLApply a modified repair machine model to reduce harvesting costs by analyzing performance and scheduling workers and machines.Complex, mixed outcomes
Lambert et al. [66]FLA modified Mamdani fuzzy model was used to increase production yield and fruit quality of Persian lime.Complex, mixed outcomes
Munhoz and Morabito [67]ROPropose a robust optimization model developed from an LP model to optimize the midterm production plan of orange juice with the goal of minimizing costsComplex, one outcome
Rocco and Morabito [68]LP/MIPA DSS based on mixed integer programing model was proposed to optimize operations scheduling and fuel logistics of steam production systems for tomato processing in Brazil.Complex, mixed outcomes
Velychko [69]LP/MIPDevelop a model that was integration of decision tree method and linear programming, to minimize operations costs and to maximize profit for every party of the fruit and vegetable cooperative.Complex, mixed outcomes
González-Araya et al. [70]LP/MIPPresent a tactical decision support system to optimize labor and resource scheduling during apple harvesting season with the objective of minimization of labor costs and maximization of quantity and quality apples to harvest.Complex, mixed outcomes
Nadal-Roig and Plà-Aragonés [71]LP/MIPA prototype based on mixed integer program was proposed to support operational decision making for fruit logistic center to optimize transport planning with the objective of minimizing costs.Complex, one outcome
Catalá et al. [72]MOLPFormulate a multiobjective integer linear programming to a pome supply chain including production, processing, distribution, and inventory stages with the objective of satisfying both two conflict goals as minimizing supply shortage and maximizing profit.Complex, mixed outcomes
Rocco and Morabito [73]LP/MIPForm a prototype based on linear programming to support tactical planning in tomato processing industry in Brazil aiming to maximize profits.Complex, one outcome
Grillo et al. [74]LP/MIPA multigoal programing model was developed to optimize a fruit supply chain in Spain with objectives of satisfying two conflict goals: maximizing total profit and minimizing shelf life of products.Complex, mixed outcomes
Soto-Silva et al. [75]MOLPThree models covering actives such as purchasing, storing, and transporting apples of processing factories in Chile were developed to minimize costs.Complex, one outcome
Cheraghalipour et al. [76]HEUThe first proposed model was applied to minimized costs of the rice supply chain in Iran by implementing an integration of genetic algorithm and particle swarm optimization.Complex, one outcome
Foong et al. [77]LP/MIPA mathematical model named input–output optimization model was developed to deal with palm planting and harvesting planning problems with objectives of maximizing of yield but minimizing of planting areas and gas emissions.Complex, mixed outcomes
Gokarn and Kuthambalayan [78]C&AA study based on collecting and analyzing data was developed to evaluate uncertainties of the supply chain of fresh produce, and relationships among all outbound and inbound parties of supply chains of companies in IndiaComplex, one outcome
Ji et al. [79]MIP/ROTo minimize the cost objective of a two-echelon inventory routing problem for perishable products, a robust optimization model was developed from an MIP model.Complex, mixed outcomes
Varas et al. [80]MOLPPropose a multiobjective integer linear programming model to achieve conflicted goals that are maximization of harvesting quality and minimization of operation costs in Chilean wineries.Complex, mixed outcomes
Alemany et al. [81]MIP/FLTo deal with uncertainties in planting and harvesting fresh tomatoes, a fuzzy model developed from an MIP model was used to support decision makers with the objectives of maximizing income and minimizing costs.Complex, mixed outcomes
Gómez-Lagos et al. [82]MIP/HEUAn MIP model was proposed for tactical fruit harvest planning with the objective of minimizing the total cost by using greedy randomized adaptive search procedure metaheuristic method.Complex, one outcome
Ktenioudaki et al. [83]STATo predict weight loss and to improve quality in blueberry processing, the boosted regression tree was implementedComplex, one outcome
Lim et al. [84]MIP/NLPA harvesting and evacuation route optimization model was proposed to minimize travelling distance but maximize the quantity of palm harvested in Malaysia.Complex, one outcome
Trivedi et al. [85]MIPPresent a multistage integer linear program to optimize tactical transportation plans for apple supply chain in India with the goal of minimizing of costs and maximizing of demand.Complex, mixed outcomes
C&A: collecting and analyzing data, DP: dynamic programming, FL: fuzzy logic, HEU: heuristics algorithms, LP: linear programming, MIP: mixed integer programming, ML: machine learning model, MOLP: multiobjective linear programming, ND: network designing, NLP: nonlinear programming, RO: robust optimization, SDP: stochastic dynamic programming, SFA: stochastic frontier approach, SM: simulation models, SP: stochastic programming, STA: statistical methods, TH: triple helix model.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Nguyen, T.-D.; Nguyen-Quang, T.; Venkatadri, U.; Diallo, C.; Adams, M. Mathematical Programming Models for Fresh Fruit Supply Chain Optimization: A Review of the Literature and Emerging Trends. AgriEngineering 2021, 3, 519-541. https://doi.org/10.3390/agriengineering3030034

AMA Style

Nguyen T-D, Nguyen-Quang T, Venkatadri U, Diallo C, Adams M. Mathematical Programming Models for Fresh Fruit Supply Chain Optimization: A Review of the Literature and Emerging Trends. AgriEngineering. 2021; 3(3):519-541. https://doi.org/10.3390/agriengineering3030034

Chicago/Turabian Style

Nguyen, Tri-Dung, Tri Nguyen-Quang, Uday Venkatadri, Claver Diallo, and Michelle Adams. 2021. "Mathematical Programming Models for Fresh Fruit Supply Chain Optimization: A Review of the Literature and Emerging Trends" AgriEngineering 3, no. 3: 519-541. https://doi.org/10.3390/agriengineering3030034

APA Style

Nguyen, T. -D., Nguyen-Quang, T., Venkatadri, U., Diallo, C., & Adams, M. (2021). Mathematical Programming Models for Fresh Fruit Supply Chain Optimization: A Review of the Literature and Emerging Trends. AgriEngineering, 3(3), 519-541. https://doi.org/10.3390/agriengineering3030034

Article Metrics

Back to TopTop