Digital Mapping of Topsoil Texture Classes Using a Hybridized Classical Statistics–Artificial Neural Networks Approach and Relief Data
Abstract
:1. Introduction
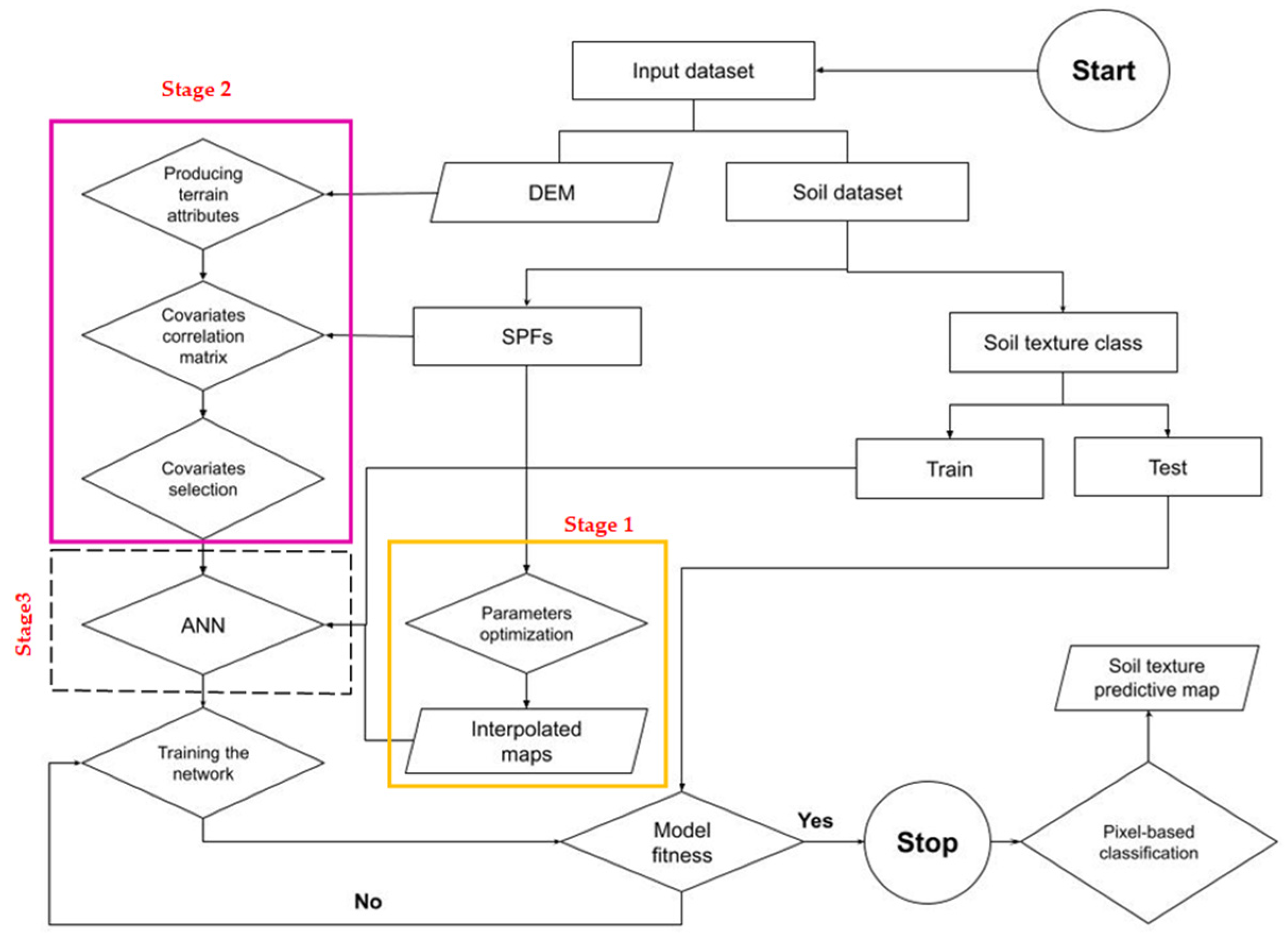
2. Materials and Methods
2.1. Study Area
2.2. Soil Data
2.3. Parameter Optimization of STF Spatial Interpolation
2.4. STF Interpolation
2.5. Covariate Selection
2.6. Covariate Reduction and Selection
2.7. The Predictive Soil Texture Class Models Built with ANN
2.7.1. Data Split into Training and Testing Sets
2.7.2. Training the Machine Learning Algorithms
2.7.3. Testing the Prediction Results and Covariate Importance
2.8. Model Evaluation
2.8.1. Interpolated Data Evaluation
2.8.2. ANN-Predicted Soil Texture Class Evaluation
2.9. Spatial Predictions
3. Results and Discussion
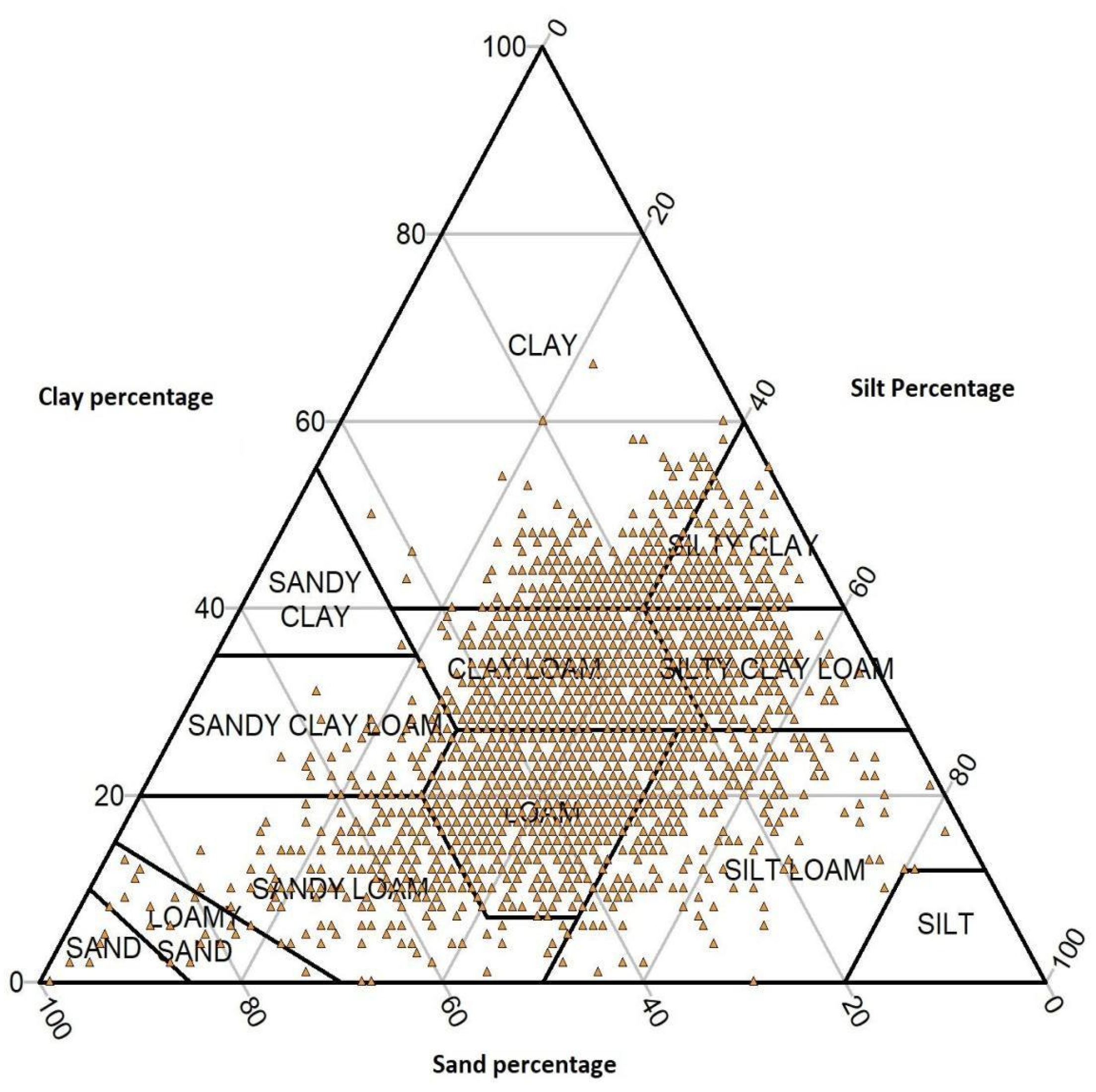
3.1. Soil Dataset Descriptive Statistics
3.2. Soil Texture Class Evaluation
3.3. STF Spatial Structure
3.4. Soil Texture Fraction Mapping
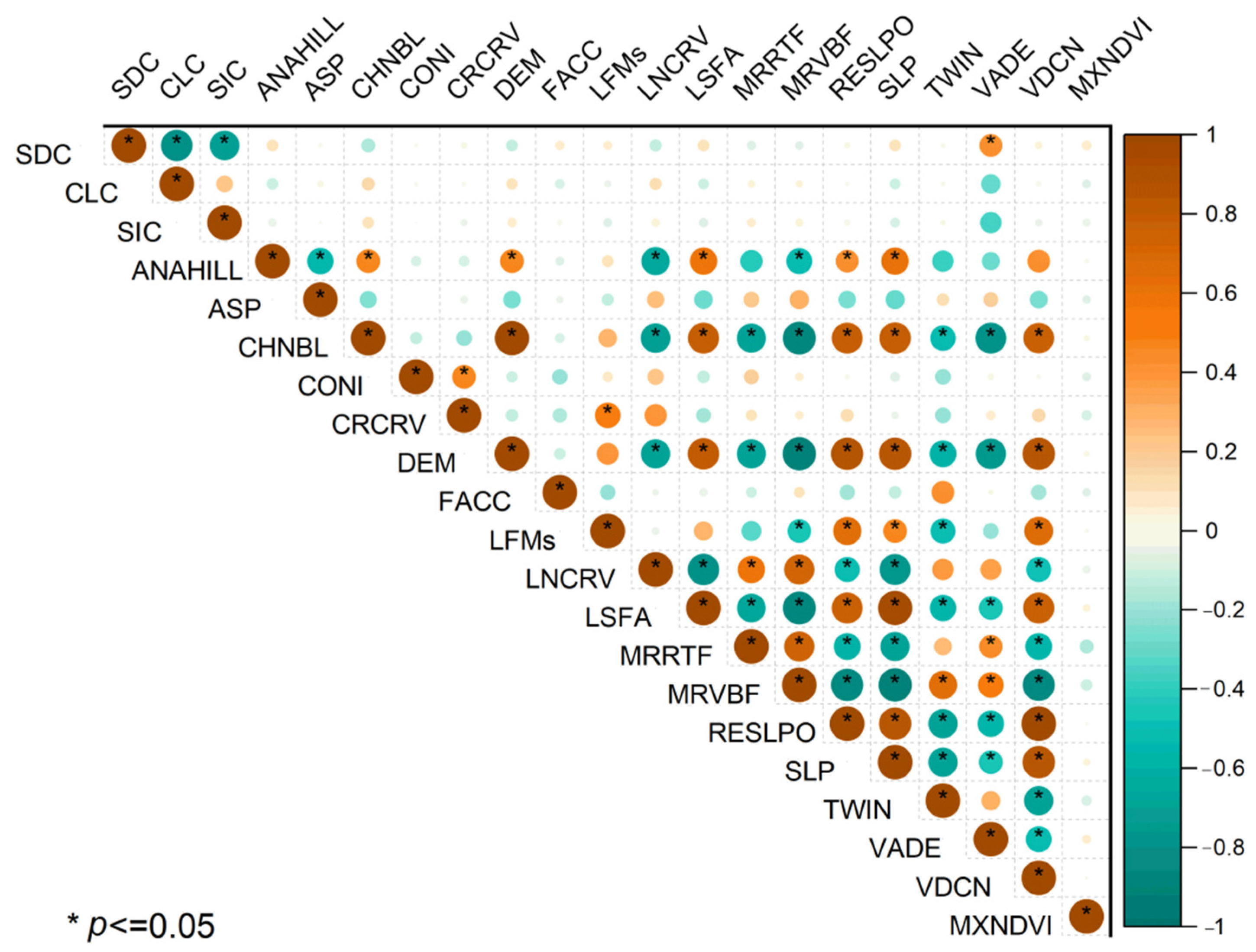
3.5. Important Covariates
3.6. Soil Texture Class Prediction Performance
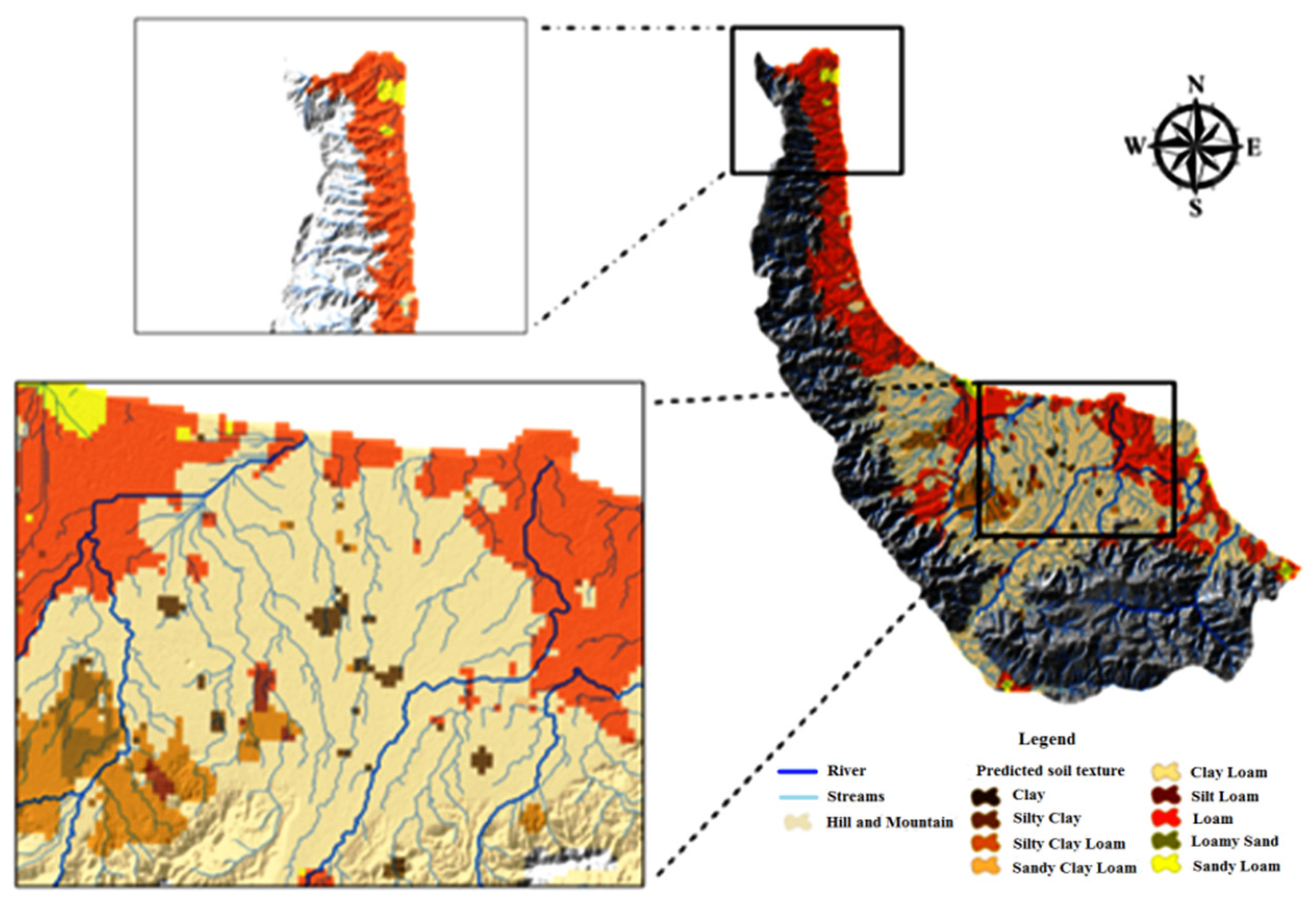
3.7. Predicted Soil Texture Class Map
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, Y.; Wu, W.; Wang, H.; Zhang, X.; Yang, C.; Liu, H. Identification of Soil Texture Classes Under Vegetation Cover Based on Sentinel-2 Data with SVM and SHAP Techniques. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3758–3770. [Google Scholar] [CrossRef]
- Gozdowski, D.; Stępień, M.; Samborski, S.; Dobers, E.S.; Szatyłowicz, J.; Chormański, J. Determination of the Most Relevant Soil Properties for the Delineation of Management Zones in Production Fields. Commun. Soil Sci. Plant Anal. 2014, 45, 2289–2304. [Google Scholar] [CrossRef]
- Bakker, A. Soil Texture Mapping on a Regional Scale with Remote Sensing Data. Ph.D. Thesis, Wageningen University, Wageningen, The Netherlands, 2012. [Google Scholar]
- Bouma, J.; Stoorvogel, J.; Van Alphen, B.; Booltink, H. Pedology, Precision Agriculture, and the Changing Paradigm of Agricultural Research. Soil Sci. Soc. Am. J. 1999, 63, 1763–1768. [Google Scholar] [CrossRef] [Green Version]
- Ding, X.; Zhao, Z.; Yang, Q.; Chen, L.; Tian, Q.; Li, X.; Meng, F.-R. Model Prediction of Depth-Specific Soil Texture Distributions with Artificial Neural Network: A Case Study in Yunfu, a Typical Area of Udults Zone, South China. Comput. Electron. Agric. 2020, 169, 105217. [Google Scholar] [CrossRef]
- Koseva, I.S.; Watmough, S.A.; Aherne, J. Estimating Base Cation Weathering Rates in Canadian Forest Soils Using a Simple Texture-Based Model. Biogeochemistry 2010, 101, 183–196. [Google Scholar] [CrossRef]
- Ghiri, M.N.; Abtahi, A. Factors Affecting Potassium Fixation in Calcareous Soils of Southern Iran. Arch. Agron. Soil Sci. 2012, 58, 335–352. [Google Scholar] [CrossRef]
- Goli-Kalanpa, E.; Roozitalab, M.; Malakouti, M. Potassium Availability as Related to Clay Mineralogy and Rates of Potassium Application. Commun. Soil Sci. Plant Anal. 2008, 39, 2721–2733. [Google Scholar] [CrossRef]
- Vaughan, E.; Matos, M.; Ríos, S.; Santiago, C.; Marín-Spiotta, E. Clay and Climate Are Poor Predictors of Regional-Scale Soil Carbon Storage in the US Caribbean. Geoderma 2019, 354, 113841. [Google Scholar] [CrossRef]
- Xu, H.; Liu, K.; Zhang, W.; Rui, Y.; Zhang, J.; Wu, L.; Colinet, G.; Huang, Q.; Chen, X.; Xu, M. Long-Term Fertilization and Intensive Cropping Enhance Carbon and Nitrogen Accumulated in Soil Clay-Sized Particles of Red Soil in South China. J Soils Sediments 2020, 20, 1824–1833. [Google Scholar] [CrossRef]
- Bockheim, J.; Hartemink, A. Distribution and Classification of Soils with Clay-Enriched Horizons in the USA. Geoderma 2013, 209, 153–160. [Google Scholar] [CrossRef]
- Reichardt, K.; Timm, L.C. Solo, Planta e Atmosfera: Conceitos, Processos e Aplicações; Manole: Barueri, Brazil, 2004. [Google Scholar]
- Dupuis, E.M.; Whalen, J.K. Soil Properties Related to the Spatial Pattern of Microbial Biomass and Respiration in Agroecosystems. Can. J. Soil Sci. 2007, 87, 479–484. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Mahdianpari, M.; Mohammadimanesh, F.; Behrens, T.; Toomanian, N.; Scholten, T.; Schmidt, K. Multi-Task Convolutional Neural Networks Outperformed Random Forest for Mapping Soil Particle Size Fractions in Central Iran. Geoderma 2020, 376, 114552. [Google Scholar] [CrossRef]
- Behrens, T.; Zhu, A.-X.; Schmidt, K.; Scholten, T. Multi-Scale Digital Terrain Analysis and Feature Selection for Digital Soil Mapping. Geoderma 2010, 155, 175–185. [Google Scholar] [CrossRef]
- Klein, V.A.; Baseggio, M.; Madalosso, T.; Marcolin, C.D. Soil Texture and the Estimation by Dewpoint Potential Meter of Water Retention at Wilting Point/Textura Do Solo e a Estimativa Do Teor de Agua No Ponto de Murcha Permanente Com Psicrometro. Ciência Rural 2010, 40, 1550–1557. [Google Scholar] [CrossRef] [Green Version]
- Tümsavaş, Z.; Tekin, Y.; Ulusoy, Y.; Mouazen, A.M. Prediction and Mapping of Soil Clay and Sand Contents Using Visible and Near-Infrared Spectroscopy. Biosyst. Eng. 2019, 177, 90–100. [Google Scholar] [CrossRef]
- Malone, B.P.; McBratney, A.B.; Minasny, B. Spatial Scaling for Digital Soil Mapping. Soil Sci. Soc. Am. J. 2013, 77, 890–902. [Google Scholar] [CrossRef] [Green Version]
- Paterson, S.; Minasny, B.; McBratney, A. Spatial Variability of Australian Soil Texture: A Multiscale Analysis. Geoderma 2018, 309, 60–74. [Google Scholar] [CrossRef]
- Mesgaran, M.B.; Madani, K.; Hashemi, H.; Azadi, P. Iran’s Land Suitability for Agriculture. Sci Rep 2017, 7, 7670. [Google Scholar] [CrossRef] [Green Version]
- Roozitalab, M.H.; Toomanian, N.; Ghasemi Dehkordi, V.R.; Khormali, F. Major Soils, Properties, and Classification. In The Soils of Iran; Springer: Berlin/Heidelberg, Germany, 2018; pp. 93–147. [Google Scholar]
- Zeraatpisheh, M.; Jafari, A.; Bagheri Bodaghabadi, M.; Ayoubi, S.; Taghizadeh-Mehrjardi, R.; Toomanian, N.; Kerry, R.; Xu, M. Conventional and Digital Soil Mapping in Iran: Past, Present, and Future. Catena 2020, 188, 104424. [Google Scholar] [CrossRef]
- Ryżak, M.; Bieganowski, A. Methodological Aspects of Determining Soil Particle-size Distribution Using the Laser Diffraction Method. J. Plant Nutr. Soil Sci. 2011, 174, 624–633. [Google Scholar] [CrossRef]
- Liao, K.; Xu, S.; Wu, J.; Zhu, Q. Spatial Estimation of Surface Soil Texture Using Remote Sensing Data. Soil Sci. Plant Nutr. 2013, 59, 488–500. [Google Scholar] [CrossRef]
- Wang, D.-C.; Zhang, G.-L.; Zhao, M.-S.; Pan, X.-Z.; Zhao, Y.-G.; Li, D.-C.; Macmillan, B. Retrieval and Mapping of Soil Texture Based on Land Surface Diurnal Temperature Range Data from MODIS. PLoS ONE 2015, 10, e0129977. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical Tools for Characterizing the Spatial Variability of Microbiological and Physico-Chemical Soil Properties. Biol. Fertil. Soils 1998, 27, 315–334. [Google Scholar] [CrossRef] [Green Version]
- Kaya, F.; Başayiğit, L. Spatial Prediction and Digital Mapping of Soil Texture Classes in a Floodplain Using Multinomial Logistic Regression. In International Conference on Intelligent and Fuzzy Systems; Springer: Cham, Switzerland, 2021; pp. 463–473. [Google Scholar]
- Amirian-Chakan, A.; Minasny, B.; Taghizadeh-Mehrjardi, R.; Akbarifazli, R.; Darvishpasand, Z.; Khordehbin, S. Some Practical Aspects of Predicting Texture Data in Digital Soil Mapping. Soil Tillage Res. 2019, 194, 104289. [Google Scholar] [CrossRef]
- Mallah, S.; Delsouz Khaki, B.; Davatgar, N.; Bazargan, K.; Vahed, H.S.; Rezaee, L.; Shakouri Katigari, M.; Shokri Vahed, H.; Sheikholeslam, H.; Shirinfekr, A. Comparison of Three Geostatistics Methods for Prediction of Soil Texture Classes in Crop and Orchard Lands of Guilan Province. Iran. J. Soil Res. 2019, 33, 213–225. [Google Scholar]
- Zaeri, K.; Hazbavi, S.; Toomanian, N.; Zadeh, J.T. Creating Surface Soil Texture Map with Indicator Kriging Technique: A Case Study of Central Iran Soils. Int. J. Agric. Crop Sci. (IJACS) 2013, 6, 518–521. [Google Scholar]
- Hengl, T.; Toomanian, N.; Reuter, H.I.; Malakouti, M.J. Methods to Interpolate Soil Categorical Variables from Profile Observations: Lessons from Iran. Geoderma 2007, 140, 417–427. [Google Scholar] [CrossRef]
- Ma, Y.; Minasny, B.; Malone, B.P.; Mcbratney, A.B. Pedology and Digital Soil Mapping (DSM). Eur. J. Soil Sci. 2019, 70, 216–235. [Google Scholar] [CrossRef]
- McBratney, A.B.; Mendonça Santos, M.L.; Minasny, B. On Digital Soil Mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Zhang, S.; Shen, C.; Chen, X.; Ye, H.; Huang, Y.; Lai, S. Spatial Interpolation of Soil Texture Using Compositional Kriging and Regression Kriging with Consideration of the Characteristics of Compositional Data and Environment Variables. J. Integr. Agric. 2013, 12, 1673–1683. [Google Scholar] [CrossRef] [Green Version]
- Padarian, J.; Minasny, B.; McBratney, A.B. Machine Learning and Soil Sciences: A Review Aided by Machine Learning Tools. Soil 2020, 6, 35–52. [Google Scholar] [CrossRef] [Green Version]
- Greve, M.H.; Kheir, R.B.; Greve, M.B.; Bøcher, P.K. Quantifying the Ability of Environmental Parameters to Predict Soil Texture Fractions Using Regression-Tree Model with GIS and LIDAR Data: The Case Study of Denmark. Ecol. Indic. 2012, 18, 1–10. [Google Scholar] [CrossRef]
- Khanbabakhani, E.; Torkashvand, A.M.; Mahmoodi, M.A. The Possibility of Preparing Soil Texture Class Map by Artificial Neural Networks, Inverse Distance Weighting, and Geostatistical Methods in Gavoshan Dam Basin, Kurdistan Province, Iran. Arab. J. Geosci. 2020, 13, 237. [Google Scholar] [CrossRef]
- Mehrabi-Gohari, E.; Matinfar, H.R.; Jafari, A. The Spatial Prediction of Soil Texture Fractions in Arid Regions of Iran. Soil Syst. 2019, 3, 65. [Google Scholar] [CrossRef] [Green Version]
- Song, X.-D.; Liu, F.; Zhang, G.-L.; Li, D.-C.; Zhao, Y.-G. Estimation of Soil Texture at a Regional Scale Using Local Soil-Landscape Models. Soil Sci. 2016, 181, 435–445. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, W.; Zhou, W.; Li, X.; Yue, T. Comparison of Additive and Isometric Log-Ratio Transformations Combined with Machine Learning and Regression Kriging Models for Mapping Soil Particle Size Fractions. Geoderma 2020, 365, 114214. [Google Scholar] [CrossRef]
- Wu, W.; Li, A.-D.; He, X.-H.; Ma, R.; Liu, H.-B.; Lv, J.-K. A Comparison of Support Vector Machines, Artificial Neural Network and Classification Tree for Identifying Soil Texture Classes in Southwest China. Comput. Electron. Agric. 2018, 144, 86–93. [Google Scholar] [CrossRef]
- Zhao, Z.; Chow, T.L.; Rees, H.W.; Yang, Q.; Xing, Z.; Meng, F.-R. Predict Soil Texture Distributions Using an Artificial Neural Network Model. Comput. Electron. Agric. 2009, 65, 36–48. [Google Scholar] [CrossRef]
- Heung, B.; Ho, H.C.; Zhang, J.; Knudby, A.; Bulmer, C.E.; Schmidt, M.G. An Overview and Comparison of Machine-Learning Techniques for Classification Purposes in Digital Soil Mapping. Geoderma 2016, 265, 62–77. [Google Scholar] [CrossRef]
- Yang, L.; Cai, Y.; Zhang, L.; Guo, M.; Li, A.; Zhou, C. A Deep Learning Method to Predict Soil Organic Carbon Content at a Regional Scale Using Satellite-Based Phenology Variables. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102428. [Google Scholar] [CrossRef]
- Chen, T.; Niu, R.; Wang, Y.; Li, P.; Zhang, L.; Du, B. Assessment of Spatial Distribution of Soil Loss over the Upper Basin of Miyun Reservoir in China Based on RS and GIS Techniques. Environ. Monit. Assess. 2011, 179, 605–617. [Google Scholar] [CrossRef] [PubMed]
- Gomez, C.; Dharumarajan, S.; Féret, J.-B.; Lagacherie, P.; Ruiz, L.; Sekhar, M. Use of Sentinel-2 Time-Series Images for Classification and Uncertainty Analysis of Inherent Biophysical Property: Case of Soil Texture Mapping. Remote Sens. 2019, 11, 565. [Google Scholar] [CrossRef]
- Jafari, A.; Finke, P.; Vande Wauw, J.; Ayoubi, S.; Khademi, H. Spatial Prediction of USDA-great Soil Groups in the Arid Zarand Region, Iran: Comparing Logistic Regression Approaches to Predict Diagnostic Horizons and Soil Types. Eur. J. Soil Sci. 2012, 63, 284–298. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Minasny, B.; Sarmadian, F.; Malone, B.P. Digital Mapping of Soil Salinity in Ardakan Region, Central Iran. Geoderma 2014, 213, 15–28. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Guided Tour. In Soft Computing and Intelligent Systems: Theory and Applications; McMaster University: Hamilton, ON, USA, 1999; p. 71. [Google Scholar]
- Merdun, H.; Çınar, Ö.; Meral, R.; Apan, M. Comparison of Artificial Neural Network and Regression Pedotransfer Functions for Prediction of Soil Water Retention and Saturated Hydraulic Conductivity. Soil Tillage Res. 2006, 90, 108–116. [Google Scholar] [CrossRef]
- Pentoś, K.; Pieczarka, K.; Lejman, K. Application of Soft Computing Techniques for the Analysis of Tractive Properties of a Low-Power Agricultural Tractor under Various Soil Conditions. Complexity 2020, 2020, 7607545. [Google Scholar] [CrossRef]
- Rajurkar, M.P.; Kothyari, U.C.; Chaube, U.C. Modeling of the Daily Rainfall-Runoff Relationship with Artificial Neural Network. J. Hydrol. 2004, 285, 96–113. [Google Scholar] [CrossRef]
- Ray, A.; Halder, T.; Jena, S.; Sahoo, A.; Ghosh, B.; Mohanty, S.; Mahapatra, N.; Nayak, S. Application of Artificial Neural Network (ANN) Model for Prediction and Optimization of Coronarin D Content in Hedychium Coronarium. Ind. Crops Prod. 2020, 146, 112186. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, Q.; Sun, D.; Ding, X.; Meng, F.-R. Extended Model Prediction of High-Resolution Soil Organic Matter over a Large Area Using Limited Number of Field Samples. Comput. Electron. Agric. 2020, 169, 105172. [Google Scholar] [CrossRef]
- Li, Q.-Q.; Wang, C.-Q.; Zhang, W.-J.; Yu, Y.; Li, B.; Yang, J.; Bai, G.-C.; Cai, Y. Prediction of Soil Nutrients Spatial Distribution Based on Neural Network Model Combined with Goestatistics. Ying Yong Sheng Tai Xue Bao J. Appl. Ecol. 2013, 24, 459–466. [Google Scholar]
- Song, Y.-Q.; Yang, L.-A.; Li, B.; Hu, Y.-M.; Wang, A.-L.; Zhou, W.; Cui, X.-S.; Liu, Y.-L. Spatial Prediction of Soil Organic Matter Using a Hybrid Geostatistical Model of an Extreme Learning Machine and Ordinary Kriging. Sustainability 2017, 9, 754. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Z.; Zhang, F.; Chai, X.; Zhu, Z.; Ma, F. Spatial Estimation of Soil Moisture and Salinity With Neural Kriging. In Computer and Computing Technologies in Agriculture II, Volume 2; IFIP Advances in Information and Communication Technology; Li, D., Zhao, C., Eds.; Springer US: Boston, MA, USA, 2009; Volume 294, pp. 1227–1237. ISBN 978-1-4419-0210-8. [Google Scholar]
- De Martonne, E. Une Nouvelle Function Climatologique: L’indice d’aridité. Meteorologie 1926, 2, 449–459. [Google Scholar]
- Banai, M.; MH, B. Soil Moisture and Temperature Regime Map of Iran. In Proceedings of the International Congress of Soil Science, Edmonton, AB, Canada, 19–27 June 1998. [Google Scholar]
- Haghipour, A.; Aghanabati, A. Geological Map of Iran 1: 2.500. 000 Scale; Geological Survey of Iran: Tehran, Iran, 1989. [Google Scholar]
- Saadat, S. Soil Quality Monitoring in Agricultural Lands; Soil and Water Research Institute: Karaj, Iran, 2018; p. 992. [Google Scholar]
- Gee, G.; Bauder, J. Particle-Size Analysis. In Methods of Soil Analysis. Part 1. Agron. Monogr. 9; Klute, A., Ed.; ASA and SSSA: Madison, WI, USA, 1986; pp. 383–411. [Google Scholar]
- Gerakis, A.; Baer, B. A Computer Program for Soil Textural Classification. Soil Sci. Soc. Am. J. 1999, 63, 807–808. [Google Scholar] [CrossRef]
- Jackson, R.D.; Bell, M.M.; Gratton, C. Assessing Ecosystem Variance at Different Scales to Generalize about Pasture Management in Southern Wisconsin. Agric. Ecosyst. Environ. 2007, 122, 471–478. [Google Scholar] [CrossRef]
- Ali, S.M.; Malik, R.N. Spatial Distribution of Metals in Top Soils of Islamabad City, Pakistan. Env. Monit. Assess 2011, 172, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Robertson, G. GS+:“Geostatistics for the Environmental Sciences”; Gamma Design Software: Plainwell, MI, USA, 2008; Available online: https://geostatistics.com/files/GSPlusUserGuide.pdf (accessed on 20 February 2022).
- Trangmar, B.B.; Yost, R.S.; Uehara, G. Application of Geostatistics to Spatial Studies of Soil Properties. In Advances in Agronomy; Elsevier: Amsterdam, The Netherlands, 1986; Volume 38, pp. 45–94. ISBN 978-0-12-000738-7. [Google Scholar]
- Isaaks, E.H.; Srivastava, R.M. Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989; p. 561. [Google Scholar]
- Kravchenko, A.; Bullock, D.G. A Comparative Study of Interpolation Methods for Mapping Soil Properties. Agron. J. 1999, 91, 393–400. [Google Scholar] [CrossRef]
- Mueller, T.G.; Pierce, F.J.; Schabenberger, O.; Warncke, D.D. Map Quality for Site-Specific Fertility Management. Soil Sci. Soc. Am. J. 2001, 65, 1547–1558. [Google Scholar] [CrossRef]
- Conrad, C.; Lamers, J.P.A.; Ibragimov, N.; Löw, F.; Martius, C. Analysing Irrigated Crop Rotation Patterns in Arid Uzbekistan by the Means of Remote Sensing: A Case Study on Post-Soviet Agricultural Land Use. J. Arid Environ. 2016, 124, 150–159. [Google Scholar] [CrossRef]
- Karegowda, A.G.; Manjunath, A.; Jayaram, M. Comparative Study of Attribute Selection Using Gain Ratio and Correlation Based Feature Selection. Int. J. Inf. Technol. Knowl. Manag. 2010, 2, 271–277. [Google Scholar]
- Cleveland, W.S.; Loader, C. Smoothing by Local Regression: Principles and Methods. In Statistical Theory and Computational Aspects of Smoothing; Springer: Berlin/Heidelberg, Germany, 1996; pp. 10–49. [Google Scholar]
- Zhang, W.; Goh, A.T.C. Multivariate Adaptive Regression Splines and Neural Network Models for Prediction of Pile Drivability. Geosci. Front. 2016, 7, 45–52. [Google Scholar] [CrossRef] [Green Version]
- Jamieson, P.; Porter, J.; Wilson, D. A Test of the Computer Simulation Model ARCWHEAT1 on Wheat Crops Grown in New Zealand. Field Crops Res. 1991, 27, 337–350. [Google Scholar] [CrossRef]
- Landis, J.R.; Koch, G.G. The Measurement of Observer Agreement for Categorical Data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matinfar, H.; Sarmadian, F.; Alavi Panah, S.; Heck, R. Comparisons of Object-Oriented and Pixel-Based Classification of Land Use/Land Cover Types Based on Lansadsat7, Etm+ Spectral Bands (Case Study: Arid Region of Iran). Am. Eurasian J. Agric. Environ. Sci. 2007, 2, 448–456. [Google Scholar]
- Versluis, A.; Rogan, J. Mapping Land-Cover Change in a Haitian Watershed Using a Combined Spectral Mixture Analysis and Classification Tree Procedure. Geocarto Int. 2010, 25, 85–103. [Google Scholar] [CrossRef]
- Barthold, F.K.; Wiesmeier, M.; Breuer, L.; Frede, H.-G.; Wu, J.; Blank, F.B. Land Use and Climate Control the Spatial Distribution of Soil Types in the Grasslands of Inner Mongolia. J. Arid Environ. 2013, 88, 194–205. [Google Scholar] [CrossRef]
- Brungard, C.W.; Boettinger, J.L.; Duniway, M.C.; Wills, S.A.; Edwards Jr, T.C. Machine Learning for Predicting Soil Classes in Three Semi-Arid Landscapes. Geoderma 2015, 239, 68–83. [Google Scholar] [CrossRef]
- Pahlavan Rad, M.R.; Toomanian, N.; Khormali, F.; Brungard, C.W.; Komaki, C.B.; Bogaert, P. Updating Soil Survey Maps Using Random Forest and Conditioned Latin Hypercube Sampling in the Loess Derived Soils of Northern Iran. Geoderma 2014, 232–234, 97–106. [Google Scholar] [CrossRef]
- Roecker, S.M.; Howell, D.W.; Haydu-Houdeshell, C.A.; Blinn, C. A Qualitative Comparison of Conventional Soil Survey and Digital Soil Mapping Approaches. In Digital Soil Mapping; Boettinger, J.L., Howell, D.W., Moore, A.C., Hartemink, A.E., Kienast-Brown, S., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 369–384. ISBN 978-90-481-8862-8. [Google Scholar]
- Stum, A.K.; Boettinger, J.L.; White, M.A.; Ramsey, R.D. Random Forests Applied as a Soil Spatial Predictive Model in Arid Utah. In Digital Soil Mapping; Boettinger, J.L., Howell, D.W., Moore, A.C., Hartemink, A.E., Kienast-Brown, S., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 179–190. ISBN 978-90-481-8862-8. [Google Scholar]
- Zeraatpisheh, M.; Ayoubi, S.; Jafari, A.; Finke, P. Comparing the Efficiency of Digital and Conventional Soil Mapping to Predict Soil Types in a Semi-Arid Region in Iran. Geomorphology 2017, 285, 186–204. [Google Scholar] [CrossRef]
- Al-Omran, A.M.; Al-Wabel, M.I.; El-Maghraby, S.E.; Nadeem, M.E.; Al-Sharani, S. Spatial Variability for Some Properties of the Wastewater Irrigated Soils. J. Saudi Soc. Agric. Sci. 2013, 12, 167–175. [Google Scholar] [CrossRef] [Green Version]
- Emadi, M.; Baghernejad, M.; Maftoun, M. Assessment of Some Soil Properties by Spatial Variability in Saline and Sodic Soils in Arsanjan Plain, Southern Iran. Pak. J. Biol. Sci. PJBS 2008, 11, 238–243. [Google Scholar] [CrossRef] [Green Version]
- Taghizadeh-Mehrjardi, R.; Emadi, M.; Cherati, A.; Heung, B.; Mosavi, A.; Scholten, T. Bio-Inspired Hybridization of Artificial Neural Networks: An Application for Mapping the Spatial Distribution of Soil Texture Fractions. Remote Sens. 2021, 13, 1025. [Google Scholar] [CrossRef]
- Kiani-Harchegani, M.; Sadeghi, S.H.; Asadi, H. Comparing Grain Size Distribution of Sediment and Original Soil under Raindrop Detachment and Raindrop-Induced and Flow Transport Mechanism. Hydrol. Sci. J. 2018, 63, 312–323. [Google Scholar] [CrossRef]
- Javad, S.M. The Effect of Toposequence on Physical and Chemical Characteristics of Paddy Soils of Guilan Province, Northern Iran, Rasht. Afr. J. Agric. Res. 2013, 8, 1975–1982. [Google Scholar]
- Mallah, S.; Delsouz Khaki, B.; Davatgar, N.; Scholten, T.; Amirian-Chakan, A.; Emadi, M.; Kerry, R.; Mosavi, A.H.; Taghizadeh-Mehrjardi, R. Predicting Soil Textural Classes Using Random Forest Models: Learning from Imbalanced Dataset. Agronomy 2022, 12, 2613. [Google Scholar] [CrossRef]
- Kaya, F.; Başayiğit, L.; Keshavarzi, A.; Francaviglia, R. Digital Mapping for Soil Texture Class Prediction in Northwestern Türkiye by Different Machine Learning Algorithms. Geoderma Reg. 2022, 31, e00584. [Google Scholar] [CrossRef]
- Adhikari, K.; Kheir, R.B.; Greve, M.B.; Bøcher, P.K.; Malone, B.P.; Minasny, B.; McBratney, A.B.; Greve, M.H. High-Resolution 3-D Mapping of Soil Texture in Denmark. Soil Sci. Soc. Am. J. 2013, 77, 860–876. [Google Scholar] [CrossRef]
- Akpa, S.I.C.; Odeh, I.O.A.; Bishop, T.F.A.; Hartemink, A.E. Digital Mapping of Soil Particle-Size Fractions for Nigeria. Soil Sci. Soc. Am. J. 2014, 78, 1953–1966. [Google Scholar] [CrossRef]
- Muzzamal, M.; Huang, J.; Nielson, R.; Sefton, M.; Triantafilis, J. Mapping Soil Particle-Size Fractions Using Additive Log-Ratio (ALR) and Isometric Log-Ratio (ILR) Transformations and Proximally Sensed Ancillary Data. Clays Clay Miner. 2018, 66, 9–27. [Google Scholar] [CrossRef]
- Torabi Golsefidi, H.; Karimian Eghbal, M.; Kalbasi, M. Clay Mineral Investigation of Paddy Soils of Different Landforms of Eastern Guilan Province. J. Water Soil Sci. 2001, 15, 122–138. [Google Scholar]
- De Wit, A.; Clevers, J. Efficiency and Accuracy of Per-Field Classification for Operational Crop Mapping. Int. J. Remote Sens. 2004, 25, 4091–4112. [Google Scholar] [CrossRef]



| Reference | Variables | Strongest Correlation | Climate/Soil Moisture Regime | Scale/Location | |
|---|---|---|---|---|---|
| Dependent | Independent | ||||
| Zhao et al., 2009 [42] | STFs: Sand; Clay. | The hydrographic parameters derived from DEM; SD; SDR; VSP. | Hydrographic parameters derived from DEM. | Average annual rainfall, snowfall, and daily temperatures are 730.7 mm, 306.7 cm and 3.7 °C, respectively. | Watershed, Canada |
| Greve et al., 2012 [36] | STFs: Coarse sand; Fine sand; Silt; Clay. | Seven primary terrain parameters: ELV; Slope gradient; Slope aspect. Existing maps: parent materials, landscape types, geographic region, profile curvature. Available pluviometric station data: yearlyprecipitation, seasonalprecipitation. CTI-extracted, generated usingLIDAR. Others: plan curvature, flow direction, flow accumulation. | Coarse sand: elevation (13%); fine sand: slope aspect (14%), ELV (12%), CTI (9%). Common in all STFs: parent materials (47–100%), geographic regions (31–100%) and landscape types (68–100%). Clay: Yearly-precipitation, Seasonal-precipitation, ELV (10%) Silt: Yearlyprecipitation, Seasonalprecipitation, parent materials (47% and 100%), geographic regions (31–100%), landscape types (68–100%). | Temperate climate with a mean winter temperature of 0 °C and a summer mean of 16 °C. | Denmark |
| Bakker A., 2012 [3] | STFs: Sand; Silt; Clay. | PC3; NDVI; DEM; Slope; TWI; CURVATURE; Profile; Planform; Temperature; Seasonal precipitation; SWI; CI; MI; QI. | STFs: Clay: temperature, seasonal precipitation, DEM, QI; Silt: seasonal precipitation, SLOPE, planform, CURVATURE, MI, NDVI; Sand: seasonal precipitation, NDVI, DEM, planform; | Warm, temperate with dry and hot summer. | Morocco |
| ST | Slope; CURVATURE; Mineral indices; ASTER SWIR bands; ASTER TIR bands. | ||||
| Liao et al., 2013 [24] | STFs: Sand; Silt; Clay. | Six bands DN of Landsat ETM: Bands 1–5 and Band 7; DN of Band 7. | Band 7 ETM | ||
| Wang et al., 2015 [25] | STFs: Sand; Clay; Physical clay content. | LSDT; LSNT; DTR. (During 2004, 2007 and 2008) | DTR | Not reported. | Farmland/ river plain, East China |
| Song et al., 2016 [39] | STFs: Sand; Clay. | ELV; TWI; Slope; ASP. Plan curvature; Profile curvature; MAP; MAAT; SR; NDVI; Land cover; ST. | Sand: DEM, MAAT, TWI, slope, SR, plan curvature, land cover. Clay: NDVI, ST, MAP, TWI, profile curvature. | Humid and cold. | Mountains/ Qinghai-Tibetan plateau, China, covered primarily by alpine meadow |
| Wu et al., 2018 [41] | STC: Sandy; Loamy; Clayey. | ELV; TCI_Low; Flow-PathL. | ELV; TCI_Low; Flow- PathLength. | MAP: 1037.7 mm. | Small mountainous watershed located in the core areas of a river in southwest China |
| Mehrabi-Gohari et al., 2019 [38] | STFs: Sand; Silt; Clay. | Terrain attributes extracted from DEM—90 m resolution (Slope, ASP, TWI, NDVI, etc.) B2, B3, B4, B5, B6, B7, B8, B10 and B11 Landsat 8 bands. Soil spectral data; | Soil spectral data. Spectrometric data; multi-resolution, valley-bottom flatness index and wetness index. | Arid. | Approximately 70 km awayfrom Kerman, city of Zarand, southeastern Iran |
| Amrian-Chakan et al., 2019 [28] | STFs: Sand; Silt; Clay; TIW; AWC. | Terrain attributes; B1, B2, B3, B4, B5, B7; Landsat 8 bands; BS2, BS3, BS4, BS6, BS7, BS8, BS12 Sentinel-2 bands; NDVI; Clay index. | MRVBF; NDVI; Elevation; Slope; B3. | Semi-arid region with mean annual temperature, mean annual rainfall and annual evaporation of 25 °C, 323 mm and 2818 mm. | Northeast of Behbahan city in Khuzestan province, southwestern Iran |
| Wang et al., 2020 [40] | STFs: Sand; Silt; Clay. | MAP; Temperature; SOC; Thickness; NDVI; ELV; Vegetation types; ST; Geomorphology types; Land-use types. | Temperature; MAP; ELV; ST; SOC; NDVI. | Extremely hot in summer and severely cold in winter with low MAP, strong solar radiation and high evaporation rate. | River basin, China |
| Ding et al., 2020 [5] | STFs: Sand; Clay. | Nine topo-hydrogenic from DEM (ELV, Slope, PSR, ASP, SDR, VSP, FD, FL) with 10 m resolution. | DEM-derived topo-hydrologic variables(ASP, ELV, SDR, PSR, FL, VSF, PSR, STF). | Udults. | Forest, China |
| Khanbabakhani et al., 2020 [37] | STFs: Sand; Silt; Clay. | Longitude; Altitude; ELV; Slope (%). | Not reported. | Not reported. | Gavoshan dam basin in Kurdistan Province |
| Taghizadeh-Mehrjardi et al., 2020 [14] | STFs: Sand; Silt; Clay. | Terrain attributes; RS data; Climatic data; Soil data. | B12 and B7 of Sentinel-2 and Landsat-8 images; NDVI; Clay index. | Arid and semi-arid average annual rainfall: 96–359 mm. | Central Iran |
| Zhou et al., 2022 [1] | ST | Multitemporal Sentinel-2 image; DEM derivatives and stratum; B5, B6, B7, B8A, B11, B12, red-edge factors, MCARI, NDI45, CI, BI, NDVI, SAVI. | Elevation, stratum, red-edge factors. | Multi-crop farming and subtropical monsoon, humid climate. | Southwestern China |
| Attr. | Def. | Abr. | Res. | Sor. |
|---|---|---|---|---|
| Analytical hill-shading | ANHL | 90 m | SAGA GIS | |
| Aspect | ASP | 90 m | SAGA GIS | |
| Channel network base level | CHNBL | 90 m | SAGA GIS | |
| Convergence index | CONI | 90 m | SAGA GIS | |
| Cross-sectional curvature | CRCRV | 90 m | SAGA GIS | |
| Digital elevation model | DEM | 90 m | SRTM | |
| Flow accumulation | FACC | 90 m | SAGA GIS | |
| Landforms | LFMs | 90 m | SAGA GIS | |
| Longitudinal curvature | LNCRV | 90 m | SAGA GIS | |
| LS factor | LSFA | 90 m | SAGA GIS | |
| Multiresolution index of the ridgetop’sflatness | MRRTF | 90 m | SAGA GIS | |
| Multiresolution index of valley bottom’sflatness | MRVBF | 90 m | SAGA GIS | |
| Relative slope position | RESLPO | 90 m | SAGA GIS | |
| Slope | SLP | 90 m | SAGA GIS | |
| Topographic wetness index | TWIN | 90 m | SAGA GIS | |
| Valley depth | VADE | 90 m | SAGA GIS | |
| Vertical distance to channel Network | VDCN | 90 m | SAGA GIS | |
| Clay particle content | CLC | 90 m | [61] | |
| Silt particle content | SIC | 90 m | [61] | |
| Sand particle content | SDC | 90 m | [61] |
| Particle | Min | Max | AM | GM | Mode | Median | St. Dev | Skewness | Kurtosis | % C.V |
|---|---|---|---|---|---|---|---|---|---|---|
| Clay (%) | 1 | 66 | 39.4 | 29.3 | 40 | 29.7 | 10.6 | −0.408 * | −0.408 * | 27 |
| Sand (%) | 1 | 99 | 31.5 | 30.8 | 24 | 30.4 | 13.4 | −1.197 * | 0.709 * | 43 |
| Silt (%) | 1 | 81 | 39.8 | 39.8 | 42 | 39.6 | 9.14 | −1.493 * | 0.158 * | 23 |
| STFs | Model | (C0) | (C0 + C) | A0 (m) | C0/(C0 + C) (%) | R2 | RSS |
|---|---|---|---|---|---|---|---|
| Clay | Expo | 60 | 110 | 4000 | 0.54 | 0.91 | 86 |
| Sand | Expo | 0/13 | 0/24 | 6000 | 0.54 | 0.94 | 0.001 |
| Silt | Expo | 62 | 89 | 8000 | 0.7 | 0.93 | 16.8 |
| Variable | Interpolation Method | R2 | RMSE | NRMSE | d | ME | Equation |
|---|---|---|---|---|---|---|---|
| Clay | OK | 0.54 | 7.3 | 0.25 | 0.8 | 0.006 | y = 0.4365x + 16.366 |
| IDW | 0.64 | 6.4 | 0.22 | 0.87 | 0.023 | y = 0.5962x + 11.762 | |
| Sand | OK | 0.52 | 9.3 | 0.29 | 0.8 | 0.29 | y = 0.4565x + 17.429 |
| IDW | 0.67 | 7.9 | 0.25 | 0.87 | 0.03 | y = 0.6039x + 12.518 |
| Reference | No of Samples | Depth (cm) | Method | Particles | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sand | Silt | Clay | |||||||||||
| Fine Sand | Coarse Sand | Sand | |||||||||||
| ME | RMSE | ME | RMSE | ME | RMSE | ME | RMSE | ME | RMSE | ||||
| Zhao et al., 2009 [42] | 442 | NA | ANN LM | NA | NA | NA | NA | 8.11 | 16.6 | NA | NA | 1.18 | 7.9 |
| ANN RP | NA | NA | NA | NA | 1.12 | 14.9 | NA | NA | 2.07 | 8.5 | |||
| Greve et al., 2012 [36] | 45,224 | 0–30 | RT | 7.54 | 11.31 | 8.64 | 12.46 | NA | NA | 2.51 | 12.41 | 2.27 | 11.41 |
| Wang et al., 2015 [25] | 62 | Topsoil | LRM | NA | NA | NA | NA | 8.72 | 10.69 | NA | NA | 3.44 | 4.57 |
| Song et al., 2016 [39] | 119 | 0–120 | ANN RF | NA | NA | NA | NA | NA | 12.5 | NA | NA | NA | 3 |
| Mehrabi et al., 2019 [38] | 115 | 0–5 | RT | NA | NA | NA | NA | 0.09 | 6.98 | 0.21 | 4.64 | 0.04 | 5.07 |
| ANN | NA | NA | NA | NA | 0.06 | 4.07 | 0.1 | 2.75 | 0.02 | 2.02 | |||
| ANFIS | NA | NA | NA | NA | 0.06 | 4 | 0.09 | 2.68 | 0.02 | 2 | |||
| Wang et al., 2020 [40] | 640 | 0–20 | ALR-BRT | NA | NA | NA | NA | 0.57 | 15.99 | −2.23 | 15.1 | NA | 1.75 |
| ALR-RF | NA | NA | NA | NA | 0.38 | 15.7 | −1.78 | 14.53 | NA | 1.4 | |||
| ALR-RK | NA | NA | NA | NA | −2.34 | 17.92 | 0.86 | 17.05 | NA | 1.49 | |||
| ILR-BRT | NA | NA | NA | NA | 0.84 | 15.56 | −2.44 | 14.71 | NA | 1.6 | |||
| ILR-RF | NA | NA | NA | NA | 0.51 | 15.35 | −1.89 | 14.2 | NA | 1.38 | |||
| ILR-RK | NA | NA | NA | NA | −2.66 | 16.91 | 1.77 | 16.6 | NA | 0.89 | |||
| Khanbabakhani et al., 2020 | 105 | 0–15 | ANN | NA | NA | NA | NA | NA | 4 | NA | 4 | NA | 4 |
| Zhou et al., 2022 [1,37] | 943 | 0–20 | SVM and SHAP | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| Covariates | B | Std. Error | St. B | P.co | T | p-Value |
|---|---|---|---|---|---|---|
| CLC | 0.051 | 0.005 | 0.156 | 0.162 | 10.270 | 0.000 |
| SIC | −0.007 | 0.006 | −0.019 | −0.031 | −1.273 | 0.038 |
| ANAHILL | −0.383 | 0.531 | −0.012 | −0.006 | −0.721 | 0.471 |
| ASP | 0.009 | 0.026 | 0.006 | 0.007 | 0.371 | 0.662 |
| CHNBL | 0.014 | 0.014 | 0.160 | 0.083 | 1.009 | 0.000 |
| CONI | 0.002 | 0.003 | 0.007 | 0.005 | 0.483 | 0.629 |
| CRCRV | 229.050 | 288.751 | 0.014 | 0.027 | 0.793 | 0.428 |
| DEM | −0.008 | 0.014 | −0.111 | 0.080 | −0.588 | 0.000 |
| FACC | 2.820 × 10−10 | 0.000 | 0.003 | −0.002 | 0.209 | 0.835 |
| LFMs | −0.059 | 0.157 | −0.007 | 0.032 | −0.375 | 0.034 |
| LNCRV | 287.705 | 247.781 | 0.022 | 0.004 | 1.161 | 0.246 |
| LSFA | −0.157 | 0.099 | −0.056 | 0.032 | −1.586 | 0.031 |
| MRRTF | −0.145 | 0.034 | −0.072 | −0.0081 | −4.308 | 0.000 |
| MRVBF | 0.061 | 0.051 | 0.028 | −0.053 | 1.196 | 0.232 |
| RESLPO | −247.250 | 67.044 | −0.563 | 0.042 | −3.688 | 0.000 |
| SLP | 5.694 | 2.881 | 0.086 | 0.053 | 1.976 | 0.000 |
| TWIN | 0.004 | 0.022 | 0.003 | −0.019 | 0.161 | 0.202 |
| VADE | 0.000 | 0.001 | −0.010 | −0.053 | −0.495 | 0.000 |
| VDCN | 0.132 | 0.036 | 0.591 | 0.047 | 3.688 | 0.000 |
| MXNDVI | −0.313 | 0.432 | −0.011 | −0.012 | −0.725 | 0.468 |
| Class | C | S | LS | SL | SIC | SICL | SC | SCL | CL | SIL | L | Observation |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | 147 | - | 0 | 0 | 19 | 24 | - | 0 | 334 | 0 | 25 | 549 |
| S | 0 | - | 3 | 0 | 0 | 0 | - | 0 | 1 | 0 | 2 | 6 |
| LS | 0 | - | 1 | 7 | 0 | 0 | - | 1 | 3 | 0 | 5 | 17 |
| SL | 0 | - | 2 | 53 | 0 | 0 | - | 3 | 26 | 1 | 137 | 222 |
| SIC | 20 | - | 0 | 0 | 92 | 75 | - | 0 | 157 | 2 | 6 | 352 |
| SICL | 2 | - | 0 | 0 | 12 | 146 | - | 0 | 201 | 13 | 40 | 414 |
| SC | 0 | - | 0 | 0 | 0 | 0 | - | 0 | 1 | 0 | 0 | 1 |
| SCL | 0 | - | 0 | 2 | 0 | 0 | - | 9 | 24 | 0 | 40 | 75 |
| CL | 20 | - | 0 | 5 | 6 | 39 | - | 5 | 979 | 2 | 218 | 1274 |
| SIL | 1 | - | 0 | 2 | 0 | 18 | - | 0 | 59 | 93 | 171 | 344 |
| L | 3 | - | 1 | 12 | 4 | 11 | - | 1 | 345 | 22 | 840 | 1239 |
| Total | 193 | - | 7 | 81 | 133 | 313 | - | 19 | 2130 | 133 | 1484 | 4493 |
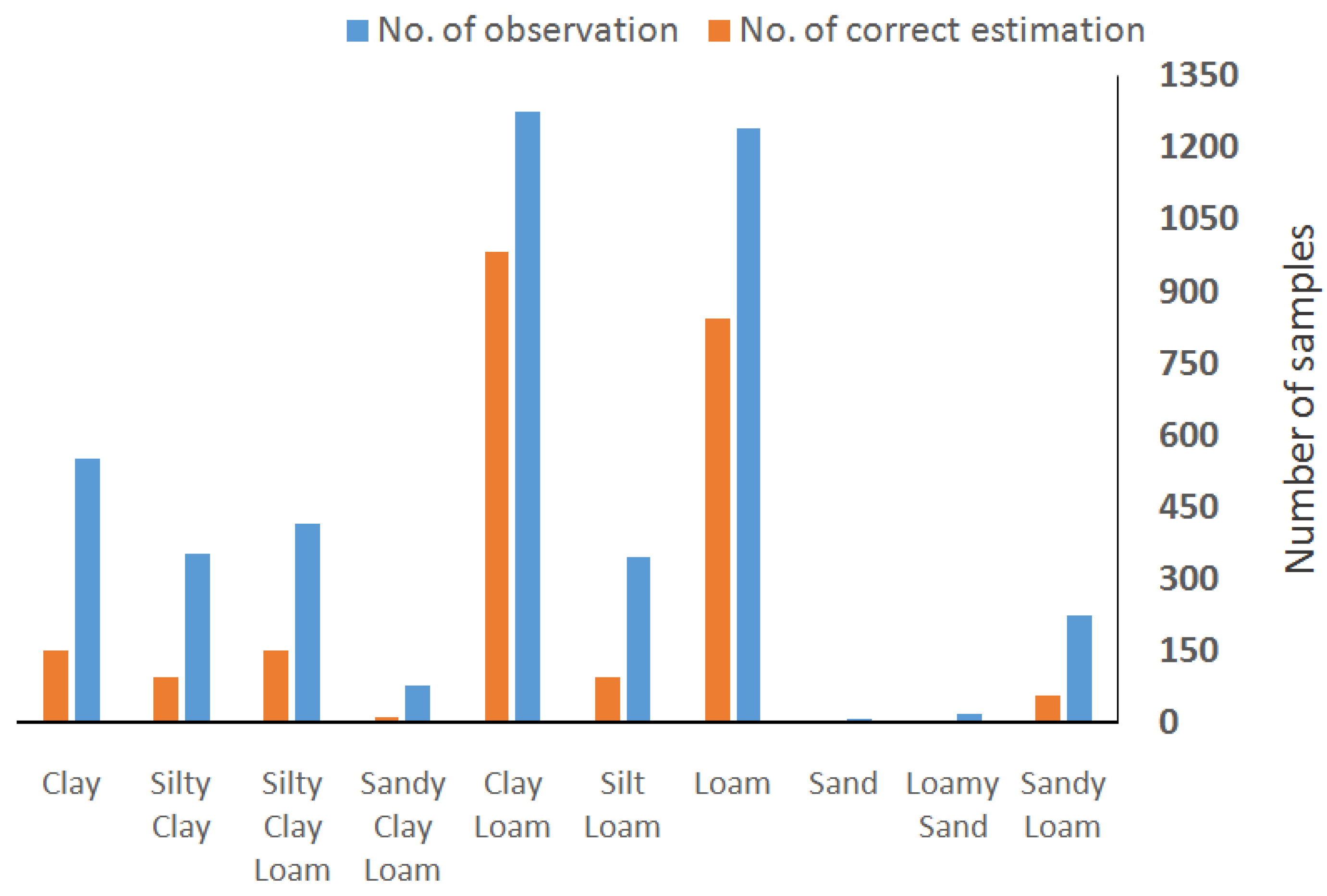
| Soil Texture Class | Reference Totals | Classified Totals | Number Correct | PA | UA |
|---|---|---|---|---|---|
| Clay | 193 | 549 | 147 | 76% | 27% |
| Sand | 0 | 6 | 0 | 0% | 0% |
| Loamy sand | 7 | 17 | 1 | 14% | 6% |
| Sandy loam | 81 | 222 | 53 | 65% | 24% |
| Silty clay | 133 | 352 | 92 | 69% | 26% |
| Silty clay loam | 313 | 414 | 146 | 46% | 35% |
| Sandy clay | 0 | 1 | 0 | 0% | 0% |
| Sandy clay loam | 19 | 75 | 9 | 47% | 12% |
| Clay loam | 2130 | 1274 | 979 | 46% | 77% |
| Silt loam | 133 | 344 | 93 | 70% | 27% |
| Loam | 1484 | 1239 | 840 | 56% | 68% |
| Total | 4493 | 4493 | 2360 | 55% | 33.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mallah, S.; Delsouz Khaki, B.; Davatgar, N.; Poppiel, R.R.; Demattê, J.A.M. Digital Mapping of Topsoil Texture Classes Using a Hybridized Classical Statistics–Artificial Neural Networks Approach and Relief Data. AgriEngineering 2023, 5, 40-64. https://doi.org/10.3390/agriengineering5010004
Mallah S, Delsouz Khaki B, Davatgar N, Poppiel RR, Demattê JAM. Digital Mapping of Topsoil Texture Classes Using a Hybridized Classical Statistics–Artificial Neural Networks Approach and Relief Data. AgriEngineering. 2023; 5(1):40-64. https://doi.org/10.3390/agriengineering5010004
Chicago/Turabian StyleMallah, Sina, Bahareh Delsouz Khaki, Naser Davatgar, Raul Roberto Poppiel, and José A. M. Demattê. 2023. "Digital Mapping of Topsoil Texture Classes Using a Hybridized Classical Statistics–Artificial Neural Networks Approach and Relief Data" AgriEngineering 5, no. 1: 40-64. https://doi.org/10.3390/agriengineering5010004
APA StyleMallah, S., Delsouz Khaki, B., Davatgar, N., Poppiel, R. R., & Demattê, J. A. M. (2023). Digital Mapping of Topsoil Texture Classes Using a Hybridized Classical Statistics–Artificial Neural Networks Approach and Relief Data. AgriEngineering, 5(1), 40-64. https://doi.org/10.3390/agriengineering5010004








