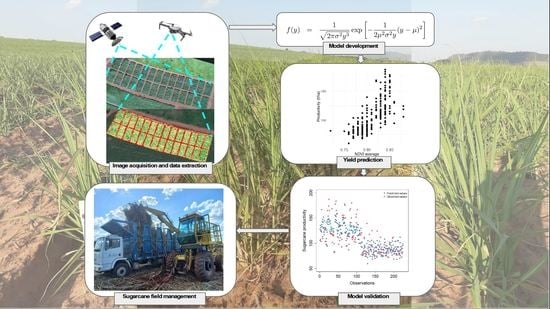
Development and Validation of a Model Based on Vegetation Indices for the Prediction of Sugarcane Yield
Abstract
:1. Introduction
2. Material and Methods
2.1. Field Experiments
2.2. Vegetation Indices
- is the reflectance factor of the red band; and
- is the reflectance factor of the near-infrared band.
- is the reflectance factor of the blue band;
- is the reflectance factor of the green band; and
- is the reflectance factor of the red band.
2.3. Data Acquisition, Preparation, and Processing
2.4. Statistical Modeling
2.5. Model Validation
3. Results and Discussion
3.1. Descriptive Analysis for the Model Development
- : sugarcane yield (t/ha);
- : block (I, II, III, and IV). In this case, we need three dummy variables, namely: (, and );
- : local (Field A and Field B); and
- : variety (0 = CTC1007, 1 = CV0618, 2 = CV7870 and 3 = RB966928). Here, three dummy variables were also used and defined as follows: (, and );
- : average NDVI; and
- : average VARI, for .
3.2. Results of the IG Semiparametric Regression Model
3.3. Use of Spectral Indices as Predictors
- Figure 8a shows the average NDVI values: the average sugarcane yield increased between NDVIs of approximately 0.70 and 0.85, but then remained constant for an average NDVI close to 0.85.
- Figure 8b shows the average VARI values: the average sugarcane yield increased between VARIs of approximately 0.25 and 0.60.
3.4. Climate
4. Validating the Model with Data from Commercial Production Fields
4.1. Descriptive Analysis of the Validation Data
- : average sugarcane productivity (t/ha);
- : location (A, B, C, D, E, and F), with five dummy variables, namely (, , …, );
- : area (ha);
- : average NDVI; and
- : average VARI, for .
4.2. Results of the IG Semiparametric Regression Model
- Figure 14a shows the area values in hectares (ha). Note that the average sugarcane productivity was highest for areas between approximately 1 and 6 ha but then declined for areas above 6 ha.
- Figure 14b shows that the average sugarcane productivity increased between average values of NDVI of approximately 0.75 and 0.80 but remained constant for average NDVI values above 0.80.
- Finally, Figure 14c shows that the average sugarcane productivity increased between average VARI values of approximately 0.10 and 0.33, decreased between average VARI values of approximately 0.33 and 0.45, and increased for average VARI values of approximately 0.45 and higher.
4.3. Model Comparison
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vandenberghe, L.P.S.; Valladares-Diestra, K.K.; Bittencourt, G.A.; Zevallos Torres, L.A.; Karp, S.G.; Sydney, E.B.; de Carvalho, J.C.; Thomaz, S.; Soccol, C.R. Beyond sugar and ethanol: The future of sugarcane biorefineries in Brazil. Renew. Sustain. Energy Rev. 2022, 167, 1–18. [Google Scholar] [CrossRef]
- Cursi, D.E.; Hoffmann, H.P.; Barbosa, G.V.S.; Bressiani, J.A.; Gazaffi, R.; Chapola, R.G.; Fernandes, A.R., Jr.; Balsalobre, T.W.A.; Diniz, C.A.; Santos, J.M.; et al. History and current status of sugarcane breeding, germplasm development and molecular genetics in Brazil. Sugar Tech 2022, 24, 112–133. [Google Scholar] [CrossRef]
- Hoffman, M.T.; Todd, S.W. Impact of environmental change on ecosystem services and human well-being in Africa. Clim. Vulnerability 2013, 1, 49–67. [Google Scholar] [CrossRef]
- Simøes, M.D.S.; Rocha, J.V.; Lamparelli, R.A.C. Spectral variables, growth analysis and yield of sugarcane. Sci. Agric. 2005, 62, 199–207. [Google Scholar] [CrossRef] [Green Version]
- Gupta, R.K.; Vijayan, D.; Prasad, T.S. Comparative analysis of red-edge hyperspectral indices. Adv. Space Res. 2003, 32, 2217–2222. [Google Scholar] [CrossRef]
- Shukla, G.; Tiwari, P.; Dugesar, S.; Srivastava, P.K. Estimation of evapotranspiration using surface energy balance system and satellite datasets. In Agricultural Water Management; Academic Press: Hoboken, NJ, USA, 2021; pp. 157–183. [Google Scholar] [CrossRef]
- Rojo-Baio, F.H.; Neves, D.C.; Teodoro, P.E. Soil chemical attributes, soil type, and rainfall effects on normalized difference vegetation index and cotton fiber yield variability. Agron. J. 2019, 111, 2910–2919. [Google Scholar] [CrossRef]
- Gonzáles, H.H.S.; Penuelas-Rubio, O.; Argentel-Martinez, L.; Ponce, A.L.; Andrade, M.H.H.; Aguilera, J.G.; Hasanuzzaman, M.; Teodoro, P.E. Salinity effects on water potential and the normalized difference vegetation index in four species of a saline semi-arid ecosystem. PeerJ 2021, 9, e12297. [Google Scholar] [CrossRef]
- Sumesh, K.C.; Sarawut, N.; Jaturong, S. Integration of RGB-based vegetation index, crop surface model and object-based image analysis approach for sugarcane yield estimation using unmanned aerial vehicle. Comput. Electron. Agric. 2021, 180, 105903. [Google Scholar] [CrossRef]
- Akbarian, S.; Xu, C.; Wang, W.; Ginns, S.; Lim, S. Sugarcane yields prediction at the row level using a novel cross-validation approach to multi-year multispectral images. Comput. Electron. Agric. 2022, 198, 107024. [Google Scholar] [CrossRef]
- Cho, Y.; Khosravikia, F.; Rathje, E.M. A comparison of artificial neural network and classical regression models for earthquake-induced slope displacements. Soil Dyn. Earthq. Eng. 2022, 152, 107024. [Google Scholar] [CrossRef]
- Xi, L.; Afshin, D.; Petersen, A. Truncated estimation in functional generalized linear regression models. Comput. Stat. Data Anal. 2022, 169, 107421. [Google Scholar]
- Chahboun, S.; Maaroufi, M. Performance comparison of k-nearest neighbor, random forest, and multiple linear regression to predict photovoltaic panels’ power output. In Advances on Smart and Soft Computing: Proceedings of ICACIn 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 301–311. [Google Scholar]
- Green, P.; Yandell, B. Semi-Parametric Generalized Linear Models; Springer: New York, NY, USA, 1985. [Google Scholar]
- Hastie, T.J.; Tibshirani, R.J. Generalized Additive Models; CRC Press: Boca Raton, FL, USA, 1990; Volume 43. [Google Scholar]
- Ruppert, D.; Wand, M.P.; Carroll, R.J. Semiparametric Regression; Cambridge University Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Rigby, R.A.; Stasinopoulos, D.M. Generalized additive models for location, scale and shape. J. R. Stat. Soc. Ser. C (Appl. Stat.) 2005, 54, 507–554. [Google Scholar] [CrossRef] [Green Version]
- Hudson, I.L.; Kim, S.W.; Keatley, M.R. Climatic influences on the flowering phenology of four Eucalypts: A GAMLSS approach. In Phenological Research; Springer: Dordrecht, The Netherlands, 2010; pp. 209–228. [Google Scholar]
- Ibacache-Pulgar, G.; Paula, G.A.; Cysneiros, F.J.A. Semiparametric additive models under symmetric distributions. Test 2013, 22, 103–121. [Google Scholar] [CrossRef]
- Etienne, X.L.; Ferrara, G.; Mugabe, D. How efficient is maize production among smallholder farmers in Zimbabwe? A comparison of semiparametric and parametric frontier efficiency analyses. Appl. Econ. 2019, 51, 2855–2871. [Google Scholar] [CrossRef]
- Jackson, R.D.; Huete, A.R. Interpreting vegetation indices. Prev. Vet. Med. 1991, 11, 185–200. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ. 1973, 351, 309. [Google Scholar]
- Gitelson, A.A.; Stark, R.; Grits, U.; Rundquist, D.; Kaufman, Y.; Derry, D. Vegetation and soil lines in visible spectral space: A concept and technique for remote estimation of vegetation fraction. Int. J. Remote. Sens. 2002, 23, 2537–2562. [Google Scholar] [CrossRef]
- Monteiro, L.A.; Sentelhas, P.C.; Pedra, G.U. Assessment of NASA/POWER satellite-based weather system for Brazilian conditions and its impact on sugarcane yield simulation. Int. J. Climatol. 2018, 38, 1571–1581. [Google Scholar] [CrossRef]
- The Power Data Access Viewer. Available online: https://power.larc.nasa.gov/data-access-viewer/ (accessed on 15 June 2021).
- Nelson, R.W. What Agronomists, Crop Consultants, Producers, and Growers Need to Know before Choosing a Crop Scouting Sensor; Sentera, LLC: Saint Paul, MN, USA, 2017. [Google Scholar]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, 2nd ed.; Wiley: New York, NY, USA, 1994; Volume 1. [Google Scholar]
- Stasinopoulos, D.M.; Rigby, R.A. Generalized additive models for location scale and shape (GAMLSS) in R. J. Stat. Softw. 2007, 23, 1–46. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing. Version 3.6.3. R Foundation for Statistical Computing, Vienna, Austria. 2020. Available online: https://www.R-project.org/ (accessed on 10 January 2023).
- Stasinopoulos, M.D.; Rigby, R.A.; Heller, G.Z.; Voudouris, V.; De Bastiani, F. Flexible Regression and Smoothing: Using Gamlss in R; CRC Press: New York, NY, USA, 2017. [Google Scholar]
- Green, P.J.; Silverman, B.W. Nonparametric Regression and Generalized Linear Models: A Roughness Penalty Approach; Chapman and Hall: London, UK, 1993. [Google Scholar]
- Dunn, P.K.; Smyth, G.K. Randomized quantile residuals. J. Comput. Graph. Stat. 1996, 5, 236–244. [Google Scholar]
- Royston, J.P. An extension of Shapiro and Wilk’s W test for normality to large samples. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1982, 31, 115–124. [Google Scholar] [CrossRef]
- Wang, X.; Xu, D. An inverse Gaussian process model for degradation data. Technometrics 2010, 52, 188–197. [Google Scholar] [CrossRef]
- Shamany, R.; Alobaidi, N.N.; Algamal, Z.Y. A new two-parameter estimator for the inverse Gaussian regression model with application in chemometrics. Electron. J. Appl. Stat. Anal. 2019, 12, 453–464. [Google Scholar]
- Kinat, S.; Amin, M.; Mahmood, T. GLM-based control charts for the inverse Gaussian distributed response variable. Qual. Reliab. Eng. Int. 2020, 36, 765–783. [Google Scholar] [CrossRef]
- Allison, J.S.; Betsch, S.; Ebner, B.; Visagie, J. On testing the adequacy of the inverse Gaussian distribution. Mathematics 2022, 10, 350. [Google Scholar] [CrossRef]
- Nagelkerke, N.J. A note on a general definition of the coefficient of determination. Biometrika 1991, 78, 691–692. [Google Scholar] [CrossRef]
- Buuren, S.V.; Fredriks, M. Worm plot: A simple diagnostic device for modeling growth reference curves. Stat. Med. 2001, 20, 1259–1277. [Google Scholar] [CrossRef]
- Acker, J.; Williams, R.; Chiu, L.; Ardanuy, P.; Miller, S.; Schueler, C.; Vachon, P.W.; Manore, M. Remote Sensing from Satellites. Ref. Modul. Earth Syst. Environ. Sci. 2014. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote. Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef] [Green Version]
- Shendryk, Y.; Sofonia, J.; Garrard, R.; Rist, Y.; Skocaj, D.; Thorburn, P. Fine-scale prediction of biomass and leaf nitrogen content in sugarcane using UAV LiDAR and multispectral imaging. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102177. [Google Scholar] [CrossRef]
- Luciano, A.C.S.; Picoli, M.C.A.; Duft, D.G.; Rocha, J.V.; Leal, M.R.L.V.; Maire, G.L. Empirical model for forecasting sugarcane yield on a local scale in Brazil using Landsat imagery and random forest algorithm. Comput. Electron. Agric. 2021, 184, 106063. [Google Scholar] [CrossRef]
- Priya, S.R.K.; Bajpai, P.K.; Suresh, K.K. Use of data reduction technique for sugarcane yield forecast. Indian J. Sugarcane Technol. 2014, 29, 77–80. [Google Scholar]
- Wieg, G.L.; Richardson, A.J.; Escobar, D.E. Vegetation indices in crop assessment. Remote. Sens. Environ. 1991, 35, 105–119. [Google Scholar] [CrossRef]
- CONAB—Companhia Nacional de Abastecimento. Available online: https://www.conab.gov.br/info-agro/safras/cana/boletim-da-safra-de-cana-de-acucar (accessed on 1 February 2023).
- Esquerdo, J.C.D.M.; Antunes, J.F.G.; Coutinho, A.C.; Speranza, E.A.; Kondo, A.A.; dos Santos, J.L. SATVeg: A web-based tool for visualization of MODIS vegetation indices in South America. Comput. Electron. Agric. 2020, 175, 105516. [Google Scholar] [CrossRef]
- Jacon, A.D.; Galvão, L.S.; dos Santos, J.R.; Sano, E.E. Seasonal characterization and discrimination of savannah physiognomies in Brazil using hyperspectral metrics from Hyperion/EO-1. Int. J. Remote. Sens. 2017, 38, 4494–4516. [Google Scholar] [CrossRef]
















| # | Sugarcane Varieties Used in Field A | Sugarcane Varieties Used in Field B | Varieties Cycle |
|---|---|---|---|
| 1 | CTC1007 | CTC1007 | Normal |
| 2 | RB966928 | RB966928 | Early |
| 3 | CV0618 | CV0618 | Early to normal |
| 4 | CV7870 | CV7870 | Normal |
| Effects | Parameter | Estimate | SE | p-Value |
|---|---|---|---|---|
| Intercept | 1.461 | 0.415 | <0.001 | |
| Block II | −0.003 | 0.025 | 0.899 | |
| Block III | −0.053 | 0.025 | 0.037 | |
| Block IV | −0.043 | 0.025 | 0.079 | |
| Field B | 0.257 | 0.033 | <0.001 | |
| Variety CV0618 | −0.077 | 0.025 | 0.002 | |
| Variety CV7870 | −0.101 | 0.025 | <0.001 | |
| Variety RB966928 | −0.029 | 0.025 | 0.251 | |
| −4.377 | 0.047 | <0.001 |
| Hypotheses | Estimate | SE | p-Value |
|---|---|---|---|
| CV0618–CTC1007 | −0.077 | 0.025 | 0.002 |
| CV7870–CTC1007 | −0.101 | 0.025 | <0.001 |
| RB966928–CTC1007 | −0.029 | 0.025 | 0.251 |
| CV7870–CV0618 | −0.024 | 0.024 | 0.313 |
| RB966928–CV0618 | 0.048 | 0.024 | 0.045 |
| RB966928–CV7870 | 0.072 | 0.024 | 0.003 |
| Effects | Parameter | Estimate | SE | p-Value |
|---|---|---|---|---|
| Intercept | 4.653 | 0.685 | <0.001 | |
| Location B | −0.036 | 0.050 | 0.491 | |
| Location C | −0.562 | 0.042 | <0.001 | |
| Location D | −0.386 | 0.048 | <0.001 | |
| Location E | −0.284 | 0.047 | <0.001 | |
| Location F | −0.535 | 0.153 | 0.005 | |
| −5.034 | 0.129 | <0.001 |
| Hypotheses | Estimate | SE | p-Value |
|---|---|---|---|
| C–B | −0.526 | 0.047 | <0.001 |
| D–B | −0.350 | 0.046 | <0.001 |
| E–B | −0.248 | 0.044 | <0.001 |
| F–B | −0.499 | 0.139 | 0.004 |
| D–C | 0.176 | 0.039 | 0.001 |
| E–C | 0.278 | 0.045 | <0.001 |
| F–C | 0.027 | 0.144 | 0.853 |
| E–D | 0.102 | 0.046 | 0.051 |
| F–D | −0.148 | 0.132 | 0.285 |
| F–E | −0.250 | 0.149 | 0.123 |
| Statistical Measures | IG Semiparametric Regression Model | Multiple Regression Model |
|---|---|---|
| Field experiment data | ||
| R2 | 0.737 | 0.651 |
| RMSE | 16.109 | 16.776 |
| Commercial production field data | ||
| R2 | 0.921 | 0.826 |
| RMSE | 5.998 | 8.657 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasconcelos, J.C.S.; Speranza, E.A.; Antunes, J.F.G.; Barbosa, L.A.F.; Christofoletti, D.; Severino, F.J.; de Almeida Cançado, G.M. Development and Validation of a Model Based on Vegetation Indices for the Prediction of Sugarcane Yield. AgriEngineering 2023, 5, 698-719. https://doi.org/10.3390/agriengineering5020044
Vasconcelos JCS, Speranza EA, Antunes JFG, Barbosa LAF, Christofoletti D, Severino FJ, de Almeida Cançado GM. Development and Validation of a Model Based on Vegetation Indices for the Prediction of Sugarcane Yield. AgriEngineering. 2023; 5(2):698-719. https://doi.org/10.3390/agriengineering5020044
Chicago/Turabian StyleVasconcelos, Julio Cezar Souza, Eduardo Antonio Speranza, João Francisco Gonçalves Antunes, Luiz Antonio Falaguasta Barbosa, Daniel Christofoletti, Francisco José Severino, and Geraldo Magela de Almeida Cançado. 2023. "Development and Validation of a Model Based on Vegetation Indices for the Prediction of Sugarcane Yield" AgriEngineering 5, no. 2: 698-719. https://doi.org/10.3390/agriengineering5020044
APA StyleVasconcelos, J. C. S., Speranza, E. A., Antunes, J. F. G., Barbosa, L. A. F., Christofoletti, D., Severino, F. J., & de Almeida Cançado, G. M. (2023). Development and Validation of a Model Based on Vegetation Indices for the Prediction of Sugarcane Yield. AgriEngineering, 5(2), 698-719. https://doi.org/10.3390/agriengineering5020044