Tractor Three-Point Hitch Control for an Independent Lower Arms System
Abstract
:1. Introduction
- Roll control without any accessory: Independent cylinders on each arm of the tractor provide easy control of the roll of the implement without requiring an extra adjustment arm on the implement. For example, in the case of a box scraper [26], the operators can easily choose an implement without the hydraulic cylinder that would have been used for adjustment of the implement roll. The tractor can save the configuration for the hitch height as well as the roll angle and also allows the operators to actuate the implement with these parameters in real time.
- Modularity and Serviceability: Using two independent cylinders, we took a modular approach since each set of cylinders and lower arms in one module is independent of the other. This facilitates better serviceability, which can include repairing or replacing existing components.
- Packaging: Without the rock shaft assembly, the packaging in the tractor becomes less complex, and it saves space for other components and accessories.
- Cost reduction: By removing the physical rock shaft assembly, we were able to simplify the mechanical design and reduce material costs.
- Ease of attaching implements: Since the arms can be moved up and down independently, it is easy to attach an implement to the three-point hitch system. Also, the architecture of the hydraulics in MK-V tractors allows individual cylinders to float independently, which makes it easy to move each cylinder without any hydraulic assistance while attaching implements [27].
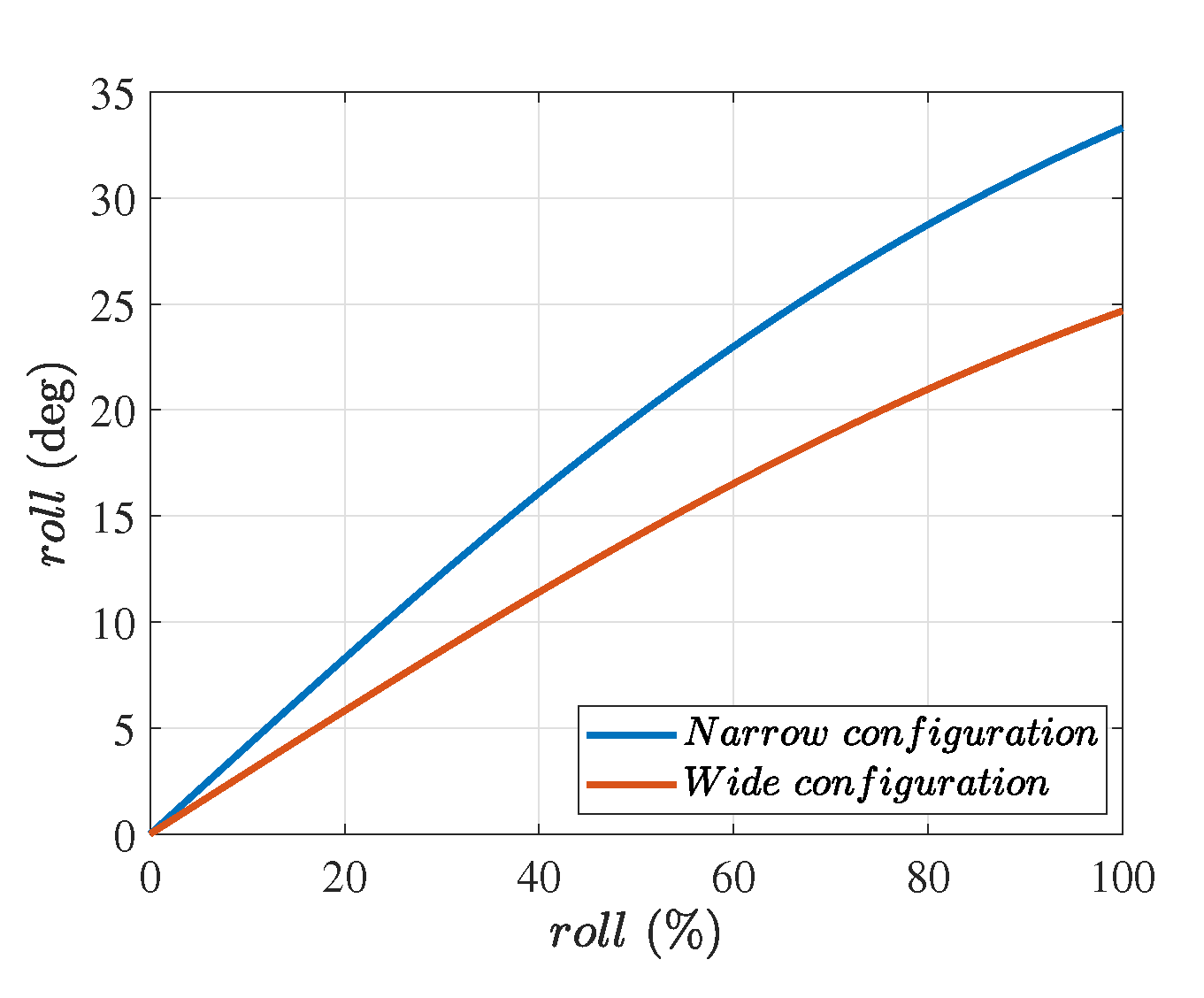
- Extreme roll: In traditional tractors, solid links are used for three-point hitch lower arms, which can move together because of the physical constraints imposed by the rock shaft. In some implementations, one of these arms is replaced with a hydraulic cylinder [2], which can be actuated to achieve roll in the implement. However, the amount of roll is limited due to the limited stroke length of the add-on cylinder, whereas, in our case, a significantly large amount of roll can be achieved. An extreme roll angle is achieved when one cylinder is fully retracted, and the other is fully extended.
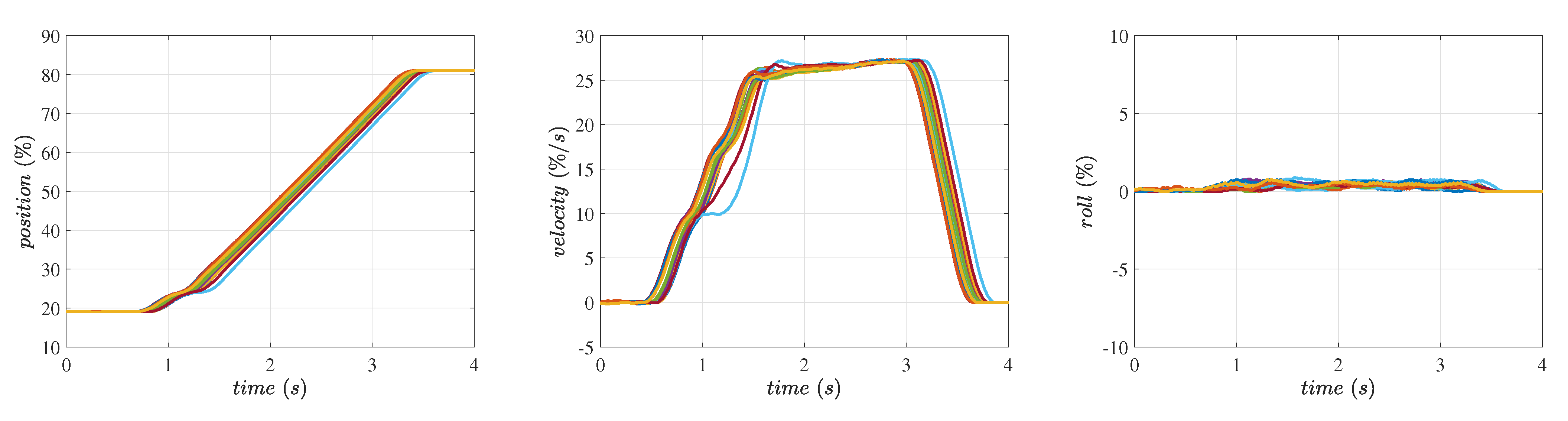
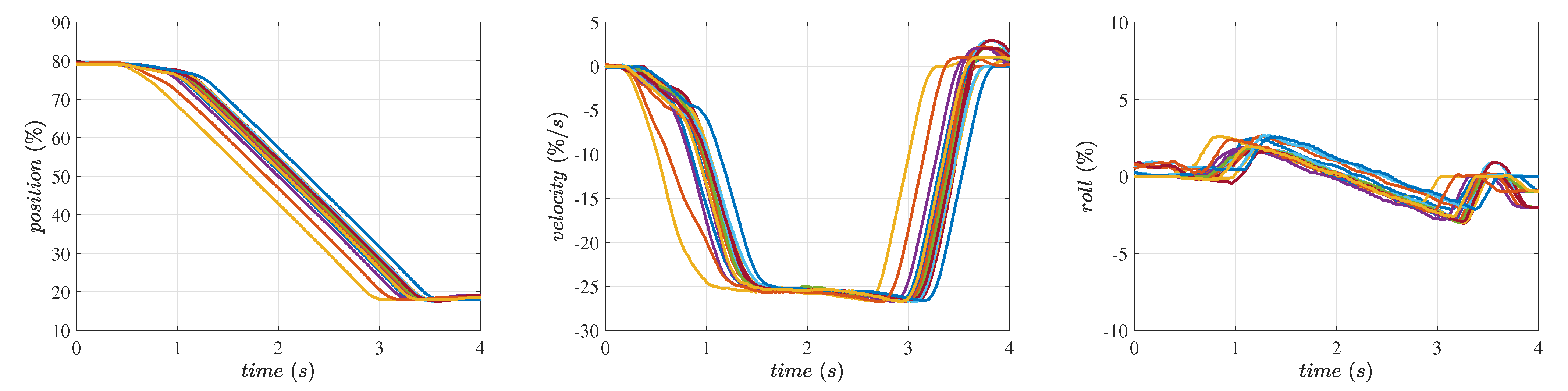
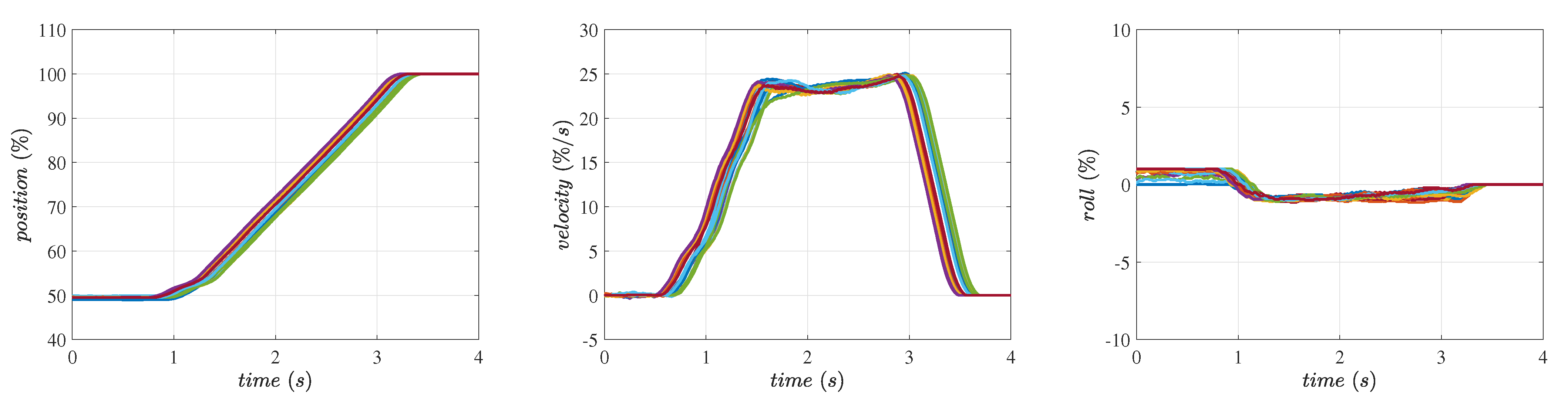
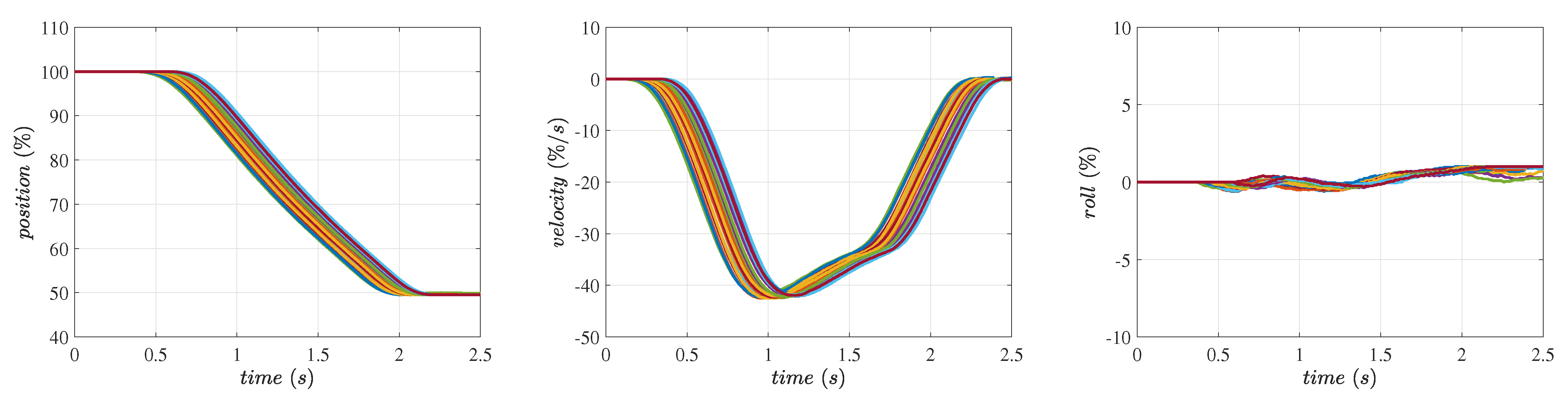
- Position control: It is often necessary to control the position of the implements in the vertical direction without any roll with respect to the tractor. This basic requirement leads to a challenge as it demands the arms to move up and down in a synchronized manner. We have introduced the roll control algorithm that is coupled with the position control algorithm for the hitch height motion. We have conducted experiments that exhibit the performance of the position control algorithm through step responses.
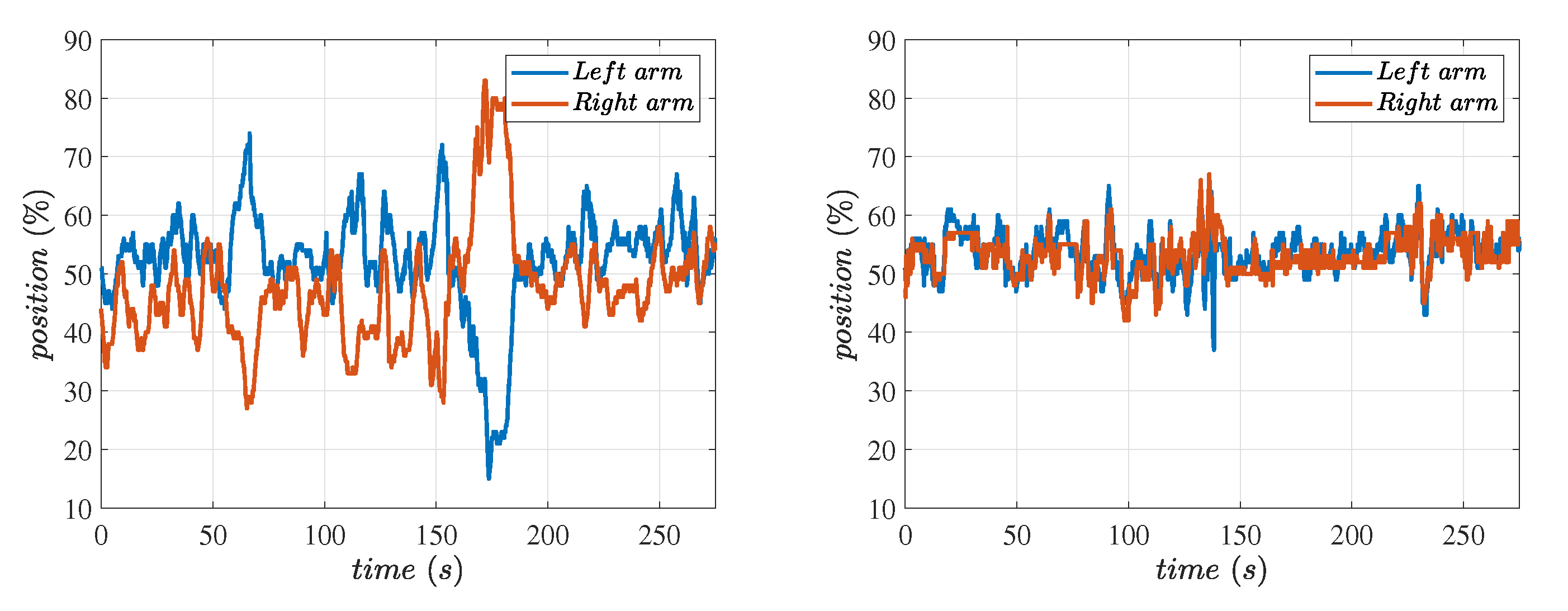
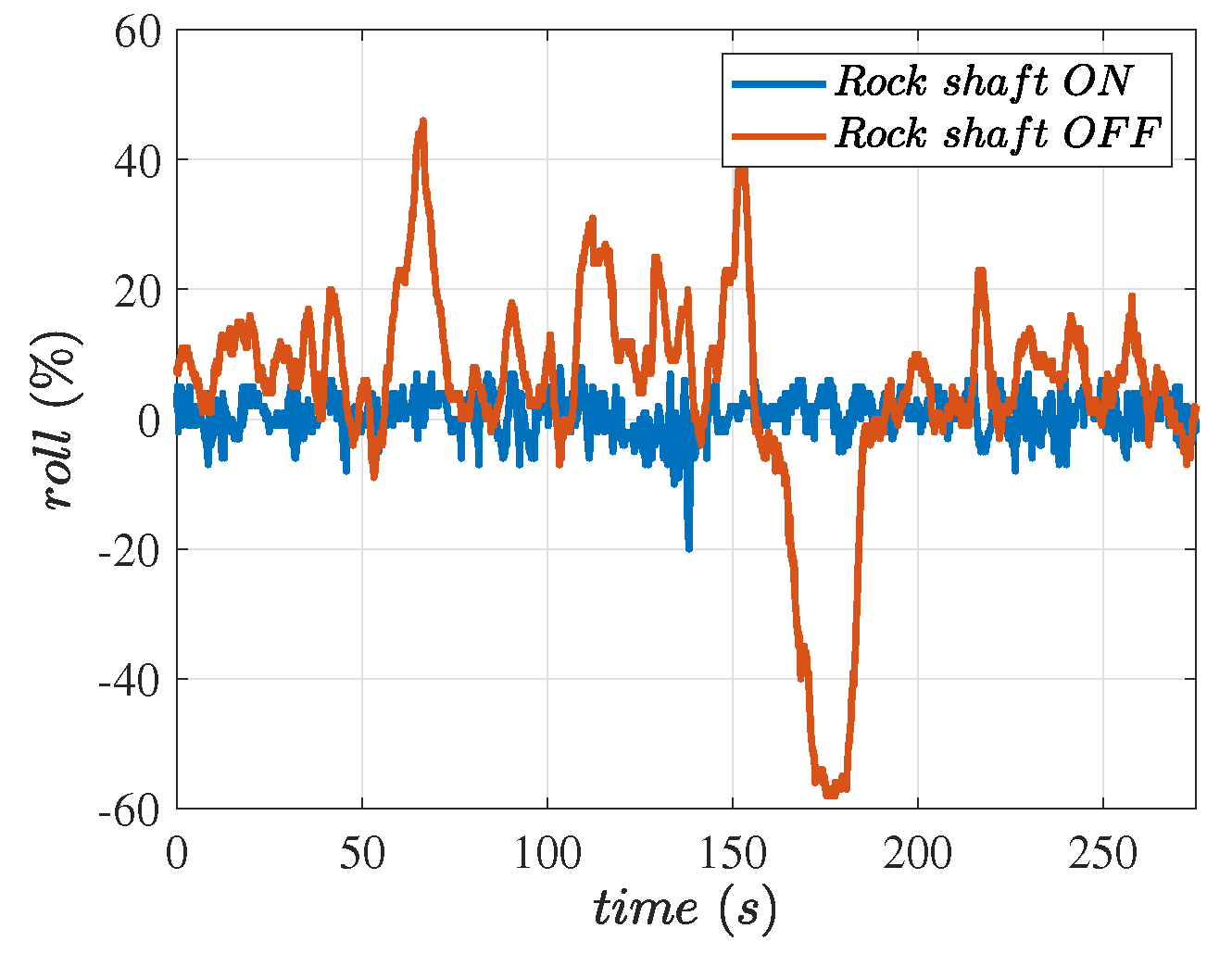
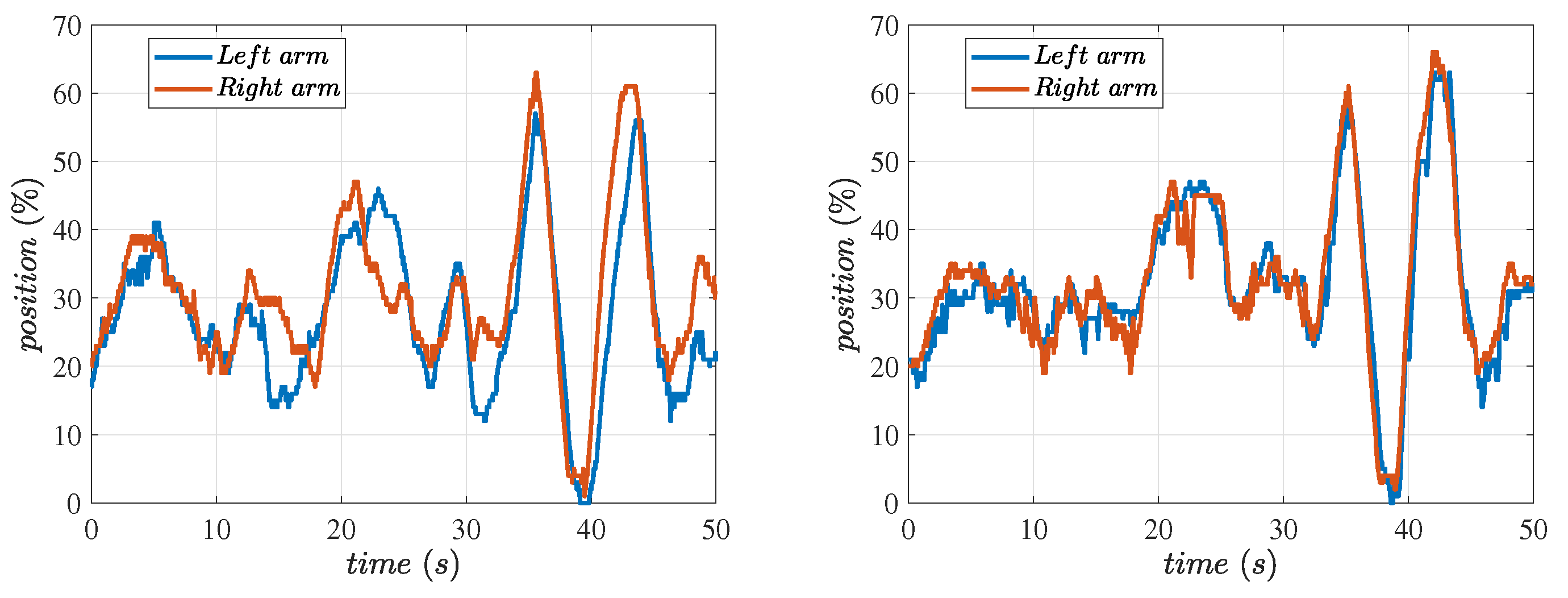
- Follow the terrain around the roll axis: The hitch system allows the implement to follow the terrain, instead of the tractor, around the roll axis when in float mode. However, if we need the implement to follow the tractor, it is often not feasible without a rock shaft. The importance of implements following the terrain while in float mode is thoroughly explained in [28,29,30]. This motivates our work on a software rock shaft, which we discuss in detail in the following sections and show results from the experiments. The algorithm ensures that the implement does not rotate around the roll axis while making sure it moves up and down to follow the terrain along that axis of the tractor’s motion.
- Additional actuators and sensors: Since the lower arm cylinders are independent, two sets of actuators and sensors are required to actuate the cylinders and track their positions, as opposed to one actuator and one sensor on traditional tractors. Although an advantage of having a sensor on each arm is the ability to detect a multitude of cases of sensor failures, which is not possible with just one sensor, it adds additional computational load on the controller.
2. Hardware
2.1. Mechanical Platform
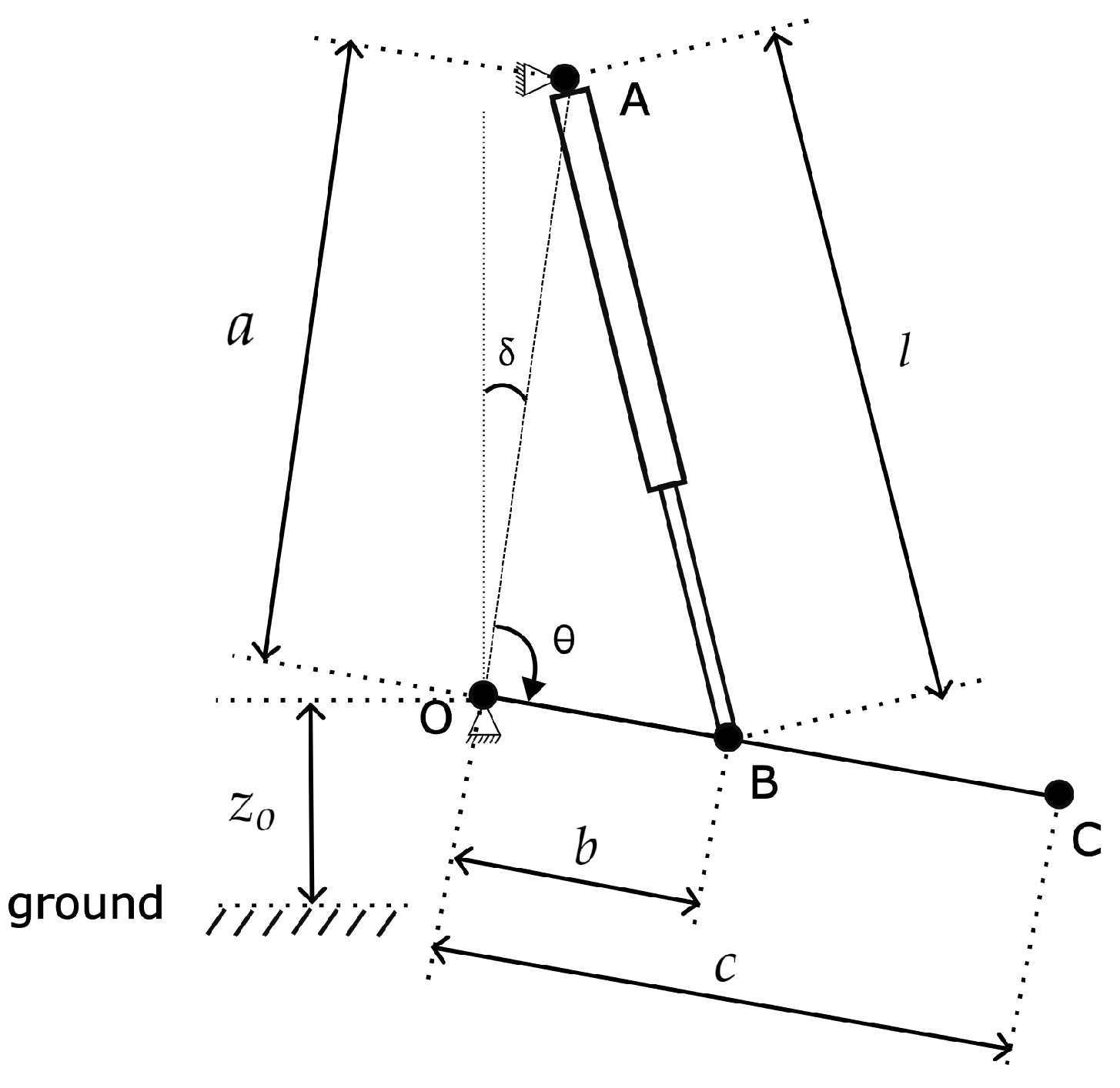
2.2. Geometry of the Actuator
2.3. Actuation and Sensing
2.4. Embedded Microcontroller
3. Controller Design
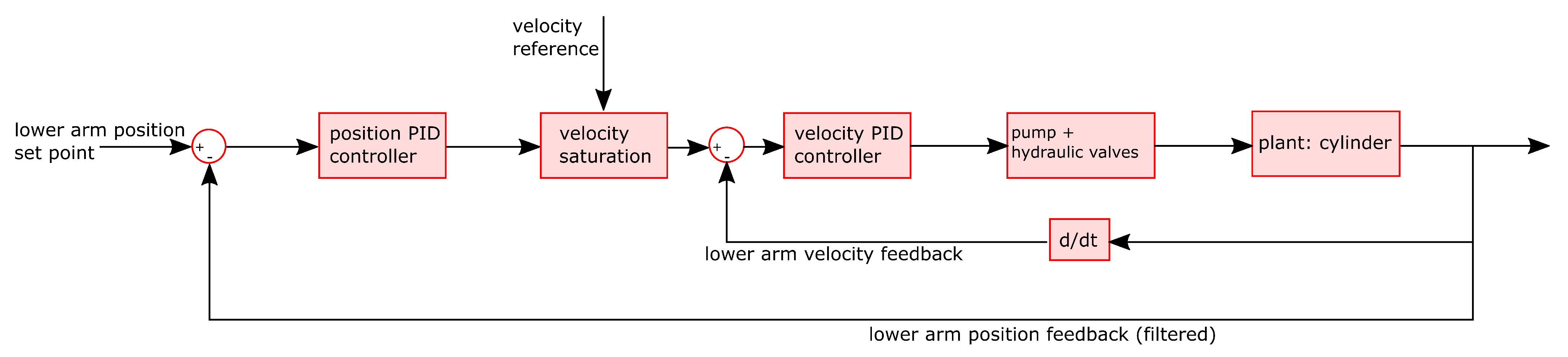
3.1. Plant and Its Actuation
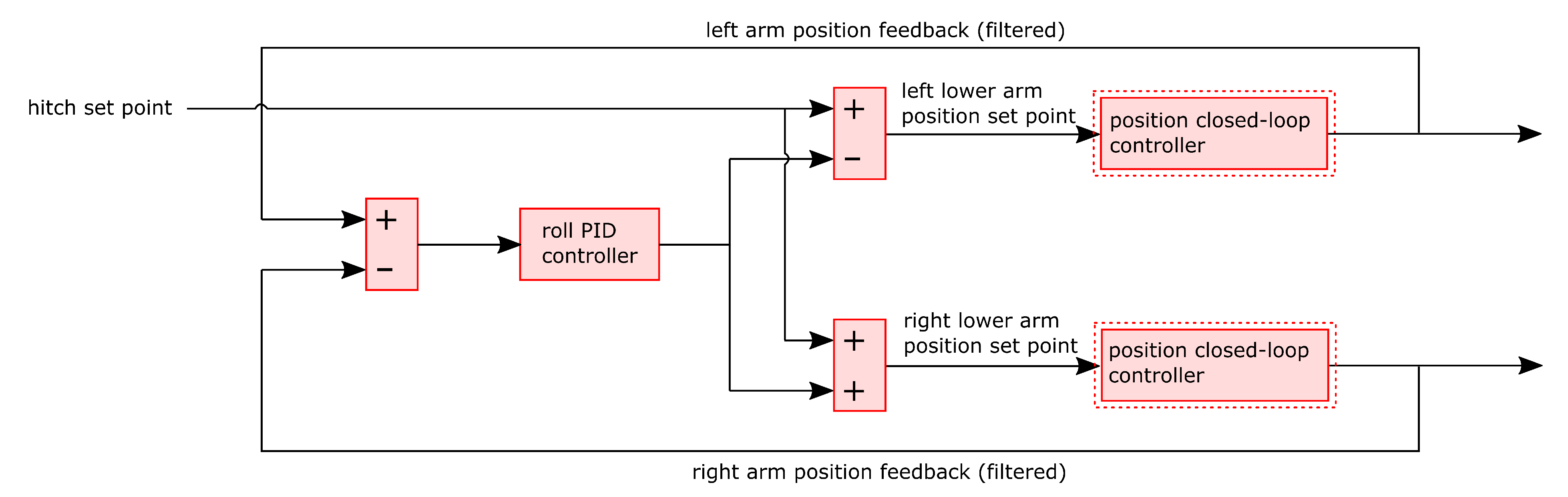
3.2. Closed-Loop Hitch Position Control
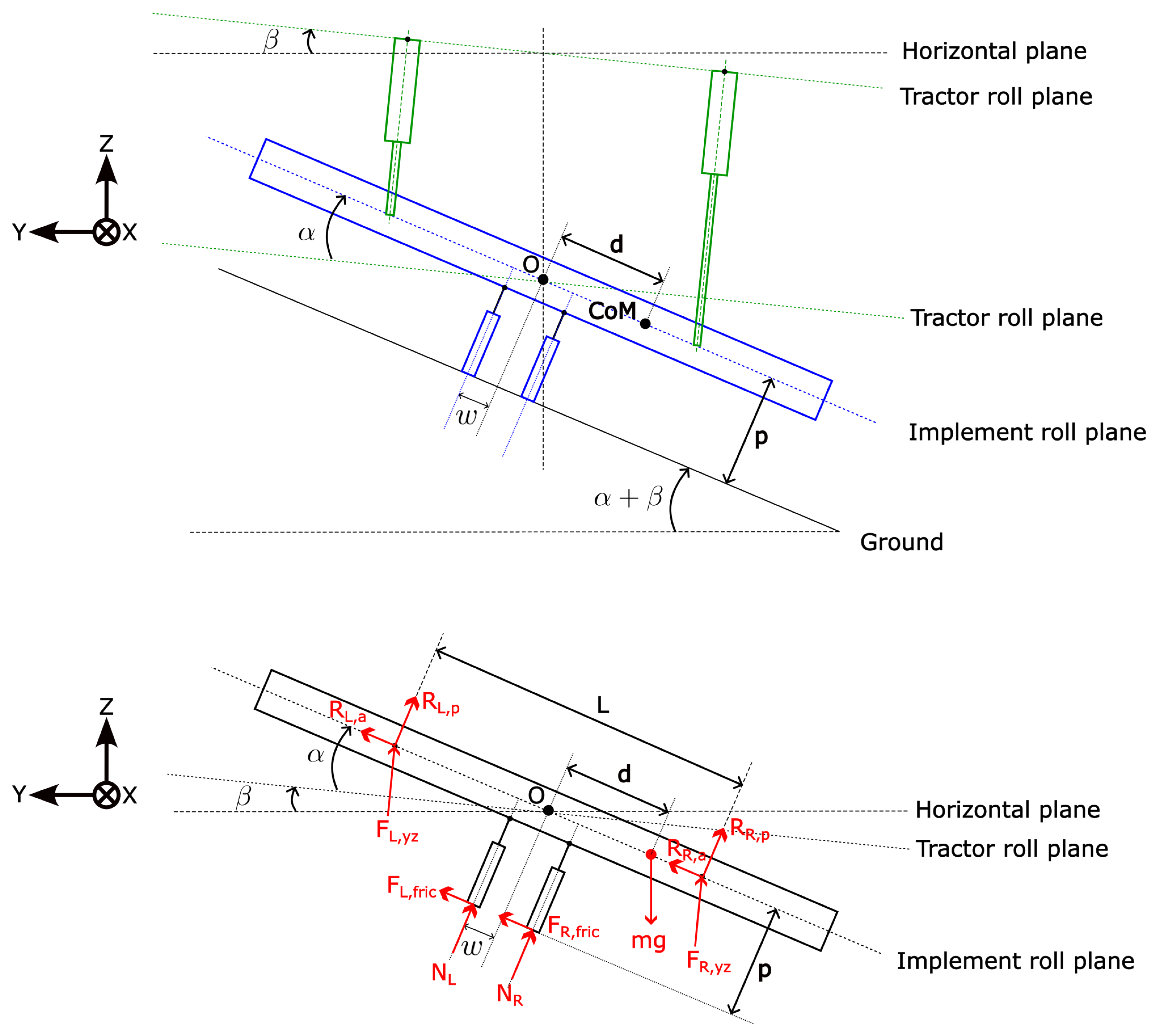
3.3. Software Rock Shaft Algorithm for Float Mode
| Algorithm 1 Software rock shaft algorithm, which emulates the physical rock shaft found on traditional tractors. The algorithm ensures that the implement attached to the hitch moves up and down with the terrain while ensuring zero roll with respect to the tractor. |
| Input: : Position of the left arm : Position of the right arm : Boolean for upward force detected on the left arm : Boolean for upward force detected on the right arm : Boolean for system’s float mode
|
4. Methodology
5. Results and Discussion
5.1. Position Control of the Hitch System
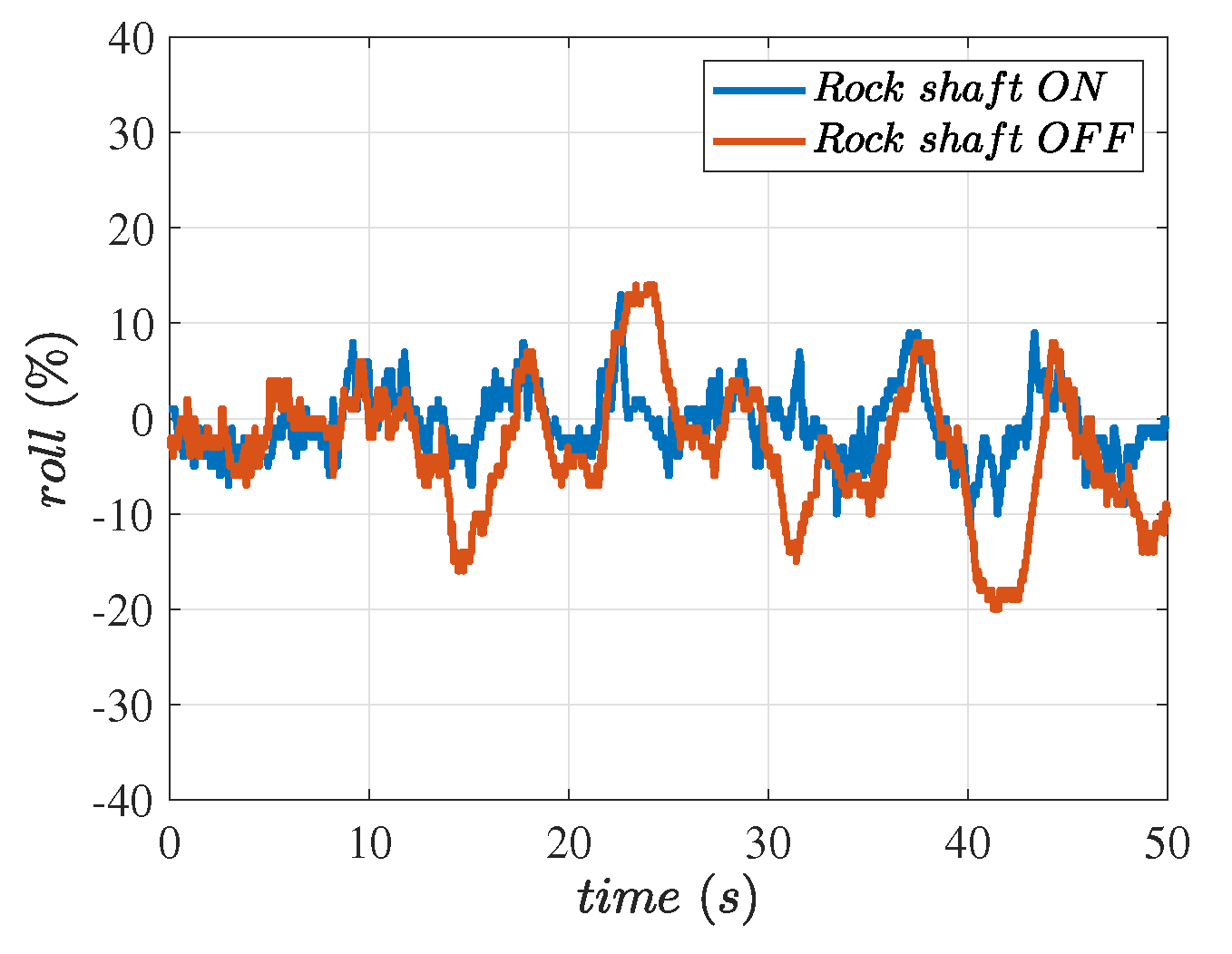
5.2. Float Control of the Hitch System Using Software Rock Shaft Algorithm
6. Conclusions
7. Patents
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moreda, G.; Muñoz-García, M.; Barreiro, P. High voltage electrification of tractor and agricultural machinery–A review. Energy Convers. Manag. 2016, 115, 117–131. [Google Scholar] [CrossRef]
- Yu, J.H.; Park, J.K.; Cheon, S.H.; Byeon, S.J.; Lee, J.W. Development of a rolling angle estimation algorithm to improve the performance of implement leveling-control systems for agricultural tractors. Adv. Mech. Eng. 2022, 14, 16878132221138310. [Google Scholar] [CrossRef]
- Florentsev, S.; Izosimov, D.; Makarov, L.; Baida, S.; Belousov, A. Complete traction electric equipment sets of electro-mechanical drive trains for tractors. In Proceedings of the 2010 IEEE Region 8 International Conference on Computational Technologies in Electrical and Electronics Engineering (SIBIRCON), Irkutsk, Russia, 11–15 July 2010; pp. 611–616. [Google Scholar]
- Ueka, Y.; Yamashita, J.; Sato, K.; Doi, Y. Study on the development of the electric tractor: Specifications and traveling and tilling performance of a prototype electric tractor. Eng. Agric. Environ. Food 2013, 6, 160–164. [Google Scholar] [CrossRef]
- Mocera, F.; Somà, A. Analysis of a parallel hybrid electric tractor for agricultural applications. Energies 2020, 13, 3055. [Google Scholar] [CrossRef]
- Mousazadeh, H.; Keyhani, A.; Javadi, A.; Mobli, H.; Abrinia, K.; Sharifi, A. Life-cycle assessment of a Solar Assist Plug-in Hybrid electric Tractor (SAPHT) in comparison with a conventional tractor. Energy Convers. Manag. 2011, 52, 1700–1710. [Google Scholar] [CrossRef]
- Chen, Y.C.; Chen, L.W.; Chang, M.Y. A design of an unmanned electric tractor platform. Agriculture 2022, 12, 112. [Google Scholar] [CrossRef]
- Monarch Tractor MK-V. Available online: https://www.monarchtractor.com/mk-v-electric-tractor (accessed on 25 April 2024).
- Boe, T.E.; Bergene, M.A. Tractor three-point hitch control system. SAE Trans. 1989, 98, 229–236. [Google Scholar]
- Kushwah, A.; Chouriya, A.; Tewari, V.; Gupta, C.; Chowdhury, M.; Shrivastava, P.; Bhagat, P. A novel embedded system for tractor implement performance mapping. Cogent Eng. 2024, 11, 2311093. [Google Scholar] [CrossRef]
- Bhondave, B.; Ganesan, T.; Varma, N.; Renu, R.; Sabarinath, N. Design and development of electro hydraulics hitch control for agricultural tractor. SAE Int. J. Commer. Veh. 2017, 10, 405–410. [Google Scholar] [CrossRef]
- Kumar, S.; Tewari, V.K.; Bharti, C.K.; Ranjan, A. Modeling, simulation and experimental validation of flow rate of electro-hydraulic hitch control valve of agricultural tractor. Flow Meas. Instrum. 2021, 82, 102070. [Google Scholar] [CrossRef]
- Sun, X.; Lu, Z.; Song, Y.; Cheng, Z.; Jiang, C.; Qian, J.; Lu, Y. Development status and research progress of a tractor electro-hydraulic hitch system. Agriculture 2022, 12, 1547. [Google Scholar] [CrossRef]
- Nataraj, E.; Sarkar, P.; Raheman, H.; Upadhyay, G. Embedded digital display and warning system of velocity ratio and wheel slip for tractor operated active tillage implements. J. Terramechanics 2021, 97, 35–43. [Google Scholar] [CrossRef]
- Xi, Z.; Feng, T.; Liu, Z.; Xu, H.; Zheng, J.; Xu, L. Estimation of Soil Characteristic Parameters for Electric Mountain Tractor Based on Gauss–Newton Iteration Method. World Electr. Veh. J. 2024, 15, 217. [Google Scholar] [CrossRef]
- Ro, Y.M.; Moon, J.H.; Kim, K.U. Performance improvement of the horizontal control system for a tractor implement using sensor signal from the front axle. J. Biosyst. Eng. 2016, 41, 67–74. [Google Scholar] [CrossRef]
- Cheng, Z.; Lu, Z. Research on the PID control of the ESP system of tractor based on improved AFSA and improved SA. Comput. Electron. Agric. 2018, 148, 142–147. [Google Scholar] [CrossRef]
- Khalaji, A.K. PID-based target tracking control of a tractor-trailer mobile robot. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4776–4787. [Google Scholar] [CrossRef]
- David, S.A.; de Sousa, R.V.; Valentim Jr, C.A.; Tabile, R.A.; Machado, J.A.T. Fractional PID controller in an active image stabilization system for mitigating vibration effects in agricultural tractors. Comput. Electron. Agric. 2016, 131, 1–9. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Dai, D.; Wang, X.; Wang, S. Review of electro-hydraulic hitch system control method of automated tractors. Int. J. Agric. Biol. Eng. 2021, 14, 1–11. [Google Scholar] [CrossRef]
- Li, M.; Wang, L.; Liu, J.; Ye, J. Method study on fuzzy-PID adaptive control of electric-hydraulic hitch system. In Proceedings of the International Conference on Advances in Materials, Machinery, Electronics (AMME 2017), Wuhan, China, 25–26 February 2017; Volume 1820. [Google Scholar]
- Meena, K.; Dhavalikar, M.; Thorat, S. A review on the position control of hydraulic cylinder for accuracy and response time. Mater. Today Proc. 2023, 72, 995–999. [Google Scholar] [CrossRef]
- Manring, N.D.; Fales, R.C. Hydraulic Control Systems; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Cundiff, J.S. Fluid Power Circuits and Controls: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Hook, R.; Murphy, K. Depth Control of Integral Flexible Implements; Technical Report, SAE Technical Paper; SAE International: Warrendale, PA, USA, 1969. [Google Scholar]
- Land Pride Box Scraper BB12. Available online: https://www.landpride.com/products/58/BB12-Series-Box-Scrapers (accessed on 29 April 2024).
- Omohundro, Z.M.; Chenjia, Y.; Jutkowitz, A.; Chukewad, Y.M. Three-Point Hitch Hook Up Assist System. US Patent App. 18/164,592, 5 February 2023. [Google Scholar]
- White, E. Relation of the Tractor to the Implement. SAE Trans. 1919, 14, 323–334. [Google Scholar]
- Johannsen, B. Tractor Hitches and Hydraulic Systems—An Implement Designer’s Viewpoint. SAE Trans. 1954, 62, 173–185. [Google Scholar]
- Kubota Float Function Demonstration. Available online: https://www.wickhamtractor.com/kubota-float-function (accessed on 3 June 2024).
- Shafaei, S.; Loghavi, M.; Kamgar, S. Development and implementation of a human machine interface-assisted digital instrumentation system for high precision measurement of tractor performance parameters. Eng. Agric. Environ. Food 2019, 12, 11–23. [Google Scholar] [CrossRef]
- Al-Janobi, A. A data-acquisition system to monitor performance of fully mounted implements. J. Agric. Eng. Res. 2000, 75, 167–175. [Google Scholar] [CrossRef]
- Yahya, A.; Zohadie, M.; Kheiralla, A.; Giew, S.; Boon, N. Mapping system for tractor-implement performance. Comput. Electron. Agric. 2009, 69, 2–11. [Google Scholar] [CrossRef]
- Sandeep, T.; Prashant, K.; Abhijit, H.; Swarupanand, S.; Sanjeev, H. Study on Various Position Sensing Technologies in Tractor Hitch Application: Paper No.: 2023-JL-05. ARAI J. Mobil. Technol. 2023, 3, 820–834. [Google Scholar] [CrossRef]
- Novotechnik Novohall Rotary Sensor. Available online: https://www.novotechnik.com/resources/data-sheets/rotary-shaft-type/59_DS_295_RSA-3200_Ratiometric–enUS.pdf (accessed on 21 April 2024).
- Hydac Proportional Needle Valve PWSM06020W. Available online: https://www.hydac.com/_de-es/productos/valves/proportional-valves/proportional-needle-valves-poppet-type/pwsm06020w.html?type=9999 (accessed on 7 May 2024).
- Hydac Electronic Pressure Transmitter HPT 146K-R-0250-077. Available online: https://www.hydac.com/shop/en/sensors/pressure-sensors/pressure-transmitters (accessed on 29 April 2024).
- HYDAC HY-TTC-580 Series. Available online: https://catalog.hydac.com/viewitems/controllers/hy-ttc-580 (accessed on 14 April 2024).
- Cunha, M.A.; Guenther, R.; De Pieri, E.R.; De Negri, V.J. Design of cascade controllers for a hydraulic actuator. Int. J. Fluid Power 2002, 3, 35–46. [Google Scholar] [CrossRef]
- Tierre Lupo 140. Available online: https://www.tierreonline.com/en/grass-cutter/lupo-revers/ (accessed on 26 April 2024).
- Schmeiser Seed Drill VD48PW. Available online: https://www.tgschmeiser.com/products/vineyarddrills/no-till.html (accessed on 26 April 2024).
- FHM Standard Ditch Bank Flail Mower AGL125. Available online: https://www.farmer-helper.com/proDetail.aspx?id=2999 (accessed on 29 April 2024).
- Omohundro, Z.M.; Chukewad, Y.M.; Jutkowitz, A. Tractor Three-Point Hitch Control for an Independent Lower Arms System. US Provisional Patent App. 63/644,704, 9 May 2024. [Google Scholar]
- Omohundro, Z.M.; Jutkowitz, A.; Chukewad, Y.M. Three-point hitch control system. US Provisional Patent App. 18/522,088, 28 November 2023. [Google Scholar]





| Parameter | Value |
|---|---|
| a | 75.0 cm |
| b | 30.0 cm |
| c | 70.0 cm |
| 25.3 cm | |
| l | 53.3 cm to 79.0 cm |
| ° to ° | |
| ° |
| Direction | Implement (Flail Mower) | Initial Position (%) | Set Point (%) | Target Speed (%/s) | Trials |
|---|---|---|---|---|---|
| Up | No | 20 | 80 | 25 | 17 |
| Down | No | 80 | 20 | −25 | 17 |
| Up | Yes | 50 | 100 | 25 | 21 |
| Down | Yes | 100 | 50 | −33 | 21 |
| Implement | Weight (kg) | Motion Direction | Mean (%) | SD (%) |
|---|---|---|---|---|
| No implement | N/A | Up | 0.26 | 0.23 |
| No implement | N/A | Down | 1.24 | |
| Tierre Lupo Flail Mower | 240 | Up | 0.66 | |
| Tierre Lupo Flail Mower | 240 | Down | 0.45 |
| Implement | Weight (kg) | Software Rock Shaft | Mean (%) | SD (%) |
|---|---|---|---|---|
| Schmeiser Seed Drill | 515 | Off | 4.64 | 16.77 |
| Schmeiser Seed Drill | 515 | On | 0.58 | 2.79 |
| Tierre Lupo Flail Mower | 240 | Off | 6.45 | |
| Tierre Lupo Flail Mower | 240 | On | 3.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chukewad, Y.M.; Chadha, S.; Jagdale, K.S.; Elkunchwar, N.; Rosa, U.A.; Omohundro, Z. Tractor Three-Point Hitch Control for an Independent Lower Arms System. AgriEngineering 2024, 6, 1725-1746. https://doi.org/10.3390/agriengineering6020100
Chukewad YM, Chadha S, Jagdale KS, Elkunchwar N, Rosa UA, Omohundro Z. Tractor Three-Point Hitch Control for an Independent Lower Arms System. AgriEngineering. 2024; 6(2):1725-1746. https://doi.org/10.3390/agriengineering6020100
Chicago/Turabian StyleChukewad, Yogesh M., Sidakdeep Chadha, Karan S. Jagdale, Nishant Elkunchwar, Uriel A. Rosa, and Zachary Omohundro. 2024. "Tractor Three-Point Hitch Control for an Independent Lower Arms System" AgriEngineering 6, no. 2: 1725-1746. https://doi.org/10.3390/agriengineering6020100
APA StyleChukewad, Y. M., Chadha, S., Jagdale, K. S., Elkunchwar, N., Rosa, U. A., & Omohundro, Z. (2024). Tractor Three-Point Hitch Control for an Independent Lower Arms System. AgriEngineering, 6(2), 1725-1746. https://doi.org/10.3390/agriengineering6020100





