Subsoiler Tool with Bio-Inspired Attack Edge for Reducing Draft Force during Soil Tillage
Abstract
:1. Introduction
2. Materials and Methods
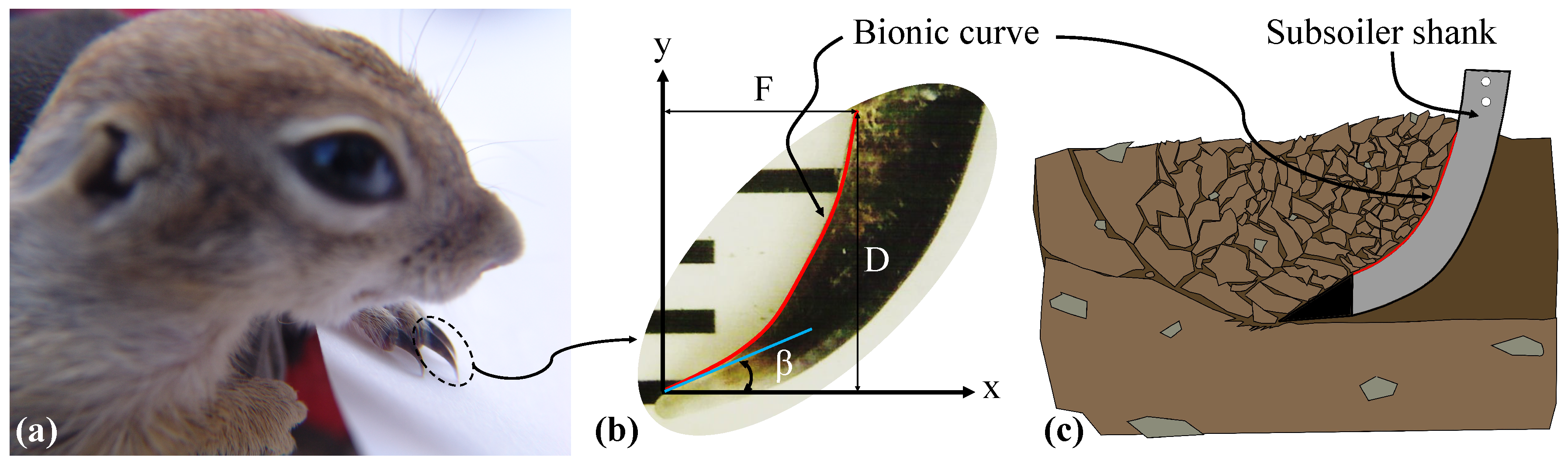
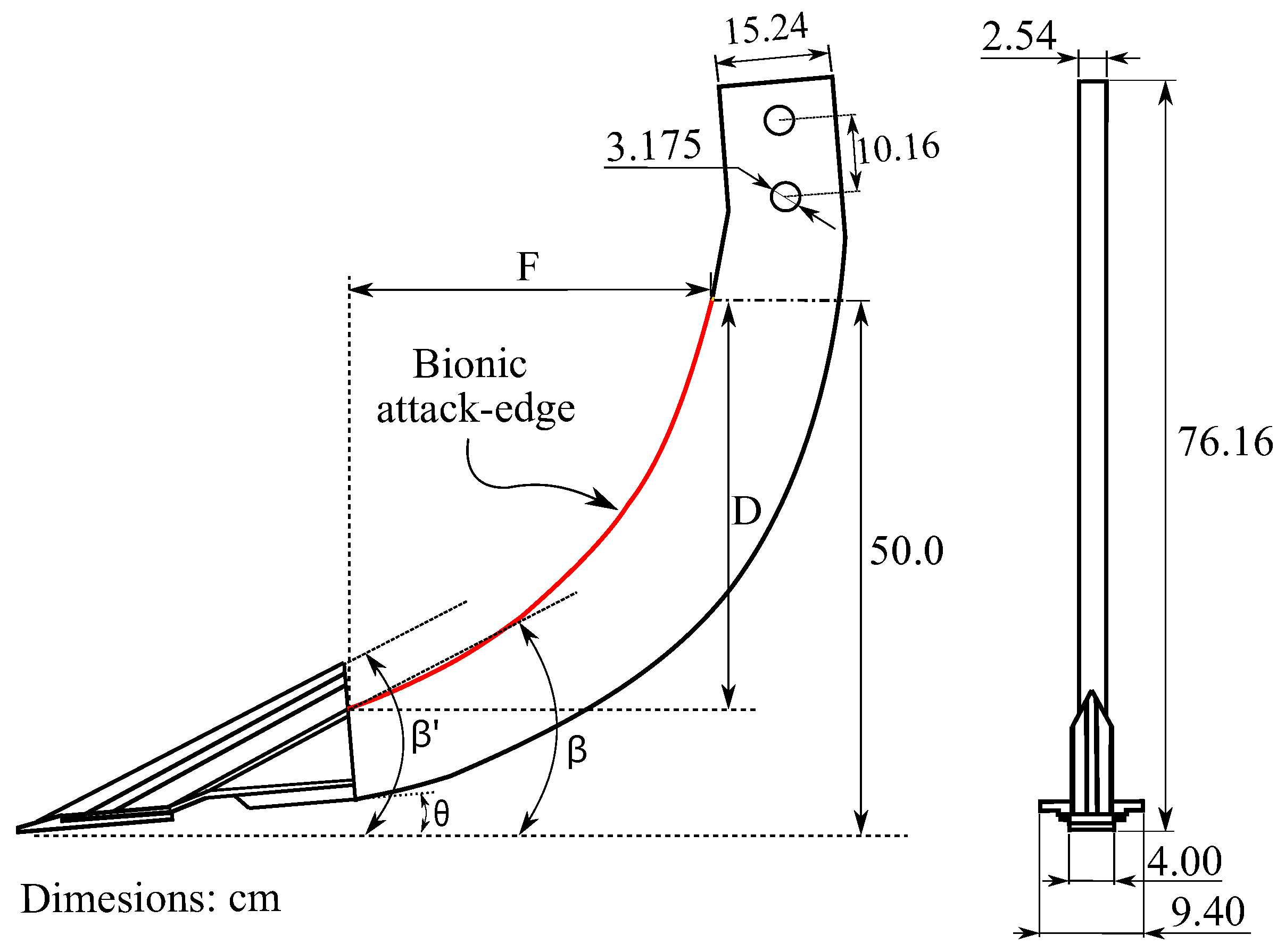
2.1. Bionic Attack-Edge of Subsoiler Bodies
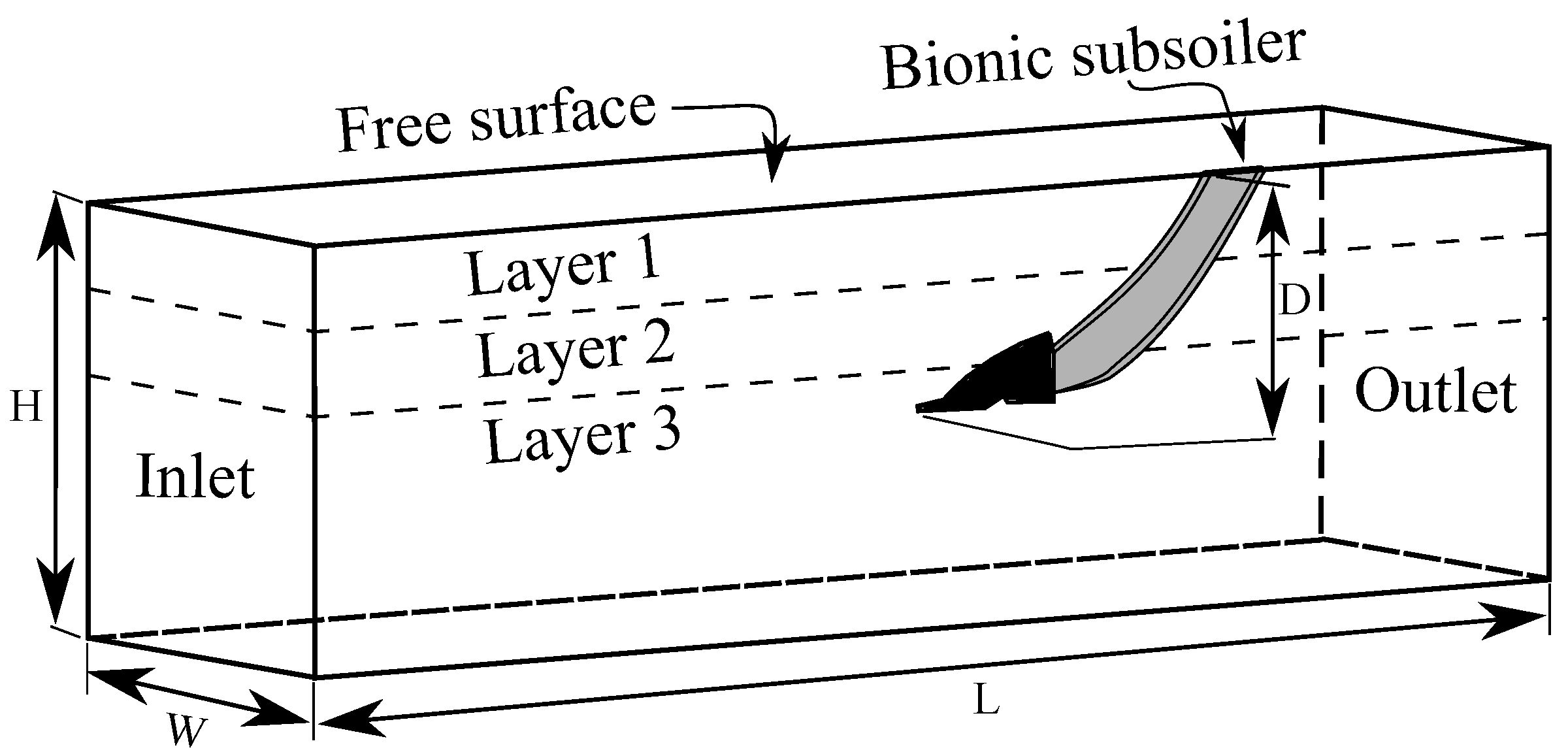
2.2. Numerical Modeling
2.2.1. Governing Equations
2.2.2. Modeling, Boundary Conditions and Soil Parameters
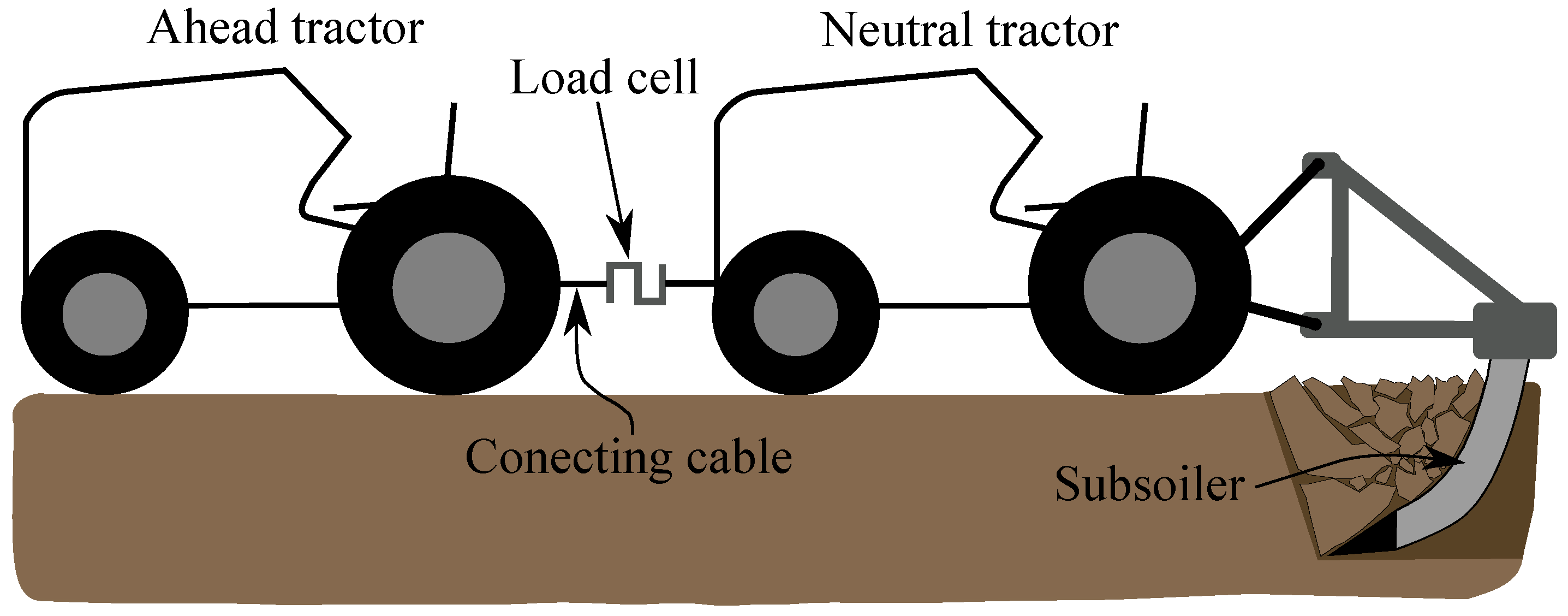
2.3. Field Estimation of the Draft Force
Field Experiment
3. Results and Discussion
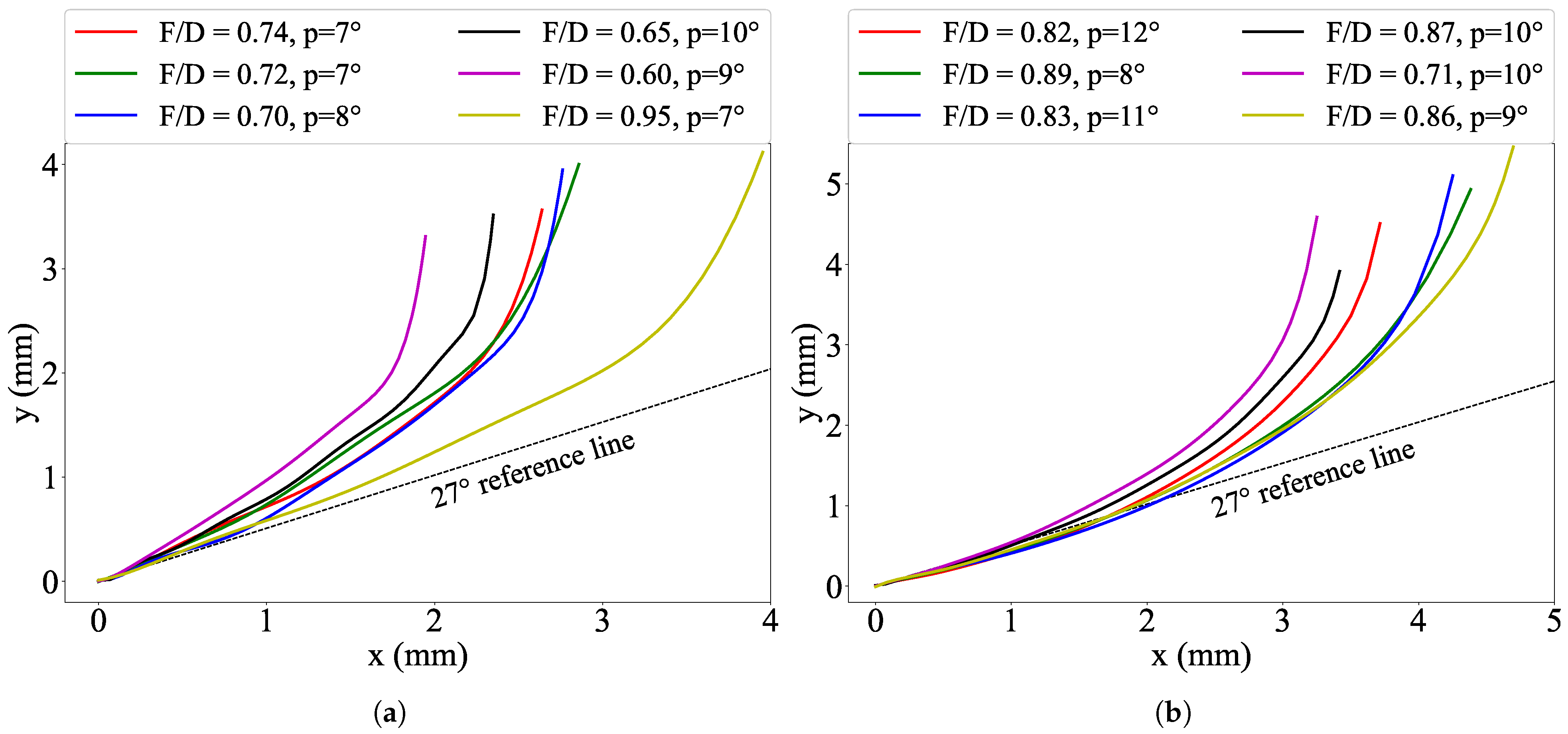
3.1. Bionic Subsoiler Body
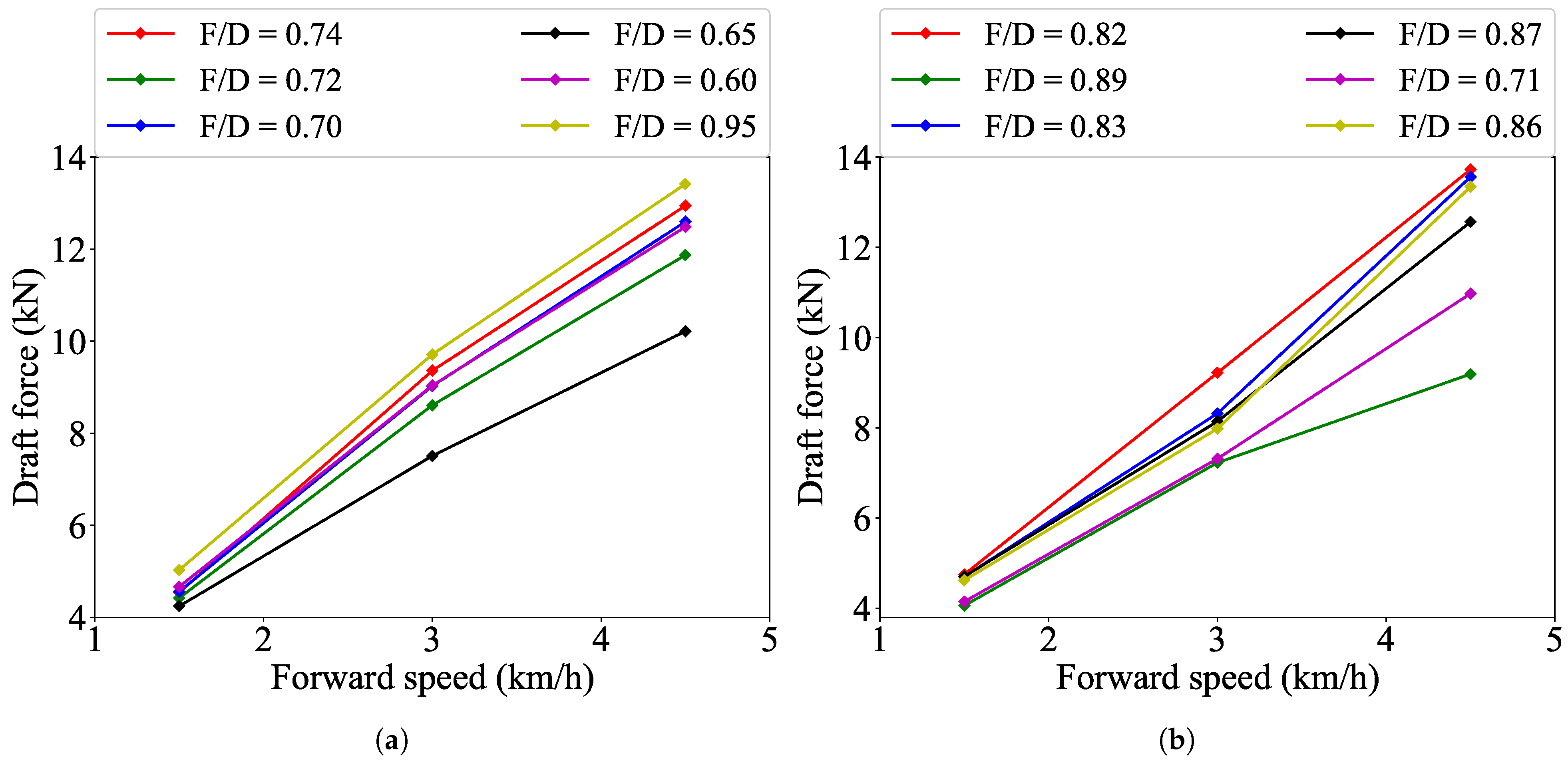
3.2. Draft Force Determined via Numerical Modeling
3.3. Draft Force in the Real Field Experiment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Internal and External Equations of the Fitting Contour Lines of the Claws
| Coeff. | ||||||
|---|---|---|---|---|---|---|
| 0.74 | 0.72 | 0.70 | 0.65 | 0.60 | 0.95 | |
| 374 | ||||||
| – | – | – | ||||
| – | – | – | – | |||
| – | – | – | – | – | ||
| Coeff. | ||||||
|---|---|---|---|---|---|---|
| 0.82 | 0.89 | 0.83 | 0.87 | 0.71 | 0.86 | |
| – | ||||||
| – | – | |||||
| – | – | – | – | |||
| – | – | – | – | – | ||
References
- Tong, J.; Jiang, A.H.; Wang, Y.M.; Ma, Y.H.; Li, J.W.; Sun, J.Y. Tillage force and disturbance characteristics of different geometric-shaped sub-soilers via DEM. Adv. Manuf. 2020, 8, 392–404. [Google Scholar] [CrossRef]
- Tim Chamen, W.C.; Moxey, A.P.; Towers, W.; Balana, B.; Hallett, P.D. Mitigating arable soil compaction: A review and analysis of available cost and benefit data. Soil Tillage Res. 2015, 146, 10–25. [Google Scholar] [CrossRef]
- Acquah, K.; Chen, Y. Soil Compaction from Wheel Traffic under Three Tillage Systems. Agriculture 2022, 12, 219. [Google Scholar] [CrossRef]
- Hakansson, I.; Reeder, R.C. Subsoil compaction by vehicles with high axle load—Extent, persistence and crop response. Soil Tillage Res. 1994, 29, 277–304. [Google Scholar] [CrossRef]
- Raper, R.L.; Reeves, D.W.; Shaw, J.N.; van Santen, E.; Mask, P.L. Using site specific subsoiling to minimize draft and optimize corn yields. Trans. ASAE 2005, 48, 2047–2052. [Google Scholar] [CrossRef]
- de Campos, M.; Rossato, O.B.; Marasca, I.; Martello, J.M.; de Siqueira, G.F.; Garcia, C.P.; Rossetto, R.; Calonego, J.C.; Cantarella, H.; Crusciol, C.A.C. Deep tilling and localized liming improve soil chemical fertility and sugarcane yield in clayey soils. Soil Tillage Res. 2022, 222, 10542. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z.; Shao, X.; Kong, Y.; Lyu, Y.; Wang, Y. Deep tillage improves the grain yield and nitrogen use efficiency of maize (Zea mays L.) under a wide–narrow row alternative system in northeast china. Int. J. Plant Prod. 2022, 16, 63–76. [Google Scholar] [CrossRef]
- Brezinščak, L.; Kontek, K.; Bogunović, I.; Horvat, D. Impact of conservation tillage on grain yield and yield components of maize in north-west Croatia. Agric. Conspec. Sci. 2022, 87, 103–109. [Google Scholar]
- Aday, S.H.; AL-Haliphy, A.R.; Majeed, H. Field study for a modified subsoiler draft requirement in a heavy soil. Iraqi J. Agric. 2004, 9, 155–166. [Google Scholar]
- Song, W.; Jiang, X.; Li, L.; Jin, T. Increasing the width of disturbance of plough pan with bionic inspired subsoilers. Soil Tillage Res. 2022, 220, 105356. [Google Scholar] [CrossRef]
- Raper, R.L. Subsoiler shapes for site-specific tillage. Trans. ASAE 2005, 21, 25–30. [Google Scholar] [CrossRef]
- Nichols, M.L.; Reaves, C.A. Soil reaction to subsoiling equipment. Agric. Eng. 1958, 39, 340–343. [Google Scholar]
- Smith, L.A.; Williford, J.L. Power requirements of conventional, triplex, and parabolic subsoilers. Trans. ASAE 1988, 31, 1685–1688. [Google Scholar] [CrossRef]
- Mollazade, K.; Jafari, A.; Ebrahimi, E. Application of dynamical analysis to choose best subsoiler’s shape using ANSYS. N. Y. Sci. J. 2010, 3, 93–100. [Google Scholar]
- Tong, J.; Sun, J.; Chen, D.; Zhang, S. Geometrical features and wettability of drug beetles and potential biomimetic engineering applications in tillage implements. Soil Tillage Res. 2005, 80, 1–12. [Google Scholar] [CrossRef]
- Guo, Z.; Zhou, Z.; Zhang, Y.; Li, Z. Bionic optimization research of soil cultivating component design. Sci. China Ser. E Tech. Sci. 2009, 52, 955–965. [Google Scholar] [CrossRef]
- Zhang, J.; Tong, J.; Ma, Y. Simulation of bionic anti-drag subsoiler with exponential curve feature using discrete element method. Appl. Mech. Mater. 2014, 461, 461–543. [Google Scholar] [CrossRef]
- Young, C.J.; Jones, J. Spermophilus mexicanus. Mamm. Species 1982, 164, 1–4. [Google Scholar] [CrossRef]
- Godwin, R.J.; Spoor, G. Soil failure with narrow tines. J. Agric. Eng. Res. 1977, 22, 213–228. [Google Scholar] [CrossRef]
- Yates, R.C. A Handbook on Curves and Their Properties; J.W. Edwards: Ann Arbor, MI, USA, 1947. [Google Scholar]
- Karmakar, S.; Kushwaha, R.L. Dynamic modeling of soil-tool interaction: An overview from a fluid flow perspective. J. Terramech. 2006, 43, 411–425. [Google Scholar] [CrossRef]
- El-Borhamy, M. Numerical study of the stationary generalized viscoplastic fluid flows. Alex. Eng. J. 2018, 57, 2007–2018. [Google Scholar] [CrossRef]
- Zhu, L.; Ge, J.R.; Cheng, X.; Peng, S.S.; Qi, Y.Y.; Zhang, S.W.; Zhu, D.Q. Modeling of share/soil interaction of a horizontally reversible plow using computational fluid dynamics. J. Terramech. 2017, 72, 1–8. [Google Scholar] [CrossRef]
- Karmakar, S.; Kushwaha, R.L.; Lague, C. Numerical modeling of soil stress and pressure distribution on a flat tillage tool using computational fluid dynamics. Biosyst. Eng. 2007, 97, 407–414. [Google Scholar] [CrossRef]
- Al-Shammary, A.A.G.; Kouzani, A.; Kaynak, A.; Khoo, S.; Norton, M.; Gates, W. Soil bulk density estimation methods: A review. Pedosphere 2018, 28, 581–596. [Google Scholar] [CrossRef]
- Godwin, R.J. A review of the effect of implement geometry on soil failure and implement forces. Soil Tillage 2007, 97, 331–340. [Google Scholar] [CrossRef]
- Karmakar, S.; Ashrafizadeh, S.R.; Kushwaha, R.L. Experimental validation of computational fluid dynamics modeling for narrow tillage tool draft. J. Terramech. 2009, 46, 277–283. [Google Scholar] [CrossRef]
- Zhang, Z.; Gan, S.; Zuo, G.; Tong, J. Bionic design and performance experiment of Sandfish head inspired subsoiler tine. Trans. Chin. Soc. Agric. Mach. 2021, 52, 33–42. [Google Scholar]
- Wang, X.; Du, R.; Geng, L.; Zhou, H.; Ji, J. Performance Evaluation of a Cicada-Inspired Subsoiling Tool Using DEM Simulations. Biomimetics 2024, 9, 25. [Google Scholar] [CrossRef]





| Soil Layer (m) | Bulk Density () | Moisture Content (%) | Cone Index (kPa) | Yield Stress (kPa) | Viscosity (kPa s) |
|---|---|---|---|---|---|
| 0–0.15 | 1380 | ||||
| 0.15–0.30 | 1360 | ||||
| 0.30–0.45 | 1390 |
| Soil Layer (m) | Bulk Density () | Moisture Content (%) | Cone Index (kPa) |
|---|---|---|---|
| 0–0.10 | 1378 | ||
| 0.10–0.20 | 1363 | ||
| 0.20–0.30 | 1387 | ||
| 0.30–0.40 | 1403 |
| Subsoiler | Tillage Depth (m) |
|---|---|
| SS | 0.2412 c 1 |
| CS | 0.3026 b |
| BS | 0.3210 a |
| Subsoiler | Draft Force (kN) |
|---|---|
| SS | a 1 |
| CS | b |
| BS | c |
| Speed (km/h) | Draft force (kN) |
| 2.7 | b |
| 4.0 | a |
| 5.8 | a |
| Subsoiler × Speed (km/h) | Draft force (kN) |
| SS—2.7 | b |
| SS—4.0 | a |
| SS—5.8 | a |
| CS—2.7 | c |
| CS—4.0 | b |
| CS—5.8 | ab |
| BS—2.7 | c |
| BS—4.0 | c |
| BS—5.8 | c |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garibaldi-Márquez, F.; Martínez-Reyes, E.; Morales-Morales, C.; Ramos-Cantú, L.; Castro-Bello, M.; González-Lorence, A. Subsoiler Tool with Bio-Inspired Attack Edge for Reducing Draft Force during Soil Tillage. AgriEngineering 2024, 6, 2678-2693. https://doi.org/10.3390/agriengineering6030156
Garibaldi-Márquez F, Martínez-Reyes E, Morales-Morales C, Ramos-Cantú L, Castro-Bello M, González-Lorence A. Subsoiler Tool with Bio-Inspired Attack Edge for Reducing Draft Force during Soil Tillage. AgriEngineering. 2024; 6(3):2678-2693. https://doi.org/10.3390/agriengineering6030156
Chicago/Turabian StyleGaribaldi-Márquez, Francisco, Ernesto Martínez-Reyes, Cornelio Morales-Morales, Lenin Ramos-Cantú, Mirna Castro-Bello, and Armida González-Lorence. 2024. "Subsoiler Tool with Bio-Inspired Attack Edge for Reducing Draft Force during Soil Tillage" AgriEngineering 6, no. 3: 2678-2693. https://doi.org/10.3390/agriengineering6030156
APA StyleGaribaldi-Márquez, F., Martínez-Reyes, E., Morales-Morales, C., Ramos-Cantú, L., Castro-Bello, M., & González-Lorence, A. (2024). Subsoiler Tool with Bio-Inspired Attack Edge for Reducing Draft Force during Soil Tillage. AgriEngineering, 6(3), 2678-2693. https://doi.org/10.3390/agriengineering6030156







