Justification of the Crank Tedder Parameters for Mineral Fertilizers

Abstract

The aim of the research was to reduce the irregularity of mineral fertilizer granule flow by developing a tedder-vaulting breaker that prevents the formation of vaults over the sowing windows of the seeder hopper. Existing dosing devices for mineral fertilizers do not provide stable application of the required doses of mineral fertilizers due to vaulting as well as accumulation and sticking of fertilizers in hoppers. In order to achieve a stable and precise metering of high fertilizer doses, a crank tedder is suggested to be mounted inside the hopper. Its function is to break the constantly appearing dynamic vaults above the sowing windows and to crush the fertilizer clods, i.e., to provide the fertilizer sowing units with a continuous flow of material. Theoretical studies were carried out using methods of classical and applied mechanics, special sections of higher mathematics. The following optimal parameters were established: the tedder blade width 0.05–0.09 m, the radius of the elbow 0.028–0.034 m, the blade installation angle 23–27°, and the kinematic mode of the tedder k = 1.5–1.9. Experimental studies have shown that the use of a crank tedder provides a stable flow of mineral fertilizer granules through sowing windows and reduces the sowing unevenness between seeding units by 12–15% and sowing instability by 7–10%. At the same time, the degree of damage to granules of 1–5 mm size is insignificant and is within 2.8–3.5%.

1. Introduction

Fertilizer application systems are one of the key elements in agricultural technology, as they have a direct impact on fertilizer efficiency and production costs [1,2,3]. Important elements of fertilizer machines are the hoppers and the seeding system, which must ensure stable, uniform, and accurate distribution of material. One of the problems faced by designers and operators of fertilizer machines is vaulting in hoppers—the accumulation and sticking of granules (fertilizer) in the corners and over the outlet windows of the hoppers [4,5]. Formation of vaults above the outlet windows makes it difficult to dose fertilizer evenly and, by disrupting the agrotechnological process of fertilizer application, leads to a reduction in crop yield [6,7,8]. This phenomenon is often related to the physical-technological properties of fertilizers and also to the design features of hoppers [9].

As a result of the formation of voids and vaults, the technological process of sowing is disturbed, which leads to unevenness of sowing and low yields. Thus, at uneven distribution of fertilizer at 40–60% the yield of grain and row crops decreases by 4–6%, at unevenness of 80%—by 15%. Even at application of optimal doses of fertilizers with irregularity of 50–70% the expected grain yield decreases by 14–15% [10].

Various devices such as vault breakers and tedders are being actively developed to solve this problem, to prevent or minimize the vaulting process in the hoppers of fertilizer machines. One of them is systems with vibrators, which are mounted on the hopper walls or on the hopper bottom [11,12]. Vibration helps to break down the vaults and fertilizer clumps, improving their flowability [13,14,15]. Such systems can be either pneumatic or electric.

Vertical tedders have also been applied to prevent vaulting, which provides the required outflow from hoppers [16]. The most common are rotary devices—various versions of tedders in the form of rotating petals, hammers, blades, and cylindrical or conical springs located at the bottom of the hopper [17,18]. They mainly cope with the task of breaking clumps of fertilizer and preventing the formation of dense vaults. However, they do not fully ensure the quality of the material output through the outlet windows, and seeding irregularities exceed the agrotechnical requirements [19,20,21].

Devices based on the supply of compressed air to the fertilizer storage area are often developed to prevent vaulting [22]. Pneumatic systems create an air flow which, as it passes through the fertilizer, helps to break up the clumps. The advantage of these systems is their ability to distribute air evenly throughout the hopper [23]. However, the complexity of the design does not allow for their wide application in the hoppers of fertilizer machines. The same disadvantages are inherent in the vault breakers and tedders working by electrostatic and magnetic methods. These methods are not widespread; however, they are promising and have been investigated with interest in recent years.

Several studies are also aimed at improving the structural characteristics of hoppers. It is proposed to change the shape and inclination angles of the hopper walls, to use flexible materials or inserts on the walls, which contributes to a natural reduction in the formation of vaults and a more uniform distribution of material [24,25,26,27]. However, for different types of fertilizers, different shapes and inclination angles will be required as well, which leads to additional design solutions.

To solve the above-mentioned problem, a tedder is installed inside the box, above the seeding windows. The purpose of the tedder is to crush fertilizer clumps and turn them into flowing granules, and to move these granules into the receiving windows of the metering unit. Despite advances in the development of tedders and vault breakers, there are problems in ensuring a uniform flow of fertilizer granules from the discharge windows of seeders and fertilizer hoppers.

The aim of the research is to reduce the irregularity of the flow of mineral fertilizer granules by developing a vault breaker tedder that prevents the formation of vaults over the sowing windows and provides the sowing machine with a continuous flow of fertilizer with low damage to granules.

2. Materials and Methods

The proposed cranked tedder consists of three supports B, D, and C and four elbows, L, M, N, and F. Blades are attached to the edges of the elbows, as shown in Figure 1. If necessary, additional elbows can be connected depending on the number of outlet windows.

When the tedder rotates with angular velocity ω on supports B, D, and C, the blades L, M, N, and F are one by one immersed in the fertilizer mass. During this immersion, they crush the encountered fertilizer clods, bring them to the receiving window of the sowing unit, and thus carry out a natural fertilizer feeding process into the window.

Theoretical studies were carried out using methods of classical and applied mechanics, special sections of higher mathematics. According to theoretically determined optimal parameters mock-up crank tedder was made and exploited in experiments.

The experimental setup is designed on the basis of the seeding hopper (1) of the SZS-2.0 (Manufacturer: Tselinselmash, Kazakhstan) seeder—a type of stubble seed-fertilizer drill (Figure 2). An experimental fluted roller feed unit as a metering device was adopted. Seeding units (apparatuses) consist of a fluted roller (5) and a funnel (2) for supplying fertilizer to the working bodies. The distance between the seeding units is 23.0 cm. The crank tedder (3) is placed in the hopper above the sowing windows. For visual observation of the crank tedder operation, the visible part of the hopper wall and part of the sowing unit housing are made of organic glass (4). Fluted rollers (5) and blades (6) of the crank tedder were 3D printed from PLA. The experimental setup is installed on a belt conveyor (7) to further study the uniformity of fertilizer distribution.

The purpose of the experiments was to evaluate the influence of the application of the crank tedder on the quality of the technological process—unevenness of seeding between the seeding units and instability of seeding. These indicators were determined with and without the cranked tedder and then compared.

Experimental research was carried out under the guidance of [28,29]. Accordingly, results were processed by determining the seeding unevenness between the seeding units and the seeding instability using the method of variation statistics. The coefficient of variation of the fertilizer mass, which fell on individual trays, installed at a common width perpendicular to the direction of movement, is taken as the sowing unevenness between the units. The coefficient of variation of the average fertilizer mass sown per repetition is taken as the sowing instability.

The presence of dust-like particles in the fertilizer leads to their sticking to the machine’s working elements (metering units, vault breakers, fertilizer pipelines), which ultimately leads to a disruption of the technological process. Therefore, an important indicator of the crank tedder’s performance is the degree of damage to granulated fertilizer. It was determined as follows. By preliminary sieving on sieves the initial fractions were obtained: (a) 5–15 mm, (b) 3–5 mm, (c) 2–3 mm, (d) 1–2 mm, each of 3 kg Each of the fractions was passed through the crank tedder with completely removed fluted roller and open sowing windows and again subjected to sieve analysis. The ratio of the weight of the fractions passed to the lower class to the original weight is the degree of damage to the granules; the higher the damage to the granules, the greater the likelihood of uneven seeding. For this purpose, granular ammophos with a moisture content of 4.2% was used.

3. Results and Discussions

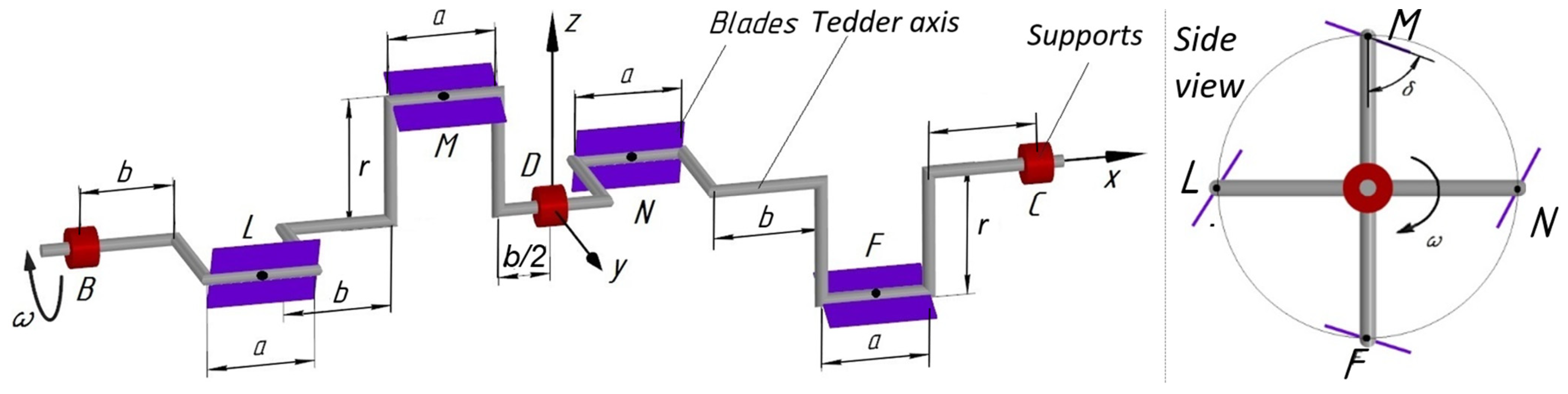
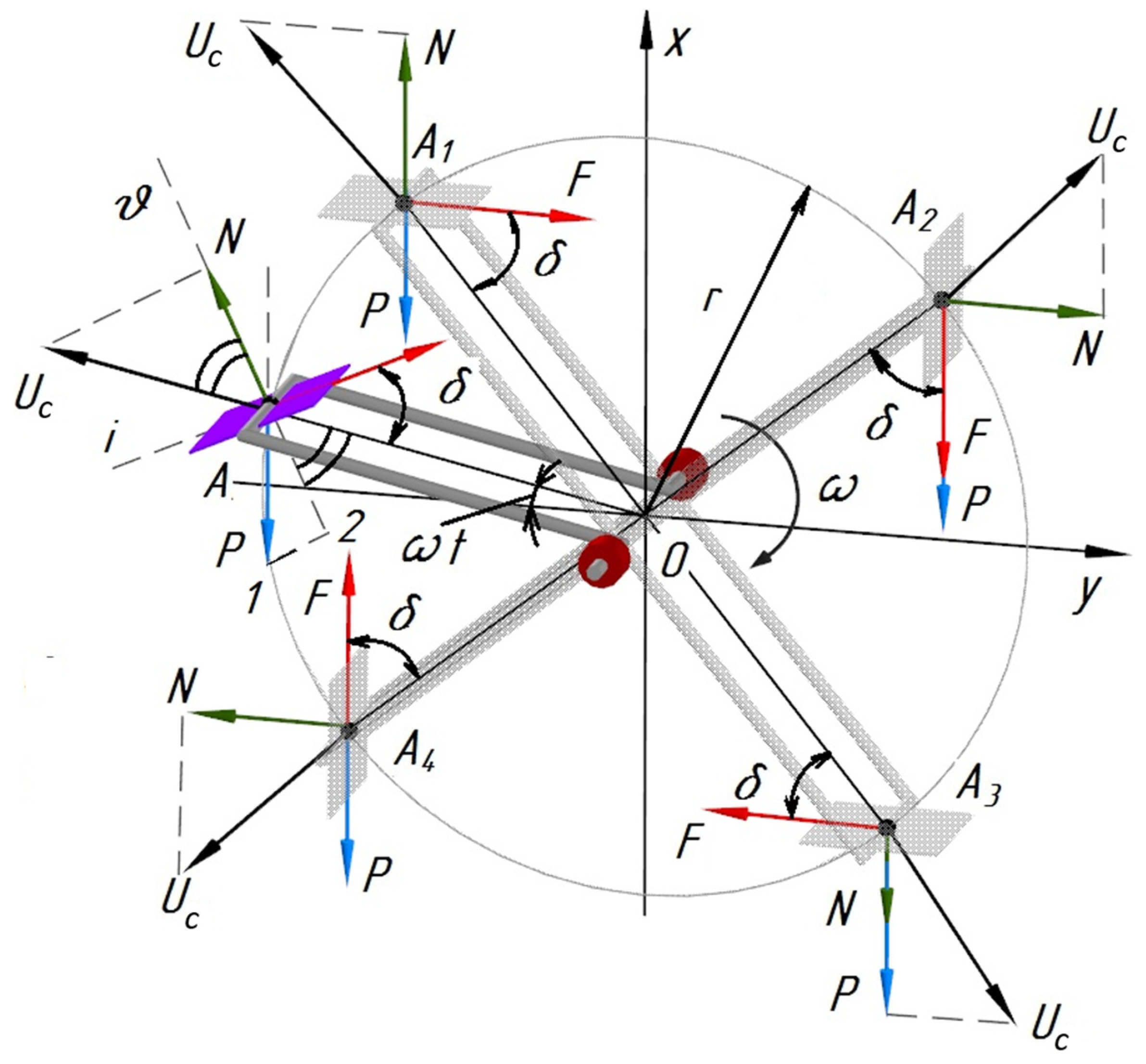
3.1. Theoretical Studies

In the diagram (Figure 1), the tedders‘ elbows L and N are located on the horizontal plane xy, and elbows M and F are located on the vertical plane xz.

The centrifugal moment of inertia of the crankshaft (J_xy, J_xz, J_yz) has to be determined. The mass of the crankshaft can be considered concentrated at the points L, M, N, and F and equal to each other, since the links along the x-axis do not give the centrifugal moment of inertia.

In classical mechanics, the centrifugal moment of inertia of a solid body is calculated by the following formulae [30,31]:

$$\begin{gathered} J_{xy}=\sum _{k=1}^n{m}_k·x_k·y_k; \\ {J}_{xz}=\sum _{k=1}^n{m}_k·x_k·z_k \\ {J}_{yz}=\sum _{k=1}^n{m}_k·y_k·z_k. \end{gathered}$$

(1)

Let us decompose the sums in Equation (1) into points whose masses are concentrated at the points m_L, m_M, m_N, m_F:

$$\begin{array}{c}\begin{array}{ll}{J}_{yx}=\sum _{k=1}^n{m}_L{x}_L{y}_L& =m_L{x}_L{y}_L+m_M{x}_M{y}_M+m_N{x}_N{y}_N+m_F{x}_F{y}_F\\ & =m_L·b\left[-\left(1.5a+1.5b\right)\right]+m_M\left(-b\right)\left({\displaystyle \frac{a}{2}}+{\displaystyle \frac{b}{2}}\right)\\ & =-{\displaystyle \frac{3}{2}}{m}_{L}ab-{\displaystyle \frac{3}{2}}{m}_L{b}^2-m_M{\displaystyle \frac{ab}{2}}-m_M{\displaystyle \frac{b^2}{2}}\\ & =-m2ab-m2b^2=-2m\left(ab+b^2\right)=-2\mathrm{T}b\left(a+b\right);\end{array}\\ { J}_{yz}=\sum _{k=1}^n{m}_L{y_{L}z}_L+m_M{y}_M{z}_M+m_N{y}_N{z}_N+m_F{y}_F{z}_F=0,\end{array}$$

(2)

This is because the x-axis is the main axis of symmetry of the tedder, and the centrifugal moment of low inertia is zero around the main axis of inertia:

$$\begin{array}{ll}{J}_{zx}=\sum _{k=1}^n{m}_L{z}_L{x}_L& =m_L{z}_L{x}_L+m_M{z}_M{x}_M+m_N{z}_N{x}_N+m_F{z}_F{x}_F\\ & =m_M\left(b\right)·\left[-\left(0.5a+0.5b\right)\right]+m_F\left(-b\right)·\left[1.5a+1.5b\right]\\ & =-0.5m_{M}b·a-0.5m_M{b}^2-1.5m_{F}a·b-1.5m_F·b^2\\ & =-2mab-2m{b}^2=-2mb\left(a+b\right)\end{array}$$

(3)

The conclusion from Equations (2) and (3) is that the centrifugal moment of inertia of the crank tedder maintains equality on two mutually perpendicular planes:

$$J_{yx}=J_{xz}=-2mb\left(a+b\right)$$

(4)

Let us consider the operation of one tedder elbow with a blade immersed in the fertilizer medium. Figure 3 (side view) considers one tedder elbow 0A. An important point to consider is that part of the blade A is not perpendicular to the radial direction (r), there is an angle δ between the blade and the radius 0A. The function of this angle can be understood by the following analysis. If the direction of the blade and the tangent line coincide (δ = π/2), the blade plunges directly into the fertilizer mass at right angles, so the relative motion is minimal.

As a result, the tedding process must also be at a low level. If this angle δ > π/2, the blade pushes the fertilizer toward the center (0) with its surface and compacts it instead of loosening it. If the angle under consideration is δ < π/2, the blade pushes the fertilizer from the center outwards, resulting in an accelerated loosening process.

While all external forces acting on the fertilizer above the blade maintain mutual equality, the fertilizer also remains at relative rest.

External forces acting on the fertilizer:

• N—normal reaction of the surface of the blade on the fertilizer;
• P = mg—gravity of the fertilizer;
• F = fN—friction force between the blade and the fertilizer;
• U_c = mω²r—centrifugal force of the fertilizer in transport movement;
• f = tg φ—friction coefficient between fertilizer and metal;
• φ—angle of friction between fertilizer and metal;
• ω—angle of rotation of the crank tedder;
• r—radius of the blade elbow;
• t—mass of fertilizer in contact point with the blade.

The blade, with the fertilizer on top, is rotated by an angle ωt during time t. Its position is defined by point A. During the traveling time t₁, t₂, … the blade together with the fertilizer occupies the points A₁, A₂, … The angle of movement depends on the value of ωt. Depending on it, the above-mentioned forces also change their direction.

At point A with respect to the axis Oy, the blade is rotated by the angle ωt₁. The forces N and P are opposite and are balanced. The tedding process is influenced by the forces of inertia and friction U_c, F. At the point A₂ the forces F, P act in one direction, and the projection of the inertial force acts against them. At point A₃, the forces N, P, and the projection of the force U_c are involved in tedding in one direction. At point A₄, the forces F and P are opposite and are balanced. The force U_c participates in tedding.

Important to find out the parametric equations of point A at any location:

x = r sin ωt;
y = r cos ωt.

(5)

From the first derivatives of the above equations, the blade velocities can be determined:

$$\begin{gathered} V_x={\displaystyle \frac{dx}{dx}}=\omega rcos\omega t; \\ {V}_y={\displaystyle \frac{dy}{dt}}=-\omega rsin\omega t. \end{gathered}$$

(6)

From the derivatives of the last equations, the blade accelerations can be determined:

$$\begin{gathered} W_x={\displaystyle \frac{d{V}_x}{dt}}=-{\omega }^{2}rsin\omega t; \\ {W}_y={\displaystyle \frac{d{V}_y}{dt}}=-{\omega }^{2}rcos\omega t. \end{gathered}$$

(7)

If the fertilizer blade is assumed to be stationary with respect to the natural axis v, then all forces must observe the equality:

N + U_C cos (∠U_C AN) = P cos (∠1 A2).

(8)

The angles in the last equation:

$$\angle 1A0=\pi -\left({\displaystyle \frac{\pi }{2}}+\omega t\right)={\displaystyle \frac{\pi }{2}}-\omega t;$$

$$\angle U_{c}AN=\angle 2A0={\displaystyle \frac{\pi }{2}}-\delta .$$

$$\angle 1A2=\angle 1A0-\angle 2A0=\delta -\omega t.$$

Using the values of the terms of Equation (8) and the defined angles, we will find:

$$\begin{gathered} N+m{\omega }^{2}tcos\left({\displaystyle \frac{\pi }{2}}-\delta \right)=mgcos\left(\delta -\omega t\right); \\ N+m{\omega }^{2}r sin \delta =mg cos\left(\delta -\omega t\right); \\ N=mg\left[cos\left(\delta -\omega t\right)-k\mathit{sin}\delta \right]. \end{gathered}$$

(9)

In Equation (9), the conventional notation is accepted:

$$k={\displaystyle \frac{{\omega }^{2}r}{g}}.$$

(10)

In the following, we consider the sign k as an indicator of the kinematic mode of the crank tedder and define its value as the ratio of centrifugal and free fall acceleration.

If the fertilizer is under the action of the blade, the normal reaction must be positive, i.e., N > 0. In this case, the following condition must be fulfilled:

$$\mathit{cos}(\delta -\omega t) > k \mathit{sin} \delta .$$

(11)

Let’s examine the last equation:

$$\begin{gathered} cos\delta ·cos\omega t+sin\delta ·sin \omega t>ksin\delta ; \\ k<ctg\delta ·cos\omega t+sin\omega t. \end{gathered}$$

(12)

$$tg\delta <{\displaystyle \frac{cos\omega t}{k-sin\omega t}}.$$

(13)

According to Equations (12) and (13), the kinematic mode index of the crank tedder, and through which (Equation (6)), the angular velocity of the tedder ω, its radius r and the blade position angle δ can be determined. When the cranked tedder rotates in time t₁, it rotates by angle ωt₁ and the blade goes into position A₁. At this point N = P, i.e., the fertilizer loses its connection with the blade and separates from it, performing its own independent movement. The case of this position occurs when the angles ωt₁ and δ are equal: ωt₁ = $\delta$.

For such a case, Equation (12) can be rewritten:

$$\begin{gathered} k\le ctg \omega t·\mathit{cos}\omega t+{\mathit{sin}}^2\omega t; \\ k\le {\displaystyle \frac{{cos}^2\omega t+sin\omega t}{\mathit{sin}\omega t}}; \\ k\le {\displaystyle \frac{1}{\mathit{sin}\omega t}}. \end{gathered}$$

(14)

Conclusion from the last equation: the kinematic mode index of the crank tedder, is inversely proportional to the sine of the angle of rotation of the crank.

Let us consider the balance of external forces acting on the blade in the following case A₁:

$$\begin{gathered} \sum x=N+U_c\mathit{cos}\left({\displaystyle \frac{\pi }{2}}-\delta \right)-P=0; \\ \sum y=U_{c}sin\left({\displaystyle \frac{\pi }{2}}-\delta \right)-F=0. \end{gathered}$$

(15)

Let’s substitute the values of the terms of the created system of equations:

$$\begin{gathered} N+m{\omega }^{2}rsin\delta =mg; \\ m{\omega }^{2}rcos\delta =fN. \end{gathered}$$

(16)

From the second equation of the system (16), we will find:

$$N={\displaystyle \frac{1}{f}}m{\omega }^{2}rcos\delta .$$

(17)

It is known from theoretical mechanics [30] that in rotational motion the mass can be compensated by the moment of centrifugal inertia. On this basis, from Equation (4), we can find the moment of centrifugal inertia with respect to the x-axis:

$$J=\sqrt{J_{yx}^2+J_{xz}^2}=\sqrt{8m^2{b}^2{\left(a+b\right)}^2}=2\sqrt{2}mb\left(a+b\right).$$

(18)

Substituting (18) into (17), we define:

$$N={\displaystyle \frac{1}{⨍}}{w}^{2}rcos\delta ·2\sqrt{2}mb(a+b).$$

(19)

From the first equation of the system (16), taking into account (19), we find:

$$N=mq-m{w}^{2}rsin\delta .$$

(20)

From (19) and (20) we have:

$${\displaystyle \frac{1}{⨍}}{w}^{2}rcos\delta ·2\sqrt{2}mb\left(a+b\right)=mq-m{w}^{2}rsin\delta .$$

Divide both sides of the equality by mg:

$${\displaystyle \frac{1}{⨍}}{\displaystyle \frac{w^{2}r}{q}}cos\delta ·2\sqrt{2}b\left(a+b\right)=1-{\displaystyle \frac{w^{2}r}{q}}sin\delta .$$

(21)

Let’s accept the designation ${\displaystyle \frac{w^{2}r}{q}}=k,$ and we can call it the kinematic mode coefficient of the crank tedder:

$$\begin{gathered} {\displaystyle \frac{1}{⨍}}kcos\delta ·2\sqrt{2}b\left(a+b\right)=1-ksin\delta ; \\ {\displaystyle \frac{k}{⨍}}\left[\left(cos\delta ·2\sqrt{2}b\left(a+b\right)\right)\right]+sin\delta =1; \\ k[cos\delta ·2\surd 2b(a+b)+⨍sin\delta ]=⨍; \\ {k=⨍\left[2\sqrt{2}b\left(a+b\right)cos\delta +⨍sin\delta \right]}^{-1} \end{gathered}$$

(22)

In the case when b = r:

$${k=⨍\left[2\sqrt{2}r\left(a+b\right)cos\delta +⨍sin\delta \right]}^{-1}.$$

(23)

To clarify the obtained results, we derive the formula for the kinematic mode without taking into account the influence of blade parameters.

From the first Equation (16):

$$N=mq-m{w}^{2}rsin\delta .$$

(24)

From the second Equation (16) we determine:

$$N={\displaystyle \frac{1}{⨍}}m{w}^{2}rcos\delta .$$

(25)

Equalize the right sides (24) and (25):

$$mq-m{w}^{2}rsin\delta ={\displaystyle \frac{1}{⨍}}m{w}^{2}rcos\delta .$$

We divide both sides by mq and take notation ${\displaystyle \frac{w^{2}r}{q}}=k$

$$\begin{gathered} 1-ksin\delta ={\displaystyle \frac{1}{⨍}}kcos\delta ; \\ ⨍=\mathrm{k}(\mathit{cos}\delta +⨍sin\delta ); \\ {k=⨍(cos\delta +⨍sin\delta )}^{-1} \end{gathered}$$

(26)

As can be seen from (23) and (26), the structure of both formulas is identical, the only difference is the cosine function coefficient, that is $2\sqrt{2}b\left(a+b\right)$, which characterizes the influence of the blades on the crank tedder operation. In Formula (26), only one important factor is taken into account—the angle of the blades. k is dimensionless as in (10) and also in (26). However, in (23) k becomes a dimension, because the influence of the blades is introduced by replacing the mass with the moment of centrifugal inertia in order to take into account the blade parameters. Formula (26) can be used for simplified production calculations, and Formula (23) can be used for refined calculations.

To verify the obtained expression, let us substitute the generally accepted values of coefficients and design parameters of the tedder:

• r = 0.06 m—radius of the elbow;
• a = 0.04 m—width of the blade;
• b = 0.23 m—distance between neighboring elbows;
• f = 0.5—coefficient of friction;
• δ = 60°—angle of location of crank blades.

  $$k=0.5{\left[2\sqrt{2}·0.06\left(0.04+0.23\right)0.5+0.5·0.87\right]}^{-1}=1.09.$$

The result is expected. Further it is necessary to perform a numerical analysis of Formula (23) in order to justify the design and technological parameters of the tedder.

For numerical analysis of (23), we take numerical values of the terms of the equations from scientific sources. The distance between the seeding units of the SZS-2.0 seeder is 23.0 cm. A crank tedder is placed in the hopper of this drill. The distance between the tedder blades must therefore also be 23.0 cm [32,33,34]:

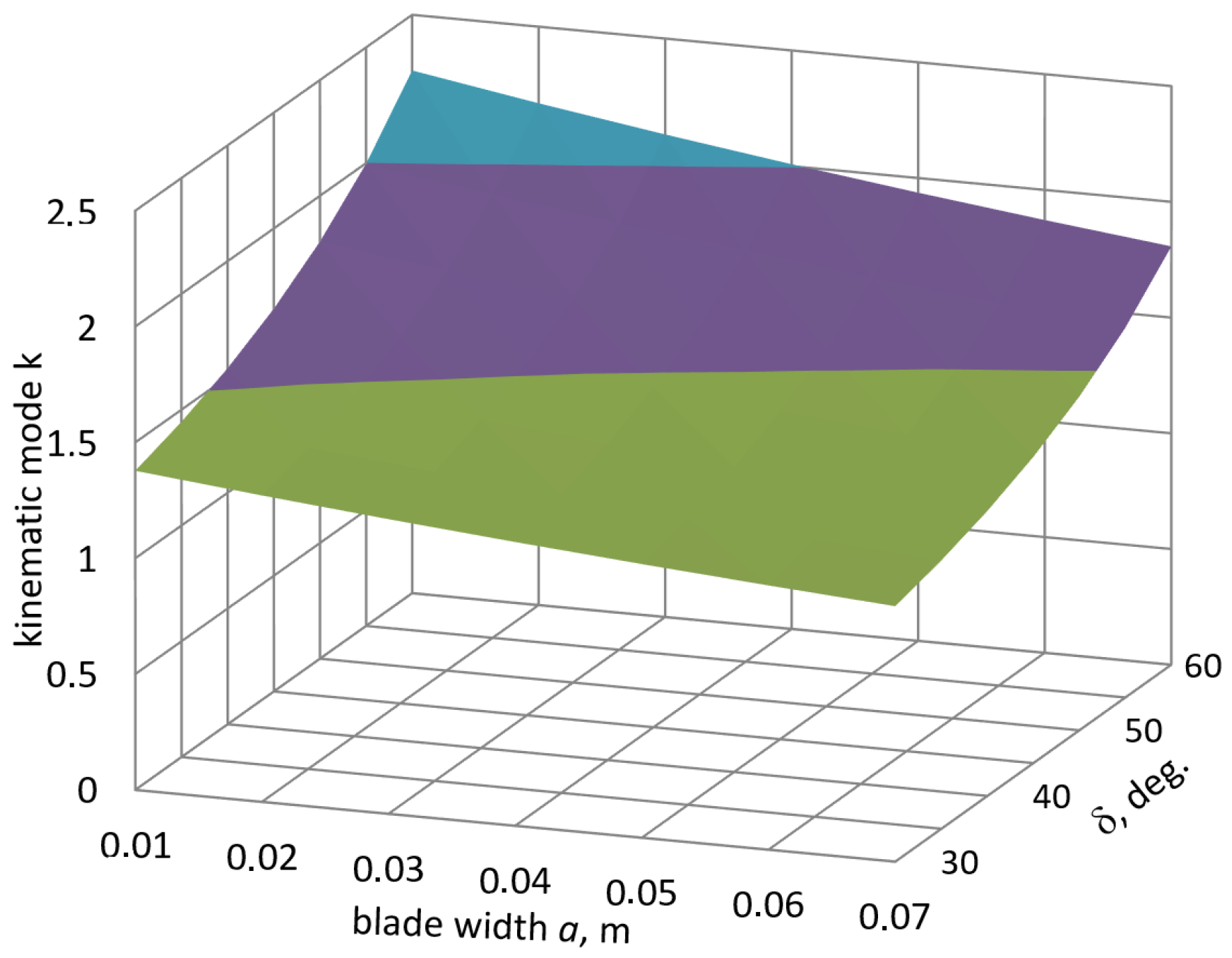
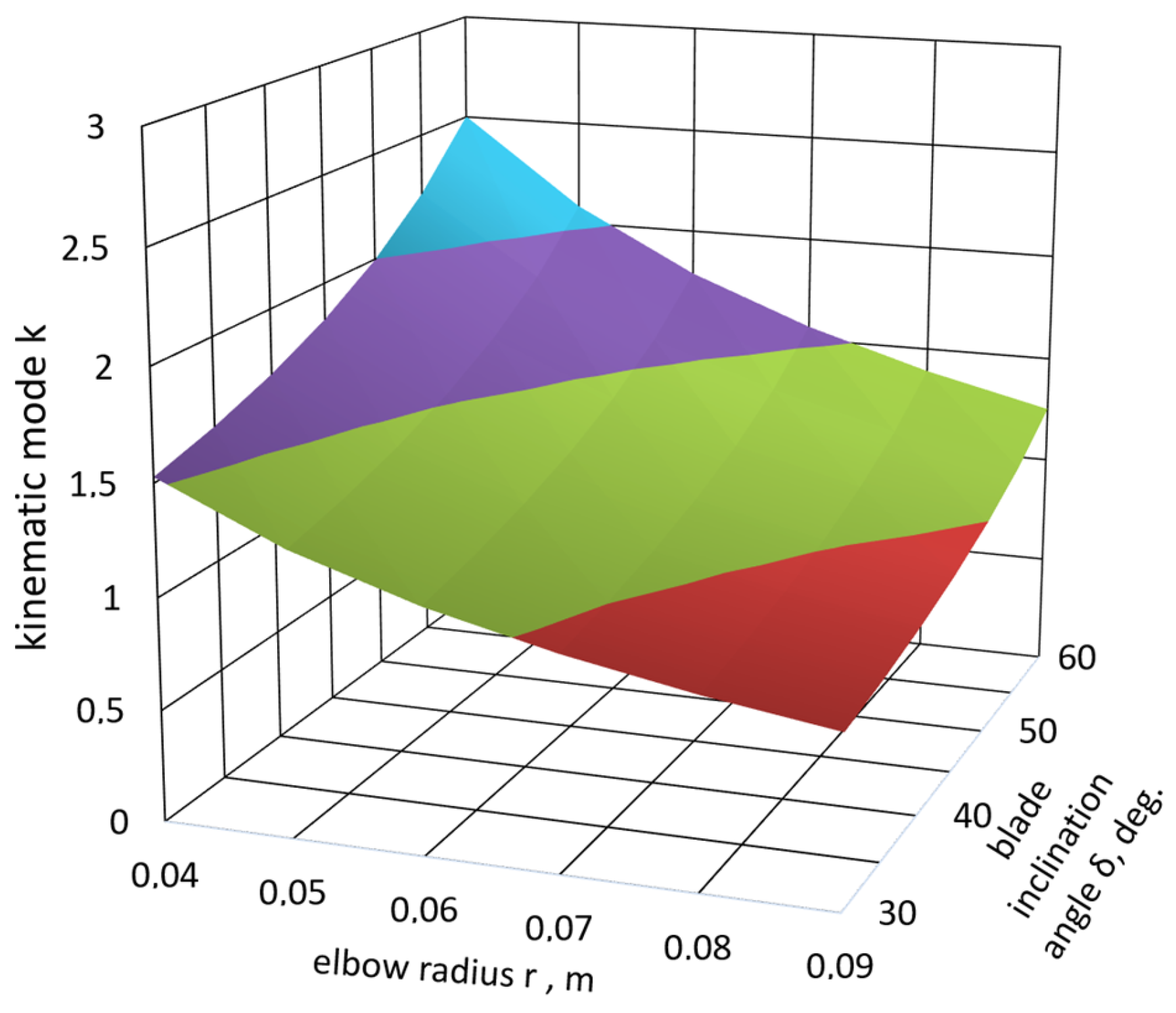
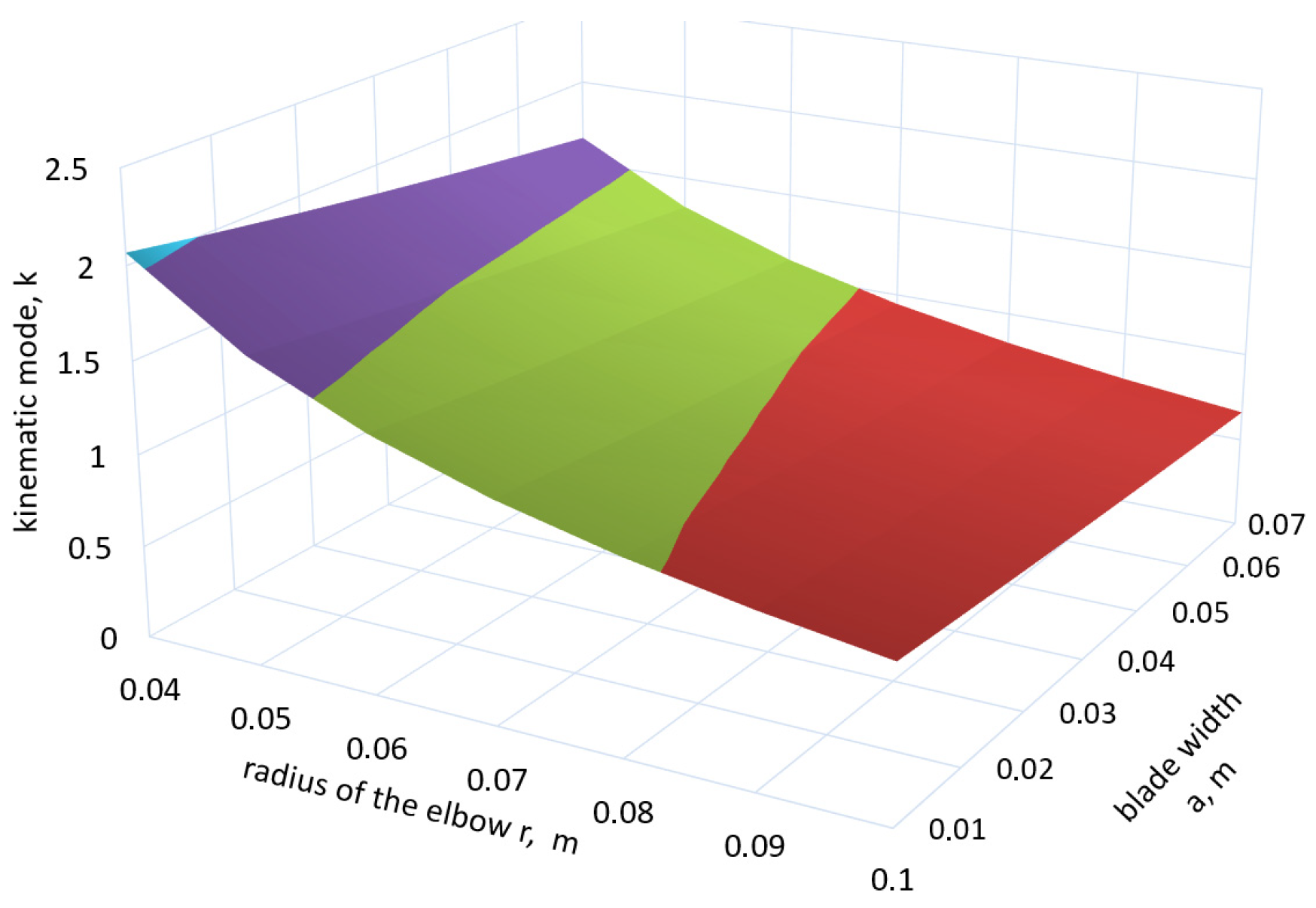
• δ = 20–65°—angle of location of crank blades;
• r = 0.01–0.1 m—radius of the elbow;
• a = 0.05–0.2 m—width of the blade.

Dependences of design parameters and kinematic mode of the crank tedder are shown in Figure 4.

The most significant influence on the kinematic mode is the angle δ. Thus, increasing the blade mounting angle by 75%, from 20° to 35°, led to a decrease in the kinematic mode by 51.6%, that is from 2.35 to 1.55. On the contrary, increasing the width of the tedder blade from 0.05 m to 0.01 m resulted in a decrease in the kinematic mode by 3%, from 1.72 m to 1.67. The radius of the tedder elbow has a similar effect on the kinematic mode. Thus, when reducing the specified radius from 0.07 m to 0.01 m, the kinematic mode increases from 1.69 to 1.95, that is 15.4%.

The obtained indicators testify to the correctness of the solution of the technical problem on the destruction of constantly appearing vaults over sowing windows, crushing of fertilizer clods due to the impact of blades, as the blade installation angle δ have most significant influence on the kinematic mode.

Figure 5, Figure 6, Figure 7 and Figure 8 show the dependence of kinematic mode on different parameters of the crank tedder. It can be seen that increasing the blade inclination angle, blade width, and radius of the elbow allows for reducing the kinematic mode, hence reducing its rotational speed. However, the extent of their influence differs.

Thus, the dependences f (r) and f (δ) intersect at the coordinate points (Figure 4): k = 1.87, a = 0.07 m, r = 0.031 m, δ = 25.2°.

Consequently, the optimal parameters of the crank tedder are:

• blade width—0.07 m;
• radius of the elbow—0.031 m;
• elbow angle—25.2°
• kinematic mode coefficient, k = 1.87.

3.2. Results of Experiments

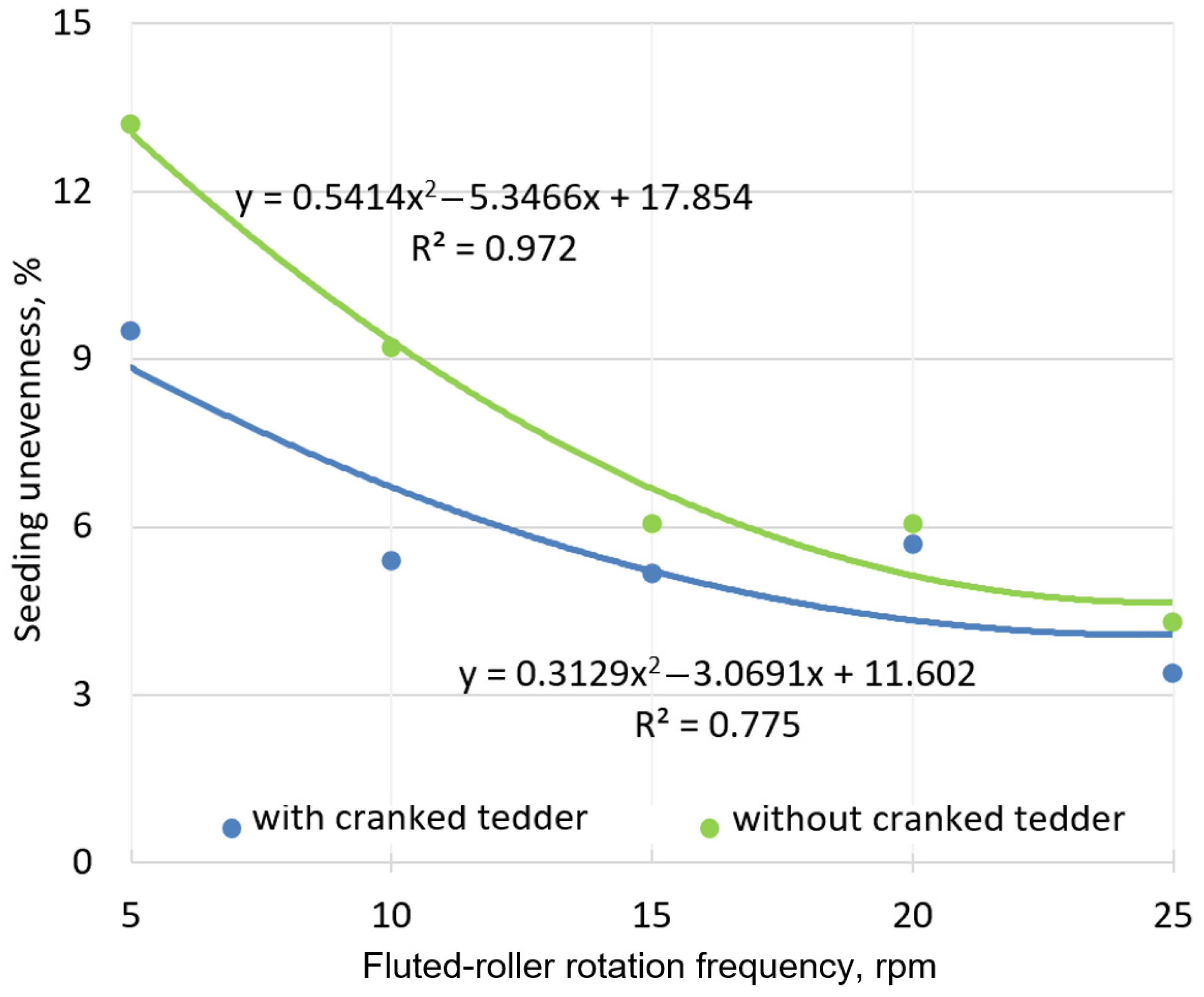
3.2.1. Determination of Sowing Quality

Experiments have shown that the use of a crank tedder provides a steady flow of granules through the sowing windows and reduces the unevenness of sowing between the devices by 12–15% and 7–10% sowing instability (Figure 9).

3.2.2. Degree of Granule Damage in Fertilizer

The fracture and damage behavior of granules under impact is very important in many industrial processes [35].

Table 1. Damage to ammophos granules by crank tedder.

Granule Size, mm	Granule Damage,%
>5	14.64
3–5	3.38
2–3	2.95
1–2	2.84

shows that the degree of damage to granules and particles of larger sizes is higher in comparison with particles of smaller sizes. Visual observations showed that large granules (lumps) are destroyed at the moment of meeting with the elbows and pushing them into the sowing windows by the blades of the crank tedder. The degree of damage to granules 1–5 mm in size is insignificant and ranges from 2.8–3.5%. Since they constitute the main part of the fertilizer (about 90%), the degree of granule damage by the crank tedder is acceptable.

Further research will be directed to the study of the proposed tedder-vaulting breaker for sowing of hard-to-flow materials—grass seeds.

4. Conclusions

Physical and mechanical properties of mineral fertilizers, design features of hoppers, and shapes or dimensions of the sowing opening lead to the formation of vaults (arches) over the seeding window, which causes the violation of the technological process of seeding. Based on the analysis of known devices, it is proposed to install a crank tedder above the seeding windows of fertilizer hoppers or seed drills. The performed theoretical study allowed us to establish optimal parameters of the crank tedder for hopper or the grain-fertilizer seeder: width of the tedder blade 0.05–0.09 m, radius of the elbow 0.028–0.034 m, the blade installation angle 23–27°, kinematic mode of the tedder k = 1.5–1.9. Experimental studies have shown that the use of the crank tedder provides a stable flow of granules through the sowing windows, reduces the unevenness of seeding between the devices by 12–15%, and decreases the seeding instability by 7–10%. The degree of damage to granules of 1–5 mm size is insignificant and ranges between 2.8 and 3.5%. Further research plans to equip the experimental seed drill (SZS-2.0) with the crank tedder and conduct field experiments for performance evaluation.