Abstract
We consider a finite-size spherical bubble with a nonequilibrium value of the q-field, where the bubble is immersed in an infinite vacuum with the constant equilibrium value for the q-field (this has already cancelled an initial cosmological constant). Numerical results are presented for the time evolution of such a q-bubble with gravity turned off and with gravity turned on. For small enough bubbles and a q-field energy scale sufficiently below the gravitational energy scale , the vacuum energy of the q-bubble is found to disperse completely. For large enough bubbles and a finite value of , the vacuum energy of the q-bubble disperses only partially and there occurs gravitational collapse near the bubble center.
PACS:
95.36.+x; 98.80.Es; 98.80.Jk
1. Introduction
The energy density of the vacuum, the dark energy, and the cosmological constant are highly debated topics today, as quantum field theory suggests a typical number that is some 120 orders of magnitude larger [1,2] than what has been observed [3]. The mismatch is so large and so significant as to make it the main outstanding problem of modern physics. However, a similar vacuum energy problem exists in condensed-matter systems, and its solution may provide a hint for the solution of the cosmological constant problem. In condensed matter, the zero-point energy of the quantum fields is fully cancelled by the microscopic (atomic) degrees of freedom, if the system is in its ground state. If the system is slightly out of equilibrium, the vacuum energy is not fully compensated, but its magnitude is determined by the infrared energy scale rather than by the ultraviolet (atomic) energy scale.
Still, in order to apply this condensed-matter scenario of the cancellation of the vacuum energy to the quantum vacuum of our Universe, we need to know the proper variables to describe this quantum vacuum. One example of such a variable is the four-form field strength used by Hawking in particular [4]. The nonlinear extension of this approach, which goes under the name of q-theory [5,6,7], demonstrates the nullification of the vacuum energy density in a full-equilibrium vacuum without matter present. A small cosmological constant appears if the vacuum is out of equilibrium. Its value is then determined by infrared physics and is proportional either to the matter content of the Universe or to the Hubble expansion rate.
While q-theory solves the main cosmological problem (other realizations of the q variable are presented in Refs. [8,9] and a one-page review appears as Appendix A in Ref. [10]), the dynamical process of equilibration of the vacuum towards the full equilibrium is still under investigation. The previously obtained results [6] concern the decay of an initially homogeneous high-energy state emerging immediately after the Big Bang. These calculations demonstrated that, with generic initial conditions, the high-energy state prefers to relax to a de-Sitter vacuum rather than to the Minkowski vacuum. On the other hand, the possibility of the final decay of the de-Sitter vacuum to the Minkowski vacuum is under intensive debate. This is because of the special symmetry of de-Sitter spacetime; see, e.g., Refs. [11,12] and references therein.
One way to circumvent this de-Sitter controversy is to consider the case that the Big Bang takes place not over the whole of space but only in a finite region of space, which is surrounded by equilibrium Minkowski vacuum. This possibility is also suggested by condensed-matter experiments [13], where a hot spot created within the equilibrium state finally relaxes to the full equilibrium by radiating the extra energy away to infinity.
Concretely, we propose to calculate, in the q-theory framework [5,6], the time evolution of a finite-size spherical bubble with , which is immersed in an infinite equilibrium vacuum with , where has already cancelled an initial cosmological constant . The expectation is that the interior field relaxes to , while the bubble wall (or its remnant) ultimately moves outwards. However, gravity may hold surprises in store. Remark that our proposed calculation corresponds to the scenario discussed in the second paragraph of Sec. V A in Ref. [6], which mentioned the possibility that “the starting nonequilibrium state could, in turn, be obtained by a large perturbation of an initial equilibrium vacuum.” We emphasize that the calculation of the present article is the first-ever calculation of the inhomogeneous dynamics of the quantum vacuum in the q-theory framework.
Before we start with this calculation, we have three clarifying comments. The first comment is that it may be instructive to compare our q-bubble to the vacuum bubble as discussed by Coleman and collaborators [14,15,16]. That discussion starts from a classical field theory of a fundamental scalar field with nonderivative interactions. The interactions are, in fact, determined by a potential term in the action. The potential is assumed to have various local minima: one or more “false” vacua and the single “true” vacuum , where the “false” vacua have a larger energy density than the value of the “true” vacuum. Coleman’s vacuum bubble, then, corresponds to a finite-size spherical bubble with “true” vacuum inside and “false” vacuum outside (in other words, the energy density inside is lower than outside). The dynamic behavior of a single vacuum bubble is that the bubble expands (cf. Figure 4 in Ref. [14]) with the true-vacuum region increasing but, at a given finite time, the far-away region remaining in a false-vacuum state. Such a vacuum bubble is essentially different from our q-bubble which has an infinite equilibrium vacuum with outside (in Coleman’s terminology, “true” q-vacuum outside). In a way, the q-bubble resembles Coleman’s vacuum bubble with interior and exterior regions switched. It is clear that, already energetically, the dynamic behavior of the q-bubble will be different from that of Coleman’s vacuum bubble.
The second comment concerns the different role of a fundamental scalar field and the vacuum variable for the cosmological constant problem. In the fundamental-scalar-field approach, the nullification of the energy density in the equilibrium vacuum requires fine-tuning [2]. In the q-field approach, the vacuum is a self-sustained system, which, in equilibrium, automatically acquires a zero value for the thermodynamic potential that enters the Einstein equation by a cosmological-constant-type term. See, in particular, the discussion of Section 2 in Ref. [8].
The third comment expands on the second and concerns the actual dynamics of the q-field. At first glance, the dynamical equations used in the present article are identical to the equations of general relativity coupled to a “scalar” field with a potential to be defined later. The dynamics of a fundamental scalar field interacting with gravity has been extensively studied, in particular by Choptuik and collaborators [17,18,19] (see also Refs. [20,21] for two recent reviews on numerical relativity). In general, however, the q-field has only locally the property of a scalar field, while it globally obeys a conservation law. It is precisely this conservation law that makes the four-form field strength appropriate for the description of the phenomenology of the quantum vacuum. All this makes the dynamics of the quantum vacuum essentially different from the dynamics of a fundamental scalar field. This issue will be discussed further in Section 2.
We, now, turn to the calculation of the time evolution of a q-bubble. After a brief review of the theory, we, first, consider a q-bubble with gravity effects turned off and, then, with gravity effects turned on. Throughout, we use natural units with and take the metric signature .
2. Theory and Setup
In this article, we use q-theory in the four-form-field-strength realization with explicit derivative terms of the q-field in the action [22,23,24,25]. Specifically, we take the simplest possible theory with the following action [23]:
where g is the determinant of the metric , R the Ricci curvature scalar, G a gravitational coupling constant, and A a three-form gauge field with corresponding four-form field strength (see Refs. [5,6] and further references therein). In Equation (1a), and are generic even functions of q. We use the same conventions for the curvature tensors as in Ref. [26]. For the moment, we have omitted in the integrand on the right-hand side of Equation (1a) the Lagrange density of the fields of the Standard Model of elementary particle physics.
The Hamilton principle for variations and of the action (1) produces two field equations, a generalized Maxwell equation involving and the Einstein equation involving a particular combination of energy-density terms,
These Maxwell-type and Einstein field equations are given by Equations (3) and (5), respectively, in Ref. [23]. One particular solution has the flat-spacetime Minkowski metric,
and the constant nonvanishing q-field,
where the equilibrium value gives
with and , respectively, the vacuum energy density and vacuum pressure entering the Einstein equation (see below). Note that the mass dimension of is 2 in the four-form-field-strength realization.
The solution of the generalized Maxwell equation introduces an integration constant and is given by Equation (4) in Ref. [23]. A particular value for is , which corresponds to the constant equilibrium value of the q-field [obtained from the condition ] and is explicitly defined by:
The solution of the generalized Maxwell equation now takes the form of a nonlinear Klein–Gordon equation for the special case of constant ,
This nonlinear Klein–Gordon equation then reads [23]:
in terms of the vacuum energy density defined by:
with the constant from Equation (4). Precisely, this vacuum energy density enters the Einstein equation [23],
where is the Ricci curvature tensor and the energy-momentum tensor of the q-field.
As mentioned in Section 1 and in Ref. [23], the final dynamic Equations (6) and (8) are identical to those of a gravitating fundamental scalar field with a potential from (7) with q replaced by . However, the constant entering our two dynamic equations via arises as an integration constant for the solution of an underlying dynamic equation, namely, the generalized Maxwell equation obtained by variation of the three-form gauge field A in the action. Concretely, the equilibrium value is found to depend on the cosmological constant from Equation (1b),
and the same holds for the integration constant from Equation (4),
This point will be clarified by an example in the penultimate paragraph of this section.
Remark also that the nonlinear Klein–Gordon Equation (6) only appears for the special case of constant and constant (here, we have taken ). The advantage of considering this simplified case of q-theory is that, if necessary, we may appeal to established numerical methods [17,18,19,20,21] for a gravitating fundamental scalar field . But, here, we will only perform an exploratory numerical analysis, leaving refinements to the future.
Using , we introduce the dimensionless coordinates for , the dimensionless function for , the dimensionless constant for , the dimensionless cosmological constant for the cosmological constant , and the dimensionless vacuum energy density for . By abuse of notation, we also have the dimensionless vacuum energy density for the dimensional quantity . Recall that is the equilibrium value of the “chemical potential” corresponding to the conserved vacuum variable q; see Ref. [5] for further discussion.
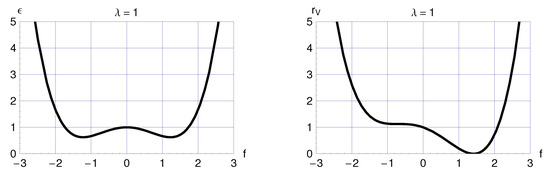
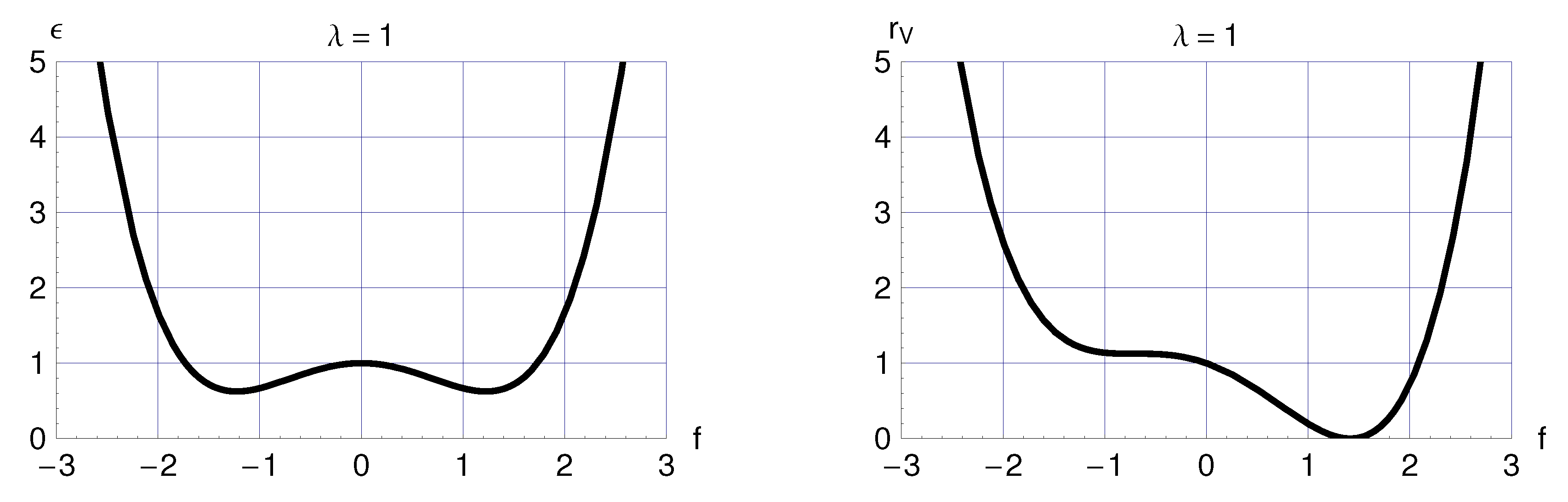
In order to be specific, we take the following Ansatz for the dimensionless energy density appearing in the action of Equation (1a):
with a dimensionless bare cosmological constant (the case of an arbitrary-sign initial cosmological constant has been considered in Ref. [7]). The equilibrium condition
gives the following constant equilibrium value of the f-field ( is taken to be positive) and corresponding “chemical potential” :
The dimensionless gravitating vacuum energy density corresponding to Equation (7) is given by:
where the numerical value for from Equation (12b) holds for the specific Ansatz (10). At equilibrium, the function has
where in Equation (14c) is the dimensionless version of the equilibrium vacuum compressibility [5].
Observe that as defined by Equation (13) has a direct dependence from the energy density (10) and an indirect dependence from the equilibrium value (4) of the chemical potential, explicitly given by Equation (12b). Let us briefly discuss the implications of this indirect dependence. Write the energy density from Equation (10) as
and the gravitating energy density from Equation (13) as
Now, consider
for generic positive and . It then follows that
But the behavior is different,
simply because of the shift of the q-field equilibrium value if is changed to and the corresponding shift of the equilibrium chemical potential (4), as shown by the explicit dimensionless expression (12a). The additive behavior (17a) is what is expected for a fundamental scalar field, but the behavior (17b) from the composite scalar field q is different. Precisely this nontrivial behavior of , different from the behavior of for a fundamental scalar , allows for the natural compensation of an initial cosmological constant , as mentioned in the second comment of Section 1.
3. Bubble without Gravity
3.1. Preliminaries
It is relatively easy to get a result for a special case. First, we set:
so that we just have Minkowski spacetime to consider.
Second, we recall from Section 2 that the generalized Maxwell equation [5,6] gives rise to the nonlinear-Klein–Gordon Equation (6), which reads explicitly:
with the flat-spacetime d’Alembertian .
Third, introducing spherical coordinates, the q-field of a spherical bubble is given by:
Fourth, we start from a bubble with essentially and . Outside the bubble, the q-field has already compensated the initial cosmological constant (the case of an arbitrary-sign initial cosmological constant has been considered in Ref. [7]). The question, now, is how the inside q-field evolves with time.
3.2. Numerics
The numerical solution will be obtained by use of the dimensionless variables introduced in Section 2. The partial differential equation (PDE) from Equation (19) for the spherically symmetric q-field (20) then reads:
where is given by Equation (13) with Equations (10) and (12b). The initial values at and the boundary conditions at and are:
Practically, we restrict the range to with and . In addition, we use the following explicit start function:
where, for now, we set and take
Note that the fourth power of the sine-function in Equation (23) makes for a continuous second-order derivative at .
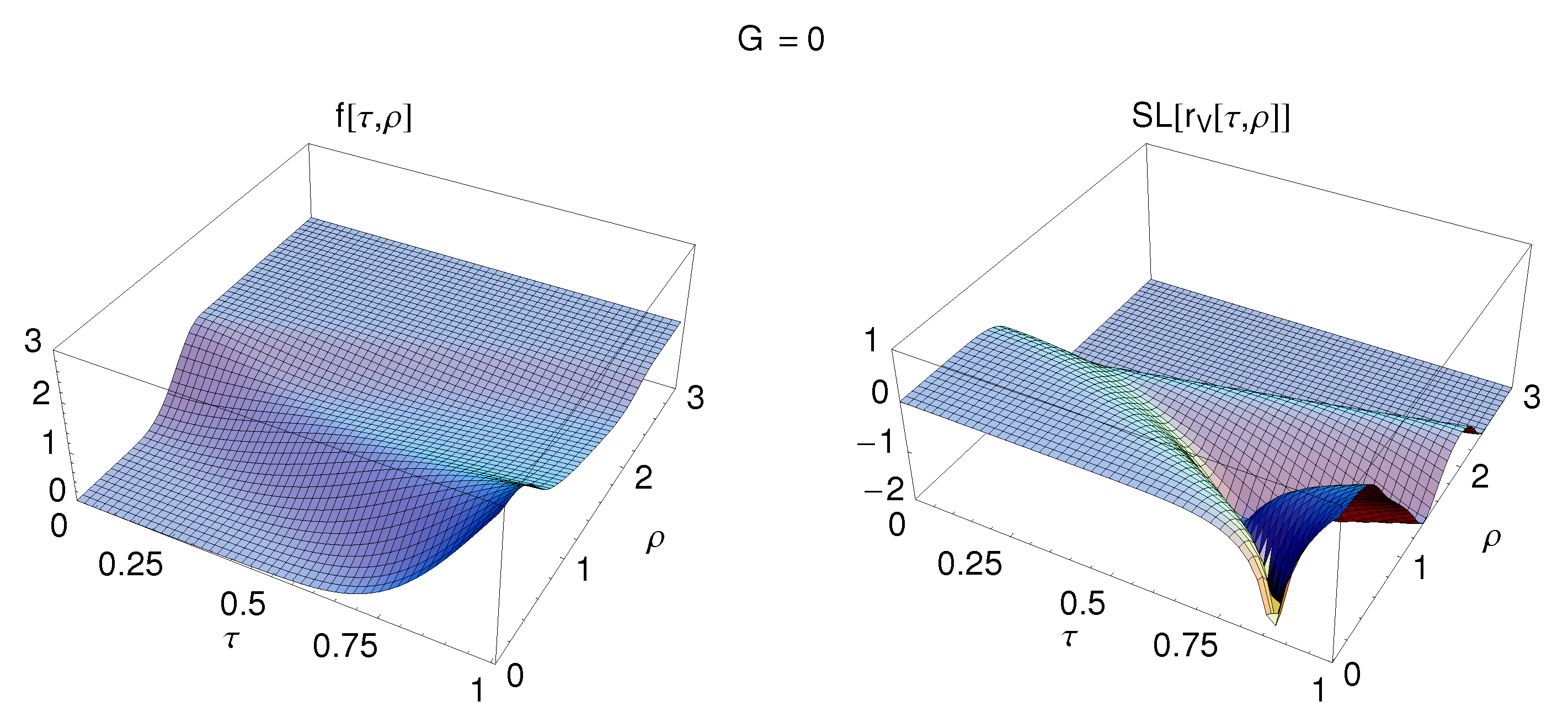
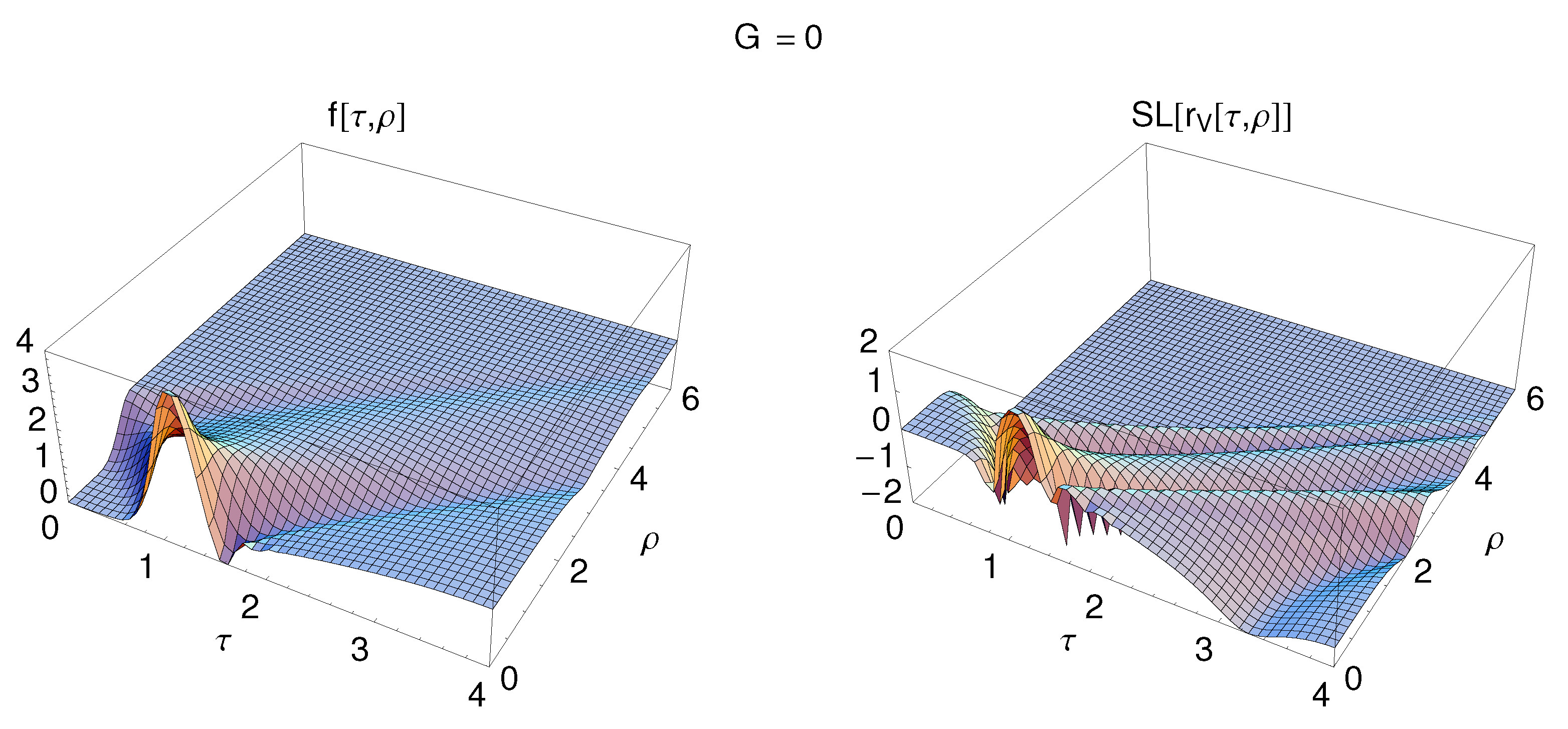
The general behavior of the numerical solution is displayed in Figure 2 and Figure 3 and four time-slices are given in Figure 4. These results show the disappearance of the bubble “domain-wall” and the start of the outward motion of its remnant. Observe, in Figure 3, both spatial oscillations (for example, at ) and temporal oscillations (for example, at ). The temporal oscillations were first observed for a homogeneous context in Ref. [6], but new here is that energy can escape towards the surrounding unperturbed space.
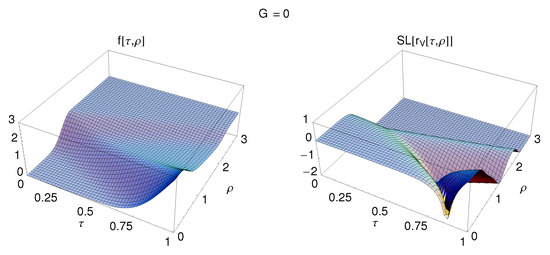
Figure 2.
Numerical solution of the flat-spacetime PDE from Equation (21) for the case of a nonzero cosmological constant, . The initial values are Equation (22a) from the start function (23) with and Equation (22b). The boundary conditions are Equation (22c) at and Equation (22d) at . The field is calculated over a relatively short time interval, . The corresponding energy density is also plotted, using the shift-log function defined by for . This vacuum energy density for is given by Equation (13) with Equations (10) and (12b). The vacuum energy density is, in fact, the quantity that would gravitate if G were nonzero.
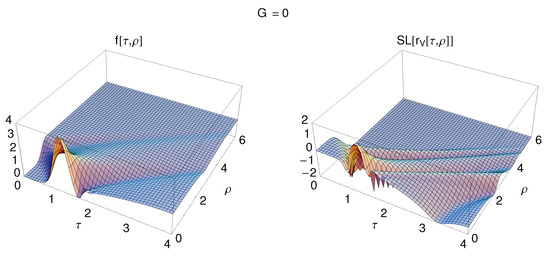
Figure 3.
Same as Figure 2, but now evolved over a larger time interval, .
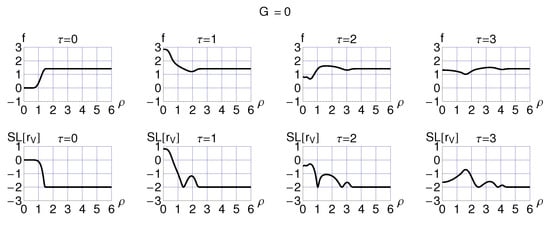
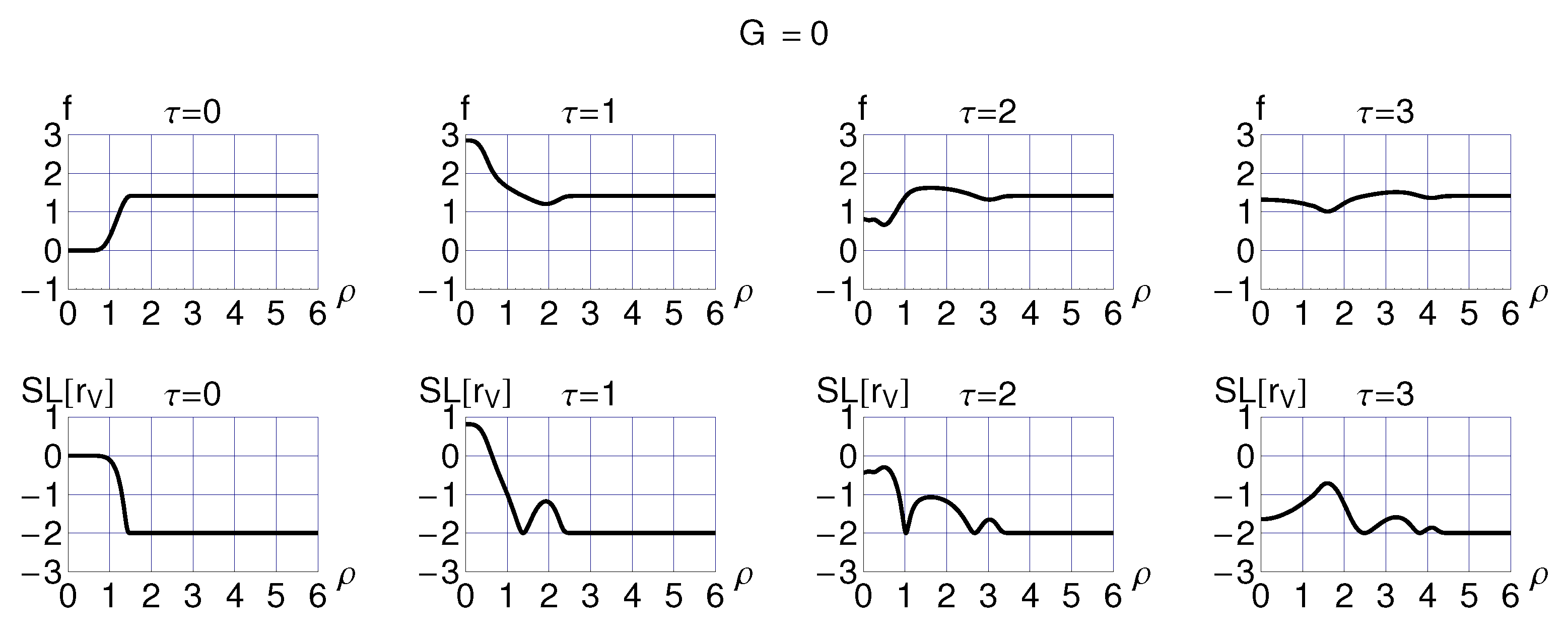
Figure 4.
Four time-slices from the numerical solution of Figure 3.
These numerical results demonstrate that the out-moving disturbance has a rapidly decreasing amplitude. Incidentally, the quality of the numerical solution can be monitored by evaluating the numerical value of the integral of motion (energy) corresponding to the field Equation (21); see also Section 4.2.
3.3. Discussion
The numerical results of Section 3.2 show two characteristics of the q-bubble time evolution in the absence of gravitational effects:
- initially, the bubble wall gives rise to both out-moving and in-moving disturbances of the dimensionless vacuum energy density , where the in-moving disturbance makes for an increased energy density at the center;
- ultimately, there is an out-moving disturbance with a rapidly diminishing amplitude (asymptotically, from energy conservation).
Even for the simple case of zero gravity, this makes the numerical calculation of large bubbles difficult. There are, then, two very different scales, namely the bubble radius () and the width of the bubble wall ().
Remark, finally, that the above two characteristics of the q-bubble dynamics are very different from those of Coleman’s vacuum bubble, as mentioned already in Section 1. Indeed, Coleman’s vacuum bubble [14] has no in-moving disturbance and an essentially constant domain-wall profile in its rest-frame, energy being supplied by the “false” vacuum.
4. Bubble with Gravity
4.1. Preliminaries and Ansätze
From now on, we set:
where is Newton’s gravitational coupling constant [3].
The spherically symmetric Ansatz for the metric in Kodama–Schwarzschild coordinates reads [27]:
and the spherically symmetric Ansatz for the matter field is simply:
It is a straightforward exercise to insert these Ansätze into the field Equations (6) and (8) from the action (1). In this way, the reduced nonlinear-Klein–Gordon equation and the reduced Einstein equations are obtained (these expressions will be given in Section 4.2).
4.2. Dimensionless PDEs
As mentioned in Section 2, specifically in the paragraph above Equation (10), we make all variables dimensionless by use of , which we now take to have the following numerical value:
With , the number g here can be interpreted as a hierarchy factor,
Added to our previous dimensionless q-field Ansatz function , we now have two dimensionless metric Ansatz functions, making for a total of three Ansatz functions:
A useful definition is
as precisely this combination enters the metric Ansatz (25) by the square bracket factors in and , using dimensionless coordinates and instead of t and r.
The reduced nonlinear-Klein–Gordon equation corresponds to the following PDE:
where an overdot stands for differentiation with respect to the dimensionless time coordinate and a prime for differentiation with respect to the dimensionless radial coordinate . The reduced Einstein equations give the following first-order PDEs:
and the following second-order PDE:
Note that we have used Equation (32a) to get the expression on the right-hand side of Equation (32c).
The following consistency check holds: the second-order PDE (33) is solved by the solutions of the first-order PDEs (32) and the second-order PDE (31). It is a well-known fact that the same holds for the reduced ordinary differential equations (ODEs) of the standard Friedmann–Robertson–Walker universe. Specifically, the second-order reduced Einstein ODE follows from the first-order reduced Einstein ODE (a.k.a. the Friedmann equation) by use of the energy-momentum-conservation relations of the perfect fluid considered. Ultimately, this redundancy of the reduced field equations traces back to the invariance of the theory under general coordinate transformations; cf. Section 15.1, p. 473 of Ref. [26].
We can also obtain a useful g-independent relation from Equations (32a) and (32b) in three steps. First, we extract from Equation (32a) and take the derivative. Second, we extract from Equation (32b) and take the derivative, Third, we equate the two expressions for . The obtained relation is
which may be interpreted as a current-conservation relation. Indeed, for the setup of our initial-value problem (with for at ), the integral of Equation (34) gives the following conserved energy E:
where the equilibrium value of the q variable in the four-form-field-strength realization (1c) has been used to make lengths and times dimensionless (Section 2). Incidentally, the relation (34) reproduces the reduced nonlinear-Klein–Gordon Equation (31) upon use of (32).
Consistent with the expected de-Sitter behavior near the center and the expected Schwarzschild behavior towards spatial infinity, we take the following boundary conditions on the dimensionless metric function :
For the other metric function , we take
The boundary conditions on have already been given in Equations (22c) and (22d). From the boundary conditions (36), we find that the reduced Einstein Equations (32) and (33), for the case , give and , so that Equation (31) reproduces the flat-spacetime PDE (21).
4.3. Numerics
4.3.1. Numerical Procedure
Finding the numerical solution of the PDEs (31)–(33) is a nontrivial task. In the following local approach, we are inspired by the discussion of Appendix A.
4.3.2. Numerical Solutions
For the presentation of our numerical results, we will employ time-slice plots (cf. Figure 4) rather than surface plots (cf. Figure 2 and Figure 3). The various time-slices will be collected in a single plot by color-coding the different time values.
The numerical solution for (Figure 5) can now be compared with the one for (Figure 6). For the last case, in particular, it has been verified that the numerically obtained functions , , and give residuals of the first-order PDEs (32a) and (32b) that drop to zero as the number of grid points increases.
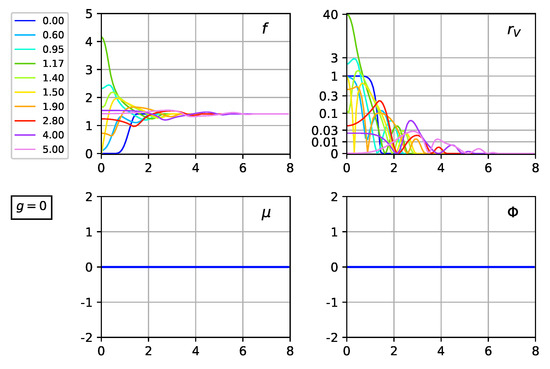
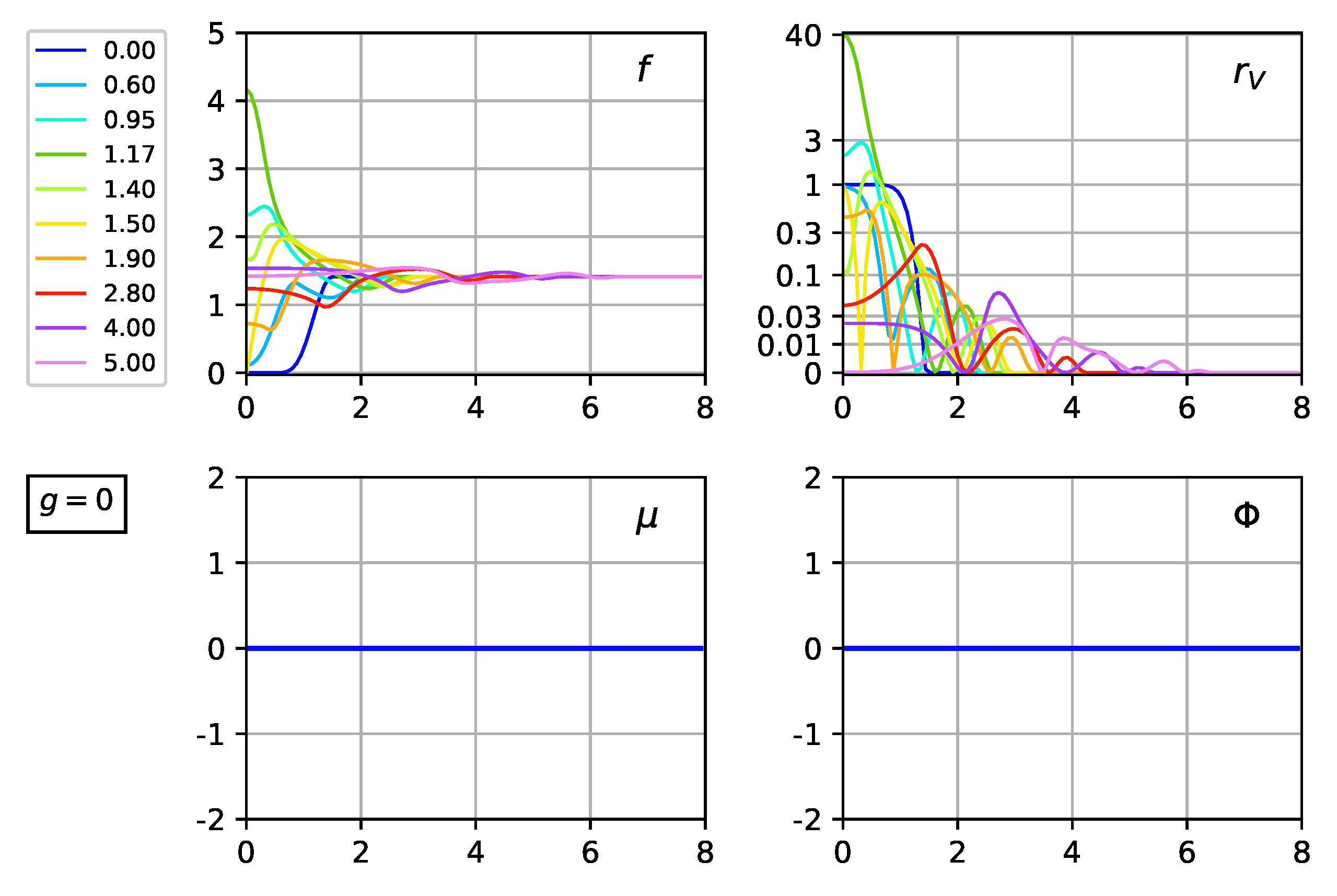
Figure 5.
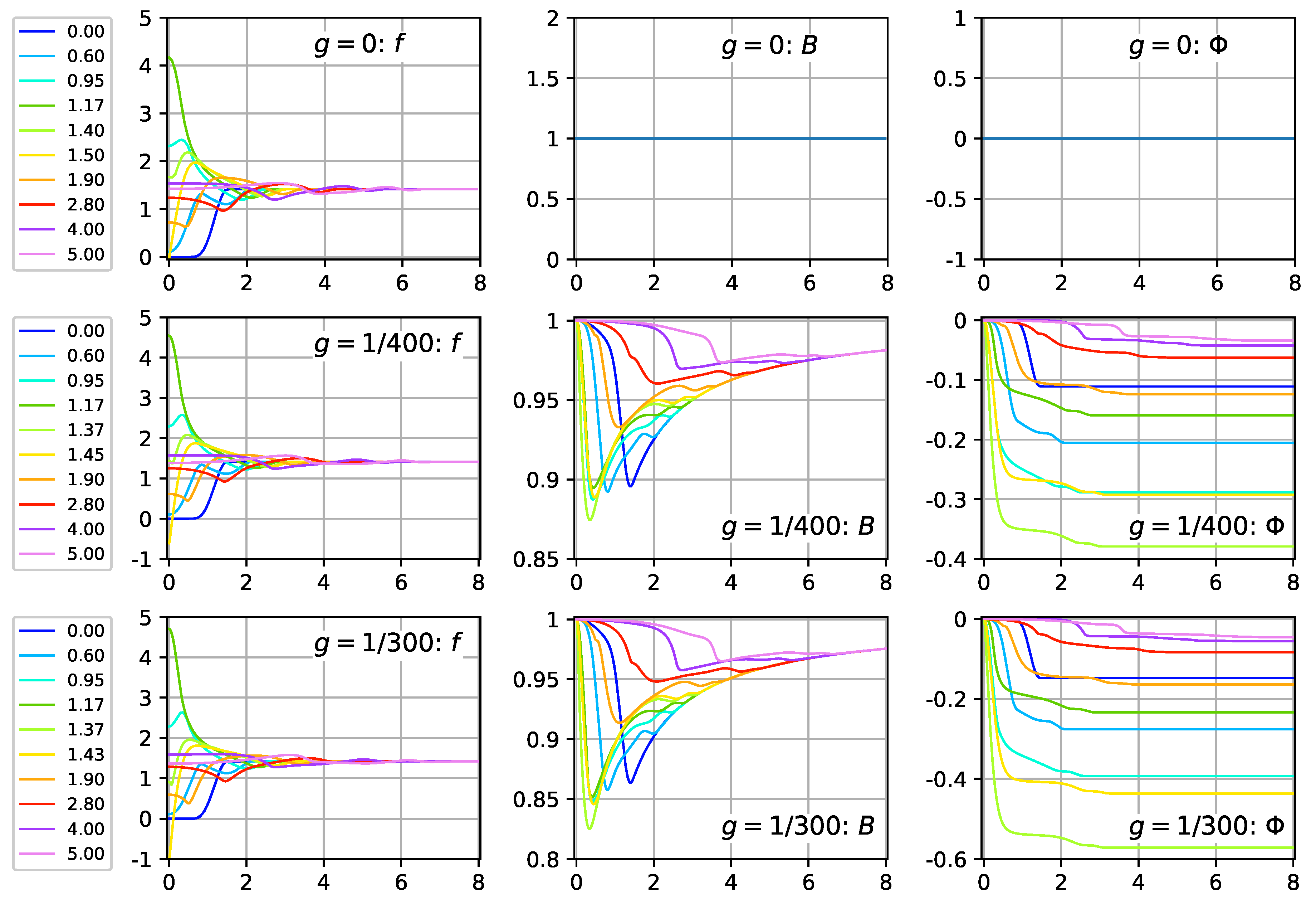
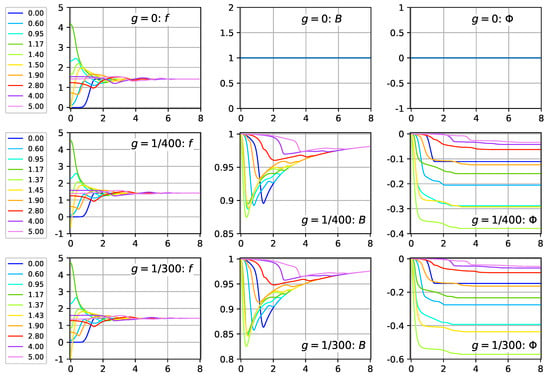
Numerical solution of the PDEs (31)–(33): plots of , , , and at different time slices, with values given in the legend on the left-hand side. The model parameters are and . The initial values are: as given by Equation (23) with and . The metric functions and vanish identically. The vacuum energy density is plotted as .
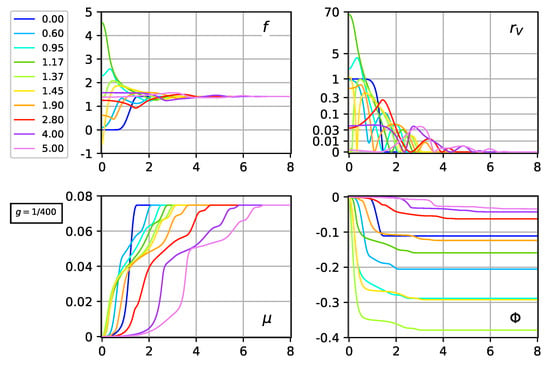
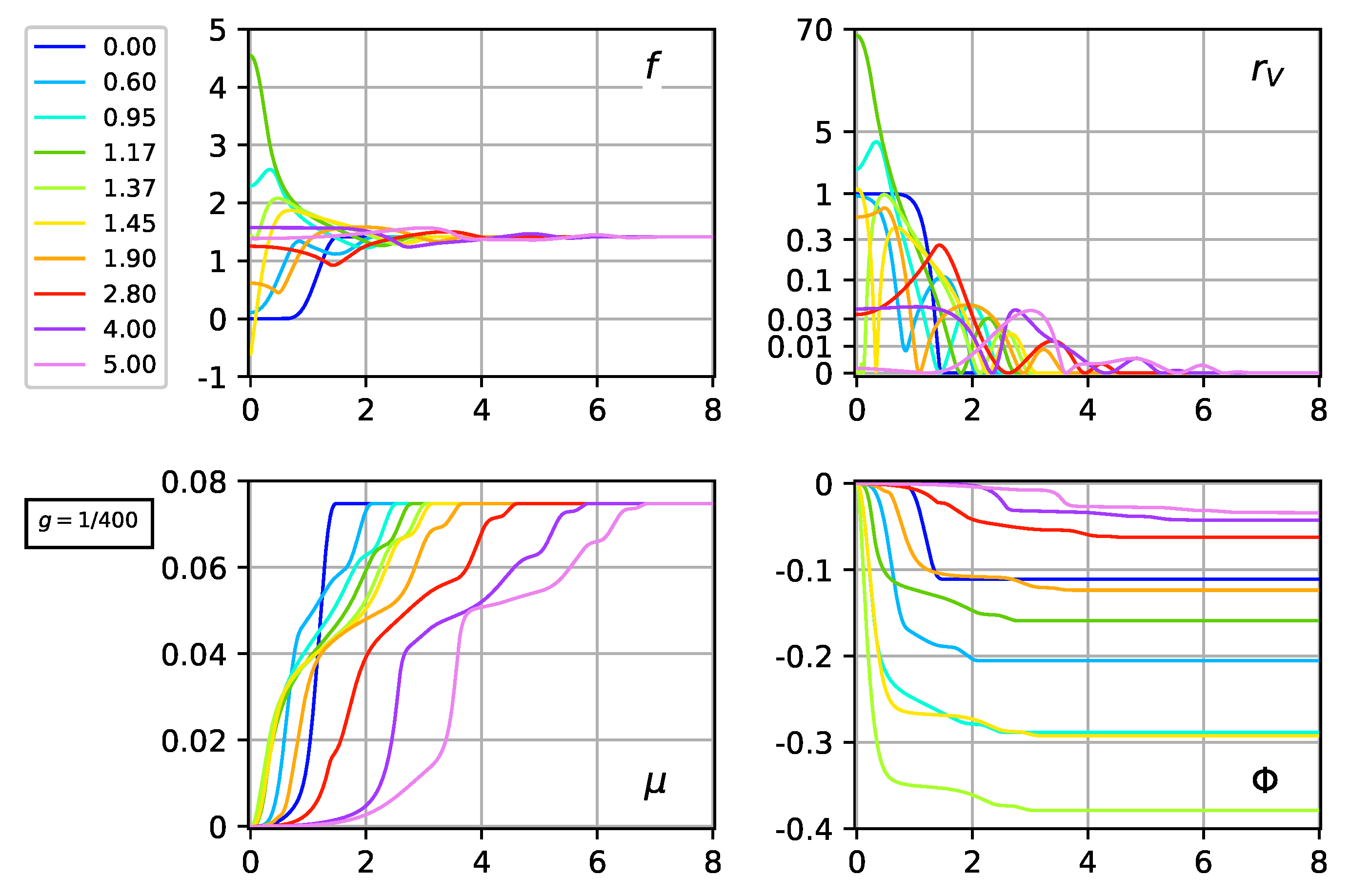
For somewhat larger g values, a Schwarzschild-type horizon is formed, as the energy density e becomes large close to the center . This horizon is apparently different from a de-Sitter-type horizon that arises from a constant vacuum energy density far away from the center; see Appendix B for a brief discussion of the de-Sitter-type spacetime near the q-bubble origin. With the setup and boundary conditions from Figure 6, we estimate horizon formation to occur for . The regular numerical solution at is shown in Figure 7. The evolution towards the formation of a horizon, with from Equation (30) dipping to zero, is illustrated in Figure 8.
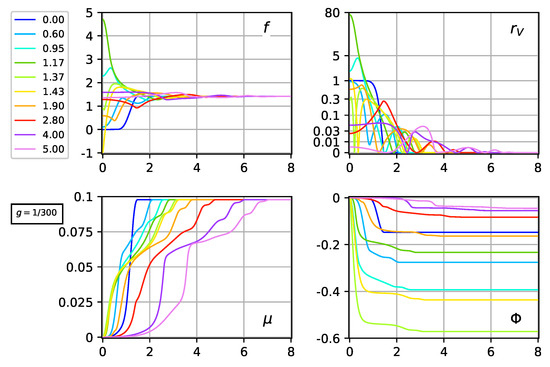
Figure 7.
Same as Figure 6, but now for .
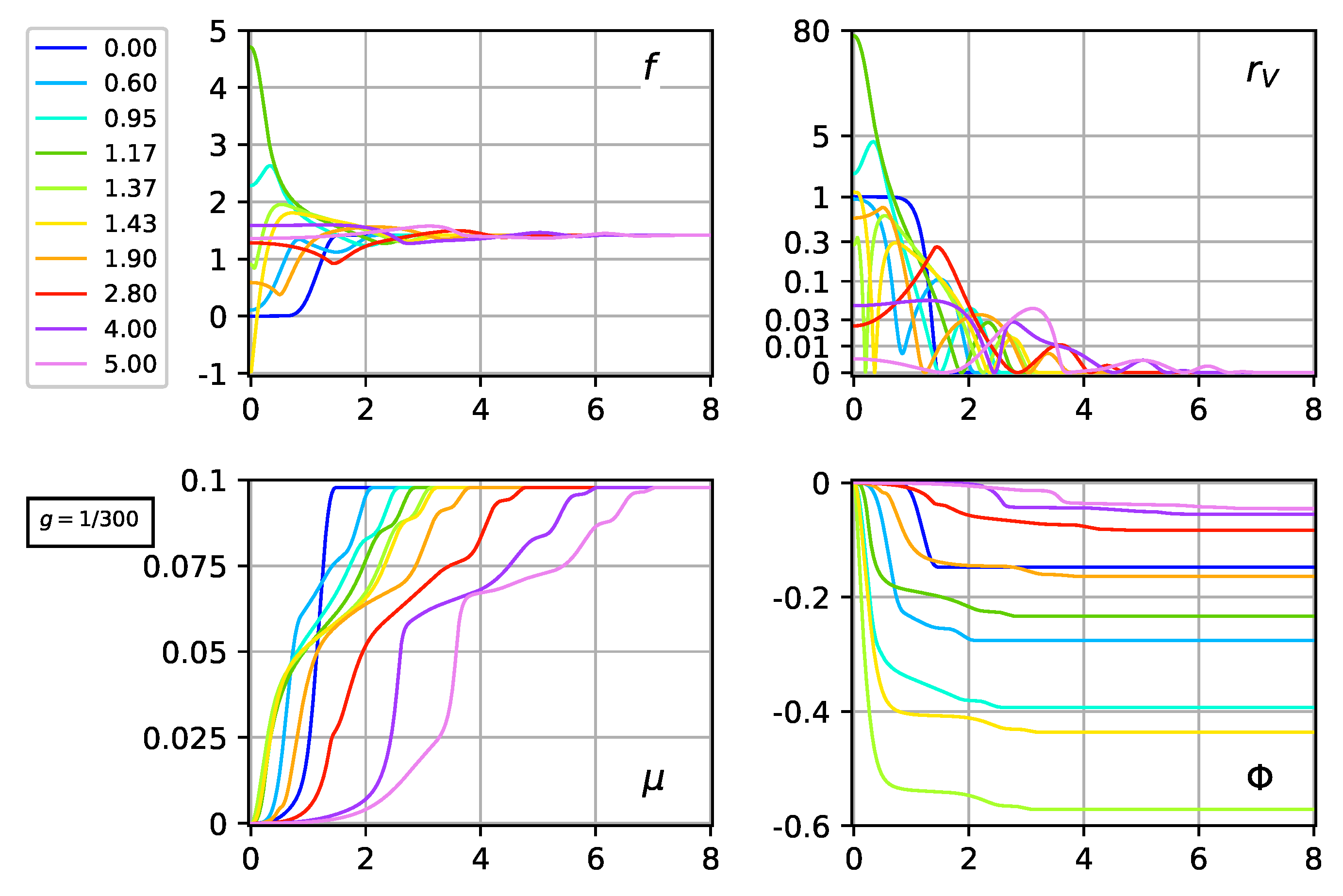
For a large bubble, we expect that, from the ingoing disturbance (cf. Figure 2 and Figure 3), the peak close to the origin will be higher than the one for a small bubble. This behavior is confirmed by comparing Figure 9 with Figure 6. The f-panel in Figure 9 also shows that the quantities and are large at , with both terms contributing significantly to the energy density e close to the center .
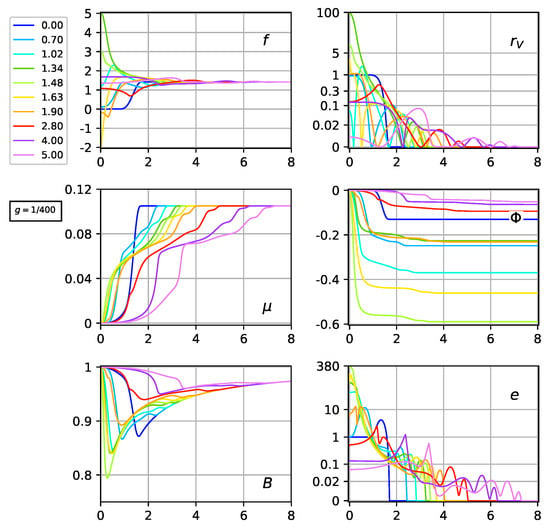
Figure 9.
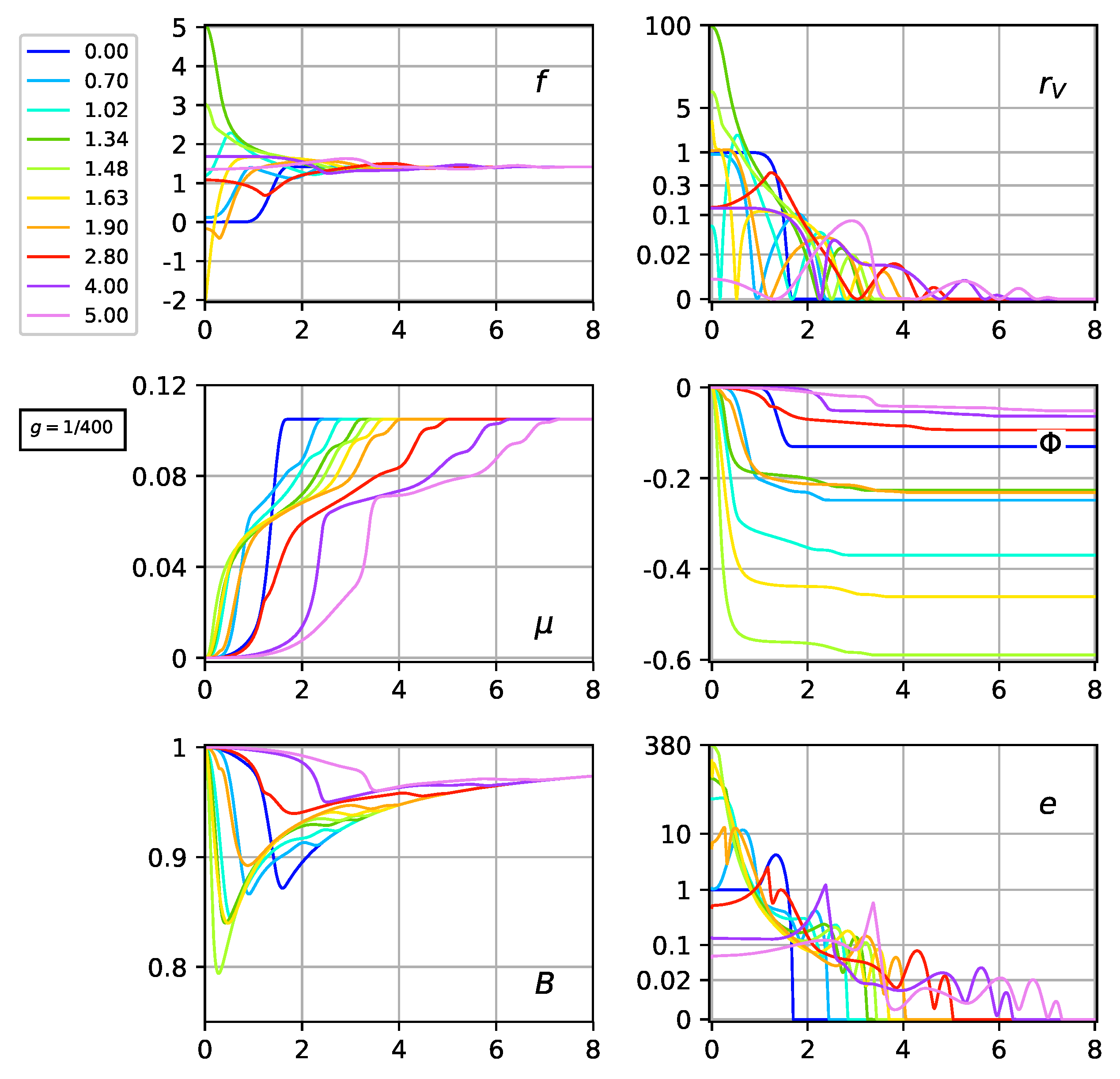
Same as Figure 6, but now with instead of . Two additional panels show the metric quantity from Equation (30) and the energy density from Equation (35b). The energy densities e and are plotted using the same scale function but with different over-all factors. The peak at of the solution is significantly larger than the corresponding peak of the solution in Figure 6. Similarly, the B dip of the solution is significantly lower than the corresponding dip of the solution in the B panel of the middle row of Figure 8.
4.4. Discussion
The numerical results of Section 4.3.2 show that the vacuum energy density of a nonequilibrium q-bubble embedded in the equilibrium vacuum with evolves in a complicated way. For a sufficiently small q-bubble, part of the vacuum energy density of the bubble wall first moves inwards towards the center and then rapidly disperses (cf. Figure 2 and Figure 3).
The numerical calculations were performed for the case with gravity turned off () and turned on (). Qualitatively, the main effect of gravity is to give a larger maximum value of the vacuum energy density at the center (compare the panels of Figure 5 and Figure 6).
If the hierarchy ratio g from Equation (28) is approximately equal to or somewhat above , the particular solution develops a Schwarzschild-type horizon near the center and different coordinates need to be chosen (cf. Appendix B). We postpone this analysis to a future publication, as the focus of the present article is on the dispersion of vacuum energy if the Big Bang occurs in a finite region of space surrounded by equilibrium vacuum (where any form of initial vacuum energy has already been cancelled [5,6,7]).
5. Conclusions
In the present article, we have obtained a first glimpse of the inhomogeneous dynamics of the gravitating vacuum energy density as described by the vacuum variable q originating from a four-form field strength (earlier work [6,7] considered the time-evolution of spatially-constant q-fields). In this new probe of q-theory, we start from a large vacuum energy density in a finite region of space surrounded by equilibrium vacuum, and follow the time evolution of the vacuum energy density.
Our numerical results show the possibility of obtaining different evolution scenarios depending on the initial conditions and the parameters of the vacuum energy. These results suggest that there may be de-Sitter expansion within a finite region of space, gravitational collapse of the vacuum medium with the formation of a singularity, and formation of cosmological and/or black-hole horizons.
It may also be of interest to study the vacuum structure at the black hole singularity. The singularity may be smoothened, as the gravitational coupling depends, in general, on the value of the q variable and gravity may be effectively turned off near the center. We leave this study to a future investigation.
Author Contributions
All authors contributed equally to this paper.
Funding
The work of G.E.V. has been supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No. 694248). O.P.S is supported by the Beca Externa Jovenes Investigadores of CONICET. The APC was funded by ERC Grant No. 694248.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Integro-Differential Equations
The role of in the PDEs (31)–(33) is rather subtle. From Equation (32c), we have
which can be integrated to give
where the prime in the numerator of the integrand stands for differentiation with respect to . Hence, is determined nonlocally by the functions and at the same time slice .
The PDEs (31) and (33) still involve and its time-derivative [the spatial derivatives and can be eliminated by use of Equation (32c)]. Replacing by from Equation (A2), these two equations become
integro-differential equations solely involving the functions and . Explicitly, these equations read:
with given by the expression (A2) and having the -derivative pulled inside the integral.
Appendix B. Bubble Interior
The q-bubble setup considered in this article has a start configuration determined by Equation (23) and the further initial condition . Then, the reduced field Equation (32a) gives that the metric Ansatz function behaves near the center as . This behavior of allows for the following definition of the quantity :
Near the spacetime origin () of the q-bubble considered, we have
with constants and . In fact, the reduced field Equation (32a) gives
where g has been defined in Equation (27). The resemblance of Equation (A6) with the spatially flat Friedmann equation [26] of a universe with constant vacuum energy will become clear later on.
Writing the metric (25) in terms of dimensionless variables gives
With the behavior (A4) and (A5), the metric (A7) near the spacetime origin of the q-bubble () becomes
which corresponds to the metric of de-Sitter spacetime in so-called static coordinates [28,29,30]. Note that, if were allowed to be large enough, the metric on the right-hand side of Equation (A8) would display a coordinate singularity at .
Now, introduce new dimensionless coordinates (denoted by a hat) from the following relations:
With these new coordinates, the metric (A8) near the spacetime origin of the q-bubble () becomes
Note that the spatially-flat Robertson–Walker metric on the right-hand side of Equation (A10a) with the scale factor (A10b) no longer has the nontrivial coordinate singularity. From the scale factor in Equation (A10b), we obtain , so that the quantity , which was originally defined by Equations (A4) and (A5), can be interpreted as a Hubble constant. The scale factor of Equation (A10) displays, for , the well-known exponential expansion of de-Sitter spacetime [28,29,30].
The numerical solution of Figure 6, however, has for and does not show the exponential expansion. Needed is an initial bubble (23) with (the required order of magnitude for is ). But there are three problems with such large bubbles. First, as noted in Section 3.3, the numerics of a large q-bubble are challenging.
Second, the coordinate singularity of Equation (A8) at suggests that the metric Ansatz (A7) is inappropriate. Most likely, this problem can be evaded by use of another metric Ansatz, possibly inspired by Painlevé–Gullstrand coordinates [31,32,33,34].
Third, large bubbles may give gravitational collapse close to the center , as the energy density e from Equation (35b) becomes large at the center. See Figure 2, where the initial () bubble-wall disturbance of the vacuum energy density separates around into an outgoing and ingoing disturbance, the latter giving a peak of at for . See also Figure 9, which shows that the numerical solution with a somewhat larger value of has a significantly larger peak at the origin than the numerical solution of Figure 6.
References
- Zel’dovich, Y.B. The cosmological constant and the theory of elementary particles. Sov. Phys. Usp. 1968, 11, 381–393. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Review of Particle Physics. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Hawking, S.W. The cosmological constant is probably zero. Phys. Lett. B 1984, 134, 403–404. [Google Scholar] [CrossRef]
- Klinkhamer, F.R.; Volovik, G.E. Self-tuning vacuum variable and cosmological constant. Phys. Rev. D 2008, 77, 085015. [Google Scholar] [CrossRef]
- Klinkhamer, F.R.; Volovik, G.E. Dynamic vacuum variable and equilibrium approach in cosmology. Phys. Rev. D 2008, 78, 063528. [Google Scholar] [CrossRef]
- Klinkhamer, F.R.; Volovik, G.E. Dynamic cancellation of a cosmological constant and approach to the Minkowski vacuum. Mod. Phys. Lett. A 2016, 31, 1650160. [Google Scholar] [CrossRef]
- Klinkhamer, F.R.; Volovik, G.E. Brane realization of q-theory and the cosmological constant problem. JETP Lett. 2016, 103, 627–630. [Google Scholar] [CrossRef]
- Klinkhamer, F.R.; Volovik, G.E. Tetrads and q-theory. JETP Lett. 2019, 109, 364–367. [Google Scholar] [CrossRef]
- Klinkhamer, F.R.; Volovik, G.E. Dynamics of the quantum vacuum: Cosmology as relaxation to the equilibrium state. J. Phys. Conf. Ser. 2011, 314, 012004. [Google Scholar] [CrossRef]
- Markkanen, T. De Sitter stability and coarse graining. Eur. Phys. J. C 2018, 78, 97. [Google Scholar] [CrossRef] [PubMed]
- Matsui, H. Instability of de Sitter spacetime induced by quantum conformal anomaly. JCAP 2019, 1901, 003. [Google Scholar] [CrossRef]
- Ruutu, V.M.H.; Eltsov, V.B.; Gill, A.J.; Kibble, T.W.B.; Krusius, M.; Makhlin, Y.G.; Placais, B.; Volovik, G.E.; Xu, W. Vortex formation in neutron-irradiated superfluid 3He as an analogue of cosmological defect formation. Nature 1996, 382, 334–336. [Google Scholar] [CrossRef]
- Coleman, S.R. The fate of the false vacuum. 1. Semiclassical theory. Phys. Rev. D 1977, 15, 2929–2936, Erratum in Phys. Rev. D 1977, 16, 1248. [Google Scholar] [CrossRef]
- Callan, C.G., Jr.; Coleman, S.R. The fate of the false vacuum. 2. First, quantum corrections. Phys. Rev. D 1977, 16, 1762–1768. [Google Scholar] [CrossRef]
- Coleman, S.R.; de Luccia, F. Gravitational effects on and of vacuum decay. Phys. Rev. D 1980, 21, 3305–3315. [Google Scholar] [CrossRef]
- Choptuik, M.W. Universality and scaling in gravitational collapse of a massless scalar field. Phys. Rev. Lett. 1993, 70, 9–12. [Google Scholar] [CrossRef]
- Marsa, R.L.; Choptuik, M.W. Black-hole–scalar-field interactions in spherical symmetry. Phys. Rev. D 1996, 54, 4929–4943. [Google Scholar] [CrossRef]
- Honda, E.P.; Choptuik, M.W. Fine structure of oscillons in the spherically symmetric ϕ4 Klein-Gordon model. Phys. Rev. D 2002, 65, 084037. [Google Scholar] [CrossRef]
- Choptuik, M.W.; Lehner, L.; Pretorius, F. Probing strong field gravity through numerical simulations. arXiv 2015, arXiv:1502.06853. [Google Scholar]
- Cardoso, V.; Gualtieri, L.; Herdeiro, C.; Sperhake, U. Exploring new physics frontiers through numerical relativity. Living Rev. Relativ. 2015, 18, 1. [Google Scholar] [PubMed]
- Klinkhamer, F.R.; Volovik, G.E. Propagating q-field and q-ball solution. Mod. Phys. Lett. A 2017, 32, 1750103. [Google Scholar] [CrossRef]
- Klinkhamer, F.R.; Volovik, G.E. Dark matter from dark energy in q-theory. JETP Lett. 2017, 105, 74–77. [Google Scholar] [CrossRef]
- Klinkhamer, F.R.; Volovik, G.E. More on cold dark matter from q-theory. arXiv 2016, arXiv:1612.04235. [Google Scholar]
- Klinkhamer, F.R.; Mistele, T. Classical stability of higher-derivative q-theory in the four-form-field-strength realization. Int. J. Mod. Phys. A 2017, 32, 1750090. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; John Wiley and Sons: New York, NY, USA, 1972. [Google Scholar]
- Abreu, G.; Visser, M. Kodama time: Geometrically preferred foliations of spherically symmetric spacetimes. Phys. Rev. D 2010, 82, 044027. [Google Scholar] [CrossRef]
- Schrödinger, E. Expanding Universes; Cambridge University Press: Cambridge, UK, 1956. [Google Scholar]
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Space-Time; Cambridge University Press: Cambridge, UK, 1973. [Google Scholar]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Painlevé, P. La mécanique classique et la théorie de la relativité. C. R. Acad. Sci. (Paris) 1921, 173, 677–680. [Google Scholar]
- Gullstrand, A. Allgemeine Lösung des statischen Einkörper-problems in der Einsteinschen Gravitations-theorie. Arkiv. Mat. Astron. Fys. 1922, 16, 1–15. [Google Scholar]
- Martel, K.; Poisson, E. Regular coordinate systems for Schwarzschild and other spherical space-times. Am. J. Phys. 2001, 69, 476–480. [Google Scholar] [CrossRef]
- Volovik, G.E. Particle decay in de Sitter spacetime via quantum tunneling. JETP Lett. 2009, 90, 1–4. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).