Force Metrology with Plane Parallel Plates: Final Design Review and Outlook
Abstract
1. Introduction
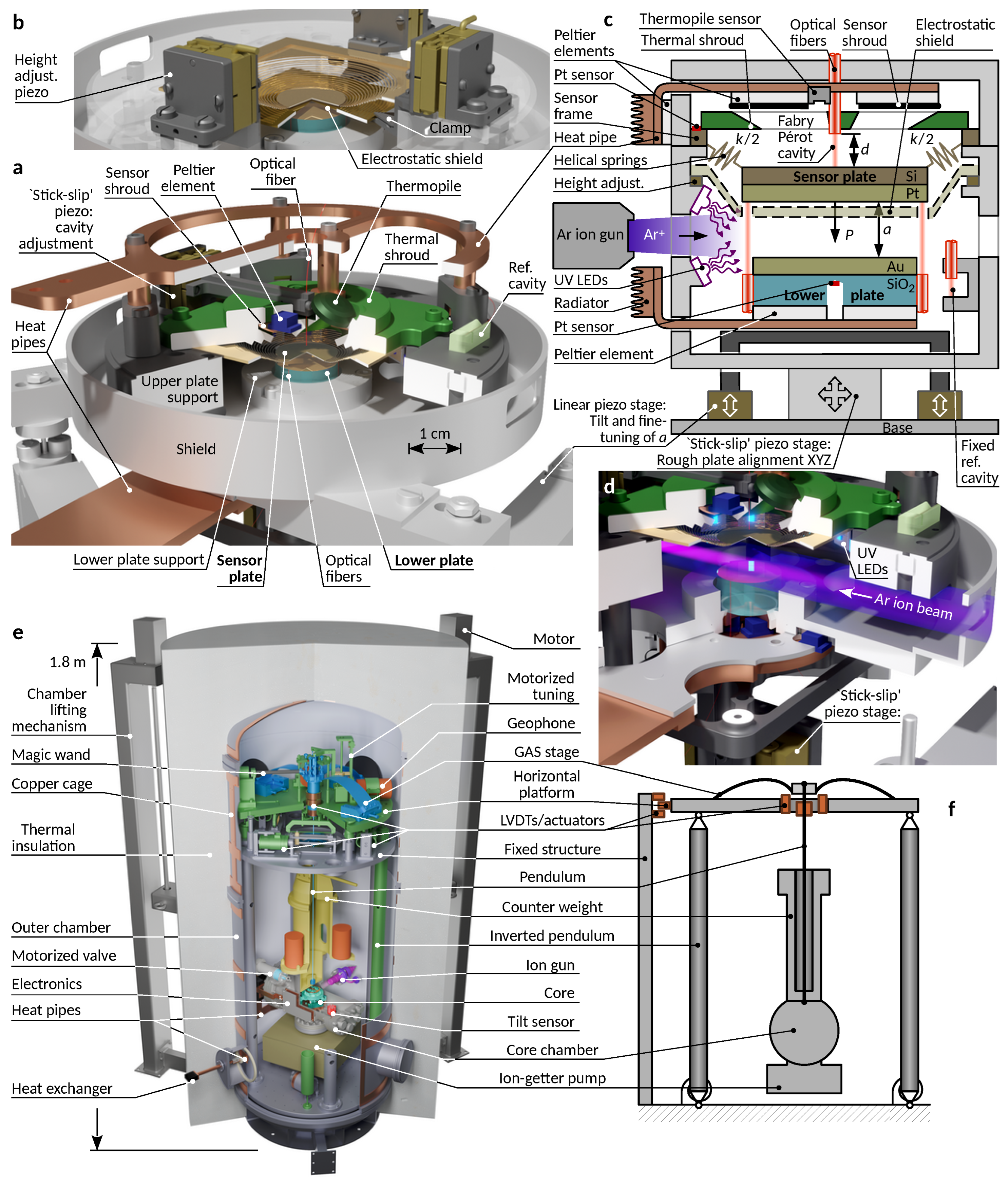
2. Experimental Design
2.1. Seismic Attenuation
2.2. Surface Charge Cancellation
2.3. Temperature Control
2.4. AFM/KPFM Setup
2.5. Optical Detection System: Force and Distance Measurements
2.5.1. Force and Force Gradient Detection
2.5.2. Calibration
3. Error Budget
3.1. Seismic Noise
3.2. Detection Noise
3.3. Updated Error Budget
4. Prospective Results
4.1. Casimir Effect
4.1.1. Material Properties

4.1.2. The Geometry of the System
4.1.3. The Thermodynamic State of the System: Configurations out of Thermal Equilibrium
4.2. Scalar Dark Energy
4.2.1. Theoretical Background
4.2.2. Dilaton Constraints
4.2.3. Symmetron Constraints
4.2.4. Chameleon Constraints
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Alternate Current |
| AFM | Atomic Force Microscope |
| AM | Amplitude Modulation |
| ATI | Atominstitut |
| Cannex | Casimir And Non-Newtonian force EXperiment |
| COBS | Conrad OBServatory |
| CKM | Cabibbo–Kobayashi–Maskawa matrix |
| CP(T) | Charge Parity (Time) |
| cal | calibration |
| DAMA | DArk MAtter |
| DAQ | Data Acquisition |
| DC | Direct Current |
| DE | Dark Energy |
| DM | Dark Matter |
| det | detector |
| ESS | Electrostatic Shield |
| EW | Evanescent Wave |
| exc | excitation |
| FEM | Finite Element Method |
| FM | Frequency Modulation |
| GAS | Geometric Anti-Spring |
| GR | General Relativity |
| KPFM | Kelvin Probe Force Microscopy |
| LED | Light-Emitting Diode |
| LI | Lock-In amplifier |
| Lif | Lifshitz |
| LVDT | Linear Variable Differential Transformer |
| CDM | Lambda Cold Dark Matter model |
| MC | Monte Carlo |
| MEMS | MicroElectroMechanical System |
| NHNM | New High-Noise Model |
| NEMS | NanoElectroMechanical System |
| NLNM | New Low-Noise Model |
| PE | Peltier Element |
| PID | Proportional–Integral–Derivative |
| PLL | Phase-Locked Loop |
| PW | Propagating Wave |
| QCD | Quantum ChromoDynamics |
| QED | Quantum ElectroDynamics |
| RC | Resistor–Capacitor |
| RCWA | Rigorous Coupled Wave Approach |
| RMS | Root Mean Square |
| SAS | Seismic Attenuation System |
| SB | Stefan–Boltzmann |
| STS | STreckeisen Seismometer |
| SM | Standard Model |
| SNR | Signal-to-Noise Ratio |
| SpI | Spectral Integration |
| sig | signal |
| TD | Temperature Drift |
| TE | Transverse Electric |
| TM | Transverse Magnetic |
| TU | Technische Universität |
| UHV | Ultra-High Vacuum |
| UV | UltraViolet |
| WIMP | Weakly Interacting Massive Particle |
Appendix A. Details of the Error Budget
| Parameter | Value | Description |
|---|---|---|
| 2.0 s | integration time for a single DC voltage measurement | |
| 83.0 s | lock-in integration time for a single AC amplitude, frequency, or phase measurement | |
| m | 26.13 mg | effective dynamic sensor mass |
| 2 9.8 s−1 | free sensor resonance frequency | |
| d | 500 | nominal sensor cavity size |
| A | 1.035 cm2 | sensor interaction area |
Appendix A.1. DC Signals
Appendix A.1.1. Statistical Errors
- DAQ noise, , containing the aliasing error from 34470A datasheet (first term). Keysight specifies [263] that the error given in the datasheet is for a temperature range of ±1 °C and can be adapted if the real temperature variation is below that. We add 1 (second term) to account for noise picked up by cabling, estimated from actual measurements with the device.
- Detector noise, . At , the detectors have a noise level of /, at a total incident flux of 1 from the fiber interferometer into the detector (based on laser power and the optical properties of the cavity and fiber). We consider a 1 bandwidth for the low-pass filter, resulting in 60 RMS noise.
- Laser power fluctuations, (SpI). We received actual TLX1 intensity noise spectra from the manufacturer ranging from to 10 . From these data, we determined a temperature correlation coefficient of , but not all of the drift is temperature-related. We, thus, use the measured Allan deviation as error here. For integration times 2, 83, and 1000 s, using Equation (A2), we obtain RMS relative intensity errors , , and , respectively. To the first order, this error is canceled exactly by the normalization in Equation (7).
- Laser bandwidth, . Given by the datasheet to be 10 (0.08 fm), nominally, as the low-frequency limit of the frequency noise.
- Laser frequency noise, (SpI). Derived from manufacturer data of the spectral frequency noise in the range 3 Hz–100 MHz. At lower frequencies, the noise is assumed to stay constant at /, which is three orders of magnitude larger than the specified linewidth but serves as a worst-case estimate. We convert these data to wavelength noise by for the mean wavelength nm after integration over the spectrum as described at the start of Appendix A, resulting in RMS values , , and for = 2, 83 and 1000 s, respectively.
- Reference cavity signal, . Respective values are obtained from the total without seismic vibrations and thermal distance fluctuations, as the reference cavity is a monolithic block made of a material with thermal expansion coefficient of less than 2 . We obtain a total and for 1000 s and 72 h integration time, indicating the errors for , and , respectively. This error could be reduced in practice, as power fluctuations being the main error here also have a significant temperature dependence.
Appendix A.1.2. Systematic Errors
- DAQ error, (TD). We use the temperature drift according to manufacturer specifications with V. For longer measurements, we consider a reset of this error by the Keysight 34470A’s auto-calibration routing after s.
- Cavity drift, (TD). The effective temperature coefficient of d can only be measured, as uncertainties in the material properties lead to rather different values. Considering the actual geometry and materials, we obtain an estimate of m/K, which, together with a preliminary stability 0.1 mK of the core temperature and , results in the second-strongest error at large . Knowing the actual temperature, this error could be removed from the results but we do not consider this possibility in the error budget here. We rather assume that can be reset using a -sweep calibration preceding each measurement point, leading to respective statistical averaging and consider with amplitude pm. We add to the uncertainty of determination obtained from simulated calibration data. For this purpose, we computed 100 -sweep datasets considering independently randomized , , , and fixed with their respective known statistical widths. The single sweep data are fit to Equation (6) with free parameters , , d, and . is then the standard deviation of all the MC results and the mean parameter error (added as systematic errors) of the fits. The same procedure is used for the reference cavity size determination error , where we set for data generation. For the computation of the 72 h reference signal, we assume periodic re-calibration and reset of every , with calibration time s.
- Wavelength drift, (TD), is derived from the GHz accuracy of the TLX1 for a range 10–40 °C. As the absolute wavelength can be re-calibrated using the frequency-locked reference laser, we assume for operation at COBS a pessimistic maximal error of as amplitude for . This error averages with the number of measurement points of both data and reference signal; we assume periodic re-calibration and reset of every .
- Reference cavity signal (TD): systematic component of and for 1000 s and 72 h integration time, respectively. Obtained in the same way as .
Appendix A.1.3. Constant Errors
- DAQ error, , for the Keysight 34470A offset error, exceeding the specifications from the datasheet.
- Reference cavity signal: constant component of , similar as for .
Appendix A.2. AC Signals
Appendix A.2.1. Statistical Errors
- PLL frequency noise, . The short-time stability of the lock-in amplifier’s phase-tracking based on phase stability was measured as the RMS value of the phase using a first-order passive RC-lowpass as a device under test over 3 h, without feedback. This error combines internal electrical noise, aliasing errors, and internal oscillator stability (without an external Rubidium reference clock). We obtained (for and ).
- Frequency measurement, . This noise quantifies the stability of the frequency tracking algorithm of the PLL together with PID feedback. We measured it using the same first-order passive RC lowpass, resulting in .
- Signal noise, (SpI, indirectly; see Appendix A.1). Voltage noise (containing all error sources described in Appendix A.1) can be converted into time jitter of a sinusoidal signal at frequency , as explained in the main text in Section 3.2, resulting in and V, and for and s integration time, respectively and .
Appendix A.2.2. Systematic Errors
- PLL phase stability, (TD). This error quantifies the ppm/°C drift of the internal oscillator of the lock-in amplifier with temperature, and the respective deviation at COBS. For multiple measurements, we consider periodic re-calibration to average this error. and for and s integration time, respectively.
- Resonance frequency calibration error, . The resonance frequency is calibrated prior to each distance sweep or once per day. We use the combined standard deviation and parameter error obtained from MC simulations of the calibration data as described in Section 2.5.2. .
- Signal drift, (TD, indirectly; see Appendix A.1). Drifts of the voltage signal, converted to frequency error, as described in Section 3.2. We obtain and V, and for and s integration time, respectively, and .
Appendix A.2.3. Constant Errors
- PLL phase error, . This error reflects the absolute ppm frequency accuracy of the reference Rubidium atomic clock, applied to the sensor resonance frequency ( Hz).
- Resonance frequency calibration error, . This error comes from the mean constant offset error seen in our MC simulations. It is caused by non-linearities in combination with other errors, leading to a constant estimation error .
- Signal error: constant component of the signal error, amounting to or nHz (see Section 2.5.2).
Appendix A.3. Pressure Gradient
Appendix A.3.1. Statistical Errors
- Frequency measurement, (SpI, indirectly; see Appendix A.1. This error is propagated from the AC error described in Appendix A.2 and amounts for to and for and s, respectively, at .
Appendix A.3.2. Systematic Errors
- Frequency measurement, (TD, indirectly; see see Appendix A.1). This error is propagated from the AC error described in Appendix A.2. We obtain and for and s, respectively.
- Resonance frequency calibration error, . This error (described already in Appendix A.2) is considered separately here, as it appears in the expression for the total gradient , expressed from Equation (5). .
- Mass calibration error, . We again use the standard deviation and parameter error determined from MC simulations of calibration data (see Section 2.5.2). = kg.
Appendix A.3.3. Constant Errors
- Frequency measurement, , is the constant part of the error propagated from the AC frequency detection.
- Resonance frequency error, . Mean parameter offset from fits to MC simulation data (see Section 2.5.2).
- Mass calibration error, kg. Mean parameter offset from fits to MC simulation data (see Section 2.5.2).
Appendix A.4. Pressure
Appendix A.4.1. Statistical Errors
- Signal fluctuation, . Propagated statistical error from the DC signal. Amounts to and for and s integration time, respectively, at .
- Reference signal, . Statistical error of the zero-force reference signal taken at (do not confuse with from the reference cavity). As DC detection is independent of a, we use the same models as for described in Appendix A.1. for s integration time.
- Force gradient, . Correcting the spring constant k introduces a dependence on the force gradient. We propagate the corresponding error described in Appendix A.3, resulting in and nN/m for and s integration time, respectively.
Appendix A.4.2. Systematic Errors
- Mass calibration error, kg, was described in Appendix A.3.
- Resonance frequency error, = . This is the same error described in Appendix A.2.
- Wavelength error, (TD, partially). While can be measured and brought close to zero by the beat method (see Section 2.5.2), it can also be obtained from a fit to a -sweep (see above). We use the average parameter uncertainty of the fits combined with the standard deviation of the results using 300 sets of calibration data, resulting in pm. In addition, we use the known temperature dependence, as described in Appendix A.1: , and add the two uncertainties.
- Cavity size determination error, . Same as described in Appendix A.1.
- Signal error, (TD, indirectly; see Appendix A.1). Systematic component of the signal error from Appendix A.1. We use and for and s, respectively.
- Reference signal error, (TD, indirectly; see Appendix A.1). Systematic error of the zero-force reference, from Appendix A.1 for s. .
- Force gradient error, (TD, indirectly; see Appendix A.3. Systematic error of the synchronous force gradient measurement, considering all errors from Appendix A.3, for both and s, respectively.
Appendix A.4.3. Constant Errors
- Resonance frequency error, . Mean offset from MC simulations, see Appendix A.3.
- Mass calibration error, kg. Mean offset from MC simulations, see Appendix A.3.
- Wavelength offset error, . Absolute error of the Thorlabs LLD1530 reference laser from manufacturer data, adjusted for better thermal stability at COBS, as described in Section 3.2. During the experiment, this may turn out to be a systematic error. Conservatively, we consider it to be constant here. fm.
- Signal error, . Propagated constant error of the DC signal . .
- Reference signal error, . Constant error of the zero-force reference signal. .
- Force gradient error, . Constant part as described in Appendix A.3, amounting to nN/m.
Appendix A.5. Other Errors
Appendix B. Evaluation of the Out of Thermal Equilibrium Casimir Pressure
References
- Keshavarzi, A.; Khaw, K.S.; Yoshioka, T. Muon g − 2: A Review. Nucl. Phys. B 2022, 975, 115675. [Google Scholar] [CrossRef]
- Gao, H.; Vanderhaeghen, M. The Proton Charge Radius. Rev. Mod. Phys. 2022, 94, 015002. [Google Scholar] [CrossRef]
- Tiesinga, E.; Mohr, P.J.; Newell, D.B.; Taylor, B.N. CODATA Recommended Values of the Fundamental Physical Constants: 2018. Rev. Mod. Phys. 2021, 93, 025010. [Google Scholar] [CrossRef]
- Burger, F.A.; Corkery, R.W.; Buhmann, S.Y.; Fiedler, J. Comparison of Theory and Experiments on van der Waals Forces in Media—A Survey. J. Phys. Chem. C 2020, 124, 24179–24186. [Google Scholar] [CrossRef]
- Workman, R.L. et al. [Particle Data Group] Review of Particle Physics. Prog. Theor. Exp. Phys. 2022, 2022, 083C01. [Google Scholar] [CrossRef]
- Hardy, J.C.; Towner, I.S. Superallowed 0+ → 0+ nuclear β decays: 2020 critical survey, with implications for Vud and CKM unitarity. Phys. Rev. C 2020, 102, 045501. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Pseudoparticles. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. Constraints Imposed by CP Conservation in the Presence of Pseudoparticles. Phys. Rev. D 1977, 16, 1791–1797. [Google Scholar] [CrossRef]
- Weinberg, S. A New Light Boson? Phys. Rev. Lett. 1978, 40, 223–226. [Google Scholar] [CrossRef]
- Wilczek, F. Problem of Strong P and T Invariance in the Presence of Instantons. Phys. Rev. Lett. 1978, 40, 279–282. [Google Scholar] [CrossRef]
- Zwicky, F. Die Rotverschiebung von extragalaktischen Nebeln. Helv. Phys. Acta 1933, 6, 110–127. Available online: https://www.e-periodica.ch/digbib/view?pid=hpa-001:1933:6#112 (accessed on 7 February 2024).
- Aghanim, N. et al. [Planck Collaboration] Planck 2018 Results. VI. Cosmological Parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Angulo, R.E.; Hahn, O. Large-Scale Dark Matter Simulations. Liv. Rev. Comput. Astrophys. 2022, 8, 1. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; della Valle, M.; Deustua, S.; Ellis, R.S.; Fabbro, S.; Fruchter, A.; Goldhaber, G.; Groom, D.E.; Hook, I.M.; et al. Discovery of a Supernova Explosion at Half the Age of the Universe. Nature 1998, 391, 51–54. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astrophys. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Schmidt, B.P.; Suntzeff, N.B.; Phillips, M.M.; Schommer, R.A.; Clocchiatti, A.; Kirshner, R.P.; Garnavich, P.; Challis, P.; Leibundgut, B.; Spyromilio, J.; et al. The High-Z Supernova Search: Measuring Cosmic Deceleration and Global Curvature of the Universe Using Type Ia Supernovae. Astrophys. J. 1998, 507, 46–63. [Google Scholar] [CrossRef]
- Hu, J.P.; Wang, F.Y. Hubble Tension: The Evidence of New Physics. Universe 2023, 9, 94. [Google Scholar] [CrossRef]
- Koch, B.; Käding, C.; Pitschmann, M.; Sedmik, R.I.P. Vacuum Energy, the Casimir Effect, and Newton’s Non-Constant. Universe 2023, 9, 476. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An Update. New Astron. Rev. 2022, 95, 101659. [Google Scholar] [CrossRef]
- Solà, J. Cosmological Constant and Vacuum Energy: Old and New Ideas. J. Phys. Conf. Ser. 2013, 453, 012015. [Google Scholar] [CrossRef]
- Martin, J. Everything You Always Wanted to Know about the Cosmological Constant Problem (but Were Afraid to Ask). Comptes Rendus Phys. 2012, 13, 566–665. [Google Scholar] [CrossRef]
- Padmanabhan, T. Why Does Gravity Ignore the Vacuum Energy? Int. J. Mod. Phys. D 2006, 15, 2029–2058. [Google Scholar] [CrossRef]
- Weinberg, S. Theories of the Cosmological Constant. arXiv 1996, arXiv:astro-ph/9610044. [Google Scholar] [CrossRef]
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1. [Google Scholar] [CrossRef]
- Cree, S.S.; Davis, T.M.; Ralph, T.C.; Wang, Q.; Zhu, Z.; Unruh, W.G. Can the Fluctuations of the Quantum Vacuum Solve the Cosmological Constant Problem? Phys. Rev. D 2018, 98, 063506. [Google Scholar] [CrossRef]
- Adler, R.J.; Casey, B.; Jacob, O.C. Vacuum Catastrophe: An Elementary Exposition of the Cosmological Constant Problem. Am. J. Phys. 1995, 63, 620–626. [Google Scholar] [CrossRef]
- Nobbenhuis, S. The Cosmological Constant Problem, an Inspiration for New Physics. Ph.D. Thesis, Utrecht University, Utrecht, The Netherlands, 2006. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Bussolotti, A.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Dai, C.-J.; D’Angelo, A.; Di Marco, A.; He, H.-L.; et al. First Model Independent Results from DAMA/LIBRA–Phase2. Universe 2018, 4, 116. [Google Scholar] [CrossRef]
- Bulbul, E.; Markevitch, M.; Foster, A.; Smith, R.K.; Loewenstein, M.; Randall, S.W. Detection of an Unidentified Emission Line in the Stacked X-ray Spectrum of Galaxy Clusters. Astrohpys. J. 2014, 789, 13. [Google Scholar] [CrossRef]
- Hofmann, F.; Wegg, C. 7.1 keV Sterile Neutrino Dark Matter Constraints from a Deep Chandra X-ray Observation of the Galactic Bulge Limiting Window. Astron. Astrophys. 2019, 625, L7. [Google Scholar] [CrossRef]
- Barkana, R. Possible Interaction between Baryons and Dark-Matter Particles Revealed by the First Stars. Nature 2018, 555, 71–74. [Google Scholar] [CrossRef]
- Colladay, D.; Kostelecký, V.A. Lorentz-Violating Extension of the Standard Model. Phys. Rev. D 1998, 58, 116002. [Google Scholar] [CrossRef]
- Moody, J.E.; Wilczek, F. New Macroscopic Forces? Phys. Rev. D 1984, 30, 130–138. [Google Scholar] [CrossRef]
- Fadeev, P.; Stadnik, Y.V.; Ficek, F.; Kozlov, M.G.; Flambaum, V.V.; Budker, D. Revisiting Spin-Dependent Forces Mediated by New Bosons: Potentials in the Coordinate-Space Representation for Macroscopic- and Atomic-Scale Experiments. Phys. Rev. A 2019, 99, 022113. [Google Scholar] [CrossRef]
- Sponar, S.; Sedmik, R.I.P.; Pitschmann, M.; Abele, H.; Hasegawa, Y. Tests of Fundamental Quantum Mechanics and Dark Interactions with Low-Energy Neutrons. Nat. Rev. Phys. 2021, 3, 309–327. [Google Scholar] [CrossRef]
- Casimir, H.B.G. On the Attraction between Two Perfectly Conducting Plates. Proc. Kon. Ned. Akad. Wet. B 1948, 51, 793–795. Available online: https://dwc.knaw.nl/DL/publications/PU00018547.pdf (accessed on 7 February 2024).
- Lamoreaux, S. Demonstration of the Casimir Force in the 0.6 to 6 μm Range. Phys. Rev. Lett. 1997, 78, 5. [Google Scholar] [CrossRef]
- Mohideen, U.; Roy, A. Precision Measurement of the Casimir Force from 0.1 to 0.9 µm. Phys. Rev. Lett. 1998, 81, 4549–4552. [Google Scholar] [CrossRef]
- Roy, A.; Mohideen, U. Demonstration of the Nontrivial Boundary Dependence of the Casimir Force. Phys. Rev. Lett. 1999, 82, 4380–4383. [Google Scholar] [CrossRef]
- Tang, L.; Wang, M.; Ng, C.Y.; Nikolic, M.; Chan, C.T.; Rodriguez, A.W.; Chan, H.B. Measurement of Non-Monotonic Casimir Forces between Silicon Nanostructures. Nat. Photon. 2017, 11, 97. [Google Scholar] [CrossRef]
- Garrett, J.L.; Somers, D.A.T.; Munday, J.N. Measurement of the Casimir Force between Two Spheres. Phys. Rev. Lett. 2018, 120, 040401. [Google Scholar] [CrossRef]
- Chen, F.; Mohideen, U.; Klimchitskaya, G.L.; Mostepanenko, V.M. Demonstration of the Lateral Casimir Force. Phys. Rev. Lett. 2002, 88, 101801. [Google Scholar] [CrossRef]
- Chiu, H.C.; Klimchitskaya, G.L.; Marachevsky, V.N.; Mostepanenko, V.M.; Mohideen, U. Demonstration of the Asymmetric Lateral Casimir Force between Corrugated Surfaces in the Nonadditive Regime. Phys. Rev. B 2009, 80, 121402. [Google Scholar] [CrossRef]
- Lisanti, M.; Iannuzzi, D.; Capasso, F. Observation of the Skin-Depth Effect on the Casimir Force between Metallic Surfaces. Proc. Natl. Acad. Sci. USA 2005, 102, 11989. [Google Scholar] [CrossRef]
- Chen, F.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Demonstration of the Difference in the Casimir Force for Samples with Different Charge-Carrier Densities. Phys. Rev. Lett. 2006, 97, 170402. [Google Scholar] [CrossRef]
- de Man, S.; Heeck, K.; Wijngaarden, R.J.; Iannuzzi, D. Halving the Casimir Force with Conductive Oxides. Phys. Rev. Lett. 2009, 103, 040402. [Google Scholar] [CrossRef]
- Torricelli, G.; van Zwol, P.J.; Shpak, O.; Binns, C.; Palasantzas, G.; Kooi, B.J.; Svetovoy, V.B.; Wuttig, M. Switching Casimir Forces with Phase-Change Materials. Phys. Rev. A 2010, 82, 010101. [Google Scholar] [CrossRef]
- Torricelli, G.; Pirozhenko, I.; Thornton, S.; Lambrecht, A.; Binns, C. Casimir Force between a Metal and a Semimetal. Europhys. Lett. 2011, 93, 51001. [Google Scholar] [CrossRef]
- Banishev, A.A.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Demonstration of the Casimir Force between Ferromagnetic Surfaces of a Ni-Coated Sphere and a Ni-Coated Plate. Phys. Rev. Lett. 2013, 110, 137401. [Google Scholar] [CrossRef]
- Banishev, A.A.; Wen, H.; Xu, J.; Kawakami, R.K.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Measuring the Casimir Force Gradient from Graphene on a SiO2 Substrate. Phys. Rev. B 2013, 87, 205433. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Y.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Demonstration of an Unusual Thermal Effect in the Casimir Force from Graphene. Phys. Rev. Lett. 2021, 126, 206802. [Google Scholar] [CrossRef]
- Ardito, R.; Frangi, A.; Corigliano, A.; Masi, B.D.; Cazzaniga, G. The Effect of Nano-Scale Interaction Forces on the Premature Pull-in of Real-Life Micro-Electro-Mechanical Systems. Microel. Reliab. 2012, 52, 271. [Google Scholar] [CrossRef]
- Broer, W.; Palasantzas, G.; Knoester, J.; Svetovoy, V.B. Significance of the Casimir Force and Surface Roughness for Actuation Dynamics of MEMS. Phys. Rev. B 2013, 87, 125413. [Google Scholar] [CrossRef]
- Somers, D.A.T.; Garrett, J.L.; Palm, K.J.; Munday, J.N. Measurement of the Casimir Torque. Nature 2018, 564, 386–389. [Google Scholar] [CrossRef]
- Lee, S.w.; Sigmund, W.M. Repulsive van der Waals Forces for Silica and Alumina. J. Coloid Interf. Sci. 2001, 243, 365–369. [Google Scholar] [CrossRef]
- Feiler, A.A.; Bergström, L.; Rutland, M.W. Superlubricity Using Repulsive van der Waals Forces. Langmuir 2008, 24, 2274–2276. [Google Scholar] [CrossRef]
- Munday, J.N.; Capasso, F.; Parsegian, V.A. Measured Long-Range Repulsive Casimir–Lifshitz Forces. Nature 2009, 457, 170–173. [Google Scholar] [CrossRef]
- Mostepanenko, V.M. Casimir Puzzle and Casimir Conundrum: Discovery and Search for Resolution. Universe 2021, 7, 84. [Google Scholar] [CrossRef]
- Bimonte, G.; López, D.; Decca, R.S. Isoelectronic Determination of the Thermal Casimir Force. Phys. Rev. B 2016, 93, 184434. [Google Scholar] [CrossRef]
- Chen, F.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Control of the Casimir force by the modification of dielectric properties with light. Phys. Rev. B 2007, 76, 035338. [Google Scholar] [CrossRef]
- van Zwol, P.; Svetovoy, V.; Palasantzas, G. Characterization of Optical Properties and Surface Roughness Profiles: The Casimir Force Between Real Materials. In Casimir Physics; Dalvit, D., Milonni, P., Roberts, D., da Rosa, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 311–343. [Google Scholar] [CrossRef]
- Behunin, R.O.; Intravaia, F.; Dalvit, D.A.R.; Neto, P.A.M.; Reynaud, S. Modeling Electrostatic Patch Effects in Casimir Force Measurements. Phys. Rev. A 2012, 85, 012504. [Google Scholar] [CrossRef]
- Sushkov, A.O.; Kim, W.J.; Dalvit, D.A.R.; Lamoreaux, S.K. Observation of the Thermal Casimir Force. Nat. Phys. 2011, 7, 230–233. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. An Alternative Response to the Off-Shell Quantum Fluctuations: A Step Forward in Resolution of the Casimir Puzzle. Eur. Phys. J. C 2020, 80, 900. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Violation of the Nernst Heat Theorem in the Theory of the Thermal Casimir Force between Drude Metals. Phys. Rev. A 2004, 69, 022119. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Sedmik, R.I.P. Casimir Pressure between Metallic Plates out of Thermal Equilibrium: Proposed Test for the Relaxation Properties of Free Electrons. Phys. Rev. A 2019, 100, 022511. [Google Scholar] [CrossRef]
- Bordag, M.; Geyer, B.; Klimchitskaya, G.L.; Mostepanenko, V.M. Stronger Constraints for Nanometer Scale Yukawa-type Hypothetical Interactions from the New Measurement of the Casimir Force. Phys. Rev. D 1999, 60, 055004. [Google Scholar] [CrossRef]
- Mostepanenko, V.M.; Novello, M. Constraints on Non-Newtonian Gravity from the Casimir Force Measurements between Two Crossed Cylinders. Phys. Rev. D 2001, 63, 115003. [Google Scholar] [CrossRef]
- Decca, R.S.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; López, D.; Mostepanenko, V.M. Improved Tests of Extra-Dimensional Physics and Thermal Quantum Field Theory from New Casimir Force Measurements. Phys. Rev. D 2003, 68, 116003. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Chan, H.B.; Fischbach, E.; Krause, D.E.; Jamell, C.R. Constraining New Forces in the Casimir Regime Using the Isoelectronic Technique. Phys. Rev. Lett. 2005, 94, 240401. [Google Scholar] [CrossRef]
- Decca, R.; López, D.; Fischbach, E.; Klimchitskaya, G.; Krause, D.; Mostepanenko, V. Novel Constraints on Light Elementary Particles and Extra-Dimensional Physics from the Casimir Effect. Eur. Phys. J. C 2007, 51, 963–975. [Google Scholar] [CrossRef]
- Mostepanenko, V.M.; Decca, R.S.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; López, D. Stronger Constraints on Non-Newtonian Gravity from the Casimir Effect. J. Phys. A 2008, 41, 164054. [Google Scholar] [CrossRef]
- Masuda, M.; Sasaki, M. Limits on Nonstandard Forces in the Submicrometer Range. Phys. Rev. Lett. 2009, 102, 171101. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Advance and Prospects in Constraining the Yukawa-type Corrections to Newtonian Gravity from the Casimir Effect. Phys. Rev. D 2010, 81, 055003. [Google Scholar] [CrossRef]
- Sushkov, A.O.; Kim, W.J.; Dalvit, D.A.R.; Lamoreaux, S.K. New Experimental Limits on Non-Newtonian Forces in the Micrometer Range. Phys. Rev. Lett. 2011, 107, 171101. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Constraints on Corrections to Newtonian Gravity from Two Recent Measurements of the Casimir Interaction between Metallic Surfaces. Phys. Rev. D 2013, 87, 125031. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Romero, C. Constraints on axion-nucleon coupling constants from measuring the Casimir force between corrugated surfaces. Phys. Rev. D 2014, 90, 055013. [Google Scholar] [CrossRef]
- Chen, Y.J.; Tham, W.K.; Krause, D.E.; López, D.; Fischbach, E.; Decca, R.S. Stronger Limits on Hypothetical Yukawa Interactions in the 30–8000 Nm Range. Phys. Rev. Lett. 2016, 116, 221102. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Constraints on Axionlike Particles and Non-Newtonian Gravity from Measuring the Difference of Casimir Forces. Phys. Rev. D 2017, 95, 123013. [Google Scholar] [CrossRef]
- Kuz’min, V.A.; Tkachev, I.I.; Shaposhnikov, M.E. Restrictions Imposed on Light Scalar Particles by Measurements of van der Waals Forces. JETP Lett. 1982, 36, 59–62. [Google Scholar]
- Behunin, R.O.; Dalvit, D.A.R.; Decca, R.S.; Speake, C.C. Limits on the Accuracy of Force Sensing at Short Separations Due to Patch Potentials. Phys. Rev. D 2014, 89, 051301. [Google Scholar] [CrossRef]
- Wang, J.; Guan, S.; Chen, K.; Wu, W.; Tian, Z.; Luo, P.; Jin, A.; Yang, S.; Shao, C.; Luo, J. Test of Non-Newtonian Gravitational Forces at Micrometer Range with Two-Dimensional Force Mapping. Phys. Rev. D 2016, 94, 122005. [Google Scholar] [CrossRef]
- Adelberger, E.G.; Stubbs, C.W.; Heckel, B.R.; Su, Y.; Swanson, H.E.; Smith, G.; Gundlach, J.H.; Rogers, W.F. Testing the Equivalence Principle in the Field of the Earth: Particle Physics at Masses below 1 μeV? Phys. Rev. D 1990, 42, 3267–3292. [Google Scholar] [CrossRef] [PubMed]
- Hoyle, C.D.; Kapner, D.J.; Heckel, B.R.; Adelberger, E.G.; Gundlach, J.H.; Schmidt, U.; Swanson, H.E. Submillimeter Tests of the Gravitational Inverse-Square Law. Phys. Rev. D 2004, 70, 042004. [Google Scholar] [CrossRef]
- Adelberger, E.G.; Heckel, B.R.; Hoedl, S.; Hoyle, C.D.; Kapner, D.J.; Upadhye, A. Particle-Physics Implications of a Recent Test of the Gravitational Inverse-Square Law. Phys. Rev. Lett. 2007, 98, 131104. [Google Scholar] [CrossRef]
- Hammond, G.D.; Speake, C.C.; Trenkel, C.; Patón, A.P. New Constraints on Short-Range Forces Coupling Mass to Intrinsic Spin. Phys. Rev. Lett. 2007, 98, 081101. [Google Scholar] [CrossRef]
- Schlamminger, S.; Choi, K.Y.; Wagner, T.A.; Gundlach, J.H.; Adelberger, E.G. Test of the Equivalence Principle Using a Rotating Torsion Balance. Phys. Rev. Lett. 2008, 100, 041101. [Google Scholar] [CrossRef]
- Heckel, B.R.; Adelberger, E.G.; Cramer, C.E.; Cook, T.S.; Schlamminger, S.; Schmidt, U. Preferred-Frame and CP-Violation Tests with Polarized Electrons. Phys. Rev. D 2008, 78, 092006. [Google Scholar] [CrossRef]
- Geraci, A.A.; Smullin, S.J.; Weld, D.M.; Chiaverini, J.; Kapitulnik, A. Improved Constraints on Non-Newtonian Forces at 10 Microns. Phys. Rev. D 2008, 78, 022002. [Google Scholar] [CrossRef]
- Hoedl, S.A.; Fleischer, F.; Adelberger, E.G.; Heckel, B.R. Improved Constraints on an Axion-Mediated Force. Phys. Rev. Lett. 2011, 106, 041801. [Google Scholar] [CrossRef]
- Heckel, B.R.; Terrano, W.A.; Adelberger, E.G. Limits on Exotic Long-Range Spin-Spin Interactions of Electrons. Phys. Rev. Lett. 2013, 111, 151802. [Google Scholar] [CrossRef]
- Terrano, W.A.; Adelberger, E.G.; Lee, J.G.; Heckel, B.R. Short-Range, Spin-Dependent Interactions of Electrons: A Probe for Exotic Pseudo-Goldstone Bosons. Phys. Rev. Lett. 2015, 115, 201801. [Google Scholar] [CrossRef]
- Tan, W.-H.; Yang, S.-Q.; Shao, C.-G.; Li, J.; Du, A.-B.; Zhan, B.-F.; Wang, Q.-L.; Luo, P.-S.; Tu, L.-C.; Luo, J. New Test of the Gravitational Inverse-Square Law at the Submillimeter Range with Dual Modulation and Compensation. Phys. Rev. Lett. 2016, 116, 131101. [Google Scholar] [CrossRef] [PubMed]
- Tan, W.-H.; Du, A.-B.; Dong, W.-C.; Yang, S.-Q.; Shao, C.-G.; Guan, S.-G.; Wang, Q.-L.; Zhan, B.-F.; Luo, P.-S.; Tu, L.-C.; et al. Improvement for Testing the Gravitational Inverse-Square Law at the Submillimeter Range. Phys. Rev. Lett. 2020, 124, 051301. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.G.; Adelberger, E.G.; Cook, T.S.; Fleischer, S.M.; Heckel, B.R. New Test of the Gravitational 1/r2 Law at Separations down to 52 µm. Phys. Rev. Lett. 2020, 124, 101101. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.-L.; Tan, Y.-J.; Wu, W.-H.; Luo, J.; Shao, C.-G. Constraining the Chameleon Model with the HUST-2020 Torsion Pendulum Experiment. Phys. Rev. D 2021, 103, 104005. [Google Scholar] [CrossRef]
- Sedmik, R.I.P.; Almasi, A.; Iannuzzi, D. Locality of Surface Interactions on Colloidal Probes. Phys. Rev. B 2013, 88, 165429. [Google Scholar] [CrossRef]
- van Zwol, P.J.; Svetovoy, V.B.; Palasantzas, G. Distance upon Contact: Determination from Roughness Profile. Phys. Rev. B 2009, 80, 235401. [Google Scholar] [CrossRef]
- Sedmik, R.I.P.; Pitschmann, M. Next Generation Design and Prospects for Cannex. Universe 2021, 7, 234. [Google Scholar] [CrossRef]
- Bressi, G.; Carugno, G.; Onofrio, R.; Ruoso, G. Measurement of the Casimir Force between Parallel Metallic Surfaces. Phys. Rev. Lett. 2002, 88, 041804. [Google Scholar] [CrossRef] [PubMed]
- Antonini, P.; Bimonte, G.; Bressi, G.; Carugno, G.; Galeazzi, G.; Messineo, G.; Ruoso, G. An Experimental Apparatus for Measuring the Casimir Effect at Large Distances. J. Phys. Conf. Ser. 2009, 161, 012006. [Google Scholar] [CrossRef]
- Almasi, A.; Brax, P.; Iannuzzi, D.; Sedmik, R.I.P. Force Sensor for Chameleon and Casimir Force Experiments with Parallel-Plate Configuration. Phys. Rev. D 2015, 91, 102002. [Google Scholar] [CrossRef]
- Sedmik, R.; Brax, P. Status Report and First Light from Cannex: Casimir Force Measurements between Flat Parallel Plates. J. Phys. Conf. Ser. 2018, 1138, 012014. [Google Scholar] [CrossRef]
- Sedmik, R.I.P. Casimir and Non-Newtonian Force Experiment (CANNEX): Review, Status, and Outlook. Int. J. Mod. Phys. A 2020, 35, 2040008. [Google Scholar] [CrossRef]
- Fischer, H.; Käding, C.; Sedmik, R.I.P.; Abele, H.; Brax, P.; Pitschmann, M. Search for Environment-Dependent Dilatons. Phys. Dark Univ. 2024, 43, 101419. [Google Scholar] [CrossRef]
- Brax, P.; van de Bruck, C.; Davis, A.C.; Shaw, D.J.; Iannuzzi, D. Tuning the Mass of Chameleon Fields in Casimir Force Experiments. Phys. Rev. Lett. 2010, 104, 241101. [Google Scholar] [CrossRef]
- Stochino, A.; DeSalvo, R.; Huang, Y.; Sannibale, V. Improvement of the Seismic Noise Attenuation Performance of the Monolithic Geometric Anti-Spring Filters for Gravitational Wave Interferometric Detectors. Nucl. Instrum. Meth. A 2007, 580, 1559–1564. [Google Scholar] [CrossRef]
- Stochino, A.; Abbot, B.; Aso, Y.; Barton, M.; Bertolini, A.; Boschi, V.; Coyne, D.; DeSalvo, R.; Galli, C.; Huang, Y.; et al. The Seismic Attenuation System (SAS) for the Advanced LIGO Gravitational Wave Interferometric Detectors. Nucl. Inst. Methods A 2009, 598, 737. [Google Scholar] [CrossRef][Green Version]
- Blom, M.R.; Beker, M.G.; Bertolini, A.; van den Brand, J.F.J.; Bulten, H.J.; Doets, M.; Hennes, E.; Mul, F.A.; Rabeling, D.S.; Schimmel, A. Vertical and Horizontal Seismic Isolation Performance of the Advanced Virgo External Injection Bench Seismic Attenuation System. Phys. Procedia 2015, 61, 641–647. [Google Scholar] [CrossRef][Green Version]
- van Heijningen, J.V.; Bertolini, A.; Hennes, E.; Beker, M.G.; Doets, M.; Bulten, H.J.; Agatsuma, K.; Sekiguchi, T.; van den Brand, J.F.J. A Multistage Vibration Isolation System for Advanced Virgo Suspended Optical Benches. Class. Quant. Grav. 2019, 36, 075007. [Google Scholar] [CrossRef]
- Cella, G.; Sannibale, V.; DeSalvo, R.; Márka, S.; Takamori, A. Monolithic Geometric Anti-Spring Blades. Nucl. Instr. Meth. A 2005, 540, 502–519. [Google Scholar] [CrossRef]
- Takamori, A.; Raffai, P.; Márka, S.; DeSalvo, R.; Sannibale, V.; Tariq, H.; Bertolini, A.; Cella, G.; Viboud, N.; Numata, K.; et al. Inverted Pendulum as Low-Frequency Pre-Isolation for Advanced Gravitational Wave Detectors. Nucl. Instrum. Meth. A 2007, 582, 683–692. [Google Scholar] [CrossRef]
- Peterson, J.R. Observations and Modeling of Seismic Background Noise; USGS Numbered Series 93-322; U.S. Geological Survey: Reston, VA, USA, 1993. [CrossRef]
- Beker, M.G.; Bertolini, A.; van den Brand, J.F.J.; Bulten, H.J.; Hennes, E.; Rabeling, D.S. State Observers and Kalman Filtering for High Performance Vibration Isolation Systems. Rev. Sci. Instrum. 2014, 85, 034501. [Google Scholar] [CrossRef]
- Rossi, F.; Opat, G.I. Observations of the Effects of Adsorbates on Patch Potentials. J. Phys. D Appl. Phys. 1992, 25, 1349–1353. [Google Scholar] [CrossRef]
- Garrett, J.L.; Kim, J.; Munday, J.N. Measuring the Effect of Electrostatic Patch Potentials in Casimir Force Experiments. Phys. Rev. Res. 2020, 2, 023355. [Google Scholar] [CrossRef]
- Robertson, N.A.; Blackwood, J.R.; Buchman, S.; Byer, R.L.; Camp, J.; Gill, D.; Hanson, J.; Williams, S.; Zhou, P. Kelvin Probe Measurements: Investigations of the Patch Effect with Applications to ST-7 and LISA. Class. Quant. Grav. 2006, 23, 2665. [Google Scholar] [CrossRef]
- Speake, C.C.; Trenkel, C. Forces between Conducting Surfaces due to Spatial Variations of Surface Potential. Phys. Rev. Lett. 2003, 90, 160403. [Google Scholar] [CrossRef]
- Kim, W.J.; Sushkov, A.O.; Dalvit, D.A.R.; Lamoreaux, S.K. Surface Contact Potential Patches and Casimir Force Measurements. Phys. Rev. A 2010, 81, 022505. [Google Scholar] [CrossRef]
- Fosco, C.D.; Lombardo, F.C.; Mazzitelli, F.D. Electrostatic Interaction due to Patch Potentials on Smooth Conducting Surfaces. Phys. Rev. A 2013, 88, 062501. [Google Scholar] [CrossRef]
- Liu, M.; Schafer, R.; Xu, J.; Mohideen, U. Elimination of Electrostatic Forces in Precision Casimir Force Measurements Using UV and Argon Ion Radiation. Mod. Phys. Lett. A 2020, 35, 2040001. [Google Scholar] [CrossRef]
- de Man, S.; Heeck, K.; Iannuzzi, D. No Anomalous Scaling in Electrostatic Calibrations for Casimir Force Measurements. Phys. Rev. A 2009, 79, 024102. [Google Scholar] [CrossRef]
- Sedmik, R.I.P.; Borghesani, A.F.; Heeck, K.; Iannuzzi, D. Hydrodynamic Force Measurements under Precisely Controlled Conditions: Correlation of Slip Parameters with the Mean Free Path. Phys. Fluids 2013, 25, 042103. [Google Scholar] [CrossRef]
- Sedmik, R.I.P.; Urech, A.; Zalevsky, Z.; Carmeli, I. Efficient Reduction of Casimir Forces by Self-assembled Bio-molecular Thin Films. arXiv 2023, arXiv:2306.16209. [Google Scholar] [CrossRef]
- Turetta, N.; Sedona, F.; Liscio, A.; Sambi, M.; Samorì, P. Au(111) Surface Contamination in Ambient Conditions: Unravelling the Dynamics of the Work Function in Air. Adv. Mater. Interf. 2021, 8, 2100068. [Google Scholar] [CrossRef]
- Chavan, D.; Gruca, G.; de Man, S.; Slaman, M.; Rector, J.H.; Heeck, K.; Iannuzzi, D. Ferrule-Top Atomic Force Microscope. Rev. Sci. Instrum. 2010, 81, 123702. [Google Scholar] [CrossRef]
- Behunin, R.O.; Dalvit, D.A.R.; Decca, R.S.; Genet, C.; Jung, I.W.; Lambrecht, A.; Liscio, A.; López, D.; Reynaud, S.; Schnoering, G.; et al. Kelvin Probe Force Microscopy of Metallic Surfaces Used in Casimir Force Measurements. Phys. Rev. A 2014, 90, 062115. [Google Scholar] [CrossRef]
- Zerweck, U.; Loppacher, C.; Otto, T.; Grafström, S.; Eng, L.M. Accuracy and Resolution Limits of Kelvin Probe Force Microscopy. Phys. Rev. B 2005, 71, 125424. [Google Scholar] [CrossRef]
- Axt, A.; Hermes, I.M.; Bergmann, V.W.; Tausendpfund, N.; Weber, S.A.L. Know Your Full Potential: Quantitative Kelvin Probe Force Microscopy on Nanoscale Electrical Devices. Beilstein J. Nanotechnol. 2018, 9, 1809–1819. [Google Scholar] [CrossRef]
- Ma, Z.M.; Mu, J.L.; Tang, J.; Xue, H.; Zhang, H.; Xue, C.Y.; Liu, J.; Li, Y.J. Artifacts in KPFM in FM, AM and Heterodyne AM Modes. Key Engin. Mater. 2014, 609–610, 1362–1368. [Google Scholar] [CrossRef]
- Burke, S.A.; LeDue, J.M.; Miyahara, Y.; Topple, J.M.; Fostner, S.; Grütter, P. Determination of the Local Contact Potential Difference of PTCDA on NaCl: A Comparison of Techniques. Nanotechnol. 2009, 20, 264012. [Google Scholar] [CrossRef]
- Garrett, J.L.; Munday, J.N. Fast, High-Resolution Surface Potential Measurements in Air with Heterodyne Kelvin Probe Force Microscopy. Nanotechnology 2016, 27, 245705. [Google Scholar] [CrossRef]
- Sugawara, Y.; Kou, L.; Ma, Z.; Kamijo, T.; Naitoh, Y.; Jun Li, Y. High Potential Sensitivity in Heterodyne Amplitude-Modulation Kelvin Probe Force Microscopy. Appl. Phys. Lett. 2012, 100, 223104. [Google Scholar] [CrossRef]
- Sugawara, Y.; Miyazaki, M.; Li, Y.J. Surface Potential Measurement by Heterodyne Frequency Modulation Kelvin Probe Force Microscopy in MHz Range. J. Phys. Commun. 2020, 4, 075015. [Google Scholar] [CrossRef]
- Ma, Z.M.; Kou, L.; Naitoh, Y.; Li, Y.J.; Sugawara, Y. The Stray Capacitance Effect in Kelvin Probe Force Microscopy Using FM, AM and Heterodyne AM Modes. Nanotechnology 2013, 24, 225701. [Google Scholar] [CrossRef]
- Miyazaki, M.; Sugawara, Y.; Li, Y.J. Dual-Bias Modulation Heterodyne Kelvin Probe Force Microscopy in FM Mode. Appl. Phys. Lett. 2022, 121, 241602. [Google Scholar] [CrossRef]
- Nonnenmacher, M.; O’Boyle, M.P.; Wickramasinghe, H.K. Kelvin Probe Force Microscopy. Appl. Phys. Lett. 1991, 58, 2921–2923. [Google Scholar] [CrossRef]
- Dobosz, M.; Kożuchowski, M. Overview of the Laser-Wavelength Measurement Methods. Opt. Lasers Engin. 2017, 98, 107–117. [Google Scholar] [CrossRef]
- Thorlabs GmbH (Newton, NJ, USA). Private communication, 2023.
- Rabinovich, S.G. Measurement Errors and Uncertainties: Theory and Practice; AIP Press/Springer Science & Business Media: New York, NY, USA, 2005. [Google Scholar] [CrossRef]
- Bordag, M.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Lifshitz, E.M. The Theory of Molecular Attractive Force between Solids. Sov. Phys. JETP 1956, 2, 73–83. Available online: http://jetp.ras.ru/cgi-bin/e/index/e/2/1/p73?a=list (accessed on 7 February 2024).
- Iannuzzi, D.; Lisanti, M.; Capasso, F. Effect of Hydrogen-Switchable Mirrors on the Casimir force. Proc. Natl. Acad. Sci. USA 2004, 101, 4019–4023. [Google Scholar] [CrossRef]
- Lamoreaux, S.K. Reanalysis of Casimir Force Measurements in the 0.6-to-6-μm Range. Phys. Rev. A 2010, 82, 024102. [Google Scholar] [CrossRef]
- Banishev, A.A.; Chang, C.C.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Measurement of the Gradient of the Casimir Force between a Nonmagnetic Gold Sphere and a Magnetic Nickel Plate. Phys. Rev. B 2012, 85, 195422. [Google Scholar] [CrossRef]
- Zhao, R.; Li, L.; Yang, S.; Bao, W.; Xia, Y.; Ashby, P.; Wang, Y.; Zhang, X. Stable Casimir Equilibria and Quantum Trapping. Science 2019, 364, 984–987. [Google Scholar] [CrossRef]
- Dzyaloshinskii, I.E.; Lifshitz, E.M.; Pitaevskii, L.P. General Theory of the van der Waals’ Forces. Sov. Phys. Usp. 1961, 4, 153–176. [Google Scholar] [CrossRef]
- Rodriguez, A.W.; Reid, M.T.H.; Intravaia, F.; Woolf, A.; Dalvit, D.A.R.; Capasso, F.; Johnson, S.G. Geometry-Induced Casimir Suspension of Oblate Bodies in Fluids. Phys. Rev. Lett. 2013, 111, 180402. [Google Scholar] [CrossRef]
- Esteso, V.; Carretero-Palacios, S.; Míguez, H. Nanolevitation Phenomena in Real Plane-Parallel Systems Due to the Balance between Casimir and Gravity Forces. J. Phys. Chem. C 2015, 119, 5663–5670. [Google Scholar] [CrossRef]
- Esteso, V.; Frustaglia, D.; Carretero-Palacios, S.; Míguez, H. Casimir-Lifshitz Optical Resonators: A New Platform for Exploring Physics at the Nanoscale. Adv. Phys. Res. 2023, 3, 2300065. [Google Scholar] [CrossRef]
- Bostrom, M.; Sernelius, B.E. Thermal Effects on the Casimir Force in the 0.1-5 μm Range. Phys. Rev. Lett. 2000, 84, 4757. [Google Scholar] [CrossRef]
- Brevik, I.; Shapiro, B.; Silveirinha, M.G. Fluctuational electrodynamics in and out of equilibrium. Int. J. Mod. Phys. A 2022, 37, 2241012. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Current status of the problem of thermal Casimir force. Int. J. Mod. Phys. A 2022, 37, 2241002. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Tests of new physics from precise measurements of the Casimir pressure between two gold-coated plates. Phys. Rev. D 2007, 75, 077101. [Google Scholar] [CrossRef]
- Liu, M.; Xu, J.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Precision measurements of the gradient of the Casimir force between ultraclean metallic surfaces at larger separations. Phys. Rev. A 2019, 100, 052511. [Google Scholar] [CrossRef]
- Bimonte, G.; Spreng, B.; Maia Neto, P.A.; Ingold, G.L.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Decca, R.S. Measurement of the Casimir Force between 0.2 and 8 μm: Experimental Procedures and Comparison with Theory. Universe 2021, 7, 93. [Google Scholar] [CrossRef]
- Garcia-Sanchez, D.; Fong, K.Y.; Bhaskaran, H.; Lamoreaux, S.; Tang, H.X. Casimir Force and ’In Situ’ Surface Potential Measurements on Nanomembranes. Phys. Rev. Lett. 2012, 109, 027202. [Google Scholar] [CrossRef]
- Behunin, R.O.; Zeng, Y.; Dalvit, D.A.R.; Reynaud, S. Electrostatic Patch Effects in Casimir-force Experiments Performed in the Sphere-Plane Geometry. Phys. Rev. A 2012, 86, 052509. [Google Scholar] [CrossRef]
- Garrett, J.L.; Somers, D.; Munday, J.N. The Effect of Patch Potentials in Casimir Force Measurements Determined by Heterodyne Kelvin Probe Force Microscopy. J. Phys. Cond. Matter 2015, 27, 214012. [Google Scholar] [CrossRef][Green Version]
- Torgerson, J.R.; Lamoreaux, S.K. Low-frequency Character of the Casimir Force between Metallic Films. Phys. Rev. E 2004, 70, 047102. [Google Scholar] [CrossRef]
- Bimonte, G. Johnson Noise and the Thermal Casimir Effect. New J. Phys. 2007, 9, 281. [Google Scholar] [CrossRef]
- Intravaia, F.; Henkel, C. Casimir Interaction from Magnetically Coupled Eddy Currents. Phys. Rev. Lett. 2009, 103, 130405. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Casimir Effect Invalidates the Drude Model for Transverse Electric Evanescent Waves. Physics 2023, 5, 952–967. [Google Scholar] [CrossRef]
- van Leeuwen, H.J. Problèmes de la théorie électronique du magnétisme. J. Phys. Radium 1921, 2, 361–377. [Google Scholar] [CrossRef]
- Bimonte, G. Bohr–van Leeuwen theorem and the thermal Casimir effect for conductors. Phys. Rev. A 2009, 79, 042107. [Google Scholar] [CrossRef]
- London, F.; London, H. The Electromagnetic Equations of the Supraconductor. Proc. R. Soc. A Math. Phys. Engin. Sci. 1935, 149, 71–88. [Google Scholar] [CrossRef]
- Intravaia, F. How Modes Shape Casimir Physics. Int. J. Mod. Phys. A 2022, 37, 2241014. [Google Scholar] [CrossRef]
- Intravaia, F.; Ellingsen, S.; Henkel, C. Casimir–Foucault Interaction: Free Energy and Entropy at Low Temperature. Phys. Rev. A 2010, 82, 032504. [Google Scholar] [CrossRef]
- Henkel, C.; Intravaia, F. On the Casimir Entropy between ‘Perfect Crystals’. Int. J. Mod. Phys. A 2010, 25, 2328–2336. [Google Scholar] [CrossRef]
- Reiche, D.; Busch, K.; Intravaia, F. Quantum Thermodynamics of Overdamped Modes in Local and Spatially Dispersive Materials. Phys. Rev. A 2020, 101, 012506. [Google Scholar] [CrossRef]
- Bimonte, G.; Santamato, E. General Theory of Electromagnetic Fluctuations near a Homogeneous Surface in Terms of Its Reflection Amplitudes. Phys. Rev. A 2007, 76, 013810. [Google Scholar] [CrossRef]
- Guérout, R.; Lambrecht, A.; Milton, K.A.; Reynaud, S. Derivation of the Lifshitz–Matsubara Sum Formula for the Casimir Pressure between Metallic Plane Mirrors. Phys. Rev. E 2014, 90, 042125. [Google Scholar] [CrossRef]
- Svetovoy, V.B.; Esquivel, R. Nonlocal Impedances and the Casimir Entropy at Low Temperatures. Phys. Rev. E 2005, 72, 036113. [Google Scholar] [CrossRef]
- Intravaia, F.; Henkel, C. Casimir Energy and Entropy between Dissipative Mirrors. J. Phys. A Math. Gen. 2008, 41, 164018. [Google Scholar] [CrossRef][Green Version]
- Klimchitskaya, G.L.; Blagov, E.V.; Mostepanenko, V.M. Problems in the Lifshitz Theory of Atom–Wall Interaction. Int. J. Mod. Phys. A 2009, 24, 1777–1788. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. The Casimir Force between real Materials: Experiment and Theory. Rev. Mod. Phys. 2009, 81, 1827–1885. [Google Scholar] [CrossRef]
- Milton, K. The Casimir Force: Feeling the Heat. Nat. Phys. 2011, 7, 190–191. [Google Scholar] [CrossRef]
- Shelden, C.; Spreng, B.; Munday, J.N. Enhanced Repulsive Casimir Forces between Gold and Thin Magnetodielectric Plates. Phys. Rev. A 2023, 108, 032817. [Google Scholar] [CrossRef]
- Banishev, A.A.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Casimir Interaction between Two Magnetic Metals in Comparison with Nonmagnetic Test Bodies. Phys. Rev. B 2013, 88, 155410. [Google Scholar] [CrossRef]
- Bordag, M.; Fialkovsky, I.V.; Gitman, D.M.; Vassilevich, D.V. Casimir Interaction between a Perfect Conductor and Graphene Described by the Dirac Model. Phys. Rev. B 2009, 80, 245406. Available online: http://jetpletters.ru/ps/1330/article_20101.shtml (accessed on 7 February 2024). [CrossRef]
- Fialkovsky, I.V.; Marachevsky, V.N.; Vassilevich, D.V. Finite-Temperature Casimir Effect for Graphene. Phys. Rev. B 2011, 84, 035446. [Google Scholar] [CrossRef]
- Egerland, C.H.; Busch, K.; Intravaia, F. Polaritonic Contribution to the Casimir Energy between Two Graphene Layers. Phys. Rev. B 2019, 100, 235418. [Google Scholar] [CrossRef]
- Woods, L.M.; Dalvit, D.A.R.; Tkatchenko, A.; Rodriguez-Lopez, P.; Rodriguez, A.W.; Podgornik, R. Materials Perspective on Casimir and van der Waals Interactions. Rev. Mod. Phys. 2016, 88, 045003. [Google Scholar] [CrossRef]
- Fialkovsky, I.; Khusnutdinov, N.; Vassilevich, D. Quest for Casimir Repulsion between Chern-Simons Surfaces. Phys. Rev. B 2018, 97, 165432. [Google Scholar] [CrossRef]
- Chen, L.; Chang, K. Chiral-Anomaly-Driven Casimir-Lifshitz Torque between Weyl Semimetals. Phys. Rev. Lett. 2020, 125, 047402. [Google Scholar] [CrossRef]
- Farias, M.B.; Zyuzin, A.A.; Schmidt, T.L. Casimir Force between Weyl Semimetals in a Chiral Medium. Phys. Rev. B 2020, 101, 235446. [Google Scholar] [CrossRef]
- Intravaia, F.; Lambrecht, A. Surface Plasmon Modes and the Casimir Energy. Phys. Rev. Lett. 2005, 94, 110404. [Google Scholar] [CrossRef]
- Intravaia, F.; Henkel, C.; Lambrecht, A. Role of Surface Plasmons in the Casimir Effect. Phys. Rev. A 2007, 76, 033820. [Google Scholar] [CrossRef]
- Boyer, T.H. Quantum Electromagnetic Zero-Point Energy of a Conducting Spherical Shell and the Casimir Model for a Charged Particle. Phys. Rev. 1968, 174, 1764–1766. [Google Scholar] [CrossRef]
- Graham, N.; Quandt, M.; Weigel, H. Attractive Electromagnetic Casimir Stress on a Spherical Dielectric Shell. Phys. Lett. B 2013, 4–5, 846–849. [Google Scholar] [CrossRef]
- Büscher, R.; Emig, T. Nonperturbative Approach to Casimir Interactions in Periodic Geometries. Phys. Rev. A 2004, 69, 062101. [Google Scholar] [CrossRef]
- Davids, P.S.; Intravaia, F.; Rosa, F.S.S.; Dalvit, D.A.R. Modal Approach to Casimir Forces in Periodic Structures. Phys. Rev. A 2010, 82, 062111. [Google Scholar] [CrossRef]
- Lambrecht, A.; Marachevsky, V.N. Casimir Interaction of Dielectric Gratings. Phys. Rev. Lett. 2008, 101, 160403. [Google Scholar] [CrossRef]
- Intravaia, F.; Davids, P.S.; Decca, R.S.; Aksyuk, V.A.; López, D.; Dalvit, D.A.R. Quasianalytical Modal Approach for Computing Casimir Interactions in Periodic Nanostructures. Phys. Rev. A 2012, 86, 042101. [Google Scholar] [CrossRef]
- Messina, R.; Maia Neto, P.A.; Guizal, B.; Antezza, M. Casimir Interaction between a Sphere and a Grating. Phys. Rev. A 2015, 92, 062504. [Google Scholar] [CrossRef]
- Hartmann, M.; Ingold, G.L.; Neto, P.A.M. Plasma versus Drude Modeling of the Casimir Force: Beyond the Proximity Force Approximation. Phys. Rev. Lett. 2017, 119, 043901. [Google Scholar] [CrossRef]
- Antezza, M.; Chan, H.B.; Guizal, B.; Marachevsky, V.N.; Messina, R.; Wang, M. Giant Casimir Torque between Rotated Gratings and the θ = 0 Anomaly. Phys. Rev. Lett. 2020, 124, 013903. [Google Scholar] [CrossRef]
- Schoger, T.; Spreng, B.; Ingold, G.L.; Lambrecht, A.; Maia Neto, P.A.; Reynaud, S. Universal Casimir Interactions in the Sphere–Sphere Geometry. Int. J. Mod. Phys. A 2022, 37, 2241005. [Google Scholar] [CrossRef]
- Emig, T.; Bimonte, G. Multiple Scattering Expansion for Dielectric Media: Casimir Effect. Phys. Rev. Lett. 2023, 130, 200401. [Google Scholar] [CrossRef]
- Reid, M.T.H.; White, J.; Johnson, S.G. Computation of Casimir Interactions between Arbitrary three-dimensional objects with arbitrary material properties. Phys. Rev. A 2011, 84, 010503. [Google Scholar] [CrossRef]
- Johnson, S. Numerical Methods for Computing Casimir Interactions. In Casimir Physics; Dalvit, D., Milonni, P., Roberts, D., da Rosa, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 175–218. [Google Scholar] [CrossRef]
- Rodriguez, A.W.; Capasso, F.; Johnson, S.G. The Casimir Effect in Microstructured Geometries. Nat. Photon. 2011, 5, 211–221. [Google Scholar] [CrossRef]
- Reid, M.T.H.; White, J.; Johnson, S.G. Fluctuating Surface Currents: An Algorithm for Efficient Prediction of Casimir Interactions among Arbitrary Materials in Arbitrary Geometries. Phys. Rev. A 2013, 88, 022514. [Google Scholar] [CrossRef]
- Kristensen, P.T.; Beverungen, B.; Intravaia, F.; Busch, K. High-Accuracy Casimir–Polder Force Calculations using the Discontinuous Galerkin Time-Domain method. Phys. Rev. B 2023, 108, 205424. [Google Scholar] [CrossRef]
- Chan, H.B.; Aksyuk, V.A.; Kleiman, R.N.; Bishop, D.J.; Capasso, F. Quantum Mechanical Actuation of Microelectromechanical Systems by the Casimir Force. Science 2001, 291, 1941–1944. [Google Scholar] [CrossRef]
- Chan, H.B.; Aksyuk, V.A.; Kleiman, R.N.; Bishop, D.J.; Capasso, F. Nonlinear Micromechanical Casimir Oscillator. Phys. Rev. Lett. 2001, 87, 211801. [Google Scholar] [CrossRef]
- Derjaguin, B.V.; Abrikosova, I.I.; Lifshitz, E.M. Direct Measurement of Molecular Attraction between Solids Separated by a Narrow Gap. Quart. Rev. Chem. Soc. 1956, 10, 295–329. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Precise Comparison of Theory and New Experiment for the Casimir Force Leads to Stronger Constraints on Thermal Quantum Effects and Long-Range Interactions. Ann. Phys. 2005, 318, 37–80. [Google Scholar] [CrossRef]
- Sparnaay, M.J. Attractive Forces between Flat Plates. Nature 1957, 180, 334–335. [Google Scholar] [CrossRef]
- Chan, H.B.; Bao, Y.; Zou, J.; Cirelli, R.A.; Klemens, F.; Mansfield, W.M.; Pai, C.S. Measurement of the Casimir Force between a Gold Sphere and a Silicon Surface with Nanoscale Trench Arrays. Phys. Rev. Lett. 2008, 101, 030401. [Google Scholar] [CrossRef]
- Bao, Y.; Guèrout, R.; Lussange, J.; Lambrecht, A.; Cirelli, R.A.; Klemens, F.; Mansfield, W.M.; Pai, C.S.; Chan, H.B. Casimir Force on a Surface with Shallow Nanoscale Corrugations: Geometry and Finite Conductivity Effects. Phys. Rev. Lett. 2010, 105, 250402. [Google Scholar] [CrossRef]
- Lussange, J.; Guérout, R.; Lambrecht, A. Casimir Energy between Nanostructured Gratings of Arbitrary Periodic Profile. Phys. Rev. A 2012, 86, 062502. [Google Scholar] [CrossRef]
- Intravaia, F.; Koev, S.; Jung, I.W.; Talin, A.A.; Davids, P.S.; Decca, R.S.; Aksyuk, V.A.; Dalvit, D.A.R.; López, D. Strong Casimir Force Reduction through Metallic Surface Nanostructuring. Nat. Commun. 2013, 4, 2515. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Tang, L.; Ng, C.Y.; Messina, R.; Guizal, B.; Crosse, J.A.; Antezza, M.; Chan, C.T.; Chan, H.B. Strong Geometry Dependence of the Casimir Force between Interpenetrated Rectangular Gratings. Nat. Commun. 2021, 12, 600. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.T.; Taylor, A.J.; Yu, N. A Review of Metasurfaces: Physics and Applications. Rep. Prog. Phys. 2016, 79, 076401. [Google Scholar] [CrossRef] [PubMed]
- Kort-Kamp, W.J.M.; Azad, A.K.; Dalvit, D.A.R. Space-Time Quantum Metasurfaces. Phys. Rev. Lett. 2021, 127, 043603. [Google Scholar] [CrossRef]
- Qiu, C.W.; Zhang, T.; Hu, G.; Kivshar, Y. Quo Vadis, Metasurfaces? Nano Lett. 2021, 21, 5461–5474. [Google Scholar] [CrossRef]
- Rahi, S.J.; Emig, T.; Graham, N.; Jaffe, R.L.; Kardar, M. Scattering Theory Approach to Electrodynamic Casimir Forces. Phys. Rev. D 2009, 80, 085021. [Google Scholar] [CrossRef]
- Rahi, S.J.; Emig, T.; Jaffe, R.L. Geometry and Material Effects in Casimir Physics-Scattering Theory. In Casimir Physics; Dalvit, D., Milonni, P., Roberts, D., da Rosa, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 129–174. [Google Scholar] [CrossRef]
- Lambrecht, A.; Canaguier-Durand, A.; Guérout, R.; Reynaud, S. Casimir Effect in the Scattering Approach: Correlations between Material Properties, Temperature and Geometry. In Casimir Physics; Dalvit, D., Milonni, P., Roberts, D., da Rosa, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 97–127. [Google Scholar] [CrossRef]
- Ingold, G.L.; Lambrecht, A. Casimir Effect from a Scattering Approach. Am. J. Phys. 2015, 83, 156–162. [Google Scholar] [CrossRef]
- Busch, K.; von Freymann, G.; Linden, S.; Mingaleev, S.; Tkeshelashvili, L.; Wegener, M. Periodic Nanostructures for Photonics. Phys. Rep. 2007, 444, 101–202. [Google Scholar] [CrossRef]
- Matsubara, T. A New Approach to Quantum Statistical Mechanics. Prog. Theor. Phys. 1955, 14, 351–378. [Google Scholar] [CrossRef]
- Chiu, H.C.; Klimchitskaya, G.L.; Marachevsky, V.N.; Mostepanenko, V.M.; Mohideen, U. Lateral Casimir Force between Sinusoidally Corrugated Surfaces: Asymmetric Profiles, Deviations from the Proximity Force Approximation, and Comparison with Exact Theory. Phys. Rev. B 2010, 81, 115417. [Google Scholar] [CrossRef]
- Antezza, M.; Pitaevskii, L.P.; Stringari, S.; Svetovoy, V.B. Casimir-Lifshitz Force Out of Thermal Equilibrium and Asymptotic Nonadditivity. Phys. Rev. Lett. 2006, 97, 223203. [Google Scholar] [CrossRef]
- Volokitin, A.I.; Persson, B.N.J. Near-Field Radiative Heat Transfer and Noncontact Friction. Rev. Mod. Phys. 2007, 79, 1291–1329. [Google Scholar] [CrossRef]
- Reiche, D.; Intravaia, F.; Busch, K. Wading through the Void: Exploring Quantum Friction and Nonequilibrium fluctuations. APL Photon. 2022, 7, 030902. [Google Scholar] [CrossRef]
- Antezza, M.; Pitaevskii, L.P.; Stringari, S.; Svetovoy, V.B. Casimir–Lifshitz Force out of Thermal Equilibrium. Phys. Rev. A 2008, 77, 022901. [Google Scholar] [CrossRef]
- Obrecht, J.M.; Wild, R.J.; Antezza, M.; Pitaevskii, L.P.; Stringari, S.; Cornell, E.A. Measurement of the Temperature Dependence of the Casimir-Polder Force. Phys. Rev. Lett. 2007, 98, 063201. [Google Scholar] [CrossRef]
- Messina, R.; Antezza, M. Scattering-Matrix Approach to Casimir–Lifshitz Force and Heat Transfer out of Thermal Equilibrium between Arbitrary Bodies. Phys. Rev. A 2011, 84, 042102. [Google Scholar] [CrossRef]
- Bartolo, N.; Messina, R.; Dalvit, D.A.R.; Intravaia, F. Nonequilibrium Casimir–Polder Plasmonic Interactions. Phys. Rev. A 2016, 93, 042111. [Google Scholar] [CrossRef]
- Fuchs, S.; Bennett, R.; Krems, R.V.; Buhmann, S.Y. Nonadditivity of Optical and Casimir-Polder Potentials. Phys. Rev. Lett. 2018, 121, 083603. [Google Scholar] [CrossRef] [PubMed]
- Bimonte, G.; Emig, T.; Krüger, M.; Kardar, M. Dilution and Resonance-enhanced Repulsion in Nonequilibrium Fluctuation Forces. Phys. Rev. A 2011, 84, 042503. [Google Scholar] [CrossRef]
- Zhang, B.; Henkel, C.; Haller, E.; Wildermuth, S.; Hofferberth, S.; Krüger, P.; Schmiedmayer, J. Relevance of Sub-Surface Chip Layers for the Lifetime of Magnetically Trapped Atoms. Eur. Phys. J. D 2005, 35, 97–104. [Google Scholar] [CrossRef]
- Yariv, A.; Yeh, P. Optical Waves in Crystals. Propagation and Control of Laser Radiation; John Wiley & Sons: New York, NY, USA, 1983. [Google Scholar]
- Mendoza Herrera, L.J.; Arboleda, D.M.; Santillán, J.M.J.; Fernández van Raap, M.B.; Scaffardi, L.B.; Schinca, D.C. Nanoscale Dielectric Function of Fe, Pt, Ti, Ta, Al, and V: Application to Characterization of Al Nanoparticles Synthesized by Fs Laser Ablation. Plasmonics 2017, 12, 1813–1824. [Google Scholar] [CrossRef]
- Ordal, M.A.; Bell, R.J.; Alexander, R.W.; Long, L.L.; Querry, M.R. Optical Properties of Fourteen Metals in the Infrared and Far Infrared: Al, Co, Cu, Au, Fe, Pb, Mo, Ni, Pd, Pt, Ag, Ti, V, and W. Appl. Opt. 1985, 24, 4493–4499. [Google Scholar] [CrossRef] [PubMed]
- Pirozhenko, I.; Lambrecht, A. Influence of Slab Thickness on the Casimir Force. Phys. Rev. A 2008, 77, 013811. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon Cosmology. Phys. Rev. D 2004, 69, 044026. [Google Scholar] [CrossRef]
- Khoury, J. Les Houches Lectures on Physics beyond the Standard Model of Cosmology. arXiv 2013, arXiv:1312.2006. [Google Scholar] [CrossRef]
- Brax, P.; Burrage, C.; Davis, A.C. Screening Fifth Forces in K-Essence and DBI Models. J. Cosmol. Astropart. Phys. 2013, 1, 020. [Google Scholar] [CrossRef]
- Brax, P.; Valageas, P. K-Mouflage Cosmology: The Background Evolution. Phys. Rev. D 2014, 90, 023507. [Google Scholar] [CrossRef]
- Vainshtein, A.I. To the Problem of Nonvanishing Gravitation Mass. Phys. Lett. B 1972, 39, 393–394. [Google Scholar] [CrossRef]
- Damour, T.; Polyakov, A.M. The String Dilaton and a Least Coupling Principle. Nucl. Phys. 1994, B423, 532–558. [Google Scholar] [CrossRef]
- Brax, P.; van de Bruck, C.; Davis, A.C.; Shaw, D. Dilaton and Modified Gravity. Phys. Rev. D 2010, 82, 063519. [Google Scholar] [CrossRef]
- Sakstein, J.A. Astrophysical Tests of Modified Gravity. Ph.D. Thesis, Downing College, University of Cambridge, Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Cronenberg, G.; Brax, P.; Filter, H.; Geltenbort, P.; Jenke, T.; Pignol, G.; Pitschmann, M.; Thalhammer, M.; Abele, H. Acoustic Rabi Oscillations between Gravitational Quantum States and Impact on Symmetron Dark Energy. Nat. Phys. 2018, 14, 1022–1026. [Google Scholar] [CrossRef]
- Brax, P.; Pitschmann, M. Exact Solutions to Nonlinear Symmetron Theory: One- and Two-Mirror Systems. Phys. Rev. D 2018, 97, 064015. [Google Scholar] [CrossRef]
- Pitschmann, M. Exact Solutions to Nonlinear Symmetron Theory: One- and Two-Mirror Systems. II. Phys. Rev. D 2021, 103, 084013. [Google Scholar] [CrossRef]
- Burrage, C.; Sakstein, J. Tests of Chameleon Gravity. Living Rev. Relativ. 2018, 21, 1. [Google Scholar] [CrossRef]
- Gasperini, M.; Piazza, F.; Veneziano, G. Quintessence as a Runaway Dilaton. Phys. Rev. D 2001, 65, 023508. [Google Scholar] [CrossRef]
- Damour, T.; Piazza, F.; Veneziano, G. Violations of the Equivalence Principle in a Dilaton Runaway Scenario. Phys. Rev. D 2002, 66, 046007. [Google Scholar] [CrossRef]
- Damour, T.; Piazza, F.; Veneziano, G. Runaway Dilaton and Equivalence Principle Violations. Phys. Rev. Lett. 2002, 89, 081601. [Google Scholar] [CrossRef] [PubMed]
- Brax, P.; Burrage, C.; Davis, A.C. Laboratory Constraints. Int. J. Mod. Phys. D 2018, 27, 1848009. [Google Scholar] [CrossRef]
- Burrage, C.; Copeland, E.J.; Hinds, E.A. Probing Dark Energy with Atom Interferometry. J. Cosmol. Astropart. Phys. 2015, 2015, 042. [Google Scholar] [CrossRef]
- Burrage, C.; Copeland, E.J. Using Atom Interferometry to Detect Dark Energy. Contemp. Phys. 2016, 57, 164–176. [Google Scholar] [CrossRef]
- Upadhye, A. Symmetron Dark Energy in Laboratory Experiments. Phys. Rev. Lett. 2013, 110, 031301. [Google Scholar] [CrossRef] [PubMed]
- Jenke, T.; Bosina, J.; Micko, J.; Pitschmann, M.; Sedmik, R.; Abele, H. Gravity Resonance Spectroscopy and Dark Energy Symmetron Fields. Eur. Phys. J. Spec. Top. 2021, 230, 1131–1136. [Google Scholar] [CrossRef]
- Brax, P.; Davis, A.C.; Elder, B. Screened Scalar Fields in Hydrogen and Muonium. Phys. Rev. D 2023, 107, 044008. [Google Scholar] [CrossRef]
- Fischer, H.; Käding, C.; Lemmel, H.; Sponar, S.; Pitschmann, M. Search for Dark Energy with Neutron Interferometry. Prog. Theor. Exp. Phys. 2024, 2, 023E02. [Google Scholar] [CrossRef]
- Brax, P.; Fischer, H.; Käding, C.; Pitschmann, M. The Environment Dependent Dilaton in the Laboratory and the Solar System. Eur. Phys. J. C 2022, 82, 934. [Google Scholar] [CrossRef]
- Ivanov, A.N.; Cronenberg, G.; Höllwieser, R.; Jenke, T.; Pitschmann, M.; Wellenzohn, M.; Abele, H. Exact Solution for Chameleon Field, Self-Coupled through the Ratra–Peebles Potential with n = 1 and Confined between Two Parallel Plates. Phys. Rev. D 2016, 94, 085005. [Google Scholar] [CrossRef]
- Keysight Technologies (Santa Rosa, CA, USA). Private communication, 2023.














| Error | Symbol | Value [V] | Error | |
|---|---|---|---|---|
| Type | ||||
| Detector noise | stat. | |||
| DAQ input noise | stat. | |||
| Laser power fluct. (canceled) | 0 | 0 | stat. | |
| Laser bandwidth | stat. | |||
| Laser frequency noise | stat. | |||
| Seismic vibrations | stat. | |||
| Tot. ref. measurement noise (72 h) | stat. | |||
| DAQ input error | syst. | |||
| Laser wavelength drift | syst. | |||
| Cavity size drift | syst. | |||
| Tot. ref. measurement error (72 h) | syst. | |||
| DAQ calibration | const. | |||
| Tot. ref. measurement error (72 h) | const. | |||
| Error | Symbol | Value [Hz] | Error | |
|---|---|---|---|---|
| Type | ||||
| Signal noise | stat. | |||
| f-detection | stat. | |||
| PLL frequency noise | stat. | |||
| Signal drift | syst. | |||
| PLL phase stability | syst. | |||
| Resonance freq. error | syst. | |||
| Signal noise | const. | |||
| PLL phase error | const. | |||
| Resonance freq. error | const. | |||
| Error | Symbol | Value [N/m3] | Error | |
|---|---|---|---|---|
| Type | ||||
| Frequency detection error | stat. | |||
| Mass calibr. uncertainty | syst. | |||
| Resonance freq. uncert. | syst. | |||
| Frequency detection error | syst. | |||
| Mass calibration error | const. | |||
| Resonance freq. error | const. | |||
| Frequency detection error | const. | |||
| Error | Symbol | Value [N/m2] | Error | |
|---|---|---|---|---|
| Type | ||||
| Force gradient error | stat. | |||
| DC signal error | stat. | |||
| Zero force DC signal error | stat. | |||
| Mass calibr. uncertainty | syst. | |||
| Resonance freq. uncertainty | syst. | |||
| Cavity size error | syst. | |||
| Wavelength drift | syst. | |||
| Fringe amplitude uncertainty | syst. | |||
| Force gradient error | syst. | |||
| DC signal error | syst. | |||
| Zero force DC signal error | syst. | |||
| Mass cal. uncertainty | const. | |||
| Resonance freq. uncertainty | const. | |||
| Cavity size error | const. | |||
| Wavelength accuracy | const. | |||
| Force gradient error | const. | |||
| DC signal error | const. | |||
| Zero force DC signal error | const. | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haghmoradi, H.; Fischer, H.; Bertolini, A.; Galić, I.; Intravaia, F.; Pitschmann, M.; Schimpl, R.A.; Sedmik, R.I.P. Force Metrology with Plane Parallel Plates: Final Design Review and Outlook. Physics 2024, 6, 690-741. https://doi.org/10.3390/physics6020045
Haghmoradi H, Fischer H, Bertolini A, Galić I, Intravaia F, Pitschmann M, Schimpl RA, Sedmik RIP. Force Metrology with Plane Parallel Plates: Final Design Review and Outlook. Physics. 2024; 6(2):690-741. https://doi.org/10.3390/physics6020045
Chicago/Turabian StyleHaghmoradi, Hamid, Hauke Fischer, Alessandro Bertolini, Ivica Galić, Francesco Intravaia, Mario Pitschmann, Raphael A. Schimpl, and René I. P. Sedmik. 2024. "Force Metrology with Plane Parallel Plates: Final Design Review and Outlook" Physics 6, no. 2: 690-741. https://doi.org/10.3390/physics6020045
APA StyleHaghmoradi, H., Fischer, H., Bertolini, A., Galić, I., Intravaia, F., Pitschmann, M., Schimpl, R. A., & Sedmik, R. I. P. (2024). Force Metrology with Plane Parallel Plates: Final Design Review and Outlook. Physics, 6(2), 690-741. https://doi.org/10.3390/physics6020045





