Simulative Assessment of Novel Parallel-Hybrid-Electric Powertrains: Consideration of Transmission System Power Losses
Abstract
:1. Introduction
2. Novel Parallel-Hybrid-Electric Powertrain Topology
Optimization-Based Initial Draft of a 3D Design for Powertrain Topologies
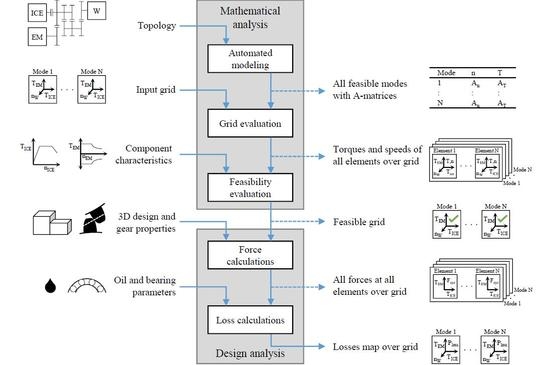
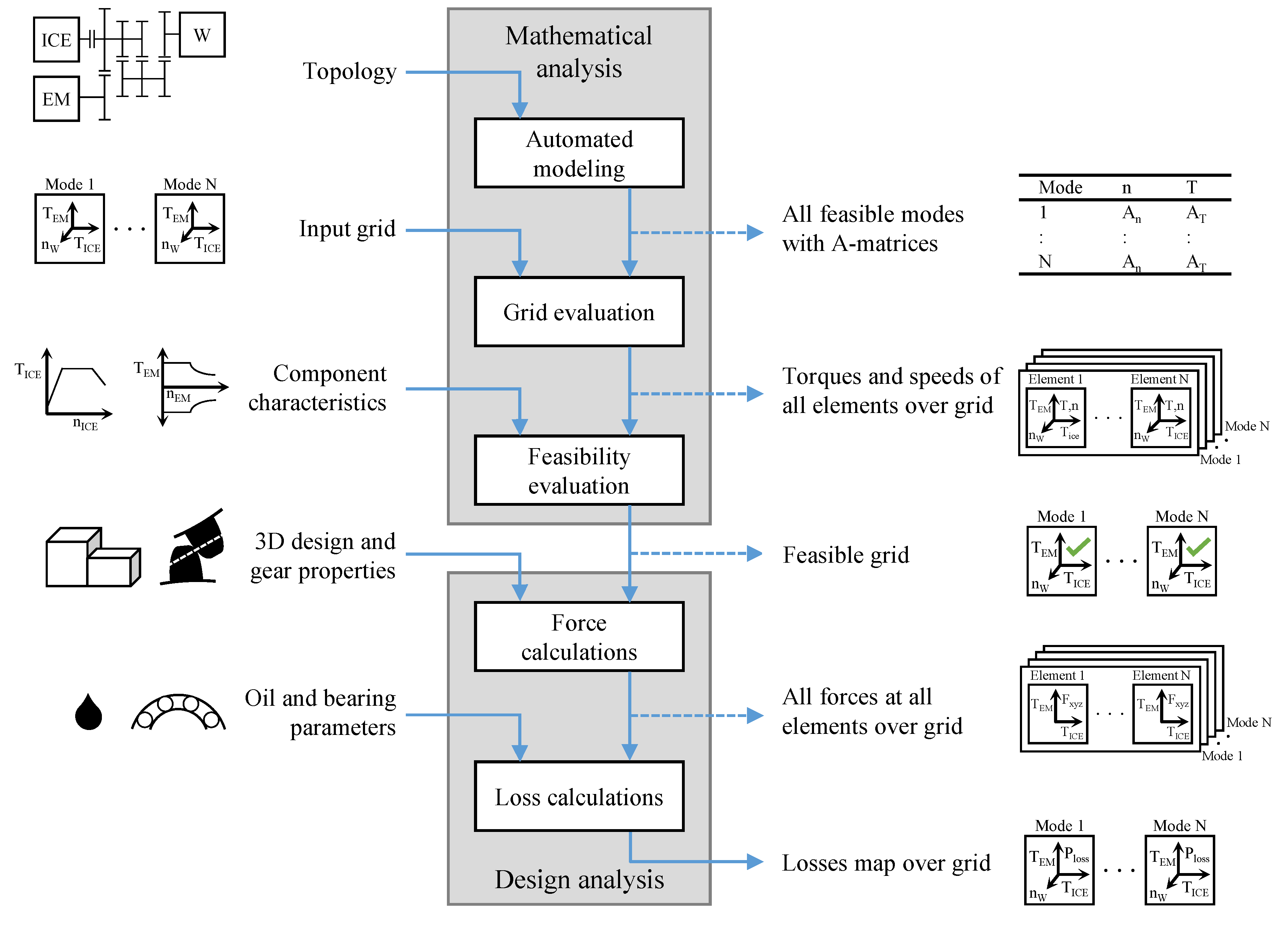
3. MIMO-Transmission Systems Power Loss Estimation Method for Novel Parallel-Hybrid-Electric Powertrains
3.1. Mathematical Analysis of General Hybrid-Electric Powertrain Topologies
3.1.1. Automated Modeling
3.1.2. Grid Evaluation
3.1.3. Feasibility Evaluation
3.2. Design Analysis: Transmission Power Loss Calculation
3.2.1. Force Calculations
3.2.2. Loss Calculations
3.3. Resulting Multidimensional Transmission System Power Loss Maps
4. Simulative Assessment of Parallel-Hybrid-Electric Powertrains
4.1. Operating Strategy
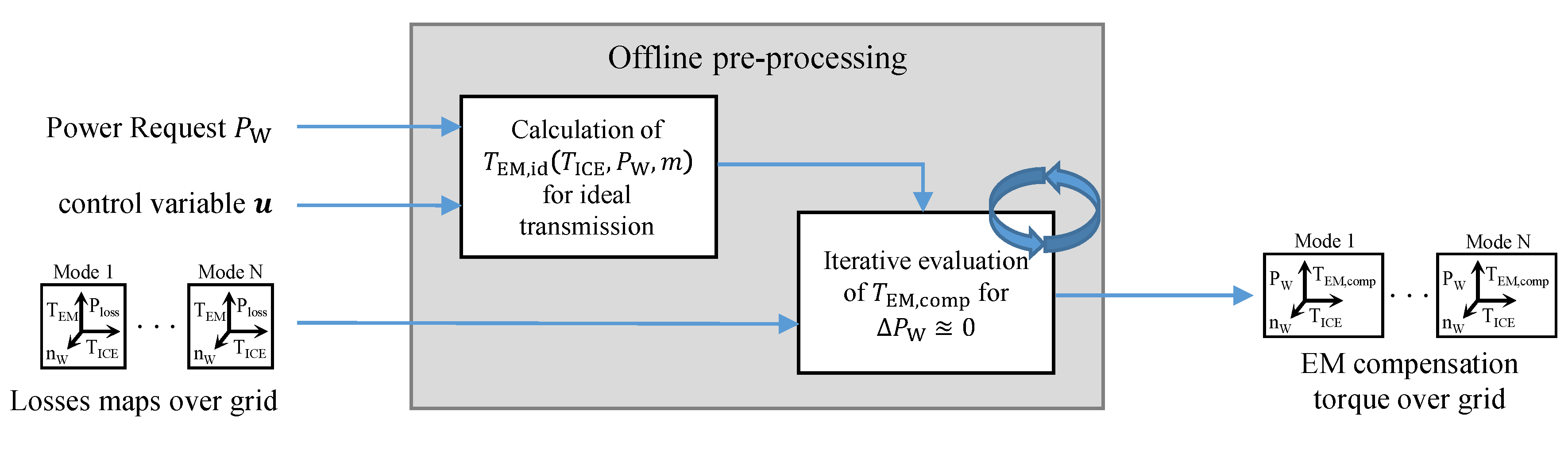
4.2. Consideration of Multidimensional Transmission Power Losses in the Operating Strategy
5. Case Study
5.1. Boundary Conditions and Assumptions
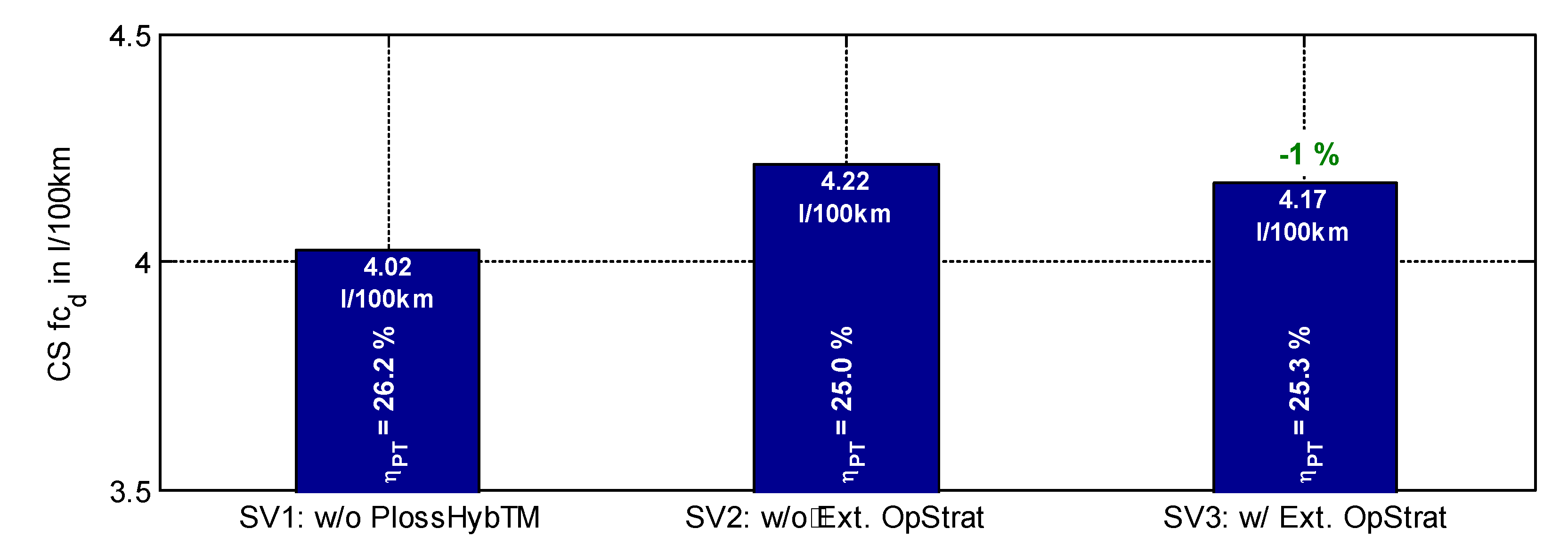
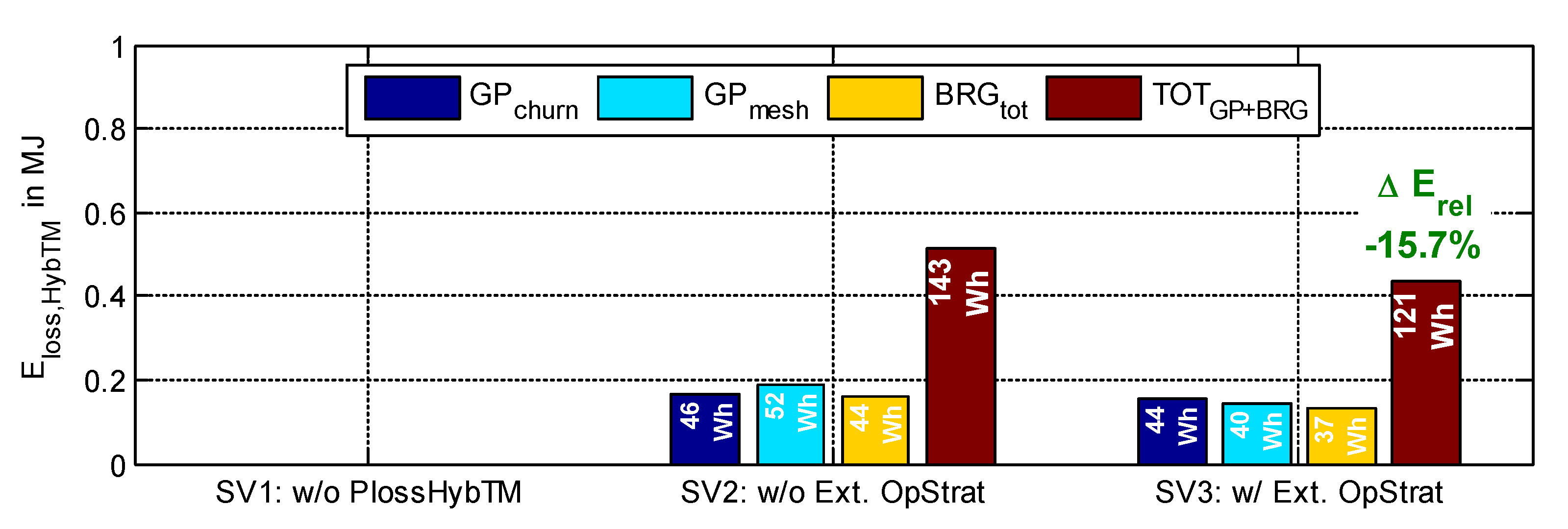
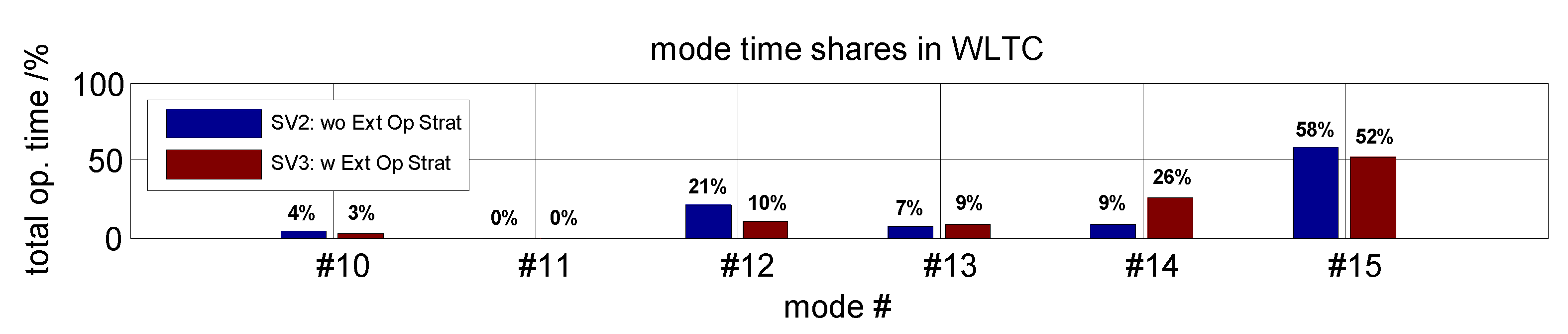
5.2. Results of the Simulative Assessment
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Silvas, E.; Hofman, T.; Murgovski, N.; Etman, L.F.P.; Steinbuch, M. Review of Optimization Strategies for System-Level Design in Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2017, 66, 57–70. [Google Scholar] [CrossRef] [Green Version]
- Hofmann, P. Hybridfahrzeuge: Ein Alternatives Antriebssystem für die Zukunft, 2nd ed.; Springer: Wien, Austria, 2014. [Google Scholar]
- Schleiffer, J.-E.; Lange, A.; Rinderknecht, S.; Kücükay, F. BEREIT: Optimization of Parallel Hybrid Electric Vehicle (HEV) Fleets. CTI MAG 2015, 2015, 25–28. [Google Scholar]
- Nüesch, T.; Cerofolini, A.; Mancini, G.; Cavina, N.; Onder, C.; Guzzella, L. Equivalent Consumption Minimization Strategy for the Control of Real Driving NOx Emissions of a Diesel Hybrid Electric Vehicle. Energies 2014, 7, 3148–3178. [Google Scholar] [CrossRef] [Green Version]
- Meier, T. Multikriterielle Optimierung hybrider Antriebsstränge Mittels Statistischer Versuchsplanung. Ph.D. Thesis, TU Darmstadt, Darmstadt, Germany, 2014. [Google Scholar]
- Danzer, C. Systematische Synthese, Variation, Simulation und Bewertung von Mehrgang- und Mehrantrieb-Systemen Rein Elektrischer und Hybrider Fahrzeugantriebsstränge. Ph.D. Thesis, TU Chemnitz, Chemnitz, Germany, 2016. [Google Scholar]
- Seidel, T.; Lange, A.; Küçükay, F. DHT concepts based on DCT design. In Drivetrain for Vehicles 2017; VDI: Bonn, Germany, 2017; Volume 2313. [Google Scholar]
- Brouwer, M.; Schleiffer, J.-E. Hybrid Drive Device for a Motor Vehicle. DE102016002863A1, 30 November 2016. [Google Scholar]
- Changenet, C.; Oviedo-Marlot, X.; Velex, P. Power Loss Predictions in Geared Transmissions Using Thermal Networks-Applications to a Six-Speed Manual Gearbox. J. Mech. Des. 2005, 128, 618–625. [Google Scholar] [CrossRef]
- Shen, Y.; Rinderknecht, S. A method on modelling and analyzing the power losses in vehicle transmission. Forsch. Ing. 2018, 82, 261–270. [Google Scholar] [CrossRef]
- Van Harselaar, W.; Hofman, T.; Brouwer, M. Automated Dynamic Modeling of Arbitrary Hybrid and Electric Drivetrain Topologies. IEEE Trans. Veh. Technol. 2018, 67, 6921–6934. [Google Scholar] [CrossRef]
- Naunheimer, H.; Fietkau, P.; Lechner, G. Automotive Transmissions: Fundamentals, Selection, Design, and Application, 2nd ed.; Springer: Heidelberg, Germany; New York, NY, USA, 2011. [Google Scholar]
- ISO/TR 14179-2:2001. Gears—Thermal capacity—Part 2: Thermal Load-Carrying Capacity; ISO: Geneva, Switzerland, 2001. [Google Scholar]
- SKF. Bearing Friction, Power Loss and Starting Torque. Available online: https://www.skf.com/binary/21-299767/0901d1968065e9e7-The-SKF-model-for-calculating-the-frictional-movement_tcm_12-299767.pdf (accessed on 2 March 2020).
- Winke, F.; Bargende, M. Dynamic Simulation of Urban Hybrid Electric Vehicles. MTZ Worldw. 2013, 74, 56–63. [Google Scholar] [CrossRef]
- Paganelli, G.; Delprat, S.; Guerra, T.M.; Rimaux, J.; Santin, J.J. Equivalent consumption minimization strategy for parallel hybrid powertrains. In Proceedings of the Vehicular Technology Conference, IEEE 55th Vehicular Technology Conference, VTC Spring 2002, Birmingham, AL, USA, 6–9 May 2002; Volume 4, pp. 2076–2081. [Google Scholar]
- Serrao, L.; Onori, S.; Rizzoni, G. A Comparative Analysis of Energy Management Strategies for Hybrid Electric Vehicles. J. Dyn. Sys. Meas. Control 2011, 133, 031012. [Google Scholar] [CrossRef] [Green Version]
- Koot, M.; Kessels, J.T.B.A.; de Jager, B.; Heemels, W.P.M.H.; van den Bosch, P.P.J.; Steinbuch, M. Energy Management Strategies for Vehicular Electric Power Systems. IEEE Trans. Veh. Technol. 2005, 54, 771–782. [Google Scholar] [CrossRef]
- Musardo, C.; Rizzoni, G.; Staccia, B. A-ECMS: An Adaptive Algorithm for Hybrid Electric Vehicle Energy Management. In Proceedings of the 44th IEEE Conference on Decision and Control, European Control Conference 2005, Seville, Spain, 12–15 December 2005; pp. 1816–1823. [Google Scholar]
- Alles, J. Erweiterung von Modell und Betriebsstrategie zur simulativen Bewertung von Parallelhybrid-fahrzeug Varianten. Master’s Thesis, TU Darmstadt, Darmstadt, Germany, 2016. [Google Scholar]
- Lange, A. Optimierung modularer Elektro- und Hybridantriebe. Ph.D. Thesis, TU Braunschweig, Braunschweig, Germany, 2018. [Google Scholar]
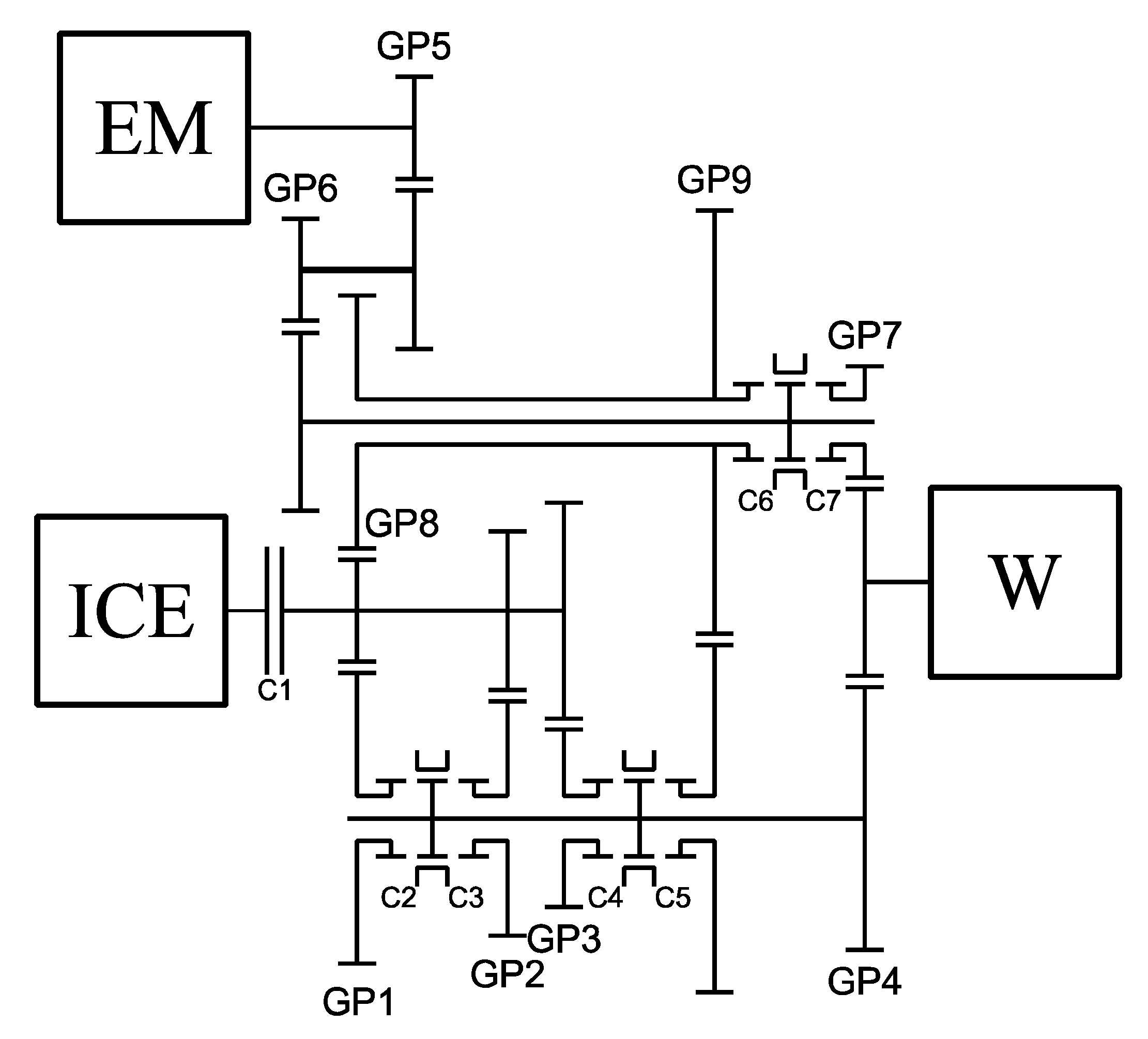

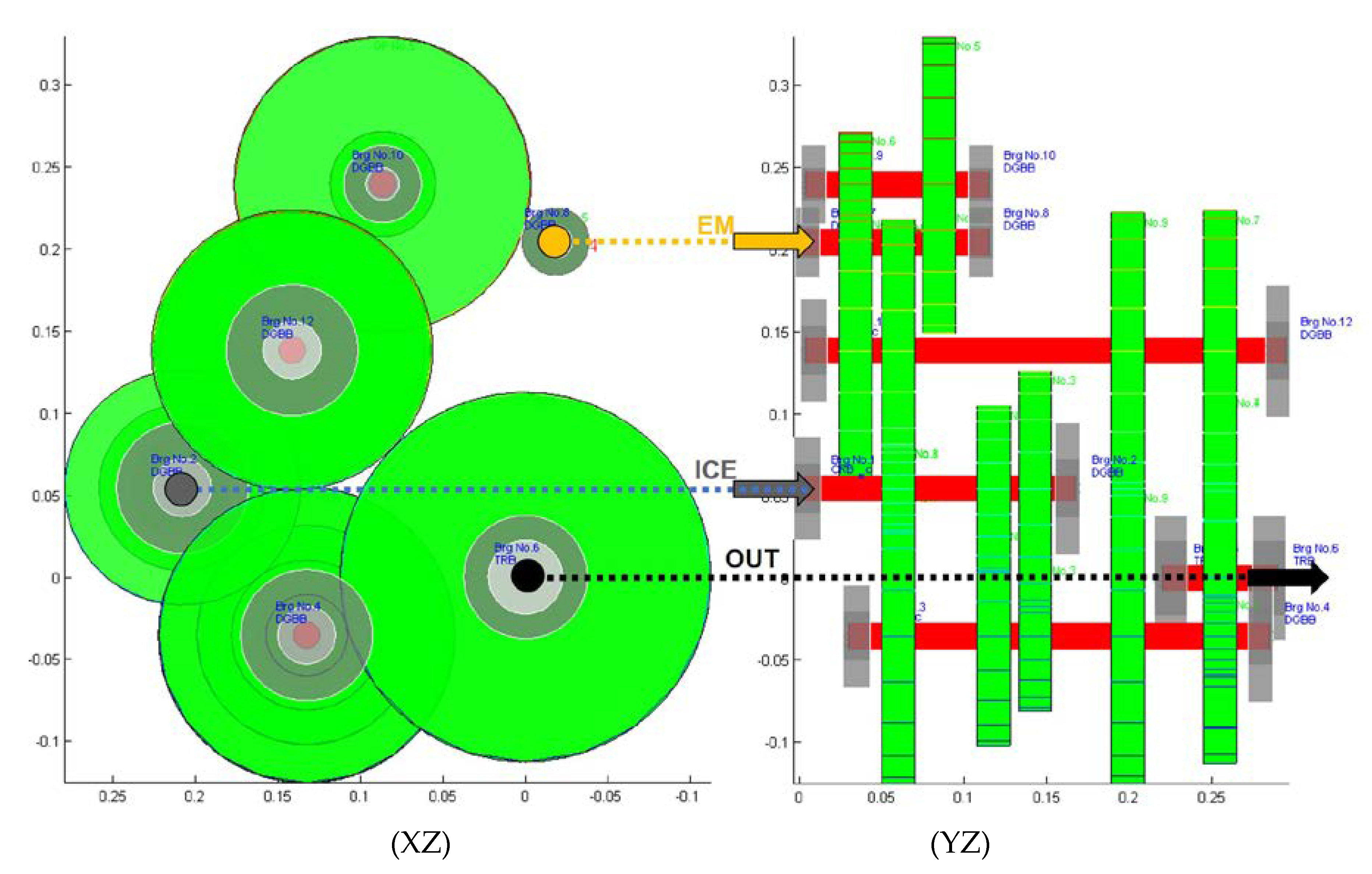



| Transmission Mode # | Mode Type | C1 | C2 | C3 | C4 | C5 | C6 | C7 | ICE Gear | EM Gear |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ICE only | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | - |
| 2 | ICE only | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 2 | - |
| 3 | ICE only | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 3 | - |
| 4 | ICE only | 1 | 0 | 0 | 0 | 1 | 0 | 0 | R | - |
| 5 | EV | 0 | 1 | 0 | 0 | 0 | 1 | 0 | - | P2–1 |
| 6 | EV | 0 | 0 | 0 | 0 | 1 | 1 | 0 | - | R |
| 7 | EV | 0 | 0 | 1 | 0 | 0 | 1 | 0 | - | P2–2 |
| 8 | EV | 0 | 0 | 0 | 0 | 0 | 0 | 1 | - | P3 |
| 9 | EV | 0 | 0 | 0 | 1 | 0 | 1 | 0 | - | P2–3 |
| 10 | Fixed gear parallel | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | P2–1 |
| 11 | Fixed gear parallel | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | P3 |
| 12 | Fixed gear parallel | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 2 | P2–2 |
| 13 | Fixed gear parallel | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 2 | P3 |
| 14 | Fixed gear parallel | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 3 | P3 |
| 15 | Fixed gear parallel | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 3 | P2–3 |
| 16 | Fixed gear parallel | 1 | 0 | 0 | 0 | 1 | 1 | 0 | R | R |
| 17 | Fixed gear parallel | 1 | 0 | 0 | 0 | 1 | 0 | 1 | R | P3 |
| 18 | Charge | 1 | 0 | 0 | 0 | 0 | 1 | 0 | - | - |
| Parameter | Value | Unit | |
|---|---|---|---|
| Vehicle mass | 1700 | kg | |
| Air resistance coefficient | 0.632 | m² | |
| Dynamic wheel radius | 0.31 | m | |
| Rolling resistance coefficient | 0.01 | - | |
| Power demand for auxiliaries | 800 | W |
| SV2: w/o Extended Operating Strategy | SV3: w/Extended Operating Strategy | ||
|---|---|---|---|
| Transmission Power Losses | |||
| Operating Strategy | Local optimal distribution of only on basis of
& | Local optimal distribution of only on basis of & | Extended local optimal distribution under consideration of |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schleiffer, J.-E.; van Harselaar, W.; Shen, Y.; Rinderknecht, S. Simulative Assessment of Novel Parallel-Hybrid-Electric Powertrains: Consideration of Transmission System Power Losses. Vehicles 2020, 2, 173-190. https://doi.org/10.3390/vehicles2010010
Schleiffer J-E, van Harselaar W, Shen Y, Rinderknecht S. Simulative Assessment of Novel Parallel-Hybrid-Electric Powertrains: Consideration of Transmission System Power Losses. Vehicles. 2020; 2(1):173-190. https://doi.org/10.3390/vehicles2010010
Chicago/Turabian StyleSchleiffer, Jean-Eric, Wilco van Harselaar, Ye Shen, and Stephan Rinderknecht. 2020. "Simulative Assessment of Novel Parallel-Hybrid-Electric Powertrains: Consideration of Transmission System Power Losses" Vehicles 2, no. 1: 173-190. https://doi.org/10.3390/vehicles2010010
APA StyleSchleiffer, J.-E., van Harselaar, W., Shen, Y., & Rinderknecht, S. (2020). Simulative Assessment of Novel Parallel-Hybrid-Electric Powertrains: Consideration of Transmission System Power Losses. Vehicles, 2(1), 173-190. https://doi.org/10.3390/vehicles2010010