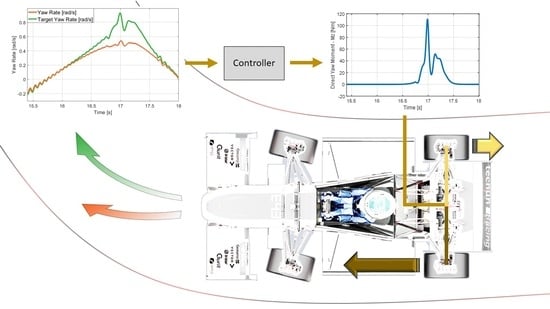
Comparison of Typical Controllers for Direct Yaw Moment Control Applied on an Electric Race Car
Abstract
:1. Introduction
2. Vehicle Modelling
2.1. Vehicle Specifications
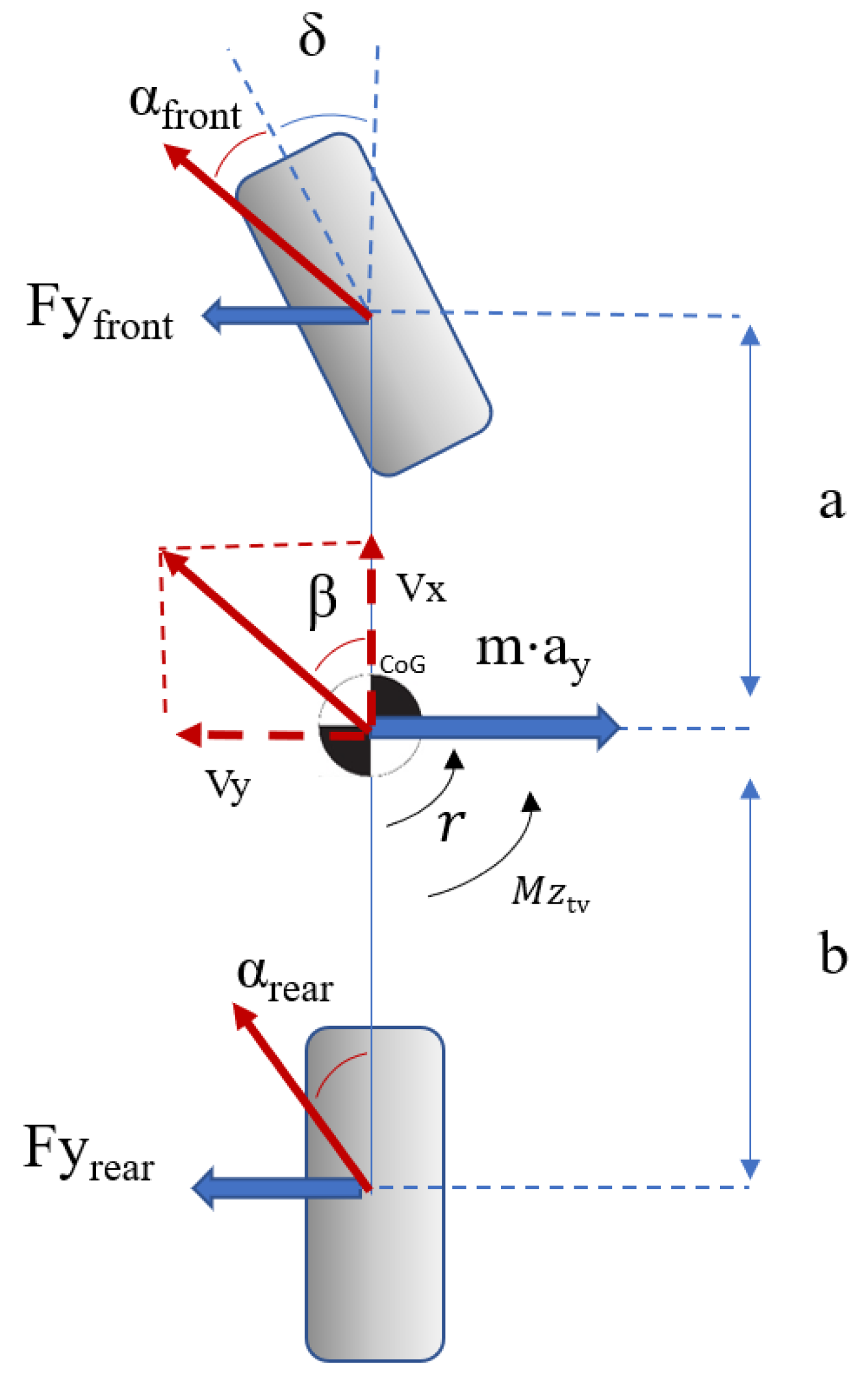
2.2. Linearized Bicycle Model
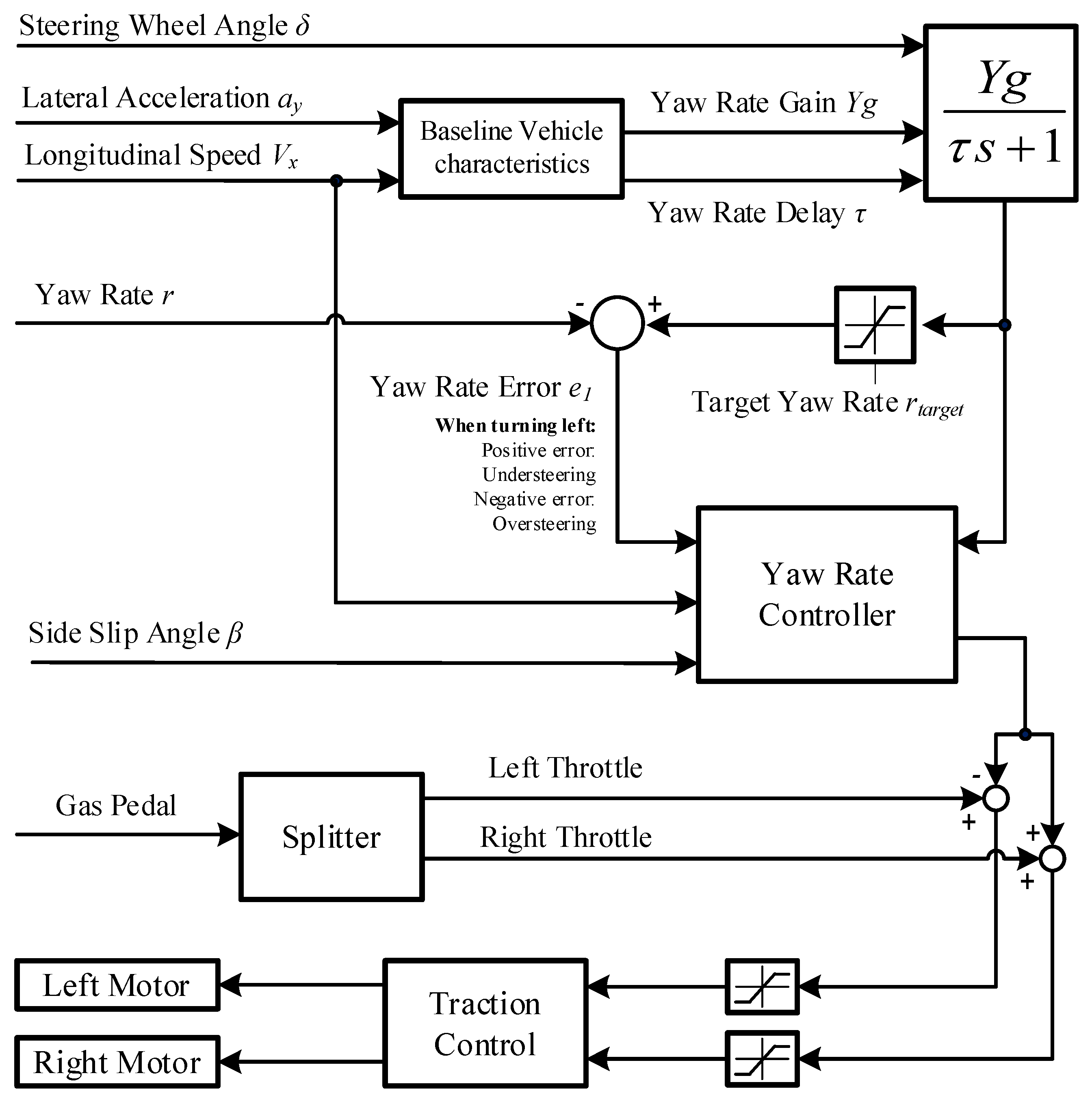
3. Controllers Description
3.1. PID
3.2. Sliding Mode Controller
3.3. Linear Quadratic Regulator
3.4. Linear Model Predictive Control
3.5. Linear Parameter Varying Model Predictive Control
4. Simulation Model
4.1. Vehicle Parameters
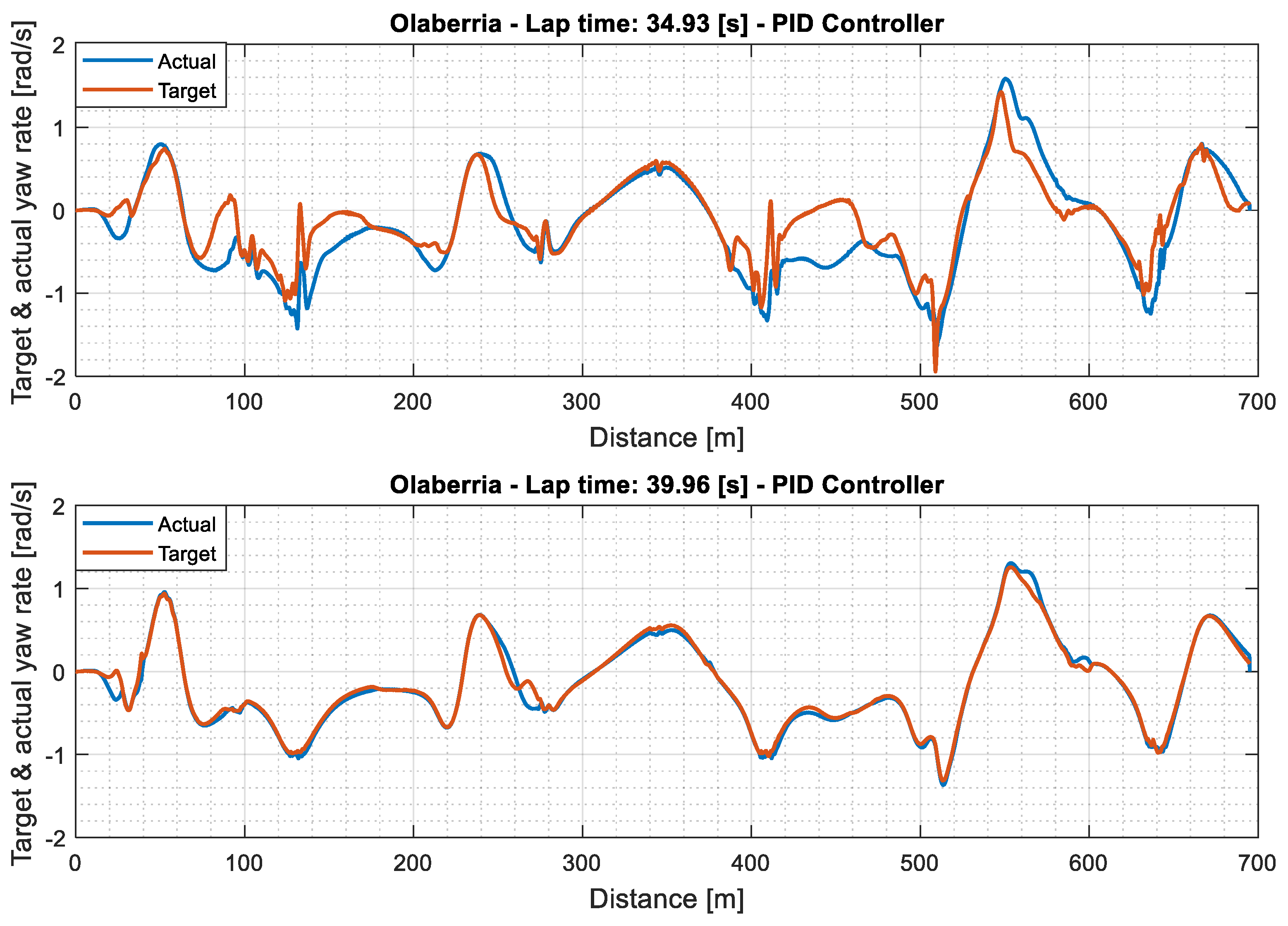
4.2. Olaberria Circuit
4.3. Hockenheim 2010 Formula Student Endurance Track
5. Results
- Integral of the absolute yaw rate error (IAE):
- Integral of the absolute value of the control action (IACA):
- The braking locations at Hockenheim require less combined G (the vehicleheads straight when braking).
- Vehicle speed at the braking areas at Hockenheim is lower than in the critical braking point of Olaberria, where the front axle lock occurs. At lower speed, the ratio of apparent front wheels weight over the apparent weight on the rear wheels is higher, so it is more difficult to lock the front wheels.
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Crolla, D.A.; Cao, D. The impact of hybrid and electric powertrains on vehicle dynamics, control systems and energy regeneration. Veh. Syst. Dyn. 2012, 50, 95–109. [Google Scholar] [CrossRef] [Green Version]
- Shyrokau, B.; Wang, D.; Savitski, D.; Hoepping, K.; Ivanov, V. Vehicle motion control with subsystem prioritization. Mechatronics 2015, 30, 297–315. [Google Scholar] [CrossRef]
- Shyrokau, B.; Savitski, D.; Wang, D. Influence of Active Subsystems on Electric Vehicle Behavior and Energy Characteristics. In SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2014; Volume 1. [Google Scholar]
- Ivanov, V.; Savitski, D.; Shyrokau, B. A Survey of Traction Control and Antilock Braking Systems of Full Electric Vehicles with Individually Controlled Electric Motors; IEEE Transactions on Vehicular Technology: Miami, FL, USA, 2015; Volume 64. [Google Scholar]
- Ghosh, J.; Tonoli, A.; Amati, N. A Torque Vectoring Strategy for Improving the Performance of a Rear Wheel Drive Electric Vehicle. In Proceedings of the 2015 IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19–22 October 2015; pp. 1–6. [Google Scholar]
- Sugano, T.; Fukuba, H.; Suetomi, T. A study of dynamics performance improvement by rear right and left independent drive system. Veh. Syst. Dyn. 2010, 48, 1285–1303. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, H.; Huang, Y.; Chen, H.; Guo, K.; Li, Q. An Analytical Approach to Improve Vehicle Maneuverability via Torque Vectoring Control: Theoretical Study and Experimental Validation. IEEE Trans. Veh. Technol. 2019, 68, 4514–4526. [Google Scholar] [CrossRef]
- Fu, C.; Hoseinnezhad, R.; Jazar, R.; Bab-Hadiashar, A.; Watkins, S. Electronic differential design for vehicle side-slip control. In Proceedings of the 2012 International Conference on Control, Automation and Information Sciences (ICCAIS), Saigon, Vietnam, 26–29 November 2012; pp. 306–310. [Google Scholar]
- Pinheiro, H.D.C.; Messana, A.; Sisca, L.; Ferraris, A.; Airale, A.G.; Carello, M. Torque Vectoring in Electric Vehicles with In-wheel Motors. Adv. Serv. Ind. Robot. 2019, 73, 3127–3136. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J. Vehicle Lateral Dynamics Control Through AFS/DYC and Robust Gain-Scheduling Approach. IEEE Trans. Veh. Technol. 2016, 65, 489–494. [Google Scholar] [CrossRef]
- Zainal, Z.; Rahiman, W.; Baharom, M.N.R. Yaw Rate and Sideslip Control using PID Controller for Double Lane Changing. J. Telecommun. Electron. Comput. Eng. 2017, 9, 99–103. [Google Scholar]
- De Novellis, L.; Sorniotti, A.; Gruber, P.; Orus, J.; Fortun, J.-M.R.; Theunissen, J.; De Smet, J. Direct yaw moment control actuated through electric drivetrains and friction brakes: Theoretical design and experimental assessment. Mechatronics 2015, 26, 1–15. [Google Scholar] [CrossRef] [Green Version]
- De Novellis, L.; Sorniotti, A.; Gruber, P. Wheel Torque Distribution Criteria for Electric Vehicles With Torque-Vectoring Differentials. IEEE Trans. Veh. Technol. 2013, 63, 1593–1602. [Google Scholar] [CrossRef] [Green Version]
- Lu, Q.; Gentile, P.; Tota, A.; Sorniotti, A.; Gruber, P.; Costamagna, F.; De Smet, J. Enhancing vehicle cornering limit through sideslip and yaw rate control. Mech. Syst. Signal Process. 2016, 75, 455–472. [Google Scholar] [CrossRef]
- Murua, A.M.; Bistue, G.; Rubio, A.; Gonzalez, J. A Direct Yaw-Moment Control Logic for an Electric 2WD Formula SAE Using an Error-Cube Proportional Derivative Controller. SAE Int. J. Connect. Autom. Veh. 2020, 3, 139–148. [Google Scholar] [CrossRef]
- De Novellis, L.; Sorniotti, A.; Gruber, P.; Pennycott, A. Comparison of Feedback Control Techniques for Torque-Vectoring Control of Fully Electric Vehicles. IEEE Trans. Veh. Technol. 2014, 63, 3612–3623. [Google Scholar] [CrossRef] [Green Version]
- Goggia, T.; Sorniotti, A.; De Novellis, L.; Ferrara, A.; Gruber, P.; Theunissen, J.; Steenbeke, D.; Knauder, B.; Zehetner, J. Integral Sliding Mode for the Torque-Vectoring Control of Fully Electric Vehicles: Theoretical Design and Experimental Assessment. IEEE Trans. Veh. Technol. 2015, 64, 1701–1715. [Google Scholar] [CrossRef]
- Ghosh, J.; Tonoli, A.; Amati, N. Improvement of Lap-Time of a Rear Wheel Drive Electric Racing Vehicle by a Novel Motor Torque Control Strategy. SAE Tech. Pap. Ser. 2017, 1. [Google Scholar] [CrossRef]
- Rieveley, R.J.; Minaker, B.P. Variable Torque Distribution Yaw Moment Control for Hybrid Powertrains. SAE Tech. Pap. Ser. 2007. [Google Scholar] [CrossRef]
- Canale, M.; Fagiano, L.; Ferrara, A.; Vecchio, C. Comparing Internal Model Control and Sliding-Mode Approaches for Vehicle Yaw Control. IEEE Trans. Intell. Transp. Syst. 2008, 10, 31–41. [Google Scholar] [CrossRef]
- Chae, M.; Hyun, Y.; Yi, K.; Nam, K. Dynamic Handling Characteristics Control of an in-Wheel-Motor Driven Electric Vehicle Based on Multiple Sliding Mode Control Approach. IEEE Access 2019, 7, 132448–132458. [Google Scholar] [CrossRef]
- Mousavinejad, E.; Han, Q.-L.; Yang, F.; Zhu, Y.; Vlacic, L. Integrated control of ground vehicles dynamics via advanced terminal sliding mode control. Veh. Syst. Dyn. 2016, 55, 268–294. [Google Scholar] [CrossRef]
- Truong, D.T.; Meywerk, M.; Tomaske, W. Torque vectoring for rear axle using Adaptive Sliding Mode Control. In Proceedings of the 2013 International Conference on Control, Automation and Information Sciences (ICCAIS), Nha Trang, Vietnam, 25–28 November 2013; pp. 328–333. [Google Scholar]
- Hamzah, N.; Aripin, M.K.; Sam, Y.M.; Selamat, H.; Ismail, M.F.; Selamat, H. Vehicle stability enhancement based on second order sliding mode control. In Proceedings of the 2012 IEEE International Conference on Control System, Computing and Engineering, Penang, Malaysia, 23–25 November 2012; pp. 580–585. [Google Scholar]
- Tota, A.; Lenzo, B.; Lu, Q.; Sorniotti, A.; Gruber, P.; Fallah, S.; Velardocchia, M.; Galvagno, E.; De Smet, J. On the Experimental Analysis of Integral Sliding Modes for Yaw Rate and Sideslip Control of an Electric Vehicle with Multiple Motors. Int. J. Automot. Technol. 2018, 19, 811–823. [Google Scholar] [CrossRef]
- Fadali, M.S.; Visioli, A. Optimal Control. In Digital Control Engineering; Elsevier BV: Amsterdam, The Netherlands, 2013; pp. 399–438. [Google Scholar]
- Van Zanten, A.T.; Erhardt, R.; Pfaff, G. VDC, The Vehicle Dynamics Control System of Bosch. In SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 1995. [Google Scholar]
- Van Zanten, A.T. Bosch ESP Systems: 5 Years of Experience. In SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2000. [Google Scholar]
- Esmailzadeh, E.; Goodarzi, A.; Vossoughi, G. Optimal yaw moment control law for improved vehicle handling. Mechatronics 2003, 13, 659–675. [Google Scholar] [CrossRef]
- Mirzaei, M. A new strategy for minimum usage of external yaw moment in vehicle dynamic control system. Transp. Res. Part C Emerg. Technol. 2010, 18, 213–224. [Google Scholar] [CrossRef]
- Wang, Z.; Montanaro, U.; Fallah, S.; Sorniotti, A.; Lenzo, B. A gain scheduled robust linear quadratic regulator for vehicle direct yaw moment Control. Mechatronics 2018, 51, 31–45. [Google Scholar] [CrossRef]
- Antunes, J.; Antunes, A.; Outeiro, P.; Cardeira, C.; Oliveira, P. Testing of a torque vectoring controller for a Formula Student prototype. Robot. Auton. Syst. 2019, 113, 56–62. [Google Scholar] [CrossRef]
- Yu, H.; Liang, W.; Kuang, M.; McGee, R. Vehicle handling assistant control system via independent rear axle torque biasing. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 695–700. [Google Scholar]
- Kaiser, G.; Holzmann, F.; Chrétien, B.; Korte, M.; Werner, H. Torque Vectoring with a feedback and feed forward controller-applied to a through the road hybrid electric vehicle. 2011 IEEE Intell. Veh. Symp. (IV) 2011, 448–453. [Google Scholar] [CrossRef]
- Kaiser, G.; Liu, Q.; Hoffmann, C.; Korte, M.; Werner, H.; Kaiser, G. Torque vectoring for an electric vehicle using an LPV drive controller and a torque and slip limiter. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 5016–5021. [Google Scholar]
- Jalali, K.; Uchida, T.; McPhee, J.; Lambert, S. Integrated Stability Control System for Electric Vehicles with In-wheel Motors using Soft Computing Techniques. SAE Int. J. Passeng. Cars Electron. Electr. Syst. 2009, 2, 109–119. [Google Scholar] [CrossRef]
- Jager, B.; Neugebauer, P.; Kriesten, R.; Parspour, N.; Gutenkunst, C. Torque-vectoring stability control of a four wheel drive electric vehicle. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015; Volume 2015-Augus, pp. 1018–1023. [Google Scholar]
- Jaafari, S.M.M.; Shirazi, K.H. Integrated Vehicle Dynamics Control Via Torque Vectoring Differential and Electronic Stability Control to Improve Vehicle Handling and Stability Performance. J. Dyn. Syst. Meas. Control. 2018, 140, 071003. [Google Scholar] [CrossRef]
- Parra, A.; Zubizarreta, A.; Pérez, J.; Dendaluce, M. Intelligent Torque Vectoring Approach for Electric Vehicles with Per-Wheel Motors. Complexity 2018, 2018, 7030184. [Google Scholar] [CrossRef] [Green Version]
- Canale, M.; Fagiano, L. Vehicle yaw control using a fast NMPC approach. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 5360–5365. [Google Scholar]
- Siampis, E.; Velenis, E.; Longo, S. Rear wheel torque vectoring model predictive control with velocity regulation for electric vehicles. Veh. Syst. Dyn. 2015, 53, 1555–1579. [Google Scholar] [CrossRef] [Green Version]
- Siampis, E.; Velenis, E.; Gariuolo, S.; Longo, S. A Real-Time Nonlinear Model Predictive Control Strategy for Stabilization of an Electric Vehicle at the Limits of Handling. IEEE Trans. Control. Syst. Technol. 2018, 26, 1982–1994. [Google Scholar] [CrossRef]
- Vasiljevic, G.; Bogdan, S. Model predictive control based torque vectoring algorithm for electric car with independent drives. In Proceedings of the 2016 24th Mediterranean Conference on Control and Automation (MED), Athens, Greece, 21–24 June 2016; pp. 316–321. [Google Scholar]
- Jalali, M.; Khajepour, A.; Chen, S.-K.; Litkouhi, B.B. Handling Delays in Yaw Rate Control of Electric Vehicles Using Model Predictive Control With Experimental Verification. J. Dyn. Syst. Meas. Control. 2017, 139, 121001. [Google Scholar] [CrossRef]
- Mikulas, E.; Gulan, M.; Takacs, G. Model Predictive Torque Vectoring Control for a Formula Student Electric Racing Car. In Proceedings of the 2018 European Control Conference (ECC), Limassol, Cyprus, 12–15 June 2018; pp. 581–588. [Google Scholar]
- Ferreau, H.J.; Kirches, C.; Potschka, A.; Bock, H.G.; Diehl, M. qpOASES: A parametric active-set algorithm for quadratic programming. Math. Program. Comput. 2014, 6, 327–363. [Google Scholar] [CrossRef]
- Houska, B.; Ferreau, H.J.; Diehl, M. ACADO toolkit-An open-source framework for automatic control and dynamic optimization. Optim. Control. Appl. Methods 2010, 32, 298–312. [Google Scholar] [CrossRef]
- Han, K.; Park, G.; Sankar, G.S.; Nam, K.; Choi, S.B. Model Predictive Control Framework for Improving Vehicle Cornering Performance Using Handling Characteristics. IEEE Trans. Intell. Transp. Syst. 2020, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Tahouni, A.; Mirzaei, M.; Najjari, B. Novel Constrained Nonlinear Control of Vehicle Dynamics Using Integrated Active Torque Vectoring and Electronic Stability Control. IEEE Trans. Veh. Technol. 2019, 68, 9564–9572. [Google Scholar] [CrossRef]
- Oh, K.; Joa, E.; Lee, J.; Yun, J.; Yi, K. Yaw Stability Control of 4WD Vehicles Based on Model Predictive Torque Vectoring with Physical Constraints. Int. J. Automot. Technol. 2019, 20, 923–932. [Google Scholar] [CrossRef]
- Parra, A.; Tavernini, D.; Gruber, P.; Sorniotti, A.; Zubizarreta, A.; Perez, J. On Nonlinear Model Predictive Control for Energy-Efficient Torque-Vectoring. IEEE Trans. Veh. Technol. 2021, 70, 173–188. [Google Scholar] [CrossRef]
- Milliken, W.F.; Milliken, D.L. Race car vehicles dynamics. Soc. Automot. Eng. 1994, 400, 16. [Google Scholar]
- Pacejka, H. Tire and Vehicle Dynamics, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2012; pp. 87–147. [Google Scholar]
- Murray, R.M. Optimization-Based Control; California Institute of Technology: Pasadena, CA, USA, 2009; pp. 111–128. [Google Scholar]
- Murua, A.M.; Camo, P.M.; Lozano, M.S. Modelado 3D Low-Cost para integrar en un simulador un circuito existente de karting mediante fotogrametría aérea con drones. DYNA 2021, 96, 73–78. [Google Scholar]
- Harsh, D.; Shyrokau, B. Tire Model with Temperature Effects for Formula SAE Vehicle. Appl. Sci. 2019, 9, 5328. [Google Scholar] [CrossRef] [Green Version]
- Pretagostini, F.; Ferranti, L.; Berardo, G.; Ivanov, V.; Shyrokau, B. Survey on Wheel Slip Control Design Strategies, Evaluation and Application to Antilock Braking Systems. IEEE Access 2020, 8, 10951–10970. [Google Scholar] [CrossRef]







| Ref(s). | FF 1 Terms | Comments |
|---|---|---|
| [5] | No | Reduces slip angle difference between front and rear axle to achieve maximum lateral acceleration. |
| [6] | Yes | Focuses on rear cornering stiffness to avoid instability, evaluates control using a driving simulator. |
| [7] | Yes | Derives an analytical formula to improve the steady and transient dynamics of the vehicle. |
| [8] | Yes | Minimizes sideslip angle. |
| [9] | Yes | Minimizes yaw rate error between a reference model and the real vehicle. |
| [10] | Yes | Combined with active front steering. |
| [11] | No | Reference tracking and proposes a tuning method. Tested on the ISO 3888-2 Double Lane Change Test at 40 km/h and 90 km/h. |
| [12] | Yes | Estimates sideslip angle and cornering stiffness through a Kalman filter. Compared vs. friction brake actuation. |
| [13] | Yes | Wheel torque distribution criteria using offline optimization and Control Allocation (CA). |
| [14] | Yes | Performance comparison with H-infinity controller. |
| [15] | No | Uses a cubic-error PD controller for yaw rate and sideslip control. |
| Ref(s). | Order 1 | Comments |
|---|---|---|
| [16] | 2 | Two second-order sliding-mode controllers are evaluated against a feedforward controller combined with either a conventional or an adaptive Proportional Integral Derivative (PID) controller. |
| [17] | −1 | Implements Integral Sliding Mode Control (ISMC) to avoid chattering |
| [18] | 1 | Combines SMC with PID. Include a low pass filter to reduce chattering. Reduces the difference between front and rear slip angles. |
| [19] | 1 | Includes saturation to reduce chattering. |
| [20] | −1, 2 | Compares Internal Mode Control (IMC) and Second-Order Sliding Mode Control (SOSM), both using feedforward terms. With both control techniques, stability in demanding oversteering conditions, such as braking in a high-speed turn, can be worse than the uncontrolled case, depending on the longitudinal deceleration level. |
| [21] | 1 | Multiple Adaptive Sliding Mode Control (MASMC). |
| [22] | - | Compares Integral Terminal Sliding Mode (ITSM) and Nonsingular Fast Terminal Sliding Model (NFTSM) to improve the transient response of the vehicle sideslip angle and yaw rate. |
| [23] | 1 | Adaptive. Lyapunov-based stability analysis. Performance studied on a double lane change test simulation. |
| [24] | 1, 2 | Compares first order, SOSM, and PID controllers. SOSM is the winner of the comparison based on a Sine with Dwell test manoeuvre (no chattering, best tracking performance, better slip-angle). |
| [25] | −1 | Integral Sliding Mode Control (ISMC) compared LQR controller with and without non-linear feedforward. ISMC outperforms LQR both in tracking performance and yaw damping. |
| Ref(s) | Controller | Comments |
|---|---|---|
| [27,28] | LQR | Applied to production vehicles. |
| [29] | LQR | Tracks vehicle yaw rate, minimization of the optimal handling performance index. |
| [30] | LQR | Tracks yaw rate and sideslip angle, minimizes the use of external yaw moment. |
| [31] | RLQR | Robust controller. Robustness is achieved through gain-scheduling and additional closed-loop control terms. Outperforms standard LQR. |
| [32] | LQR | Applied to Formula Student vehicle. Showed promising results compared to PD controller. |
| [33,34] | LQG | Improved disturbance rejection ability if compared to LQR. |
| [35] | LPV | DYC combined with torque and slip limitation applied to a front-wheel-drive electric vehicle. |
| Ref(s) | Comments |
|---|---|
| [36] | A high-level supervisory module operated by a genetic fuzzy yaw moment controller. |
| [37] | Comparison to an LQR. Fuzzy logic shows better results on ISO3888-2 and Sine with Dwell manoeuvres. |
| [38] | A unified controller with three control layers based on fuzzy control strategy is designed for this purpose and applied on a vehicle with an electronic differential. |
| [39] | A neuro-fuzzy vertical tire forces estimator combined with a fuzzy yaw moment controller is compared to a more traditional PID controller using a high-fidelity vehicle dynamics simulator; results show that the proposed controller can increase vehicle efficiency by 10%. |
| Ref(s) | Controller | Comments |
|---|---|---|
| [40] | Non-linear | Nearest point approach. Applied to step steer and split braking manoeuvre. |
| [41] | Standard | Applied to U-turn and double lane change. Outperforms LQR. |
| [42] | Non-linear | Robust controller. Robustness achieved using gain-Model In combination with an SMC to compute the necessary torques on the rear wheels based on the requested longitudinal slips. Outperforms LQR. |
| [43] | Standard | The linear vehicle model is used for the MPC and compared with an equal torque algorithm. Evaluation is performed by simulation. |
| [44] | Adapted to deal with delay | Yaw response of the vehicle is improved through torque vectoring to track the desired yaw rate, even with the presence of delays in the control loop which could degrade controller performance. Effectiveness is verified by simulation and by experiments with a rear-wheel-drive electric vehicle |
| [45] | 2 controllers: Standard and non-linear | Applied to Formula Student car. Both use the qpOASES solver [46]. The nonlinear model uses ACADO code generation tool [47]. Tested for U-turn and step steer. |
| [48] | Standard | Requires no road friction information. Estimated using the relative difference between front and rear slip angles. |
| [49] | Non-linear | Both torque vectoring and Electronic Stability Control (ESC). Non-linearity includes constraints in the actuators. Tested on line-change and J-turn manoeuvres. |
| [50] | Standard with physical constraints | Applied to 4WD. Tested on step steer and double lane-change manoeuvres. Outperforms LQR. |
| [51] | Non-linear | Concurrent optimization of the reference yaw rate and wheel torque allocation. Cost function weights on-line varied using fuzzy logic to adaptively prioritize vehicle dynamics or energy efficiency. |
| Parameter | Value |
|---|---|
| Vehicle mass (driver included), m | 296 kg |
| Yaw Inertia, Iz | 153 kg m2 |
| Wheelbase, L | 1.58 m |
| Distance from the front axle to the centre of gravity, a | 0.798 m |
| Distance from the rear axle to the centre of gravity, b | 0.782 m |
| Front axle cornering stiffness, Cα,front (absolute value) | |
| At 20 km/h | 37,530 N/rad |
| At 40 km/h | 42,660 N/rad |
| At 60 km/h | 47,780 N/rad |
| At 80 km/h | 52,900 N/rad |
| At 100 km/h | 58,000 N/rad |
| Rear axle cornering stiffness, Cα,rear (absolute value) | |
| At 20 km/h | 39,400 N/rad |
| At 40 km/h | 49,100 N/rad |
| At 60 km/h | 58,800 N/rad |
| At 80 km/h | 68,500 N/rad |
| At 100 km/h | 78,200 N/rad |
| Race Driver Parameters | Lap Times | |||||
|---|---|---|---|---|---|---|
| Learning Rate: 0: Sensitive 1.5: Aggressive | Driver Target G-G Exponent | PID | SMC | LQR | MPC | LPV-MPC |
| 0 | 1 | 36.92 | 36.94 | 36.73 | 36.78 | 36.80 |
| 0.5 | 1.2 | 36.13 | 36.26 | 35.97 | 35.99 | 36.07 |
| 0.7 | 1.4 | 35.68 | 35.78 | 35.50 | 35.55 | 35.62 |
| 1 | 1.6 | 35.33 | 35.48 | 35.14 | 35.28 | 35.32 |
| 1.5 | 1.8 | 35.12 | 35.42 | 34.98 | 35.16 | 35.11 |
| 1.5 | 2 | 35.1 | 35.27 | 34.80 | 35.13 | 35.00 |
| 1.5 | 2.2 | 34.85 | 35.23 | 34.82 | 34.82 | 34.78 |
| 1.5 | 2.3 | DNF | DNF | DNF | DNF | DNF |
| Controller | Best Lap Olaberria | ||
|---|---|---|---|
| Lap Time (s) | IACA (Nm·s) | IAE (rad) | |
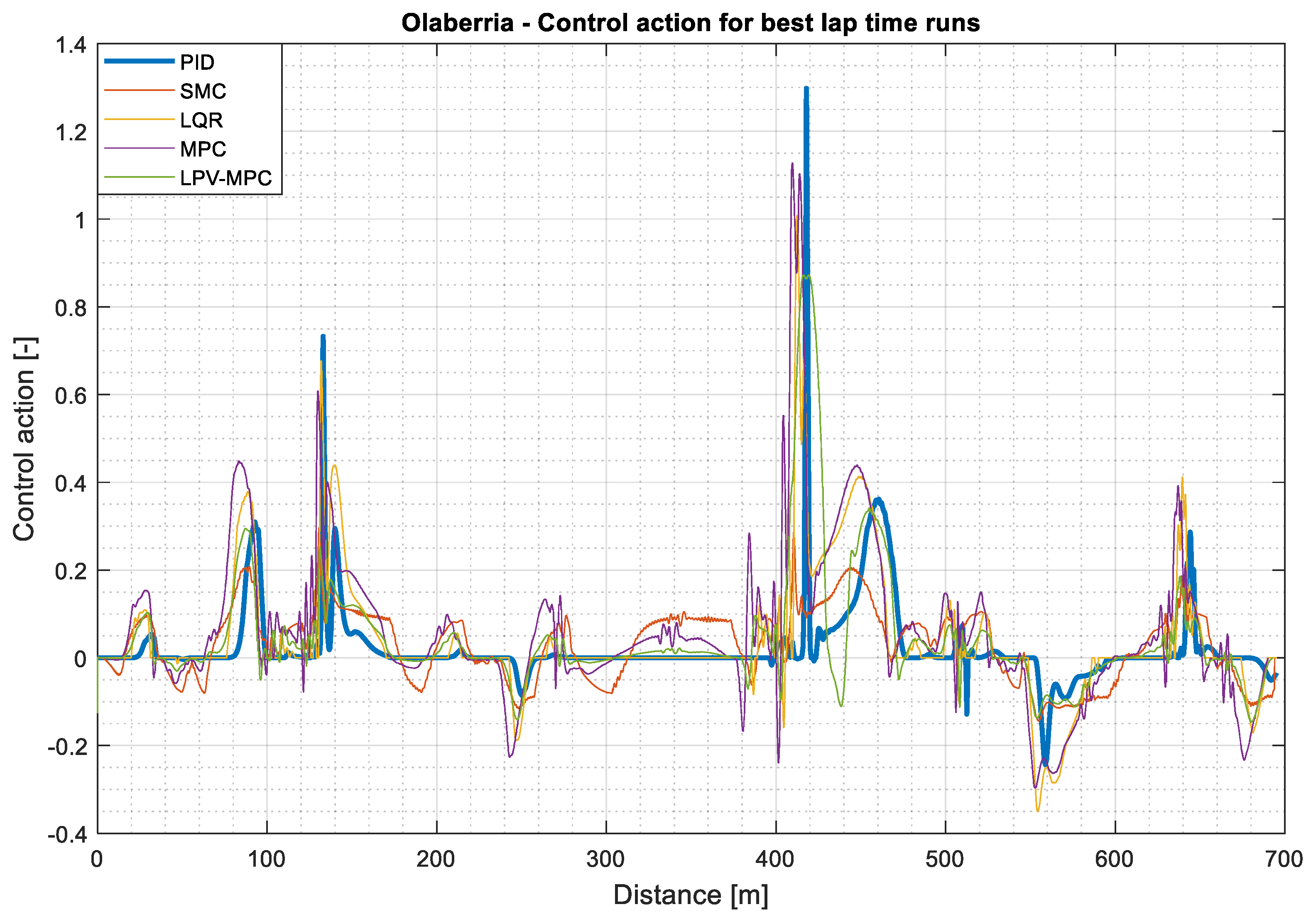
| PID | 34.85 | 3103 | 7.34 |
| SMC | 35.23 | 6660 | 7.70 |
| LQR | 34.80 | 6867 | 6.77 |
| MPC | 34.82 | 8105 | 5.63 |
| LPV-MPC | 34.78 | 5130 | 8.39 |
| Race Driver Parameters | Lap Times (s) | |||||
|---|---|---|---|---|---|---|
| Learning Rate: 0: Sensitive 1.5: Aggressive | Driver Target G-G Exponent | PID | SMC | LQR | MPC | LPV-MPC |
| 0 | 1 | 49.97 | 49.96 | 49.96 | 49.97 | 49.95 |
| 0.5 | 1.2 | 49.28 | 49.19 | 49.30 | 49.31 | 49.21 |
| 0.7 | 1.4 | 48.84 | 48.73 | 48.90 | 48.89 | 48.71 |
| 1 | 1.6 | 48.46 | 48.36 | 48.53 | 48.51 | 48.37 |
| 1.5 | 1.8 | 48.28 | 48.24 | 48.38 | 48.36 | 48.20 |
| 1.5 | 2 | 48.14 | 48.07 | 48.19 | 48.17 | 48.09 |
| 1.5 | 2.2 | 48.06 | 47.95 | 48.12 | 48.08 | 48.01 |
| 1.5 | ∞ | 47.34 | 47.31 | 47.41 | 47.38 | 47.28 |
| Controller | Best Lap Hockenheim | ||
|---|---|---|---|
| Lap Time (s) | IACA (Nm·s) | IAE (rad) | |
| PID | 47.34 | 2499 | 4.69 |
| SMC | 47.31 | 5414 | 5.29 |
| LQR | 47.41 | 3881 | 4.22 |
| MPC | 47.38 | 5483 | 4.02 |
| LPV-MPC | 47.28 | 3229 | 5.90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medina, A.; Bistue, G.; Rubio, A. Comparison of Typical Controllers for Direct Yaw Moment Control Applied on an Electric Race Car. Vehicles 2021, 3, 127-144. https://doi.org/10.3390/vehicles3010008
Medina A, Bistue G, Rubio A. Comparison of Typical Controllers for Direct Yaw Moment Control Applied on an Electric Race Car. Vehicles. 2021; 3(1):127-144. https://doi.org/10.3390/vehicles3010008
Chicago/Turabian StyleMedina, Andoni, Guillermo Bistue, and Angel Rubio. 2021. "Comparison of Typical Controllers for Direct Yaw Moment Control Applied on an Electric Race Car" Vehicles 3, no. 1: 127-144. https://doi.org/10.3390/vehicles3010008
APA StyleMedina, A., Bistue, G., & Rubio, A. (2021). Comparison of Typical Controllers for Direct Yaw Moment Control Applied on an Electric Race Car. Vehicles, 3(1), 127-144. https://doi.org/10.3390/vehicles3010008