Optimal Control of Electrified Powertrains in Offline and Online Application Concerning Dimensioning of Li-Ion Batteries
Abstract
:1. Introduction
2. Related Work
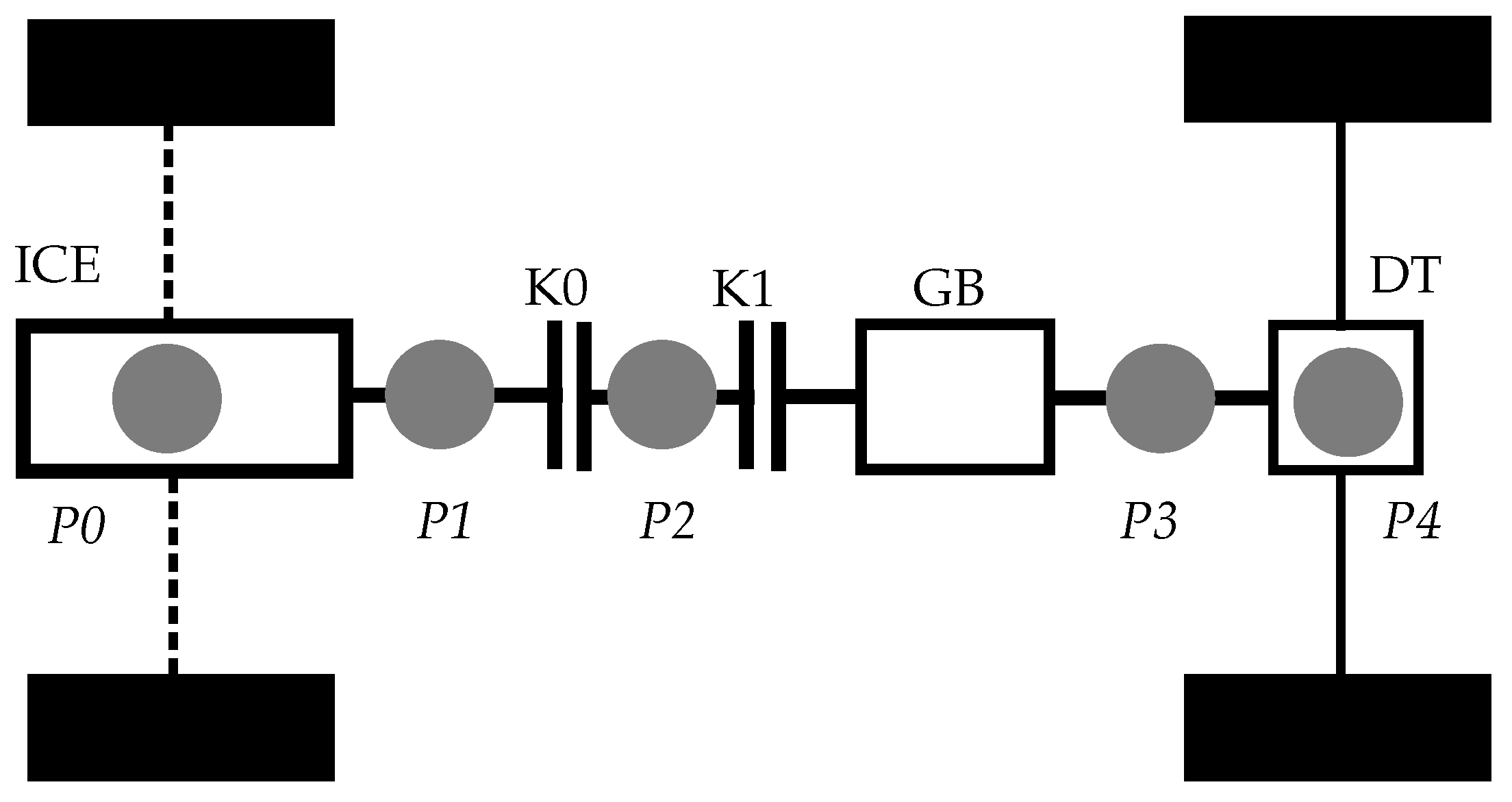
3. Modeling
3.1. Dynamic Programming (DP)
3.2. Equivalent Consumption Minimization Strategy (ECMS)
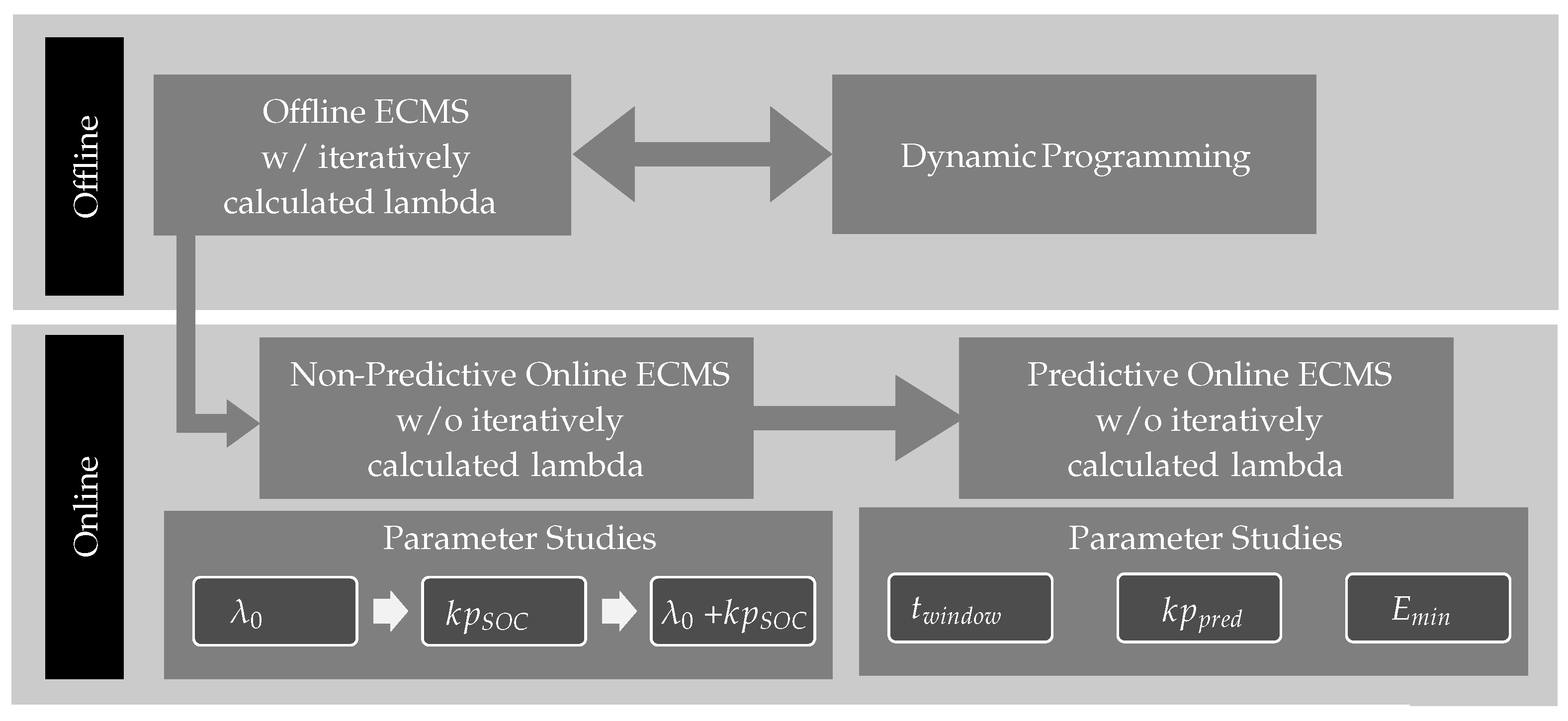
4. Results
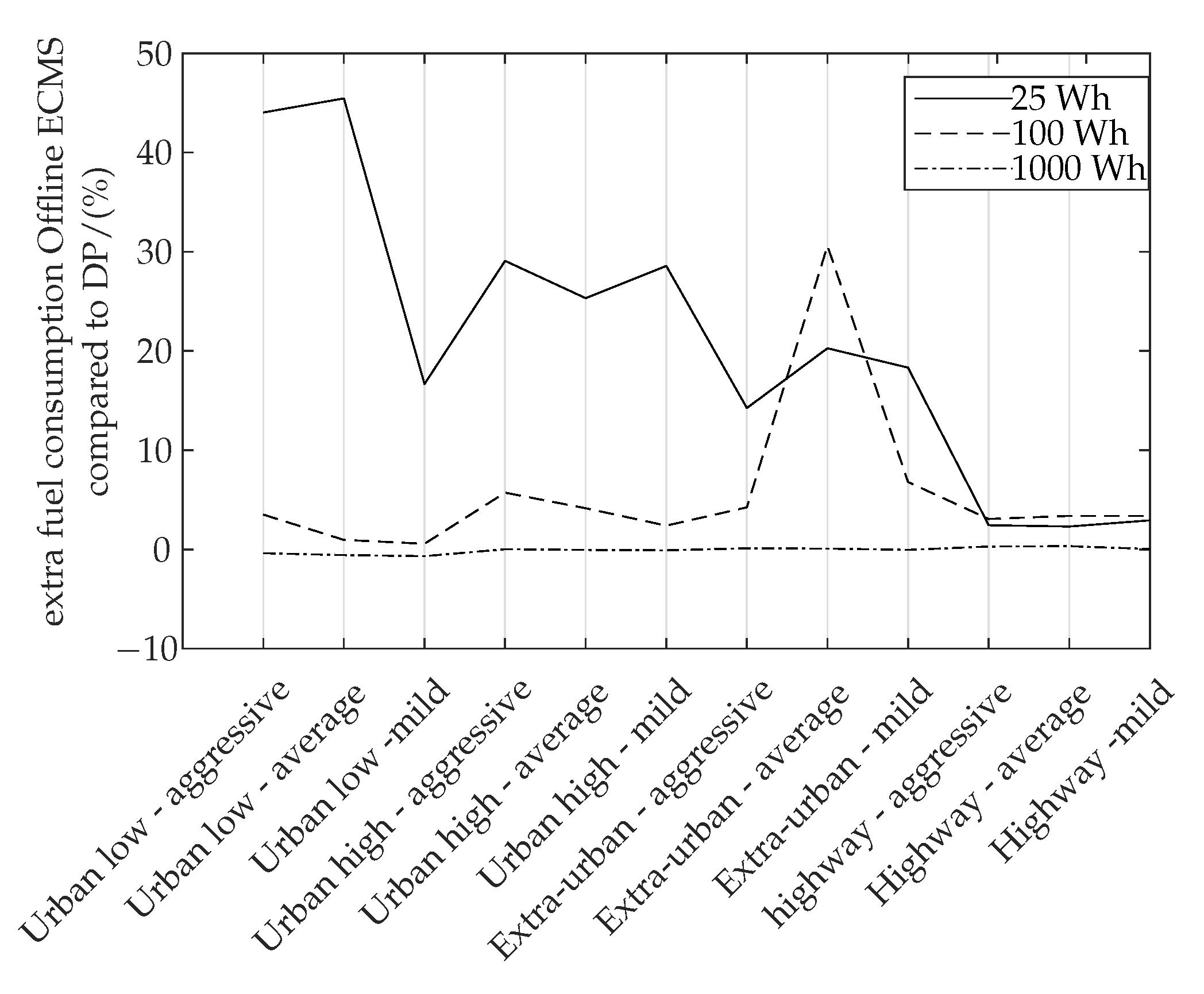
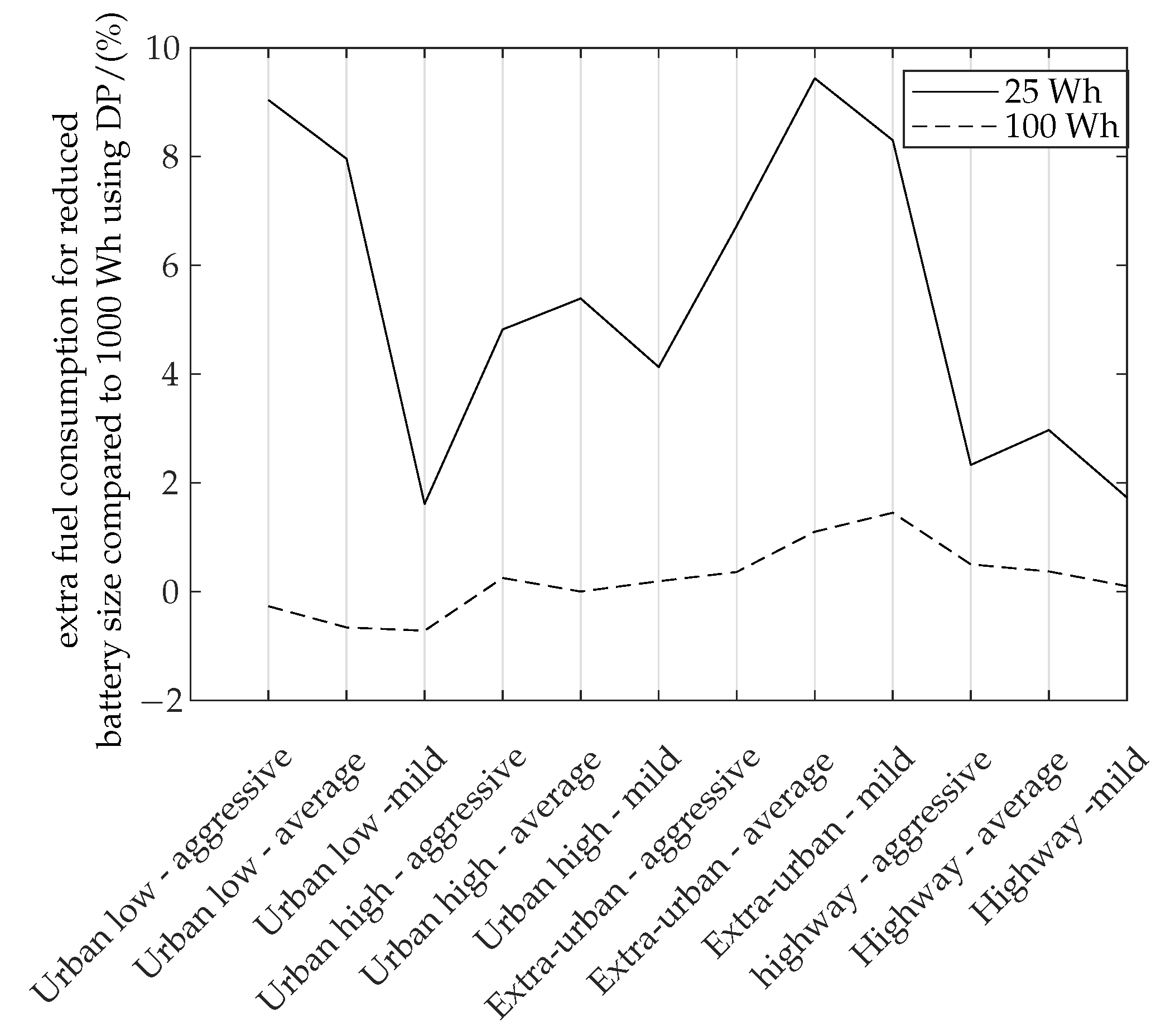
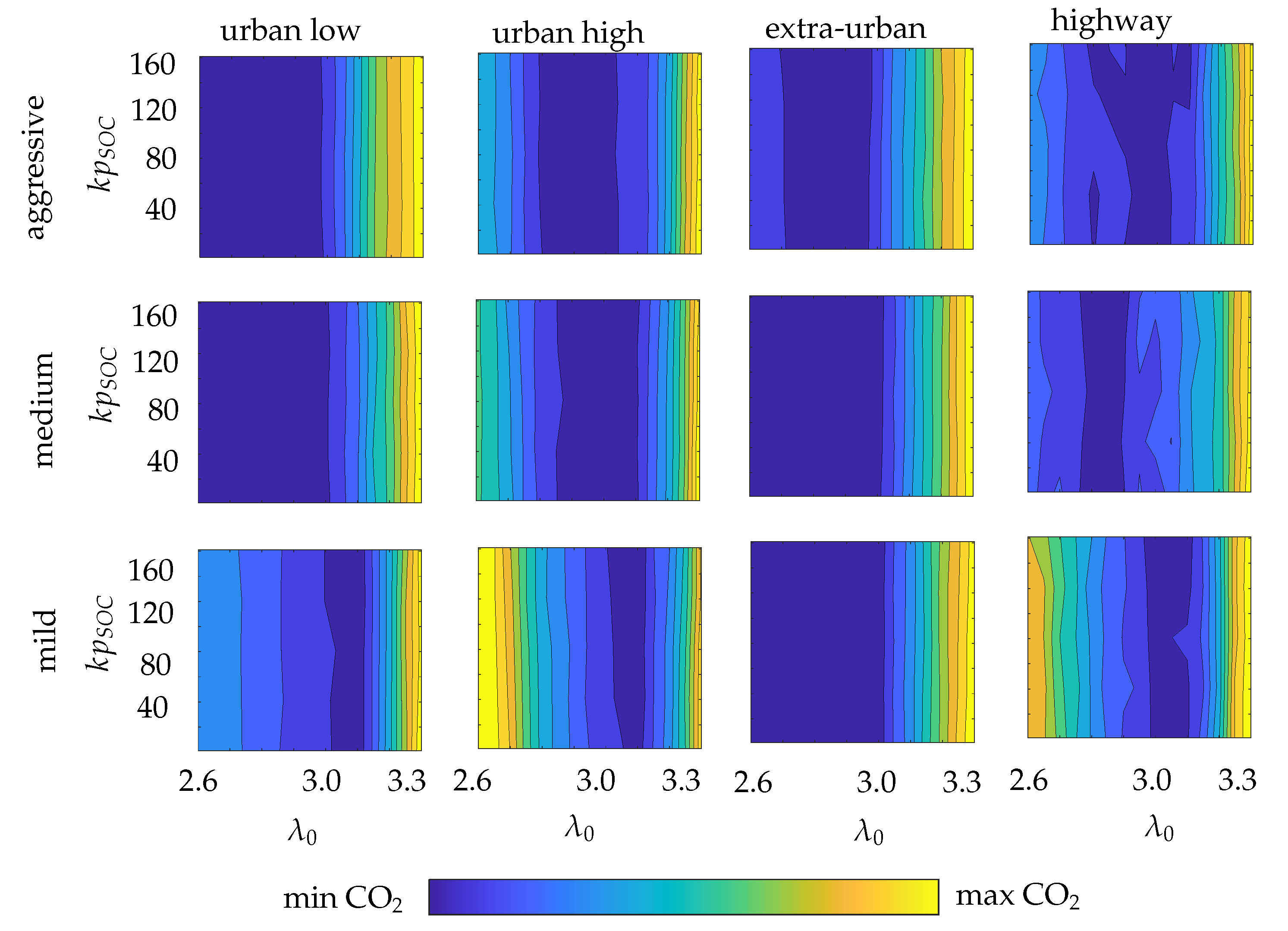
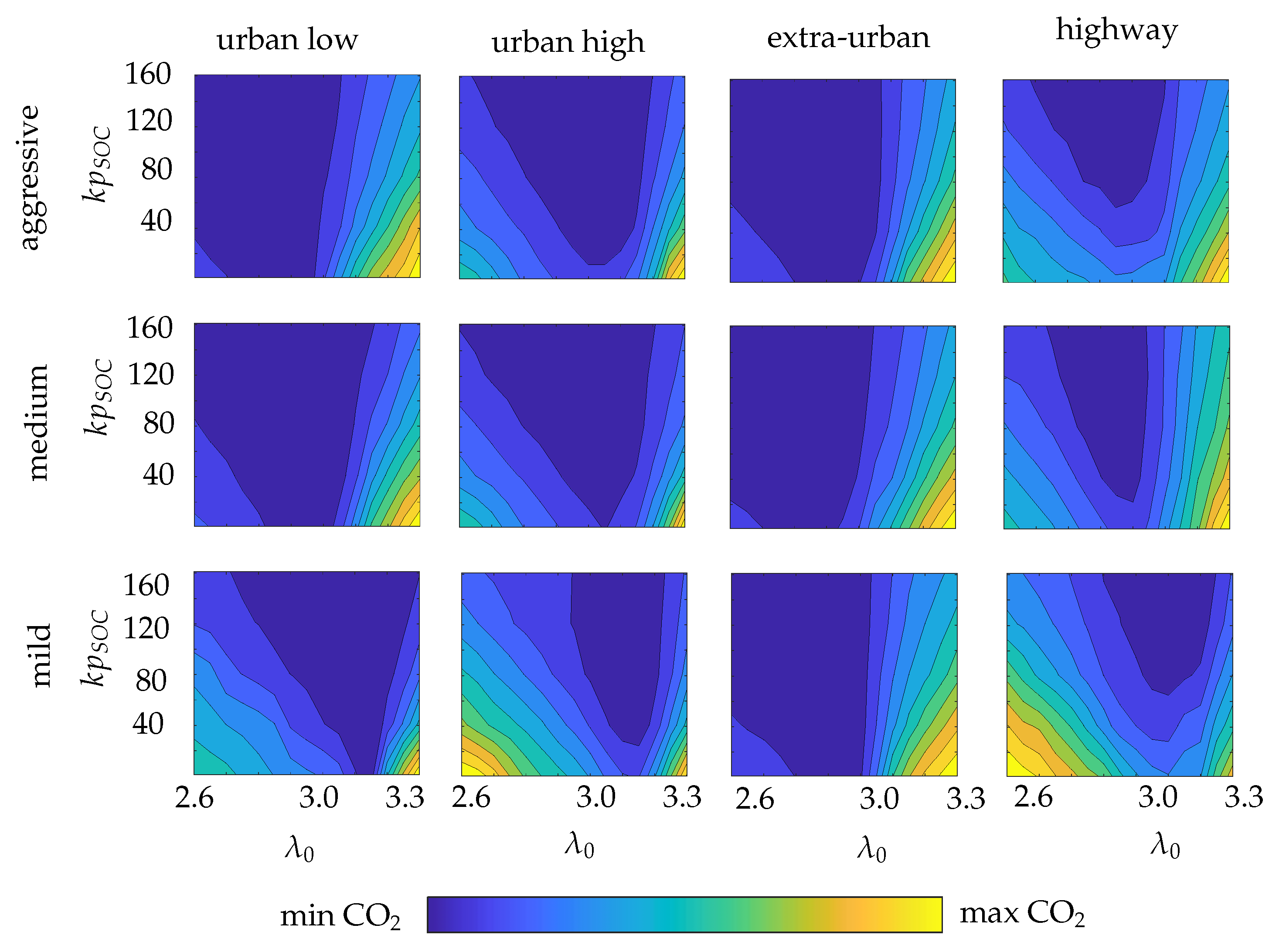
4.1. Global Optimum-Dynamic Programming vs. Offline ECMS
4.2. Online ECMS (Non-Predictive)
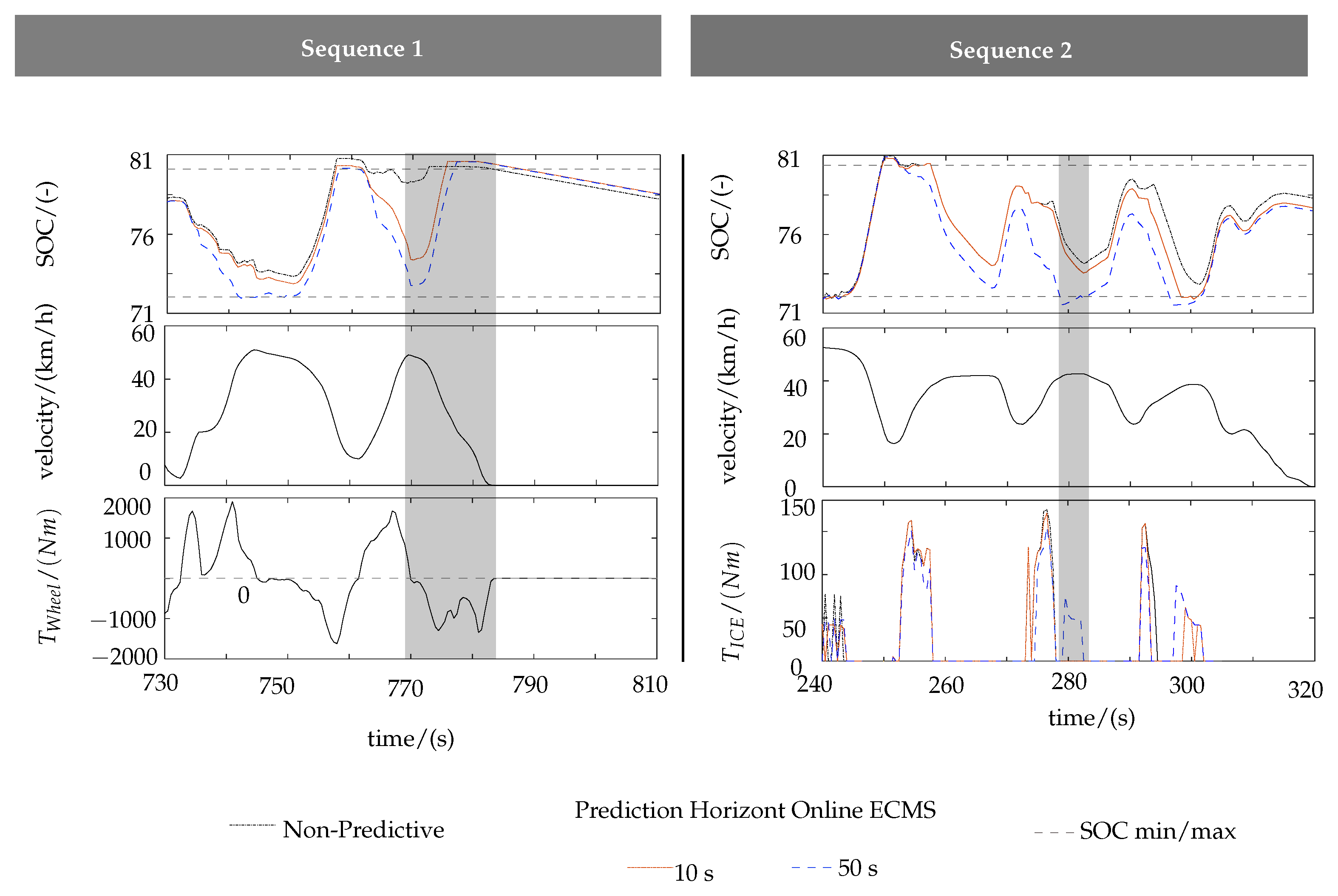
4.3. Online ECMS (Predictive)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Silvas, E.; Hofman, T.; Murgovski, N.; Etman, P.; Steinbuch, M. Review of Optimization Strategies for System-Level Design in Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2017, 66, 57–70. [Google Scholar] [CrossRef]
- Vora, A.P.; Jin, X.; Hoshing, V.; Shaver, G.; Varigonda, S.; Tyner, W.E. Integrating battery degradation in a cost of ownership framework for hybrid electric vehicle design optimization. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 1507–1523. [Google Scholar] [CrossRef]
- Cardoso, D.S.; Fael, P.O.; Espírito-Santo, A. A review of micro and mild hybrid systems. Energy Rep. 2020, 6, 385–390. [Google Scholar] [CrossRef]
- Liu, Y.; Canova, M.; Wang, Y.Y. Distributed Energy and Thermal Management of a 48-V Diesel Mild Hybrid Electric Vehicle with Electrically Heated Catalyst. IEEE Trans. Control Syst. Technol. 2020, 28, 1878–1891. [Google Scholar] [CrossRef]
- Griefnow, P.; Andert, J.; Xia, F.; Klein, S.; Stoffel, P.; Engels, M.; Jolovic, D. Real-Time Modeling of a 48V P0 Mild Hybrid Vehicle with Electric Compressor for Model Predictive Control; SAE International: Warrendale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Elektrifizierung des Antriebsstrangs; Tschöke, H.; Gutzmer, P.; Pfund, T. (Eds.) Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Tran, D.D.; Vafaeipour, M.; El Baghdadi, M.; Barrero, R.; van Mierlo, J.; Hegazy, O. Thorough state-of-the-art analysis of electric and hybrid vehicle powertrains: Topologies and integrated energy management strategies. Renew. Sustain. Energy Rev. 2020, 119, 109596. [Google Scholar] [CrossRef]
- Serrao, L. A Comparative Analysis of Energy Management Strategies for Hybrid Electric Vehicles. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2009. [Google Scholar]
- Onori, S.; Serrao, L.; Rizzoni, G. Hybrid Electric Vehicles; Springer: London, UK, 2016. [Google Scholar] [CrossRef]
- Rizzoni, G.; Onori, S. Energy Management of Hybrid Electric Vehicles: 15 years of development at the Ohio State University. Oil Gas Sci. Technol. Rev. D’IFP Energies Nouv. 2015, 70, 41–54. [Google Scholar] [CrossRef] [Green Version]
- Salmasi, F.R. Control Strategies for Hybrid Electric Vehicles: Evolution, Classification, Comparison, and Future Trends. IEEE Trans. Veh. Technol. 2007, 56, 2393–2404. [Google Scholar] [CrossRef]
- Xu, N.; Kong, Y.; Chu, L.; Ju, H.; Yang, Z.; Xu, Z.; Xu, Z. Towards a Smarter Energy Management System for Hybrid Vehicles: A Comprehensive Review of Control Strategies. Appl. Sci. 2019, 9, 2026. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Q.; Ossart, F.; Marchand, C. Comparative Study of Real-Time HEV Energy Management Strategies. IEEE Trans. Veh. Technol. 2017, 66, 10875–10888. [Google Scholar] [CrossRef] [Green Version]
- Chasse, A.; Sciarretta, A.; Chauvin, J. Online optimal control of a parallel hybrid with costate adaptation rule. IFAC Proc. Vol. 2010, 43, 99–104. [Google Scholar] [CrossRef]
- Sundström, O. Optimal Hybridization in Two Parallel Hybrid Electric Vehicles using Dynamic Programming. IFAC Proc. Vol. 2008, 41, 4642–4647. [Google Scholar] [CrossRef] [Green Version]
- Sundstrom, O.; Guzzella, L. A generic dynamic programming Matlab function. In Proceedings of the 2009 IEEE Control Applications, (CCA) & Intelligent Control, (ISIC), St. Petersburg, Russia, 8–10 July 2009; pp. 1625–1630. [Google Scholar] [CrossRef]
- Sundström, O.; Ambühl, D.; Guzzella, L. On Implementation of Dynamic Programming for Optimal Control Problems with Final State Constraints. Oil Gas Sci. Technol. Rev. De L’Institut Français Du Pétrole 2010, 65, 91–102. [Google Scholar] [CrossRef] [Green Version]
- Elbert, P.; Ebbesen, S.; Guzzella, L. Implementation of Dynamic Programming for n-Dimensional Optimal Control Problems with Final State Constraints. IEEE Trans. Control Syst. Technol. 2013, 21, 924–931. [Google Scholar] [CrossRef]
- Kim, N.; Cha, S.; Peng, H. Optimal Control of Hybrid Electric Vehicles Based on Pontryagin’s Minimum Principle. IEEE Trans. Control Syst. Technol. 2011, 19, 1279–1287. [Google Scholar] [CrossRef] [Green Version]
- Kim, N.; Rousseau, A. Sufficient conditions of optimal control based on Pontryagin’s minimum principle for use in hybrid electric vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2012, 226, 1160–1170. [Google Scholar] [CrossRef]
- Paganelli, G.; Delprat, S.; Guerra, T.M.; Rimaux, J.; Santin, J.J. Equivalent consumption minimization strategy for parallel hybrid powertrains. In Proceedings of the IEEE 55th Vehicular Technology Conference, VTC Spring 2002 (Cat. No.02CH37367), Birmingham, AL, USA, 6–9 May 2002; pp. 2076–2081. [Google Scholar] [CrossRef]
- Serrao, L.; Onori, S.; Rizzoni, G. ECMS as a realization of Pontryagin’s minimum principle for HEV control. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 3964–3969. [Google Scholar] [CrossRef]
- Zheng, C.H. Numerical Comparison Of Ecms And Pmp-Based Optimal Control Strategy In Hybrid Vehicles. Int. J. Automot. Technol. 2014, 15, 1189–1196. [Google Scholar] [CrossRef]
- Foerster, D.; Decker, L.; Doppelbauer, M.; Gauterin, F. Analysis of CO2 reduction potentials and component load collectives of 48 V-hybrids under real-driving conditions. Automot. Engine Technol. 2021, 6, 45–62. [Google Scholar] [CrossRef]
- Mayer, A. Two-Dimensional ECMS for System Analysis of Hybrid Concepts featuring Two Electric Traction Motors. In Proceedings of the 2019 International Symposium on Systems Engineering (ISSE), Edinburgh, UK, 1–3 October 2019. [Google Scholar]
- Onori, S.; Serrao, L. On Adaptive-ECMS strategies for hybrid electric vehicles. In Proceedings of the Les Rencontres Scientifiques d’IFP Energies Nouvelles–International Conference on Hybrid and Electric Vehicles–RHEVE 2011, Rueil-Malmaison, France, 6–7 December 2011. [Google Scholar]
- Onori, S.; Serrao, L.; Rizzoni, G. Adaptive Equivalent Consumption Minimization Strategy for Hybrid Electric Vechiles. In Proceedings of the ASME 2010 Dynamic Systems and Control Conference DSCC2010, Cambridge, MA, USA, 12–15 September 2010. [Google Scholar]
- Musardo, C.; Rizzoni, G.; Staccia, B. A-ECMS: An Adaptive Algorithm for Hybrid Electric Vehicle Energy Managemen: Proceedings, Seville, Spain, 12–15 December 2005; IEEE Operations Center: Piscataway, NJ, USA, 2005. [Google Scholar]
- Kessels, J.; Koot, M.; van den Bosch, P.; Kok, D.B. Online Energy Management for Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2008, 57, 3428–3440. [Google Scholar] [CrossRef]
- Liu, T.; Zou, Y.; Liu, D.X.; Sun, F.C. Real-time control for a parallel hybrid electric vehicle based on Pontryagin’s Minimum Principle. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Ouddah, O.; Adouane, L.; Abdrakhmanov, R. From Offline to Adaptive Online Energy Management Strategy of Hybrid Vehicle Using Pontryagin’s Minimum Principle. Int. J. Automot. Technol. Vol. 2017, 19, 571–584. [Google Scholar] [CrossRef]
- Sivertsson, M. Adaptive Control Using Map-Based ECMS for a PHEV. IFAC Proc. Vol. 2012, 45, 357–362. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Xu, K.; Li, L.; Langari, R. Comparative Study of Equivalent Factor Adjustment Algorithm for Equivalent Consumption Minimization Strategy for HEVs. In Proceedings of the 2018 IEEE Vehicle Power and Propulsion Conference (VPPC), Chicago, IL, USA, 27–30 August 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Fu, Z.; Liu, X. Equivalent Consumption Minimization Strategy Based on a Variable Equivalent Factor. In Proceedings of the IEEE 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017. [Google Scholar] [CrossRef]
- Enang, W.; Bannister, C. Robust proportional ECMS control of a parallel hybrid electric vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 231, 99–119. [Google Scholar] [CrossRef] [Green Version]
- Gu, B.; Rizzoni, G. An Adaptive Algorithm for Hybrid Electric Vehicle Energy Management Based on Driving Pattern Recognition. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Chicago, IL, USA, 5–10 November 2006. [Google Scholar]
- Chen, Z.; Liu, Y.; Zhang, Y.; Lei, Z.; Chen, Z.; Li, G. A neural network-based ECMS for optimized energy management of plug-in hybrid electric vehicles. Energy 2021, 243, 122727. [Google Scholar] [CrossRef]
- Xie, S.; Hu, X.; Qi, S.; Lang, K. An artificial neural network-enhanced energy management strategy for plug-in hybrid electric vehicles. Energy 2018, 163, 837–848. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Cha, S.W. Reinforcement Learning Based on Equivalent Consumption Minimization Strategy for Optimal Control of Hybrid Electric Vehicles. IEEE Access 2021, 9, 860–871. [Google Scholar] [CrossRef]
- Zhang, F.; Xi, J.; Langari, R. An adaptive equivalent consumption minimization strategy for parallel hybrid electric vehicle based on Fuzzy PI. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Gothenburg, Sweden, 19–22 June 2016; pp. 460–465. [Google Scholar] [CrossRef]
- Li, L.; Huang, H.; Lian, J.; Yao, B.; Zhou, Y.; Chang, J.; Zheng, N. Research of Ant Colony Optimized Adaptive Control Strategy for Hybrid Electric Vehicle. Math. Probl. Eng. 2014, 2014, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Huang, X.; Lopez, J.M.; Xu, X.; Dong, P. Fuzzy Adaptive-Equivalent Consumption Minimization Strategy for a Parallel Hybrid Electric Vehicle. IEEE Access 2019, 7, 133290–133303. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, H.; Hu, Y.; Xi, J. A Supervisory Control Algorithm of Hybrid Electric Vehicle Based on Adaptive Equivalent Consumption Minimization Strategy with Fuzzy PI. Energies 2016, 9, 919. [Google Scholar] [CrossRef] [Green Version]
- Kural, E.; Güvenc, B.A. Predictive-Equivalent Consumption Minimization Strategy for Energy Management of A Parallel Hybrid Vehicle for Optimal Recuperation. J. Polytech. 2015, 2015, 113–124. [Google Scholar]
- Gao, A.; Deng, X.; Zhang, M.; Fu, Z. Design and Validation of Real-Time Optimal Control with ECMS to Minimize Energy Consumption for Parallel Hybrid Electric Vehicles. Math. Probl. Eng. 2017, 2017, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Wang, H.; Khajepour, A.; He, H.; Ji, J. Model predictive control power management strategies for HEVs: A review. J. Power Sources 2017, 341, 91–106. [Google Scholar] [CrossRef]
- Josevski, M.; Abel, D. Energy Management of Parallel Hybrid Electric Vehicles based on Stochastic Model Predictive Control. IFAC Proc. Vol. 2014, 47, 2132–2137. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Q.; Du, C. A quantitative analysis of model predictive control as energy management strategy for hybrid electric vehicles: A review. Energy Rep. 2021, 7, 6733–6755. [Google Scholar] [CrossRef]
- Wahl, H.G. Optimale Regelung eines Prädiktiven Energiemanagements von Hybridfahrzeugen. Ph.D. Thesis, Institute of Vehicle System Technology, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2015. [Google Scholar]
- Bauer, K.L. Echtzeit-Strategieplanung für Vorausschauendes Automatisiertes Fahren. Ph.D. Thesis, Institute of Vehicle System Technology, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2020. [Google Scholar]
- Lian, R.; Tan, H.; Peng, J.; Li, Q.; Wu, Y. Cross-Type Transfer for Deep Reinforcement Learning Based Hybrid Electric Vehicle Energy Management. IEEE Trans. Veh. Technol. 2020, 69, 8367–8380. [Google Scholar] [CrossRef]
- Liu, T.; Tang, X.; Wang, H.; Yu, H.; Hu, X. Adaptive Hierarchical Energy Management Design for a Plug-In Hybrid Electric Vehicle. IEEE Trans. Veh. Technol. 2019, 68, 11513–11522. [Google Scholar] [CrossRef]
- Maino, C.; Mastropietro, A.; Sorrentino, L.; Busto, E.; Misul, D.; Spessa, E. Project and Development of a Reinforcement Learning Based Control Algorithm for Hybrid Electric Vehicles. Appl. Sci. 2022, 12, 812. [Google Scholar] [CrossRef]
- Forster, D.; Inderka, R.B.; Gauterin, F. Data-Driven Identification of Characteristic Real-Driving Cycles Based on k-Means Clustering and Mixed-Integer Optimization. IEEE Trans. Veh. Technol. 2020, 69, 2398–2410. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming, 1st ed.; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Görke, D. Untersuchungen zur Kraftstoffoptimalen Betriebsweise von Parallelhybridfahrzeugen und Darauf Basierende Auslegung Regelbasierter Betriebsstrategien; Springer: Wiesbaden, Germany, 2016. [Google Scholar] [CrossRef]



| Frontal Area / | 2.56 |
| Air Drag Coefficient | 0.31 |
| Rolling Coefficient | 0.01 |
| Vehicle Mass m/ | 1915 |
| Wheel Radius / | 0.36 |
| Power ICE / | 150 |
| Power EM / | 25 |
| Road Type | Driving Style | g/km | g/km | (ECMS Only) |
|---|---|---|---|---|
| urban low | aggressive | 147.9 | 147.5 | 2.92 |
| urban low | average | 136.2 | 136.7 | 3.00 |
| urban low | mild | 123.9 | 124.3 | 3.14 |
| urban high | aggressive | 120.6 | 121.6 | 3.14 |
| urban high | average | 107.4 | 108.2 | 3.17 |
| urban high | mild | 106.4 | 106.5 | 3.19 |
| extra-urban | aggressive | 169.7 | 169.7 | 3.06 |
| extra-urban | average | 136.4 | 135.6 | 2.97 |
| extra-urban | mild | 131.1 | 131.3 | 2.99 |
| highway | aggressive | 246.4 | 245.2 | 3.20 |
| highway | average | 220.5 | 221.4 | 3.18 |
| highway | mild | 204.3 | 205.7 | 3.21 |
| Road Type | Driving Style | Wh | g/km | Extra Fuel Consumption Global Optimum (DP Solution) % |
|---|---|---|---|---|
| urban low | aggressive | 53.48 | 150.82 | 1.96 |
| urban low | average | 37.63 | 138.05 | 1.38 |
| urban low | mild | −7.52 | 124.14 | 0.27 |
| urban high | aggressive | 36.96 | 122.32 | 1.33 |
| urban high | average | −27.65 | 108.62 | 1.07 |
| urban high | mild | 2.47 | 107.89 | 1.34 |
| extra-urban | aggressive | 58.33 | 172.23 | 1.36 |
| extra-urban | average | 99.34 | 139.63 | 2.32 |
| extra-urban | mild | 73.53 | 135.00 | 2.90 |
| highway | aggressive | 68.14 | 250.74 | 1.76 |
| highway | average | 65.94 | 222.88 | 1.02 |
| highway | mild | 43.5 | 206.10 | 0.85 |
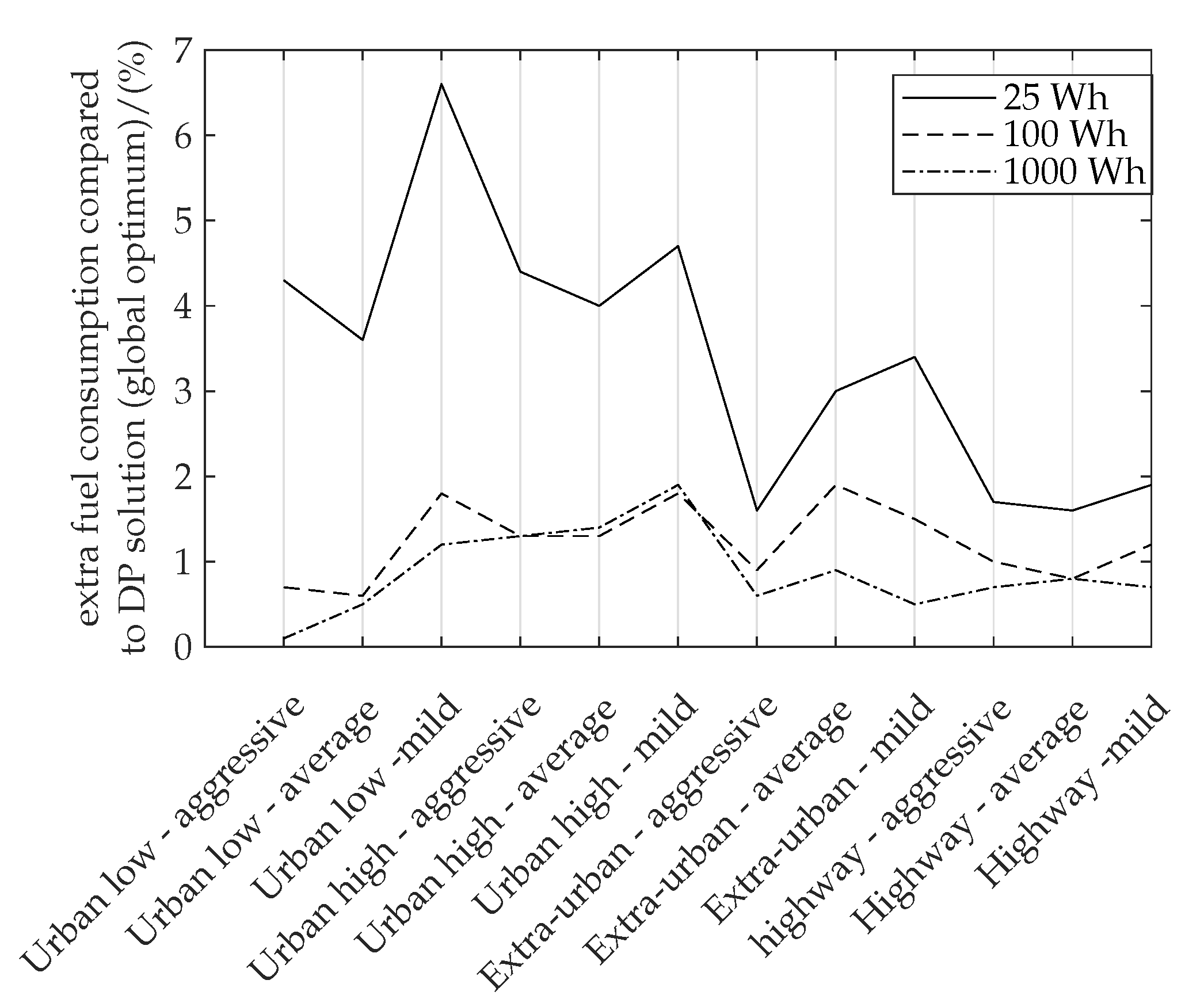
| Battery Size Wh | ⌀ Extra Fuel Consumption Global Optimum (DP Solution) % | ||
|---|---|---|---|
| 25 | 2.90 | 161 | 3.41 |
| 100 | 2.90 | 121 | 1.23 |
| 1000 | 2.85 | 41 | 0.88 |
| /(-) | /(s) | /(Wh) |
|---|---|---|
| 0.001…0.029 | 10…100 | 5…100 |
| Robust Parametrization | Individual Parametrization | ||||||||
|---|---|---|---|---|---|---|---|---|---|
s | Wh | s | Wh | ||||||
| Urban low | aggressive | 0.015 | 10 | 20 | 1.65 | 0.015 | 20 | 20 | 2.32 |
| Urban low | average | 0.015 | 10 | 20 | 1.80 | 0.009 | 20 | 10 | 1.82 |
| Urban low | mild | 0.015 | 10 | 20 | −0.47 | 0.005 | 100 | 20 | 0.18 |
| Urban high | aggressive | 0.015 | 10 | 20 | 0.54 | 0.015 | 10 | 20 | 0.54 |
| Urban high | average | 0.015 | 10 | 20 | −0.30 | 0.007 | 100 | 10 | 0.00 |
| Urban high | mild | 0.015 | 10 | 20 | −0.05 | 0.003 | 10 | 5 | 0.02 |
| Extra-urban | aggressive | 0.015 | 10 | 20 | 0.14 | 0.029 | 10 | 20 | 0.24 |
| Extra-urban | average | 0.015 | 10 | 20 | 0.38 | 0.025 | 10 | 5 | 0.90 |
| Extra-urban | mild | 0.015 | 10 | 20 | 0.78 | 0.029 | 10 | 5 | 1.39 |
| Highway | aggressive | 0.015 | 10 | 20 | 0.26 | 0.021 | 10 | 10 | 0.32 |
| Highway | average | 0.015 | 10 | 20 | 0.18 | 0.019 | 10 | 5 | 0.31 |
| Highway | mild | 0.015 | 10 | 20 | 0.06 | 0.019 | 20 | 5 | 0.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deufel, F.; Gießler, M.; Gauterin, F. Optimal Control of Electrified Powertrains in Offline and Online Application Concerning Dimensioning of Li-Ion Batteries. Vehicles 2022, 4, 464-481. https://doi.org/10.3390/vehicles4020028
Deufel F, Gießler M, Gauterin F. Optimal Control of Electrified Powertrains in Offline and Online Application Concerning Dimensioning of Li-Ion Batteries. Vehicles. 2022; 4(2):464-481. https://doi.org/10.3390/vehicles4020028
Chicago/Turabian StyleDeufel, Felix, Martin Gießler, and Frank Gauterin. 2022. "Optimal Control of Electrified Powertrains in Offline and Online Application Concerning Dimensioning of Li-Ion Batteries" Vehicles 4, no. 2: 464-481. https://doi.org/10.3390/vehicles4020028
APA StyleDeufel, F., Gießler, M., & Gauterin, F. (2022). Optimal Control of Electrified Powertrains in Offline and Online Application Concerning Dimensioning of Li-Ion Batteries. Vehicles, 4(2), 464-481. https://doi.org/10.3390/vehicles4020028






