Smart Design: Application of an Automatic New Methodology for the Energy Assessment and Redesign of Hybrid Electric Vehicle Mechanical Components
Abstract
:1. Introduction
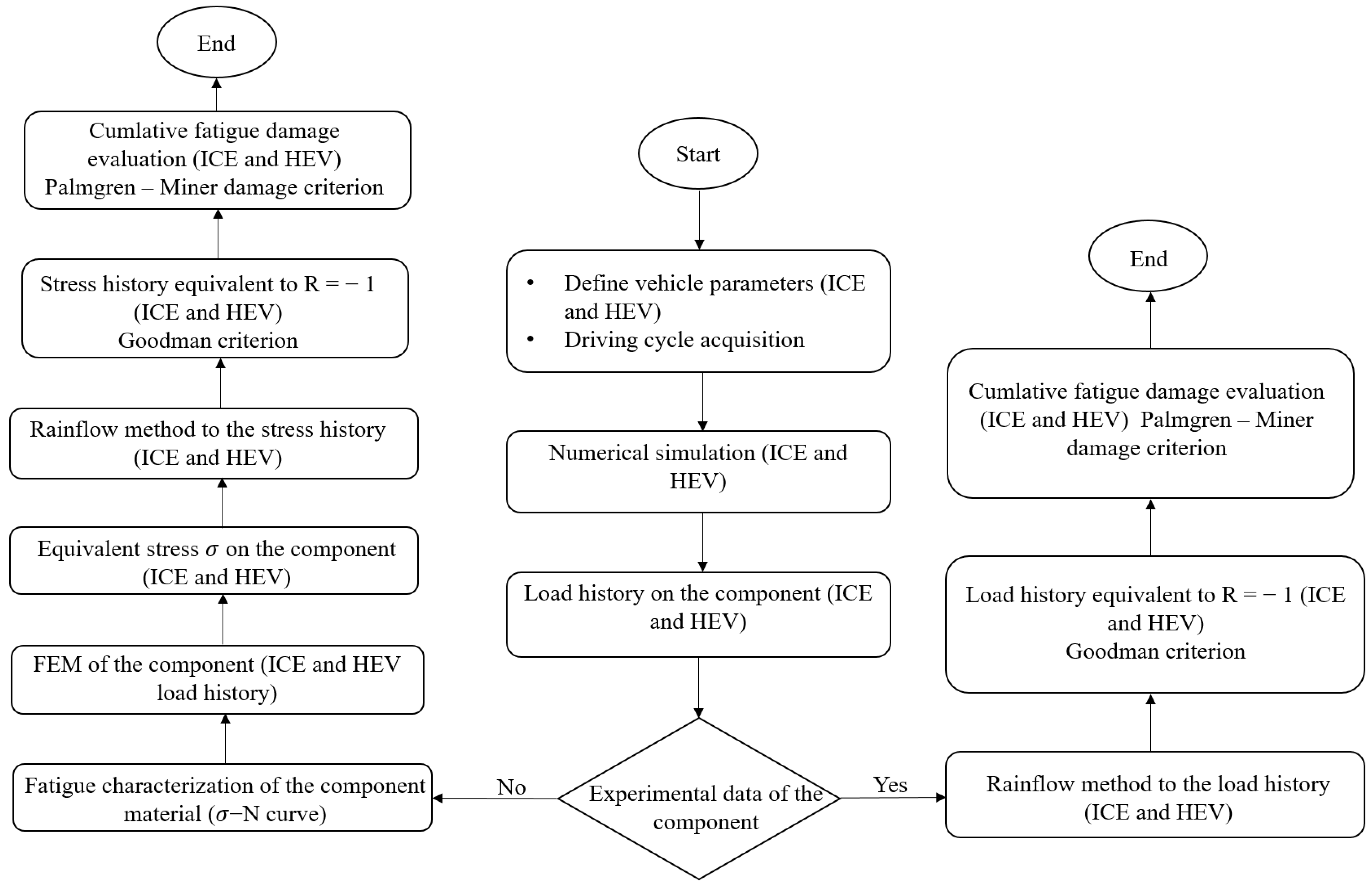
2. Materials and Methods
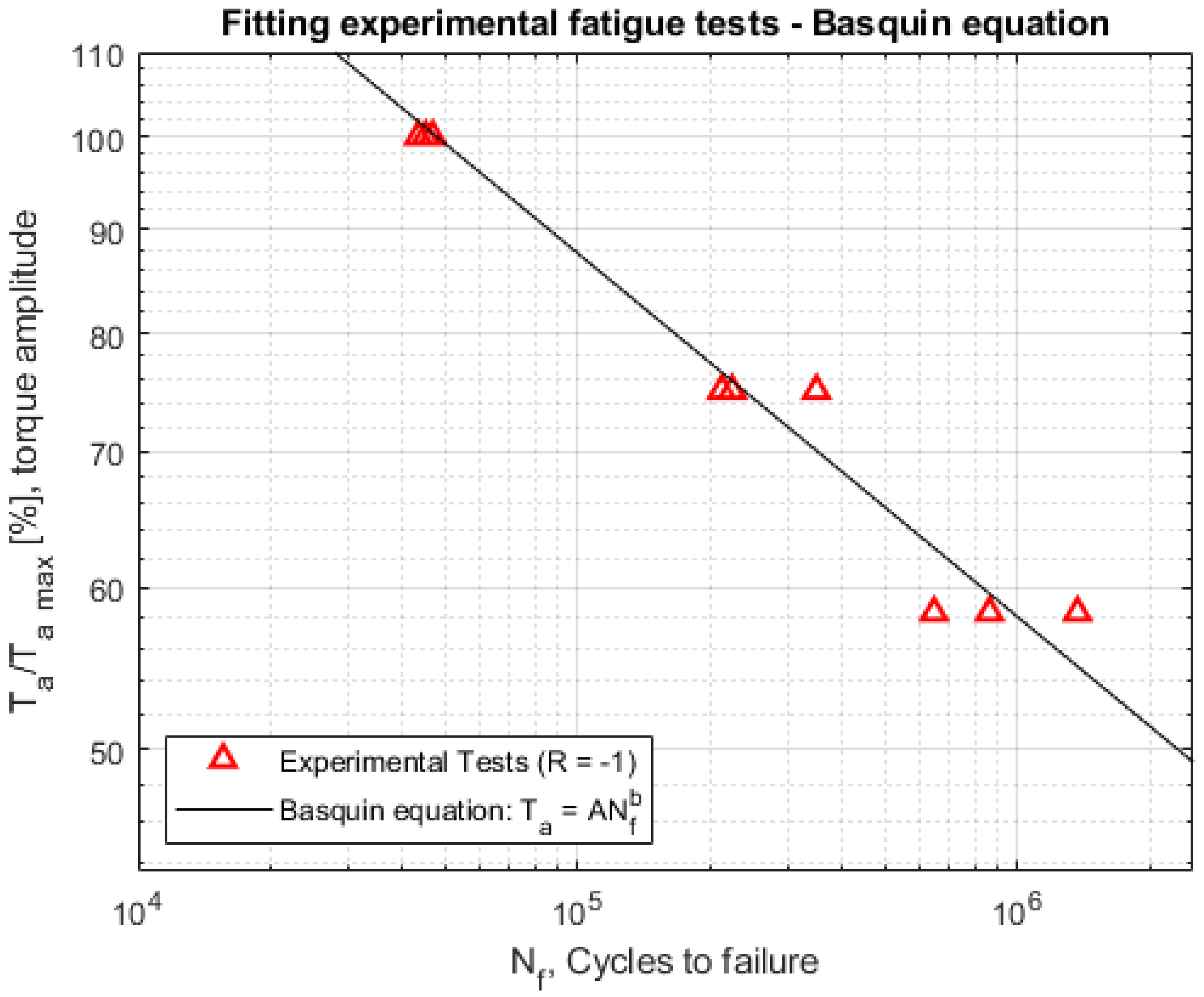
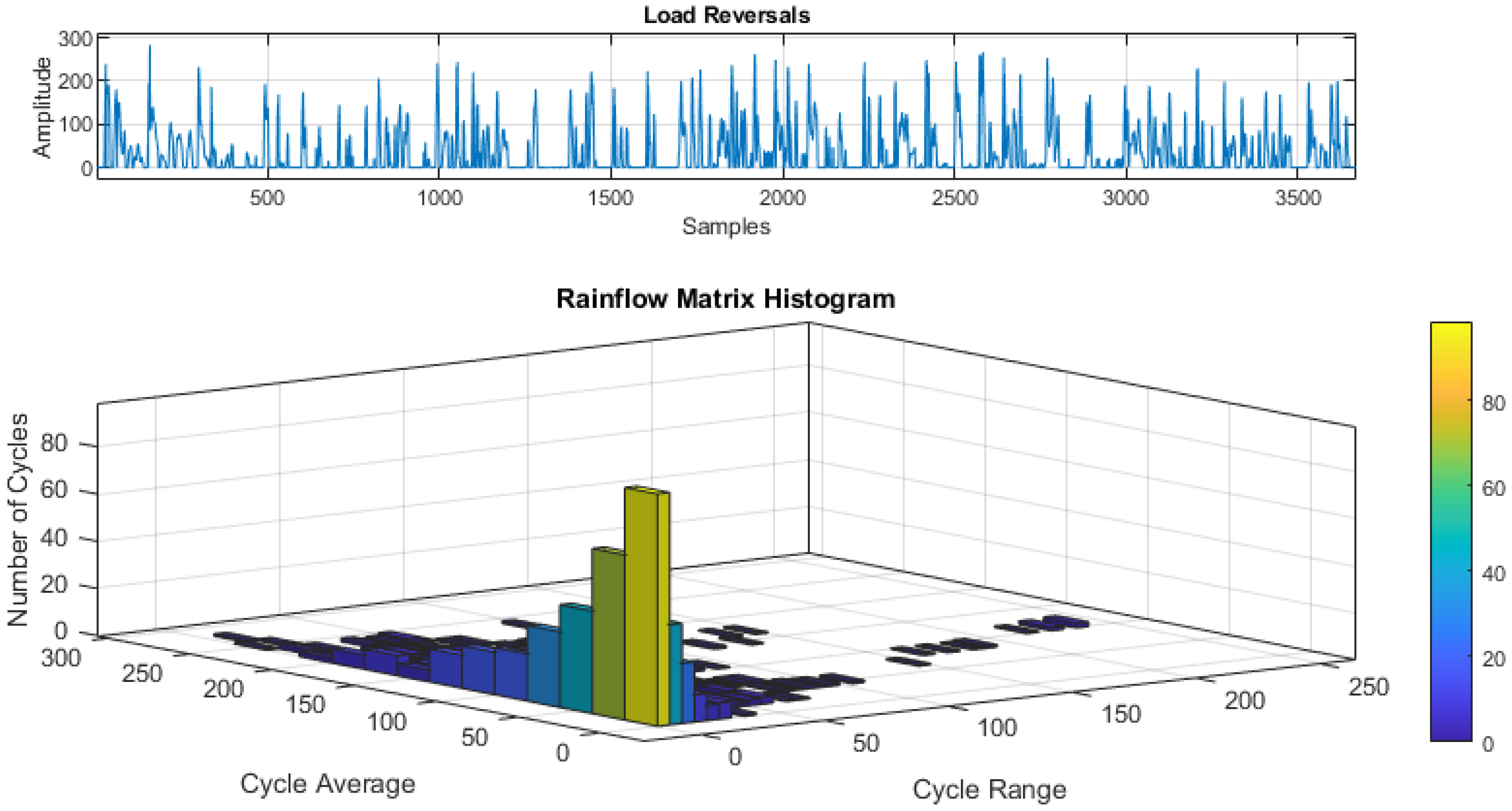
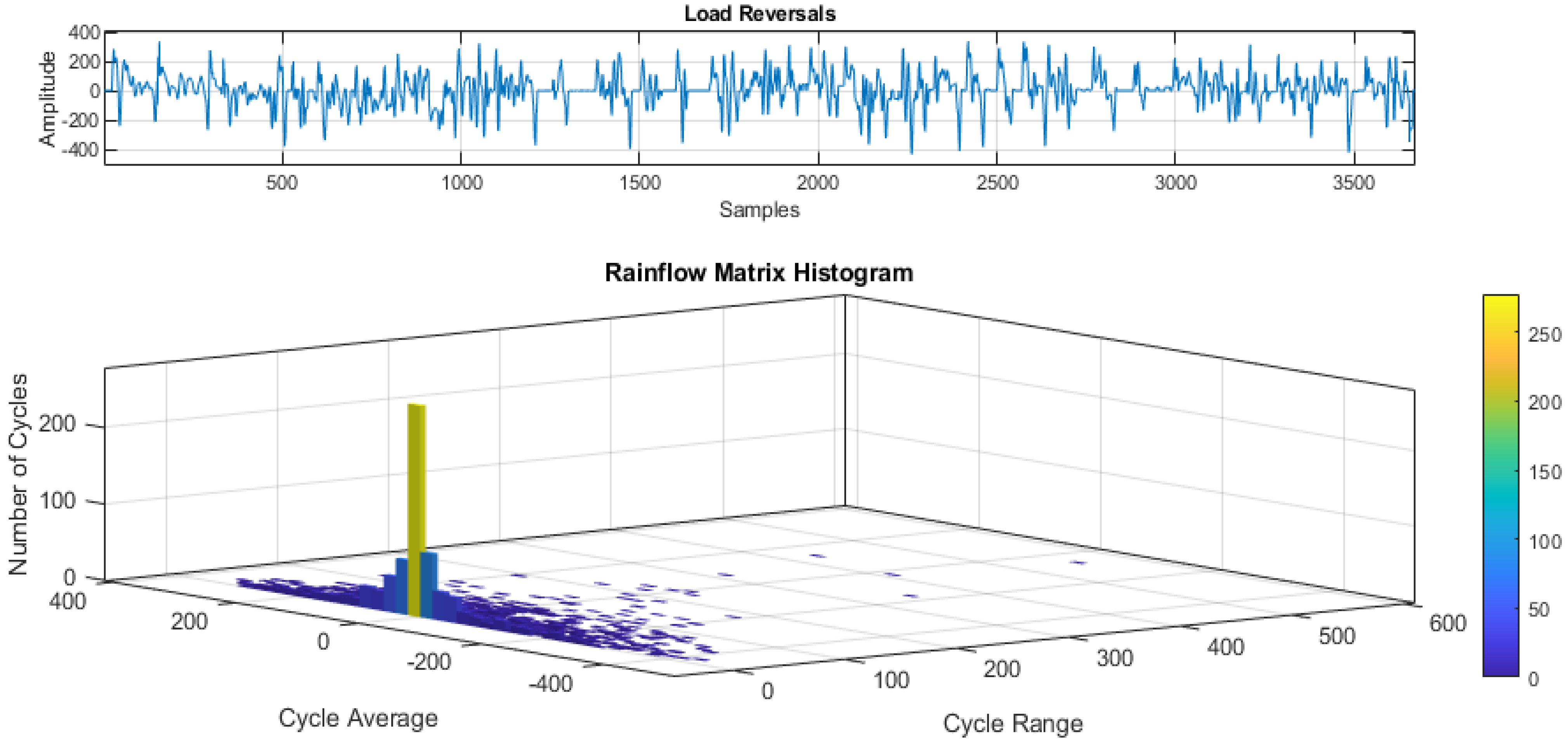
- Experimental data of the component. In this case, it was necessary, through the Rainflow method [33], to extract an equivalent load cycle in terms of stress amplitude (or, in this case, torque amplitude) and the number of cycles. Then, it was necessary to obtain an equivalent load history at load ratio R = −1, using the Goodman criterion [34]. This was done because it is common practice to test the component [32] or the material component [35] at constant amplitude. Finally, the cumulative fatigue damage was evaluated using the Palmgren-Miner criterion [36].
- No experimental data on the component. In this case, it was necessary to characterize the component material through fatigue tests, firstly. This allowed obtaining the curve (stress amplitude-number of the cycle) of the material, which would be used for the cumulative fatigue damage calculation. Then, through a Finite Element Model (FEM) of the component, it was possible to pass from load to equivalent stress on the component. Usually, for steels, the most common criterion to evaluate the equivalent stress is the Von Mises criterion [37]. At this point, the procedure followed the same steps as the previous case.
2.1. Reference Vehicle
Hybrid Electric Vehicle
2.2. Data Acquisition
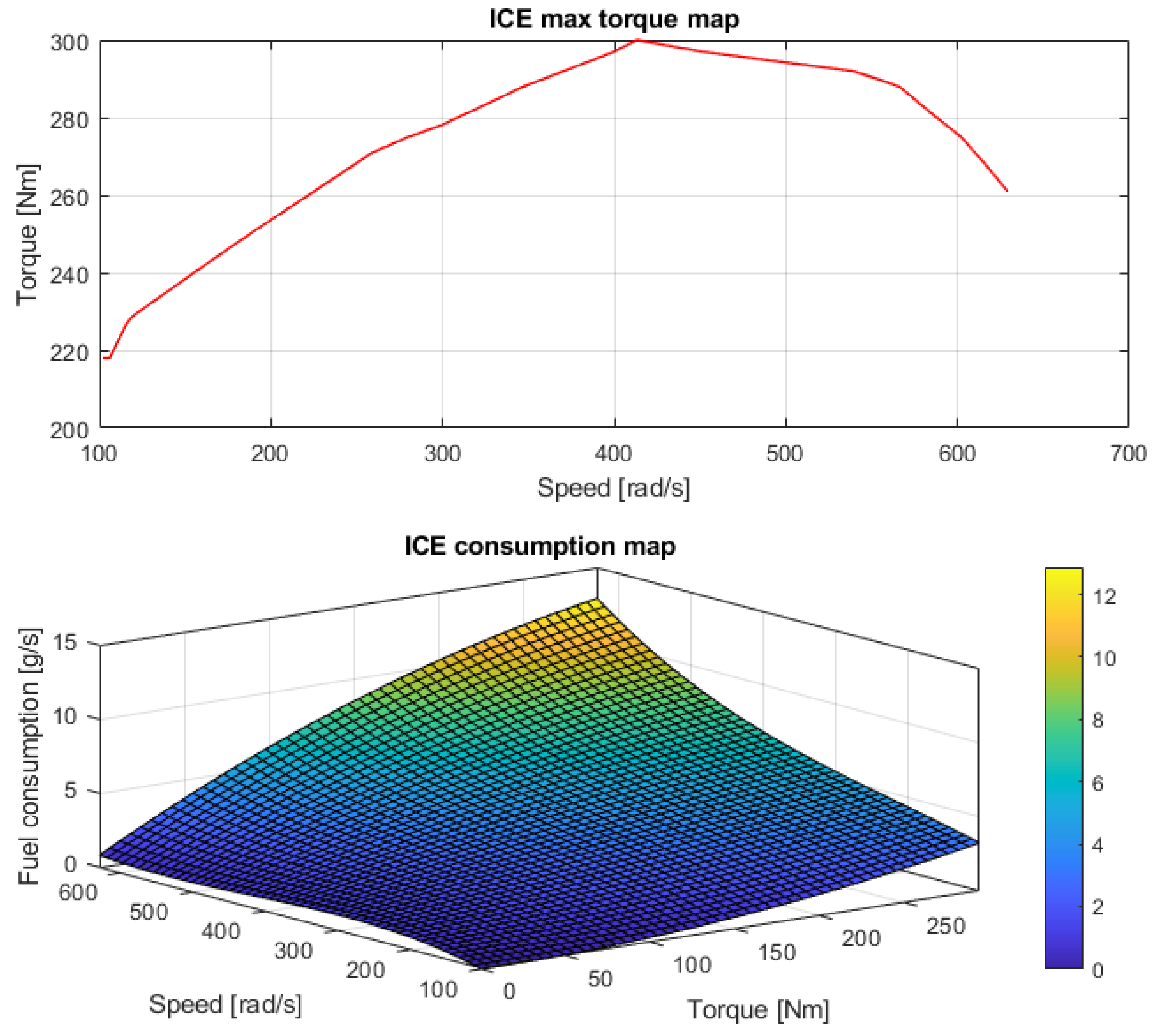
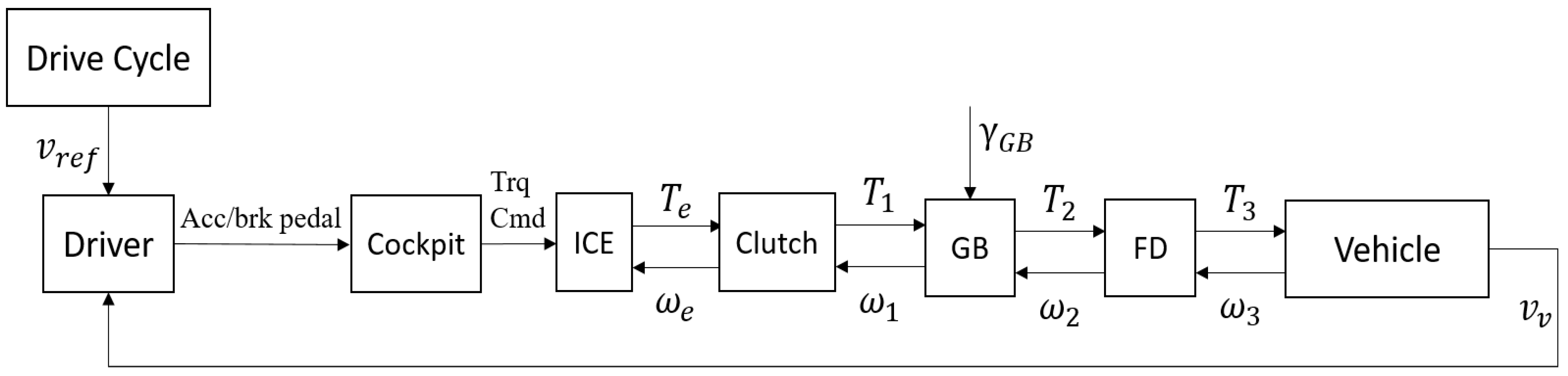
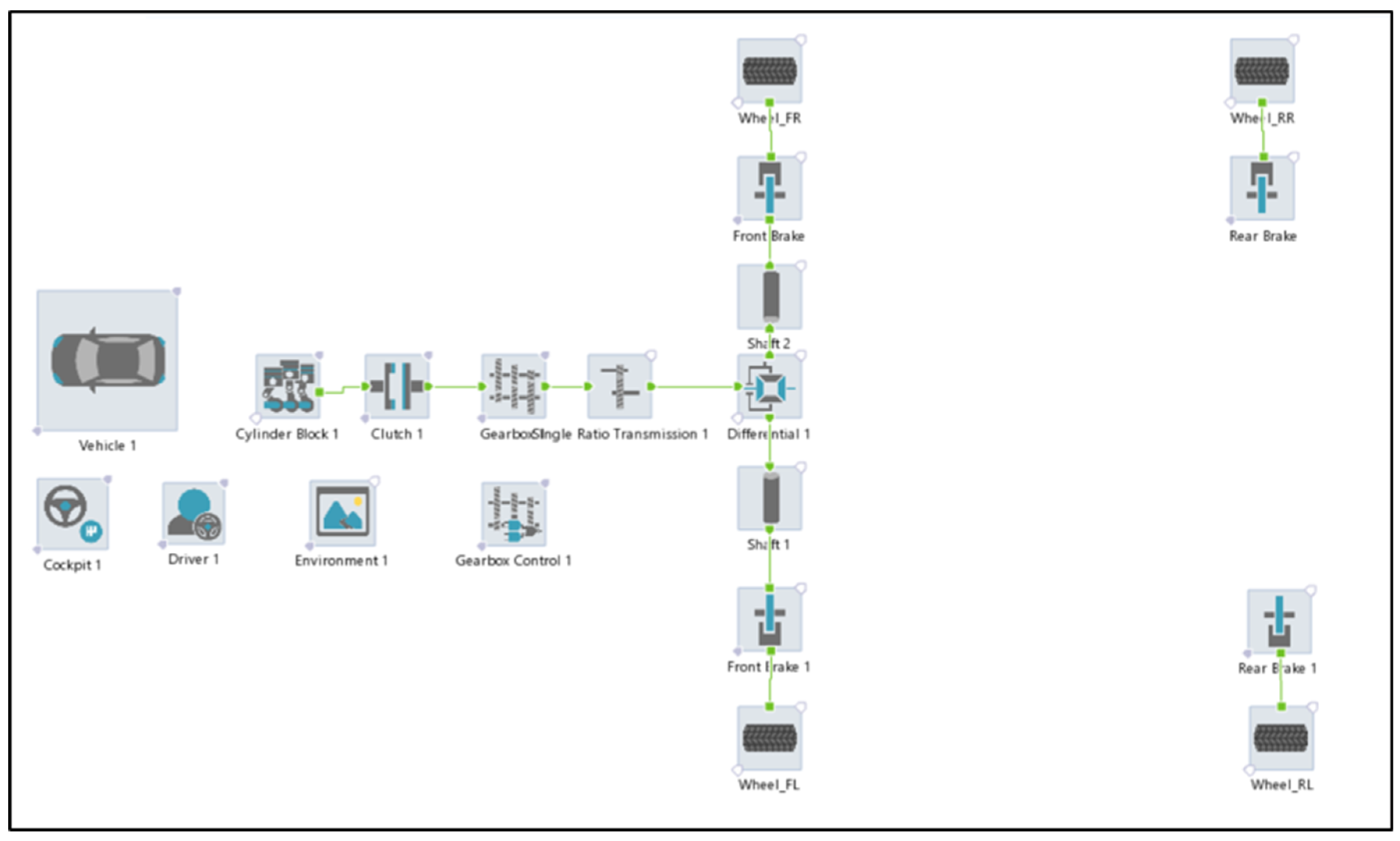
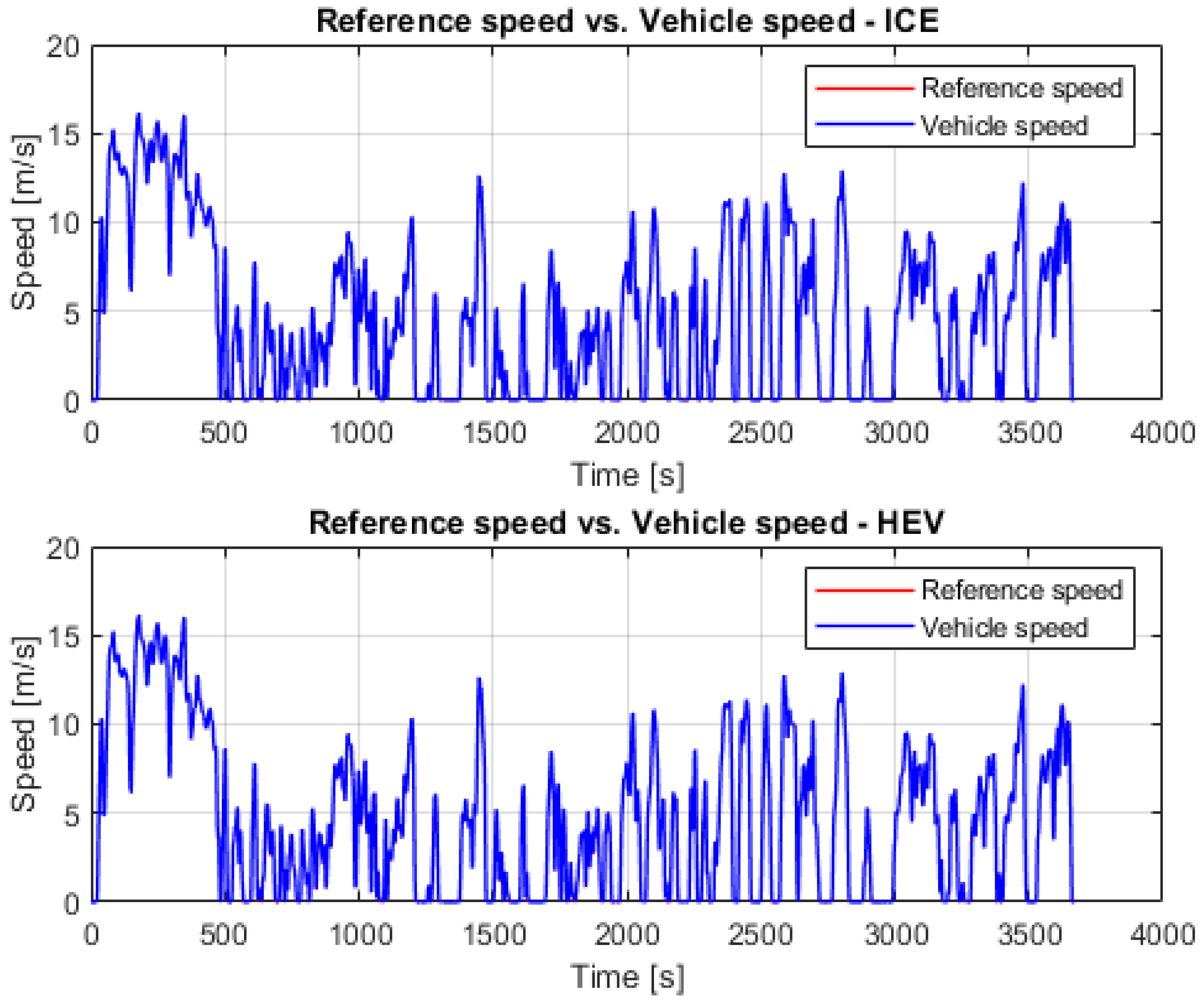
2.3. Conventional Vehicle Feed-Forward Model
- Driver. The task of the driver block was to match the vehicle speed with the reference speed acquired during the driving cycle, through a controller (PI type) acting on the throttle/brake pedal position.
- Internal Combustion Engine (ICE). It received the information from the cockpit block (torque command) in order to develop the required torque .
- Clutch. The clutch block had the task of coupling/decoupling the transmission from the ICE, letting the torque pass or not.
- Gearbox (GB). The gearbox block allowed switching the inserted gear (and hence, gear ratios). The torque level passed from to .
- Final drive (FD). It was the final element of the transmission and consisted of a gear ratio defined according to the datasheet. Also, in this case, the torque level passed from to .
- Vehicle. In the vehicle block, longitudinal vehicle dynamics equations were considered. The traction force, assumed to be applied in the longitudinal direction at the tire contact patch, would be given by the sum of the aerodynamic drag force, rolling resistance force, inertial force (chassis, wheel and engine contribution) and road inclination force.
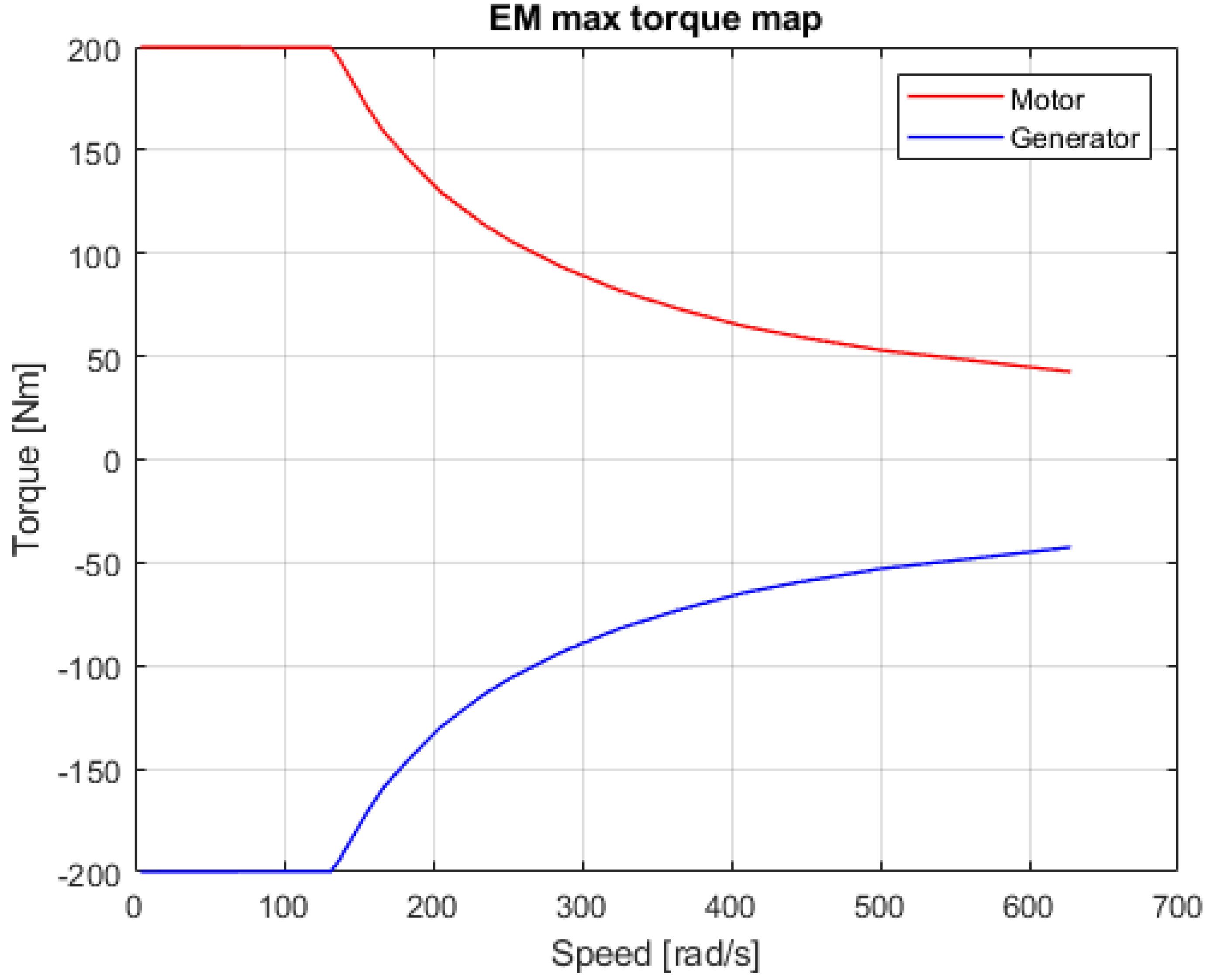
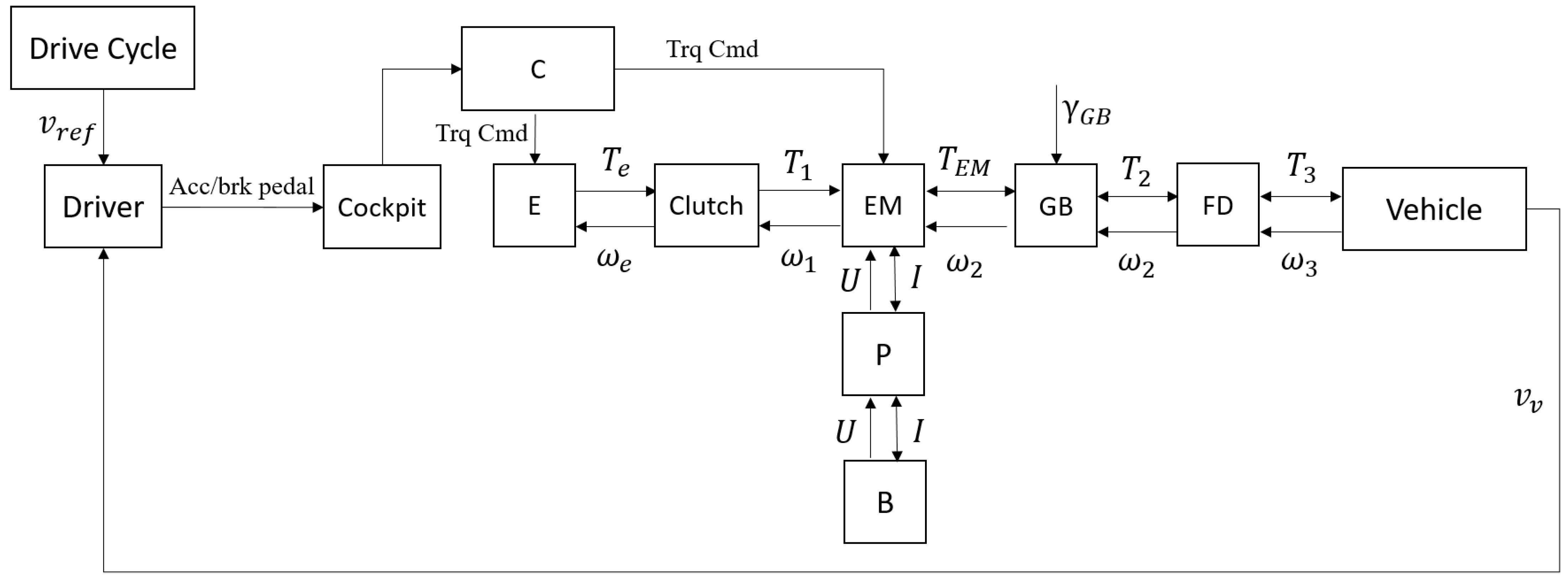
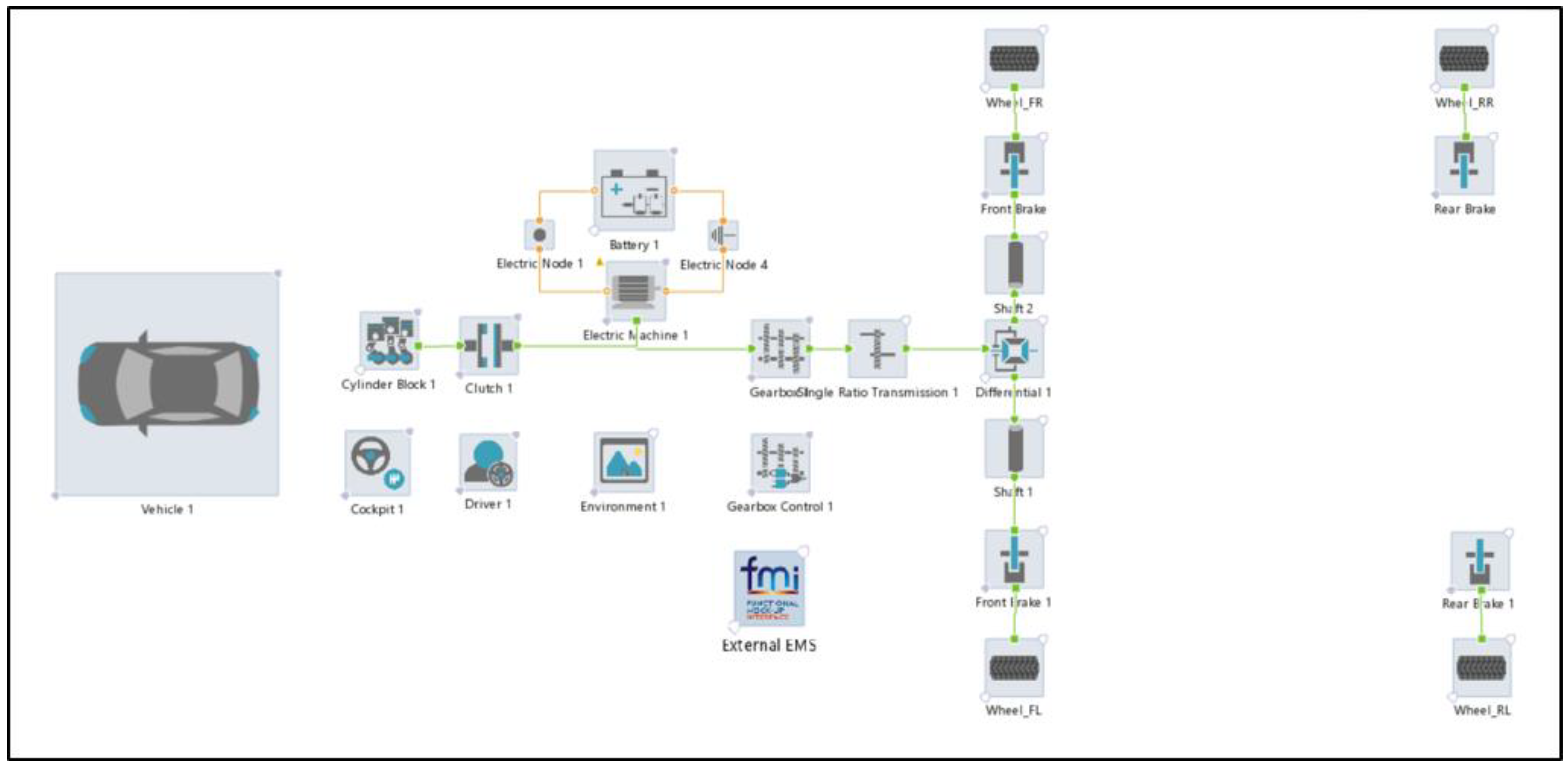
2.4. HEV Feed-Forward Model
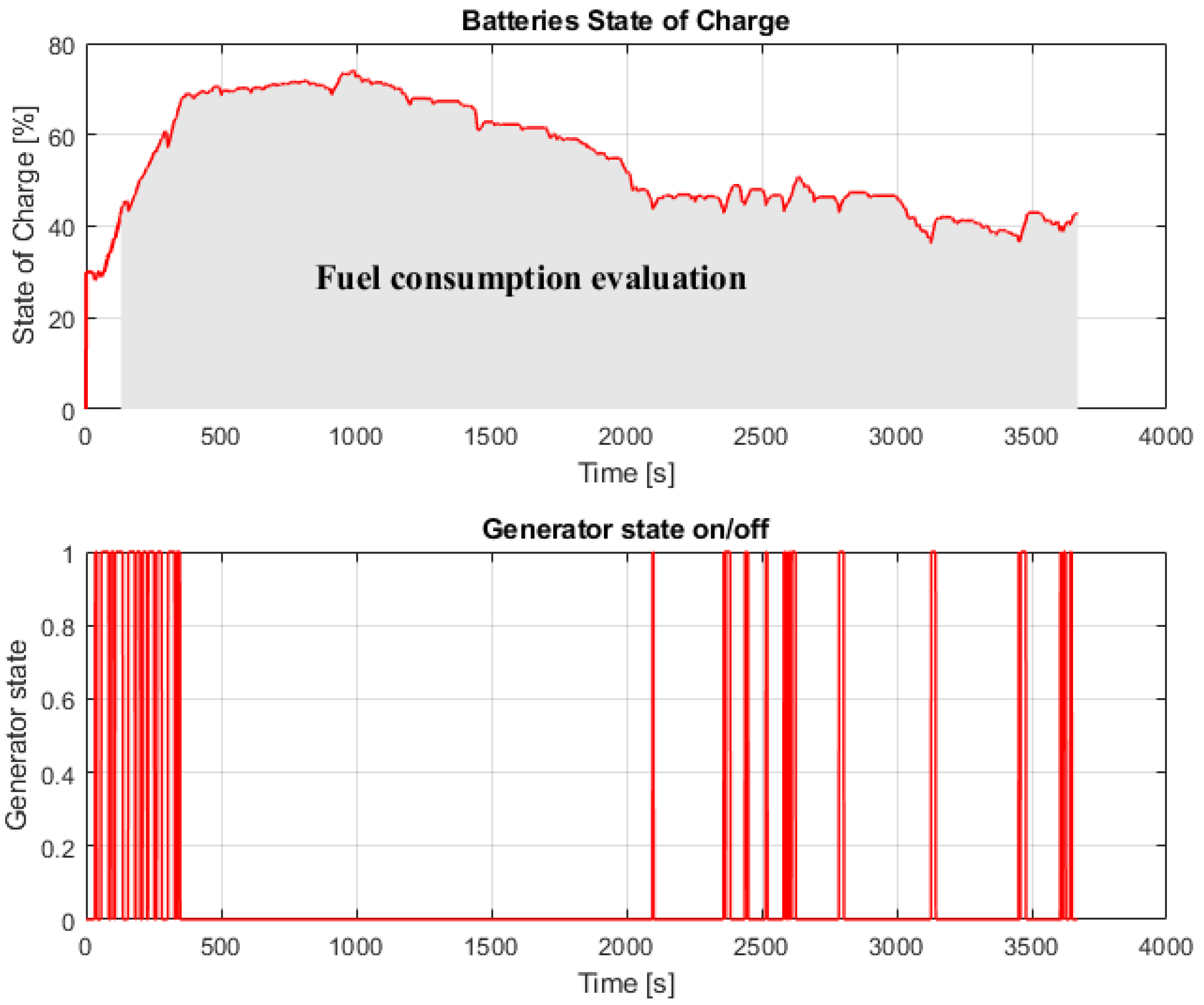
- Full electric mode. The vehicle ran in full electric mode and the power flow was B-P-EM-GB-FD-drive axis. This driving mode was activated when the batteries had a sufficiently high state of charge and the driving cycle was not so hard as to require the intervention of the ICE (for example, urban driving).
- Hybrid electric mode or power assist. The vehicle ran in hybrid mode and the thrust force was due to the combined action of both the electric motor and thermic motor.
- Battery recharging. The vehicle ran in hybrid mode but a part of the electric energy was used for battery recharging.
- Regenerative braking. The electric machine recovered the braking force by acting as generator and recharging the batteries.
- Full thermic mode. The vehicle ran in full thermic mode when the speed was such as to bring the electric motor into the overspeed condition.
2.5. Cumulative Fatigue Damage Evaluation
3. Results
3.1. ICE Vehicle Model and HEV Model Energetic Comparison
- Aerodynamic friction losses (drag force)
- Rolling friction loss, the energy dissipated in the brakes
- Force caused by gravity when driving on non-horizontal roads
- Thrust force for both configurations, as shown in Figure 11.
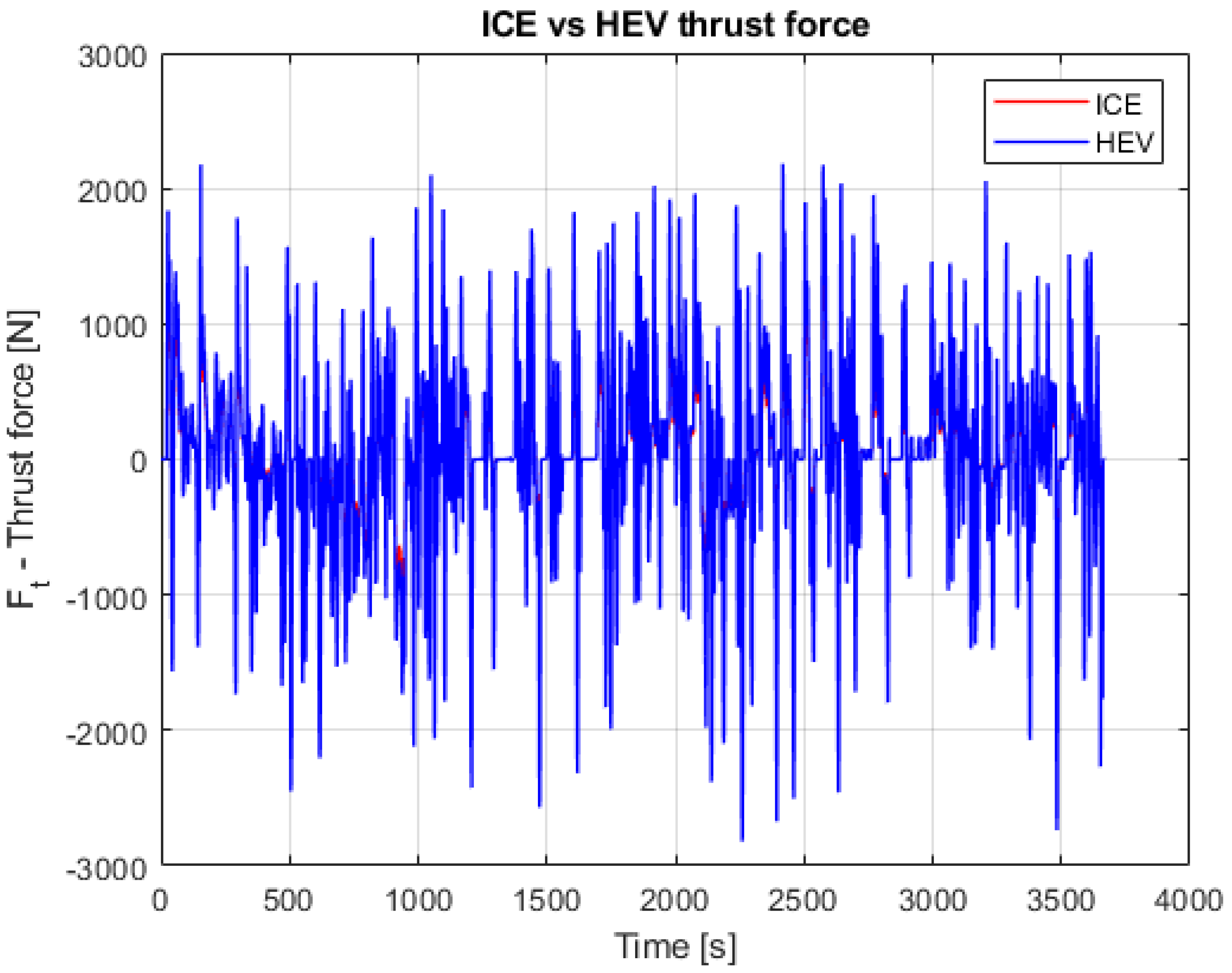
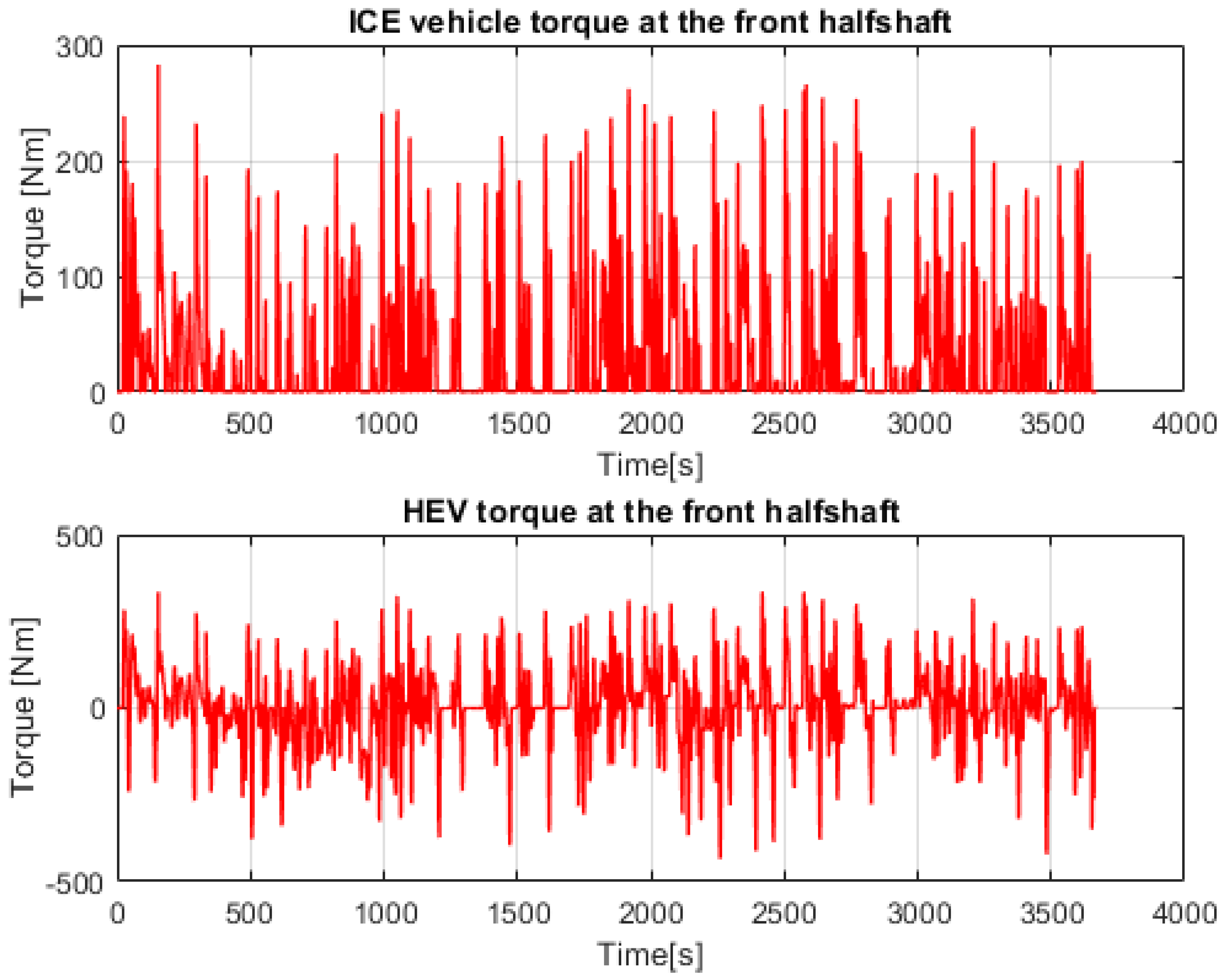
3.2. ICE Vehicle Model and HEV Model Mechanical Comparison
4. Discussion
5. Conclusions
- The results of both the ICE vehicle model and the HEV model developed in AVL CruiseMTM showed that both models were validated, based on the acquired speed profile. Moreover, the control system designed in this work was able to manage the State of Charge of the batteries until the end of the driving cycle, without damaging the batteries.
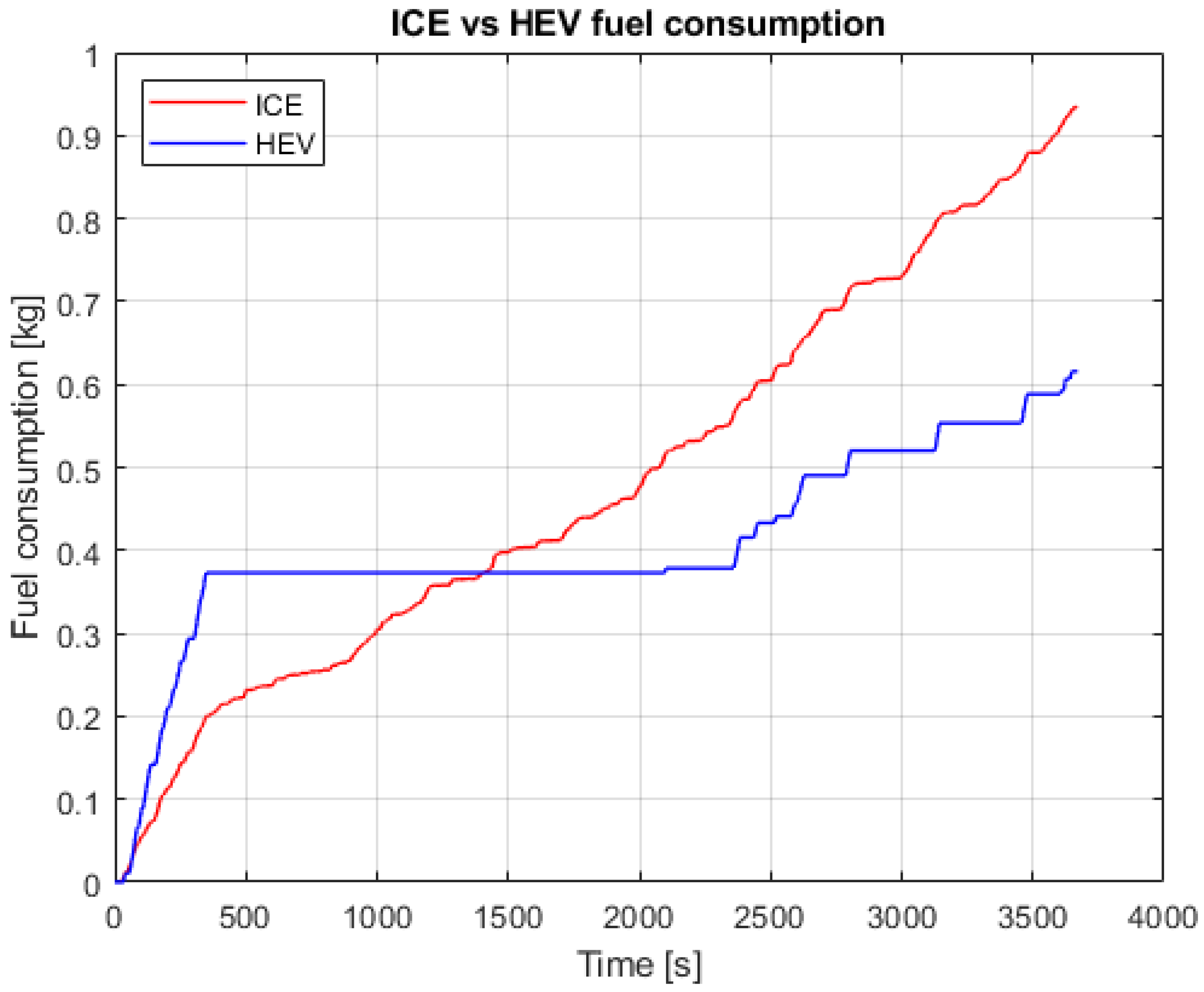
- As expected, the adoption of hybrid electric propulsion led to lower fuel consumption and, as a consequence, fewer pollutant emissions.
- It was shown that, through the application of the Palmgren-Miner criterion, the hybrid electric propulsion led to greater fatigue damage on the front half-shaft with respect to conventional propulsion.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anwar, M.B.; Muratori, M.; Jadun, P.; Hale, E.; Bush, B.; Denholm, P.; Ma, O.; Podkaminer, K. Assessing the value of electric vehicle managed charging: A review of methodologies and results. Energy Environ. Sci. 2022, 15, 466–498. [Google Scholar] [CrossRef]
- Sanguesa, J.A.; Torres-Sanz, V.; Garrido, P.; Martinez, F.J.; Marquez-Barja, J.M. A review on electric vehicles: Technologies and challenges. Smart Cities 2021, 4, 22. [Google Scholar] [CrossRef]
- Bai, S.; Liu, C. Overview of energy harvesting and emission reduction technologies in hybrid electric vehicles. Renew. Sustain. Energy Rev. 2021, 147, 111188. [Google Scholar] [CrossRef]
- Bagheri, S.; Huang, Y.; Walker, P.D.; Zhou, J.L.; Surawski, N.C. Strategies for improving the emission performance of hybrid electric vehicles. Sci. Total Environ. 2021, 771, 144901. [Google Scholar] [CrossRef]
- Jacyna, M.; Żochowska, R.; Sobota, A.; Wasiak, M. Scenario analyses of exhaust emissions reduction through the introduction of electric vehicles into the city. Energies 2021, 14, 2030. [Google Scholar] [CrossRef]
- Kazemzadeh, E.; Koengkan, M.; Fuinhas, J.A. Effect of Battery-Electric and Plug-In Hybrid Electric Vehicles on PM2.5 Emissions in 29 European Countries. Sustainability 2022, 14, 2188. [Google Scholar] [CrossRef]
- Haghbin, S.; Bahman, A.S.; Chen, H. Guest Editorial Special Issue on Novel Hybrid and Electric Powertrain Architectures. IEEE Trans. Transp. Electrif. 2022, 8, 6–8. [Google Scholar] [CrossRef]
- Iclodean, C.; Varga, B.; Burnete, N.; Cimerdean, D.; Jurchiş, B. Comparison of Different Battery Types for Electric Vehicles. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017; Volume 252. [Google Scholar] [CrossRef]
- Adegbohun, F.; von Jouanne, A.; Lee, K.Y. Autonomous battery swapping system and methodologies of electric vehicles. Energies 2019, 12, 667. [Google Scholar] [CrossRef]
- Affanni, A.; Bellini, A.; Franceschini, G.; Guglielmi, P.; Tassoni, C. Battery choice and management for new-generation electric vehicles. IEEE Trans. Ind. Electron. 2005, 52, 1343–1349. [Google Scholar] [CrossRef]
- Dixon, J. Energy storage for electric vehicles. In Proceedings of the 2010 IEEE International Conference on Industrial Technology, Via del Mar, Chile, 14–17 March 2010; pp. 20–25. [Google Scholar] [CrossRef]
- Metais, M.O.; Jouini, O.; Perez, Y.; Berrada, J.; Suomalainen, E. Too much or not enough? Planning electric vehicle charging infrastructure: A review of modeling options. Renew. Sustain. Energy Rev. 2022, 153, 111719. [Google Scholar] [CrossRef]
- Schulz, F.; Rode, J. Public charging infrastructure and electric vehicles in Norway. Energy Policy 2022, 160, 112660. [Google Scholar] [CrossRef]
- Zhang, H.; Sheppard, C.J.R.; Lipman, T.E.; Zeng, T.; Moura, S.J. Charging infrastructure demands of shared-use autonomous electric vehicles in urban areas. Transp. Res. Part D Transp. Environ. 2020, 78, 102210. [Google Scholar] [CrossRef]
- Hannan, M.A.; Azidin, F.A.; Mohamed, A. Hybrid electric vehicles and their challenges: A review. Renew. Sustain. Energy Rev. 2014, 29, 135–150. [Google Scholar] [CrossRef]
- Ehsani, M.; Gao, Y.; Miller, J.M. Hybrid electric vehicles: Architecture and motor drives. Proc. IEEE 2007, 95, 719–728. [Google Scholar] [CrossRef]
- Lanzarotto, D.; Marchesoni, M.; Passalacqua, M.; Prato, A.P.; Repetto, M. Overview of different hybrid vehicle architectures. IFAC-PapersOnLine 2018, 51, 218–222. [Google Scholar] [CrossRef]
- Singh, K.V.; Bansal, H.O.; Singh, D. A comprehensive review on hybrid electric vehicles: Architectures and components. J. Mod. Transp. 2019, 27, 77–107. [Google Scholar] [CrossRef]
- Hou, S.J.; Zou, Y.; Chen, R. Feed-forward model development of a hybrid electric truck for power management studies. In Proceedings of the 2011 2nd International Conference on Intelligent Control and Information Processing, Harbin, China, 25–28 July 2011; pp. 550–555. [Google Scholar] [CrossRef]
- Singh, K.V.; Bansal, H.O.; Singh, D. Feed-forward modeling and real-time implementation of an intelligent fuzzy logic-based energy management strategy in a series–parallel hybrid electric vehicle to improve fuel economy. Electr. Eng. 2020, 102, 967–987. [Google Scholar] [CrossRef]
- Mohan, G.; Assadian, F.; Longo, S. Comparative Analysis of Forward-Facing Models vs. Backward-Facing Models in Powertrain Component Sizing; IET Conference Publishing: London, UK, 2013; Volume 2013, pp. 1–6. [Google Scholar] [CrossRef]
- Ma, D.; Han, Y.; Qu, F.; Jin, S. Modeling and analysis of car-following behavior considering backward-looking effect. Chinese Phys. B 2021, 30, 034501. [Google Scholar] [CrossRef]
- Schnelle, S.; Wang, J.; Jagacinski, R.; Su, H. jun A feedforward and feedback integrated lateral and longitudinal driver model for personalized advanced driver assistance systems. Mechatronics 2018, 50, 177–188. [Google Scholar] [CrossRef]
- Geng, S.; Schulte, T.; Maas, J. Model-Based Analysis of Different Equivalent Consumption Minimization Strategies for a Plug-In Hybrid Electric Vehicle. Appl. Sci. 2022, 12, 2905. [Google Scholar] [CrossRef]
- D’Andrea, D.; Risitano, G.; Desiderio, E.; Quintarelli, A.; Milone, D.; Alberti, F. Artificial Neural Network Prediction of the Optimal Setup Parameters of a Seven Degrees of Freedom Mathematical Model of a Race Car: IndyCar Case Study. Vehicles 2021, 3, 19, ISBN 3933856612. [Google Scholar] [CrossRef]
- Carputo, F.; D’Andrea, D.; Risitano, G.; Sakhnevych, A.; Santonocito, D.; Farroni, F. A Neural-Network-Based Methodology for the Evaluation of the Center of Gravity of a Motorcycle Rider. Vehicles 2021, 3, 23. [Google Scholar] [CrossRef]
- D’andrea, D.; Cucinotta, F.; Farroni, F.; Risitano, G.; Santonocito, D.; Scappaticci, L. Development of machine learning algorithms for the determination of the centre of mass. Symmetry 2021, 13, 401. [Google Scholar] [CrossRef]
- Nagarkar, M.P.; El-Gohary, M.A.; Bhalerao, Y.J.; Vikhe Patil, G.J.; Zaware Patil, R.N. Artificial neural network predication and validation of optimum suspension parameters of a passive suspension system. SN Appl. Sci. 2019, 1, 569. [Google Scholar] [CrossRef]
- Du, G.; Zou, Y.; Zhang, X.; Guo, L.; Guo, N. Energy management for a hybrid electric vehicle based on prioritized deep reinforcement learning framework. Energy 2022, 241, 122523. [Google Scholar] [CrossRef]
- Galvagno, A.; Previti, U.; Famoso, F.; Brusca, S. An Innovative Methodology to Take into Account Traffic Information on WLTP Cycle for Hybrid Vehicles. Energies 2021, 14, 1548. [Google Scholar] [CrossRef]
- Farfan-Cabrera, L.I. Tribology of electric vehicles: A review of critical components, current state and future improvement trends. Tribol. Int. 2019, 138, 473–486. [Google Scholar] [CrossRef]
- Barone, C.; Casati, R.; Dusini, L.; Gerbino, F.; Guglielmino, E.; Risitano, G.; Santonocito, D. Fatigue life evaluation of car front halfshaft. Procedia Struct. Integr. 2018, 12, 3–8. [Google Scholar] [CrossRef]
- Amzallag, C.; Gerey, J.P.; Robert, J.L.; Bahuaud, J. Standardization of the rainflow counting method for fatigue analysis. Int. J. Fatigue 1994, 16, 287–293. [Google Scholar] [CrossRef]
- Nicholas, T.; Zuiker, J.R. On the use of the Goodman diagram for high cycle fatigue design. Int. J. Fract. 1989, 80, 219–235. [Google Scholar] [CrossRef]
- Dikmen, F.; Bayraktar, M.; Guclu, R. Railway axle analyses: Fatigue damage and life analysis of rail vehicle axle. Stroj. Vestn./J. Mech. Eng. 2012, 58, 545–552. [Google Scholar] [CrossRef]
- Kauzlarich, J.J. The Palmgren-Miner rule derived. Tribol. Ser. 1989, 14, 175–179. [Google Scholar] [CrossRef]
- Barsanescu, P.D.; Comanici, A.M. von Mises hypothesis revised. Acta Mech. 2017, 228, 433–446. [Google Scholar] [CrossRef]
- Starke, P.; Walther, F.; Eifler, D. New fatigue life calculation method for quenched and tempered steel SAE 4140. Mater. Sci. Eng. A 2009, 523, 246–252. [Google Scholar] [CrossRef]
- Niesłony, A.; el Dsoki, C.; Kaufmann, H.; Krug, P. New method for evaluation of the Manson-Coffin-Basquin and Ramberg-Osgood equations with respect to compatibility. Int. J. Fatigue 2008, 30, 1967–1977. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| , vehicle mass | 1505 kg |
| , frontal area | |
| , drag coefficient | 0.445 |
| , wheelbase | 2.817 m |
| , wheel rolling radius | 0.305 m |
| , gear ratio-1st | 3.54 |
| , gear ratio-2nd | 1.92 |
| , gear ratio-3rd | 1.28 |
| , gear ratio-4th | 0.91 |
| , gear ratio-5th | 0.67 |
| , gear ratio-6th | 0.53 |
| , final drive ratio-front | 4.35 |
| Parameter | Value |
|---|---|
| , vehicle mass | 1770 kg |
| , frontal area | |
| , drag coefficient | 0.445 |
| , wheelbase | 2.817 m |
| , wheel rolling radius | 0.305 m |
| , gear ratio-1st | 3.54 |
| , gear ratio-2nd | 1.92 |
| , gear ratio-3rd | 1.28 |
| , gear ratio-4th | 0.91 |
| , gear ratio-5th | 0.67 |
| , gear ratio-6th | 0.53 |
| , final drive ratio-front | 4.35 |
| , battery energy | 1299.5 Wh |
| , battery nominal voltage | 230 V |
| , battery capacity | 5.65 Ah |
| Parameter | Value |
|---|---|
| P, proportional gain | 10 |
| I, integrative gain | 0.2 |
| Parameter | Value (ICE) | Value (HEV) |
|---|---|---|
| Considered total distance | 17.28 km | 16.09 km |
| Fuel consumption | 0.9 kg | 0.5 kg |
| Fuel density (Diesel) | 0.835 kg/L | 0.835 kg/L |
| Average fuel consumption | 15.44 km/L | 27.71 km/L |
| 22.5 | 20 | 34,500 | 42.5 | −2.5 | −0.05 |
| 25 | 20 | 57,500 | 45 | −5 | −0.1 |
| 27.5 | 20 | 69,000 | 47.5 | −7.5 | −0.15 |
| 32.5 | 20 | 11,500 | 52.5 | −12.5 | −0.23 |
| 35 | 20 | 11,500 | 55 | −15 | −0.27 |
| 0 | 40 | 1,000,500 | 40 | 40 | 1 |
| 2.5 | 40 | 529,000 | 42.5 | 37.5 | 0.88 |
| 5 | 40 | 506,000 | 45 | 35 | 0.77 |
| 7.5 | 40 | 218,500 | 47.50 | 32.5 | 0.68 |
| 10 | 40 | 149,500 | 50 | 30 | 0.60 |
| 45 | −40 | 46,000 | 5 | −85 | −17 |
| 87.5 | −40 | 11,500 | 47.5 | −127.5 | −2.68 |
| 112.5 | −40 | 11,500 | 72.5 | −152.5 | −2.10 |
| 202.5 | −40 | 11,500 | 162.5 | −242.5 | −1.49 |
| 0 | −20 | 1,978,000 | −20 | −20 | 1 |
| 2.5 | −20 | 552,000 | −17.5 | −22.5 | 1.28 |
| 5 | −20 | 345,000 | −15 | −25 | 1.6 |
| 7.5 | −20 | 253,000 | −12.5 | −27.5 | 2.2 |
| 10 | −20 | 230,000 | −10 | −30 | 3 |
| 12.5 | −20 | 69,000 | −7.5 | −32.50 | 4.3 |
| 45.4 | 11,500 | 3951282.5 |
| 48 | 11,500 | 2889408.1 |
| 49.4 | 23,000 | 2516954.1 |
| 60.6 | 11,500 | 919579.2 |
| 63.4 | 34,500 | 833674.3 |
| 66.3 | 46,000 | 747769.4 |
| 45.8 | 11,500 | 3752326.1 |
| 49.2 | 11,500 | 2553792.5 |
| 54.3 | 11,500 | 1,546,168.7 |
| 102.8 | 11,500 | 69,226.8 |
| 45.48 | 11,500 | 3,917,411.8 |
| 81.8 | 11,500 | 274,118.1 |
| 49.5 | 11,500 | 2,488,406.4 |
| 50.6 | 11,500 | 2,186,339.2 |
| 49.4 | 11,500 | 2,498,245.4 |
| 55.4 | 11,500 | 1,375,488.1 |
| 78.5 | 11,500 | 374,097.2 |
| 56.1 | 11,500 | 1,286,968.4 |
| 127.1 | 11,500 | 20,284.3 |
| 49.2 | 23,000 | 2,566,367.9 |
| 69.2 | 23,000 | 657,144.8 |
| 59.2 | 11,500 | 962,304.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Previti, U.; Galvagno, A.; Risitano, G.; Alberti, F. Smart Design: Application of an Automatic New Methodology for the Energy Assessment and Redesign of Hybrid Electric Vehicle Mechanical Components. Vehicles 2022, 4, 586-607. https://doi.org/10.3390/vehicles4020034
Previti U, Galvagno A, Risitano G, Alberti F. Smart Design: Application of an Automatic New Methodology for the Energy Assessment and Redesign of Hybrid Electric Vehicle Mechanical Components. Vehicles. 2022; 4(2):586-607. https://doi.org/10.3390/vehicles4020034
Chicago/Turabian StylePreviti, Umberto, Antonio Galvagno, Giacomo Risitano, and Fabio Alberti. 2022. "Smart Design: Application of an Automatic New Methodology for the Energy Assessment and Redesign of Hybrid Electric Vehicle Mechanical Components" Vehicles 4, no. 2: 586-607. https://doi.org/10.3390/vehicles4020034
APA StylePreviti, U., Galvagno, A., Risitano, G., & Alberti, F. (2022). Smart Design: Application of an Automatic New Methodology for the Energy Assessment and Redesign of Hybrid Electric Vehicle Mechanical Components. Vehicles, 4(2), 586-607. https://doi.org/10.3390/vehicles4020034








