CFD Analysis of the Location of a Rear Wing on an Aston Martin DB7 in Order to Optimize Aerodynamics for Motorsports
Abstract
:1. Introduction
2. Methods
3. Results and Discussion
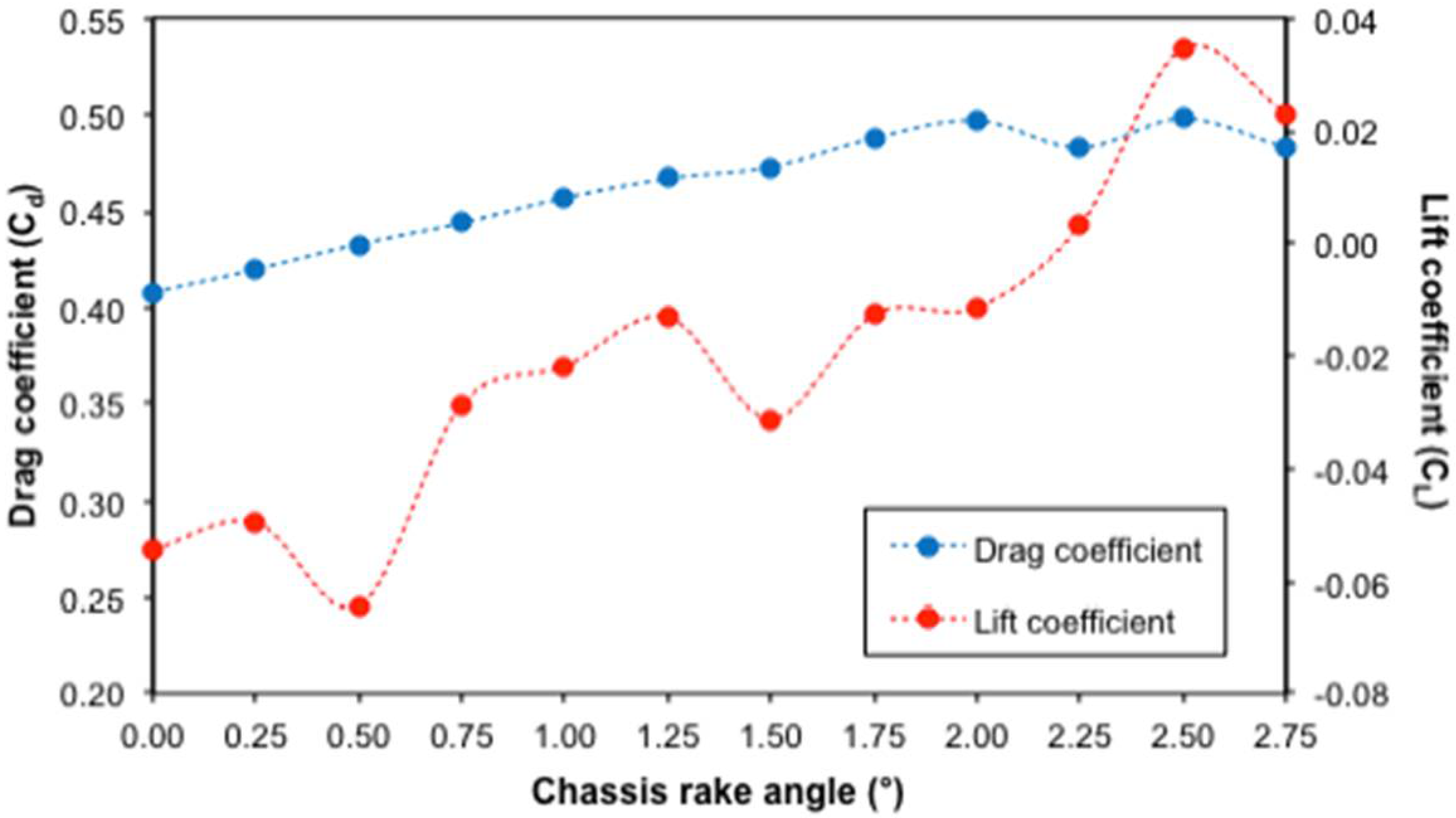
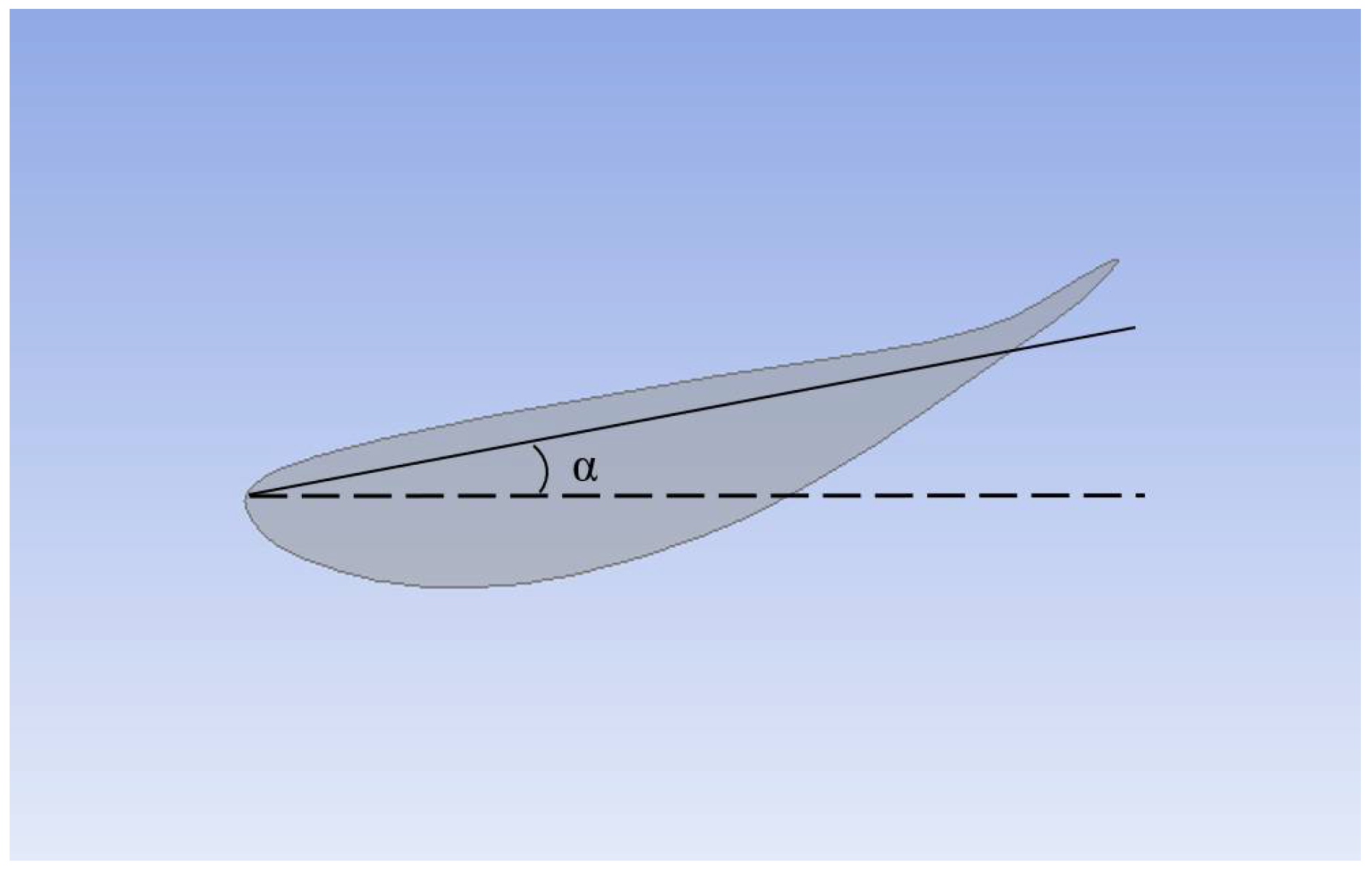
3.1. Rake Angle
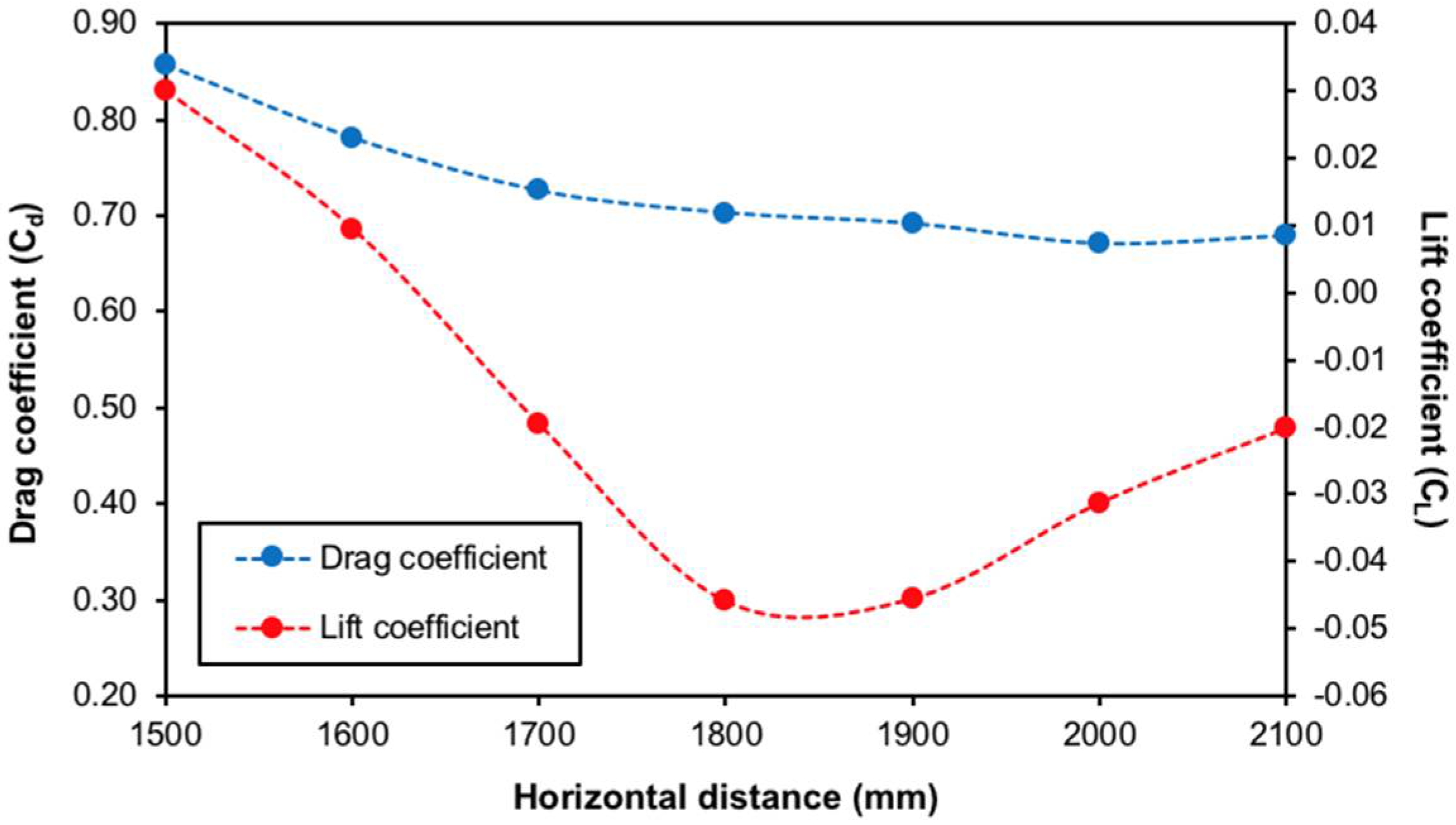
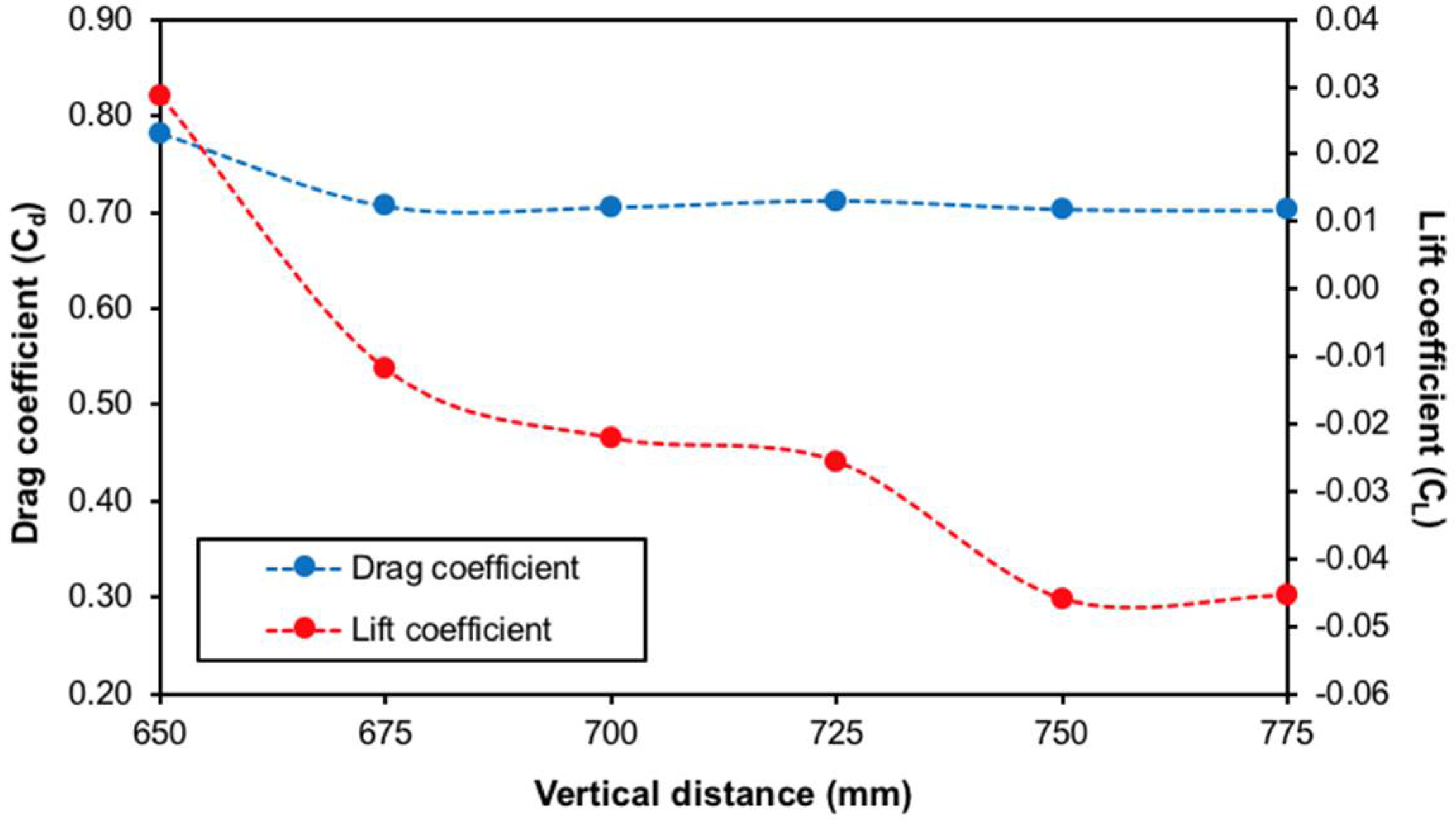
3.2. Rear Wing
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Katz, J. Race Car Aerodynamics, 2nd ed.; Bentley Publishers: Cambridge, UK, 1995. [Google Scholar]
- Wang, J.; Li, H.; Liu, Y.; Liu, T.; Gao, H. Aerodynamic research of a racing car based on wind tunnel test and computational fluid dynamics, The 4th International Conference on Mechatronics and Mechanical Engineering (ICMME 2017). In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 153, p. 04011. [Google Scholar]
- Sudin, M.N.; Abdullah, M.A.; Shamsuddin, S.A.; Ramli, F.R.; Tahir, M.M. Review of research on vehicles aerodynamic drag reduction methods. Int. J. Mech. Mechatron. Eng. 2014, 14, 35–47. [Google Scholar]
- Iljaž, J.; Škerget, L.; Štrakl, M.; Marn, J. Optimization of SAE formula rear wing. J. Mech. Eng. 2016, 62, 263–272. [Google Scholar] [CrossRef] [Green Version]
- Hetawal, S.; Gophane, M.; Ajay, B.K.; Mukkamala, Y. Aerodynamic study of formula SAE car. Procedia Eng. 2014, 97, 1198–1207. [Google Scholar] [CrossRef] [Green Version]
- Mariani, F.; Poggiani, C.; Risi, F.; Scappaticci, L. Formula-SAE racing car: Experimental and numerical analysis of the external aerodynamics. Energy Procedia 2015, 81, 1013–1029. [Google Scholar] [CrossRef] [Green Version]
- Doddegowda, P.; Bychkovsky, A.; George, A. Use of computational fluid dynamics for the design of formula SAE race car aerodynamics. In Proceedings of the 2006 SAE World Congress, Detroit, MI, USA, 3–6 April 2006. SAE Technical Paper 2006-01-0807. [Google Scholar]
- Basso, M.; Cravero, C.; Marsano, D. Aerodynamic Effect of the Gurney flap on the front wing of a F1 car and flow interactions with car components. Energies 2021, 14, 2059. [Google Scholar] [CrossRef]
- Fernandez-Gamiz, U.; Gomez-Mármol, M.; Chacón-Rebollo, T. Computational modeling of Gurney flaps and microtabs by POD method. Energies 2018, 11, 2091. [Google Scholar] [CrossRef] [Green Version]
- Damjanović, D.; Kozak, D.; Zivić, M.; Ivandić, Ž.; Baškarić, T. CFD analysis of concept car in order to improve aerodynamics. Járműipari Innováció 2011, 1, 108–115. [Google Scholar]
- Desai, M.; Channiwala, S.A.; Nagarsheth, H.J. Experimental and computational aerodynamic investigations of a car. WSEAS Trans. Fluid Mech. 2008, 3, 359–368. [Google Scholar]
- 2021 Liqui Moly New Millennium Series Regulations. Available online: https://68403ce7-faa5-44b9-9ba0-313b6d9859a7.filesusr.com/ugd/838e83_395634b45f2a41db8bf84de5f74a3920.pdf (accessed on 26 August 2021).
- Classic & Historic Thunder Saloons 2021 Championship Regs. Available online: https://classictouringcars.com/wp-content/uploads/2021/02/2021-CTCRC-Classic-Thunder-Regs.pdf (accessed on 26 August 2021).
- Reglement 2021 Trophee GT Classic. Available online: https://www.hvmracing.fr/wp-content/uploads/2021/01/Reglement-GT-Classic-2021-complet-def-avec-Visa.pdf (accessed on 26 August 2021).
- Competitors: Vehicles. Available online: https://www.motorsportuk.org/wp-content/uploads/2020/12/2021-03-08-motorsport-uk-yearbook-2021-p145-164-common-regulations-competitors-vehicles-j.pdf (accessed on 26 August 2021).
- Hu, X.; Zhang, R.; Ye, J.; Xu, Y.; Zhao, Z. Influence of different diffuser angle on Sedan’s aerodynamic characteristics. Phys. Procedia 2011, 22, 239–245. [Google Scholar] [CrossRef] [Green Version]
- Which Turbulence Model Should I Choose for My CFD Application? Available online: https://uk.comsol.com/blogs/which-turbulence-model-should-choose-cfd-application/ (accessed on 23 October 2019).
- Rajamani, G. CFD Analysis of Air Flow Interactions in Vehicle Platoons. SoA, Mechanical and Manufacturing Engineering RMIT University. 2006. Available online: https://core.ac.uk/download/pdf/15615017.pdf (accessed on 15 May 2022).
- Singh, R. CFD simulation of NASCAR racing car aerodynamics. In Proceedings of the SAE World Congress & Exhibition, Detroit, MI, USA, 14–17 April 2008. SAE Technical Paper. [Google Scholar] [CrossRef]
- Choosing the Right Turbulence Model for Your CFD Simulation. Available online: https://www.engineering.com/DesignSoftware/DesignSoftwareArticles/ArticleID/13743/Choosing-the-Right-Turbulence-Model-for-Your-CFD-Simulation.aspx (accessed on 15 April 2020).
- Cavcar, M. The International Standard Atmosphere (ISA); Anadolu University: Eskişehir, Turkey, 2000. [Google Scholar]
- Bhattacharjee, S.; Arora, B.; Kashyap, V. Optimization of race car front splitter placement using CFD. In Proceedings of the SAE World Congress & Exhibition, Detroit, MI, USA, 9–11 April 2019. SAE Technical Paper. [Google Scholar] [CrossRef]
- Cakir, M. CFD Study on Aerodynamic Effects of a Rear Wing/Spoiler on a Passenger Vehicle; MSc; Santa Clara University: Santa Clara, CA, USA, 2012. [Google Scholar]
- Full-Scale Aerodynamic Wind Tunnel. Available online: https://www.horiba-mira.com/facilities/full-scale-aerodynamic-wind-tunnel/ (accessed on 26 August 2021).
- Aston Martin DB7 Vantage: Ongoing project details. Available online: https://www.arbmotorsports.com/aston-martin-db7 (accessed on 2 April 2022).
- Džijan, I.; Pašić, A.; Buljac, A.; Kozmar, H. Aerodynamic forces acting on a race car for various ground clearances and rake angles. J. Appl. Fluid Mech. 2019, 12, 361–368. [Google Scholar] [CrossRef]
- Dowsey, D. DB7 DB Legend Revived. In Aston Martin Power Beauty and Soul, 2nd ed.; The Images Publishing Group: Victoria, Australia, 2019; pp. 124–133. [Google Scholar]
- Katz, J.; Garcia, D. Aerodynamic effects of Indy car components. SAE Trans. 2002, 111, 2322–2330. [Google Scholar]
- Nath, D.S.; Pujari, P.C.; Jain, A.; Rastogi, V. Drag reduction by application of aerodynamic devices in a race car. Adv. Aerodyn. 2021, 3, 4. [Google Scholar] [CrossRef]

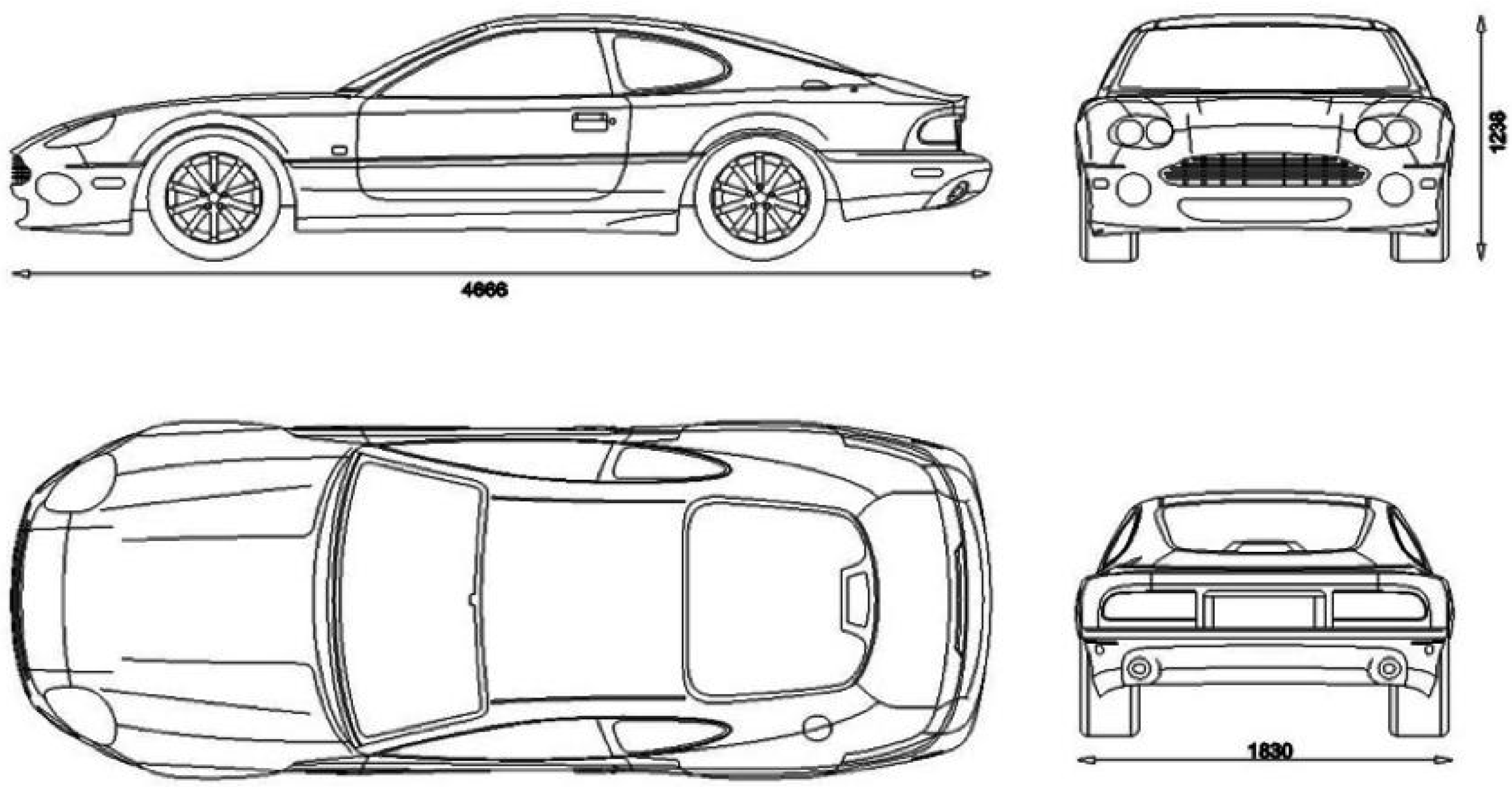

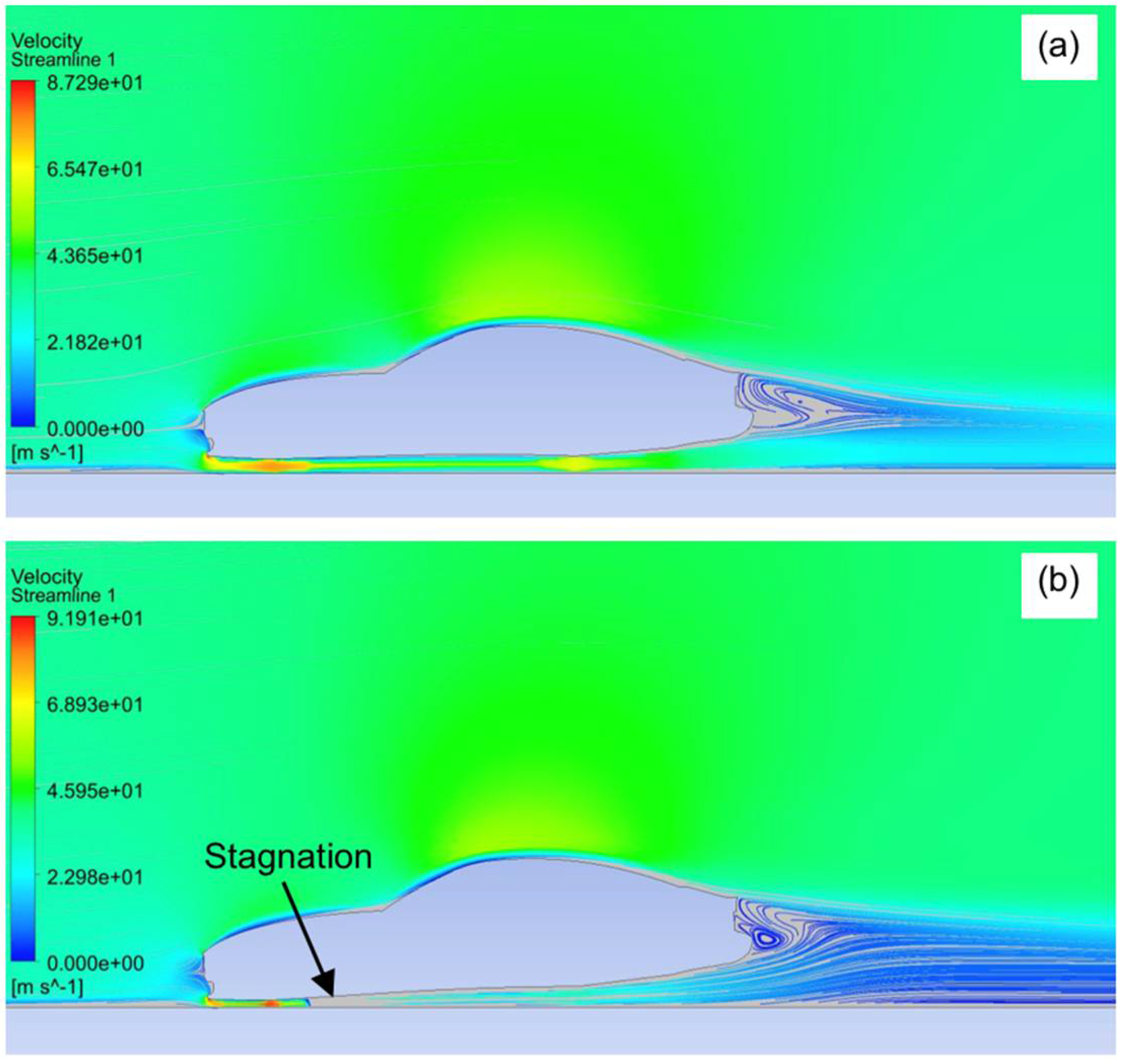





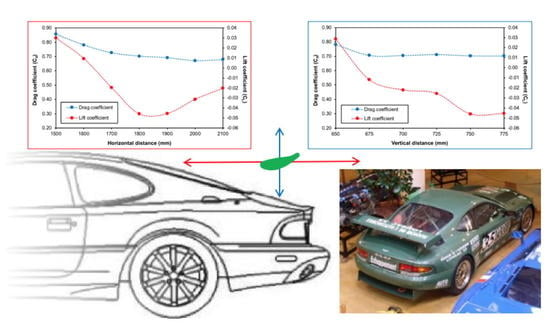
| Area | 1.959 m2 |
| Density | 1.225 kg/m3 |
| Depth | 1.83 m |
| Length | 4.666 m |
| Temperature | 288.16 K |
| Velocity | 35.76 m/s |
| Viscosity | 1.789 × 10−5 kg/m·s |
| Ratio of specific heats | 1.4 |
| Rake Angle (°) | Drag Coefficient (Cd) | Lift Coefficient (CL) | ||||
|---|---|---|---|---|---|---|
| 60 mph | 70 mph | 80 mph | 60 mph | 70 mph | 80 mph | |
| 0.00 | 0.412 | 0.408 | 0.405 | −0.054 | −0.054 | −0.055 |
| 0.25 | 0.424 | 0.420 | 0.417 | −0.049 | −0.050 | −0.050 |
| 0.5 | 0.436 | 0.433 | 0.430 | −0.065 | −0.064 | −0.064 |
| 0.75 | 0.447 | 0.444 | 0.442 | −0.028 | −0.029 | −0.029 |
| 1.00 | 0.460 | 0.457 | 0.455 | −0.022 | −0.022 | −0.022 |
| 1.25 | 0.469 | 0.467 | 0.464 | −0.013 | −0.013 | −0.013 |
| 1.5 | 0.476 | 0.473 | 0.471 | −0.030 | −0.031 | −0.032 |
| 1.75 | 0.490 | 0.488 | 0.486 | −0.012 | −0.013 | −0.013 |
| 2.00 | 0.499 | 0.497 | 0.496 | −0.011 | −0.012 | −0.011 |
| 2.25 | 0.485 | 0.483 | 0.482 | 0.003 | 0.003 | 0.003 |
| 2.5 | 0.499 | 0.498 | 0.497 | 0.034 | 0.035 | 0.035 |
| 2.75 | 0.484 | 0.483 | 0.482 | 0.023 | 0.023 | 0.023 |
| Horizontal Distance (mm) | Drag Coefficient (Cd) | Lift Coefficient (CL) | ||||
|---|---|---|---|---|---|---|
| 60 mph | 70 mph | 80 mph | 60 mph | 70 mph | 80 mph | |
| 1500 | 0.862 | 0.856 | 0.852 | 0.032 | 0.030 | 0.028 |
| 1600 | 0.787 | 0.781 | 0.776 | 0.011 | 0.009 | 0.008 |
| 1700 | 0.732 | 0.725 | 0.720 | −0.018 | −0.020 | −0.021 |
| 1800 | 0.709 | 0.702 | 0.696 | −0.042 | −0.048 | −0.048 |
| 1900 | 0.699 | 0.692 | 0.686 | −0.045 | −0.047 | −0.044 |
| 2000 | 0.677 | 0.671 | 0.665 | −0.030 | −0.032 | −0.032 |
| 2100 | 0.684 | 0.679 | 0.674 | −0.021 | −0.021 | −0.018 |
| 2200 | 0.713 | 0.709 | 0.706 | −0.008 | −0.010 | −0.011 |
| Vertical Distance (mm) | Drag Coefficient (Cd) | Lift Coefficient (CL) | ||||
|---|---|---|---|---|---|---|
| 60 mph | 70 mph | 80 mph | 60 mph | 70 mph | 80 mph | |
| 775 | 0.708 | 0.701 | 0.695 | −0.046 | −0.045 | −0.045 |
| 750 | 0.709 | 0.702 | 0.696 | −0.042 | −0.048 | −0.048 |
| 725 | 0.718 | 0.712 | 0.707 | −0.024 | −0.026 | −0.027 |
| 700 | 0.710 | 0.704 | 0.700 | −0.021 | −0.022 | −0.024 |
| 675 | 0.710 | 0.705 | 0.701 | −0.010 | −0.012 | −0.014 |
| 650 | 0.785 | 0.781 | 0.778 | 0.031 | 0.028 | 0.026 |
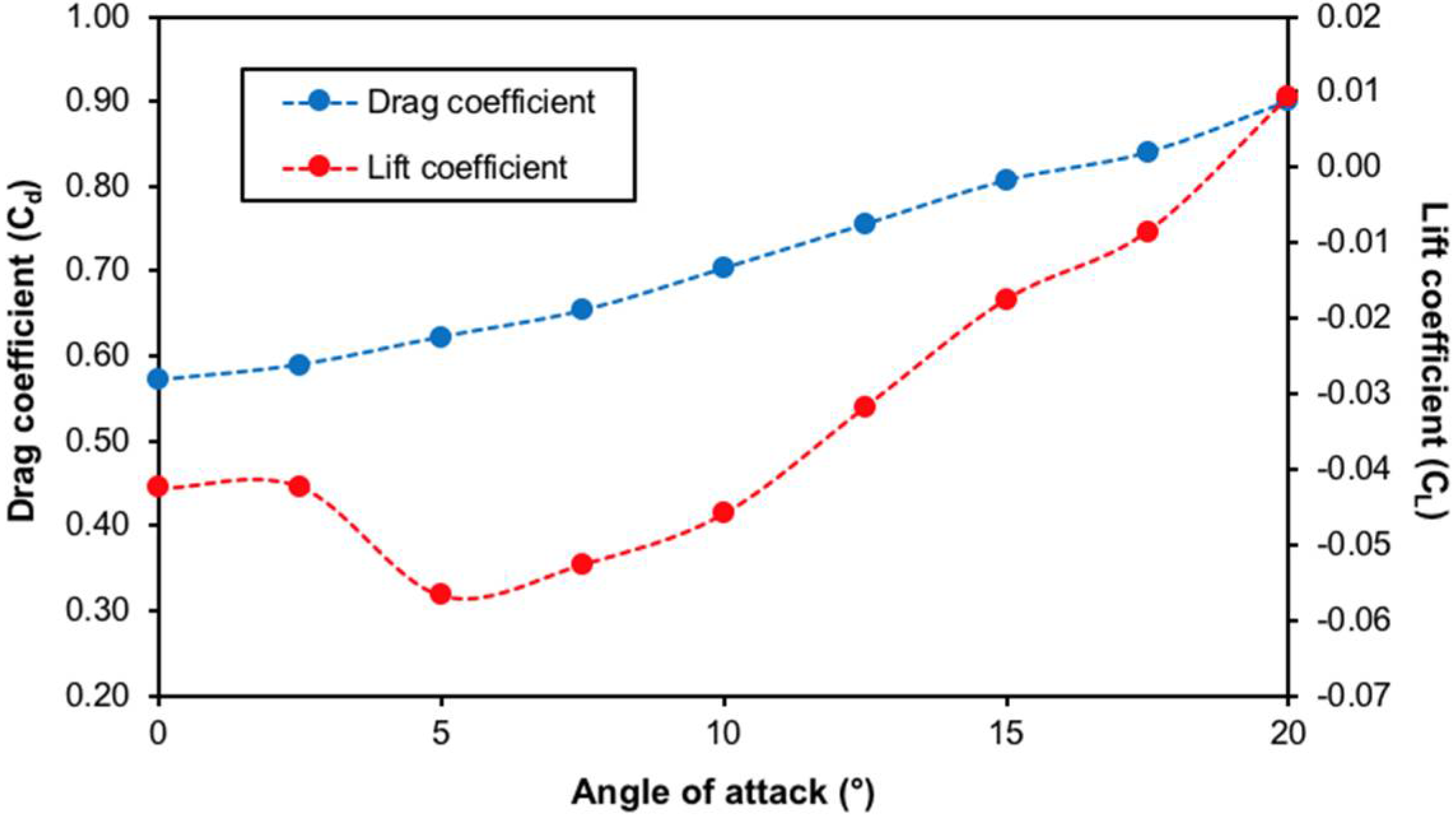
| Attack Angle (°) | Drag Coefficient (Cd) | Lift Coefficient (CL) | ||||
|---|---|---|---|---|---|---|
| 60 mph | 70 mph | 80 mph | 60 mph | 70 mph | 80 mph | |
| 0.0 | 0.575 | 0.571 | 0.567 | −0.041 | −0.045 | −0.042 |
| 2.5 | 0.593 | 0.589 | 0.584 | −0.044 | −0.042 | −0.042 |
| 5.0 | 0.627 | 0.621 | 0.616 | −0.060 | −0.055 | −0.055 |
| 7.5 | 0.658 | 0.653 | 0.648 | −0.052 | −0.053 | −0.053 |
| 10.0 | 0.709 | 0.702 | 0.696 | −0.042 | −0.048 | −0.048 |
| 12.5 | 0.762 | 0.755 | 0.750 | −0.031 | −0.032 | −0.033 |
| 15.0 | 0.813 | 0.806 | 0.801 | −0.016 | −0.018 | −0.019 |
| 17.5 | 0.847 | 0.840 | 0.834 | −0.007 | −0.009 | −0.010 |
| 20.0 | 0.907 | 0.900 | 0.895 | 0.011 | 0.009 | 0.007 |
| 22.5 | 0.957 | 0.951 | 0.946 | 0.020 | 0.017 | 0.016 |
| 25.0 | 0.998 | 0.991 | 0.985 | 0.011 | 0.020 | 0.018 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
O’Driscoll, T.P.; Barron, A.R. CFD Analysis of the Location of a Rear Wing on an Aston Martin DB7 in Order to Optimize Aerodynamics for Motorsports. Vehicles 2022, 4, 608-620. https://doi.org/10.3390/vehicles4020035
O’Driscoll TP, Barron AR. CFD Analysis of the Location of a Rear Wing on an Aston Martin DB7 in Order to Optimize Aerodynamics for Motorsports. Vehicles. 2022; 4(2):608-620. https://doi.org/10.3390/vehicles4020035
Chicago/Turabian StyleO’Driscoll, Thomas P., and Andrew R. Barron. 2022. "CFD Analysis of the Location of a Rear Wing on an Aston Martin DB7 in Order to Optimize Aerodynamics for Motorsports" Vehicles 4, no. 2: 608-620. https://doi.org/10.3390/vehicles4020035
APA StyleO’Driscoll, T. P., & Barron, A. R. (2022). CFD Analysis of the Location of a Rear Wing on an Aston Martin DB7 in Order to Optimize Aerodynamics for Motorsports. Vehicles, 4(2), 608-620. https://doi.org/10.3390/vehicles4020035