Vehicle Directional Cosine Calculation Method
Abstract
:1. Introduction
When you can measure what you are speaking about and express it in numbers, you know something about it, and when you cannot measure it, when you cannot express it in numbers, your knowledge is of a meagre and unsatisfactory kind. It may be the beginning of knowledge, but you have scarcely in your thought advanced to the stage of a science. Lord Baron Kelvin of Largs [4]
1.1. Educational Importance
1.2. History of Kinematic and Directional Cosine Matrices
1.3. Present-Day Purpose and Innovations Presented
2. Methods and Results
2.1. Dynamics
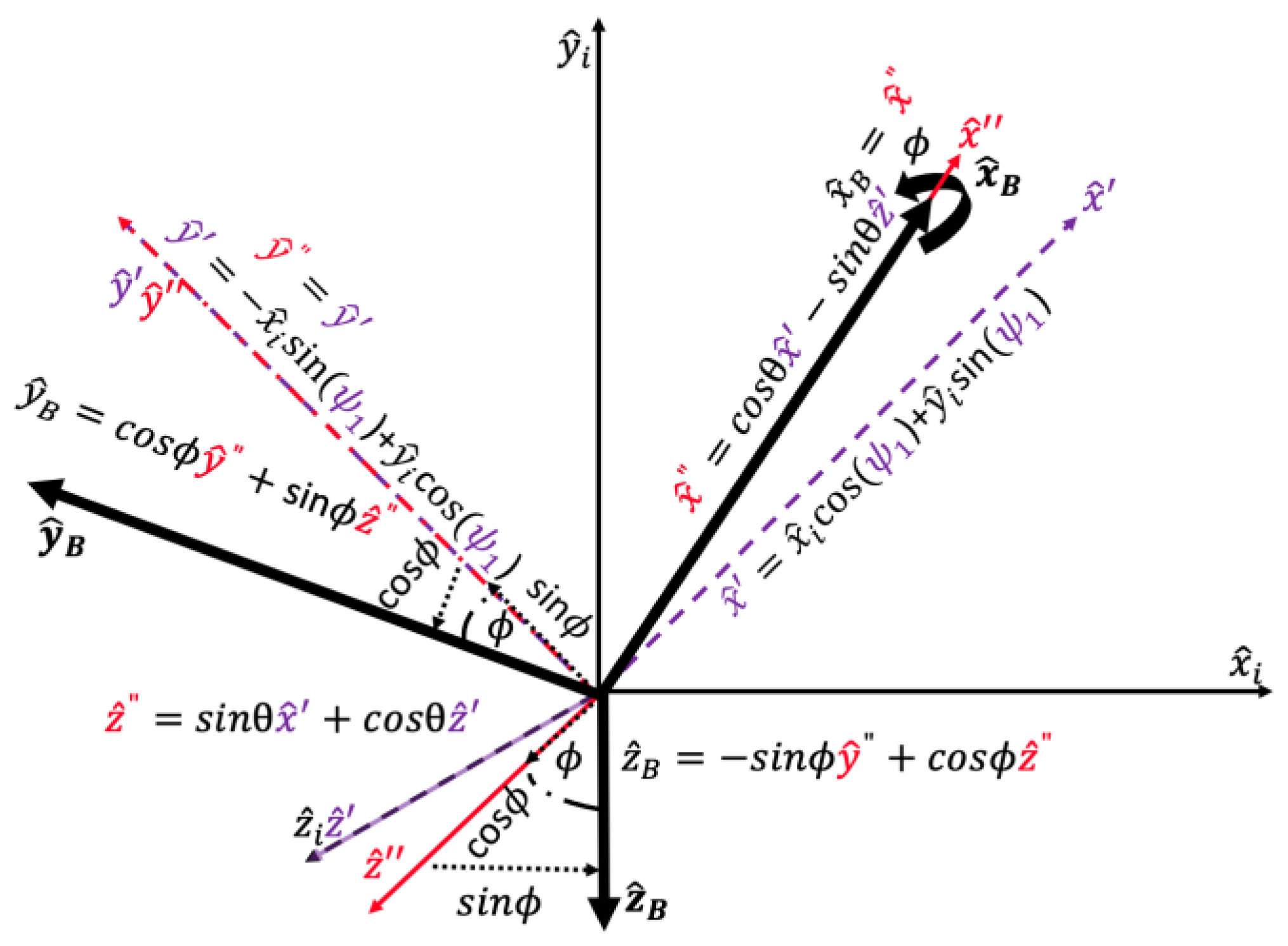
2.2. Direction Cosine Matrix
3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- NASA. First Images from the James Webb Space Telescope. Available online: https://www.nasa.gov/webbfirstimages (accessed on 30 September 2022).
- NASA. (23a) Frames of Reference: The Centrifugal Force. Available online: https://pwg.gsfc.nasa.gov/stargaze/Sframes3.htm (accessed on 30 September 2022).
- NASA. NASA Image Use Policy. 2022. Available online: https://gpm.nasa.gov/image-use-policy (accessed on 22 May 2022).
- Thomson, W. Popular Lectures and Addresses, Vol. I; MacMillan: London, UK, 1891; p. 80. ISBN 9780598775993. Available online: https://books.google.com/books?id=JcMKAAAAIAAJ&printsec=frontcover&source=gbs_ge_summary_r#v=onepage&q&f=false (accessed on 30 September 2022).
- Manurung, S.; Mihardi, S. Improving the conceptual understanding in kinematics subject matter with hypertext media learning and formal thinking ability. J. Ed. Prac. 2016, 7, 91–98. [Google Scholar]
- Ramma, Y. Physics is Taught Badly Because Teachers Struggle with Basic Concepts. The Conversation: Academic Rigor, Journalistic Flair. Published 29 October 2017. 7.12am EDT. Available online: https://theconversation.com/physics-is-taught-badly-because-teachers-struggle-with-basic-concepts-86083 (accessed on 30 September 2022).
- Ayop, S.; Ismail, M. Students’ understanding in kinematics: Assessments, conceptual difficulties, and teaching strategies. Int. J. Acad. Res. Bus. Soc. Sci. 2019, 9, 1278–1285. [Google Scholar] [CrossRef]
- Shodiqin, M.; Taqwa, M. Identification of student difficulties in understanding kinematics: Focus of study on the topic of acceleration. J. Phys. 2021, 1918, 022016. [Google Scholar] [CrossRef]
- Núñez, R.; Suárez, G.; Castro, A. Difficulties in the interpretation of kinematics graphs in secondary basic education students. J. Phys. 2022, 2159, 012019. [Google Scholar] [CrossRef]
- Moyo, N. Mathematical Difficulties Encountered by Physics Students in Kinematics; Stellenbosch University: Stellenbosch, South Africa, 2020. [Google Scholar]
- Euler, L. Formulae generales pro translatione quacunque corporum rigidorum. Euler Arch. 1776, 20, 189–207. Available online: https://scholarlycommons.pacific.edu/euler-works/478 (accessed on 2 February 2022).
- Chasles, M. Note sur les propriétés générales du système de deux corps semblables entr’eux. Bull. Sci. Math. Astron. Phys. Chem. 1830, 14, 321–326. (In French) [Google Scholar]
- Kelvin, W.; Guthrie-Tait, P. Treatise on Natural Philosophy; Google Play Books; Clarendon Press: Hong Kong, China, 1867; Available online: https://play.google.com/books/reader?id=wwO9X3RPt5kC&pg=GBS.PR8&hl=en (accessed on 30 September 2022).
- Whittaker, E.T. Chapter 1 Kinematical Preliminaries. In A Treatise on the Analytical Dynamics of Particles and Rigid Bodies: With an Introduction to the Problem of Three Bodies; Cambridge University Press: Cambridge, UK, 1917; pp. 4–5. [Google Scholar]
- Meyer, G.; Lee, H.; Wehrend, W. A method for Expanding a Direction Cosine Matrix into an Euler sequence of Rotations. NASA Technical Memorandum X-1384, 1 June 1967. Available online: https://ntrs.nasa.gov/citations/19670017935 (accessed on 30 September 2022).
- Jordan, J. Directional Cosine Computational Error. NASA Technical Report R-304, March 1969. Available online: https://ntrs.nasa.gov/api/citations/19690027619/downloads/19690027619.pdf (accessed on 30 September 2022).
- Jordan, J. An Accurate Strapdown Direction Cosine Algorithm. NASA Technical Report D-5384, September 1969. Available online: https://ntrs.nasa.gov/citations/19690027619 (accessed on 30 September 2022).
- Kane, T.; Likins, P. Kinematics of Rigid Bodies in Spaceflight. NASA Technical Report CR-119361, May 1971. Available online: https://ntrs.nasa.gov/citations/19710021700 (accessed on 30 September 2022).
- Haley, D.; Almand, B.; Thomas, M.; Krauze, L.; Gremban, K.; Sanborn, J.; Kelley, J.; Depovich, T.; Wolfe, W.; Nguyen, T. Evaluation of Automated Decisionmaking Methodologies and Development of an Integrated Robotic System Simulation. NASA Contractor Report 178050, March 1986. Available online: https://ntrs.nasa.gov/citations/19860014816 (accessed on 30 September 2022).
- King, R. Global and Regional Kinematics with GPS. NASA Conference Paper N95-14279, NASA. Goddard Space Flight Center, Satellite Laser Ranging in the 1990s: Report of the 1994 Belmont Workshop, Massachusetts Institute of Technology, Cambridge, MA, USA. 1 November 1994. Available online: https://ntrs.nasa.gov/citations/19950007865 (accessed on 30 September 2022).
- Dunn, P. Global and Regional Kinematics from SLR Stations, NASA Conference Paper N95-14278, NASA. Goddard Space Flight Center, Satellite Laser Ranging in the 1990s: Report of the 1994 Belmont Workshop, Massachusetts Institute of Technology, Cambridge, MA, USA. 1 November 1994. Available online: https://ntrs.nasa.gov/citations/19950007864 (accessed on 30 September 2022).
- Xing, G.; Parvex, S. Alternative Forms of Relative Attitude Kinematics and Dynamics Equations. NASA Goddard Space Flight Center, Greenbelt, Maryland, under Contract NAS5-99163. 1 June 2001. Available online: https://ntrs.nasa.gov/api/citations/20010084965/downloads/20010084965.pdf (accessed on 30 September 2022).
- Smeresky, B.; Rizzo, A.; Sands, T. Kinematics in the information age. Mathematics 2018, 6, 148. [Google Scholar] [CrossRef] [Green Version]
- Cole, D.; Sands, T. Effect of kinematic algorithm selection on the conceptual design of orbitally delivered vehicles. Preprints 2022, 2022020360. [Google Scholar] [CrossRef]
- Sandberg, A.; Sands, T. Autonomous Trajectory Generation Algorithms for Spacecraft Slew Maneuvers. Aerospace 2022, 9, 135. [Google Scholar] [CrossRef]
- Liu, X.; Wang, J. Parallel Kinematics: Type, Kinematics, and Optimal Design; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Dingle, H. On Inertial Reference Frames. Sci. Prog. 1962, 50, 568–583. [Google Scholar]
- Wie, B. Space Vehicle Dynamics and Control; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1998. [Google Scholar]





| Term | Definition | Term | Definition | Term | Definition | Term | Definition |
|---|---|---|---|---|---|---|---|
| External resultant force in inertial x-direction | Angular velocity about x-axis | Angular acceleration about x-axis | Moment of inertia along x with respect to x | ||||
| External resultant force in inertial y-direction | Angular velocity about y-axis | Angular acceleration about y-axis | Product of inertia along x with respect to y | ||||
| External resultant force in inertial z-direction | Angular velocity about z-axis | Angular acceleration about z-axis | Product of inertia along x with respect to z | ||||
| Acceleration in inertial x-direction | Velocity in x-direction | External resultant moment | Moment of inertia along y with respect to y | ||||
| Acceleration in inertial y-direction | Velocity in y-direction | Product of inertia along y with respect to z | |||||
| Acceleration in inertial z-direction | Velocity in z-direction | Moment of inertia along z with respect to z |
| Term | Definition | Term | Definition | Term | Definition | Term | Definition |
|---|---|---|---|---|---|---|---|
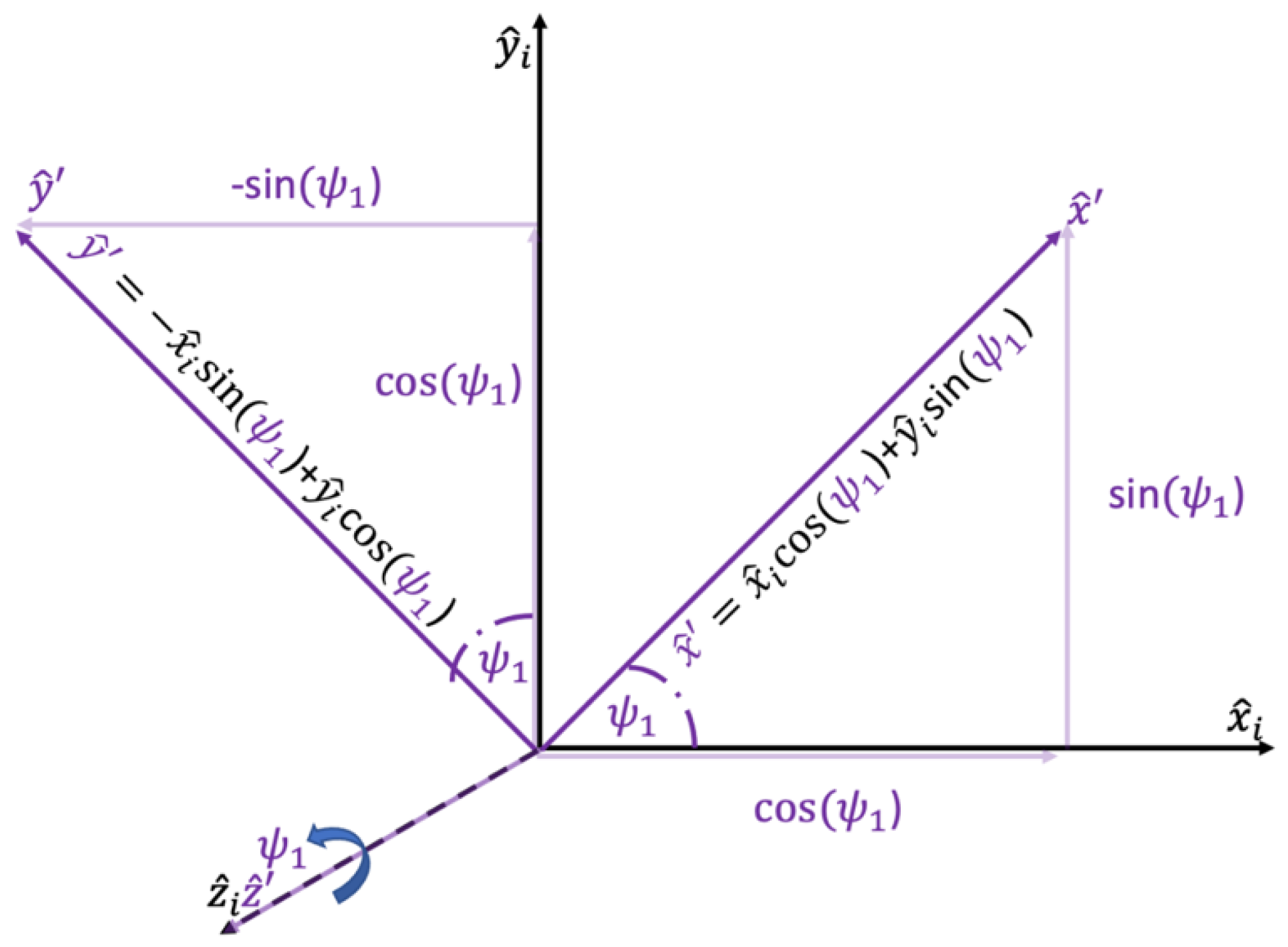
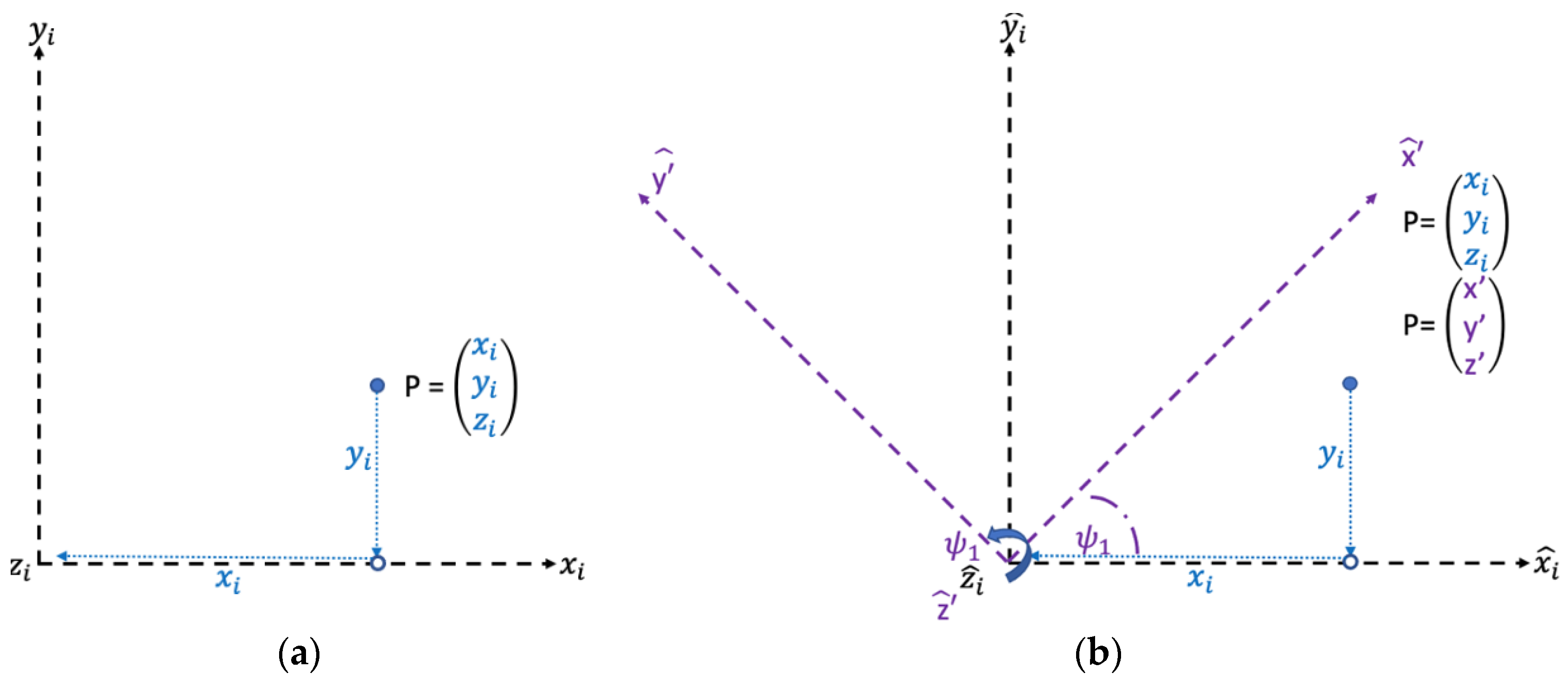
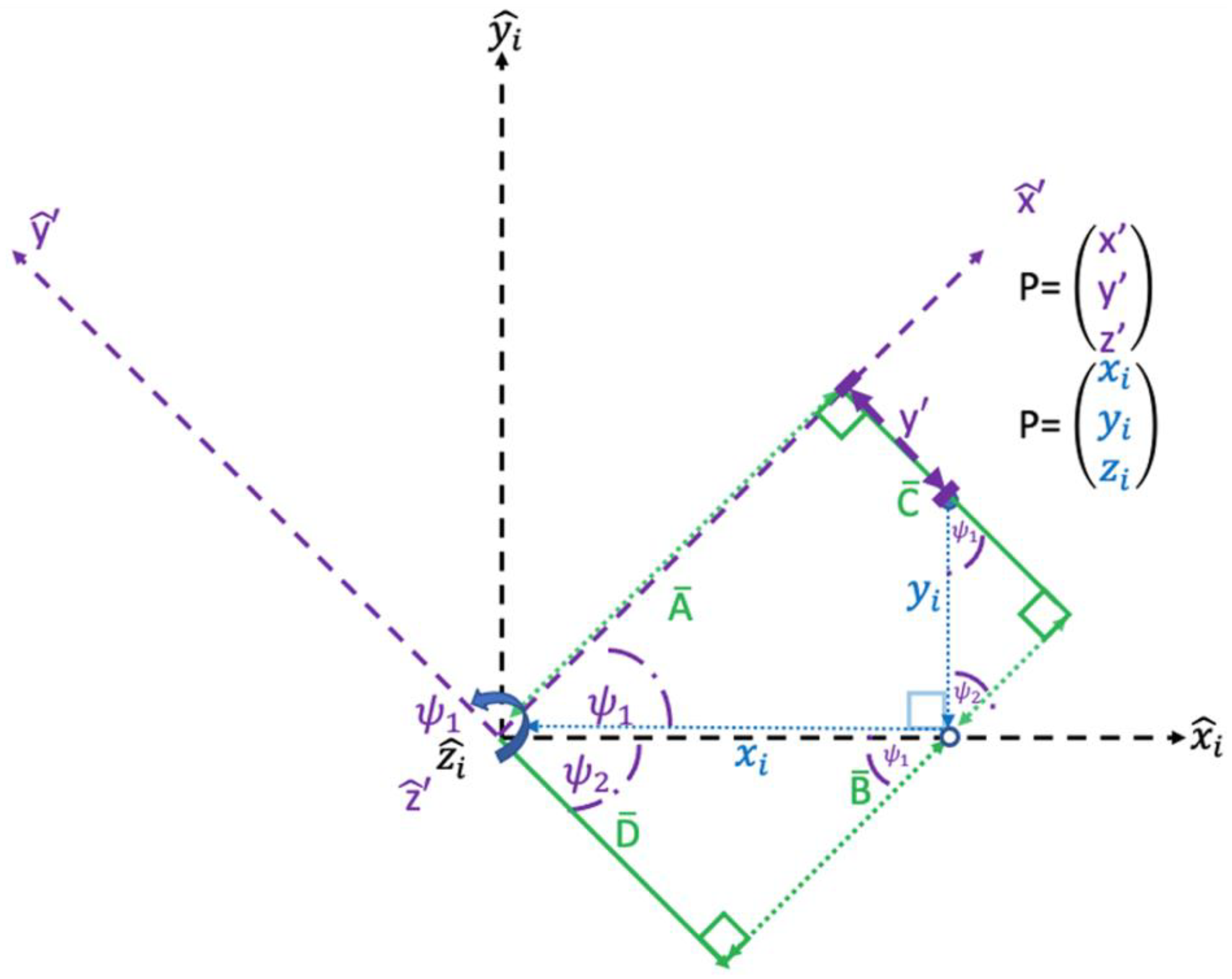
| x-axis in the inertial non-rotating reference frame | xi | Point P’s location on x-axis in the inertial non-rotating reference frame | x-axis in the new rotated reference frame about the axis to the axis | Point P’s location on the -axis after the rotation about the axis to the axis | |||
| y-axis in the inertial non-rotating reference frame | yi | Point P’s location on y-axis in the inertial non-rotating reference frame | y-axis in the new rotated reference frame about the axis to the axis | Point P’s location on the -axis after the rotation about the axis to the axis | |||
| z-axis in the inertial non-rotating reference frame | zi | Point P’s location on z-axis in the inertial non-rotating reference frame | z-axis in the new rotated reference frame about the axis to the axis | Point P’s location on the -axis after the rotation about the axis to the axis | |||
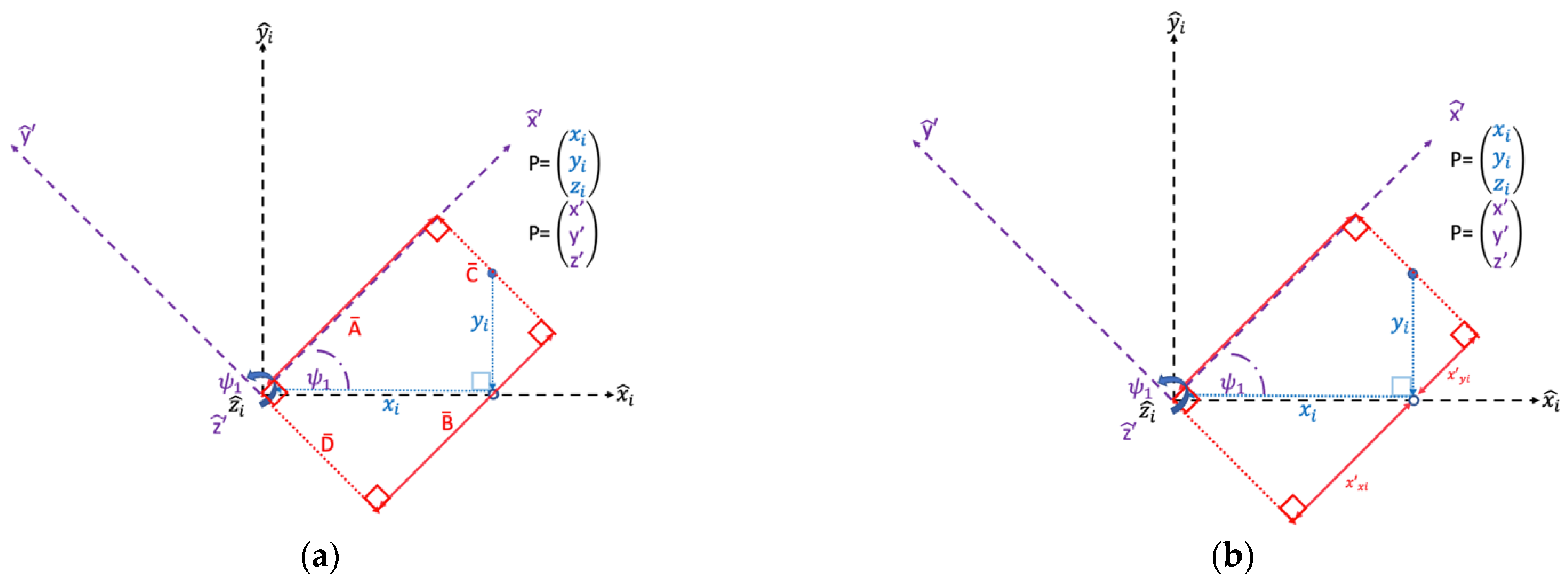
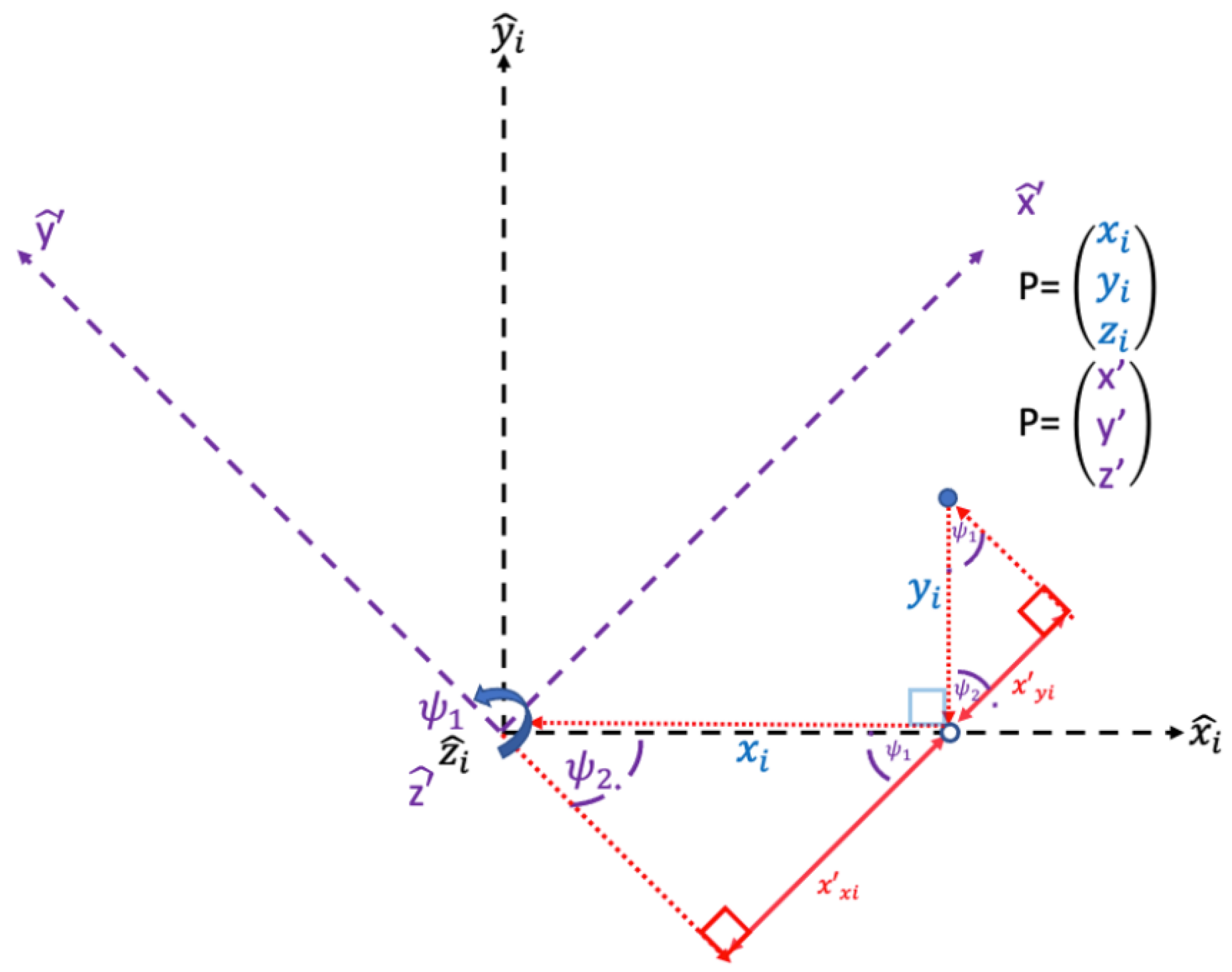
| Line B segment determined by angle ψ1 and the hypotenuse xi | . | Line B segment determined by the angle ψ1 and hypotenuse yi | ψ1 | Angle of rotation about the axis to the axis | ψ2 | Complementary angle to ψ1 | |
| Line equivalent to Point P’s measurement along the axis | Line parallel and equidistant to crossing through (xi,0,0) | Line perpendicular to and equidistant to crossing through point P | Line perpendicular to and equidistant to crossing through the origin/rotation point | ||||
| Rectangle developed by lines ,, |
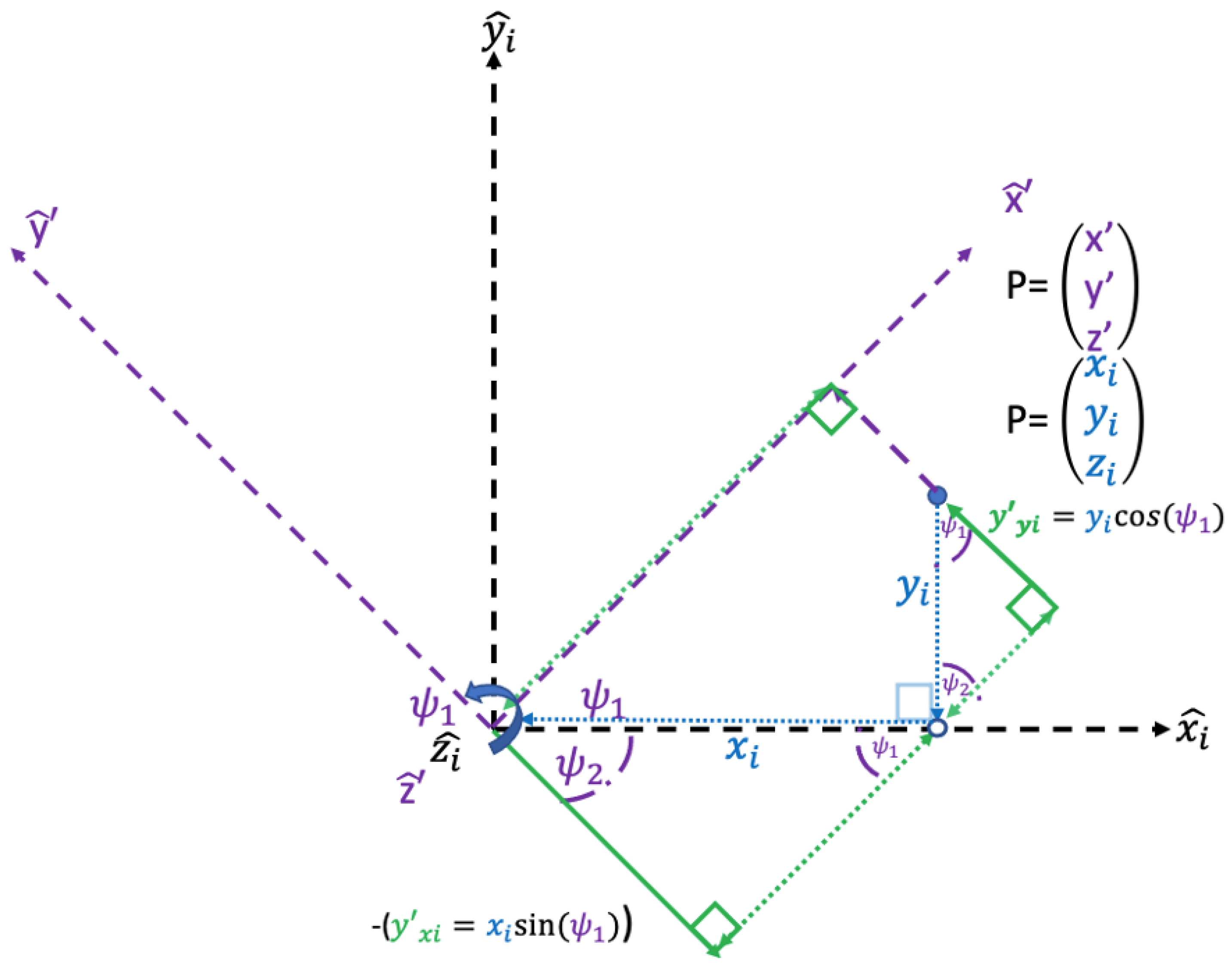
| Term | Definition | Term | Definition | Term | Definition | Term | Definition |
|---|---|---|---|---|---|---|---|
| x-axis in the inertial non-rotating reference frame | xi | Point P’s location on x-axis in the inertial non-rotating reference frame | x-axis in the new rotated reference frame about the axis to the axis | Point P’s location on the -axis after the rotation about the axis to the axis | |||
| y-axis in the inertial non-rotating reference frame | yi | Point P’s location on y-axis in the inertial non-rotating reference frame | y-axis in the new rotated reference frame about the axis to the axis | Point P’s location on the -axis after the rotation about the axis to the axis | |||
| z-axis in the inertial non-rotating reference frame | zi | Point P’s location on z-axis in the inertial non-rotating reference frame | z-axis in the new rotated reference frame about the axis to the axis | Point P’s location on the -axis after the rotation about the axis to the axis | |||
| Line segment determined by angle ψ1 and the hypotenuse xi | . | Line segment determined by the angle ψ1 and hypotenuse yi | ψ1 | Angle of rotation about the axis to the axis | ψ2 | Complementary angle to ψ1 | |
| Line equivalent to point P’s measurement along the axis | Line parallel and equidistant to crossing through (xi,0,0) | Line perpendicular to and equidistant to crossing through point P | Line perpendicular to and equidistant to crossing through the origin/rotation point | ||||
| rectangle developed by lines ,, |
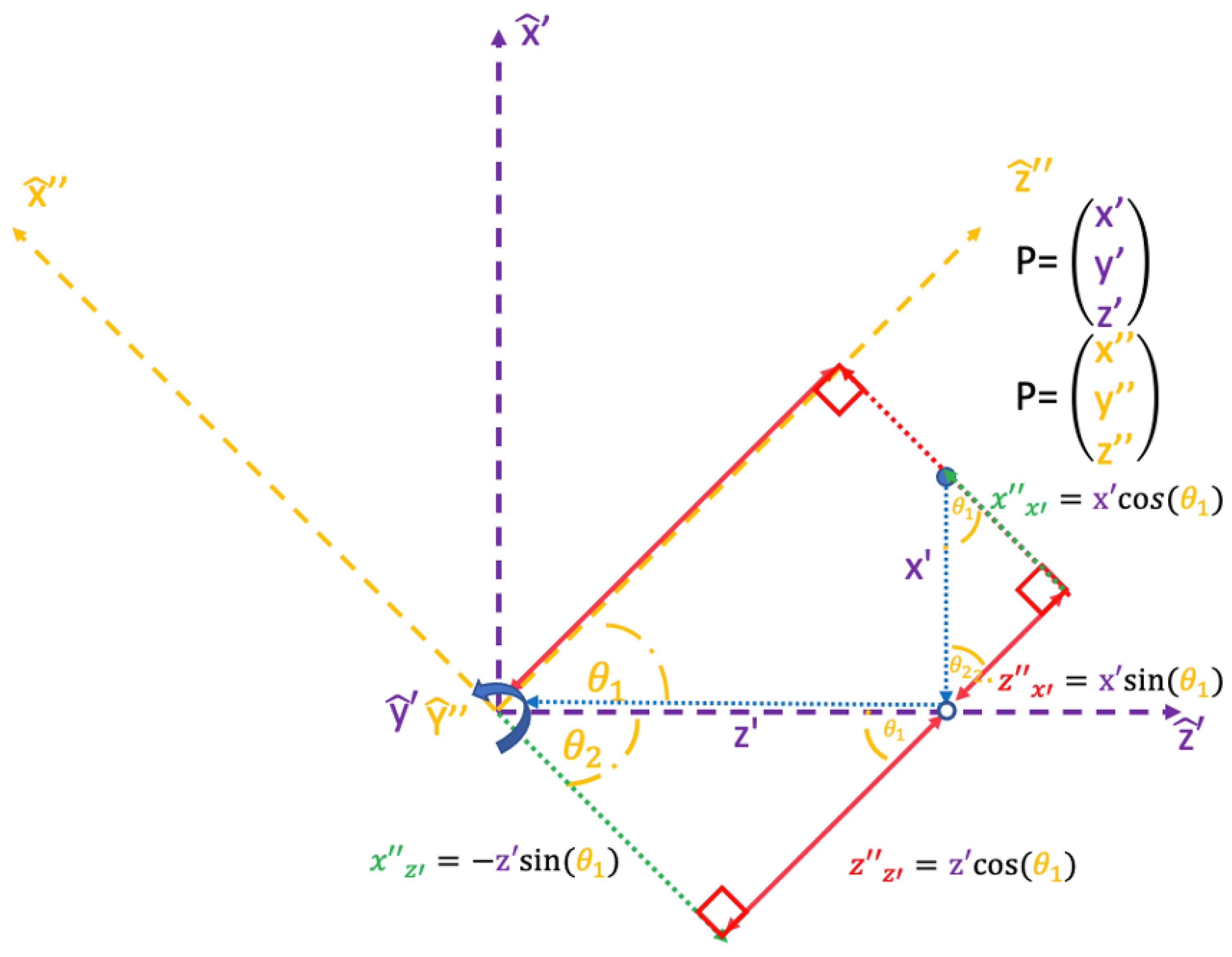
| Term | Definition | Term | Definition | Term | Definition | Term | Definition |
|---|---|---|---|---|---|---|---|
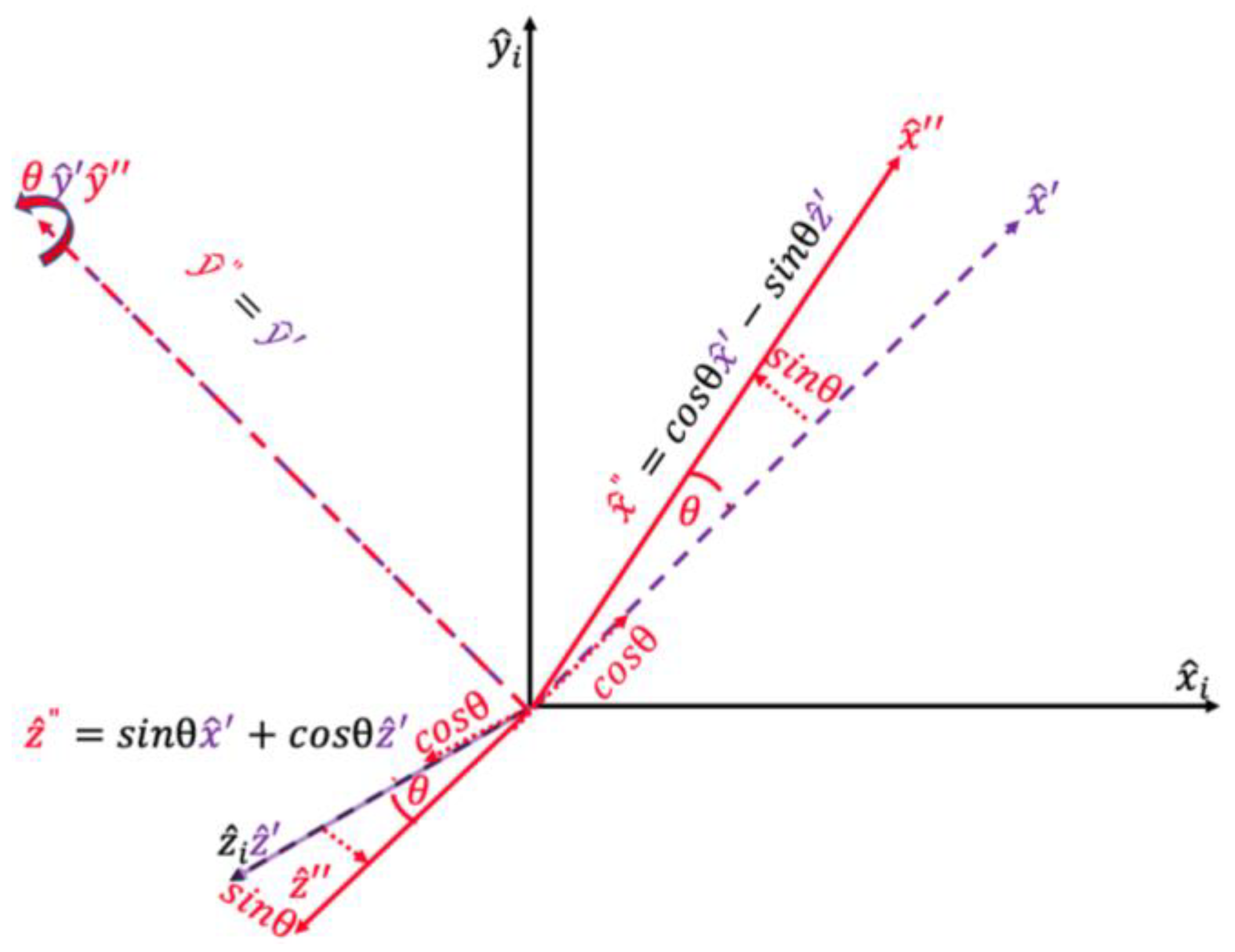
| x-axis in the new rotated reference frame about the axis to the axis | Point P’s location on the -axis after the rotation about the axis to the axis | x-axis in the rotated reference frame about the axis to the axis | Point P’s location on the, x’’-axis after the rotation about the y’. axis to the axis | ||||
| y-axis in the new rotated reference frame about the axis to the axis | Point P’s location on the -axis after the rotation about the axis to the axis | y-axis in the rotated reference frame about the axis to the axis | Point P’s location on the y’’.-axis after the rotation about the y’. axis to the axis | ||||
| z-axis in the new rotated reference frame about the axis to the axis | Point P’s location on the -axis after the rotation about the axis to the axis | z-axis in the rotated reference frame about the axis to the axis | Point P’s location on the z’’.-axis after the rotation about the y’. axis to the axis | ||||
| Determined using the same techniques as | . | Determined using the same techniques as . | θ1 | Angle of rotation about the axis to the axis | θ2 | Complementary angle to θ1 | |
| Determined using the same techniques as | . | Determined using the same techniques as . |
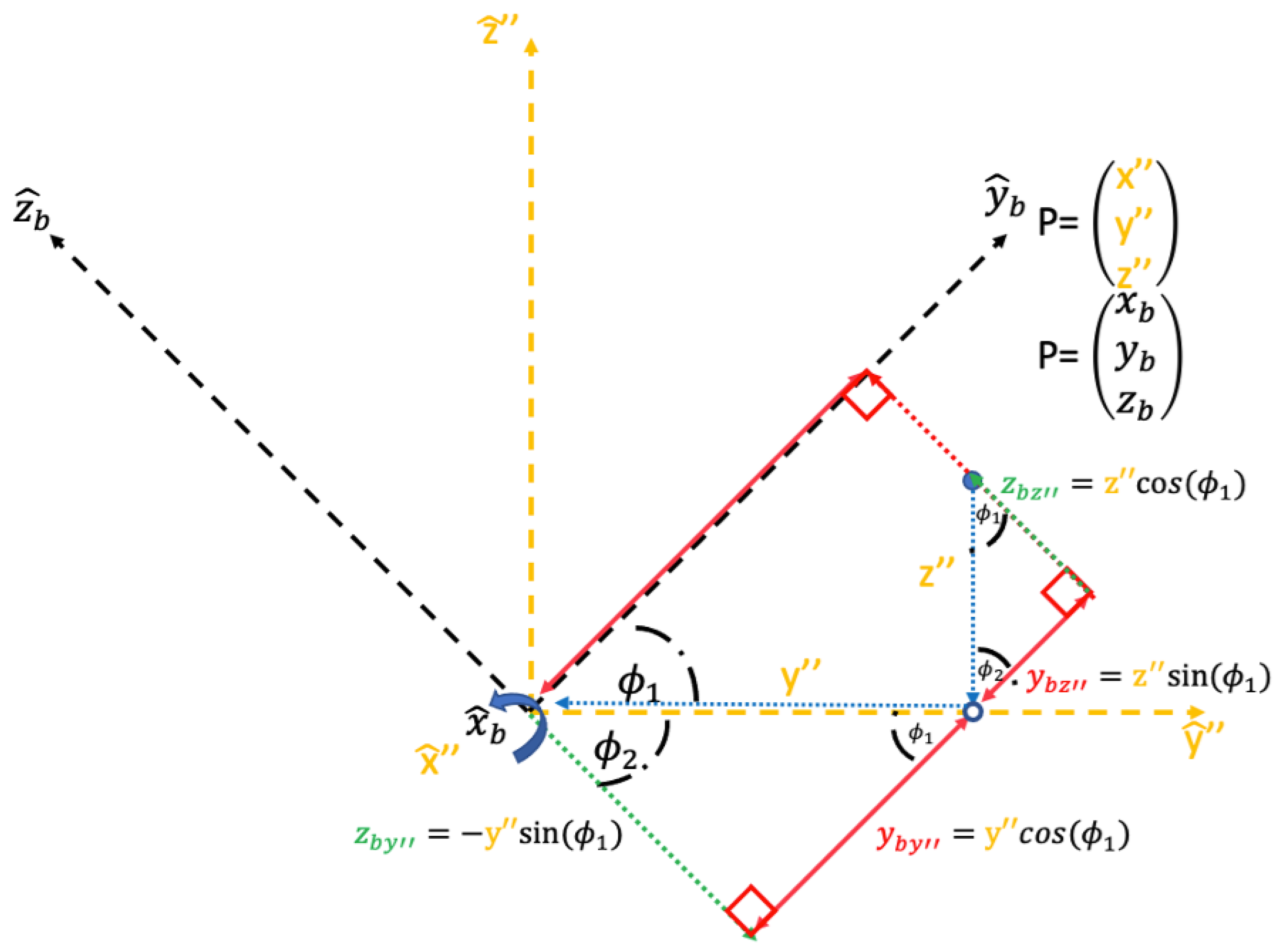
| Term | Definition | Term | Definition | Term | Definition | Term | Definition |
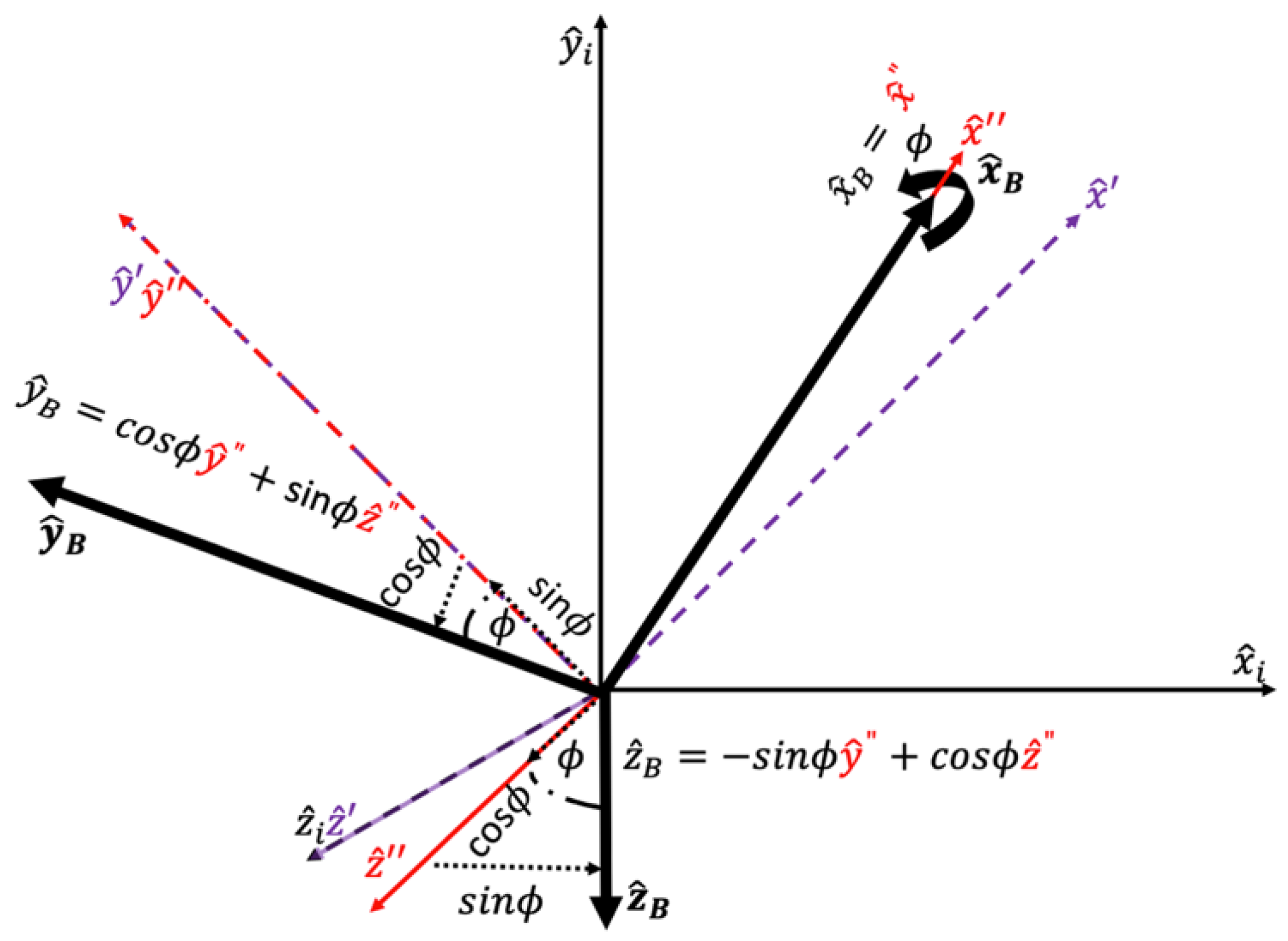
| x-axis in the rotated reference frame about the axis to the axis | Point P’s location on the, x’’.-axis after the rotation about the, y’. axis to the axis | x-axis in the rotated reference frame about the axis to the axis | Point P’s location on the, x-b..-axis after the rotation about the, y’’. axis to the axis | ||||
| y-axis in the rotated reference frame about the axis to the axis | Point P’s location on the, y’’.-axis after the rotation about the, y’. axis to the axis | y-axis in the rotated reference frame about the axis to the axis | Point P’s location on the, y-b..-axis after the rotation about the, y’’. axis to the axis | ||||
| z-axis in the rotated reference frame about the axis to the axis | Point P’s location on the, z’’.-axis after the rotation about the, y’. axis to the axis | z-axis in the rotated reference frame about the axis to the axis | Point P’s location on the, z-b..-axis after the rotation about the, y’’. axis to the axis | ||||
| Determined using the same techniques as | . | Determined using the same techniques as . | Angle of rotation about the axis to the axis | Complementary angle to | |||
| Determined using the same techniques as | . | Determined using the same techniques as . |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hall, D.; Sands, T. Vehicle Directional Cosine Calculation Method. Vehicles 2023, 5, 114-132. https://doi.org/10.3390/vehicles5010008
Hall D, Sands T. Vehicle Directional Cosine Calculation Method. Vehicles. 2023; 5(1):114-132. https://doi.org/10.3390/vehicles5010008
Chicago/Turabian StyleHall, Derek, and Timothy Sands. 2023. "Vehicle Directional Cosine Calculation Method" Vehicles 5, no. 1: 114-132. https://doi.org/10.3390/vehicles5010008
APA StyleHall, D., & Sands, T. (2023). Vehicle Directional Cosine Calculation Method. Vehicles, 5(1), 114-132. https://doi.org/10.3390/vehicles5010008







