Using Case and Error Analysis on Inspection Methods of Modeling Platforms for Automatic Emergency Call Systems Based on Generated Satellite Signals
Abstract
:1. Introduction
2. Causes and Simulation Modeling of System Errors
2.1. Frequency Errors Generated by the Environment
2.2. Time-Based Synchronization Error and Clock Error
2.3. System Output Power Error
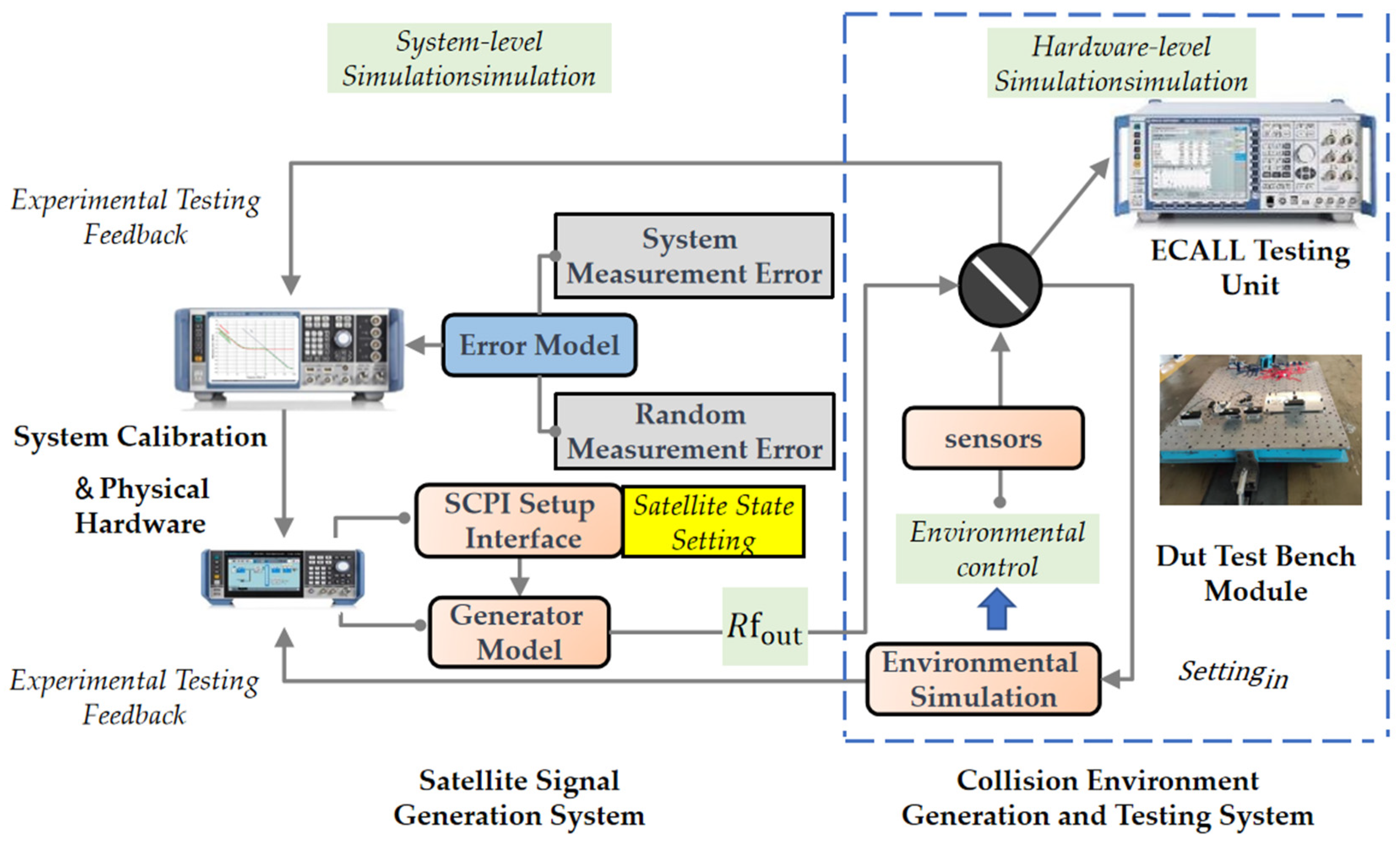
3. Semi-Physical Simulation System for Post-Collision Emergency Call
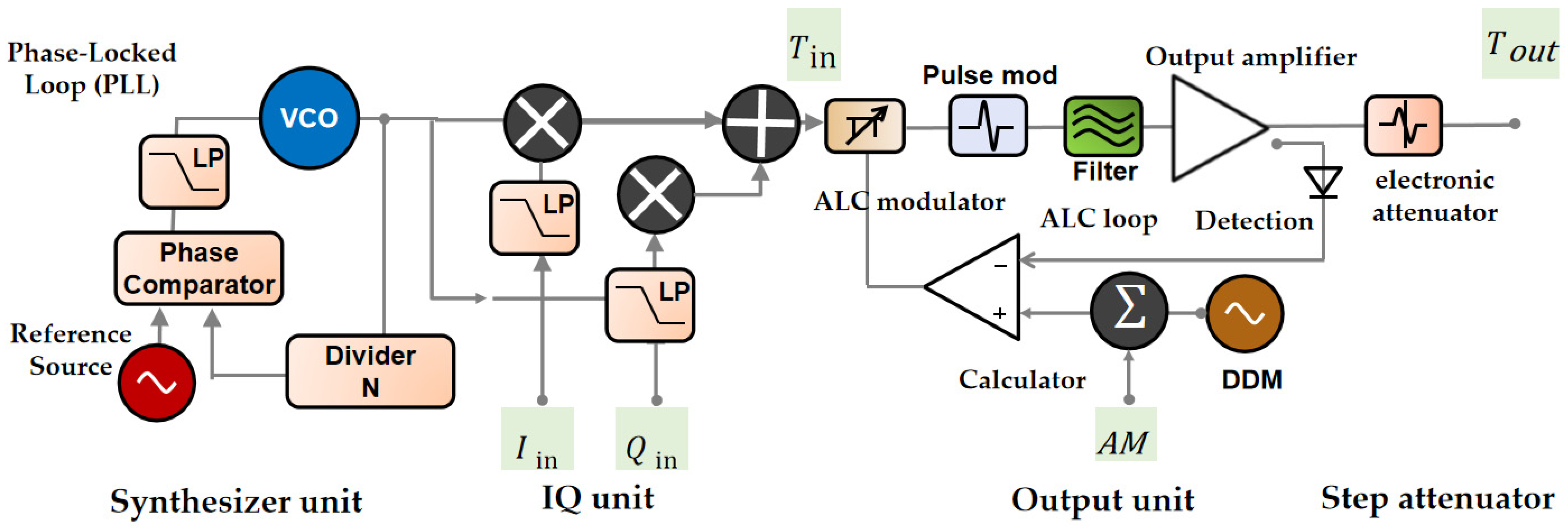
3.1. Phase Noise Error Model Based on Power Density
3.2. Positioning Information Simulation System
3.3. Emergency Call Simulation Platform
3.4. Semi-Physical Simulation Testing Process
- Using the collision testing unit in the semi-physical simulation platform, real signal observations from the testing area and system phase noise observations under generated signals are collected separately. The collected data are then subjected to outlier removal processing to ensure the reliability and accuracy of the observations.
- By controlling the parameters of the satellite signal generation system, different positioning conditions are simulated by altering the environmental conditions in which the system operates. This allows for the simulation of various vehicle collision scenarios, levels of vibration, and temperature changes. For the simulation of vibration and temperature environments, vibration characteristic parameters are calculated based on historical data from real vehicle tests and simulated collision tests to ensure an accurate environmental simulation is created.
- The weights of each error source in the error model are initialized. By triggering the emergency call device, the simulation system transmits the simulated environmental parameters to the AECS and records the system’s response and performance under different environmental conditions.
- An analysis and calculation of errors for different scenarios are performed. The timing errors and clock errors are validated by selecting a reference source with high precision. For the validation of other environmental factors, such as temperature drift, it follows the testing requirements outlined in the emergency call regulations. The samples that meet the overall qualification tests specified in UN Regulation No. 144 are selected for error analysis.
4. Results and Analysis
4.1. Experimental Setup
4.2. Results Analysis
4.3. Discussion
- The experiment categorizes the factors affecting the signal generation system into two main types: random errors and systematic errors. This categorization emphasizes the need for experimenters to use at least two different types of observations to gain a broader understanding of the phenomena observed. As the simulation model becomes more complex, further research can be conducted to explore the relationship between the signal generation system and the communication reliability of various subsystems in the AECS.
- This paper only discusses the challenges posed by the structural configuration of the semi-physical simulation platform on the experiments. However, in certain cases, different physical structures of semi-physical simulation models can also improve the communication effectiveness of an AECS. To further enhance the platform, the authors can investigate and modify the physical architecture of the semi-physical simulation model, including the number and orientation of vehicle antennas and the ground station model. These modifications aim to further improve the platform’s performance under anticipated conditions.
5. Conclusions
- The satellite signal simulation system constructed in this study provides a method for evaluating the correlation of test conditions based on a phase noise analysis using the power spectral density phase noise model. This method can optimize the existing AECS test design and is suitable for high-precision tests that require the accurate determination of error sources related to environmental factors. By improving the error model without increasing real vehicle collision tests or simulated collision tests, effective calibration and improvement measures can be developed, leading to the improved accuracy and reliability of the satellite signal simulation system.
- Through repeated experiments with different test conditions on the simulation platform, this research focused on the post-collision emergency call test method based on the simulation platform. By analyzing the errors in the environmental generation module of the system, test conditions were identified that improved the accuracy and repeatability of the experiments. Specifically, maintaining the test equipment at higher temperatures and increasing its vibration resistance can effectively enhance the accuracy of the tests. Thus, it is recommended to conduct AECS inspection tests at higher temperatures while ensuring the equipment has sufficient vibration resistance to achieve improved test accuracy.
- The analysis of the experimental results reveals that environmental factors have varying degrees of influence on different components of the satellite signal simulation system. In terms of the hardware design for the simulation system, the signal source and phase-locked loop (PLL) of the generation system are more susceptible to environmental factors. On the other hand, the voltage-controlled oscillator (VCO) in the oscillation circuit is less affected. Future research that delves deeper into the impact of environmental factors on the system accuracy can lead to targeted improvements in the system design, the optimization of testing environments, and the reduction in errors caused by environmental factors. Additionally, for components that are significantly impacted, such as the signal source and PLL, appropriate calibration and adjustment measures can be implemented to significantly enhance the accuracy and reliability of the system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.G.; Zhan, J.; Duan, C.G.; Guan, X.; Lu, P.P.; Yang, K. A Review of Vehicle Detection Techniques for Intelligent Vehicles. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 3811–3831. [Google Scholar] [CrossRef]
- Kuang, X.; Zhao, F.; Hao, H.; Liu, Z. Intelligent connected vehicles: The industrial practices and impacts on automotive value-chains in China. Asia Pac. Bus. Rev. 2018, 24, 1–21. [Google Scholar] [CrossRef]
- He, K.; Qin, K.; Wang, C.; Fang, X. Research on Cyber Security Test Method for GNSS of Intelligent Connected Vehicle. In Proceedings of the 2020 International Conference on Computer Information and Big Data Applications (CIBDA), Guiyang, China, 17–19 April 2020; pp. 200–203. [Google Scholar]
- Ma, F.W.; Shi, J.Z.; Wu, L.; Dai, K.; Zhong, S.R. Consistent Monocular Ackermann Visual–Inertial Odometry for Intelligent and Connected Vehicle Localization. Sensors 2020, 20, 5757. [Google Scholar] [CrossRef]
- Zhang, C.L.; Wei, J.M.; Dai, J.A.; Qu, S.B.; She, X.N.; Wang, Z.T. A Roadside Millimeter-Wave Radar Calibration Method Based on Connected Vehicle Technology. IEEE Intell. Transp. Syst. Mag. 2022, 15, 117–131. [Google Scholar] [CrossRef]
- Sun, C.; Zheng, S.F.; Ma, Y.L.; Chu, D.F.; Yang, J.R.; Zhou, Y.C.; Li, Y.C.; Xu, T.X. An active safety control method of collision avoidance for intelligent connected vehicle based on driving risk perception. J. Intell. Manuf. 2021, 32, 1249–1269. [Google Scholar] [CrossRef]
- Oorni, R.; Goulart, A. In-Vehicle Emergency Call Services: eCall and Beyond. IEEE Commun. Mag. 2017, 55, 159–165. [Google Scholar] [CrossRef]
- Niu, X.J.; Dai, Y.H.; Liu, T.Y.; Chen, Q.J.; Zhang, Q. Feature-based GNSS positioning error consistency optimization for GNSS/INS integrated system. GPS Solut. 2023, 27, 89. [Google Scholar] [CrossRef]
- Liu, W.; Huang, H.; Hu, Y.; Mou, M.; Hsieh, T.-H.; Hu, Q.; Wang, S. Improved GNSS vector tracking loop to enhance the navigation performance of USV. Ocean Eng. 2022, 258, 111865. [Google Scholar] [CrossRef]
- Chang, H.; Pang, C.; Zhang, L.; Guo, Z. Rotating Single-Antenna Spoofing Signal Detection Method Based on IPNN. Sensors 2022, 22, 7141. [Google Scholar] [CrossRef]
- Sulistya, B.; Taufik, N.; Renaldy, F.; Rufiyanto, A.; Trihatmo, S.; Sunandar, R.; Irawan, B.B.; Rahmatullah, R.; Mundhola, A.; Septiawan, R. GNSS Positioning Performance Monitoring of ADS-B stations for Autonomous Electric Vehicle (AEV) environment testing. In Proceedings of the 2022 International Seminar on Intelligent Technology and Its Applications (ISITIA), Surabaya, Indonesia, 20–21 July 2022; pp. 291–295. [Google Scholar]
- UN ECE Regulation No.144. Uniform provisions concerning the Accident Emergency Call Systems (AECS). 2021. 505/Rev.3/Add.143, (ECE/TRANS/WP.29).
- Abroe, G.E.; Zulkifli SA, B.M.; Kumar, K.; El Ouanjli, N.; Asirvadam, V.S.; Mossa, M.A. Comprehensive Review of Recent Advancements in Battery Technology, Propulsion, Power Interfaces, and Vehicle Network Systems for Intelligent Autonomous and Connected Electric Vehicles. Energies 2023, 16, 2925. [Google Scholar] [CrossRef]
- Yin, S.; Yang, C.; Kawsar, I.; Du, H.; Pan, Y. Longitudinal Predictive Control for Vehicle-Following Collision Avoidance in Autonomous Driving Considering Distance and Acceleration Compensation. Sensors 2022, 22, 7395. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Fan, Y.; Wang, G. An Intelligent Algorithm for USVs Collision Avoidance Based on Deep Reinforcement Learning Approach with Navigation Characteristics. J. Mar. Sci. Eng. 2023, 11, 812. [Google Scholar] [CrossRef]
- Fang, K.; Zhou, Y.; Ma, P.; Yang, M. Credibility evaluation of hardware-in-the-loop simulation systems. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 3794–3799. [Google Scholar]
- Esfandyari, M.J.; Yazdi, M.R.H.; Esfahanian, V.; Nehzati, H. A Low-Cost Single PC Based HiL Simulation Platform for Verification of The Hybrid Electric Vehicle Control Unit. In Proceedings of the Electrical Engineering (ICEE), Iranian Conference on Iranian Conference on Electrical Engineering (ICEE), Mashhad, Iran, 8–10 May 2018. [Google Scholar]
- Chen, D.; Zhang, Y.; Pang, G.; Gao, F.; Duan, L. A Hybrid Scheme for Disaster-Monitoring Applications in Wireless Sensor Networks. Sensors 2023, 23, 5068. [Google Scholar] [CrossRef]
- Ferrari, P.; Sisinni, E.; Bellagente, P.; Depari, A.; Carvalho, D.F.; Flammini, A.; Pasetti, M.; Rinaldi, S. Simulating scalability of a transparent LoRaWan enhancement for emergency communication. In Proceedings of the 2022 IEEE International Workshop on Metrology for Industry 4.0 & IoT (MetroInd4.0&IoT), Trento, Italy, 7–9 June 2022; pp. 349–353. [Google Scholar]
- Wang, J.; Wu, J.; Zheng, X.; Ni, D.; Li, K. Driving safety field theory modeling and its application in pre-collision warning system. Transp. Res. Part C Emerg. Technol. 2016, 72, 306–324. [Google Scholar] [CrossRef]
- Rana, S.; Asaduzzaman. Vibration based pavement roughness monitoring system using vehicle dynamics and smartphone with estimated vehicle parameters. Results Eng. 2021, 12, 100294. [Google Scholar] [CrossRef]
- Novat, N.; Kidando, E.; Kutela, B.; Kitali, A.E. A comparative study of collision types between automated and conventional vehicles using Bayesian probabilistic inferences. J. Saf. Res. 2023, 84, 251–260. [Google Scholar] [CrossRef]
- Chen, C.; Xiang, H.; Qiu, T.; Wang, C.; Zhou, Y.; Chang, V. A rear-end collision prediction scheme based on deep learning in the Internet of Vehicles. J. Parallel Distrib. Comput. 2018, 117, 192–204. [Google Scholar] [CrossRef]
- Chen, G.-y.; Wang, J.-q.; Hu, H.-y. An Integrated GNSS/INS/DR Positioning Strategy Considering Nonholonomic Constraints for Intelligent Vehicle. In Proceedings of the 2022 6th CAA International Conference on Vehicular Control and Intelligence (CVCI), Nanjing, China, 28–30 October 2022; pp. 1–6. [Google Scholar]
- Elsayed, H.; El-Mowafy, A.; Wang, K. Bounding of correlated double-differenced GNSS observation errors using NRTK for precise positioning of autonomous vehicles. Measurement 2023, 206, 112303. [Google Scholar] [CrossRef]
- Rafatnia, S.; Mirzaei, M. Estimation of reliable vehicle dynamic model using IMU/GNSS data fusion for stability controller design. Mech. Syst. Signal Process. 2022, 168, 108593. [Google Scholar] [CrossRef]
- Zhu, C.; Shi, L.; Li, X.; Liu, Y.; Ai, W. Lock threshold deterioration induced by antenna vibration and signal coupling effects in hypersonic vehicle carrier tracking system of Ka band. Chin. J. Aeronaut. 2018, 31, 776–781. [Google Scholar] [CrossRef]
- Bai, L.; Zhou, W.; Li, W.; Zhang, Y. Stress processing based TCXOS. Chin. J. Sci. Instrum. 2014, 35, 1594–1599. [Google Scholar]
- Da Silva, E. (Ed.) Oscillators and frequency synthesizers. In High Frequency and Microwave Engineering; Butterworth-Heinemann: Oxford, UK, 2001; pp. 357–399. [Google Scholar]
- LUO Kaiwen, L.Q.M. Damage Boundary of Crystal Oscillator under Shock Environment. Chin. J. High Press. Phys. 2021, 35, 1. [Google Scholar]
- Liu, Q.A.; Xiang, Z.Y.; Mo, J.L.; Zhang, Q.X.; Zhu, Y.G. The effects of the structural stiffness of vibration transfer path on friction-induced vibration and noise. Tribol. Int. 2022, 173, 107687. [Google Scholar] [CrossRef]
- Dishan, H. Phase error in fast Fourier transform analysis. Mech. Syst. Signal Process. 1995, 9, 113–118. [Google Scholar] [CrossRef]
- Prezelj, J.; Čurović, L.; Novaković, T.; Murovec, J. A novel approach to localization of environmental noise sources: Sub-windowing for time domain beamforming. Appl. Acoust. 2022, 195, 108836. [Google Scholar] [CrossRef]
- Ding, M.; Chen, W.; Ding, W. Performance analysis of a normal GNSS receiver model under different types of jamming signals. Measurement 2023, 214, 112786. [Google Scholar] [CrossRef]
- Dobkin, D.M. (Ed.) Chapter 4—Radio Transmitters and Receivers. In RF Engineering for Wireless Networks; Newnes: Burlington, VT, USA, 2005; pp. 107–192. [Google Scholar]
- Jin, Z.; Liu, D.; Hu, A.; Shan, X.; Zhang, C.; Su, Y.; Zou, X.; Zhao, X. An accurate ISF-based analysis and simulation method for phase noise in LC/Ring oscillators. Microelectron. J. 2021, 117, 105240. [Google Scholar] [CrossRef]
- Salzenstein, P.; Wu, T.Y. Uncertainty analysis for a phase-detector based phase noise measurement system. Measurement 2016, 85, 118–123. [Google Scholar] [CrossRef]








| Feature | AECS and ICV Research | |||
|---|---|---|---|---|
| Method 1 | Method 2 | Method 3 | Method 4 | |
| Function | Communication link reliability and collision safety distance | Machine learning-based collision risk assessment | Intelligent connected vehicle simulation platform | Development of embedded sensor and actuator systems |
| Strengths | Analyzing the entire collision process and provide logic for hardware development | Weakening the principle and analyzing from the perspective of big data | Fast iteration speed, strong targeting, and good visualization effects | Providing a generic physical emulation platform to accommodate various AECS devices |
| Weaknesses | Limited to specific calculation-constrained scenarios | Poor traceability | Poor generality | Only perform testing as regulatory requirements |
| Parameters | Range or Values |
|---|---|
| Number of Traces | 6 |
| Signal Level (dBm) | −25.506 |
| Integrated Measurements Range (Hz) | 10~10,000,000 |
| Total Simulation Duration/(s) | 138 |
| Spurious Removal Threshold (dBm) | 6 |
| Test | Signal Frequency (MHz) | Temperature Gradient | Vibration Gradient | Clock Source Precision |
|---|---|---|---|---|
| 1 | 1176.45 | 7 | 3 | High |
| 2 | 1575.42 | 7 | 3 | Low |
| 3 | 1268.52 | 7 | 1 | High |
| 4 | 1561.098 | 1 | 3 | High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Ni, X.; Yang, J.; Wang, B.; Fang, Z. Using Case and Error Analysis on Inspection Methods of Modeling Platforms for Automatic Emergency Call Systems Based on Generated Satellite Signals. Vehicles 2023, 5, 1294-1312. https://doi.org/10.3390/vehicles5040071
Fu Y, Ni X, Yang J, Wang B, Fang Z. Using Case and Error Analysis on Inspection Methods of Modeling Platforms for Automatic Emergency Call Systems Based on Generated Satellite Signals. Vehicles. 2023; 5(4):1294-1312. https://doi.org/10.3390/vehicles5040071
Chicago/Turabian StyleFu, Yining, Xindong Ni, Jingxuan Yang, Bingjian Wang, and Zhe Fang. 2023. "Using Case and Error Analysis on Inspection Methods of Modeling Platforms for Automatic Emergency Call Systems Based on Generated Satellite Signals" Vehicles 5, no. 4: 1294-1312. https://doi.org/10.3390/vehicles5040071
APA StyleFu, Y., Ni, X., Yang, J., Wang, B., & Fang, Z. (2023). Using Case and Error Analysis on Inspection Methods of Modeling Platforms for Automatic Emergency Call Systems Based on Generated Satellite Signals. Vehicles, 5(4), 1294-1312. https://doi.org/10.3390/vehicles5040071







