An Objective Evaluation Approach for Safety-Relevant Steering Feedback on a Test Bench
Abstract
:1. Introduction
2. Problem Specification
- Focus on on-center feedback and consequently neglection of boundary conditions for feedback evaluation (steering wheel angle, preload)
- Focus on distinct frequencies with constant amplitudes by a sine-sweep signal rather than superposition of different frequencies and amplitudes
- Neglection of the influence of the driver holding the steering wheel
- Generic approach without a clear connection to real-world applications.
3. Solution Approach
3.1. Quasi-Stochastic Excitation
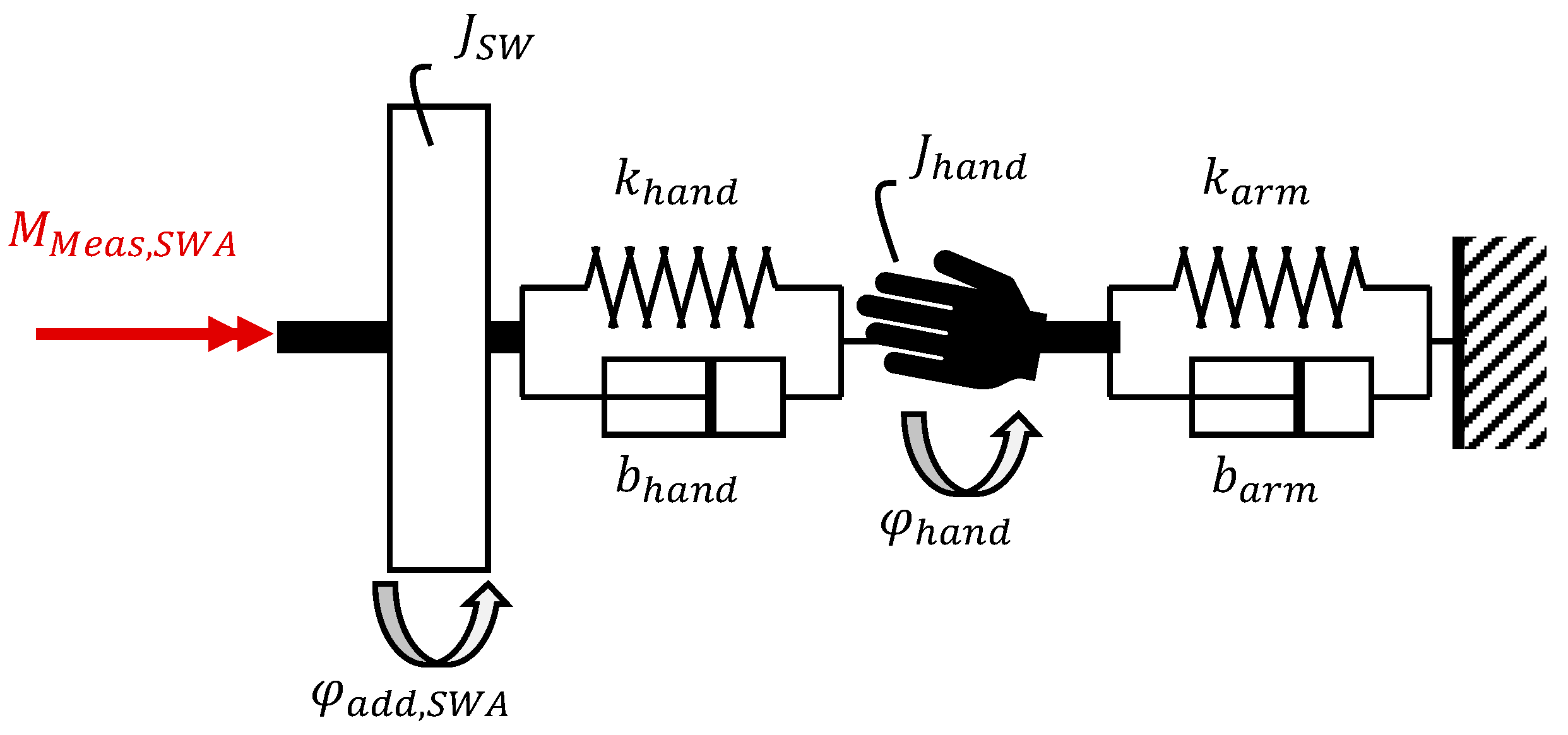
3.2. Steering Wheel Fixations
3.3. Real Driving Situations
3.4. Derivation of Applications
4. Subjective and Objective Evaluation
4.1. Subjective Evaluation
4.1.1. Questionnaire and Driver Selection
4.1.2. Evaluation Procedure
4.2. Test Bench Excitation Signals and Objective Parameters
5. Results
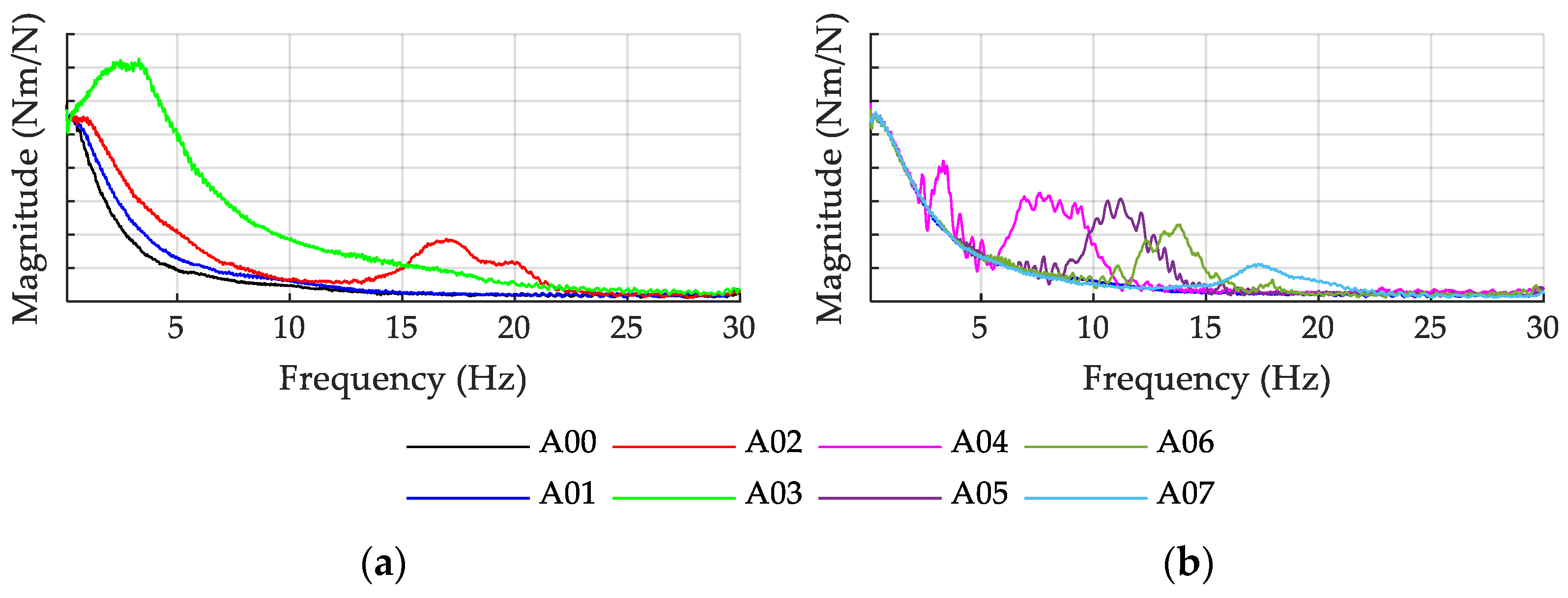
5.1. Qualitative Comparison of the Generic Approaches
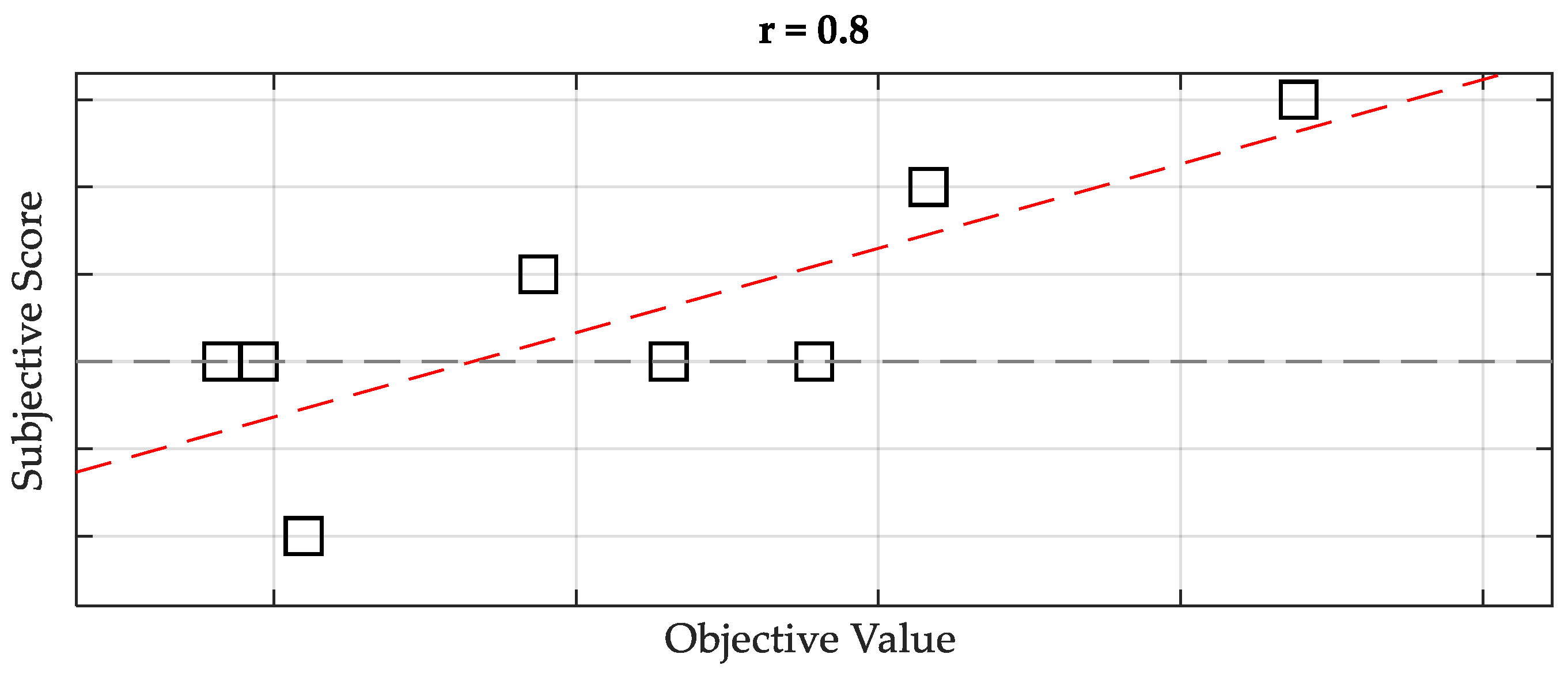
5.2. Subjective–Objective Correlation
5.2.1. Test Case Comparison
5.2.2. Comparison of the Fixation Approach
5.3. Discussion
6. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Acronyms
| DOD | Direction of Deviation |
| EPS | Electric Power Steering |
| FFT | Fast Fourier Transformation |
| HiL | Hardware-in-the-Loop |
| HPS | Hydraulic Power Steering |
| PMLSM | Permanent Magnet Linear Synchronous Motor |
| PRBS | Pseudo-Radnom-Binary-Sequence |
| PSD | Power-Spectral-Density |
| RLA | Rod Left Actuator |
| RRA | Rod Right Actuator |
| SbW | Steer-by-Wire |
| SWA | Steering Wheel Actuator |
| TMS | Ten Mark Scale |
Nomenclature
| Arm Damping Coefficient | |
| Hand Damping Coefficient | |
| Measured Rack Force at RRA | |
| Reference Rack Force at RRA | |
| Feedback Transfer Function | |
| Hand Inertia | |
| Steering Wheel Inertia | |
| Arm Stiffness Coefficient | |
| Hand Stiffness Coefficient | |
| Measured Torque at SWA | |
| Pearson Coefficient | |
| Vehicle Velocity | |
| Objective Value | |
| Subjective Value | |
| Reference Steering Wheel Angle at SWA | |
| Additional Steering Wheel Angle from the Human Grip Model |
References
- Harrer, M.; Pfeffer, P.E. Steering Handbook; Springer International Publishing: Cham, Switzerland, 2017; ISBN 978-3-319-05449-0. [Google Scholar]
- Wolf, H.J. Ergonomische Untersuchung des Lenkgefühls an Personenkraftwagen. Ph.D. Dissertation, Technische Universität München, München, Germany, 2009. [Google Scholar]
- Grau, J.; Nippold, C.; Bossdorf-Zimmer, B.; Küçükay, F.; Henze, R. Objective Evaluation of Steering Rack Force Behaviour and Identification of Feedback Information. SAE Int. J. Passeng. Cars—Mech. Syst. 2016, 9, 1279–1304. [Google Scholar] [CrossRef]
- Düsterloh, D. Funktionsoptimierung und Komplexitätsbeherrschung im Entwicklungsprozess Mechatronischer Fahrwerksysteme am Beispiel Elektromechanischer Lenksysteme. Ph.D. Dissertation, Universität Duisburg-Essen, Duisburg, Germany, 2018. [Google Scholar]
- Heißing, B.; Brandl, H.J. Subjektive Beurteilung des Fahrverhaltens, 1st ed.; Vogel: Würzburg, Germany, 2002; ISBN 3-8023-1903-6. [Google Scholar]
- Grau, J. Objektivierung des Rückmeldeverhaltens Elektromechanischer Lenksysteme. Ph.D. Dissertation, Technische Universität Braunschweig, Braunschweig, Germany, 2018. [Google Scholar]
- Brunn, P.; Harrer, M. Objektivierung der Lenkungsrückmeldung. VDI Fortschrittsberichte Reihe 2004, 12, 69–79. [Google Scholar]
- Raabe, J.; Ketzmerick, E.; Abel, H.; Prokop, G. Steering System Simulation during the Concept Phase regarding Feedback Behavior. SAE Int. J. Veh. Dyn. Stab. NVH 2022, 6, 189–206. [Google Scholar] [CrossRef]
- Pfeffer, P.E. Interaction of Vehicle and Steering System Regarding On-Centre Handling. Ph.D. Dissertation, University of Bath, Bath, UK, 2006. [Google Scholar]
- Schimpf, R. Charakterisierung von Lenksystemen mit Hilfe Eines Lenksystemprüfstands. Ph.D. Dissertation, TU Wien, Wien, Austria, 2016. [Google Scholar]
- Von Groll, M. Modifizierung von Nutz- und Störinformationen am Lenkrad durch Elektromechanische Lenksysteme. Ph.D. Dissertation, Universität Duisburg-Essen, Duisburg, Germany, 2006. [Google Scholar]
- Haas, A.; Menze, G.; Sieberg, P.M.; Schramm, D. Evaluation of Feedback Behavior of Steering Systems on a mHiL-Steering-Test-Bench. In Proceedings of the Internationales Stuttgarter Symposium—ISSYM 2023, Stuttgart, Germany, 4–5 July 2023; Kulzer, A.C., Reuss, H.-C., Wagner, A., Eds.; Springer Vieweg: Wiesbaden, Germany, 2023. [Google Scholar] [CrossRef]
- Isermann, R.; Münchhof, M. Identification of Dynamic Systems: An Introduction with Applications; Springer: Berlin/Heidelberg, Germany, 2011; ISBN 978-3-540-78879-9. [Google Scholar]
- Haas, A.; Schrage, B.; Menze, G.; Sieberg, P.M.; Schramm, D. Oscillation and Vibration Reduction Approaches on a HiL-Steering-Test-Bench. IEEE ASME Trans. Mechatron 2023, 1–11. [Google Scholar] [CrossRef]
- Haas, A.; Schrage, B.; Menze, G.; Sieberg, P.M.; Schramm, D. Improvements on the Dynamical Behavior of a HiL-Steering System Test Bench. Actuators 2023, 12, 186. [Google Scholar] [CrossRef]
- Uselmann, A.; Preising, E.; Schrage, B.; Düsterloh, D. A Test of Character for Steering Systems. dSPACE Magazine, November 2016; pp. 24–31. [Google Scholar]
- Düsterloh, D.; Schrage, B. Lenkungsentwicklung am mHiL-Lenkungsprüfstand—Parameteridentifikation und Funktionsentwicklung am mHiL-Lenkungsprüfstand. In SIMVEC Simulation und Erprobung in der Fahrzeugentwicklung; VDI Verlag: Düsseldorf, Germany, 2016. [Google Scholar]
- Nippold, C. Prüfstandsbasierte Lenkungsoptimierung im Mittenbereich. Ph.D. Dissertation, Technische Universität Braunschweig, Braunschweig, Germany, 2017. [Google Scholar]
- Barthenheier, T. Potenzial Einer Fahrertyp- und Fahrsituationabhängigen Lenkradmomentgestaltung. Ph.D. Dissertation, Technische Universität Darmstadt, Darmstadt, Germany, 2004. [Google Scholar]
- Weißbacher, J. Automatische Reglerparametrierung von Servoantriebsachsen. Ph.D. Dissertation, Technische Universität Graz, Graz, Austria, 2016. [Google Scholar]
- De Vlugt, E.; Schouten, A.C.; van der Helm, F.C.T. Closed-loop multivariable system identification for the characterization of the dynamic arm compliance using continuous force disturbances: A model study. J. Neurosci. Methods 2003, 122, 123–140. [Google Scholar] [CrossRef] [PubMed]
- Haas, A.; Schrage, B.; Menze, G.; Sieberg, P.M.; Schramm, D. Subjective and Objective Evaluation of a Steering Function on a Steering System Test Bench. In Proceedings of the AmE 2023—Automotive Meets Electronics, 14. GMM Symposium, Dortmund, Germany, 15–16 June 2023. [Google Scholar]
- Lunkeit, D. Ein Beitrag zur Optimierung des Rückmelde- und Rückstellverhaltens Elektromechanischer Servolenkungen. Ph.D. Dissertation, Universität Duisburg-Essen, Duisburg, Germany, 2014. [Google Scholar]
- Uselmann, A. Ein Beitrag zur funktionalen Entwicklung eines Elektromechanischen Lenksystems für Sportlich Orientierte Fahrzeuge. Ph.D. Dissertation, Universität Duisburg-Essen, Duisburg, Germany, 2017. [Google Scholar]
- Harrer, M. Characterisation of Steering Feel. Ph.D. Dissertation, University of Bath, Bath, UK, 2007. [Google Scholar]
- Henze, R. Beurteilung von Fahrzeugen mit Hilfe Eines Fahrermodells. Ph.D. Dissertation, Technische Universität Carolo-Wilhelmina zu Braunschweig, Braunschweig, Germany, 2004. [Google Scholar]




| Criterion | Sine Sweep | PRBS | Driving Maneuver |
|---|---|---|---|
| 1—Feedback on Road Structure | 10 Hz–30 Hz r = 0.55 | 10 Hz–50 Hz r = 0.56 | r = 0.70 |
| 2—Feedback on Wheel Load Reduction | 1 Hz–10 Hz r = 0.39 | 1 Hz–10 Hz r = 0.91 | r = 0.87 |
| 3—Feedback of single obstacles | 5 Hz–20 Hz r = 0.40 | 5 Hz–20 Hz r = 0.69 | r = 0.67 |
| Criterion | Sine Sweep | PRBS | Driving Maneuver |
|---|---|---|---|
| 1—Feedback on Road Structure | 10 Hz–30 Hz r = 0.82 (+0.27) | 10 Hz–50 Hz r = 0.70 (+0.14) | r = 0.69 (−0.01) |
| 2—Feedback on Wheel Load Reduction | 1 Hz–10 Hz r = 0.77 (+0.38) | 1 Hz–10 Hz r = 0.94 (+0.03) | r = 0.90 (+0.03) |
| 3—Feedback of single obstacles | 5 Hz–20 Hz r = 0.49 (+0.09) | 5 Hz–20 Hz r = 0.68 (−0.01) | r = 0.80 (+0.13) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haas, A.; Menze, G.; Sieberg, P.M.; Schramm, D. An Objective Evaluation Approach for Safety-Relevant Steering Feedback on a Test Bench. Vehicles 2023, 5, 1727-1742. https://doi.org/10.3390/vehicles5040094
Haas A, Menze G, Sieberg PM, Schramm D. An Objective Evaluation Approach for Safety-Relevant Steering Feedback on a Test Bench. Vehicles. 2023; 5(4):1727-1742. https://doi.org/10.3390/vehicles5040094
Chicago/Turabian StyleHaas, Alexander, Gregor Menze, Philipp Maximilian Sieberg, and Dieter Schramm. 2023. "An Objective Evaluation Approach for Safety-Relevant Steering Feedback on a Test Bench" Vehicles 5, no. 4: 1727-1742. https://doi.org/10.3390/vehicles5040094
APA StyleHaas, A., Menze, G., Sieberg, P. M., & Schramm, D. (2023). An Objective Evaluation Approach for Safety-Relevant Steering Feedback on a Test Bench. Vehicles, 5(4), 1727-1742. https://doi.org/10.3390/vehicles5040094








