Deep Learning-Based Stereopsis and Monocular Depth Estimation Techniques: A Review
Abstract
:1. Introduction
2. Datasets
2.1. KITTI
2.2. Middlebury
2.3. Scene Flow
2.4. NYU Depth V2 (NYUv2)
2.5. DTU (Technical University of Denmark)
2.6. ETH3D
3. Taxonomy—For the Deep Learning-Based Depth Estimation Models
4. Stereo Depth Estimation Methods
4.1. Supervised Stereo Models
4.2. Unsupervised Stereo Models
4.3. Self-Supervised Stereo Models
4.4. Experimental Comparison—Stereo Depth Estimation Models
5. Monocular Depth Estimation Methods
5.1. Supervised Monocular Models
5.2. Unsupervised Monocular Models
5.3. Self-Supervised Monocular Models
5.4. Experimental Comparison—Monocular Depth Estimation Models
6. Discussion—Future Research Prospects
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, C.; Hou, C.; Song, Z. Depth recovery and refinement from a single image using defocus cues. J. Mod. Opt. 2015, 62, 441–448. [Google Scholar] [CrossRef]
- Tsai, Y.-M.; Chang, Y.-L.; Chen, L.-G. Block-based vanishing line and vanishing point detection for 3D scene reconstruction. In Proceedings of the 2006 International Symposium on Intelligent Signal Processing and Communications, Yonago, Japan, 12–15 December 2006; pp. 586–589. [Google Scholar]
- Zhang, R.; Tsai, P.-S.; Cryer, J.E.; Shah, M. Shape-from-shading: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 690–706. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded up robust features. Lect. Notes Comput. Sci. 2006, 3951, 404–417. [Google Scholar]
- Bosch, A.; Zisserman, A.; Munoz, X. Image classification using random forests and ferns. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision, Rio De Janeiro, Brazil, 14–21 October 2007; pp. 1–8. [Google Scholar]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 1150–1157. [Google Scholar]
- Lafferty, J.; McCallum, A.; Pereira, F.C. Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data. 2001. Available online: https://repository.upenn.edu/entities/publication/c9aea099-b5c8-4fdd-901c-15b6f889e4a7 (accessed on 28 June 2001).
- Cross, G.R.; Jain, A.K. Markov random field texture models. IEEE Trans. Pattern Anal. Mach. Intell. 1983, PAMI-5, 25–39. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Gould, S.; Koller, D. Single image depth estimation from predicted semantic labels. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 1253–1260. [Google Scholar]
- Facil, J.M.; Ummenhofer, B.; Zhou, H.; Montesano, L.; Brox, T.; Civera, J. CAM-Convs: Camera-aware multi-scale convolutions for single-view depth. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11826–11835. [Google Scholar]
- Hao, S.; Zhou, Y.; Guo, Y. A brief survey on semantic segmentation with deep learning. Neurocomputing 2020, 406, 302–321. [Google Scholar] [CrossRef]
- Lai, Z.; Lu, E.; Xie, W. Mast: A memory-augmented self-supervised tracker. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 6479–6488. [Google Scholar]
- Wang, K.; Peng, X.; Yang, J.; Lu, S.; Qiao, Y. Suppressing uncertainties for large-scale facial expression recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 6897–6906. [Google Scholar]
- Zeng, N.; Zhang, H.; Song, B.; Liu, W.; Li, Y.; Dobaie, A.M. Facial expression recognition via learning deep sparse autoencoders. Neurocomputing 2018, 273, 643–649. [Google Scholar] [CrossRef]
- Jin, L.; Wei, L.; Li, S. Gradient-based differential neural-solution to time-dependent nonlinear optimization. IEEE Trans. Autom. Control 2022, 68, 620–627. [Google Scholar] [CrossRef]
- Gorban, A.N.; Mirkes, E.M.; Tyukin, I.Y. How deep should be the depth of convolutional neural networks: A backyard dog case study. Cogn. Comput. 2020, 12, 388–397. [Google Scholar] [CrossRef]
- Liu, C.; Gu, J.; Kim, K.; Narasimhan, S.G.; Kautz, J. Neural rgb (r) d sensing: Depth and uncertainty from a video camera. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10986–10995. [Google Scholar]
- Ren, J.; Hussain, A.; Han, J.; Jia, X. Cognitive modelling and learning for multimedia mining and understanding. Cogn. Comput. 2019, 11, 761–762. [Google Scholar] [CrossRef]
- Zbontar, J.; LeCun, Y. Stereo matching by training a convolutional neural network to compare image patches. J. Mach. Learn. Res. 2016, 17, 2287–2318. [Google Scholar]
- Zhang, P.; Liu, J.; Wang, X.; Pu, T.; Fei, C.; Guo, Z. Stereoscopic video saliency detection based on spatiotemporal correlation and depth confidence optimization. Neurocomputing 2020, 377, 256–268. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Liu, F.; Zhou, S.; Wang, Y.; Hou, G.; Sun, Z.; Tan, T. Binocular light-field: Imaging theory and occlusion-robust depth perception application. IEEE Trans. Image Process. 2019, 29, 1628–1640. [Google Scholar] [CrossRef] [PubMed]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Bhoi, A. Monocular depth estimation: A survey. arXiv 2019, arXiv:1901.09402. [Google Scholar]
- Laga, H. A survey on deep learning architectures for image-based depth reconstruction. arXiv 2019, arXiv:1906.06113. [Google Scholar]
- Scharstein, D.; Szeliski, R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms. Int. J. Comput. Vis. 2002, 47, 7–42. [Google Scholar] [CrossRef]
- Scharstein, D.; Szeliski, R. High-accuracy stereo depth maps using structured light. In Proceedings of the 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Madison, WI, USA, 18–20 June 2003; p. I. [Google Scholar]
- Hirschmuller, H.; Scharstein, D. Evaluation of cost functions for stereo matching. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The kitti vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Scharstein, D.; Hirschmüller, H.; Kitajima, Y.; Krathwohl, G.; Nešić, N.; Wang, X.; Westling, P. High-resolution stereo datasets with subpixel-accurate ground truth. In Proceedings of the Pattern Recognition: 36th German Conference, GCPR 2014, Münster, Germany, 2–5 September 2014; Proceedings 36. pp. 31–42. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets robotics: The kitti dataset. Int. J. Robot. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef]
- Mayer, N.; Ilg, E.; Hausser, P.; Fischer, P.; Cremers, D.; Dosovitskiy, A.; Brox, T. A large dataset to train convolutional networks for disparity, optical flow, and scene flow estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4040–4048. [Google Scholar]
- Mayer, N.; Ilg, E.; Fischer, P.; Hazirbas, C.; Cremers, D.; Dosovitskiy, A.; Brox, T. What makes good synthetic training data for learning disparity and optical flow estimation? Int. J. Comput. Vis. 2018, 126, 942–960. [Google Scholar] [CrossRef]
- Silberman, N.; Hoiem, D.; Kohli, P.; Fergus, R. Indoor segmentation and support inference from rgbd images. In Proceedings of the Computer Vision–ECCV 2012: 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; Proceedings, Part V 12. pp. 746–760. [Google Scholar]
- Jensen, R.; Dahl, A.; Vogiatzis, G.; Tola, E.; Aanæs, H. Large scale multi-view stereopsis evaluation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 406–413. [Google Scholar]
- Schops, T.; Schonberger, J.L.; Galliani, S.; Sattler, T.; Schindler, K.; Pollefeys, M.; Geiger, A. A multi-view stereo benchmark with high-resolution images and multi-camera videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3260–3269. [Google Scholar]
- Pang, J.; Sun, W.; Ren, J.S.; Yang, C.; Yan, Q. Cascade residual learning: A two-stage convolutional neural network for stereo matching. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 887–895. [Google Scholar]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional architecture for fast feature embedding. In Proceedings of the 22nd ACM International Conference on Multimedia, Orlando, FL, USA, 3–7 November 2014; pp. 675–678. [Google Scholar]
- Chang, J.-R.; Chen, Y.-S. Pyramid stereo matching network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5410–5418. [Google Scholar]
- Khamis, S.; Fanello, S.; Rhemann, C.; Kowdle, A.; Valentin, J.; Izadi, S. Stereonet: Guided hierarchical refinement for real-time edge-aware depth prediction. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 573–590. [Google Scholar]
- Hinton, G.; Srivastava, N.; Swersky, K. Neural networks for machine learning lecture 6a overview of mini-batch gradient descent. Cited 2012, 14, 2. [Google Scholar]
- Song, X.; Zhao, X.; Hu, H.; Fang, L. Edgestereo: A context integrated residual pyramid network for stereo matching. In Proceedings of the Computer Vision–ACCV 2018: 14th Asian Conference on Computer Vision, Perth, Australia, 2–6 December 2018; Revised Selected Papers Part V 14. pp. 20–35. [Google Scholar]
- Liu, Y.; Cheng, M.-M.; Hu, X.; Wang, K.; Bai, X. Richer convolutional features for edge detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3000–3009. [Google Scholar]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour detection and hierarchical image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 898–916. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Lew, M.S. Learning relaxed deep supervision for better edge detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 231–240. [Google Scholar]
- Mottaghi, R.; Chen, X.; Liu, X.; Cho, N.-G.; Lee, S.-W.; Fidler, S.; Urtasun, R.; Yuille, A. The role of context for object detection and semantic segmentation in the wild. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 891–898. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Wang, Y.; Lai, Z.; Huang, G.; Wang, B.H.; Van Der Maaten, L.; Campbell, M.; Weinberger, K.Q. Anytime stereo image depth estimation on mobile devices. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 5893–5900. [Google Scholar]
- Yang, G.; Manela, J.; Happold, M.; Ramanan, D. Hierarchical deep stereo matching on high-resolution images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5515–5524. [Google Scholar]
- Menze, M.; Geiger, A. Object scene flow for autonomous vehicles. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3061–3070. [Google Scholar]
- Liang, Z.; Guo, Y.; Feng, Y.; Chen, W.; Qiao, L.; Zhou, L.; Zhang, J.; Liu, H. Stereo matching using multi-level cost volume and multi-scale feature constancy. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 43, 300–315. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Tao, W. Pvsnet: Pixelwise visibility-aware multi-view stereo network. arXiv 2020, arXiv:2007.07714. [Google Scholar]
- Ji, M.; Gall, J.; Zheng, H.; Liu, Y.; Fang, L. Surfacenet: An end-to-end 3d neural network for multiview stereopsis. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2307–2315. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Fang, T.; Quan, L. Mvsnet: Depth inference for unstructured multi-view stereo. In Proceedings of the European Conference on Computer vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 767–783. [Google Scholar]
- Aanæs, H.; Jensen, R.R.; Vogiatzis, G.; Tola, E.; Dahl, A.B. Large-scale data for multiple-view stereopsis. Int. J. Comput. Vis. 2016, 120, 153–168. [Google Scholar] [CrossRef]
- Kazhdan, M.; Hoppe, H. Screened poisson surface reconstruction. ACM Trans. Graph. (ToG) 2013, 32, 1–13. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L. Pytorch: An imperative style, high-performance deep learning library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- Tankovich, V.; Hane, C.; Zhang, Y.; Kowdle, A.; Fanello, S.; Bouaziz, S. Hitnet: Hierarchical iterative tile refinement network for real-time stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14362–14372. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. pp. 234–241. [Google Scholar]
- Lipson, L.; Teed, Z.; Deng, J. Raft-stereo: Multilevel recurrent field transforms for stereo matching. In Proceedings of the 2021 International Conference on 3D Vision (3DV), London, UK, 1–3 December 2021; pp. 218–227. [Google Scholar]
- Teed, Z.; Deng, J. Raft: Recurrent all-pairs field transforms for optical flow. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part II 16. pp. 402–419. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic Differentiation in Pytorch, BibSonomy, Long Beach, California, USA. Available online: https://openreview.net/forum?id=BJJsrmfCZ (accessed on 28 October 2017).
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Zeng, L.; Tian, X. CRAR: Accelerating Stereo Matching with Cascaded Residual Regression and Adaptive Refinement. ACM Trans. Multimed. Comput. Commun. Appl. (TOMM) 2022, 18, 1–19. [Google Scholar] [CrossRef]
- Yin, Z.; Darrell, T.; Yu, F. Hierarchical discrete distribution decomposition for match density estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 6044–6053. [Google Scholar]
- Zhang, F.; Prisacariu, V.; Yang, R.; Torr, P.H. Ga-net: Guided aggregation net for end-to-end stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 185–194. [Google Scholar]
- Xu, G.; Cheng, J.; Guo, P.; Yang, X. Attention concatenation volume for accurate and efficient stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12981–12990. [Google Scholar]
- Jiang, H.; Xu, R.; Jiang, W. An Improved RaftStereo Trained with A Mixed Dataset for the Robust Vision Challenge 2022. arXiv 2022, arXiv:2210.12785. [Google Scholar]
- Shen, Z.; Dai, Y.; Song, X.; Rao, Z.; Zhou, D.; Zhang, L. Pcw-net: Pyramid combination and warping cost volume for stereo matching. In Proceedings of the Computer Vision–ECCV 2022: 17th European Conference, Tel Aviv, Israel, 23–27 October 2022; Proceedings, Part XXXI. pp. 280–297. [Google Scholar]
- Guo, X.; Yang, K.; Yang, W.; Wang, X.; Li, H. Group-wise correlation stereo network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3273–3282. [Google Scholar]
- Xu, G.; Zhou, H.; Yang, X. CGI-Stereo: Accurate and Real-Time Stereo Matching via Context and Geometry Interaction. arXiv 2023, arXiv:2301.02789. [Google Scholar]
- Khot, T.; Agrawal, S.; Tulsiani, S.; Mertz, C.; Lucey, S.; Hebert, M. Learning unsupervised multi-view stereopsis via robust photometric consistency. arXiv 2019, arXiv:1905.02706. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. Tensorflow: A system for large-scale machine learning. In Proceedings of the OSDI, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Dai, Y.; Zhu, Z.; Rao, Z.; Li, B. Mvs2: Deep unsupervised multi-view stereo with multi-view symmetry. In Proceedings of the 2019 International Conference on 3D Vision (3DV), Quebec City, QC, Canada, 16–19 September 2019; pp. 1–8. [Google Scholar]
- Pilzer, A.; Lathuilière, S.; Xu, D.; Puscas, M.M.; Ricci, E.; Sebe, N. Progressive fusion for unsupervised binocular depth estimation using cycled networks. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 2380–2395. [Google Scholar] [CrossRef] [PubMed]
- Mao, X.; Li, Q.; Xie, H.; Lau, R.Y.; Wang, Z.; Paul Smolley, S. Least squares generative adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2794–2802. [Google Scholar]
- Huang, B.; Yi, H.; Huang, C.; He, Y.; Liu, J.; Liu, X. M3VSNet: Unsupervised multi-metric multi-view stereo network. In Proceedings of the 2021 IEEE International Conference on Image Processing (ICIP), Anchorage, AK, USA, 19–22 September 2021; pp. 3163–3167. [Google Scholar]
- Qi, S.; Sang, X.; Yan, B.; Wang, P.; Chen, D.; Wang, H.; Ye, X. Unsupervised multi-view stereo network based on multi-stage depth estimation. Image Vis. Comput. 2022, 122, 104449. [Google Scholar] [CrossRef]
- Sun, D.; Yang, X.; Liu, M.-Y.; Kautz, J. Pwc-net: Cnns for optical flow using pyramid, warping, and cost volume. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8934–8943. [Google Scholar]
- Xu, H.; Zhou, Z.; Wang, Y.; Kang, W.; Sun, B.; Li, H.; Qiao, Y. Digging into uncertainty in self-supervised multi-view stereo. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 6078–6087. [Google Scholar]
- Loshchilov, I.; Hutter, F. Sgdr: Stochastic gradient descent with warm restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]
- Huang, B.; Zheng, J.-Q.; Giannarou, S.; Elson, D.S. H-net: Unsupervised attention-based stereo depth estimation leveraging epipolar geometry. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 4460–4467. [Google Scholar]
- Gan, W.; Wong, P.K.; Yu, G.; Zhao, R.; Vong, C.M. Light-weight network for real-time adaptive stereo depth estimation. Neurocomputing 2021, 441, 118–127. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, P.; Yang, R. Learning depth with convolutional spatial propagation network. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 2361–2379. [Google Scholar] [CrossRef]
- Yang, J.; Alvarez, J.M.; Liu, M. Self-supervised learning of depth inference for multi-view stereo. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 7526–7534. [Google Scholar]
- Yang, J.; Mao, W.; Alvarez, J.M.; Liu, M. Cost volume pyramid based depth inference for multi-view stereo. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 4877–4886. [Google Scholar]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual losses for real-time style transfer and super-resolution. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part II 14. pp. 694–711. [Google Scholar]
- Wang, C.; Bai, X.; Wang, X.; Liu, X.; Zhou, J.; Wu, X.; Li, H.; Tao, D. Self-supervised multiscale adversarial regression network for stereo disparity estimation. IEEE Trans. Cybern. 2020, 51, 4770–4783. [Google Scholar] [CrossRef]
- Huang, B.; Zheng, J.-Q.; Nguyen, A.; Tuch, D.; Vyas, K.; Giannarou, S.; Elson, D.S. Self-supervised generative adversarial network for depth estimation in laparoscopic images. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Strasbourg, France, 27 September–1 October 2021; Proceedings, Part IV 24. pp. 227–237. [Google Scholar]
- Zhong, Y.; Dai, Y.; Li, H. Self-supervised learning for stereo matching with self-improving ability. arXiv 2017, arXiv:1709.00930. [Google Scholar]
- Wang, H.; Fan, R.; Cai, P.; Liu, M. PVStereo: Pyramid voting module for end-to-end self-supervised stereo matching. IEEE Robot. Autom. Lett. 2021, 6, 4353–4360. [Google Scholar] [CrossRef]
- Li, J.; Wang, P.; Xiong, P.; Cai, T.; Yan, Z.; Yang, L.; Liu, J.; Fan, H.; Liu, S. Practical stereo matching via cascaded recurrent network with adaptive correlation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16263–16272. [Google Scholar]
- Zhao, H.; Zhou, H.; Zhang, Y.; Zhao, Y.; Yang, Y.; Ouyang, T. EAI-Stereo: Error Aware Iterative Network for Stereo Matching. In Proceedings of the Asian Conference on Computer Vision, Macao, China, 4–8 December 2022; pp. 315–332. [Google Scholar]
- Fu, H.; Gong, M.; Wang, C.; Batmanghelich, K.; Tao, D. Deep ordinal regression network for monocular depth estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2002–2011. [Google Scholar]
- Chen, Y.; Zhao, H.; Hu, Z.; Peng, J. Attention-based context aggregation network for monocular depth estimation. Int. J. Mach. Learn. Cybern. 2021, 12, 1583–1596. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7794–7803. [Google Scholar]
- Liu, W.; Rabinovich, A.; Berg, A.C. Parsenet: Looking wider to see better. arXiv 2015, arXiv:1506.04579. [Google Scholar]
- Chen, L.-C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.0558. [Google Scholar]
- Cao, Y.; Zhao, T.; Xian, K.; Shen, C.; Cao, Z.; Xu, S. Monocular depth estimation with augmented ordinal depth relationships. IEEE Trans. Image Process. 2019, 30, 2674–2682. [Google Scholar]
- Chang, J.; Wetzstein, G. Deep optics for monocular depth estimation and 3d object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 10193–10202. [Google Scholar]
- Yin, W.; Liu, Y.; Shen, C.; Yan, Y. Enforcing geometric constraints of virtual normal for depth prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 5684–5693. [Google Scholar]
- Cao, Y.; Wu, Z.; Shen, C. Estimating depth from monocular images as classification using deep fully convolutional residual networks. IEEE Trans. Circuits Syst. Video Technol. 2017, 28, 3174–3182. [Google Scholar] [CrossRef]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated residual transformations for deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1492–1500. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Lee, J.H.; Han, M.-K.; Ko, D.W.; Suh, I.H. From big to small: Multi-scale local planar guidance for monocular depth estimation. arXiv 2019, arXiv:1907.10326. [Google Scholar]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth map prediction from a single image using a multi-scale deep network. arXiv 2014, arXiv:1406.2283. [Google Scholar]
- Lee, S.; Lee, J.; Kim, B.; Yi, E.; Kim, J. Patch-wise attention network for monocular depth estimation. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; pp. 1873–1881. [Google Scholar]
- Xu, Y.; Peng, C.; Li, M.; Li, Y.; Du, S. Pyramid feature attention network for monocular depth prediction. In Proceedings of the 2021 IEEE International Conference on Multimedia and Expo (ICME), Shenzhen, China, 5–9 July 2021; pp. 1–6. [Google Scholar]
- Liebel, L.; Körner, M. Multidepth: Single-image depth estimation via multi-task regression and classification. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 1440–1447. [Google Scholar]
- Ochs, M.; Kretz, A.; Mester, R. Sdnet: Semantically guided depth estimation network. In Proceedings of the Pattern Recognition: 41st DAGM German Conference, DAGM GCPR 2019, Dortmund, Germany, 10–13 September 2019; Proceedings 41. pp. 288–302. [Google Scholar]
- Lei, Z.; Wang, Y.; Li, Z.; Yang, J. Attention based multilayer feature fusion convolutional neural network for unsupervised monocular depth estimation. Neurocomputing 2021, 423, 343–352. [Google Scholar] [CrossRef]
- Ji, Z.-y.; Song, X.-j.; Song, H.-b.; Yang, H.; Guo, X.-x. RDRF-Net: A pyramid architecture network with residual-based dynamic receptive fields for unsupervised depth estimation. Neurocomputing 2021, 457, 1–12. [Google Scholar] [CrossRef]
- Poggi, M.; Aleotti, F.; Tosi, F.; Mattoccia, S. Towards real-time unsupervised monocular depth estimation on cpu. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 5848–5854. [Google Scholar]
- Chen, P.-Y.; Liu, A.H.; Liu, Y.-C.; Wang, Y.-C.F. Towards scene understanding: Unsupervised monocular depth estimation with semantic-aware representation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2624–2632. [Google Scholar]
- Godard, C.; Mac Aodha, O.; Brostow, G.J. Unsupervised monocular depth estimation with left-right consistency. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 270–279. [Google Scholar]
- Repala, V.K.; Dubey, S.R. Dual cnn models for unsupervised monocular depth estimation. In Proceedings of the Pattern Recognition and Machine Intelligence: 8th International Conference, PReMI 2019, Tezpur, India, 17–20 December 2019; Proceedings, Part I. pp. 209–217. [Google Scholar]
- Ling, C.; Zhang, X.; Chen, H. Unsupervised monocular depth estimation using attention and multi-warp reconstruction. IEEE Trans. Multimed. 2021, 24, 2938–2949. [Google Scholar] [CrossRef]
- Wang, H.; Sun, Y.; Wu, Q.J.; Lu, X.; Wang, X.; Zhang, Z. Self-supervised monocular depth estimation with direct methods. Neurocomputing 2021, 421, 340–348. [Google Scholar] [CrossRef]
- Bartoccioni, F.; Zablocki, É.; Pérez, P.; Cord, M.; Alahari, K. LiDARTouch: Monocular metric depth estimation with a few-beam LiDAR. Comput. Vis. Image Underst. 2023, 227, 103601. [Google Scholar] [CrossRef]
- Zhou, T.; Brown, M.; Snavely, N.; Lowe, D.G. Unsupervised learning of depth and ego-motion from video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1851–1858. [Google Scholar]
- Godard, C.; Mac Aodha, O.; Firman, M.; Brostow, G.J. Digging into self-supervised monocular depth estimation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3828–3838. [Google Scholar]
- Lu, K.; Zeng, C.; Zeng, Y. Self-supervised learning of monocular depth using quantized networks. Neurocomputing 2022, 488, 634–646. [Google Scholar] [CrossRef]
- Kerr, A.; Merrill, D.; Demouth, J.; Tran, J.; Farooqui, N.; Tavenrath, M.; Schuster, V.; Gornish, E.; Zheng, J.; Sathe, B. CUTLASS: CUDA Template Library for Dense Linear Algebra at all levels and scales. Available online: https://on-demand.gputechconf.com/gtc/2018/presentation/s8854-cutlass-software-primitives-for-dense-linear-algebra-at-all-levels-and-scales-within-cuda.pdf (accessed on 29 March 2018).
- Choi, J.; Jung, D.; Lee, Y.; Kim, D.; Manocha, D.; Lee, D. SelfTune: Metrically Scaled Monocular Depth Estimation through Self-Supervised Learning. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 6511–6518. [Google Scholar]
- Ranftl, R.; Lasinger, K.; Hafner, D.; Schindler, K.; Koltun, V. Towards robust monocular depth estimation: Mixing datasets for zero-shot cross-dataset transfer. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 1623–1637. [Google Scholar] [CrossRef] [PubMed]
- Yin, W.; Zhang, J.; Wang, O.; Niklaus, S.; Mai, L.; Chen, S.; Shen, C. Learning to recover 3d scene shape from a single image. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 204–213. [Google Scholar]
- Qin, T.; Li, P.; Shen, S. Vins-mono: A robust and versatile monocular visual-inertial state estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Li, Z.; Snavely, N. Megadepth: Learning single-view depth prediction from internet photos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2041–2050. [Google Scholar]
- Yue, M.; Fu, G.; Wu, M.; Zhang, X.; Gu, H. Self-supervised monocular depth estimation in dynamic scenes with moving instance loss. Eng. Appl. Artif. Intell. 2022, 112, 104862. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, X.; Wang, N.; Xin, G.; Hu, W. Underwater self-supervised depth estimation. Neurocomputing 2022, 514, 362–373. [Google Scholar] [CrossRef]
- Ilg, E.; Mayer, N.; Saikia, T.; Keuper, M.; Dosovitskiy, A.; Brox, T. Flownet 2.0: Evolution of optical flow estimation with deep networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2462–2470. [Google Scholar]
- Hwang, S.-J.; Park, S.-J.; Baek, J.-H.; Kim, B. Self-supervised monocular depth estimation using hybrid transformer encoder. IEEE Sens. J. 2022, 22, 18762–18770. [Google Scholar] [CrossRef]
- Watson, J.; Mac Aodha, O.; Prisacariu, V.; Brostow, G.; Firman, M. The temporal opportunist: Self-supervised multi-frame monocular depth. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 1164–1174. [Google Scholar]
- Chawla, H.; Jeeveswaran, K.; Arani, E.; Zonooz, B. Image Masking for Robust Self-Supervised Monocular Depth Estimation. arXiv 2022, arXiv:2210.02357. [Google Scholar]
- Varma, A.; Chawla, H.; Zonooz, B.; Arani, E. Transformers in self-supervised monocular depth estimation with unknown camera intrinsics. arXiv 2022, arXiv:2202.03131. [Google Scholar]
- Cai, H.; Yin, F.; Singhal, T.; Pendyam, S.; Noorzad, P.; Zhu, Y.; Nguyen, K.; Matai, J.; Ramaswamy, B.; Mayer, F. Real-Time and Accurate Self-Supervised Monocular Depth Estimation on Mobile Device. In Proceedings of the NeurIPS 2021 Competitions and Demonstrations Track, Online, 6–14 December 2021; pp. 308–313. [Google Scholar]
- Cai, H.; Matai, J.; Borse, S.; Zhang, Y.; Ansari, A.; Porikli, F. X-distill: Improving self-supervised monocular depth via cross-task distillation. arXiv 2021, arXiv:2110.12516. [Google Scholar]
- Goldman, M.; Hassner, T.; Avidan, S. Learn stereo, infer mono: Siamese networks for self-supervised, monocular, depth estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019. [Google Scholar]
- Masoumian, A.; Rashwan, H.A.; Abdulwahab, S.; Cristiano, J.; Asif, M.S.; Puig, D. GCNDepth: Self-supervised monocular depth estimation based on graph convolutional network. Neurocomputing 2023, 517, 81–92. [Google Scholar] [CrossRef]
- Klingner, M.; Termöhlen, J.-A.; Mikolajczyk, J.; Fingscheidt, T. Self-supervised monocular depth estimation: Solving the dynamic object problem by semantic guidance. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XX 16. pp. 582–600. [Google Scholar]
- Yan, J.; Zhao, H.; Bu, P.; Jin, Y. Channel-wise attention-based network for self-supervised monocular depth estimation. In Proceedings of the 2021 International Conference on 3D Vision (3DV), London, UK, 1–3 December 2021; pp. 464–473. [Google Scholar]
- Zhang, Z.; Cui, Z.; Xu, C.; Yan, Y.; Sebe, N.; Yang, J. Pattern-affinitive propagation across depth, surface normal and semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4106–4115. [Google Scholar]
- Song, X.; Li, W.; Zhou, D.; Dai, Y.; Fang, J.; Li, H.; Zhang, L. MLDA-Net: Multi-level dual attention-based network for self-supervised monocular depth estimation. IEEE Trans. Image Process. 2021, 30, 4691–4705. [Google Scholar] [CrossRef]

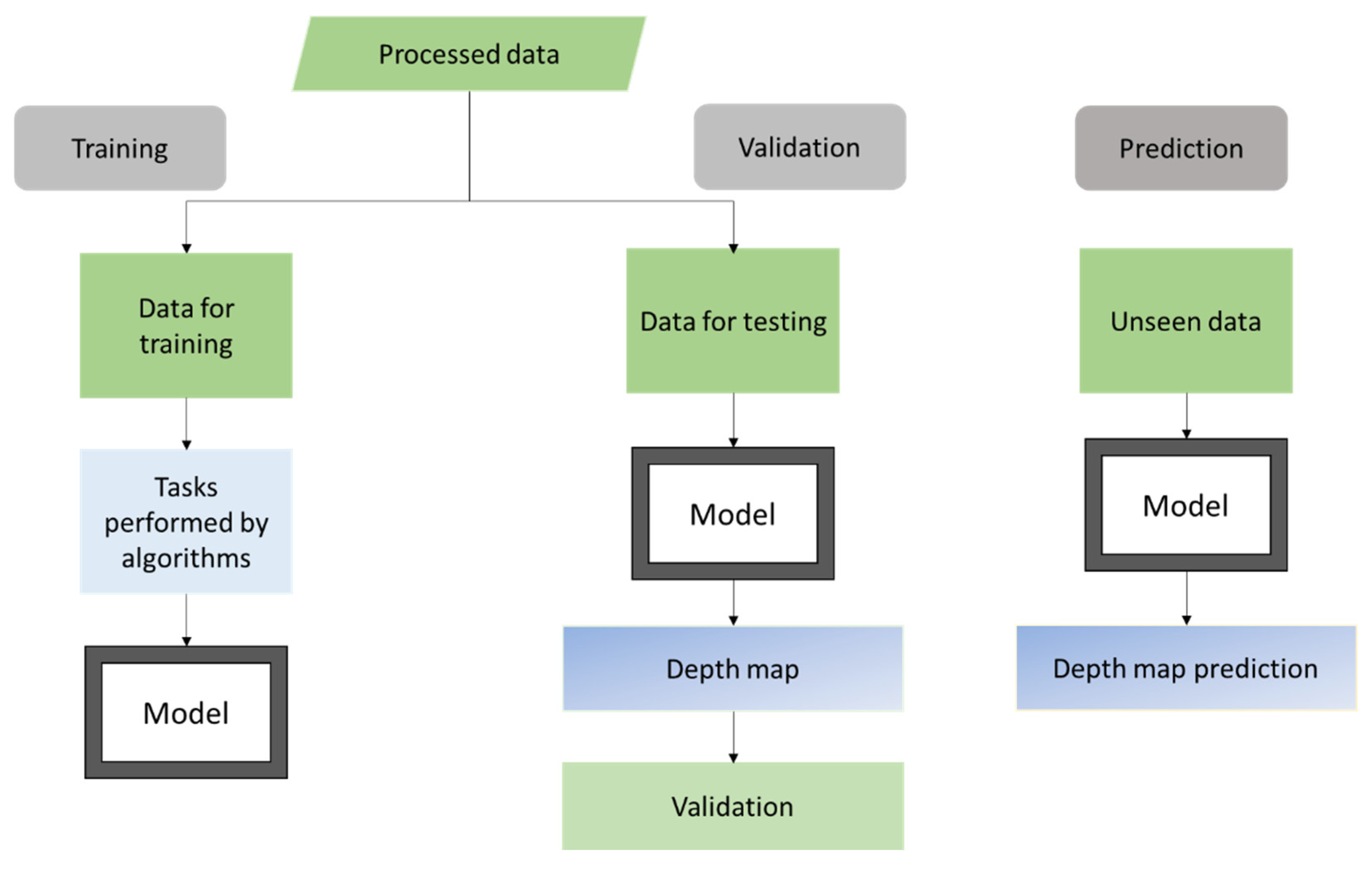
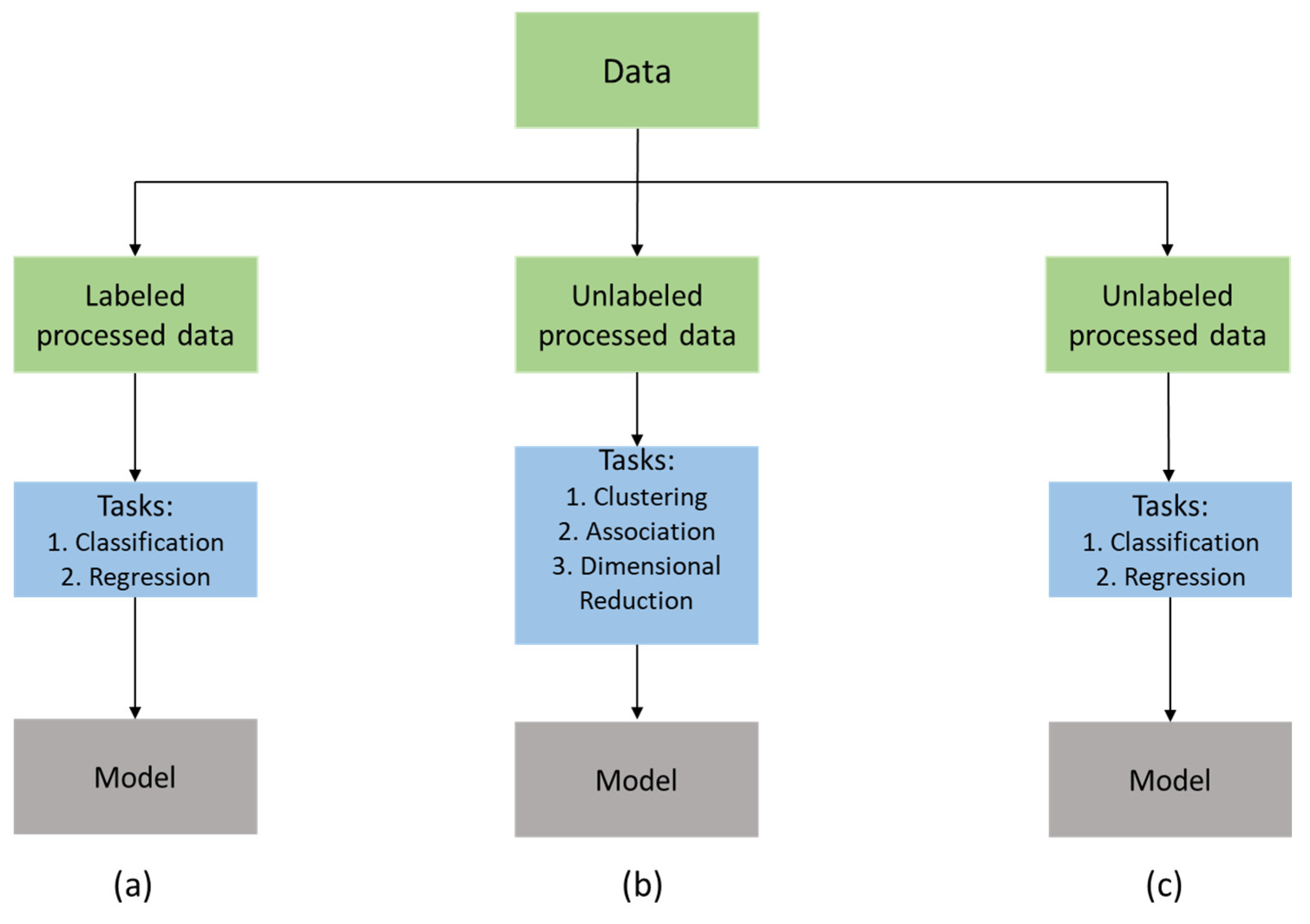

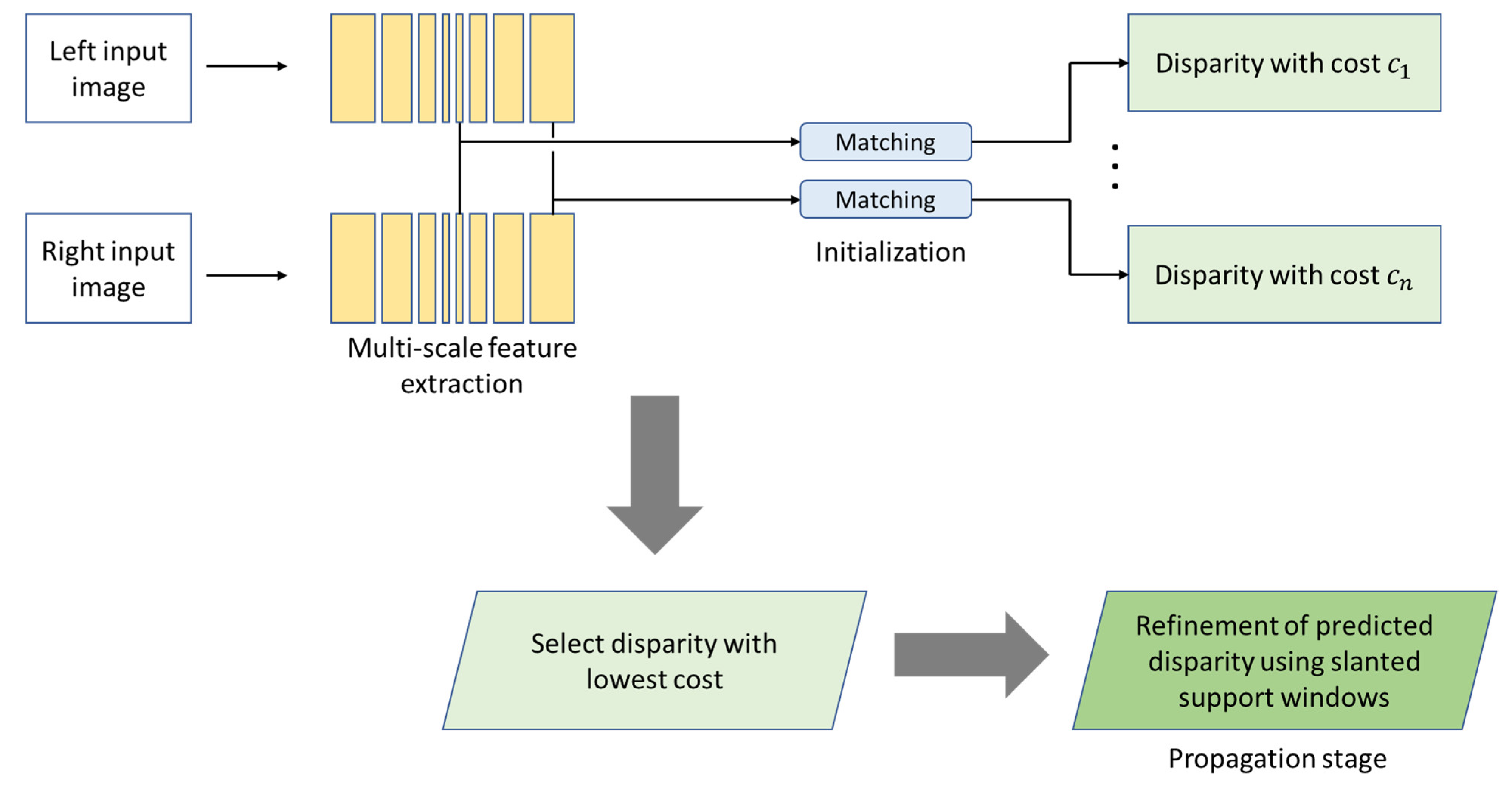

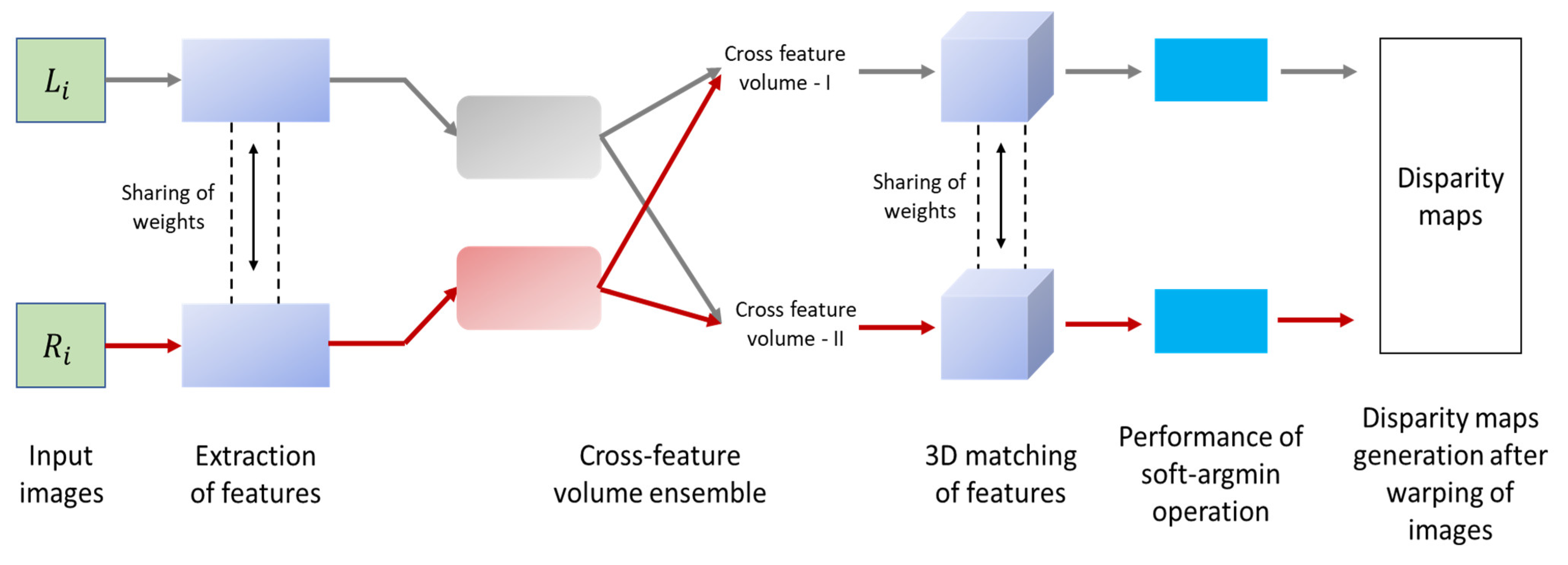
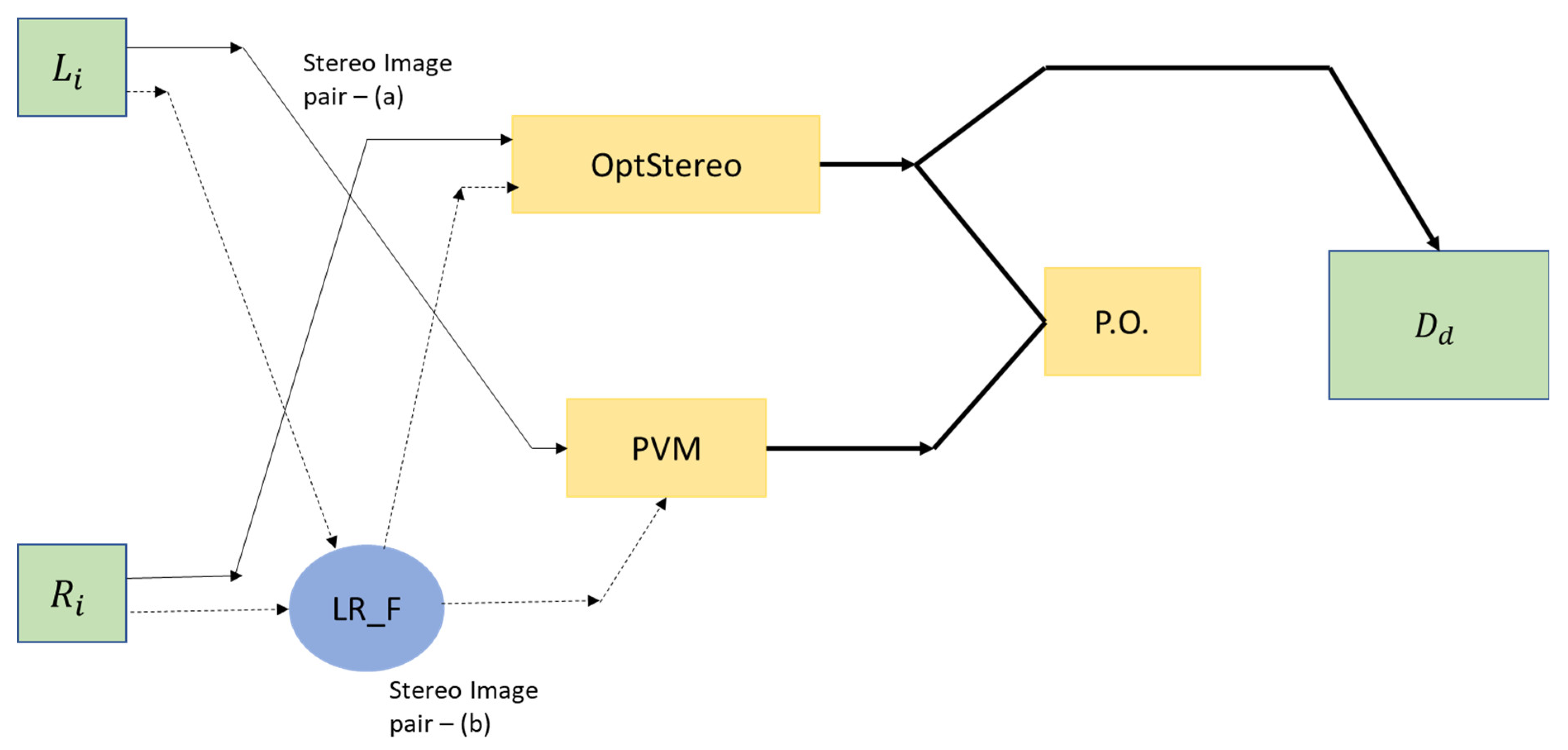

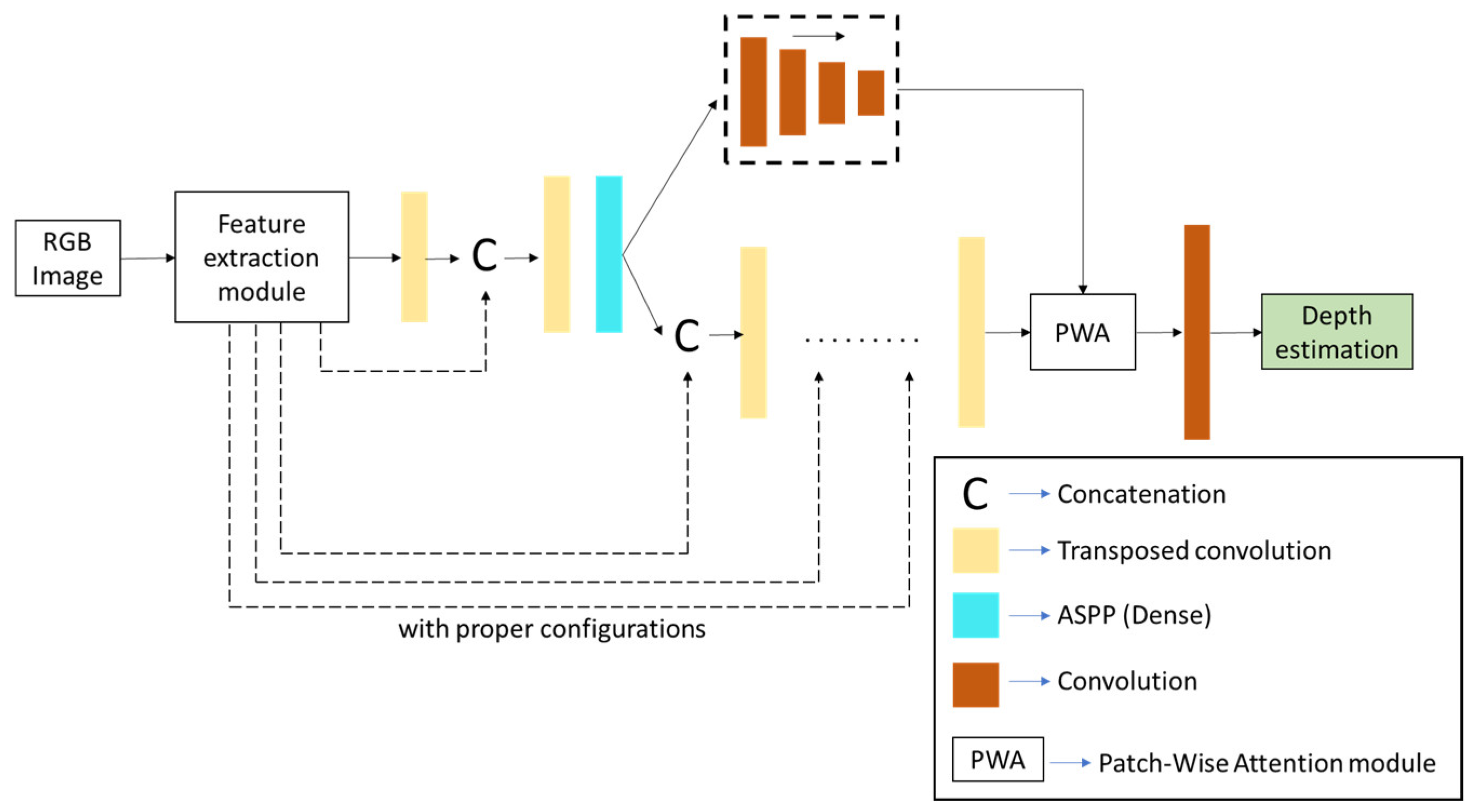
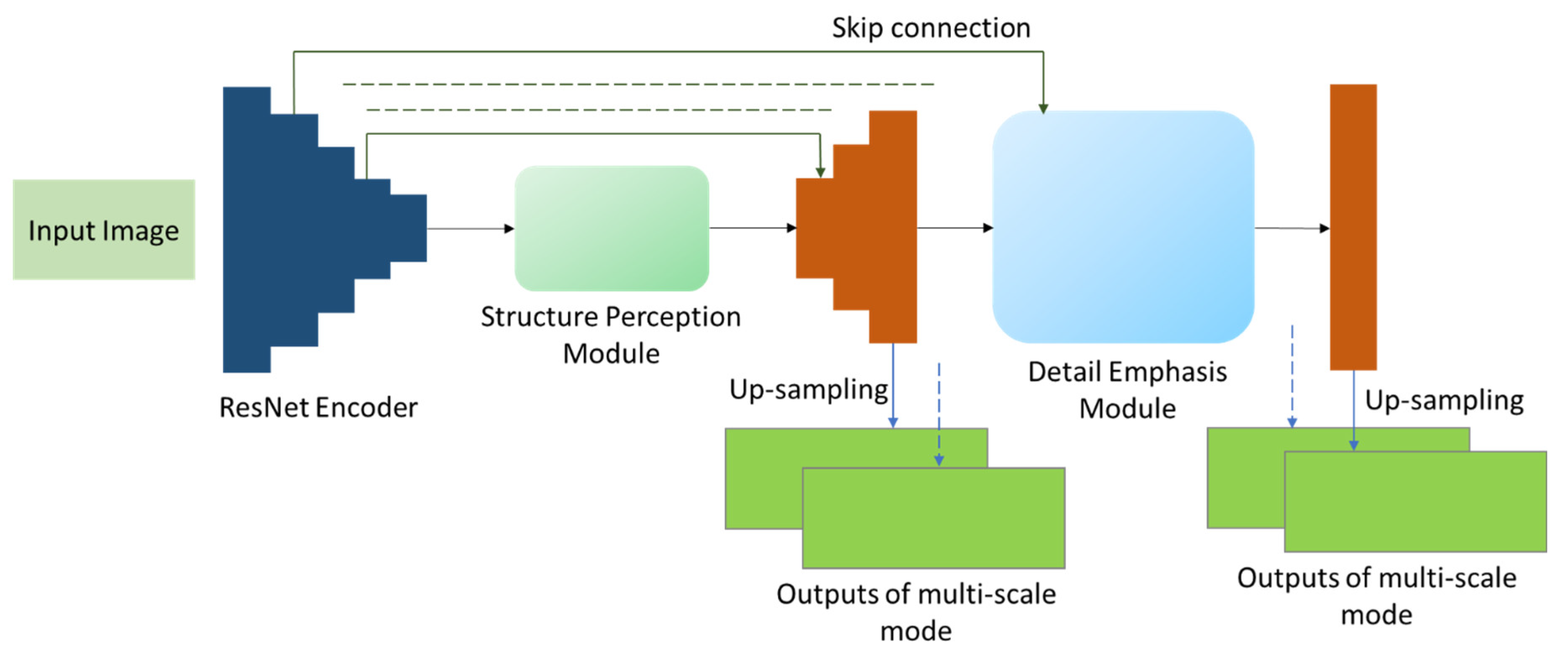
| Training Modes | Merits | Demerits |
|---|---|---|
| Supervised |
|
|
| Unsupervised |
|
|
| Self-supervised |
|
|
| Sl. No. | Algorithms | All Pixels | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| avgerr | rms | bad-4.0 | bad-2.0 | bad-1.0 | A99 | A95 | A90 | Time (s) | ||
| 1 | HSM [50] | 3.44 | 13.4 | 9.68 | 16.5 | 31.2 | 63.8 | 17.6 | 4.26 | 0.51 |
| 2 | MCV-MFC [52] | 4.54 | 13.5 | 19.1 | 31.2 | 46.7 | 68.1 | 19.5 | 9.91 | 0.35 |
| 3 | HITNet [59] | 3.29 | 14.5 | 8.66 | 12.8 | 20.7 | 77.7 | 11.4 | 3.92 | 0.14 |
| 4 | RAFT-Stereo [61] | 2.71 | 12.6 | 6.42 | 9.37 | 15.1 | 64.4 | 8.89 | 2.24 | 11.6 |
| 5 | CRAR [65] | 14.7 | 42.6 | 18.5 | 29.3 | 48.2 | 175 | 108 | 59.8 | 0.12 |
| 6 | CREStereo [93] | 2.1 | 10.5 | 5.05 | 8.13 | 14 | 49.7 | 5.48 | 1.63 | 3.55 |
| 7 | iRaftStereo_RVC [69] | 2.9 | 12.2 | 8.02 | 13.3 | 24 | 59.2 | 13.3 | 3.21 | 2.7 |
| 8 | EAI-Stereo [94] | 1.92 | 9.95 | 5.01 | 7.53 | 12.9 | 47.3 | 4.76 | 1.55 | 2.39 |
| Sl. No. | Algorithms | Non-Occluded Pixels | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| avgerr | rms | bad-4.0 | bad-2.0 | bad-1.0 | A99 | A95 | A90 | Time (s) | ||
| 1 | HSM [50] | 2.07 | 10.3 | 4.83 | 10.2 | 24.6 | 39.2 | 4.32 | 2.12 | 0.51 |
| 2 | MCV-MFC [52] | 3.13 | 10.4 | 13.4 | 24.8 | 40.8 | 41.8 | 11.7 | 6.09 | 0.35 |
| 3 | HITNet [59] | 1.71 | 9.97 | 3.81 | 6.46 | 13.3 | 30.2 | 4.26 | 2.32 | 0.14 |
| 4 | RAFT-Stereo [61] | 1.27 | 8.41 | 2.75 | 4.74 | 9.37 | 21.7 | 2.29 | 1.1 | 11.6 |
| 5 | CRAR [65] | 8.63 | 32.4 | 11.5 | 22 | 42.2 | 159 | 65 | 6.95 | 0.12 |
| 6 | CREStereo [93] | 1.15 | 7.7 | 2.04 | 3.71 | 8.25 | 22.9 | 1.58 | 0.92 | 3.55 |
| 7 | iRaftStereo_RVC [69] | 1.71 | 8.97 | 4.06 | 8.07 | 17.8 | 32.8 | 3.64 | 1.74 | 2.7 |
| 8 | EAI-Stereo [94] | 1.09 | 7.4 | 2.14 | 3.68 | 7.81 | 20.8 | 1.83 | 0.9 | 2.39 |
| Sl. No. | Algorithms | Training Mode | KITTI 2015 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| All Pixels | Non Occ Pixels | Runtime (s) | |||||||
| D1-bg | D1-fg | D1-all | D1-bg | D1-fg | D1-all | ||||
| 1 | CRL [38] | Supervised | 2.48 | 3.59 | 2.67 | 2.32 | 3.12 | 2.45 | 0.47 |
| 2 | SsMNet [91] | Self-supervised | 2.7 | 6.92 | 3.4 | 2.46 | 6.13 | 3.06 | 0.8 |
| 3 | PSMNet [40] | Supervised | 1.86 | 4.62 | 2.32 | 1.71 | 4.31 | 2.14 | 0.41 |
| 4 | EdgeStereo [43] | Supervised | 2.27 | 4.18 | 2.59 | 2.12 | 3.85 | 2.4 | 0.27 |
| 5 | HSM [50] | Supervised | 1.8 | 3.85 | 2.14 | 1.63 | 3.4 | 1.92 | 0.14 |
| 6 | MCV-MFC [52] | Supervised | 1.95 | 3.84 | 2.27 | 1.8 | 3.4 | 2.07 | 0.35 |
| 7 | HITNet [59] | Supervised | 1.74 | 3.2 | 1.98 | 1.54 | 2.72 | 1.74 | 0.02 |
| 8 | OptStereo [92] | Supervised | 1.5 | 3.43 | 1.82 | 1.36 | 3.08 | 1.64 | 0.1 |
| 9 | PVStereo [92] | Self-supervised | 2.29 | 6.5 | 2.99 | 2.09 | 5.73 | 2.69 | 0.1 |
| 10 | SMAR-Net [89] | Self-supervised | 1.95 | 4.57 | 2.38 | 1.79 | 4.31 | 2.2 | 0.48 |
| 11 | CRAR [65] | Supervised | 2.48 | 5.78 | 3.03 | 2.17 | 5.02 | 2.64 | 0.028 |
| 12 | ACVNet [68] | Supervised | 1.37 | 3.07 | 1.65 | 1.26 | 2.84 | 1.52 | 0.2 |
| 13 | iRaftStereo_RVC [69] | Supervised | 1.88 | 3.03 | 2.07 | 1.76 | 2.94 | 1.95 | 0.5 |
| 14 | PCW-Net [70] | Supervised | 1.37 | 3.16 | 1.67 | 1.26 | 2.93 | 1.53 | 0.44 |
| 15 | CGI-Stereo [72] | Supervised | 1.66 | 3.38 | 1.94 | 1.52 | 3.23 | 1.81 | 0.02 |
| Sl. No. | Algorithms | Training Mode | SILog | sqErrRel | absErrRel | iRMSE | Runtime (s) |
|---|---|---|---|---|---|---|---|
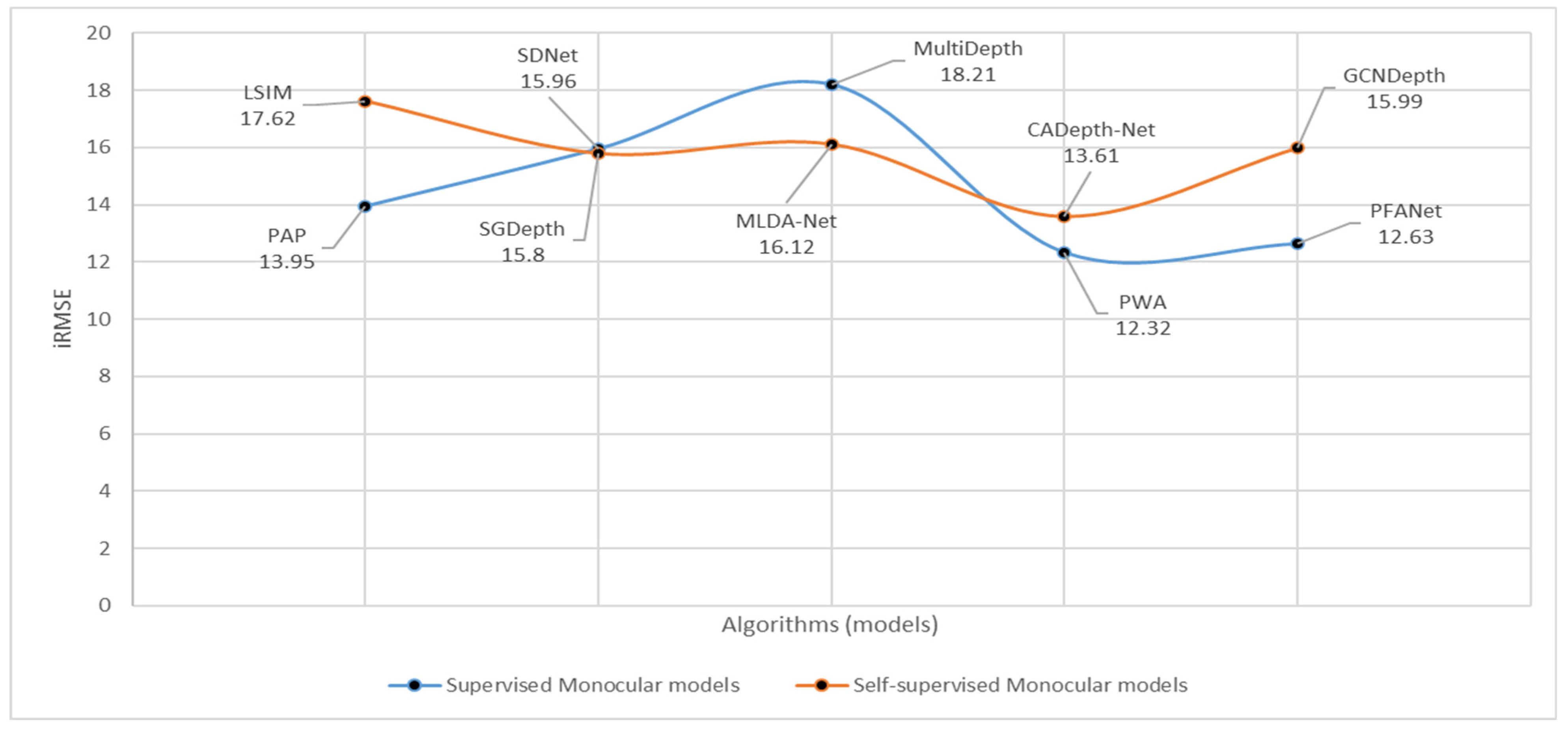
| 1 | PAP [144] | Supervised | 13.08 | 2.72 | 10.27 | 13.95 | 0.18 |
| 2 | LSIM [140] | Self-supervised | 17.92 | 6.88 | 14.04 | 17.62 | 0.08 |
| 3 | SDNet [112] | Supervised | 14.68 | 3.9 | 12.31 | 15.96 | 0.2 |
| 4 | MultiDepth [111] | Supervised | 16.05 | 3.89 | 13.82 | 18.21 | 0.01 |
| 5 | SGDepth [142] | Self-supervised | 15.3 | 5 | 13.29 | 15.8 | 0.1 |
| 6 | MLDA-Net [145] | Self-supervised | 14.42 | 3.41 | 11.67 | 16.12 | 0.2 |
| 7 | PWA [109] | Supervised | 11.45 | 2.3 | 9.05 | 12.32 | 0.06 |
| 8 | PFANet [110] | Supervised | 11.84 | 2.46 | 9.23 | 12.63 | 0.1 |
| 9 | GCNDepth [141] | Self-supervised | 15.54 | 4.26 | 12.75 | 15.99 | 0.05 |
| 10 | CADepth-Net [143] | Self-supervised | 13.34 | 3.33 | 10.67 | 13.61 | 0.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lahiri, S.; Ren, J.; Lin, X. Deep Learning-Based Stereopsis and Monocular Depth Estimation Techniques: A Review. Vehicles 2024, 6, 305-351. https://doi.org/10.3390/vehicles6010013
Lahiri S, Ren J, Lin X. Deep Learning-Based Stereopsis and Monocular Depth Estimation Techniques: A Review. Vehicles. 2024; 6(1):305-351. https://doi.org/10.3390/vehicles6010013
Chicago/Turabian StyleLahiri, Somnath, Jing Ren, and Xianke Lin. 2024. "Deep Learning-Based Stereopsis and Monocular Depth Estimation Techniques: A Review" Vehicles 6, no. 1: 305-351. https://doi.org/10.3390/vehicles6010013
APA StyleLahiri, S., Ren, J., & Lin, X. (2024). Deep Learning-Based Stereopsis and Monocular Depth Estimation Techniques: A Review. Vehicles, 6(1), 305-351. https://doi.org/10.3390/vehicles6010013








