Random Forest-Based Grouping for Accurate SOH Estimation in Second-Life Batteries
Abstract
1. Introduction
2. State-of-the-Art
3. Development Description
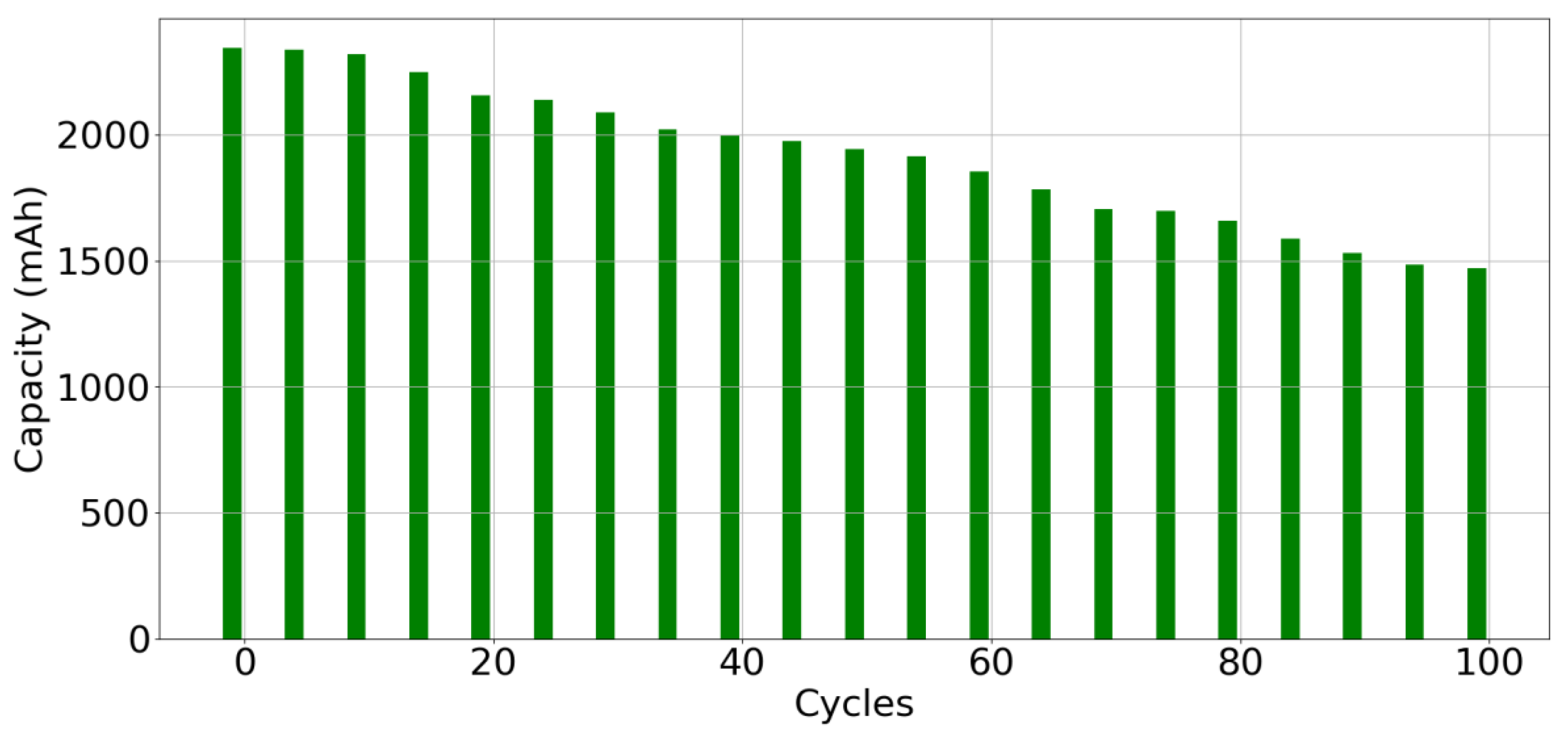
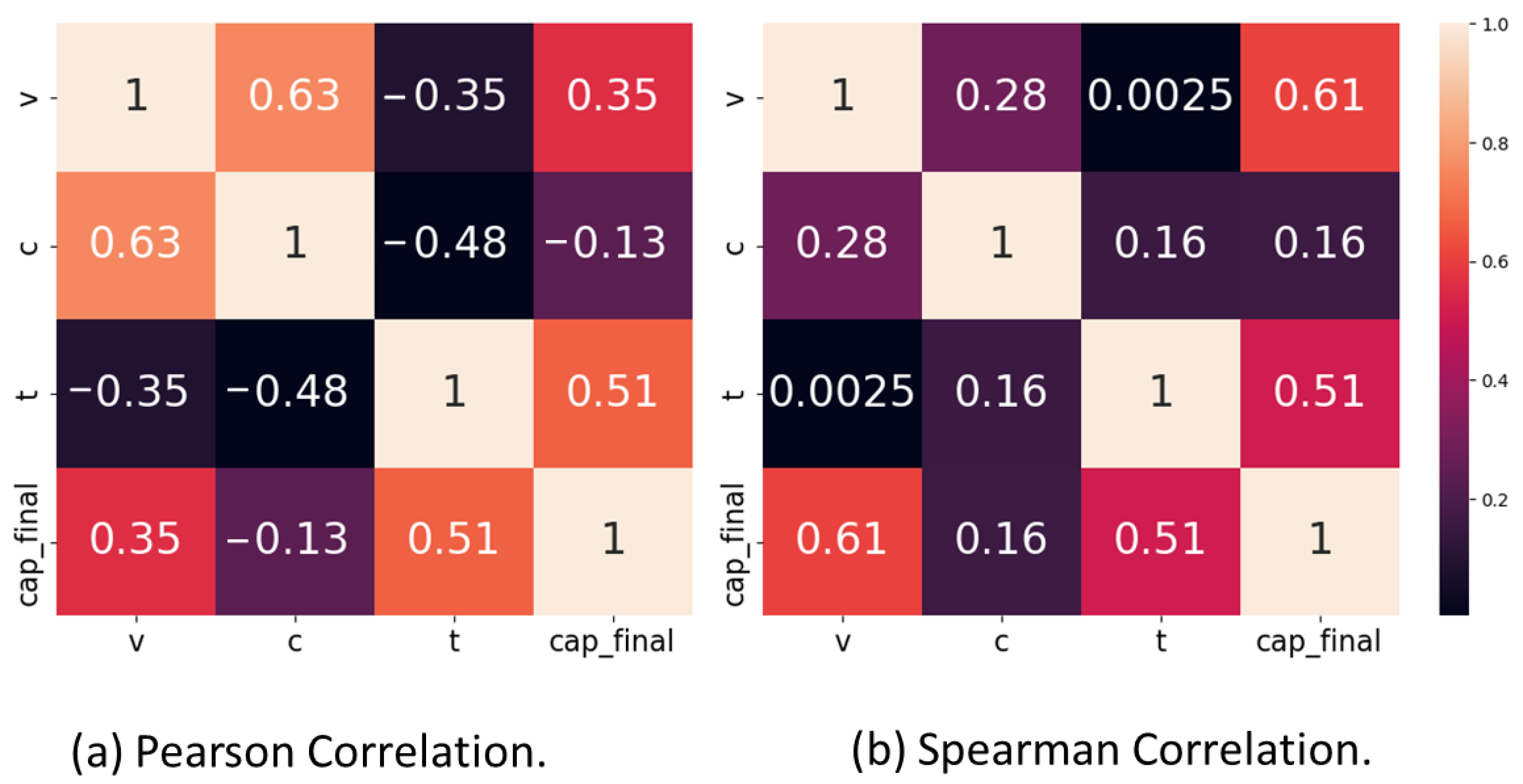
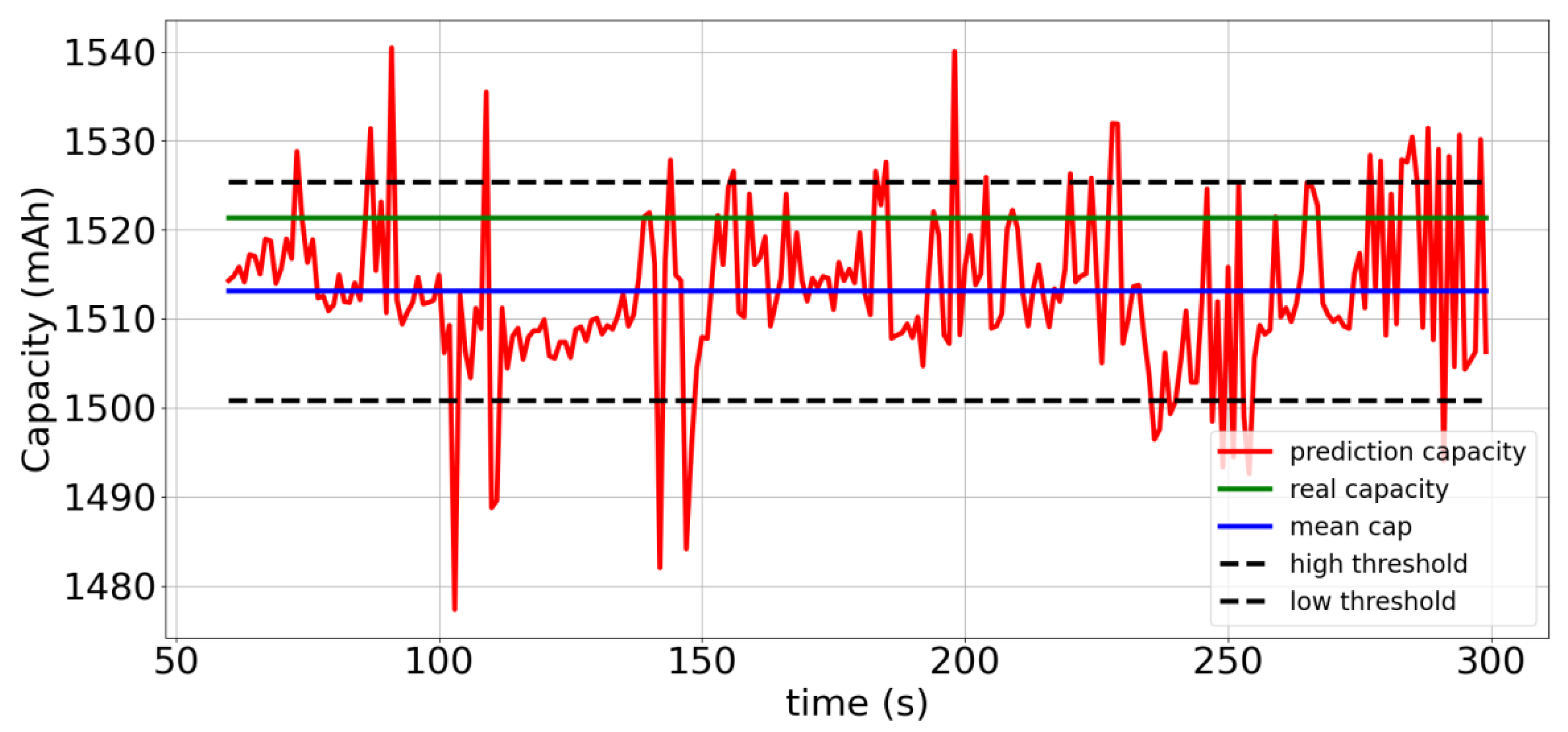
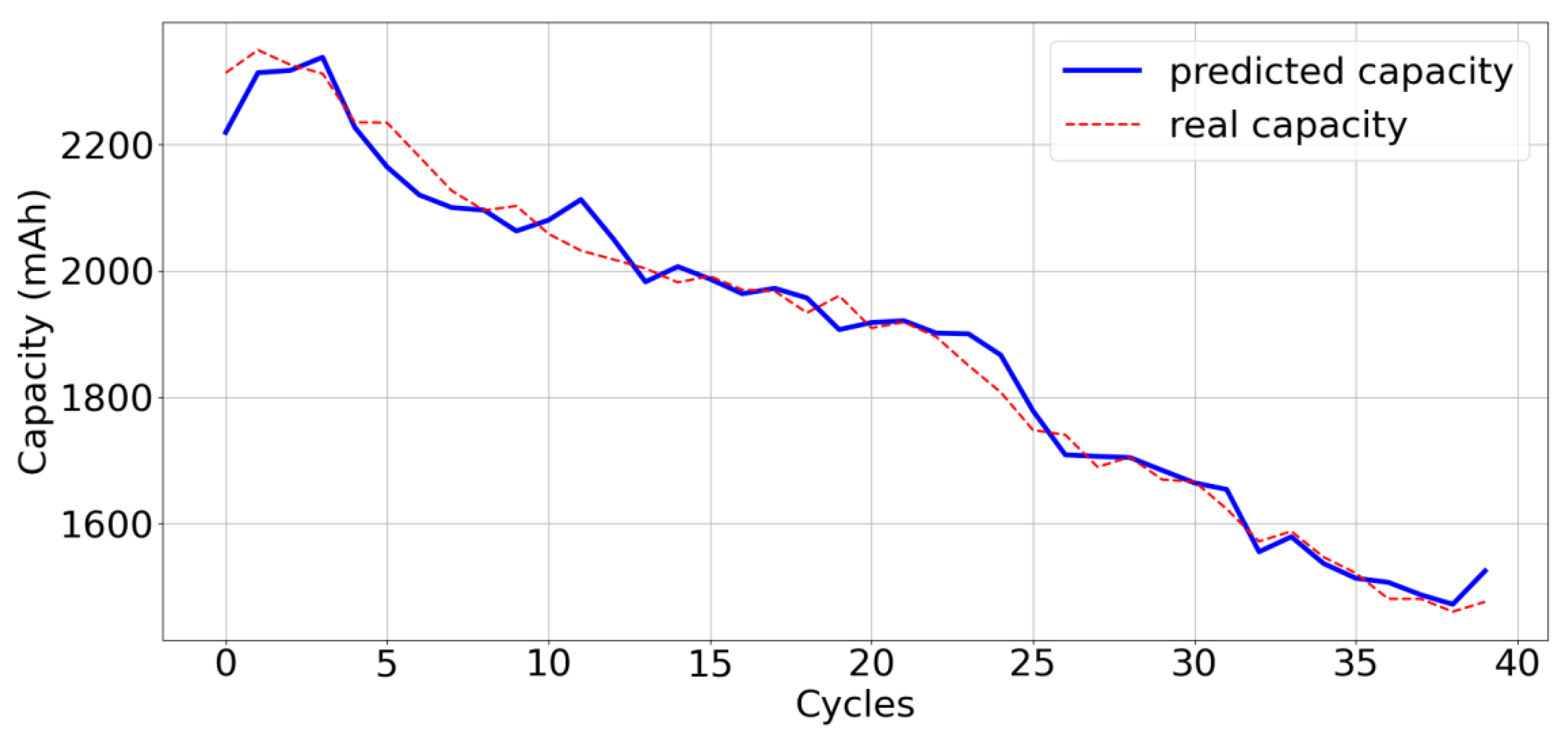
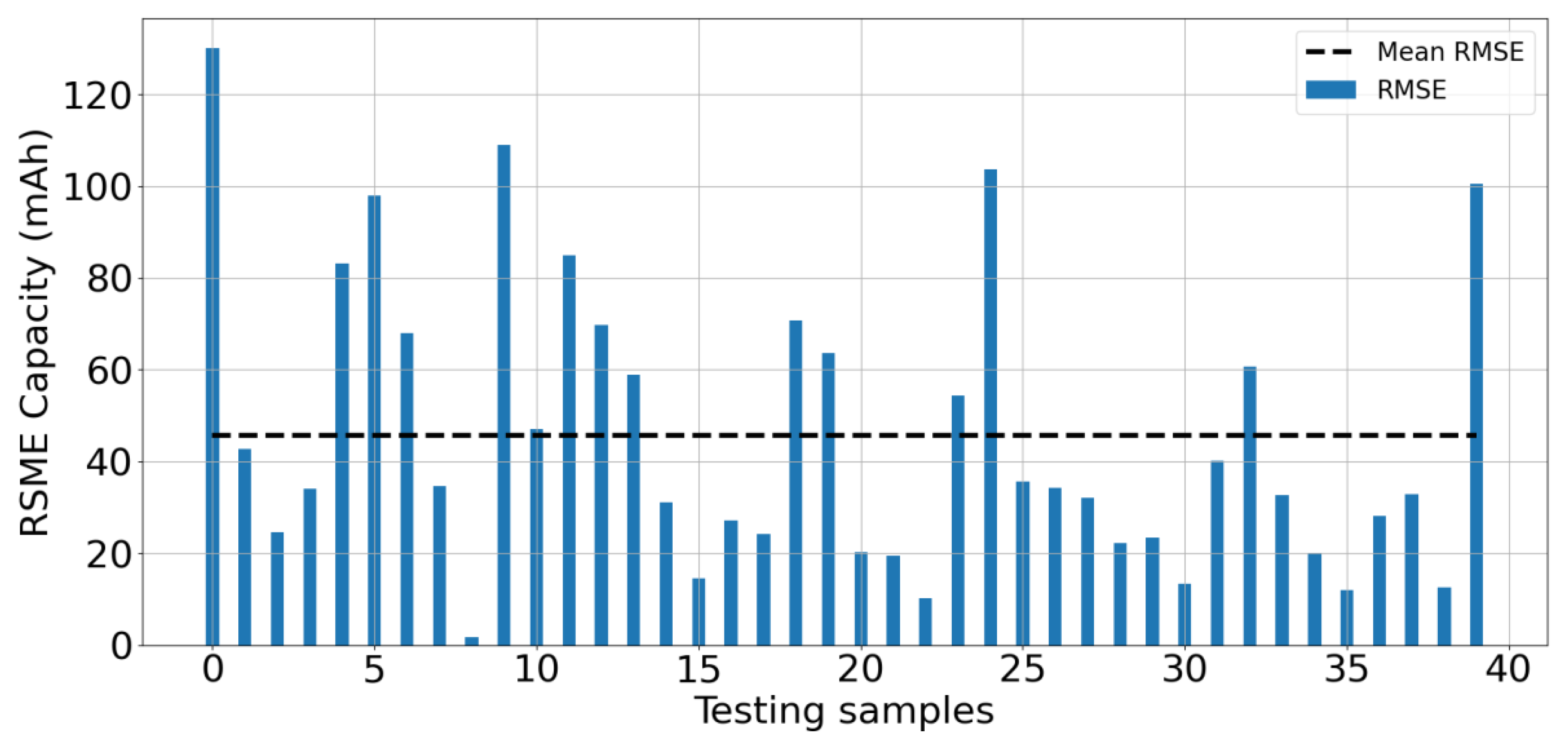
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shahjalal, M.; Roy, P.K.; Shams, T.; Fly, A.; Chowdhury, J.I.; Ahmed, M.R.; Liu, K. A review on second-life of Li-ion batteries: Prospects, challenges, and issues. Energy 2022, 241, 122881. [Google Scholar] [CrossRef]
- Rimpas, D.; Kaminaris, S.D.; Piromalis, D.D.; Vokas, G.; Orfanos, V.A. Impact of lithium battery recycling and second-life application on minimizing environmental waste. Environ. Sci. Proc. 2023, 26, 41. [Google Scholar] [CrossRef]
- Saxena, S.; Le Floch, C.; MacDonald, J.; Moura, S. Quantifying EV battery end-of-life through analysis of travel needs with vehicle powertrain models. J. Power Sources 2015, 282, 265–276. [Google Scholar] [CrossRef]
- Hu, X.; Deng, X.; Wang, F.; Deng, Z.; Lin, X.; Teodorescu, R.; Pecht, M.G. A review of second-life lithium-ion batteries for stationary energy storage applications. Proc. IEEE 2022, 110, 735–753. [Google Scholar] [CrossRef]
- Hua, Y.; Liu, X.; Zhou, S.; Huang, Y.; Ling, H.; Yang, S. Toward sustainable reuse of retired lithium-ion batteries from electric vehicles. Resour. Conserv. Recycl. 2021, 168, 105249. [Google Scholar] [CrossRef]
- Rufino Júnior, C.A.; Riva Sanseverino, E.; Gallo, P.; Koch, D.; Kotak, Y.; Schweiger, H.G.; Zanin, H. Towards a business model for second-life batteries: Barriers, opportunities, uncertainties, and technologies. J. Energy Chem. 2023, 78, 507–525. [Google Scholar] [CrossRef]
- Chen, M.; Ma, X.; Chen, B.; Arsenault, R.; Karlson, P.; Simon, N.; Wang, Y. Recycling end-of-life electric vehicle lithium-ion batteries. Joule 2019, 3, 2622–2646. [Google Scholar] [CrossRef]
- Arshad, F.; Li, L.; Amin, K.; Fan, E.; Manurkar, N.; Ahmad, A.; Yang, J.; Wu, F. A comprehensive review of advancement in recycling anode and electrolyte from spent lithium ion batteries. ACS Sustain. Chem. Eng. 2020, 8, 36. [Google Scholar] [CrossRef]
- Faessler, B. Stationary, second use battery energy storage systems and their applications: A research review. Energies 2021, 14, 2335. [Google Scholar] [CrossRef]
- Michelini, E.; Höschele, P.; Ratz, F.; Stadlbauer, M.; Rom, W.; Ellersdorfer, C.; Moser, J. Potential and most promising second-life applications for automotive lithium-ion batteries considering technical, economic and legal aspects. Energies 2023, 16, 2830. [Google Scholar] [CrossRef]
- Kampker, A.; Heimes, H.H.; Offermanns, C.; Vienenkötter, J.; Frank, M.; Holz, D. Identification of challenges for second-life battery systems—A literature review. World Electr. Veh. J. 2023, 14, 80. [Google Scholar] [CrossRef]
- Dong, Q.; Liang, S.; Li, J.; Kim, H.C.; Shen, W.; Wallington, T.J. Cost, energy, and carbon footprint benefits of second-life electric vehicle battery use. iScience 2023, 26, 107195. [Google Scholar] [CrossRef] [PubMed]
- Kebir, N.; Leonard, A.; Downey, M.; Jones, B.; Rabie, K.; Bhagavathy, S.; Hirmer, S. Second-life battery systems for affordable energy access in Kenyan primary schools. Sci. Rep. 2023, 13, 1374. [Google Scholar] [CrossRef]
- Falk, J.; Nedjalkov, A.; Angelmahr, M.; Schade, W. Applying lithium-ion second life batteries for off-grid solar powered system—A socio-economic case study for rural development. Z. Energiewirtsch. 2020, 44, 47–60. [Google Scholar] [CrossRef]
- Colarullo, L.; Thakur, J. Second-life EV batteries for stationary storage applications in Local Energy Communities. Renew. Sust. Energ. Rev. 2022, 169, 112913. [Google Scholar] [CrossRef]
- Chen, Y.; Kang, Y.; Zhao, Y.; Wang, L.; Liu, J.; Li, Y.; Liang, Z.; He, X.; Li, X.; Tavajohi, N.; et al. A review of lithium-ion battery safety concerns: The issues, strategies, and testing standards. J. Energy Chem. 2021, 59, 83–99. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, K.; Liu, K.; Lin, X.; Dey, S.; Onori, S. Advanced fault diagnosis for lithium-ion battery systems: A review of fault mechanisms, fault features, and diagnosis procedures. IEEE Ind. Electron. Mag. 2020, 14, 65–91. [Google Scholar] [CrossRef]
- Gotz, J.D.; Galvão, J.R.; Werlich, S.H.; Silveira, A.M.D.; Corrêa, F.C.; Borsato, M. Reducing the capacity loss of lithium-ion batteries with machine learning in real-time—A study case. Machines 2022, 10, 1114. [Google Scholar] [CrossRef]
- Gotz, J.D.; Galvão, J.R.; Silveira, A.; Viana, E.R.; Correa, F.C.; Borsato, M. Intelligent management for second-life lithium-ion batteries with backup cells. In Flexible Automation and Intelligent Manufacturing: Establishing Bridges for More Sustainable Manufacturing Systems; Silva, F.J.G., Ferreira, L.P., Sá, J.C., Pereira, M.T., Pinto, C.M.A., Eds.; Springer: Cham, Switzerland, 2024; pp. 1011–1018. [Google Scholar]
- Börner, M.F.; Frieges, M.H.; Späth, B.; Spütz, K.; Heimes, H.H.; Sauer, D.U.; Li, W. Challenges of second-life concepts for retired electric vehicle batteries. Cell Rep. Phys. Sci. 2022, 3, 101095. [Google Scholar] [CrossRef]
- Lee, K.; Kum, D. Development of cell selection framework for second-life cells with homogeneous properties. Int. J. Electr. Power Energy Syst. 2019, 105, 429–439. [Google Scholar] [CrossRef]
- Canals Casals, L.; García, B.; González Benítez, M. A cost analysis of electric vehicle batteries second life businesses. In Project Management and Engineering Research, Proceedings of the XVIII Congreso Internacional de Dirección e Ingeniería de Proyectos, Alcañiz, Spain, 16–18 July 2014; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Teng, J.H.; Chen, R.J.; Lee, P.T.; Hsu, C.W. Accurate and efficient SOH estimation for retired batteries. Energies 2023, 16, 1240. [Google Scholar] [CrossRef]
- Goh, H.H.; Lan, Z.; Zhang, D.; Dai, W.; Kurniawan, T.A.; Goh, K.C. Estimation of the state of health (SOH) of batteries using discrete curvature feature extraction. J. Energy Storage 2022, 50, 104646. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, H.; Ge, J.; Che, L. State-of-health estimation for lithium-ion battery using model-based feature optimization and deep extreme learning machine. J. Energy Storage 2023, 72, 108732. [Google Scholar] [CrossRef]
- Cacciato, M.; Nobile, G.; Scarcella, G.; Scelba, G. Real-time model-based estimation of SOC and SOH for energy storage systems. IEEE Trans. Power Electron. 2016, 32, 794–803. [Google Scholar] [CrossRef]
- Dai, H.; Zhao, G.; Lin, M.; Wu, J.; Zheng, G. A novel estimation method for the state of health of lithium-ion battery using prior knowledge-based neural network and Markov chain. IEEE Trans. Ind. Electron. 2019, 66, 7706–7716. [Google Scholar] [CrossRef]
- Reis, M.S.; Saraiva, P.M. Data-driven process system engineering–Contributions to its consolidation following the path laid down by George Stephanopoulos. Comput. Chem. Eng. 2022, 159, 107675. [Google Scholar] [CrossRef]
- Sheng, H.; Zhou, Y.; Bai, L.; Shi, L. Transfer state of health estimation based on cross-manifold embedding. J. Energy Storage 2022, 47, 103555. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, D.; Du, J.; Sun, H.; Li, L.; Wang, L.; Wang, K. A review of SOH prediction of Li-ion batteries based on data-driven algorithms. Energies 2023, 16, 3167. [Google Scholar] [CrossRef]
- Wang, X.; Hu, B.; Su, X.; Xu, L.; Zhu, D. State of health estimation for lithium-ion batteries using Random Forest and Gated Recurrent Unit. J. Energy Storage 2024, 76, 109796. [Google Scholar] [CrossRef]
- Jia, J.; Liang, J.; Shi, Y.; Wen, J.; Pang, X.; Zeng, J. SOH and RUL prediction of lithium-ion batteries based on Gaussian process regression with indirect health indicators. Energies 2020, 13, 375. [Google Scholar] [CrossRef]
- Wang, J.; Deng, Z.; Yu, T.; Yoshida, A.; Xu, L.; Guan, G.; Abudula, A. State of health estimation based on modified Gaussian process regression for lithium-ion batteries. J. Energy Storage 2022, 51, 104512. [Google Scholar]
- Chen, Z.; Sun, M.; Shu, X.; Xiao, R.; Shen, J. Online state of health estimation for lithium-ion batteries based on support vector machine. Appl. Sci. 2018, 8, 925. [Google Scholar] [CrossRef]
- Nguyen Van, C.; Quang, D.T. Estimation of SoH and internal resistances of Lithium ion battery based on LSTM network. Int. J. Electrochem. Sci. 2023, 18, 100166. [Google Scholar] [CrossRef]
- Zhang, L.; Ji, T.; Yu, S.; Liu, G. Accurate prediction approach of SOH for lithium-ion batteries based on LSTM method. Batteries 2023, 9, 177. [Google Scholar] [CrossRef]
- Xu, H.; Wu, L.; Xiong, S.; Li, W.; Garg, A.; Gao, L. An improved CNN-LSTM model-based state-of-health estimation approach for lithium-ion batteries. Energy 2023, 276, 127585. [Google Scholar] [CrossRef]
- Li, Y.; Luo, L.; Zhang, C.; Liu, H. State of health assessment for lithium-ion batteries using incremental energy analysis and bidirectional long short-term memory. World Electr. Veh. J. 2023, 14, 188. [Google Scholar] [CrossRef]
- Ramadan, M.; Pramana, B.; Widayat, S.; Amifia, L.; Cahyadi, A.; Wahyunggoro, O. Comparative study between internal ohmic resistance and capacity for battery state of health estimation. J. Mechatron. Electr. Power Veh. Technol. 2015, 6, 113. [Google Scholar] [CrossRef]
- Hoque, M.A.; Nurmi, P.; Kumar, A.; Varjonen, S.; Song, J.; Pecht, M.G.; Tarkoma, S. Data driven analysis of lithium-ion battery internal resistance towards reliable state of health prediction. J. Power Sources 2021, 513, 230519. [Google Scholar] [CrossRef]
- Zhou, Z.; Ran, A.; Chen, S.; Zhang, X.; Wei, G.; Li, B.; Kang, F.; Zhou, X.; Sun, H. A fast screening framework for second-life batteries based on an improved bisecting K-means algorithm combined with fast pulse test. J. Energy Storage 2020, 31, 101739. [Google Scholar] [CrossRef]
- Meng, K.; Xu, G.; Peng, X.; Youcef-Toumi, K.; Li, J. Intelligent disassembly of electric-vehicle batteries: A forward-looking overview. Resour. Conserv. Recycl. 2022, 182, 106207. [Google Scholar] [CrossRef]
- Lu, Y.; Maftouni, M.; Yang, T.; Zheng, P.; Young, D.; Kong, Z.J.; Li, Z. A novel disassembly process of end-of-life lithium-ion batteries enhanced by online sensing and machine learning techniques. J. Intell. Manuf. 2023, 34, 2463–2475. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Duan, B.; Kang, Y.; Shang, Y.; Cui, N.; Chang, L.; Zhang, C. An efficient screening method for retired lithium-ion batteries based on support vector machine. J. Clean. Prod. 2020, 267, 121882. [Google Scholar] [CrossRef]
- Liu, C.; Tan, J.; Wang, X. A data-driven decision-making optimization approach for inconsistent lithium-ion cell screening. J. Intell. Manuf. 2020, 31, 833–845. [Google Scholar] [CrossRef]
- Liu, C.; Tan, J.; Shi, H.; Wang, X. Lithium-ion cell screening with convolutional Neural Networks based on two-step time-series clustering and hybrid resampling for imbalanced data. IEEE Access 2018, 6, 59001–59014. [Google Scholar] [CrossRef]
- Gu, X.; Li, J.; Zhu, Y.; Wang, Y.; Mao, Z.; Shang, Y. A quick and intelligent screening method for large-scale retired batteries based on cloud-edge collaborative architecture. Energy 2023, 285, 129342. [Google Scholar] [CrossRef]
- Zorn, M.; Ionescu, C.; Klohs, D.; Zähl, K.; Kisseler, N.; Daldrup, A.; Hams, S.; Zheng, Y.; Offermanns, C.; Flamme, S.; et al. An approach for automated disassembly of lithium-ion battery packs and high-quality recycling using computer vision, labeling, and material characterization. Recycling 2022, 7, 48. [Google Scholar] [CrossRef]
- Siqueira, H.; Santana, C.; Macedo, M.; Figueiredo, E.; Gokhale, A.; Bastos-Filho, C. Simplified binary cat swarm optimization. Integr. Comput. Aided Eng. 2021, 28, 35–50. [Google Scholar] [CrossRef]
- Belotti, J.; Siqueira, H.; Araujo, L.; Stevan, S.L., Jr.; de Mattos Neto, P.S.; Marinho, M.H.; de Oliveira, J.F.L.; Usberti, F.; de Almeida, L.F.M.; Converti, A.; et al. Neural-based ensembles and unorganized machines to predict streamflow series from hydroelectric plants. Energies 2020, 13, 4769. [Google Scholar] [CrossRef]
- Gotz, J.; Guerrero, G.; De Queiroz, J.; Viana, E.; Borsato, M. Diagnosing failures in lithium-ion batteries with Machine Learning techniques. Eng. Fail. Anal. 2023, 150, 107309. [Google Scholar] [CrossRef]
- Belouadah, E.; Popescu, A.; Kanellos, I. A comprehensive study of class incremental learning algorithms for visual tasks. Neural Netw. 2020, 135, 38–54. [Google Scholar] [CrossRef]
- Ali, J.; Khan, R.; Ahmad, N.; Maqsood, I. Random forests and decision trees. Int. J. Comput. Sci. Issues 2012, 9, 272–278. [Google Scholar]
- Gotz, J.D.; de Souza, P.H.G.; Galvão, J.R.; Corrêa, F.C.; Badin, A.A.; Viana, E.R.; Borsato, M. Enhancing SOC estimation accuracy via incremental learning techniques for second-life batteries. Sustain. Energy Technol. Assess. 2024, 65, 103753. [Google Scholar] [CrossRef]
- Zhu, N.; Zhu, C.; Zhou, L.; Zhu, Y.; Zhang, X. Optimization of the Random Forest hyperparameters for power industrial control systems intrusion detection using an improved grid search algorithm. Appl. Sci. 2022, 12, 10456. [Google Scholar] [CrossRef]
- Le, H.-L.; Le, T.-T.; Vu, T.-T.-H.; Tran, D.-H.; Chau, D.V.; Ngo, T.-T.-T. A survey on the impact of hyperparameters on Random Forest performance using multiple accelerometer datasets. Int. J. Comput. Their Appl. 2023, 30, 351–361. [Google Scholar]
- de O. Santos, D.S., Jr.; de Mattos Neto, P.S.G.; de Oliveira, J.F.L.; Siqueira, H.V.; Barchi, T.M.; Lima, A.R.; Madeiro, F.; Dantas, D.A.P.; Converti, A.; Pereira, A.C.; et al. Solar Irradiance Forecasting Using Dynamic Ensemble Selection. Appl. Sci. 2022, 12, 3510. [Google Scholar] [CrossRef]



| Item | Specification |
|---|---|
| Cathode | Nickel-cobalt-manganese |
| Anode | Graphite |
| Nominal capacity | 2200 mAh |
| Used capacity | 1700 mAh |
| Internal resistance | 70 mΩ |
| Nominal voltage | 3.7 V |
| Upper voltage | 4.25 V |
| Lower voltage | 2.5 V |
| Maximum charging current | 1C |
| Maximum discharge current | 10 A |
| Dimensions | Ø18.25 × 65 mm |
| Weight | 42 g |
| Prediction Time(s) | RMSE (mAh) |
|---|---|
| 50–100 | 48.08 |
| 50–200 | 47.85 |
| 50–300 | 45.70 |
| 50–400 | 46.23 |
| 50–500 | 43.34 |
| 50–600 | 47.51 |
| 50–700 | 51.55 |
| 50–800 | 51.83 |
| 50–900 | 51.10 |
| 50–1000 | 53.74 |
| 50–2000 | 46.10 |
| 50–3000 | 43.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gotz, J.D.; Galvão, J.R.; Corrêa, F.C.; Badin, A.A.; Siqueira, H.V.; Viana, E.R.; Converti, A.; Borsato, M. Random Forest-Based Grouping for Accurate SOH Estimation in Second-Life Batteries. Vehicles 2024, 6, 799-813. https://doi.org/10.3390/vehicles6020038
Gotz JD, Galvão JR, Corrêa FC, Badin AA, Siqueira HV, Viana ER, Converti A, Borsato M. Random Forest-Based Grouping for Accurate SOH Estimation in Second-Life Batteries. Vehicles. 2024; 6(2):799-813. https://doi.org/10.3390/vehicles6020038
Chicago/Turabian StyleGotz, Joelton Deonei, José Rodolfo Galvão, Fernanda Cristina Corrêa, Alceu André Badin, Hugo Valadares Siqueira, Emilson Ribeiro Viana, Attilio Converti, and Milton Borsato. 2024. "Random Forest-Based Grouping for Accurate SOH Estimation in Second-Life Batteries" Vehicles 6, no. 2: 799-813. https://doi.org/10.3390/vehicles6020038
APA StyleGotz, J. D., Galvão, J. R., Corrêa, F. C., Badin, A. A., Siqueira, H. V., Viana, E. R., Converti, A., & Borsato, M. (2024). Random Forest-Based Grouping for Accurate SOH Estimation in Second-Life Batteries. Vehicles, 6(2), 799-813. https://doi.org/10.3390/vehicles6020038












