Prediction of Residual Wear Resources of Composite Brake Pads of a Modernized Brake System of Freight Wagons

Abstract

This research highlights the results of a comprehensive study of the efficiency of modernized brake systems operation of freight wagons. The inspection of the modernized elements of the lever brake system of bogies and the measurement of the wear parameters of composite brake pads during each cycle of the experimental wagons in the interval of mileage from 2.1 to 197.8 thousand km were carried out. A statistical approach was used to study the wear parameters of brake pads of modernized bogies brake systems determined during operational studies. This allowed appropriate dependencies of brake pad wear to be obtained. Based on the research results, a regression model was developed. This makes it possible to predict the residual wear resource of composite brake pads with modernized braking systems of bogies for the entire inter-repair period of operation of freight wagons guaranteed by the wagon repair company. The peculiarity of the model is that it considers the total and additional mileage of the freight wagon. This makes it possible to more accurately predict the residual lifetime of composite brake pads. It was established that, under the condition of uniform wear of brake pads, the average mileage of a freight wagon during the use of modernized brake systems of bogies can reach up to 284.57 thousand km, which increases the resource of composite pads’ wear approximately by 2.59 times. The generated model was verified by the F-criterion. Approbation of experimental devices for uniform wear of composite pads in operation established that measures to modernize brake systems of freight wagons ensure the reliable and efficient operation of the brake lever system as a whole.

1. Introduction

The development of the railway industry in the modern conditions of the competitive environment is accompanied by an increase of the running speed of freight trains, axle load, the improvement of structures and materials for the manufacture of components of rail vehicles, an increase of the load factor of wagons, etc. [1,2,3,4,5]. However, special attention should be paid to the modernization of brake equipment elements of wagons as one of the most responsible factors from the ensuring traffic safety point of view [6,7,8,9].

The traffic safety analysis of the Wagon Management Department of the Ukrzaliznytsia Stock Company (Kyiv, Ukraine) has indicated in recent years that the braking equipment of freight wagons is too vulnerable in the current operating conditions. Currently, a lot of effort is being put to solve the problem of wedge-dual wear of brake pads [10,11,12,13,14,15], because this kind of wear leads to reduction of the working part of brake pads (Figure 1), and it is widespread in freight wagons bogies on the main transport network, including the tracks with a gauge of 1520 mm.

It is important to note that the uneven wear of brake pads can also affect the quality of the wheel surface of wheelsets if it is significant.

Triangles are the main element of the brake gears of freight wagons, and they work in such a way that, during the braking of a wagon, all brake pads of the bogie are pushed against the wheels. The bogie brake system (BBS) must be balanced with respect to the force load of each pad. Due to the dynamics of the interaction of the wheels with the unevenness of the rail track, this balance is disturbed, and the pads wear out most often in the upper part. As a result, this is the main reason for their wedge-dual wear. This problem causes a decrease of braking efficiency of freight wagons due to the reduction of the working part, i.e., the braking area of the contact between the brake pads and the bogie wheels. Furthermore, this leads to an increase in the frequency of repairs of rail vehicles running parts of rolling stock, additional costs of energy resources for train traction, and a total decrease in economic and environmental indicators during freight transportation.

In this regard, it is necessary to modernize the elements of the BBS to prevent the occurrence of wedge-dual wear of composite brake pads. This will make it possible to use the pads for the entire inter-repair period of operation of freight wagons.

The issues of train movement safety within railway transport are relevant and they depend on significant factors, particularly on the technical condition and the load of the brake system elements. Thus, for example, the study of the thermal load of the brake pad was carried out using the SolidWorks simulation software in the work [16]. Based on the obtained results, an alternative solution of using composite material in the form of a modified alkylbenzene resin is proposed, which helps to increase the friction coefficient of the pads.

The study in [17] established the cause of harmful wedge-dual wear of the pads, and identified possible ways to eliminate the specified deficiency, which leads to the premature replacement of brake pads that have not used their working mass resource in the inter-repair period. The work uses a statistical approach to planning experiments during field tests of freight wagons with a typical and a modernized BBS, which were included in one warehouse. However, the question of predicting the residual resource of brake pads remained ignored by the researchers.

Another approach was proposed by a group of authors in the work [18], where the issue of the uneven wear of brake pads was considered. To achieve the given task, a complex multifactorial model is proposed. However, cases were considered where the values of the studied parameters obey the normal law of distribution.

The author of the work in [19] developed a regression model of the friction of pads and wheels of industrial transport locomotives in conditions of structural uncertainty. This model is multifactorial, but it does not consider the wear of the pads by thickness during operation.

Similar studies were conducted on the processing of the statistical material of nodes of the transport and machine-building industry in the works in [20,21,22]. However, none of them reflected the features of prediction of the residual resource of elements to reduce planned and preventive repairs of brake systems of freight wagons.

In the production studies commissioned by the national Ukrzaliznytsia Stock Company (Kyiv, Ukraine), the development of design and technological documentation regarding the modernization of the freight wagons’ BBS was carried out [23]. However, no statistical studies of the wear of brake pads of the fleet of freight wagon of private enterprises were conducted in this research work. Unlike the wagon of the Ukrzaliznytsia Stock Company (Kyiv, Ukraine), they have a permanent location, and they are operated in “softened” conditions.

One of the approaches to such statistical studies is proposed in [24]. There were estimated parameters such as the force of pressing the brake pads on the rolling surface of the wheel, the hardness of the material of the pads, etc., for the set value of the braking distance, which depends on the speed of movement, the slope of the rail track, and the radius of the curve during the braking of rail vehicles. Critical slopes of the braking distance in the case of the full-service braking of the rail vehicle were statistically established. However, the work did not consider the conditions when the braking area of the contact between the pads and the wheels decreases in the presence of their wedge-dual wear. Thus, it is not possible to reliably estimate the braking efficiency of the train under such conditions.

In the works in [25,26], the teams of authors presented the results of operational studies on the assessment of factors that cause the appearance of defects of thermal origin on the rolling surface of wheelsets due to the action of composite brake pads. To prevent the occurrence of such defects, it is suggested to use improved blocks, which make it possible to significantly reduce the number of wheel malfunctions. During the examination of the brake equipment of the freight train, various malfunctions of the mechanical and pneumatic parts of the brakes were discovered. An examination of the pads was carried out, during which their wedge-shaped wear was revealed because of the interaction of the upper end with the rolling surface of the wheels. However, the mentioned works did not consider the issue of analyzing the collected statistical material of non-normative pad wear and its processing to estimate the amount of wear, which affects the reduction of the braking efficiency of the freight train and traffic safety.

The work in [27] includes the results of tests of freight rail vehicles of industrial transport regarding the evaluation of braking efficiency, as well as a structural and dynamic analysis of the braking mechanism. The conducted research consisted of determining the type and parameters of the empirical dependence of the friction coefficient of the brake pad on the wheel rolling surface, depending on the speed and braking, as well as in determining the kinetic characteristics of the brake of the freight rail vehicles of industrial transport. However, it should be noted that the specialists did not take into account the possible wedge-dual wear (clinodual wear) of the pads of freight wagons in the research, which significantly affects the evaluation of the braking efficiency of industrial wagons.

The research in [28] highlights the analysis of performance indicators of the brake pads quality for various types of rail vehicle. Individual negative factors of composite brake pads are given, and their impact on the environment and processes causing damage to the rolling surfaces of rail vehicles’ wheels are described. However, the authors did not pay attention to the issue of the effective use of the brake pad working partly under operational conditions.

As practice proves, the wedge-dual wear of brake pads occurs due to unprofessional actions of workers who perform the maintenance and repair of freight wagons in violation of regulatory technical documents [29]. That is, in some cases, brake pads previously removed from the wagons are again installed at their discretion. Therefore, their wear obviously cannot correspond to the normal distribution law, and similar studies [30,31,32] do not make sense.

The necessary cost reduction of the maintenance of rail vehicles in operation has ensured the consideration of brake pads as a commodity that is often purchased at the lowest price under the conditions of their satisfactory operation. However, this may not lead to a reduction of operation costs, and the choice of friction material may have a direct impact on the service lifetime of the wheel, which is usually much more expensive to replace than other parts of wagons. Similarly, if low-quality materials are used for the manufacture of brake pads, the resource of their working part will quickly decrease. It will lead to an increase in the braking distance of the train and a decrease in the level of traffic safety [33].

Publications [34,35,36] consider the peculiarities of the tribotechnical repairs operation. A solution of increasing the efficiency of their work is proposed. The implementation of the proposed solutions will help to increase the speed of movement, axle load, efficiency of the braking system of rail vehicles, etc. However, at the same time, there are several problems related to the wadge-dual wear of freight wagons’ brake pads that need to be solved. Thus, the problems associated with the wear of brake pads and wheels of freight wagons actually exist [37,38], and in this direction work is being carried out related to the modernization of the elements of the brake lever system of freight wagons to ensure the safety of freight trains’ operation by increasing the efficiency of their brakes.

As it is described in the overview above, the freight wagon transport is important, together with its safe operation under the various loads [39,40]. Modern designs of freight wagons should be supplemented by the reliable system of bogies with modern technical solutions of safety components [41,42].

Currently, typical freight wagons’ brake pads for 1520 mm gauge are made of composite material. The main requirements for such pads are covered in the regulatory document [43]. Other regulatory documents apply to wagons of the European gauge, for example [44,45].

To improve the strength of brake pads, research is being carried out on their production from new materials.

Thus, the study [46] is aimed at analyzing the operation of tribotechnical units and justifying the introduction of promising materials in their construction. Due to such solutions, the speed of train movement increases significantly, the load on the axle of the wagon increases significantly, the resource of tribotechnical parts increases—composite brake pads and linings; bushings used in kinetostatic units, the operation of the braking system of the rolling stock is improved, etc. However, the problems of non-normative wear of elements of the tribotechnical unit—“brake pad-wheel” were not investigated in these works.

The publication in [47] examines the influence of low temperatures on the operation of brake pads. The requirements for the material of their manufacture are specified there. It is specified that it must have high strength and wear resistance to avoid cracks and fractures, as well as sufficient hardness to ensure minimal wear of the wheel during braking. However, the authors did not investigate the issue of wear of such pads in operation.

The work in [48] has the same drawback. It analyzes the use of the latest materials in pads, including foam–aluminum inserts. The author gives options for the execution of such blocks. However, the specifics of their operation and wear are not specified.

The study of literary sources in [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48] makes it possible to conclude that the issues of analysis and processing of statistical material regarding the wear of brake pads for the purpose of prediction their residual resource in the inter-repair period of freight wagons operation are relevant and require further development.

The purpose of the study is to highlight the features of prediction of the residual resource of composite pads of modernized brake systems of freight wagons.

To achieve this goal, the following tasks are defined:

• To carry out an inspection of composite brake pads of freight wagons with the modernized BBS in operational conditions;
• To develop a regression model for prediction of the residual lifetime of composite brake pads with the modernized BBS;
• To verify the statistical hypotheses regarding the nature of the distribution of random wear values of composite brake pads and their relationship regarding the data belonging to one general whole.

2. Research Materials and Methods

To increase the reliable operation of the brakes of freight wagons, the modernization of the BBS was carried out. It is carried out with the aim of eliminating structural defects in the system of removing the brake pads from the rolling surfaces of the wheelsets. The location of the technological hinge B connecting the vertical lever with the triangle spacer was changed in the modernized BBS and was developed at the Ukrainian State University of Railway Transport (UkrSURT) (Figure 2). This hinge is located on the same line A-A with the hinges of the pendulum suspensions. Also, a curved rod is introduced. This rod keeps the BBS constantly in balance with its ends in the cylindrical sliders. This ensures strictly uniform gaps between the blocks and wheels, and it guarantees their normative wear.

The modernized BBS developed according to the UkrSURT technology works as follows. When the brakes are released, triangles with holders and brake pads move under the influence of gravitational forces on pendulum suspensions, so that they move the pads away from the wheels. Thanks to the balance of the brake system relative to the hinges of the pendulum suspensions, the pads move away from the wheels evenly. In case of accidental forces due to oscillations and tilts of the wagon during movement, the curved rod works. Due to the placement of its ends in cylindrical sliders, it does not allow the triangle to tilt, and therefore the pads to rest with the ends of the upper or lower parts on the wheels. At this time, reaction forces are created in the sliders, which are balanced on those parts of the curved rod that are contained in the sliders due to the symmetrical location of the sliders relative to the hinge hole. The parts of the rods which are bent vertically downward and are located near the ends of the cylindrical sliders keep the rod from longitudinal displacement and falling out from the action of longitudinal forces on it during braking and the action of random forces from oscillations and tilts of the wagon.

Thanks to the guide device, the horizontal movement of adjacent triangles and brake pads in the BBS occurs. Thus, the uniformity of the clearances between the blocks and wheels is ensured when the brakes of freight wagons are released.

The approbation tests were performed under operating conditions in order to verify the reliable operation of the modernized BBS and they were developed at the Department of Wagon Engineering and Product Quality of the Ukrainian State University of Railway Transport, Kharkiv, Ukraine. By the order of the Department of Wagon Management of the Ukrzaliznytsia Stock Company (Kyiv, Ukraine), modernized BBSs were installed on ten open freight wagons built for the Donetsk Railway by the Kryukiv Wagon Building Plant (Kremenchuk, Ukraine) of a specified mileage and they were unhooked on special tracks for inspections [23,49].

A commission inspection was carried out with an examination of the condition and performance evaluation of the experimental devices of the modernized BBS with the measurement of the gaps between the blocks and wheels and the thickness of the blocks to determine their wear parameters. The statistical material obtained in this way is used both to determine the reliability indicators of experimental devices as well as to evaluate their parameters that affect the intensity of wear of brake pads [50,51].

Measurements were carried out in accordance with the developed “Program and methodology for conducting scientific production research of brake systems and wheels of freight wagons”.

Examinations showed that no damage or wear was found on any of the experimental devices of the modernized BBS. The experimental devices of the modernized BBS ensure the normative remoteness of brake pads from the wheels in freight wagons. In this manner, the inclination of the brake pads upper ends and harmful friction of the upper ends of the pads on the wheels during movement in trains without braking is eliminated. Thanks to the experimental devices, the working mass of the pads wears out only during braking. This leads to significantly less overall wear of the composite brake pads (Figure 3). The obtained wear values of the composite brake pads of the examined test wagons proved the probability of their lifespan until the wagons have traveled at least 210,000 km. This means that it is before the first depot repair of new wagons without replacing the brake pads. It should be noted that the periodical adjustment of the lever transmission mechanism by rearranging the rollers in the hinged unit of the BBS is needed.

The values of the pads’ wear of their upper and lower parts as the most worn during the milage of 121.3 thousand km of freight wagons were processed by means of the Statistica 12.5 software (Informer Technologies, Altamor Drive, Los Angeles, CA, USA). The resulting histograms are created based on Χ-quadrate criterion [6] depicted in Figure 4.

It can be seen in the histograms (Figure 4) that there is a rather large range of wear values of composite brake pads—from the minimum value of 14 mm to the maximum value of 32 mm. This indicates that the nature and intensity of brake pad wear is influenced by a large number of various factors requiring the special research.

The information obtained during the research of the brake pads’ wear depending on the freight wagons’ mileage in operating conditions was subject to careful processing. The general scheme of the freight wagons’ technical condition of freight wagons is possible to visualize with the help of statistical processing methods. In this way, it is possible to create the favorable conditions for the further serial introduction of updated freight wagons designs into a production at wagon-building plants or their modernization at wagon repair enterprises of the Ukrzaliznytsia Stock Company (Kyiv, Ukraine).

Calculations were made for the wear’s average value of all examined wagons with the modernized BBS [23].

One bogie includes eight brake pads, and the total number of shoes under study was of 80 units.

Table 1. Average values of measured wear at the upper part of composite brake pads.

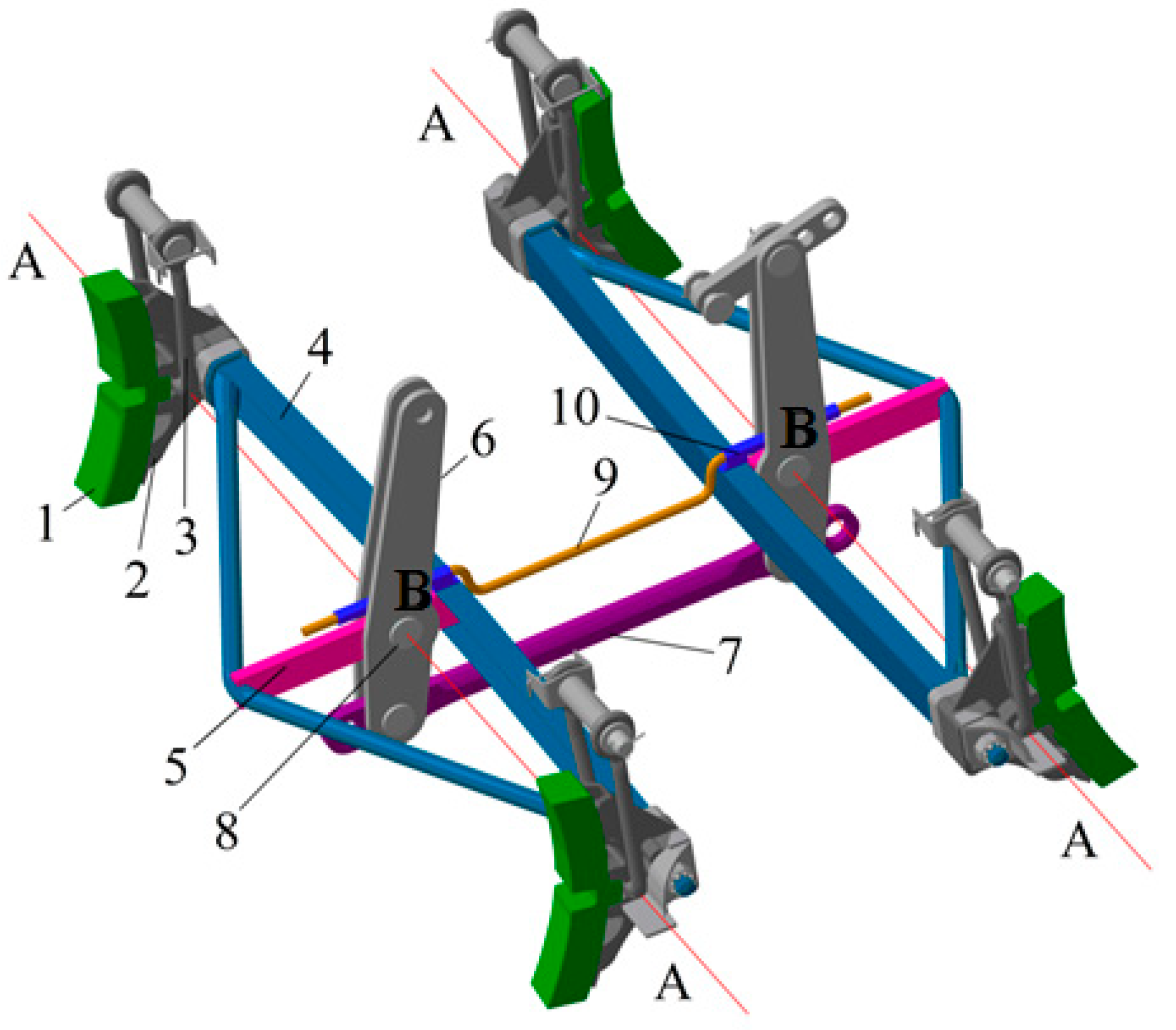
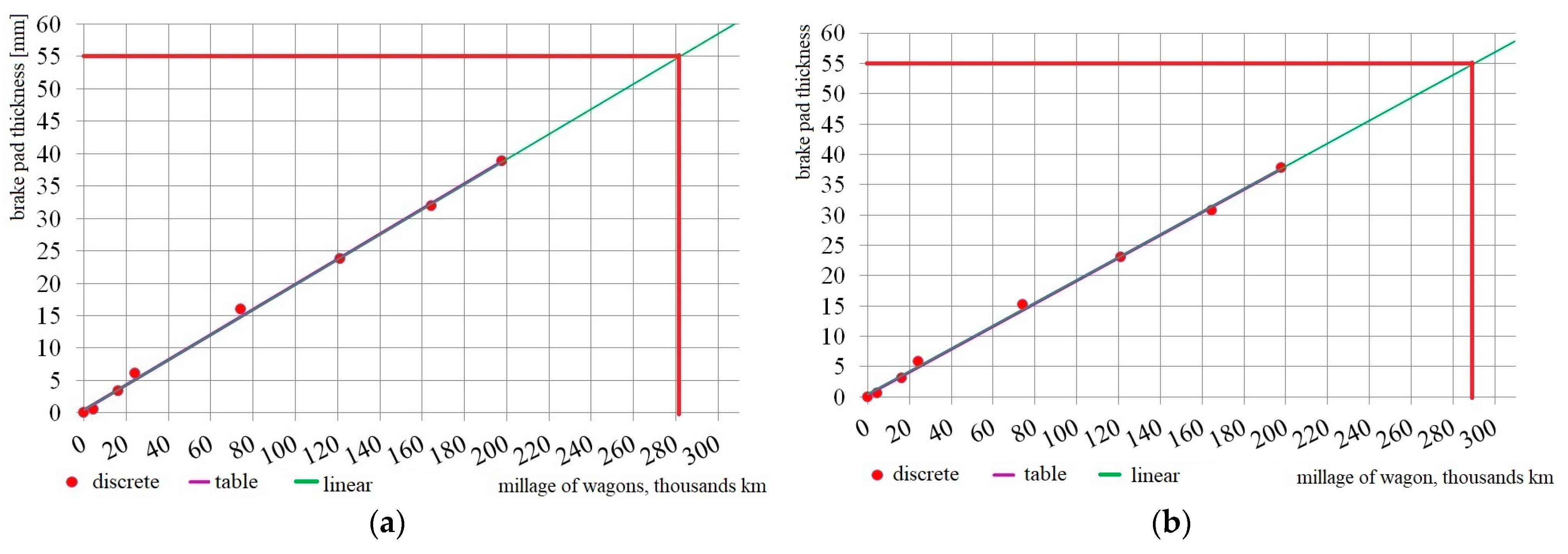
Inventory Number of an Examined Wagon	The Sequence of Thickness Reduction of the Upper Part of the Brake Pads yi [mm] with Increasing Mileage S [Thousand km]
	4.60	16.20	24.10	74.10	121.30	164.60	197.80
61138707	0.75	3.63	5.75	17.38	25.50	33.25	40.63
61139481	0.50	3.13	5.88	16.00	23.63	32.75	40.63
61138970	0.50	4.13	6.75	13.63	22.00	29.75	37.13
61139168	0.13	2.88	6.25	16.00	24.25	33.13	39.50
61139317	0.88	3.25	6.13	16.13	23.88	31.63	38.25
61139176	1.13	3.63	6.88	16.00	24.88	32.38	38.38
61139556	0.25	3.25	5.38	15.13	22.75	30.63	37.25
61139531	0.25	3.00	6.25	16.00	22.75	31.25	39.25
61140083	1.13	3.88	6.25	17.50	25.00	33.25	39.63
61140307	0.38	3.00	5.63	16.00	23.38	30.63	37.38
Average value for all wagons	0.59	3.38	6.12	15.98	23.80	31.87	38.80

and

Table 2. Average values of measured wear at the bottom part of composite brake pads.

Inventory Number of an Experimental Wagon	The Sequence of Thickness Reduction of the Bottom Part of the Brake Pads yi [mm] with Increasing Mileage S [Thousand km]
	4.60	16.20	24.10	74.10	121.30	164.60	197.80
61138707	0.50	3.25	5.25	13.25	20.63	29.50	36.50
61139481	0.63	3.25	6.25	15.88	23.38	31.75	39.38
61138970	0.63	4.00	7.00	14.00	22.38	30.25	37.00
61139168	0.38	3.38	6.13	15.38	23.63	31.38	38.25
61139317	0.63	3.25	5.88	14.5	22.25	29.75	36.38
61139176	0.38	2.63	6.00	14.75	22.25	29.75	36.50
61139556	0.63	3.13	5.88	15.38	23.13	30.88	38.00
61139531	0.63	2.88	5.50	18.00	25.88	33.25	40.50
61140083	0.38	2.50	5.13	14.88	22.75	30.63	37.50
61140307	0.88	3.13	5.88	16.13	24.13	30.75	37.25
Average value for all wagons	0.57	3.14	5.89	15.22	23.04	30.79	37.73

show the average parameter values for the pads of each wagon. The reliability of the sample was checked using the Student criterion.

$$n={\displaystyle \frac{t^2\cdot {\sigma }^2}{{\delta }^2}},$$

(1)

where t is determined from the ratio Φ(t) = γ/2; Φ(t) is the Laplace function; i is a tabled value; σ is the root mean square deviation of the random variable under study, which must be known in advance, even before experimental measurements; δ² is an absolute error of the measurement result.

As is known from the statistical theory [52,53,54], there are two sources of information when considering any task using the laws of mathematical statistics. The first source is the results of observations (examinations). In addition, the observation process can be adjusted based on the previous results (the so-called sequential analysis). The second source is a priori information about the properties of the object under the study, i.e., it is the wear and tear accumulated at this moment for a certain mileage of a wagon. This information is displayed in the model, which is selected for the task consideration.

3. The Research Results

The wear value was determined considering the theory of statistical inferences [55] based on the data given in Table 1 and Table 2, where n_i is the average value of brake pad wear for all wagons. Its value equals 60.27 mm for the upper part and it equals 58.19 mm for the bottom part of the pads. The median interval is from 24.1 to 74.1 thousand km, and the frequency equals 15.98 mm for the upper part and 15.22 mm for the bottom part of the pads.

The median is obtained by the formula:

$$M_e=x_{M_e}+{\displaystyle \frac{\frac{{\displaystyle \sum n_i}}{2}-s{n}_{M_{e-1}}}{n_{M_e}}}\cdot h$$

(2)

where $x_{M_e}$ is the beginning of the median interval, $n_{M_e}$ is the median interval frequency, and $s{n}_{M_{e-1}}$ is the accumulated frequency of the interval preceding the median.

The histograms of relative frequencies of the variation series were created (Figure 5) based on the results of the performed calculation. A horizontal axis of these histograms represents the partial intervals of the length h, and their heights equal to the relative frequency densities f_i. The area of the i-th partial rectangle is determined by the formula:

$$h{f}_i=h\left({\displaystyle \frac{{\omega }_i}{h}}\right)={\omega }_i,$$

(3)

where ω_i is the relative frequency of the options belonging to the i-th interval.

The area of the histogram of relative frequencies equals the sum of all relative frequencies, i.e., 1.0.

All calculations were performed using the Excel software (Microsoft Corporation, Redmond, Washington, DC, USA) and the results are summarized in

Table 3. The results of the calculated average wear of the upper part of the composite brake pads of the modernized BBS.

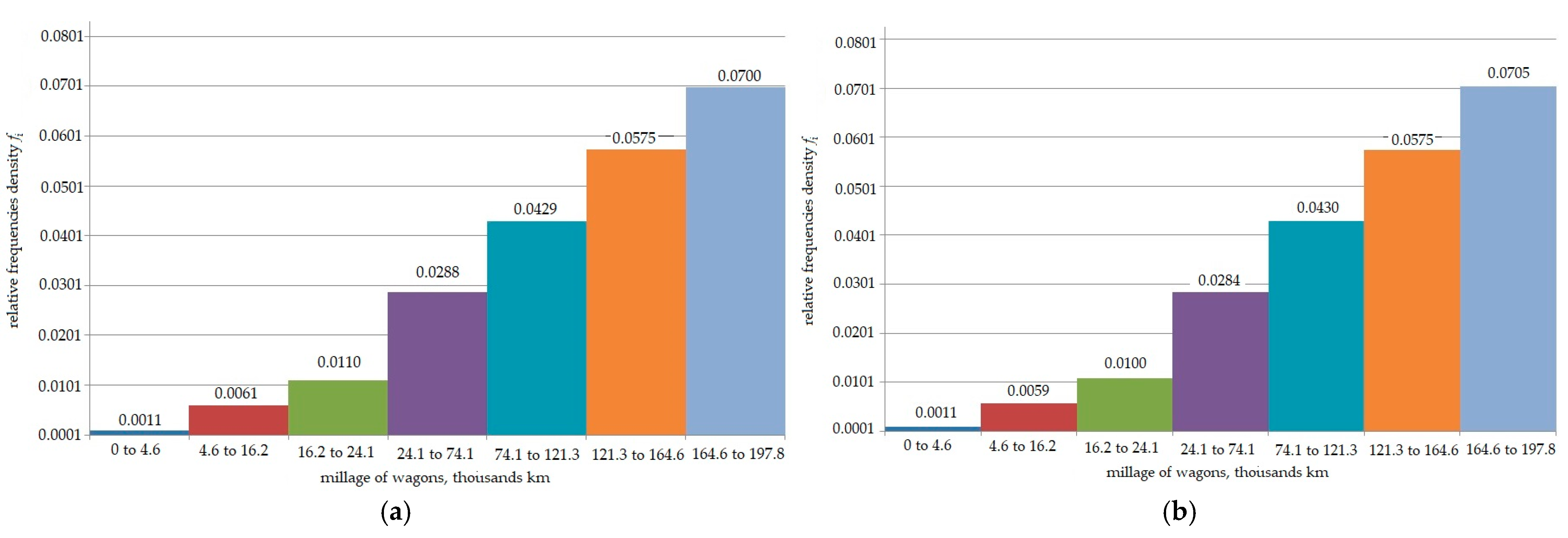
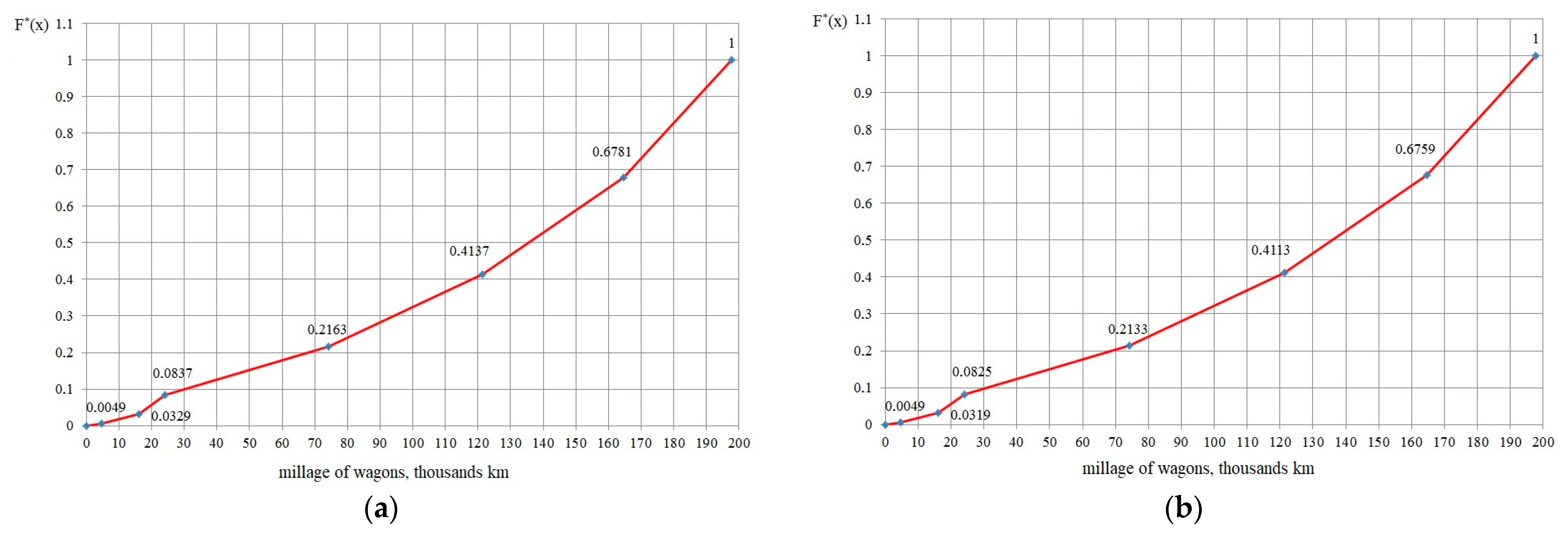
Mileage Interval (Thousand km)	ai−1	ai	xi	ni	xini	xi2ni	ωi	fi	sni	sωi
0 to 4.6	0	4.6	2.3	0.59	1.36	3.12	0.0049	0.0011	0.59	0.0049
4.6 to 16.2	4.6	16.2	10.4	3.38	35.15	365.58	0.028	0.0061	3.97	0.0329
16.2 to 24.1	16.2	24.1	20.2	6.12	123.62	2497.2	0.0508	0.011	10.09	0.0837
24.1 to 74.1	24.1	74.1	49.1	15.98	784.62	38,524.74	0.1326	0.0288	26.07	0.2163
74.1 to 121.3	74.1	121.3	97.7	23.8	2325.3	227,177.9	0.1974	0.0429	49.87	0.4137
121.3 to 164.6	121.3	164.6	143	31.87	4557.4	651,709.6	0.2644	0.0575	81.74	0.6781
164.6 to 197.8	164.6	197.8	181.2	38.8	7030.6	1,273,937	0.3219	0.07	120.54	1
Total				120.54	14,858	2,194,216	1

Note: a_i−1—the left limits of the bogie run; a_i—the right limits of the bogie run; x_i—the average mileage of wagons; n_i—the average value of pad wear for all wagons; x_in_i—weights of statistical distribution; x_i²n_i—weights of the square of the statistical distribution; ω_i—relative frequency; f_i—relative frequency density; s_in_i—accumulated frequencies; s_iω_i—accumulated relative frequencies. The width of the interval h′ = 4.6; sample mean arithmetic value of the sample x′_cp = 123.26; the arithmetic mean of the squares of the sample values ${{x^{\prime }}_{\mathrm{c}\mathrm{p}}}^2=\mathrm{18,203}$; sample variance ${D^{\prime }}_B=3010.2$; sample mean square deviation ${{\sigma }^{\prime }}_B=54.865$; the modus ${M^{\prime }}_o=6.283$; the median ${M^{\prime }}_e=1.1332$.

and

Table 4. The results of calculating the average wear of the bottom part of the composite brake pads of the modernized BBS.

Mileage Interval (Thousand km)	ai−1	ai	xi	ni	xini	xi2ni	ωi	fi	sni	sωi
0 to 4.6	0	4.6	2.3	0.57	1.31	3.02	0.0049	0.0011	0.57	0.0049
4.6 to 16.2	4.6	16.2	10.4	3.14	32.66	339.62	0.027	0.0059	3.71	0.0319
16.2 to 24.1	16.2	24.1	20.2	5.89	118.98	2403.36	0.0506	0.011	9.6	0.0825
24.1 to 74.1	24.1	74.1	49.1	15.22	747.3	36,692.53	0.1308	0.0284	24.82	0.2133
74.1 to 121.3	74.1	121.3	97.7	23.04	2251	219,923.5	0.198	0.043	47.86	0.4113
121.3 to 164.6	121.3	164.6	143	30.79	4403	629,624.7	0.2646	0.0575	78.65	0.6759
164.6 to 197.8	164.6	197.8	181.2	37.73	6836.7	1,238,806	0.3242	0.0705	116.38	1.0
Total				116.38	14,,391	2,127,792	1

Note: the interval width h″ = 4.6; the sample mean arithmetic value of the sample ${x^{″}}_{cp}=123.26$; the arithmetic mean of the squares of the sample values ${{x^{″}}_{cp}}^2=\mathrm{18,203}$; the sample variance ${D^{″}}_B=3010.2$; the sample mean square deviation ${{\sigma }^{″}}_{\mathrm{B}}=54.865$; the modus ${M^{″}}_o=6.283$; the median ${M^{″}}_e=1.1332$.

.

To characterize the properties of a statistical distribution in the mathematical statistics, the concept of an empirical distribution function is introduced as follows:

$$F_{*}(x)={\displaystyle \frac{n_x}{n}}={\displaystyle \sum _{i:x_i<x}\frac{n_i}{n}},$$

(4)

where n is the volume of a sample; n_x is the frequency of the variant of the value χ_i, which is smaller than x.

The empirical function $F_{*}(x)$ was used to estimate the theoretical distribution function of the general population. Their difference consists of the fact that the theoretical function F(x) determines the probability of the event x_i < x, and the empirical function $F_{*}(x)$ represents the relative frequency of this event [52,54].

The empirical distribution function tends to the theoretical one in probability (converges in probability to $F_{*}(x)$ in the case of a large sample volume:

$$\underset{n\to 0}{\lim }P \left(\left|F_{*}(x)-F(x)\right|<\epsilon \right)=1 \forall x, \forall \epsilon >0.$$

(5)

at which, a sample of size n with the values x₁, x₂, …, x_p of the random variable x is considered. The average indicators called as the sample numerical characteristics are used to characterize the most important properties of the statistical distribution.

Furthermore, empirical distribution functions (Figure 6) were created for the upper and bottom parts of the composite brake pads with the modernized BBS of examined wagons based on the calculation results listed in Table 3 and Table 4.

Today, there are several different software products, which implement the method of least squares (LSM). Their application is very diverse: statistics, econometrics, assessment of measurement errors, etc. [52,53,56,57].

In order to understand the practical implementation of one of them, the task of determining and predicting the composite brake pads’ wear of the modernized BBS of freight wagons using the least squares method (LSM) was considered.

The obtained results of the experiments were analyzed to compare the analytical functions in the intervals with the well-known Weierstrass theorem. The point of this procedure is to assess whether the approximate dependence of the composite brake pads’ wear on the mileage of the wagons is reliably selected. At the same time, the number of members of the polynomial series is determined from the real possibilities of carrying out scheduled and preventive repairs of wagons, although this may be the reason for the disagreement according to the criteria, such as the Fisher’s criterion, the Student’s criterion, etc. Generally, many statisticians believe that several of known criteria do not always give a positive conclusion from the calculation results’ consistency point of view. Despite that, research is confirmed in practice [58,59]. Therefore, a form of the approximate function of the regression analysis can be chosen considering the convenience of its further use. On the contrary, other experts believe that the appearance of this function should be justified.

In the performed study, a combined approach was chosen to solve this problem. The preliminary analysis of the process was investigated based on the statistical data. Then, the mathematical model has the following form:

$$\widehat{y}={\beta }_0+{\beta }_1\cdot x+{\beta }_2\cdot x^2.$$

(6)

This is a nonlinear model of the second order. In a significant number of cases of choosing the type of approximation models of the braking processes of wagons, a reliable dependence of pad wear on mileage is obtained. It corresponds to the linear model of regression analysis [48,49], which satisfactorily describes the process of the studied pad wear during braking. Therefore, the formulation (6) can be reduced to linearity. To do this, it is considered that x₁ = x and x₂ = x². This results in a linear model (for linear models, there are powerful algebraic tools for their research), which looks as follows:

$$\widehat{y}={\beta }_0+{\beta }_1\cdot x_1+{\beta }_2\cdot x_2$$

(7)

There will be deviations between the values $\widehat{y}$ calculated by the model and the experimental calculations ${\widehat{y}}_i$. This deviation will be denoted as:

$${\widehat{u}}_i=\widehat{y}-{\widehat{y}}_i,\hspace{1em}i=1, 2, \dots , n .$$

(8)

The formulation (8) is called residues. They include the influence of unaccounted factors, namely variables, random disturbances, observation errors, etc. Their values may vary from one observation to another.

LSM makes it possible to find the following values (estimates), b₀, b₁, b₂, of the model’s initial parameters β₀, β₁, β₂. This is because of the necessary criterion for selecting the coefficients of the model, which must consider the circumstance of the obtained regression function (if it is presented on a graph). It will pass as closely as possible between the experimentally obtained variables:

$$U={\displaystyle \sum _{i=1}^n{U}_i^2}\to \min .$$

(9)

Furthermore, this model will be written in the following form:

$$\widehat{y}=b_0+b_1\cdot x_1+b_2\cdot x_2.$$

(10)

when, the partial derivatives by values b₀, b₁, b₂ are considered and they equal zero, a system of three equations with three unknowns is obtained. Its solution leads to the determination of values b₀, b₁, b₂. As, in our case:

$$U={\displaystyle \sum _{i=1}^n{U}_i^2}={\displaystyle \sum _{i=1}^n({\widehat{y}}_i-b_0-b_i\cdot x_{i1}-b_2}\cdot x_{i2}{)}^2,$$

(11)

the following is obtained:

$$\left\{\begin{array}{l}{\displaystyle \frac{\partial U}{\partial b_0}}=-2\cdot {\displaystyle \sum _{i=1}^n({\widehat{y}}_i-b_0-b_i\cdot x_{i1}-b_2}\cdot x_{i2})=0,\\ {\displaystyle \frac{\partial U}{\partial b_1}}=-2\cdot {\displaystyle \sum _{i=1}^n({\widehat{y}}_i-b_0-b_i\cdot x_{i1}-b_2}\cdot x_{i2})\cdot x_{i1}=0,\\ {\displaystyle \frac{\partial U}{\partial b_2}}=-2\cdot {\displaystyle \sum _{i=1}^n({\widehat{y}}_i-b_0-b_i\cdot x_{i1}-b_2}\cdot x_{i2})\cdot x_{i2}=0.\end{array}\right.$$

(12)

The system of Equation (12) results in the following system of algebraic equations:

$$\left\{\begin{array}{l}{b}_{0}n+b_1\cdot {\displaystyle \sum _{i=1}^n{x}_{i1}}+b_2\cdot {\displaystyle \sum _{i=1}^n{x}_{i2}}={\displaystyle \sum _{i=1}^n{\widehat{y}}_i,}\\ b_0\cdot {\displaystyle \sum _{i=1}^n{x}_{i1}+b_1\cdot {\displaystyle \sum _{i=1}^n{x}_{i1}^2+b_2\cdot {\displaystyle \sum _{i=1}^n{x}_{i1}\cdot x_{i2}={\displaystyle \sum _{i=1}^n{x}_{i1}\cdot {\widehat{y}}_i,}}}}\\ b_0\cdot {\displaystyle \sum _{i=1}^n{x}_{i2}+b_1\cdot {\displaystyle \sum _{i=1}^n{x}_{i1}\cdot x_{i2}+b_2\cdot {\displaystyle \sum _{i=1}^n{x}_{i2}^2={\displaystyle \sum _{i=1}^n{x}_{i2}\cdot {\widehat{y}}_i.}}}}\end{array}\right.$$

(13)

The solution of this system (13) leads to the unknown coefficients b₀, b₁, b₂:

$$b_0=\widehat{y}-b_1\cdot x_1-b_2\cdot x_2.$$

(14)

$$b_1={\displaystyle \frac{{\displaystyle \sum _{i=1}^n(x_{i1}-{\overline{x}}_1)\cdot ({\widehat{y}}_i-\overline{y})\cdot }{\displaystyle \sum _{i=1}^n{(x_{i2}-{\overline{x}}_2)}^2}}{{\displaystyle \sum _{i=1}^n{(x_{i1}-{\overline{x}}_1)}^2}\cdot {\displaystyle \sum _{i=1}^n{(x_{i2}-{\overline{x}}_2)}^2}-{\left({\displaystyle \sum _{i=1}^n(x_{i1}-{\overline{x}}_1)\cdot (x_{i2}-{\overline{x}}_2)}\right)}^2}}-{\displaystyle \frac{{\displaystyle \sum _{i=1}^n(x_{i2}-{\overline{x}}_2)\cdot ({\widehat{y}}_i-\overline{y})\cdot }{\displaystyle \sum _{i=1}^n(x_{i1}-{\overline{x}}_1)\cdot (x_{i2}-{\overline{x}}_2)}}{{\displaystyle \sum _{i=1}^n{(x_{i1}-{\overline{x}}_1)}^2}\cdot {\displaystyle \sum _{i=1}^n{(x_{i2}-{\overline{x}}_2)}^2}-{\left({\displaystyle \sum _{i=1}^n(x_{i1}-{\overline{x}}_1)\cdot (x_{i2}-{\overline{x}}_2)}\right)}^2}}.$$

(15)

$$b_2={\displaystyle \frac{{\displaystyle \sum _{i=1}^n(x_{i2}-{\overline{x}}_2)\cdot ({\widehat{y}}_i-\overline{y})\cdot }{\displaystyle \sum _{i=1}^n{(x_{i1}-{\overline{x}}_1)}^2}}{{\displaystyle \sum _{i=1}^n{(x_{i1}-{\overline{x}}_1)}^2}\cdot {\displaystyle \sum _{i=1}^n{(x_{i2}-{\overline{x}}_2)}^2}-{\left({\displaystyle \sum _{i=1}^n(x_{i1}-{\overline{x}}_1)\cdot (x_{i2}-{\overline{x}}_2)}\right)}^2}}-{\displaystyle \frac{{\displaystyle \sum _{i=1}^n(x_{i1}-{\overline{x}}_1)\cdot ({\widehat{y}}_i-\overline{y})\cdot }{\displaystyle \sum _{i=1}^n(x_{i1}-{\overline{x}}_1)\cdot (x_{i2}-{\overline{x}}_2)}}{{\displaystyle \sum _{i=1}^n{(x_{i1}-{\overline{x}}_1)}^2}\cdot {\displaystyle \sum _{i=1}^n{(x_{i2}-{\overline{x}}_2)}^2}-{\left({\displaystyle \sum _{i=1}^n(x_{i1}-{\overline{x}}_1)\cdot (x_{i2}-{\overline{x}}_2)}\right)}^2}}.$$

(16)

Substituting their values into the general form of regression results in the so-called regression line with coefficients b₁ and b₂, which are called regression coefficients $\widehat{y}$ for x₁ and $\overline{y}$ for x₂, respectively.

The found point (b₀, b₁, b₂) is the point of satisfaction of the mentioned condition. However, regarding the mathematical analysis, there is a theorem that makes it possible to determine sufficient conditions for the extremum of a function. In our case, the minimum of a function U (b₀, b₁, b₂).

Thus, a regression model was developed for predicting the residual life of composite brake pads with the modernized BBS, which considers the mileage of the freight wagons—general and additional. The additional mileage is the distance covered by the wagon during maintenance with uncoupling or repair, i.e., shunting work at a station, shunting operations associated with the supply of wagons (loaded or empty) along the tracks to industrial enterprises, or from them to the main railway tracks.

Figure 7 shows the graphs of the linear regression created based on the results of experimental data processing (

Table 5. The results of calculating the average residual life of the upper part of composite brake pads with the modernized BBS.

x	$\widehat{\mathit{y}}$	x2	$\mathit{x}\widehat{\mathit{y}}$	ylin	dbid	d2
0	0	0	0	0.46936	−0.4694	0.22029
4.6	0.59	21.16	2.714	1.3607	−0.7707	0.59397
16.2	3.38	262.44	54.756	3.60843	−0.2284	0.05218
24.1	6.12	580.81	147.492	5.13921	0.98079	0.96195
74.1	15.98	5490.81	1184.12	14.8277	1.15229	1.32777
121.3	23.8	14,713.7	2886.94	23.9737	−0.1737	0.03016
164.6	31.87	27,093.2	5245.8	32.3639	−0.4939	0.24393
197.8	38.8	39,124.8	7674.64	38.7971	0.00295	8.7 × 10−6
602.7	120.54	87,287	17,196	-	-	3.4303

and

Table 6. The results of calculating the average residual life of the bottom part of composite brake pads with the modernized BBS.

x	$\widehat{\mathit{y}}$	x2	$\mathit{x}\widehat{\mathit{y}}$	ylin	dbid	d2
0	0	0	0	0.37035	−0.3704	0.13716
1	2	3	4	5	6	7
4.6	0.57	21.16	2.622	1.23599	−0.666	0.44354
16.2	3.14	262.44	50.868	3.4189	−0.2789	0.07778
24.1	5.89	580.81	141.949	4.90553	0.98447	0.96917
74.1	15.22	5490.81	1127.8	14.3146	0.90538	0.8197
121.3	23.04	14,713.7	2794.75	23.1968	−0.1568	0.02459
164.6	30.79	27,093.2	5068.03	31.3451	−0.5551	0.30811
197.8	37.73	39,124.8	7462.99	37.5927	0.13728	0.01885

). This makes it possible to predict the residual resource of composite brake pads for their maximum thickness of 10 mm [29] for the modernized BBS in the case of their use for the entire inter-repair operation period of freight wagons. Under the condition of installing the modernized BBS, the average mileage of a freight wagon in case of the uniform wear of brake pads can reach 284.57 thousand km.

It can be seen in the linear regression graphs (Figure 7) that it is not necessary to replace the composite brake pads by using modernized BBSs with devices for uniform removal of the pads during the inter-repair period of the wagon operation. The combined criterion applied in the studies confirms that the mileage of freight wagons repaired according to the standard frequency should be of 110,000 km after the last depot repair, and of 160,000 km for the last major repair [49].

A similar technique is used in the case of finding m regression coefficients b₀, b₁, b₂, …, b_m.

To estimate the density of the connection between x and y, the correlation coefficient and the coefficient of determination is used. It shows how much the variation of the variable x explains the variation of y. The standard error of the residuals is applied to evaluate how well the regression line explains the relationship between x and y. It shows the deviation of the empirical values from the regression line.

Testing the hypothesis about its adequacy is an important subsequent step in the creation of a regression model. To do this, the F-criterion [51,52,53] is considered. Furthermore, the t-test was applied to test the hypothesis, whether the estimated regression parameters are statistically significant or different from zero. The F-criterion of the model adequacy has the form:

$$F_{1,n-2}={\displaystyle \frac{\left(n-2\right)\cdot {\displaystyle \sum _{i=1}^n{\left({\widehat{y}}_i-\overline{y}\right)}^2}}{{\displaystyle \sum _{i=1}^n{\left({\widehat{y}}_i-\overline{y}\right)}^2}}} .$$

(17)

The observed value of the t-test to test the significance of the correlation coefficient is determined by the expression:

$$t_{n-2}={\displaystyle \frac{r\cdot \sqrt{n-2}}{\sqrt{1-r^2}}} .$$

(18)

The observed value of the t-test for testing the hypothesis:

$$H_0: b_1={\beta }_i (H_1:b_i={\beta }_i):\hspace{1em}{t}_{n-2}={\displaystyle \frac{b_i-{\beta }_i}{{\widehat{\sigma }}_{b_i}}}, i=0,1.$$

$${\widehat{\sigma }}_{b_0}={\widehat{\sigma }}_{\epsilon }\cdot \sqrt{{\displaystyle \frac{{\displaystyle \sum _{i=1}^n{x}_i^2}}{n\cdot {\displaystyle \sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2}}},\hspace{1em}}{\widehat{\sigma }}_{b_1}={\displaystyle \frac{{\widehat{\sigma }}_{\epsilon }}{\sqrt{{\displaystyle \sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2}}}},\hspace{1em}{\widehat{\sigma }}_{\epsilon }^2={\displaystyle \frac{{\displaystyle \sum _{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}}{n-2}} .$$

(19)

And, the observed value of the t-test for testing the hypothesis:

$$H_0: b_i=0 (H_1:b_i\ne 0) t_{n-2}={\displaystyle \frac{b_i}{{\widehat{\sigma }}_{b_i}}} .$$

If the straight line is placed so that the points are approximately equally placed on both sides of it, then the parameters of the linear equation can be determined quite simply.

LSM is most often used to determine the parameters of the equation of form $\overline{y}=k\cdot x+b$. At the same time, the condition of the sum of the squared deviations (distances) of all investigated points from the ordinates calculated according to the equation of the straight line ε_i, is minimal. In other words, the straight line should pass as close as possible to the peaks of the empirical regression line. This means that the parameters k and b of the regression equation must be determined from the expression:

$${\epsilon }_i={\displaystyle \sum _{i=1}^n\left(y_i-{\tilde{y}}_i\right)=\min }$$

(20)

where y_i are the ordinates of the studied points; ${\tilde{y}}_i$—the ordinates of the calculation points determined by the regression equation $\overline{y}=kx+b$ as follows:

$${\epsilon }_i=\sum _{i=1}^n{\left[y_i-\left(k\cdot x+b\right)\right]}^2=F(k,b)\min .$$

(21)

A necessary condition for the extremum of this function is the equality of partial derivatives taken by the parameters k and b:

$${\displaystyle \frac{\partial F}{\partial k}}=0 \mathrm{and} {\displaystyle \frac{\partial F}{\partial b}}=0, {\left[F\left(u\right)\right]}^{\prime }=F_u(u)*u^{\prime } .$$

(22)

From here:

$$\begin{array}{l}{\displaystyle \frac{\partial F}{\partial k}}=-2\cdot {\displaystyle \sum _{i=1}^n\left[y_i-(k\cdot x_i+b)\right]}\cdot x_i=0 ,\\ {\displaystyle \frac{\partial F}{\partial k}}=-2\cdot {\displaystyle \sum _{i=1}^n\left[y_i-(k\cdot x_i+b)\right]}=0 .\end{array}$$

(23)

Simplifying these expressions, the system of linear equations is obtained as follows:

$$\begin{array}{c}{\displaystyle \sum _{i=1}^n{y}_i\cdot x_i=k\cdot {\displaystyle \sum _{i=i}^n{x}_i^2+b\cdot {\displaystyle \sum _{i=1}^n{x}_i}}} ,\\ {\displaystyle \sum _{i=1}^n{y}_i\cdot x_i=k\cdot {\displaystyle \sum _{i=i}^n{x}_i+b\cdot n}} .\end{array}$$

(24)

The parameters k and b are found by substituting the numerical values of the corresponding quantities into the system.

Similar calculations are performed using the Cochrane quality criterion. However, due to this condition, the number of measurement points is increased to 53. The results of the calculations are described below.

The validity of the null hypothesis was checked according to the Cochrane quality criterion. The ratio of the maximum corrected variance to the sum of all corrected variances was considered:

$$G_{\mathit{ChC}}={\displaystyle \frac{S_{\mathit{max}}^2}{S_1^2+S_2^2}}={\displaystyle \frac{116.65}{116.65+109.66}}=0.5154.$$

(25)

The distribution of this random variable depends on the number of degrees of freedom k = n − 1 = 52, where n is the sample size, and it equals the value of 53.

The critical point G_cr (0.05;52;2) = 0.6543 was found according to the table in the appendix of the documents [51,57,58] at the significance level of 0.05, the number of degrees of freedom being 52, and the sample value l = 2 (wear from above and below).

As G_cr > G_ChC and their difference is insignificant, there is no reason to reject the null hypothesis. Therefore, the final general variance under the condition of homogeneity of variances is established as follows:

$$D\left(x\right)={\displaystyle \frac{1}{2}}\cdot \left(S_1^2+S_2^2\right) .$$

(26)

Thus, the corrected variances are practically equal, i.e., $S_1^2\approx S_2^2$.

Whereas the data in the task of sampling the wear of the upper and bottom parts of the composite brake pads have the same volume, the comparison of two average normal general populations is considered [54]. When the notation $d_i={\left(X_1\right)}_i-{\left(X_2\right)}_i$ is introduced, the corrected mean square deviation equals:

$$s_d=\sqrt{{\displaystyle \frac{{\displaystyle \sum d_i^2}-\frac{{\left[{\displaystyle \sum d_i}\right]}^2}{n}}{n-1}}}=0.342598 .$$

(27)

In order to test the null hypothesis for a given significance level of α = 0.05, it is necessary to determine the value of the observed criterion:

$$T_{\mathit{ChC}}={\displaystyle \frac{\overline{d}\cdot \sqrt{n}}{s_d}}=13.90331 ,$$

(28)

where $\overline{d}={\displaystyle \sum d_i}/n$ is the average difference.

Based on the critical points of the distribution, the given level of significance α = 0.05, and the number of degrees of freedom k = n − 1 = 52, the value of the critical point t_BV,cr = 2.01 is found. Hence, it can be concluded based on the findings $\left|T_{\mathit{ChC}}\right|>t_{BV,cr}$ that the obtained results are a confirmation of the fact that the wear of the upper and bottom parts of the composite brake pads has different values on average.

4. Discussion

To eliminate the wedge-dual wear of the brake pads of freight wagons with a gauge of 1520 mm, the modernization of the BBS is proposed. This modernization consists of changing the location of the technological hinge B (Figure 2), which connects the vertical lever with the strut of the triangle. The specified hinge is located on the same line A-A with the hinges of the pendulum suspensions. In addition, a curved rod is introduced, which, with its ends in the sliders, keeps the BBS constantly in balance, which ensures strictly uniform gaps between the blocks and wheels and guarantees their normative wear.

To justify the proposed modernization, complex studies of the technical condition of the BBS during the maintenance of freight wagons in the fleets of the sorting station were carried out.

Based on the collected statistical material (Table 1 and Table 2), a regression model was built. It allows the residual resource of composite brake pads to be predicted with a modernized BBS. The peculiarity of this model is that it considers the total and additional mileage of freight wagons.

As part of the study, graphic dependencies of the composite brake pads’ wear with the modernized BBS were formed in terms of thickness, which depends on the mileage of freight wagons. It was established that there is no need to replace the composite brake pads, considering the use of modernized BBSs during the inter-repair period of the wagon’s operation.

To check the adequacy of the created model, its verification was carried out using the F-criterion. The results of the calculation established that the hypothesis of adequacy is not rejected.

This study has certain advantages in comparison with known ones. For example, in contrast to works [16,17,32,33], the team of authors predicted the residual resource of brake pads, and did not determine their load in operation. In contrast to works [18,28], within the framework of this study, solutions aimed at increasing the resource of brake pads in operation are proposed. The model proposed by the authors in this research considers the brake pads’ wear by thickness during operation, which was not studied in works [19,30,31]. In comparison with the research results highlighted in works [20,21,22], this presented research proposes the improvement of the BBS to increase the resource of the brake pads. In contrast to works [23,24,27], the most unfavorable type of brake pads’ wear was considered and a solution was proposed for its elimination. In comparison with studies [25,26,29], the authors evaluated the brake pads’ wear considering the proposed modernization of the BBS and not typical designs. Unlike the works [46,47,48], the authors examined the most unfavorable operating conditions of brake pads. This will allow solutions aimed at increasing their service life in the future to be proposed.

The described methodology can be also applied to other means of railway transport, such as trams, passenger wagons, etc. [59,60,61,62].

Despite the fact described above, this presented study has a certain limitation. At this stage, the authors did not consider the influence of over-normalized modes on the brake pads’ wear of the modernized BBS, or the influence of the inherent degree of freedom of the cargo loaded in a wagon on the braking efficiency, or the malfunction of the harness device of the automatic coupler, etc.

One of the main future challenges of this study consists of the fact that the efficiency of the modernized design of the BBS has been proven only on an open wagon type so far. The effectiveness of such a BBS on other wagon types has not been considered. However, it should be noted that this wagon type makes up more than 50% of the inventory of the Ukrzaliznytsia Stock Company (Kyiv, Ukraine). These questions will be considered as a further development of the research.

The results of this study will contribute to increasing the efficiency of the operation of rail vehicles and the profitability of railway transport as a whole. The conducted research will also contribute to improving the environmental friendliness of rail transport [63,64].

5. Conclusions

1. Comprehensive experimental studies of the technical condition of modernized brake systems in operational conditions during the maintenance of freight wagons in the fleets of the sorting station were carried out. During each run of experimental freight wagons with the modernized BBS, the parameters of composite brake pads were measured during maintenance at control points in the range of 2.1 to 197.8 thousand km mileage.

2. A regression model was developed for predicting the residual life of composite brake pads with the modernized BBS, which considers the total and additional mileage of the freight wagon.

It was established that, under the condition of using the modernized BBS on freight wagons, the average mileage of a wagon with uniform wear of composite brake pads can reach up to 284.57 thousand km. It was established according to the results of mathematical calculations that the use of the modernized BBS helps to increase the resource of composite brake pads by approximately 2.59 times.

3. The verification of statistical hypotheses was carried out according to the nature of the distribution of random values of the wear of composite brake pads with the modernized BBS and their relationship regarding the data belonging to one general inventory.

It was established that the average wear of composite brake pads of the upper and bottom part of the brake pads has different values. It is proved according to the results of the calculations that the heterogeneity of the dispersion does not depend on the quantitative indicator of the sample of this experiment.