Mix Controller Design for Active Suspension of Trucks Integrated with Online Estimation of Vehicle Mass
Abstract
1. Introduction
- (1)
- A seven-degree-of-freedom vehicle active suspension model considering road excitation, lateral, and longitudinal acceleration is established.
- (2)
- A recursive least squares algorithm with a forgetting factor for vehicle mass estimation is established.
- (3)
- An active suspension mix controller, LQR controller with integrated vehicle mass estimation, is proposed.
2. Multi-Degree-of-Freedom Coupling Dynamics Model of the Vehicle
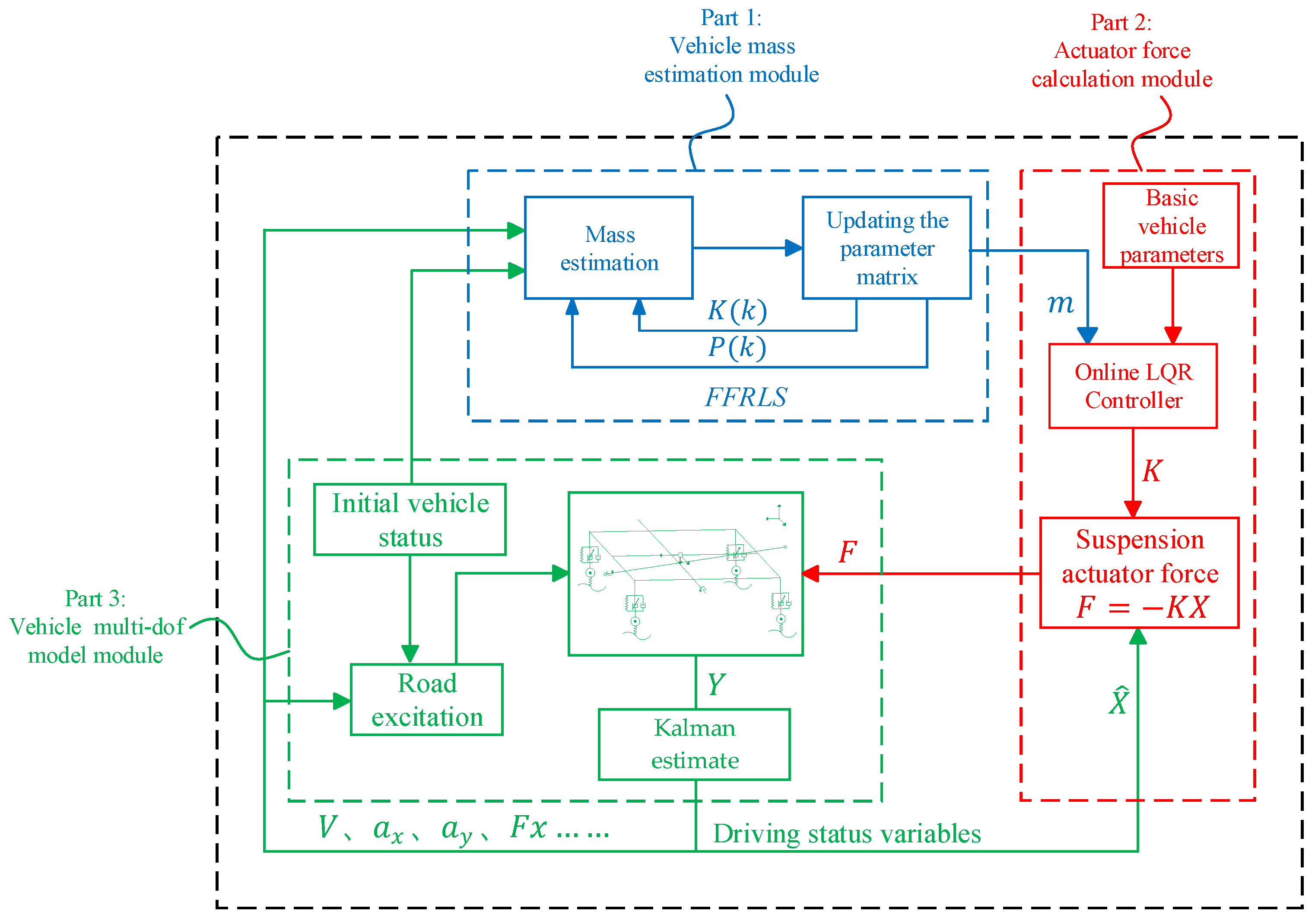
3. Mix Control System Architecture for Active Suspension Integrated with Mass Estimation
4. Design of Active Suspension Mix Controller
4.1. Module for Recursive Least Squares with Forgetting Factor for Vehicle Mass Estimation
4.1.1. Vehicle Mass Estimation Model
4.1.2. Recursive Least Squares Algorithm with Forgetting Factor
- (1)
- Solve for parameter identification gain
- (2)
- Update parameter identification
- (3)
- Update recognition error
4.2. Module for LQR-Based Actuator Force Calculation
4.3. Mix Control Logic
5. Comparative Simulation Analysis
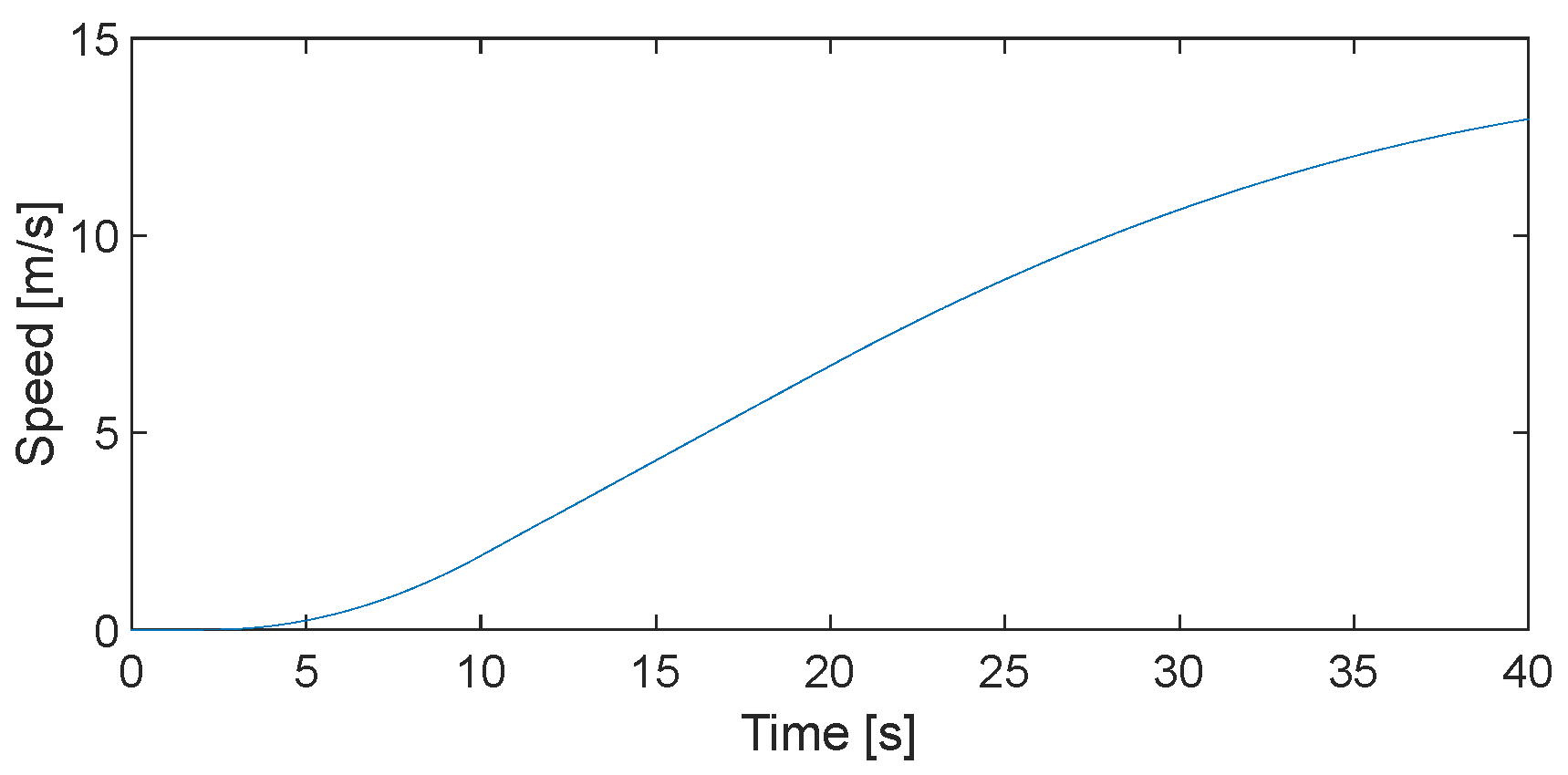
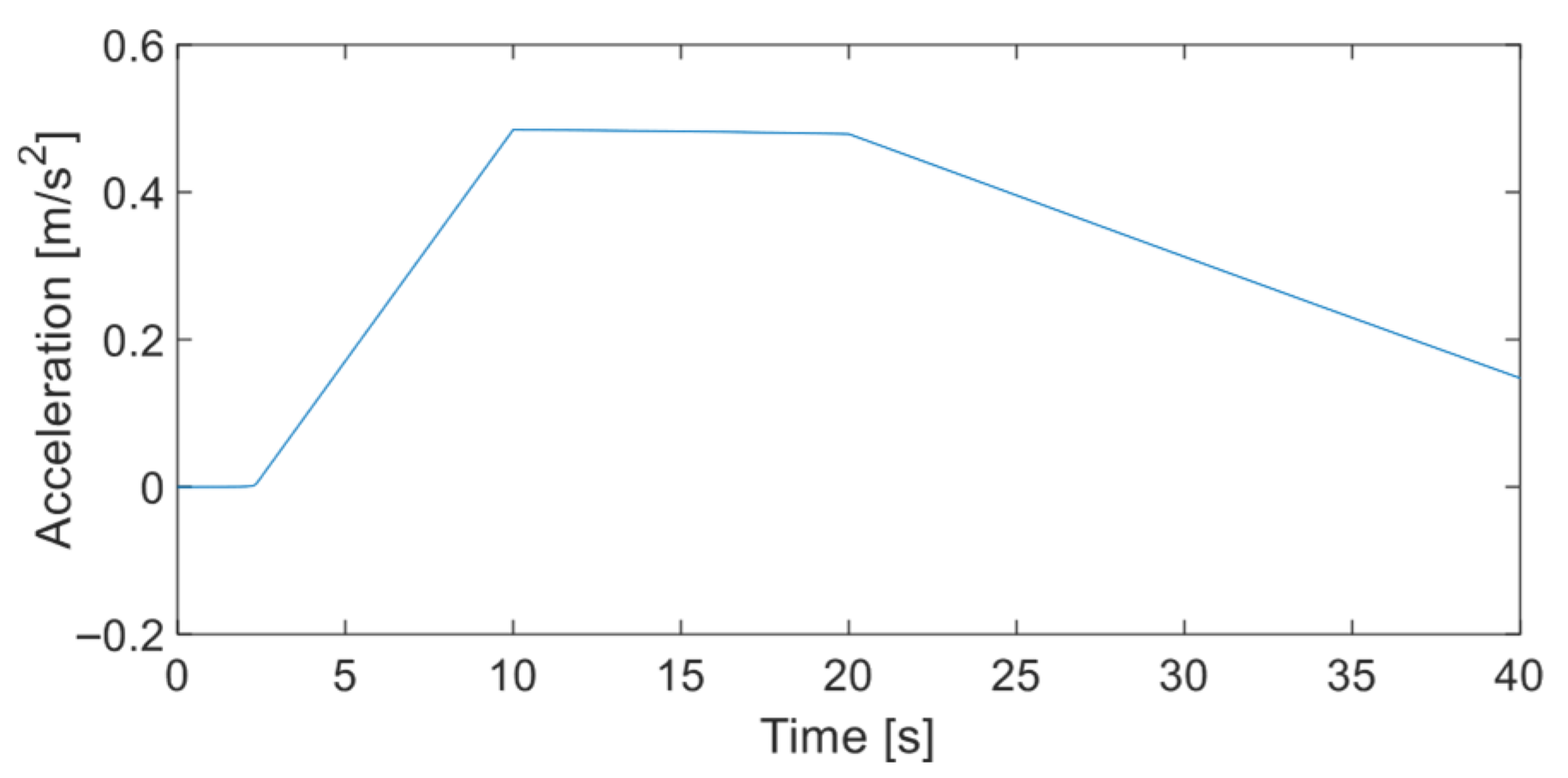
5.1. Vehicle Simulation Parameter Selection
5.2. Dynamic Response and Body Attitude Analysis Integrated with Online Estimation of Vehicle Mass
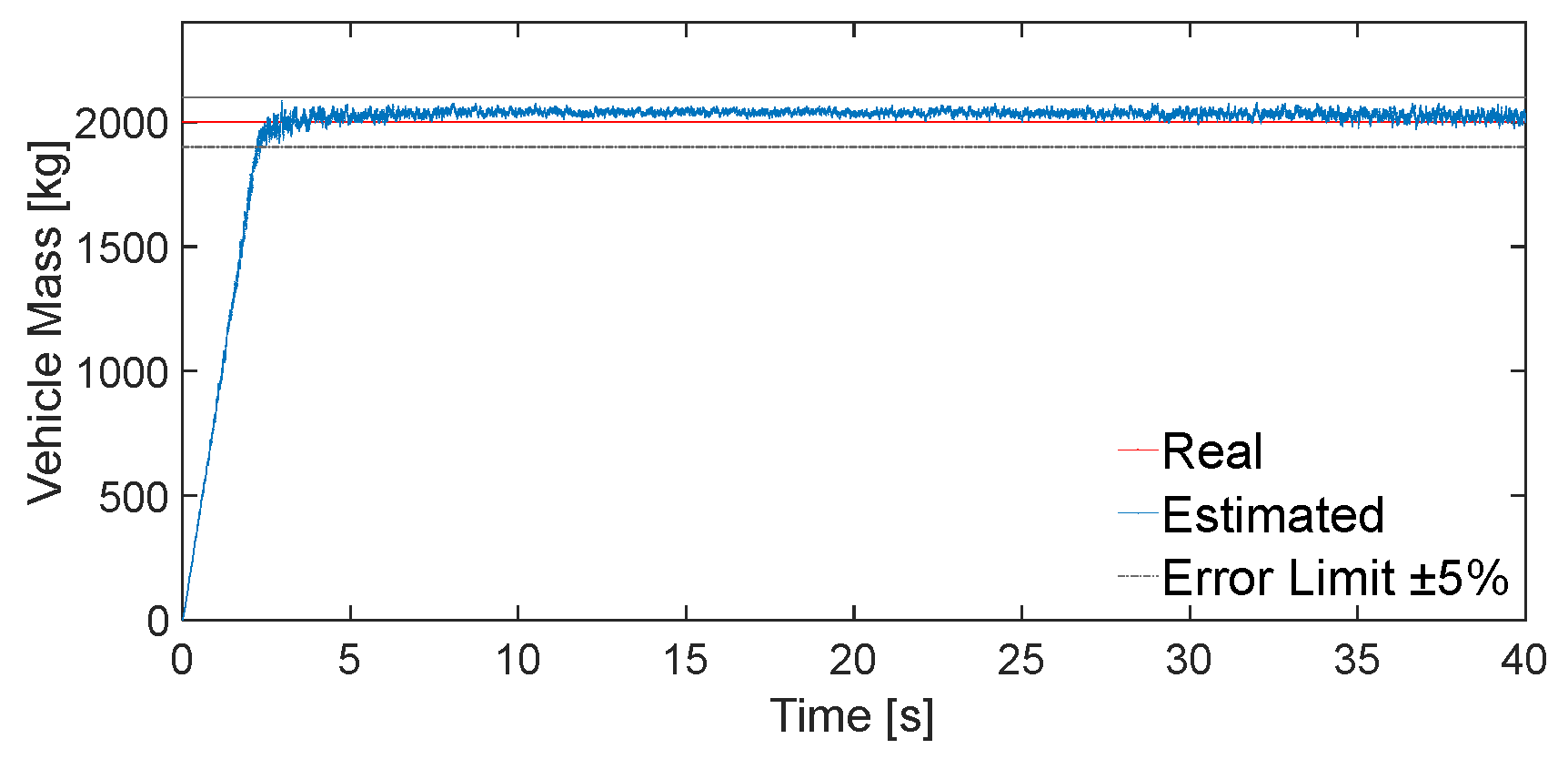
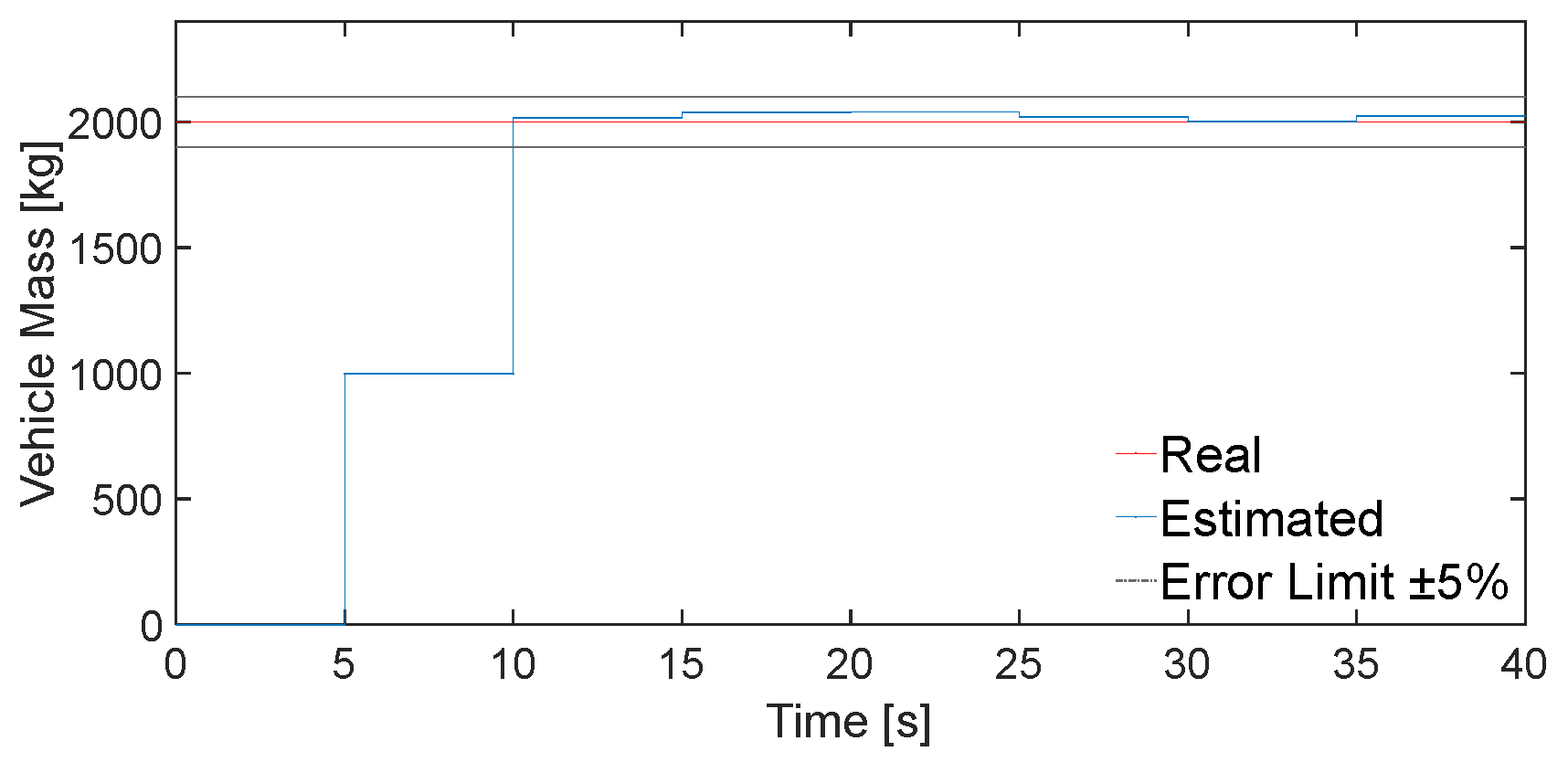
5.2.1. Vehicle Mass Estimation Simulation Analysis
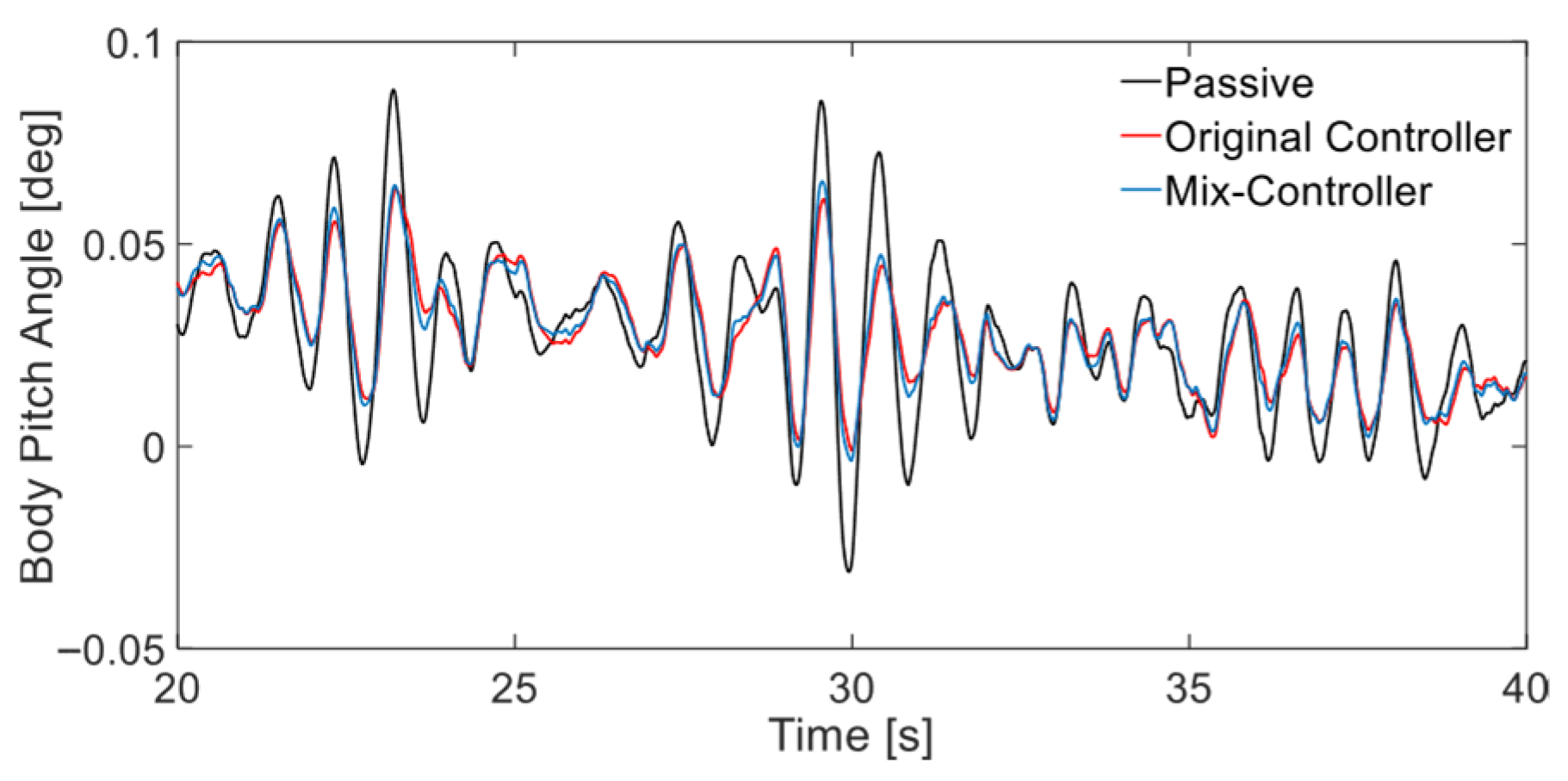
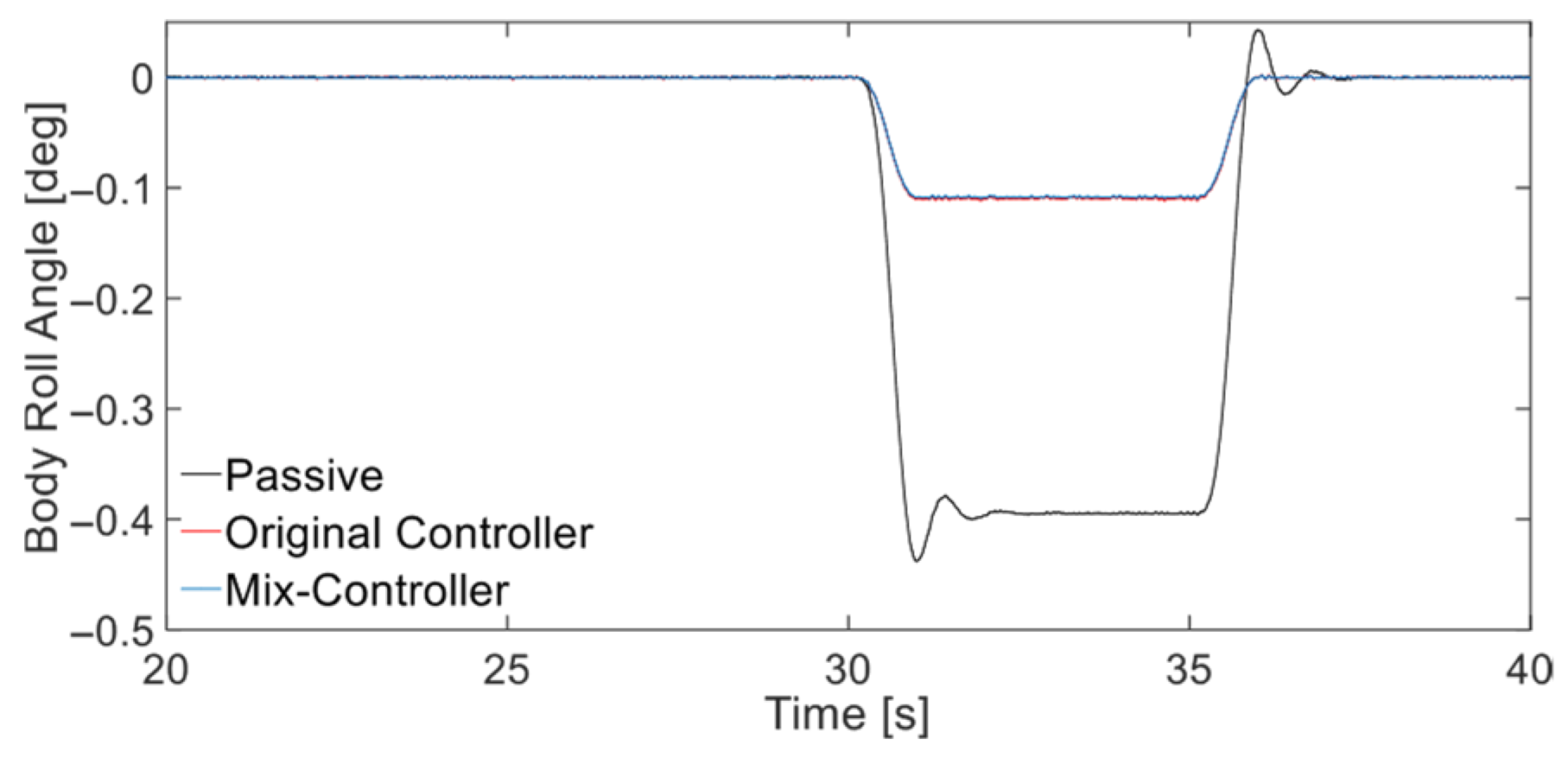
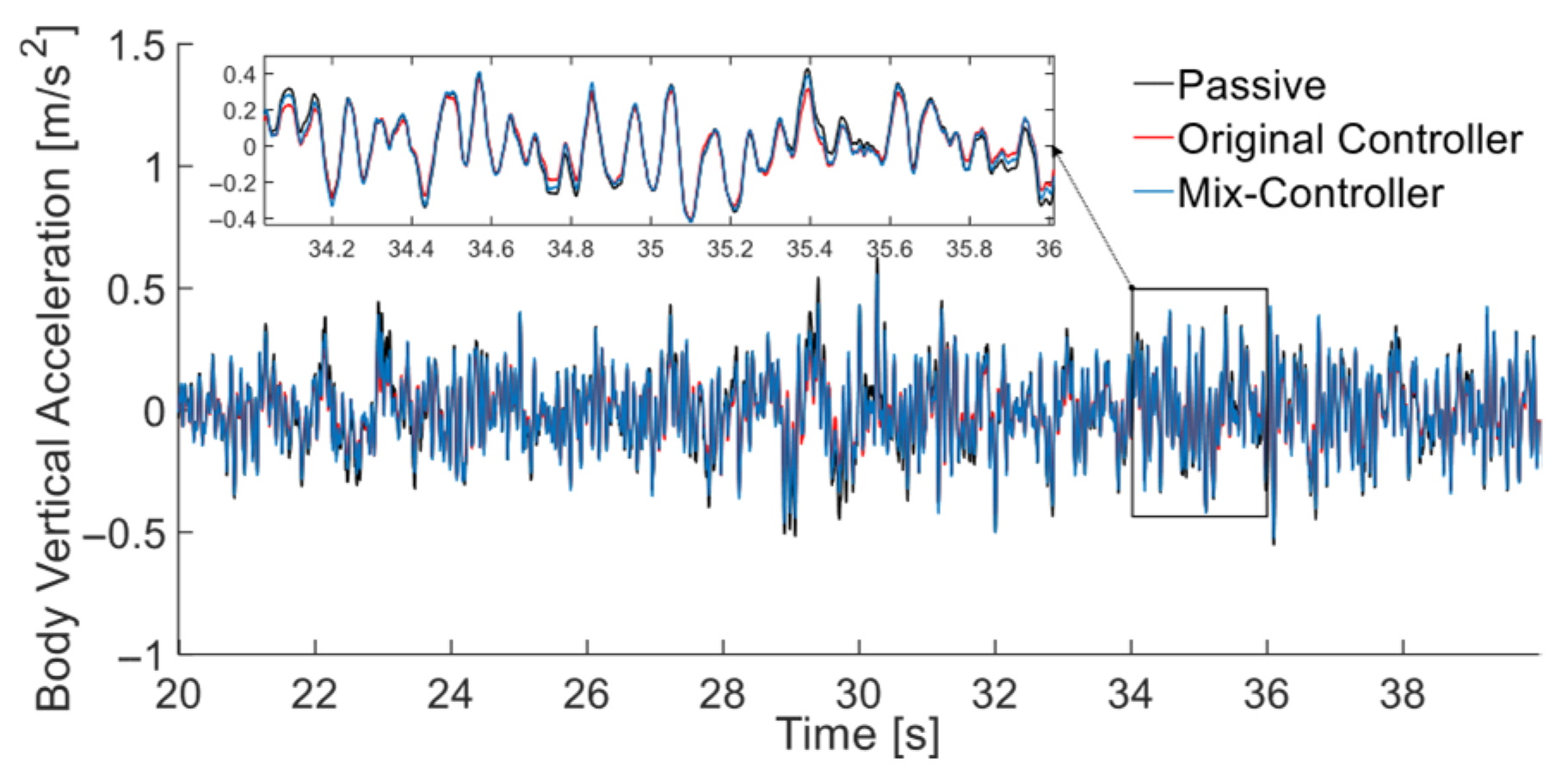
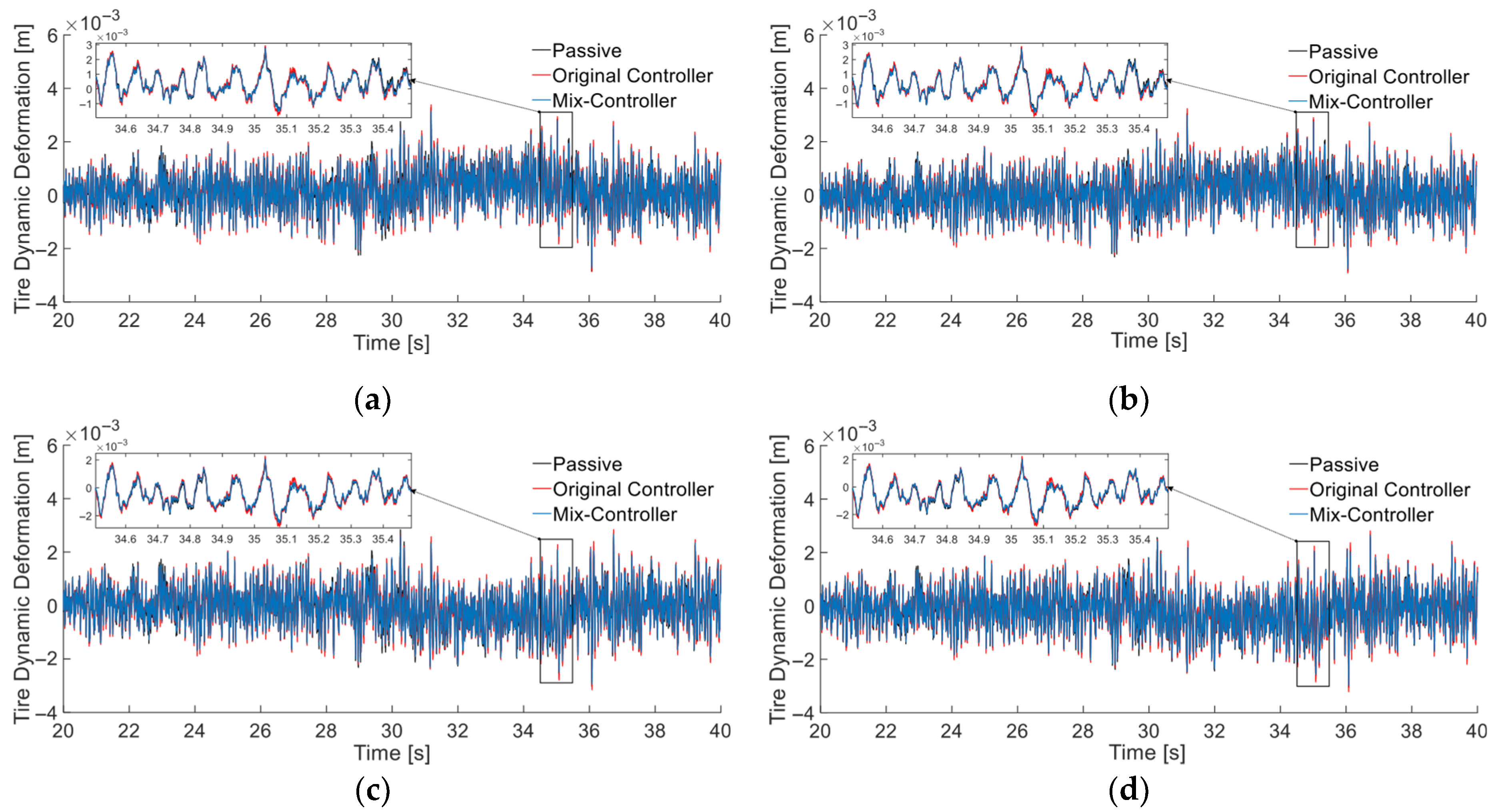
5.2.2. Vehicle Dynamic Response and Body Attitude Analysis
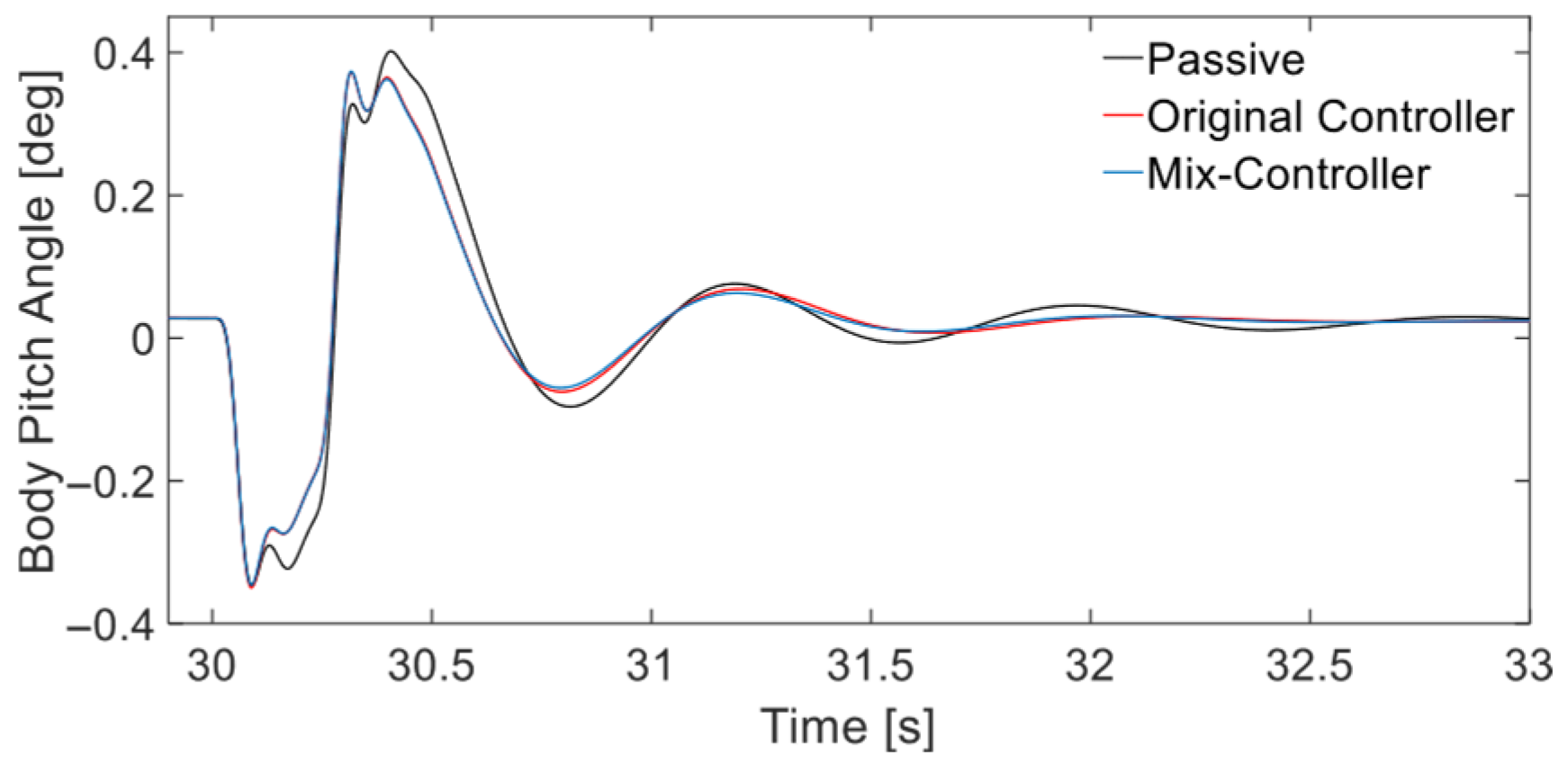
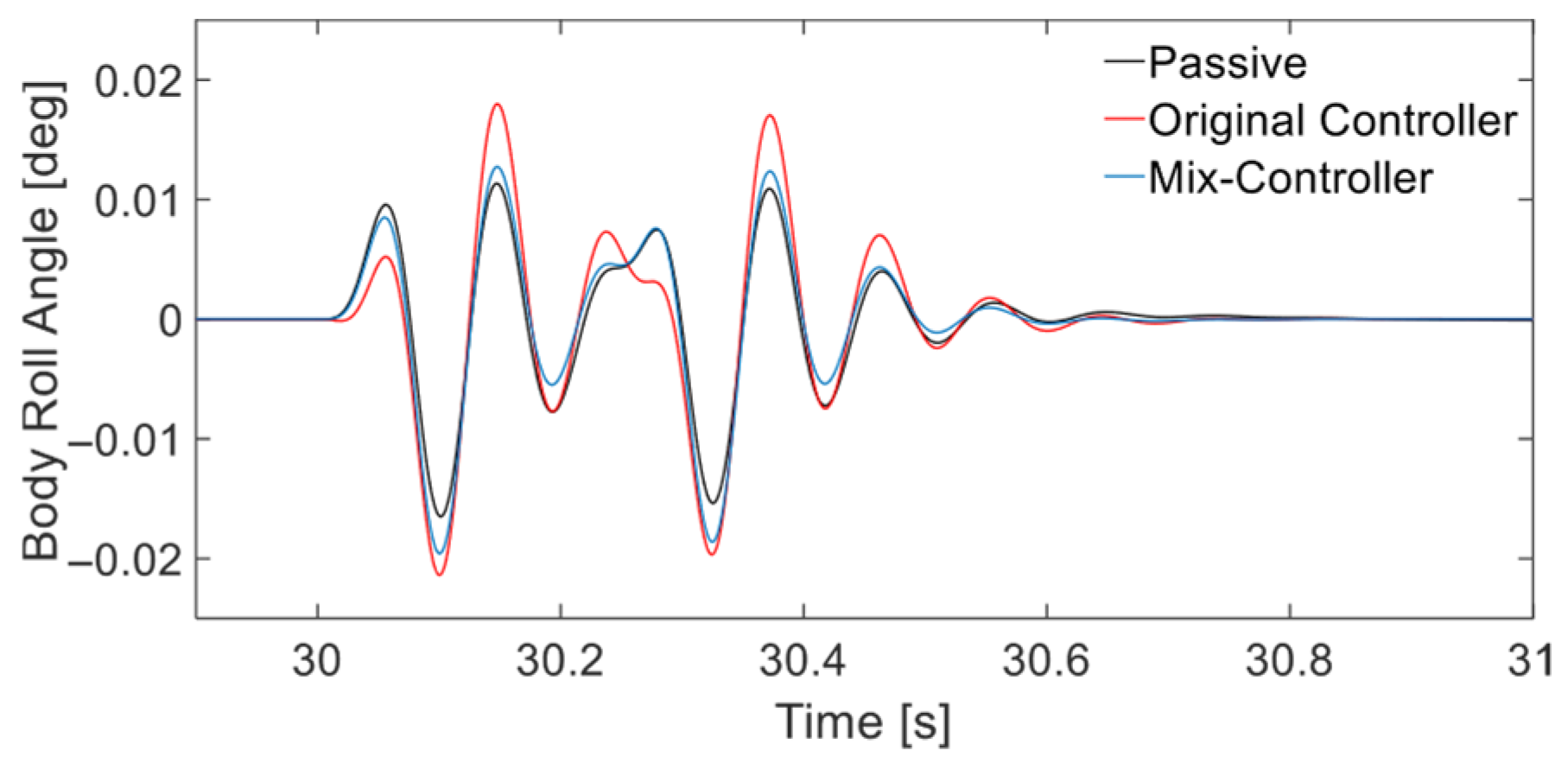
Time-Domain Response Analysis
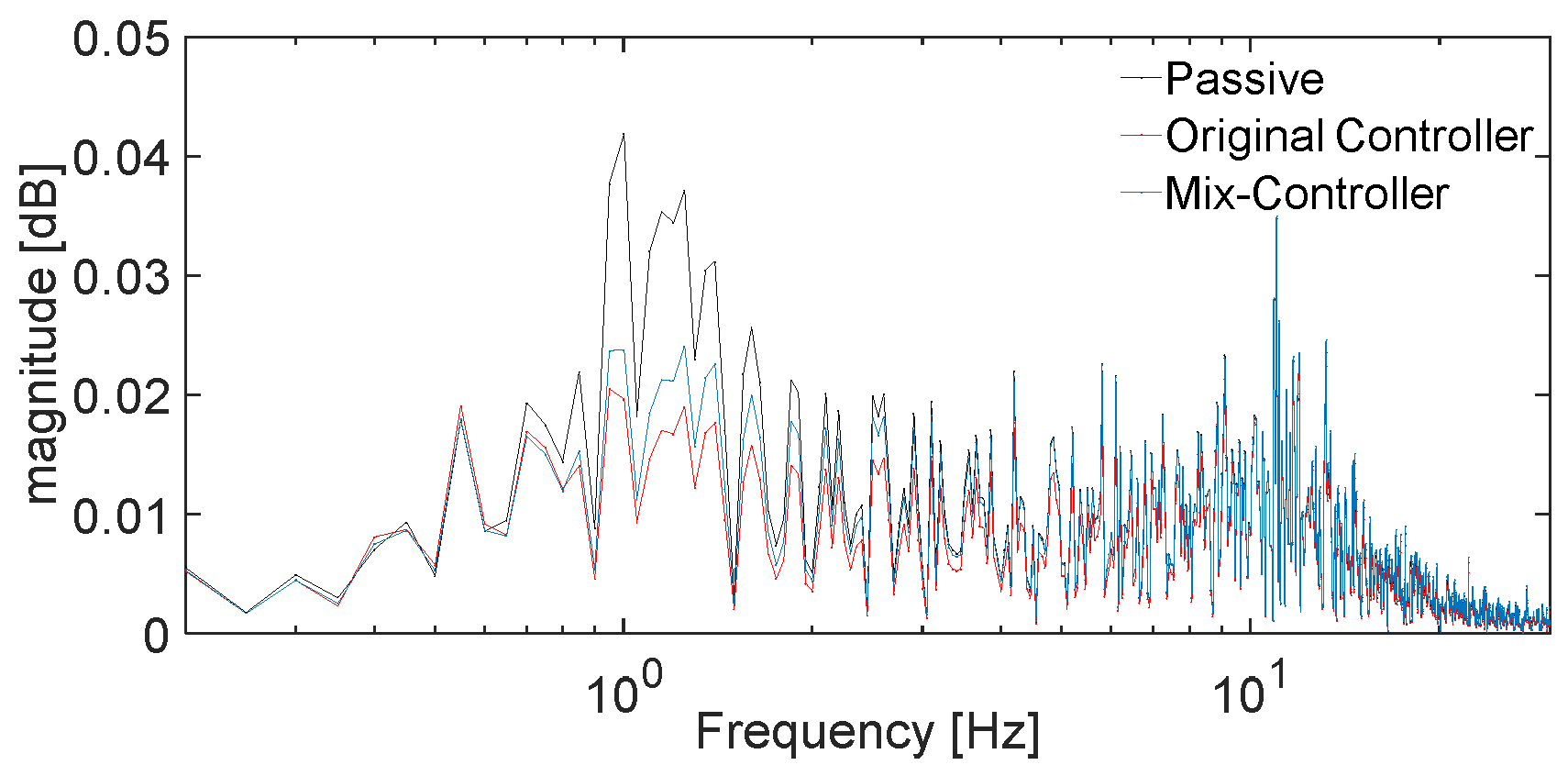
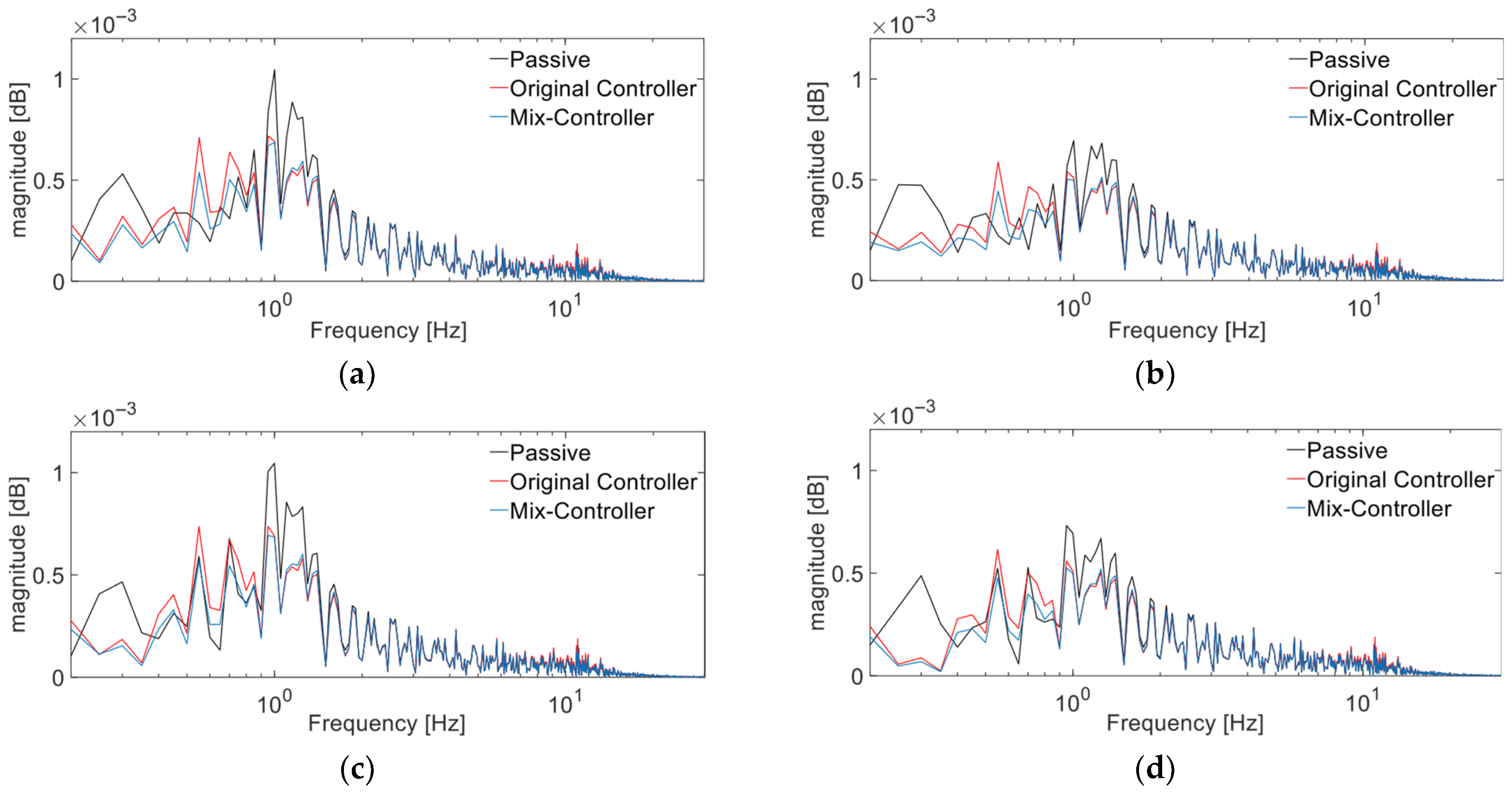
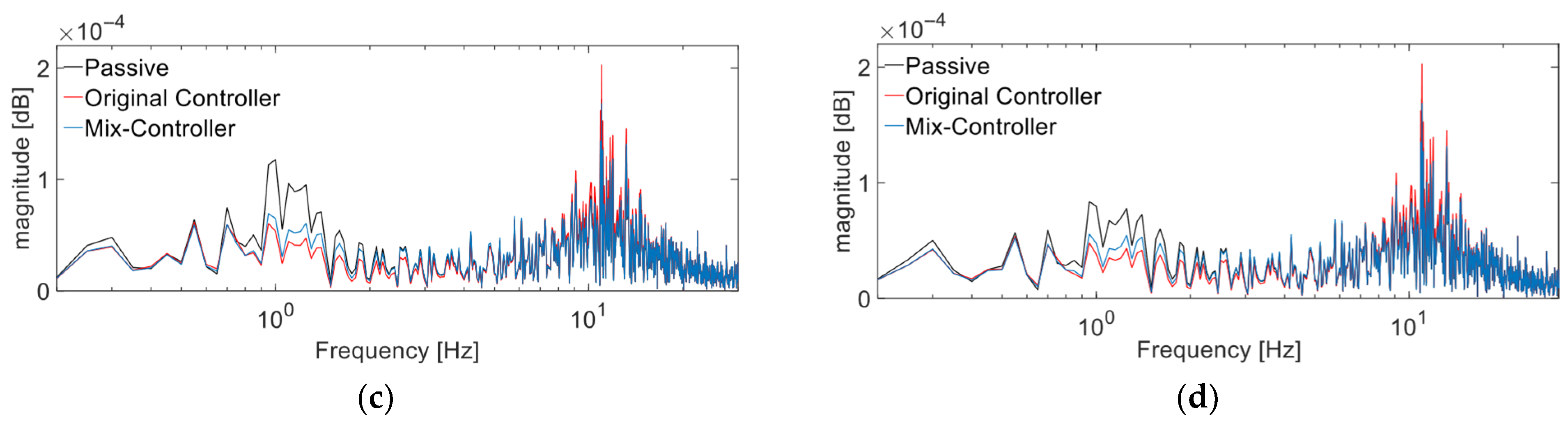
Frequency-Domain Response Analysis
5.3. Analysis of Actuator Force and Efficiency
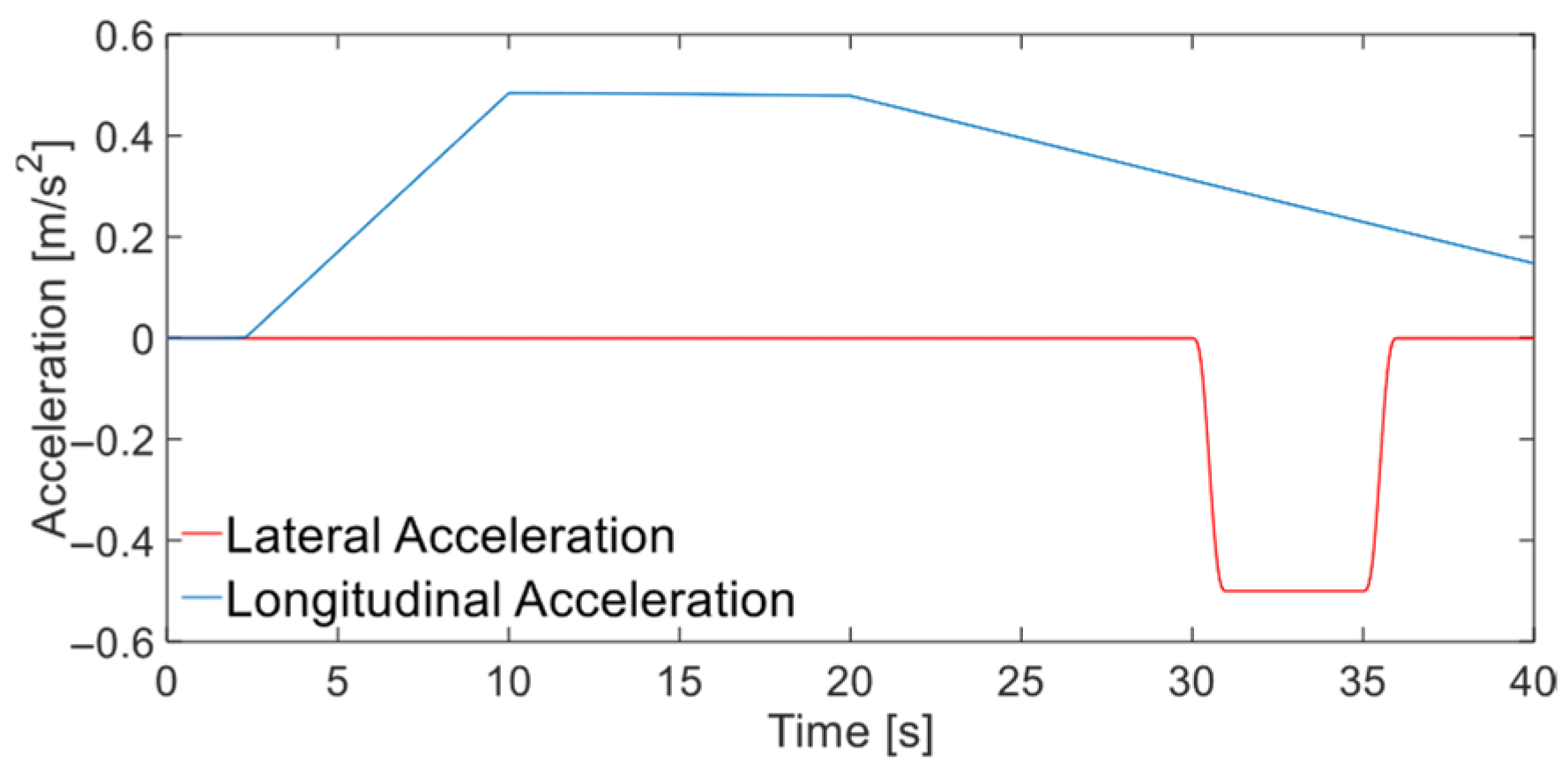
5.4. A Road Bump Experimentation Simulation Analysis
6. Conclusions
- (1)
- The mix controller for the active suspension of trucks integrated with online estimation of vehicle mass is proposed. Compared to the original controller, the mix controller can adapt to the real-time changes in vehicle mass and has a better control effect, ensuring the effectiveness of the control system.
- (2)
- According to the characteristics of parameter changes in the vehicle driving process, based on longitudinal vehicle dynamics using FFRLS and simulation test verification, the final mass estimation error results are less than 5%.
- (3)
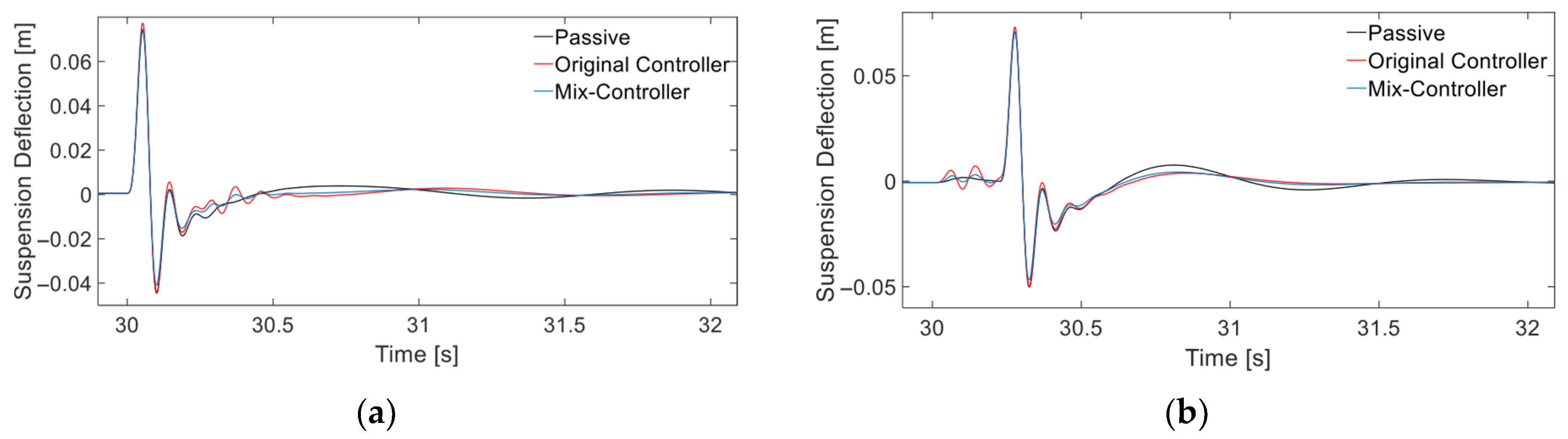
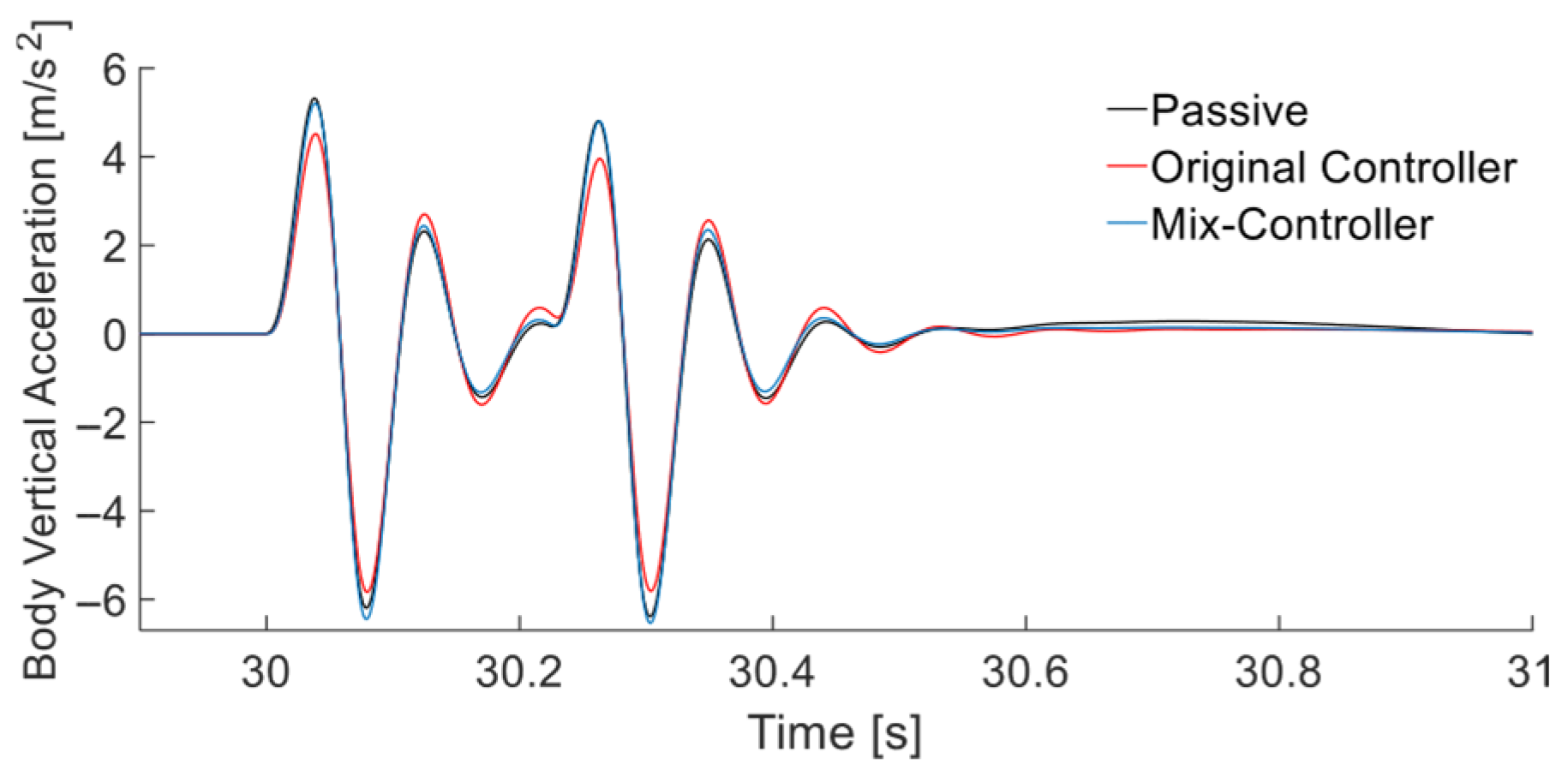
- According to the simulation results, compared to the original controller, in the time domain, the suspension dynamic deflection and tire dynamic deformation of the mix controller are reduced by an average of 3.26% and 5.91%, respectively, in the frequency domain, the suspension dynamic deflection response and tire dynamic deformation induced by external excitation of the mix controller are generally better than those of the original controller. On the other hand, although some metrics have deteriorated in the time and frequency domains, overall global optimization of comfort and stability in attitude can still be achieved.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Theunissen, J.; Tota, A.; Gruber, P.; Dhaens, M.; Sorniotti, A. Preview-based Techniques for Vehicle Suspension Control: A State-of-the-art Review. Annu. Rev. Control 2021, 51, 206–235. [Google Scholar] [CrossRef]
- Kimball, J.B.; DeBoer, B.; Bubbar, K. Adaptive Control and Reinforcement Learning for Vehicle Suspension Control: A review. Annu. Rev. Control. 2024, 58, 100974. [Google Scholar] [CrossRef]
- Yu, M.; Evangelou, S.A.; Dini, D. Advances in Vehicle Suspension Systems. Engineering 2024, 33, 160–177. [Google Scholar] [CrossRef]
- Hassan, M.A.; Abdelkareem, M.A.A.; Moheyeldein, M.M.; Elagouz, A.; Tan, G. Advanced Study of Tire Characteristics and Their Influence on Vehicle Lateral Stability and Untripped Rollover Threshold. Alex. Eng. J. 2020, 59, 1613–1628. [Google Scholar] [CrossRef]
- Wei, W.; Yu, S.J.; Li, B.Z. Research on Magnetic Characteristics and Fuzzy PID Control of Electromagnetic Suspension. Actuators 2023, 12, 203. [Google Scholar] [CrossRef]
- Liu, L.; Ren, Y.-J.; Shen, T.; Yin, G.-T.; Zhang, Y.-J. Grade Recognition for Electric Vehicles with Vehicle Mass Estimation. J. Jilin Univ. (Eng. Technol. Ed.) 2025, 55, 846–856. [Google Scholar] [CrossRef]
- Peng, C.; Wei, C.; Solernou, A.; Hagenzieker, M.; Merat, N. User Comfort and Naturalness of Automated Driving: The Effect of Vehicle Kinematic and Proxemic Factors on Subjective Response. Appl. Ergon. 2025, 122, 104397. [Google Scholar] [CrossRef]
- Zheng, W.G.; Zhang, J.-Z.; Wang, S.-C.; Feng, G.-S.; Xu, X.-H.; Ma, Q.X. A Shifting Strategy for Electric Commercial Vehicles Considering Mass and Gradient Estimation. Cmes-Comput. Model. Eng. Sci. 2023, 137, 489–508. [Google Scholar] [CrossRef]
- Yang, M.; Tian, J. Longitudinal and Lateral Stability Control Strategies for ACC Systems of Differential Steering Electric Vehicles. Electronics 2023, 12, 4178. [Google Scholar] [CrossRef]
- Liao, Y.S.; Hu, Z.-M.; Jia, H.-B.; Tian, Y.-C.; Zhong, S.-H.; Peng, X.-L. Vehicle Mass and Road Grade Estimation Based on Longitudinal-Lateral Dynamics Coupling. Automot. Eng. 2024, 1–7. [Google Scholar] [CrossRef]
- Gao, L.; Wu, Q.; He, Y. Road slope estimation for heavy-duty vehicles under the influence of multiple source factors in real complex road environments. Mech. Syst. Signal Process. 2024, 208, 110973. [Google Scholar] [CrossRef]
- Shangguan, J.Y.; Yue, M.; Xu, C.; Zhao, J. Robust Fault-Tolerant Estimation of Sideslip and Roll Angles for Distributed Drive Electric Buses with Stochastic Passenger Mass. IEEE Trans. Intell. Transp. Syst. 2023, 24, 14480–14489. [Google Scholar] [CrossRef]
- Smith, J.; Johnson, A. The Impact of Suspension System Tuning on Vehicle Handling and Ride Comfort. J. Automot. Eng. 2023, 305, 567–580. [Google Scholar]
- Liu, C.N.; Chen, L.; Lee, H.P.; Yang, Y.; Zhang, X.L. Generalized Skyhook-Groundhook Hybrid Strategy and Control on Vehicle Suspension. IEEE Trans. Veh. Technol. 2023, 72, 1689–1700. [Google Scholar] [CrossRef]
- Hussan, U.; Majeed, M.A.; Asghar, F.; Waleed, A.; Khan, A.; Javed, M.R. Fuzzy logic-based voltage regulation of hybrid energy storage system in hybrid electric vehicles. Electr. Eng. 2022, 104, 485–495. [Google Scholar] [CrossRef]
- Jovanovic, A.; Teodorovic, D. Type-2 fuzzy logic based transit priority strategy. Expert Syst. Appl. 2022, 187, 115875. [Google Scholar] [CrossRef]
- Li, H.; Yang, X. Robust optimal control of logical control networks with function perturbation. Automatica 2023, 152, 110970. [Google Scholar] [CrossRef]
- Mai, H.; Chen, X.; Yin, Z. Time-optimal L1/L2 norms optimal control for linear time-invariant systems. Optim. Control. Appl. Methods 2023, 44, 1686–1699. [Google Scholar] [CrossRef]
- Han, M.; Li, Z.; Yin, X.; Yin, X. Robust Learning and Control of Time-Delay Nonlinear Systems with Deep Recurrent Koopman Operators. IEEE Trans. Ind. Inform. 2024, 20, 4675–4684. [Google Scholar] [CrossRef]
- Kumar, L.; Kumar, P.; Dhillon, S.S. A Multiobjective Optimization Approach for Linear Quadratic Gaussian/Loop Transfer Recovery Design. Optim. Control. Appl. Methods 2020, 41, 1267–1287. [Google Scholar] [CrossRef]
- Kader, A.M.; El-Gamal, H.A.; Abdelnaeem, M. Influence of Pneumatic Tire Enveloping Behavior Characteristics on the Performance of a Half Car Suspension System Using Multi-Objective Optimization Algorithms. Alex. Eng. J. 2024, 107, 298–316. [Google Scholar] [CrossRef]
- Nan, Y.; Shao, S.J.; Ren, C.B.; Wu, K.W.; Cheng, Y.J.; Zhou, P.C. Simulation and Experimental Research on Active Suspension System with Time-Delay Feedback Control. IEEE Access 2023, 11, 88498–88510. [Google Scholar] [CrossRef]
- Wang, M.Q.; Zeng, S.H.; He, Y.X.; Su, S.; Liu, P.F. Multi-Objective Optimization of a Fractional-Order Control System for an EMS-Type Maglev Model. IEEE Trans. Veh. Technol. 2024, 73, 12652–12667. [Google Scholar] [CrossRef]
- He, L.Q.; Pan, Y.J.; He, Y.S.; Li, Z.X.; Królczyk, G.; Du, H.P. Control Strategy for Vibration Suppression of a Vehicle Multibody System on a Bumpy Road. Mech. Mach. Theory 2022, 174, 104891. [Google Scholar] [CrossRef]
- Mastinu, G.; Della Rossa, F.; Previati, G.; Gobbi, M.; Fainello, M. Global stability of road vehicle motion with driver control. Nonlinear Dyn. 2023, 111, 18043–18059. [Google Scholar] [CrossRef]
- Rong, J.L.; Deng, Z.K.; He, L.; Wang, X.; Cheng, X.Y. Time-Domain Simulation and Optimization of Ride Comfort for Vehicle Active Suspension. Trans. Beijing Inst. Technol. 2022, 42, 46–52. [Google Scholar] [CrossRef]
- Duc Ngoc, N.; Tuan Anh, N. Evaluate the stability of the vehicle when using the active suspension system with a hydraulic actuator controlled by the OSMC algorithm. Sci. Rep. 2022, 12, 19364. [Google Scholar] [CrossRef]
- Nguyen, D.N.; Nguyen, T.A. Proposing an original control algorithm for the active suspension system to improve vehicle vibration: Adaptive fuzzy sliding mode proportional-integral-derivative tuned by the fuzzy (AFSPIDF). Heliyon 2023, 9, e14210. [Google Scholar] [CrossRef]
- Viadero-Monasterio, F.; Boada, B.L.; Boada, M.J.L.; Diaz, V. H∞ dynamic output feedback control for a networked control active suspension system under actuator faults. Mech. Syst. Signal Process. 2022, 162, 10850. [Google Scholar] [CrossRef]
- Zhang, J.H.; Ding, F.; Liu, J.; Lei, F.; Wang, Y.F.; Wei, C.F. Event Triggered Finite-Time Adaptive Sliding-Mode Coordinated Control of Uncertain Hysteretic Leaf Spring Suspension with Prescribed Performance. IEEE Trans. Intell. Transp. Syst. 2025, 26, 2621–2632. [Google Scholar] [CrossRef]
- Paleologu, C.; Benesty, J.; Ciochina, S. Data-Reuse Recursive Least-Squares Algorithms. IEEE Signal Process. Lett. 2022, 29, 752–756. [Google Scholar] [CrossRef]
- Han, Z.; Zhang, F.; Zhang, Y.; Han, Y.; Jiang, P. Improved Variable Forgetting Factor Proportionate RLS Algorithm with Sparse Penalty and Fast Implementation Using DCD Iterations. China Commun. 2024, 21, 16–27. [Google Scholar] [CrossRef]
- Wu, G.Y.; Rui, X.T.; Wang, G.P.; Jiang, M.; Wang, X. Modelling and simulation of driving dynamics of wheeled launch system under random road surface excitation. Acta Mech. Sin. 2024, 40, 523310. [Google Scholar] [CrossRef]
- Xing, C.; Zhu, Y.; Wu, H. Electromechanical Coupling Braking Control Strategy Considering Vertical Vibration Suppression for Vehicles Driven by In-Wheel Motors. IEEE-Asme Trans. Mechatron. 2022, 27, 5701–5711. [Google Scholar] [CrossRef]
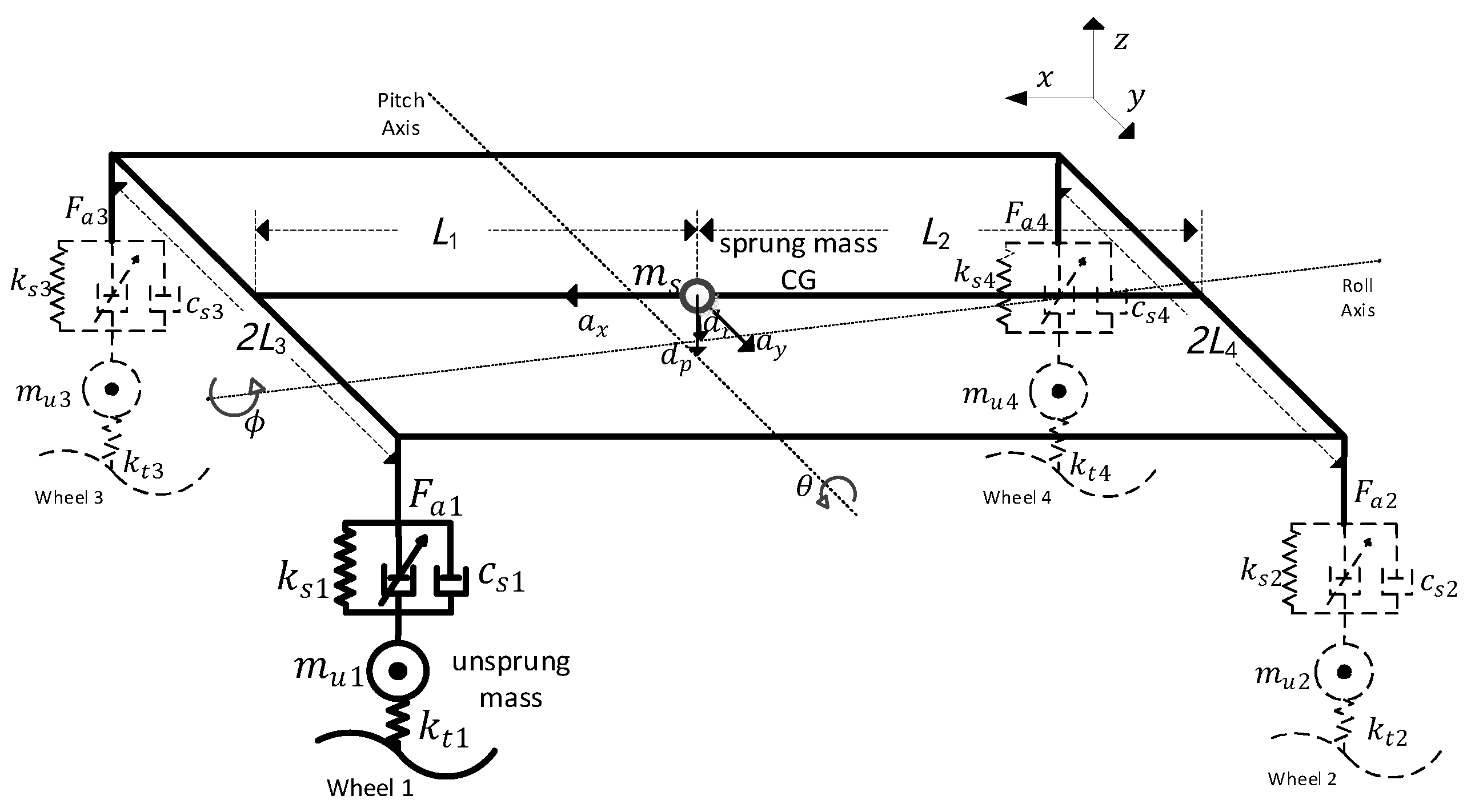





| Parameters | Symbol | Parameters | Symbol |
|---|---|---|---|
| Sprung mass | Distance from the mass center to the front axes | ||
| Vertical displacement of the sprung mass center | Distance from the mass center to the rear axes | ||
| Total suspension forces of the -th wheel | Distance from the mass center to the front half shaft base | ||
| Suspension stiffness of the -th wheel | Distance from the mass center to the rear half shaft base | ||
| Suspension damping of the -th wheel | Longitudinal accelerations of the mass center | ||
| Ideal damping force of the -th wheel | Lateral accelerations of the mass center | ||
| Unsprung mass vertical displacement of the -th wheel | Distance from the sprung mass center to the pitch axes | ||
| Sprung mass vertical displacement of the -th wheel | Distance from the sprung mass center to the roll axes | ||
| Acceleration of gravity | g | Roll angles of the sprung mass | |
| Lateral moment of inertia of the sprung mass | Pitch angles of the sprung mass | ||
| Pitch moment of inertia of the sprung mass | Unsprung mass of the -th wheel | ||
| Road input of the -th wheel | Tire stiffness of the -th wheel |
| The Range of | Effect on Historical Data |
|---|---|
| 0 < <1 | diluted |
| = 1 | unaffected |
| > 1 | enhanced |
| ~ | |||||||||
| optimization solution | 104.21 | 10−2.87 | 10−2.59 | 10+5.41 | 108.81 | 107.21 | 104.87 | 108.49 | 10−1.27 |
| Parameters | Symbol | Value | Unit |
|---|---|---|---|
| Nominal vehicle mass | 1200 | kg | |
| Vehicle actual mass | 2000 | kg | |
| Air density | 1.18 | kg·m−3 | |
| Windward area | 1.6 | m2 | |
| Coefficient of air resistance | 0.3 | ||
| Coefficient of rolling friction | 0.015 | ||
| Acceleration of gravity | g | 9.81 | m·s−2 |
| Centroid to front axes distance | 1.178 | m | |
| Centroid to rear axes distance | 1.464 | m | |
| Centroid to roll axes distance | 0.256 | m | |
| Centroid to pitch axes distance | 0.104 | m | |
| Front half shaft base | 0.729 | m | |
| Rear half shaft base | 0.7275 | m | |
| Unsprung mass at front wheels | 40.5 | kg | |
| Unsprung mass at rear wheels | 45.4 | kg | |
| Roll inertia | 522 | kg·m2 | |
| Pitch inertia | 2131 | kg·m2 | |
| Suspension stiffness | 20,000 | N·m−1 | |
| Wheel stiffness | 200,000 | N·m−1 |
| Integrator Index | Characteristic |
|---|---|
| Fast response, large overshoot, poor stability. | |
| Focuses on late response error, less consideration of pre-response errors. |
| Index | ISE | IAE |
|---|---|---|
| Vehicle mass (t) | 0.0096 | 0.28 |
| Passive | Original Controller | Rate of Change of Original Controller vs. Passive/% | Mix Controller | Rate of Change of Mix Controller vs. Passive/% | ||
|---|---|---|---|---|---|---|
| Body vertical acceleration (m·s−2) | 0.16 | 0.13 | 18.33 | 0.15 | 7.95 | |
| Body roll angle (deg) | 0.19 | 0.054 | 72.46 | 0.053 | 72.8 | |
| Body pitch angle (deg) | 0.033 | 0.031 | 7.73 | 0.031 | 7.2 | |
| Suspension deflection (m) | Wheel 1 | 0.0034 | 0.0022 | 35.16 | 0.0021 | 38.23 |
| Wheel 2 | 0.0028 | 0.0019 | 33.28 | 0.0018 | 36.52 | |
| Wheel 3 | 0.0031 | 0.0021 | 30.54 | 0.002 | 34.22 | |
| Wheel 4 | 0.0032 | 0.0021 | 35.62 | 0.002 | 38.66 | |
| Tire dynamic deformation (m) | Wheel 1 | 0.00071 | 0.00072 | −1.8 | 0.00068 | 3.76 |
| Wheel 2 | 0.00069 | 0.00071 | −3.05 | 0.00067 | 2.72 | |
| Wheel 3 | 0.00072 | 0.00074 | −2.7 | 0.00069 | 3.58 | |
| Wheel 4 | 0.00073 | 0.00075 | −3.4 | 0.00071 | 2.62 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; Hu, Y.; Zhao, W.; Zeng, D. Mix Controller Design for Active Suspension of Trucks Integrated with Online Estimation of Vehicle Mass. Vehicles 2025, 7, 71. https://doi.org/10.3390/vehicles7030071
Ma C, Hu Y, Zhao W, Zeng D. Mix Controller Design for Active Suspension of Trucks Integrated with Online Estimation of Vehicle Mass. Vehicles. 2025; 7(3):71. https://doi.org/10.3390/vehicles7030071
Chicago/Turabian StyleMa, Choutao, Yiming Hu, Weiwei Zhao, and Dequan Zeng. 2025. "Mix Controller Design for Active Suspension of Trucks Integrated with Online Estimation of Vehicle Mass" Vehicles 7, no. 3: 71. https://doi.org/10.3390/vehicles7030071
APA StyleMa, C., Hu, Y., Zhao, W., & Zeng, D. (2025). Mix Controller Design for Active Suspension of Trucks Integrated with Online Estimation of Vehicle Mass. Vehicles, 7(3), 71. https://doi.org/10.3390/vehicles7030071







