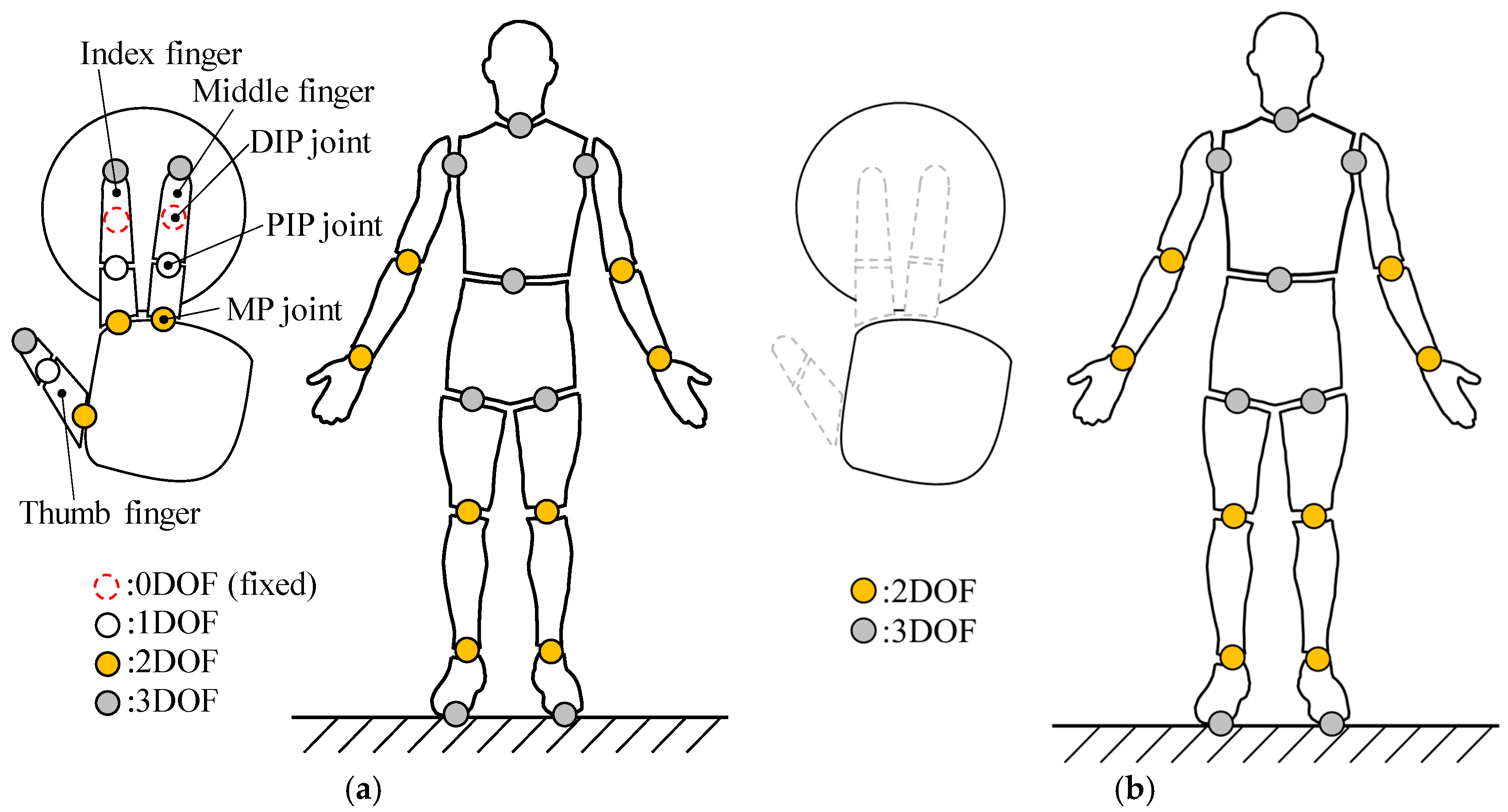
1. Introduction
Throwing a fastball would be a competitive technique of baseball pitchers. In order to obtain large ball speed, the pitchers accelerate the ball by rotating their joints through exerting joint torques (e.g., [
1]). Previous studies on high-seed swing motions based on multi-body dynamics have reported that motion-dependent term, which contains centrifugal force and Coriolis force, contributes largely to the generation of distal end points such as ball or hand in baseball pitching [
2,
3], bat head in baseball batting [
4,
5], racket head in tennis service [
6], and so on.
This study has tried to quantify functional roles of whole-body’s joint torques including fingers’ joints in the generation of ball speed and ball angular velocity (i.e., ball-spin speed) with use of two types of human whole-body models with and without consideration of finger joints. In addition to quantification of contributions of individual terms (e.g., joint torque term and gravitational term), the generating factors of the MDT was also considered using a recurrence formula with regard to the generalized velocity vectors consisting of linear and angular velocity of all segments of the system.
2. Methods
An induced speed analysis was conducted to quantify the dynamic contribution of joint torque inputs. Since the analysis needs the equation of motion for target system as well as data of pitching motion, this section mainly explains modelling of body, derivation of the equation of motion, and quantification of dynamic contributions calculated from the equation of motion in consideration of generating factors of the MDT.
2.1. Data Collection
A male collegiate right-handed baseball pitcher was instructed to pitch a ball as fast as possible to the target settled 18 m apart from him. Three-dimensional coordinate data of the pitching motion (body: 47 markers; fingers: 11 markers; ball: 6 markers) were captured using a 20-camera motion capture system (VICON-MX, Vicon Motion Systems, Oxford, UK) operating at 500 Hz. Ground reaction forces of the individual legs were measured using two force platforms (9281A and 9287B, Kistler Instruments AG, Winterthur, Switzerland) operating at 1000 Hz. This study was approved by the institution’s ethics committee (No. 28–138).
2.2. Dynamical Model of Whole Body and Ball
The whole-body segments with a ball were modelled not only as a system of twenty-two-rigid linked segments (
Figure 1a) but also as a system of sixteen-rigid linked segments (
Figure 1b). Each lower limb is assumed to be connected with the ground via a virtual joint at the center of pressure (COP) of the foot when contacting with the ground. Anatomical constraint axes (e.g., varus/valgus axis at elbow and knee joints; internal/external rotation axis at wrist joint), along which the joints cannot rotate freely, are considered.
2.3. Equation of Motion for the Whole Body and Ball System
An analytical form of the equation of motion for the whole body with ball system can be expressed as follows:
where
V is the generalized velocity vector consisting of linear velocity vectors with respect to the center of gravity (CG) and angular velocity vectors for all the segments;
ATa and
AGindicate the coefficient matrices for the active joint torque vector
Ta and gravitational force vector
G;
indicates the motion-dependent term (MDT) consisting of force and moment caused by centrifugal and Coriolis forces and gyroscopic effective moment;
AG is the coefficient matrix of gravitational acceleration vector;
AErr is the modelling error term consisting of residual joint force term, residual joint moment term and fluctuation terms caused by segments’ lengths and anatomical constraint joint axes [
7].
2.4. Contributions to Ball Variables
After integrating Equation (1) with respect to time, the ball variables are calculated as:
where the matrix
Sball denotes the transforming matrix from the generalized velocity vector to the ball CG velocity vector
, and ball angular velocity vector
ωball.
The dynamic contributions of the individual terms to the generation of the ball variables are shown as:
where the terms
CTrq,
CMDT and
CG respectively denote the contributions of joint torque term, MDT, and gravitational term; the term
CErr is the contribution of modelling error term, to the generation of ball variables;
CV0 is the contribution of the initial velocity term caused by the initial velocity state of the system at the start of analysis. For example, contribution of the joint torque term is given as follows:
2.5. Contributions to Ball Variables Considering Generating Factors of MDT
The equation of motion for the system, Equation (1), was discretized with respect to time as follows:
where
k denotes the time in the discrete-time system, and the vector
ΛV denotes the input vector consisting of the discretized terms shown as:
The generalized acceleration vector was expressed by difference approximation using the time interval
of the discretized system shown as
Combining Equations (5) and (7) yields a recurrence formula for the generalized velocity vector
V as follows [
6]:
Equations (6) and (8) provide us the information about the contributions of the input terms (i.e., the joint torque term, the gravitational term, the modelling error term) at the time k, to the generation of the generalized velocity vector at the time k + 1 in the discrete-time system without use of the MDT.
The contribution of each term at every instant to the generation of the generalized velocity vector can be derived from Equation (8). For example, the generalized velocity vector at the time
k can be calculated from the time history of the input vector
ΛV as follows:
where the function Π denotes the factorial function.
Consequently, the contribution of the active joint torque to the generation of ball variables at the time
k is expressed as follows:
The contribution of the active joint torque, Equation (10), can be furthermore divided into the contributions of the individual active joint torques about axes of the whole-body joints. Since the generalized velocity vector, Equation (9), is calculated without use of the component of the MDT, Equation (10) shows the contribution which considers generating factors of the MDT.
2.6. A Solution for Closed Loop Problem in Fingers and Ball System
When using the 22-segment model, the ball is supported by the three fingers (i.e., index, middle and thumb) that exert forces on the ball surface to grasp and manipulate the ball during fastball pitching motion. It is impossible to determine the forces exerted by individual fingers via inverse dynamics calculation because of the kinetic redundancy of the ball-fingers system. A simulation with respect to the 22-segment model, therefore, was conducted to estimate the contact forces by setting diagonal spring and damper elements between each fingertip and each contact point on the ball surface.
The position and velocity vectors of the individual fingertips are given by using contact points calculated from ball variables (i.e., ball CG’s position and velocity, ball orientation, and ball angular velocity) under the assumption that the ball contact points of fingertips maintain same location with respect to ball coordinate system until each finger loses contact with the ball. The exerting force is calculated by the following equation as:
where the vectors
p and
v denote the position and velocity vectors at fingertip (ft) calculated from the ball variables measured in experiments and the vectors at ball contact (bc) points of the individual fingers calculated from simulation described as below, and the matrices
Kc and
Cc denote diagonal matrices consisting of stiffness and viscous components, respectively.
The estimated values of the exerting forces at the ball contact points are calculated under the following condition because of avoiding pulling force components of Equation (11).
where the vector
rb with barred subscript cg-C,
j denotes position vector running from the ball CG to each fingertip.
A simulation was carried out by using the equations of ball motion for translational and rotational movements as follows:
where
mball is the mass of ball,
xball,cg is the position vector of the ball’s center of gravity (CG),
g is the gravitational acceleration vector,
is the inertia matrix of the ball expressed in the global reference coordinate system.
The inverse dynamics calculation for fingers’ joints was carried out using the estimated values of the ball contact forces exerted by the fingers. Data was analyzed with regard to the normalized time, 0–100%, from the instance when the ball is farthest from catcher to the instance when the thumb’s fingertip loses contact with the ball just prior to ball release.
3. Results and Discussions
3.1. Contribution to Ball Speed with Respect to 22-Segment Model
Figure 2a,b show the contributions of the individual terms and major contributors to the ball speed for a motion with stable data acquisition. The sum of contributions coincides with the measured speed (
Figure 2a). The joint torque term is the largest contributor to the ball speed in this model. The MDT shows small contribution to the ball speed. The PIP-joint torques of index and middle fingers are the major contributors to the ball speed (
Figure 2b).
3.2. Contribution to Ball Variables with Respect to 16-Segment Model
Figure 3a,b show the contributions of the individual terms to the ball speed and ball angular velocity with respect to the 16-segment model. In contrast to the result in
Figure 2a, the MDT is the largest contributor to the ball variables just before ball release.
3.3. Main Contributors to Ball Speed in Consideration of Generating Factors of MDT
Figure 4a–c show the main joint-torque contributors of shoulder joint, elbow and wrist joints, and torso joint to the generation of ball speed after converting MDT into other terms using Equations (9) and (10). The horizontal adduction torque is the positive contributor to the ball speed. The elbow flexion/extension-axial torque shows large magnitude of negative/positive contribution, and is the one of the largest contributors just prior to ball release. The lateral flexion-axial torus and ante/retroflexion-axial torque are positive and negative contributors to ball speed, respectively.
4. Conclusions
This study has quantified the generation mechanism of linear and angular velocities of ball by using an induced speed analysis with and without finger segments. The results show that the roles of finger joints are supporting the ball during pitching motion, and that the torques of pitching-side arm and torso joints are major positive or negative contributors to the generation of the ball variables by utilizing cumulative effects of joint torque inputs.