Design Evaluation of FFF-Printed Transtibial Prosthetic Sockets Using Follow-Up and Finite Element Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Part I: Follow-Up Study
Prosthetic Socket Production
2.2. Part II: Finite Element Model
3. Results
3.1. Part I: Follow-Up Study
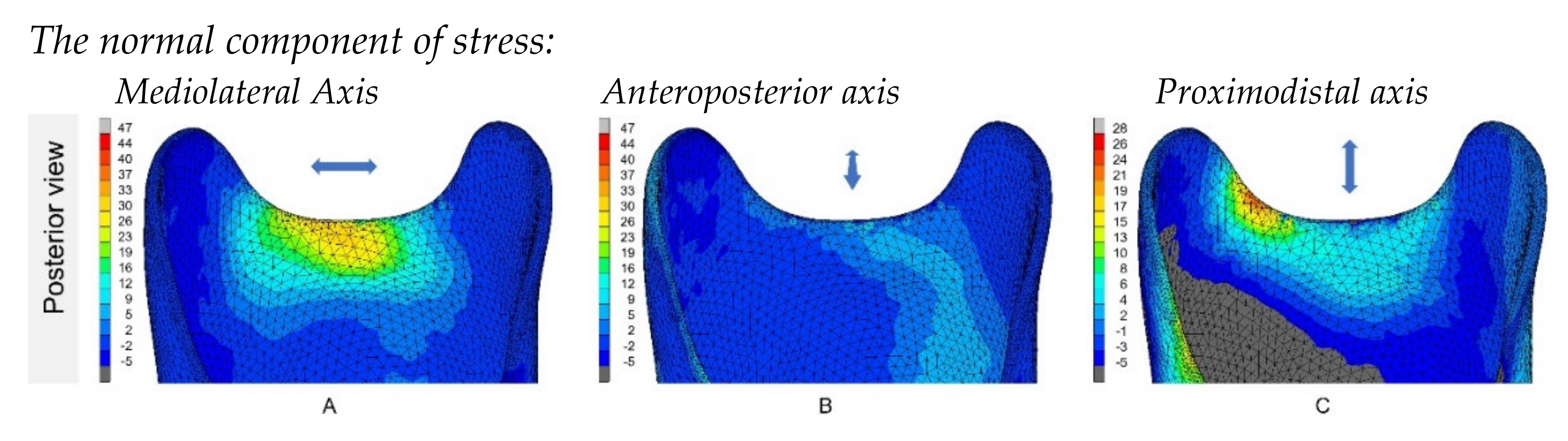
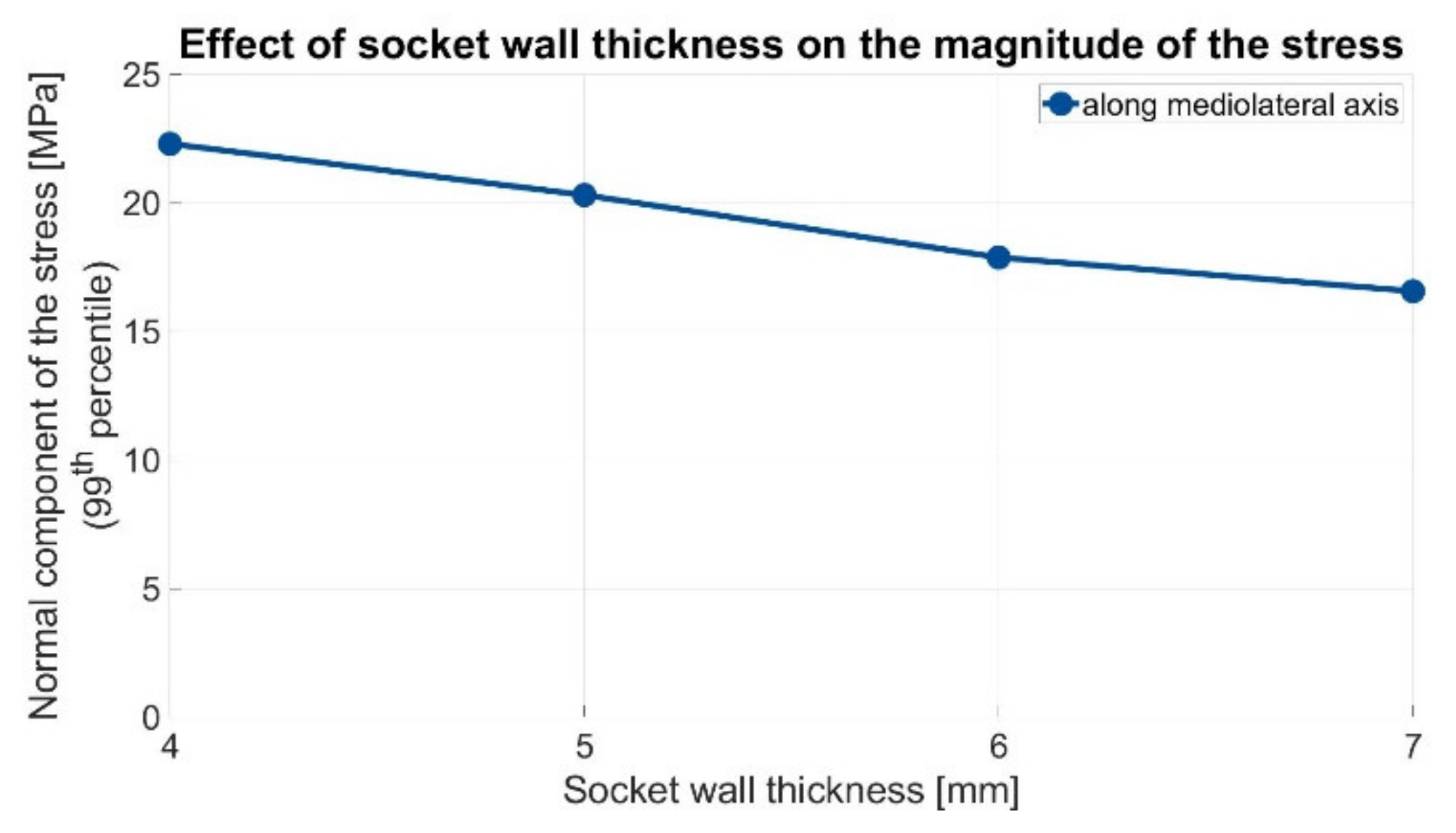
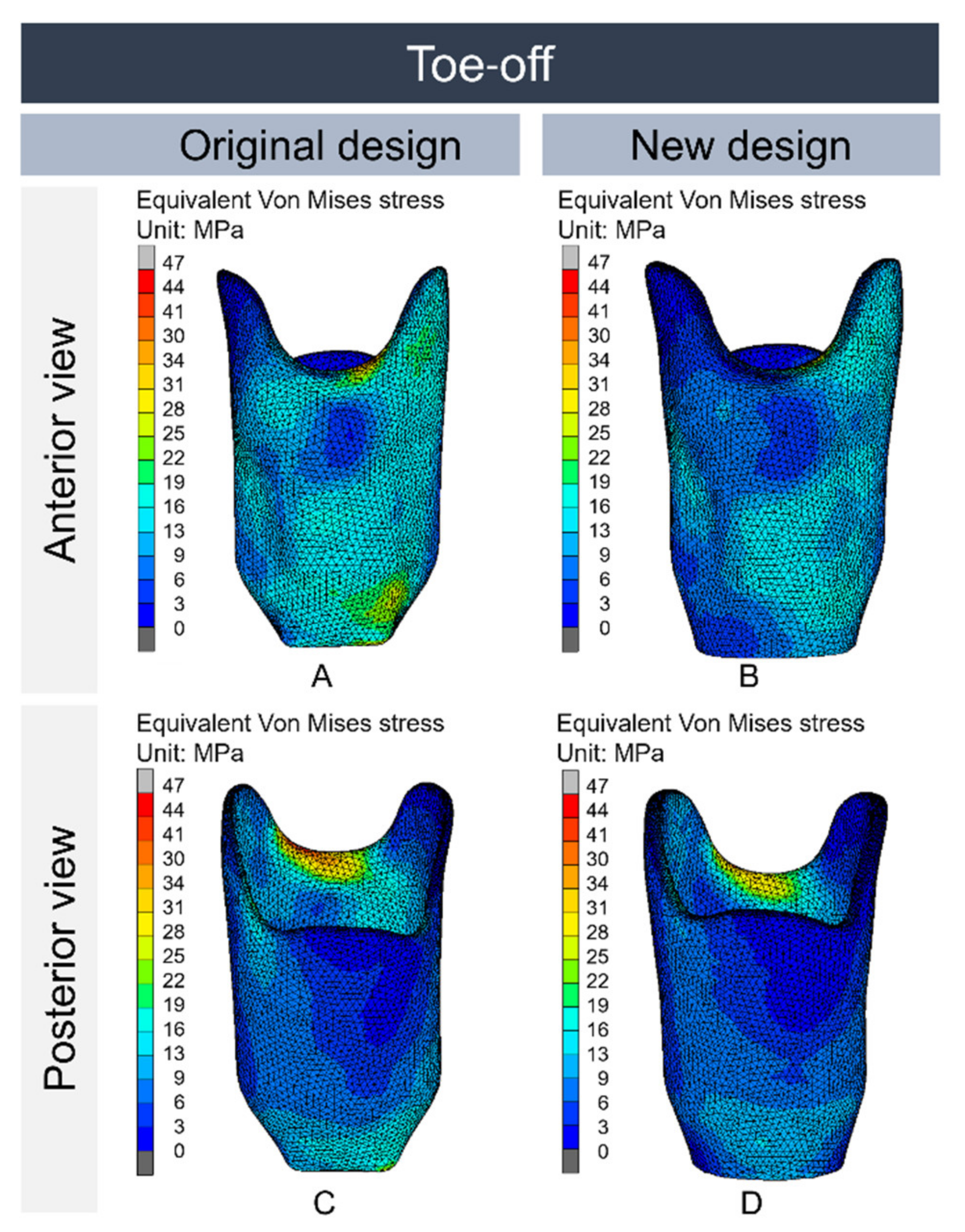
3.2. Part II: Finite Element Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. WHO Standards for Prosthetics and Orthotics; World Health Organization: Geneva, Switzerland, 2017. [Google Scholar]
- Van der Stelt, M.; Verhamme, L.; Slump, C.H.; Brouwers, L.; Maal, T.J.J. Strength testing of low-cost 3D-printed transtibial prosthetic socket. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2022, 236, 367–375. [Google Scholar] [CrossRef] [PubMed]
- NEN-EN-ISO 10328; Prosthetics—Structural Testing of Lower-Limb Prostheses—Requirements and Test Methods. European Committee for Standardization: Toronto, ON, Canada, 2016.
- Campbell, L.; Lau, A.; Pousett, B.; Janzen, E.; Raschke, S.U. How infill percentage affects the ultimate strength of 3D-printed transtibial sockets during initial contact. Can. Prosthet. Orthot. J. 2018, 1, 2. [Google Scholar] [CrossRef] [Green Version]
- Goh, J.C.H.; Lee, P.V.S.; Ng, P. Structural integrity of polypropylene prosthetic sockets manufactured using the polymer deposition technique. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2002, 216, 359–368. [Google Scholar] [CrossRef] [PubMed]
- Hsu, L.H.; Huang, G.F.; Lu, C.W.; Lai, C.W.; Chen, Y.M.; Yu, I.C. The Application of Rapid Prototyping for the Design and Manufacturing of Transtibial Prosthetic Socket. Mater. Sci. Forum 2008, 594, 273–280. [Google Scholar] [CrossRef]
- Stenvall, E.; Flodberg, G.; Pettersson, H.; Hellberg, K.; Hermansson, L.; Wallin, M.; Yang, L. Additive Manufacturing of Prostheses Using Forest-Based Composites. Bioengineering 2020, 7, 103. [Google Scholar] [CrossRef] [PubMed]
- Gariboldi, F.; Pasquarelli, D.; Cutti, A.G. Structural testing of lower-limb prosthetic sockets: A systematic review. Med. Eng. Phys. 2021, 99, 103742. [Google Scholar] [CrossRef] [PubMed]
- Nickel, E.A.; Barrons, K.J.; Owen, M.K.; Hand, B.D.; Hansen, A.H.; Desjardins, J.D. Strength Testing of Definitive Transtibial Prosthetic Sockets Made Using 3D-Printing Technology. JPO J. Prosthet. Orthot. 2020, 32, 295–300. [Google Scholar] [CrossRef]
- Faustini, M.C.; Neptune, R.R.; Crawford, R.H.; Rogers, W.E.; Bosker, G. An Experimental and Theoretical Framework for Manufacturing Prosthetic Sockets for Transtibial Amputees. IEEE Trans. Neural Syst. Rehabil. Eng. 2006, 14, 304–310. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Turner-Smith, A.R.; Tanner, A.; Roberts, V.C. Clinical investigation of the pressure and shear stress on the trans-tibial stump with a prosthesis. Med. Eng. Phys. 1998, 20, 188–198. [Google Scholar] [CrossRef]
- Faustini, M.C.; Neptune, R.R.; Crawford, R.H. The quasi-static response of compliant prosthetic sockets for transtibial amputees using finite element methods. Med. Eng. Phys. 2006, 28, 114–121. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.C.C.; Zhang, M.; Boone, D.A.; Contoyannis, B. Finite-element analysis to determine effect of monolimb flexibility on structural strength and interaction between residual limb and prosthetic socket. J. Rehabil. Res. Dev. 2004, 41, 775–786. [Google Scholar] [CrossRef] [Green Version]
- Lenka, P.K.; Choudhury, A.R. Analysis of trans tibial prosthetic socket materials using finite element method. J. Biomed. Sci. Eng. 2011, 04, 762–768. [Google Scholar] [CrossRef] [Green Version]
- Lindberg, A.; Alfthan, J.; Pettersson, H.; Flodberg, G.; Yang, L. Mechanical performance of polymer powder bed fused objects—FEM simulation and verification. Addit. Manuf. 2018, 24, 577–586. [Google Scholar] [CrossRef]
- Mubarak, A.J.M.; Rashid, A.M.A.; Wahab, A.A.; Seng, G.H.; Ramlee, M.H. Customized Designs and Biomechanical Analysis of Transtibial Prosthetic Leg. J. Physics Conf. Ser. 2021, 2071, 012014. [Google Scholar] [CrossRef]
- Jweeg, M.J.; Hammoudi, Z.S.; Alwan, B.A. Optimised Analysis, Design, and Fabrication of Trans-Tibial Prosthetic Sockets. IOP Conf. Ser. Mater. Sci. Eng. 2018, 433, 012058. [Google Scholar] [CrossRef]
- Lee, W.C.C.; Zhang, M. Design of monolimb using finite element modelling and statistics-based Taguchi method. Clin. Biomech. 2005, 20, 759–766. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zachariah, S.G.; Sanders, J.E. Finite element estimates of interface stress in the trans-tibial prosthesis using gap elements are different from those using automated contact. J. Biomech. 2000, 33, 895–899. [Google Scholar] [CrossRef]
- Ali, I.; Kumar, R.; Singh, Y. Finite element modelling and analysis of trans-tibial prosthetic socket. Glob. J. Res. Eng. 2014, 14, 43–50. [Google Scholar]
- Van der Stelt, M.; Grobusch, M.P.; Koroma, A.R.; Papenburg, M.; Kebbie, I.; Slump, C.H.; Maal, T.J.; Brouwers, L. Pioneering low-cost 3D-printed transtibial prosthetics to serve a rural population in Sierra Leone—An observational cohort study. EClinicalMedicine 2021, 35, 100874. [Google Scholar] [CrossRef] [PubMed]
- Van der Stelt, M.; Verhulst, A.; Slump, C.H.; Papenburg, M.; Grobusch, M.P.; Brouwers, L.; Maal, T.J. Design and Production of Low-Cost 3D-Printed Transtibial Prosthetic Sockets. JPO J. Prosthet. Orthot. 2021, Publish Ah, 1–7. [Google Scholar] [CrossRef]
- Thiago, R.; Ferreira, I.T.L.; Amatte, I.C.; Dutra, A.; Bürger, D. Experimental characterization and micrography of 3D printed PLA and PLA reinforced with short carbon fibers. Compos. Part B Eng. 2017, 124, 88–100. [Google Scholar] [CrossRef]
- Dickinson, A.S.; Steer, J.W.; Worsley, P.R. Finite element analysis of the amputated lower limb: A systematic review and recommendations. Med. Eng. Phys. 2017, 43, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Steer, J.W.; Worsley, P.R.; Browne, M.; Dickinson, A. Key considerations for finite element modelling of the residuum–prosthetic socket interface. Prosthet. Orthot. Int. 2020, 45, 138–146. [Google Scholar] [CrossRef] [PubMed]
- Autodesk. Autodesk Meshmixer. 2018. Available online: http://www.meshmixer.com/ (accessed on 13 September 2021).



| Bones [24] | Soft Tissue * [25] | FFF-Printed tough PLA [2,19] | |
|---|---|---|---|
| Tensile modulus | 15 Gpa | 0.2 Mpa | 1.317 Gpa |
| Poisson ratio [-] | 0.30 | 0.495 | 0.33 |
| Heel Strike (I) | Toe-Off (II) | ||
|---|---|---|---|
| Knee | Anterior-posterior offset in milimeters | 52 | 72 |
| Medio-lateral offset in milimeters | −50 | −35 | |
| Socket bottom | Anterior-posterior offset in milimeters | 20 | 90 |
| Medio-lateral offset in milimeters | −20 | −30 | |
| Participant Number | Weight: | Tibia Length | Activity Level (K-Level): | Walking Support: | Days of Use per Week: | Wearing Time per Day: (Hours) | Walking Time per Day: |
|---|---|---|---|---|---|---|---|
| 001 | 55 | 8 | 1–2 | One crutch | 7 | 10–12 | 5–15 min |
| 002 | 56.5 | 15 | 2 | Two crutches | 4 | 7–9 | 30 min–1 h |
| 003 | 55 | 9 | 2 | One crutch | 7 | 10–12 | 5–15 min |
| 004 | 54.7 | 9 | 3 | One crutch | 7 | 0–3 | 30 min–1 h |
| 005 | 47.3 | 7 | 3 | None | 7 | 10–12 | >2 h |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
van der Stelt, M.; Stenveld, F.; Bitter, T.; Maal, T.J.J.; Janssen, D. Design Evaluation of FFF-Printed Transtibial Prosthetic Sockets Using Follow-Up and Finite Element Analysis. Prosthesis 2022, 4, 589-599. https://doi.org/10.3390/prosthesis4040048
van der Stelt M, Stenveld F, Bitter T, Maal TJJ, Janssen D. Design Evaluation of FFF-Printed Transtibial Prosthetic Sockets Using Follow-Up and Finite Element Analysis. Prosthesis. 2022; 4(4):589-599. https://doi.org/10.3390/prosthesis4040048
Chicago/Turabian Stylevan der Stelt, Merel, Fianna Stenveld, Thom Bitter, Thomas J. J. Maal, and Dennis Janssen. 2022. "Design Evaluation of FFF-Printed Transtibial Prosthetic Sockets Using Follow-Up and Finite Element Analysis" Prosthesis 4, no. 4: 589-599. https://doi.org/10.3390/prosthesis4040048
APA Stylevan der Stelt, M., Stenveld, F., Bitter, T., Maal, T. J. J., & Janssen, D. (2022). Design Evaluation of FFF-Printed Transtibial Prosthetic Sockets Using Follow-Up and Finite Element Analysis. Prosthesis, 4(4), 589-599. https://doi.org/10.3390/prosthesis4040048






